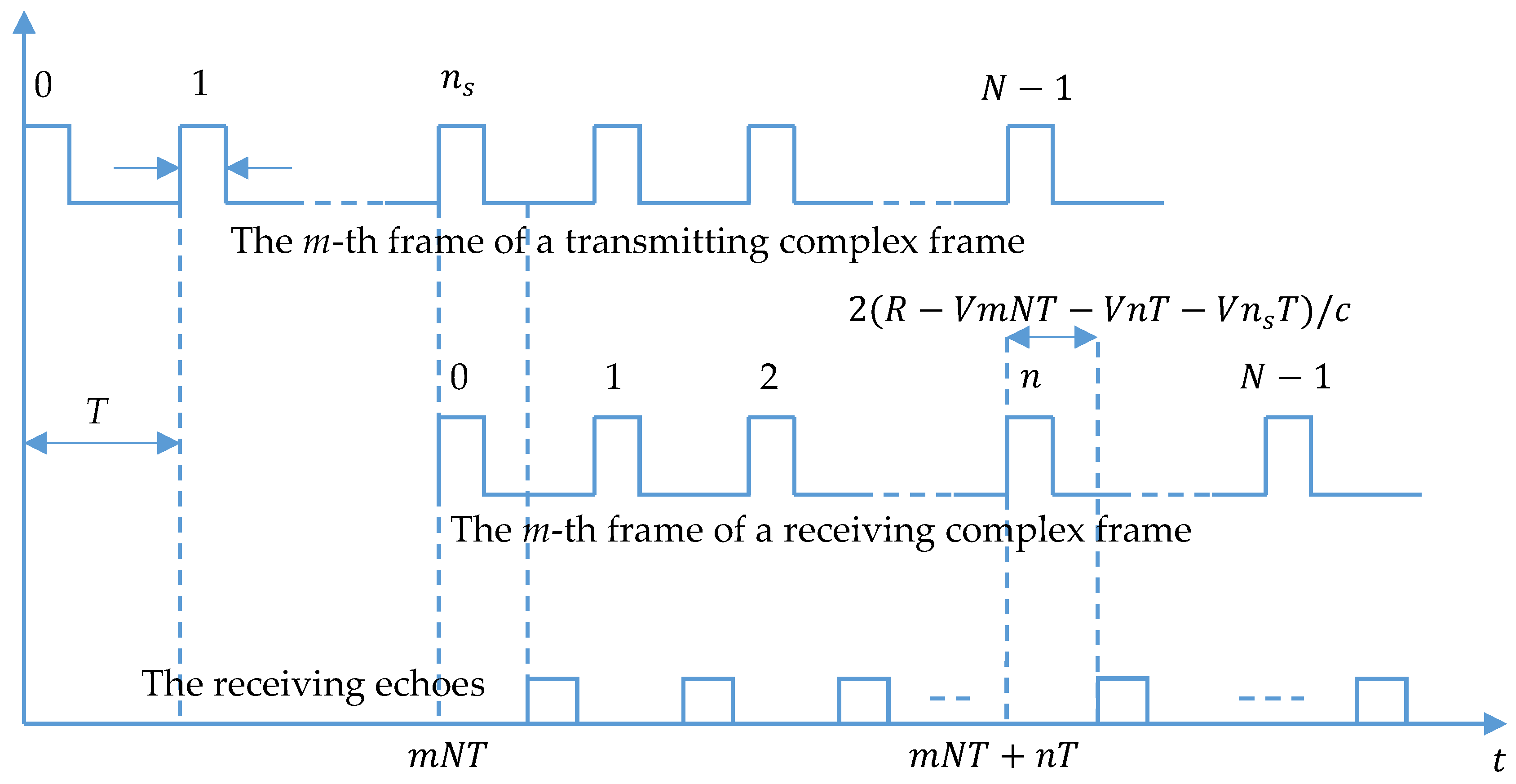
3.1. Special Range-Doppler Coupling Effect and Its Suppression
In the case of conventional stepped-frequency (SF) synthetic wideband radar system,
and
; in Equation (3),
is the frequency interval between adjacent pulses and
is the synthetic bandwidth. Each frame has the same basic frequency
and the same stepped-frequency hopping. According to Equation (3), in any frame-
m, the change of signal phase between pulses mainly depends on the phase term
, which is only related to range-
. Therefore, FFT processing or pulse compression processing in each frame can be used to obtain the distribution of scatters in the range direction; i.e., target range profile [
20]. The range resolution determined by DFT is
. The second-order phase term
in Equation (3) may cause energy diffusion of the scattering center in range profile, but the diffusion can be ignored because the synthetic bandwidth
is far smaller than the carrier frequency
f0 and the phase variation of the second-order phase term is very small. The other velocity-related phase terms
and
are linear with
n, and their influence on pulse compression is that the position of the scatter on the FFT spectrum is shifted by an offset of
, which is called range-Doppler coupling effect. The range-Doppler coupling effect in an SF radar system can cause error in range measurement, but cannot cause significant diffusion of energy or degradation of imaging quality. After pulse compression and envelope alignment of a range profile in each frame, the inter-frame phase change of each range unit mainly depends on the phase term
. Therefore, FFT processing or Doppler processing in each range unit can be used to obtain the distribution of scatters in velocity or Doppler direction. The distribution of the scatters on the 2D range-Doppler plane can be obtained by synthesizing the distributions of all the range units. As described above, in the conventional SF system, the imaging processing method of pulse compression in each frame at first, and then Doppler processing in each range resolution unit, are generally adopted.
It can be seen from Equation (3) that the phase of the signal is complexly related to the range and speed of the scatter due to HPRF and RFH. In each frame-m, the range-related phase term , changes randomly and nonlinearly between pulses because imn changes randomly. In order to use traditional FFT for pulse compression in each frame, it is necessary to rearrange the data in order of frequency from small to large, and then interpolate the non-uniform frequency-sampled data into uniform frequency-sampled data. The randomly-changed phase term is transformed to linearly-changed phase term after rearrangement and interpolation. However, data rearrangement randomizes the original linear range-Doppler coupling phase term . For supersonic/hypersonic applications, even if the clutter-center velocity compensation is made by using Equation (2), the phase change of the coupling phase term caused by the velocity residual v is still large for the scatters that are not at the direction of beam-center, and it can be close to or even more than 2π in one frame. The random change of phase is equivalent to adding multiplicative noise to the signal, and it seriously reduces the coherence of the rearranged data, which leads to serious energy-divergence of scatters and degradation of imaging quality. For inter-frame Doppler processing, because imn changes randomly, the velocity-related phase term changes randomly and nonlinearly between frames, which makes the Doppler processing complicated. The random and nonlinear range-Doppler coupling effect not only exists within the frame but occurs between frames, so it is difficult to carry out fractal-dimension processing in range and Doppler directions respectively.
In this paper, the above phenomenon is called the special range-Doppler coupling effect of RFH synthetic wideband radar in a highly dynamic application. Because of the above special effect, the conventional imaging processing method of pulse compression in each frame at first and then Doppler processing in each range resolution unit cannot be adopted in HPRF RFH radar. In order to suppress the special range-Doppler coupling effect, Doppler processing must be advanced to each frame and be synchronous with the pulse compression processing, which is called Doppler pre-processing in this paper.
The imaging algorithm of Doppler pre-processing is based on the 2D GMF algorithm, which can be executed by means of pipeline-parallel processing, and the computation can be dispersed to each frame in combination with the data acquisition process. The algorithm can be optimized in real-time ability according to different RFH modes.
As an example, the basic principle of suppressing the above special coupling effect through Doppler pre-processing is illustrated by the following intra-frame pseudo RFH mode where
and
(the basic frequency of pulse signal remains unchanged between frames; for different
n,
randomly takes different values in
without repetition); then,
Obviously, for any fixed period number n, the phase terms and vary non-randomly and linearly with the frame number m. Therefore, the M sampled data of the same period number n and the same sampling unit number k can be processed first by using FFT (Doppler pre-processing). The velocity resolution converted from the DFT spectral resolution is , and the distribution of the scatters in the velocity direction or the Doppler direction can be obtained. In the Doppler pre-processed data , the phase terms of the signal on the -th speed channel changes with n are mainly and . Due to the accumulation or filtering effect of DFT, the change range of v in this channel is . If the signal on the -th speed channel is phase-compensated by the phase factor during or after Doppler processing, the phase term becomes , where . As long as the accumulation time MNT is long enough or the resolution of velocity is high enough, Δv is small enough, and the change range of the term can be far less than π/4. Rearrange the data on each speed channel in the order of in from small to large; then, the phase term becomes , while becomes a random phase term of small value, which can be ignored.
By FFT processing of the rearranged data on each speed channel, the distribution of the scatters along range direction of each speed channel can be obtained. By synthesizing all the speed channels, the distribution of the scatters on the 2D range-Doppler plane can be obtained. It has almost the same imaging effect as the conventional imaging algorithm used in SF Radar.
For other RFH modes, Doppler pre-processing can also suppress the above special range-Doppler coupling effect, and different fast 2D range-Doppler imaging algorithms can be obtained.
3.2. Image Processing Based on 2D GMF
According to the theory of matched filtering, for any transmitting signal waveform, as long as it has a certain bandwidth and a certain time width, the 2D range-Doppler image of the detected area can be obtained from the return signal through 2D matched filtering processing at the receiving end. The range resolution of the image depends on the effective bandwidth of the transmitting signal, and the speed resolution depends on the effective time-width of the signal. If the random frequencies are uniformly-distributed, the effective bandwidth is proportional to the synthetic bandwidth .
Supposing the required non-ambiguous range depth of imaging at each sampling unit is
, the parameters
and
are designed to satisfy
. If range depth of
is divided into
range cells, the corresponding range width of each cell is
, which is exactly the nominal range resolution corresponding to the synthetic bandwidth
of RFH signal. The non-ambiguous velocity measurement range
is divided into
velocity cells, and the velocity width corresponding to each cell is
, which is exactly the velocity resolution corresponding to the accumulation time
MNT of a complex frame. According to Equation (3) and the principle of 2D GMF, the processing of 2D range-Doppler segment imaging at each sampling unit
k can be described as follows
where
is called the 2D segment image of the target area obtained by the sampling point
k.
is the value (complex number) at the pixel point
, where
is the number of pixel points in the range direction;
is the number of pixel points in the speed direction. The total number of pixels in the segment image is
MN.
The function of phase term is to calibrate the segment image, so that the starting position and the ending position of the segment image in the range direction correspond to the starting position and the ending position . The purpose of calibration is to ensure that the segment image acquired at different sampling units is not ambiguous. is the frequency-domain, non-uniform-sampling Fourier transform factor in the direction of range. The range-domain sampling after transformation is uniform, and the sampling interval is , but the frequency-domain sampling interval defined by before transformation is non-uniform and random. is the time-domain, non-uniform sampling Fourier transform factor in the velocity direction. The equivalent time-domain sampling before transformation is non-uniform because of variation of between frame, and the Doppler- frequency-domain sampling or velocity sampling after the transformation is uniform, with an interval of . is the range-Doppler coupling compensation factor, which can realize the phase compensation of the range movement within the sampling unit and across the sampling unit. Obviously, the motion compensation and 2D Fourier transform are carried out synchronously, and different phase compensation is used in different velocity channels to improve the compensation accuracy.
Obviously, when , , the RFH synthesis wideband system degenerates to the conventional SF synthesis wideband system, and the 2D GMF of Equation (4) degenerates to the conventional 2D windowed DFT operation, which can be implemented by 2D fast Fourier transform.
However, the computation complexity of 2D GMF is much higher than that of 2D FFT, so it is necessary to combine different RFH modes and use fast algorithms to realize 2D GMF to meet the real-time needs of high-speed platform-borne application.
Since the range width of echoes in each sampling unit is
, if the non-ambiguous range depth of the segment image is
, it is required that
, so that the echoes of scatters which move across sampling unit can be accumulated in-phase at the same point of panoramic image, and this is of importance in supersonic/hypersonic applications.
RI is the maximum moving range of the scatters in an imaging period of
. The overlapping width of the segment image of adjacent sampling units in the range direction is
, and the number of non-overlapping range resolution cells is
. Then, the panoramic image in the beam irradiation area can be obtained from the segment image of all the sampling units as follows:
where
U(
i) is a rectangular function with length
N, defined as:
In summary, the procedure of imaging process is shown in
Figure 2.
3.3. The Tradeoff between Randomness and Real-Time Performance
For the conventional SF radar, there is fast imaging algorithm of 2D FFT because of uniform sampling in both frequency-domain and slow-time-domain. Theoretically speaking, for the RFH radar system, the fast imaging algorithm depends on the structural characteristics of the RFH pattern. Because there are too many RFH patterns, it is impossible to design optimal imaging algorithm that has the least amount of computation for every RFH pattern. However, it is possible to design pipeline-parallel processing real-time imaging for different RFH modes combined with the data acquisition process.
In this paper, several RFH modes are defined as follows.
3.3.1. Intra-Complex-Frame Pure-RFH
In the m-th frame and the n-th pulse period of a complex frame, the frequency of the transmitting signal is randomly selected according to certain algorithm in the frequency band . The basic frequency can hop randomly in a wide frequency range between frames. In this mode of RFH, , where is the sequence number corresponding to the carrier frequency of the m-th frame and the n-th period. is randomly and un-repeatedly selected according to a certain probability density distribution in the integer set , where I = ΔF/Δfd. Different frame-m adopts different baseband frequency point set {. This mode has the best performance of randomness, low-interception, and anti-interference.
3.3.2. INTRA-Frame Pure-RFH
In each frame of a complex frame, the same frequency point set and the same hopping-order are adopted. For any frame m1 and m2, , where is randomly selected according to certain algorithm in the frequency band . Because the frequency is the same between frames, the initial phase φmn of the transmitting signal must be randomly selected according to certain algorithm between 0 and π, so as to reduce the cyclic autocorrelation of the transmitting signal and maintain the low interception performance. For different complex frames, the basic frequency randomly changes in a large range as much as possible. The same frequency between frames can simplify the Doppler processing and improve the real-time performance. However, compared with the intra-complex-frame pure-RFH mode, this mode loses performance of randomness, low-interception, and anti-interference because the same frequency point set and the same hopping-order are adopted in each frame.
In this mode of RFH, , and , where is randomly and un-repeatedly selected according to a certain probability density distribution in the range of integer set , where I = ΔF/Δfd.
3.3.3. Intra-Complex-Frames Pseudo-RFH
The baseband frequency points are obtained by uniform sampling in , , where . The basic frequency fm can hop randomly in a wide frequency range between frames, and can be randomly selected according to certain algorithm in the range of . In this mode, different frames can adopt different basic frequencies and different hopping-orders but the same uniformly sampled baseband frequency point set, and the pulse compression processing in the range direction can be done by fast Fourier transform after higher order motion compensation and data rearrangement, which improves the real-time performance. Compared with the above two modes, the shortcoming of this mode is that the non-ambiguous range depth of segment image at each sampling unit decreases because of the frequency-domain uniform sampling. It is necessary to increase N and reduce the frequency hopping interval to meet the design requirements of non-ambiguous range depth. In addition, this mode loses more performance of randomness, low-interception, and anti-interference.
In this mode, and , where is randomly and un-repeatedly selected according to a certain probability density distribution in the range of integer set .
3.3.4. Intra-Frame Pseudo-RFH
The baseband frequency points are obtained by uniform sampling in , , where . The basic frequency does not hop between frames. is randomly and un-repeatedly selected according to certain algorithm in the range of . The initial phase φmn is randomly selected according to certain algorithm between 0 and π. For different complex frames, the basic frequency randomly changes in a large range as much as possible. In this mode, both the pulse compression processing in the range direction and the Doppler processing in the speed direction can be done by fast Fourier transform, which further improves the real-time performance. Decreasing in non-ambiguous range depth, and more loss in performance of randomness, low-interception, and anti-interference, are also the shortcomings of this mode.
See
Appendix A for the specific generation of 2D RFH patterns for those four RFH modes
3.4. Online, Fast 2D Imaging Algorithms for Different RFH Modes
As mentioned before, in order to avoid image defocusing caused by the special range-Doppler coupling in the case of RFH, Doppler pre-processing must be carried out synchronized with the pulse compression process. However, Doppler processing is a kind of inter-frame processing. It will cause a serious delay in signal processing if Doppler processing is not done until the data of the last frame is collected. Considering that the data of the RFH synthetic wideband radar is obtained in the order of frames and periods, pipeline-parallel processing can be used to divide the Doppler pre-processing and pulse compression into each frame and each period, which can reduce the delay in signal processing.
3.4.1. Intra-Complex-Frame Pseudo-RFH Mode
In the 2D matched filtering (range-Doppler imaging) equation of Equation (4), in each frame of each sampling unit, the data are rearranged in the way of frequency point from small to large. Set
as the frequency point number after rearrangement and the corresponding number before rearrangement is
nm. Set the rearranged data as
. According to the definition of this RFH mode
, so the 2D matched filtering of Equation (4) can be re-written as follows:
Imaging Algorithm 1: FFT-based pulse-compression on multiple velocity channels
Step 1. Initializing, set
Step 2. For , perform the following iteration:
- (A)
Obtain the data of the k-th sampling unit of the m-th frame: .
- (B)
Data rearrangement: .
- (C)
Windowing, range calibration, multi-velocity-channel motion compensation, and Doppler pre-processing:
where
- (D)
Multi-velocity-channel fast pulse-compression processing.
It can be obtained according to Equations (5) and (6) that
The operation
is a uniform sampling DFT, which can be realized by
FFT:
- (E)
Current-frame Doppler-accumulation processing:
Obviously, .
In this algorithm, gradually, a clear image is obtained through iteration. Every additional frame of data increases the sharpness of the image. Because the rearranged frequency points are uniformly sampled, the pulse compression processing on each velocity-channel can be realized by FFT, which improves the real-time performance of the imaging algorithm.
3.4.2. Intra-Frame Pseudo-RFH Mode
This RFH mode is equivalent to making all in the intra-complex-frame pseudo-RFH mode. After data rearrangement, the nm corresponding to is the same, which is labeled as n and independent of m. In this mode, there is neither coupling phase term of lu and m, nor coupling phase term lv and n. Compared to imaging algorithm 1, the computational complexity can be further reduced by using fractal-dimension processing.
Imaging Algorithm 2. Fractal-dimension processing with Doppler pre-processing
Step 1. Data rearrangement. Rearrange the data of each frame in the order of frequency points from small to large. The rearranged data are , in which the number before rearrangement corresponding to is n.
Step 2. Windowing and velocity calibration (
corresponds to zero-velocity after compensation)
Step 3. For the data with the same sampling unit number
k, pulse period number
, and different frame number
m, carry out the non-integer sampling (
lv is an integer, but
is not an integer) IDFT processing:
Step 4. Range calibration and multi-velocity-channel motion compensation.
Step 5. Range-dimension pulse-compression processing on each velocity channel:
Obviously, the DFT processing of Equation (13) can be realized by FFT.
3.4.3. Intra-Frame Pure-RFH Mode
In this mode,
,
, and the common phase factor
can be ignored, so Equation (4) can be written as follows:
Imaging Algorithm 3. Pipeline-parallel processing 2D matching filtering algorithm
Step 1. Initialize, set .
Step 2. For , perform the following iteration:
- (A)
Obtain the data of the k-th sampling unit of the m-th frame: ;
- (B)
Windowing, range calibration, multi-velocity-channel motion compensation, and Doppler pre-processing:
where
- (C)
Multi-velocity-channel pulse-compression processing
It can be obtained according to Equations (14) and (15) that
The operation
is non-uniform sampling DFT. Even if the data are rearranged in the order of frequency points from small to large, the rearranged data are still non-uniform samples, which are difficult to be realized by FFT before inserting into uniform samples.
- (D)
Current-frame Doppler accumulation processing
Imaging Algorithm 4. Multi-velocity-channel pulse-compression based on data rearrangement/interpolation/range dimension FFT
In order to ensure the accuracy of interpolation, the interpolation processing must be done in each velocity channel. Due to the strong randomness of phase after data rearrangement, the rearranged data needs to be processed by Doppler pre-processing, so that the change range of signal phase on each speed channel is far less than one, where is the width of velocity resolution unit. On each velocity channel, the effect of rearranged random phase term is negligible. The data accumulated by Doppler pre-processing are rearranged and interpolated on each velocity channel, which makes it is easy to ensure the interpolation accuracy.
Step 1. Windowing and velocity calibration.
Step 2. For the data with the same sampling unit number
k, pulse period number
n, and different frame number
m, carry out the non-integer sampling (
lv is an integer, but
is not an integer) IDFT processing:
Step 3. Range calibration, multi-velocity-channel motion compensation:
Step 4. Data rearrangement and spline interpolation. In each sampling unit and each velocity channel, the data is rearranged in the order of n corresponding frequency points from small to large to get the non-uniformly stepped-frequency sampled data. Then, the pre trained spline interpolation model is used to interpolate the non-uniformly sampled data to uniformly sampled data , and the corresponding frequency points are unified as , , , …, .
Step 5. Perform range-dimension pulse-compression processing on each velocity channel
Obviously, the DFT processing of Equation (22) can be realized by FFT.
3.4.4. Intra-Complex Frame Pure-RFH Mode
Imaging Algorithm 5. Pipeline-parallel processing 2D matched filtering algorithm
Step 1. Initialize, set .
Step 2. For , perform the following iteration:
- (A)
Obtain the data of the k-th sampling unit of the m-th frame: ;
- (B)
Windowing, range calibration, multi-speed channel motion compensation, and pre-processing of Doppler:
where
- (C)
Multi-velocity-channel pulse-compression processing.
It can be obtained according to Equations (4) and (23) that
The operation
is non-uniform sampling DFT:
- (D)
Current-frame Doppler accumulation processing
Obviously, .