Approximations of the Aggregated Interference Statistics for Outage Analysis in Massive MTC †
Abstract
:1. Introduction
1.1. Prior Work
1.2. Contributions
- (3)
- A medium access scheme with spatial beamforming.
- (4)
- A graph-based resource allocation strategy that minimizes the average outage probability.
1.3. Organization
1.4. Notation
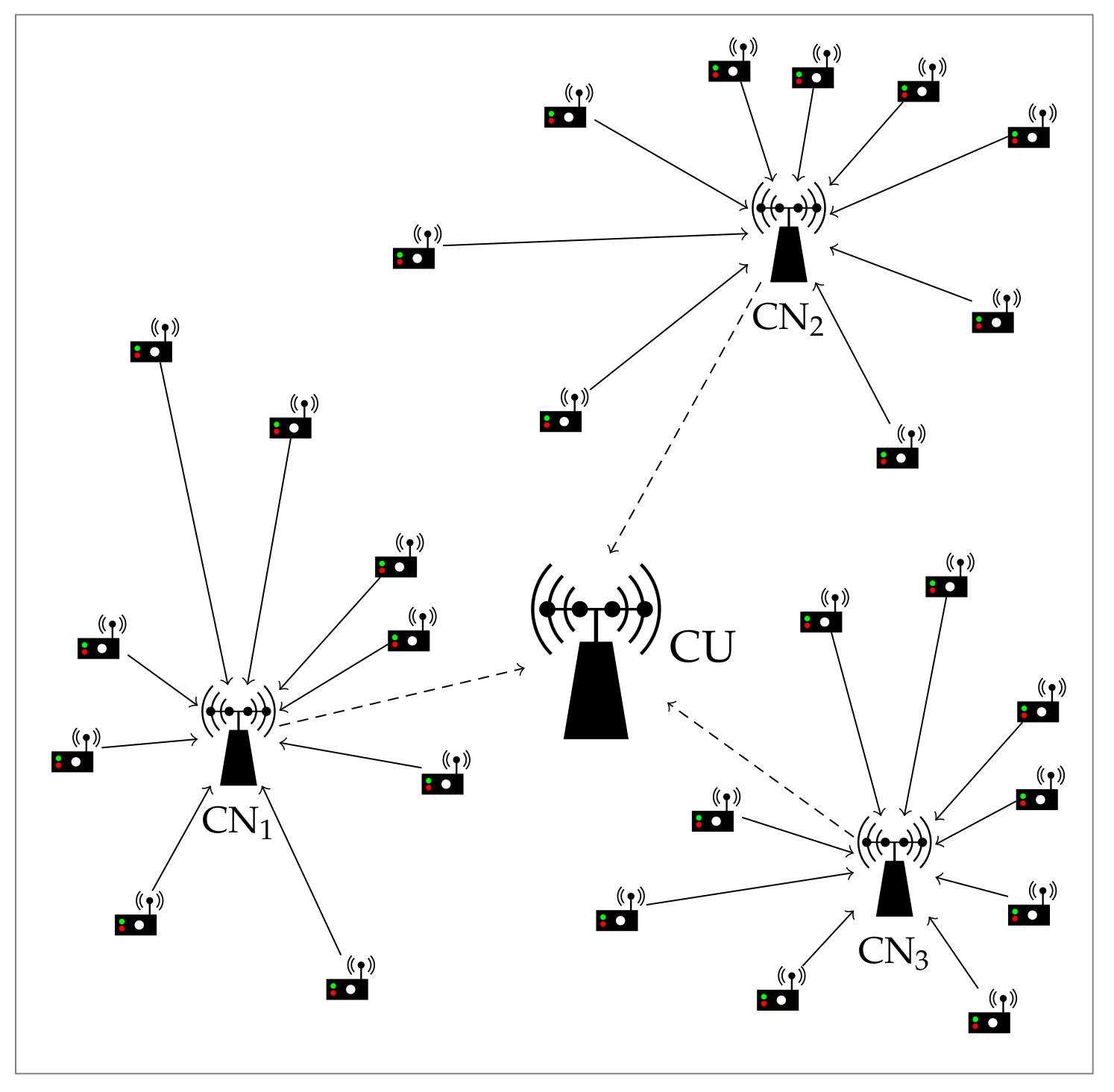
2. System Model
3. Approximations of the Statistics of the Aggregated Interference
- Outage Probability: Thanks to the approximation of the interference statistics, we are able to find an analytic closed-form expression for the outage probability (defined as the probability that the SINR is below a certain detection threshold). Based on that, and considering an orthogonal multiple access with limited number of available resources, an allocation scheme could be designed to minimize this metric improving, therefore, the system performance.
- Throughput: The approximated statistics of the aggregated interference could also be useful to obtain an analytic closed-form expression for the throughput of the sensors (e.g., through Shannon’s capacity). Note that this is indeed related to the outage probability, yet it captures different aspects of the communication.
- Harvested Energy: Given the large number of active devices in mMTC, the energy coming from the transmitted signals can be recycled (i.e., harvested). Then, we could employ the derived statistics to characterize the amount of harvested energy.
- Power Consumption: Taking into account the number of retransmissions (e.g., due to a high outage probability) and the different energy supplies (e.g., harvested energy), a power consumption model of the sensors could be derived to study and optimize the management of available energy within the network.
3.1. Characteristic Function
3.2. Gram–Charlier Approximation
4. Outage Probability
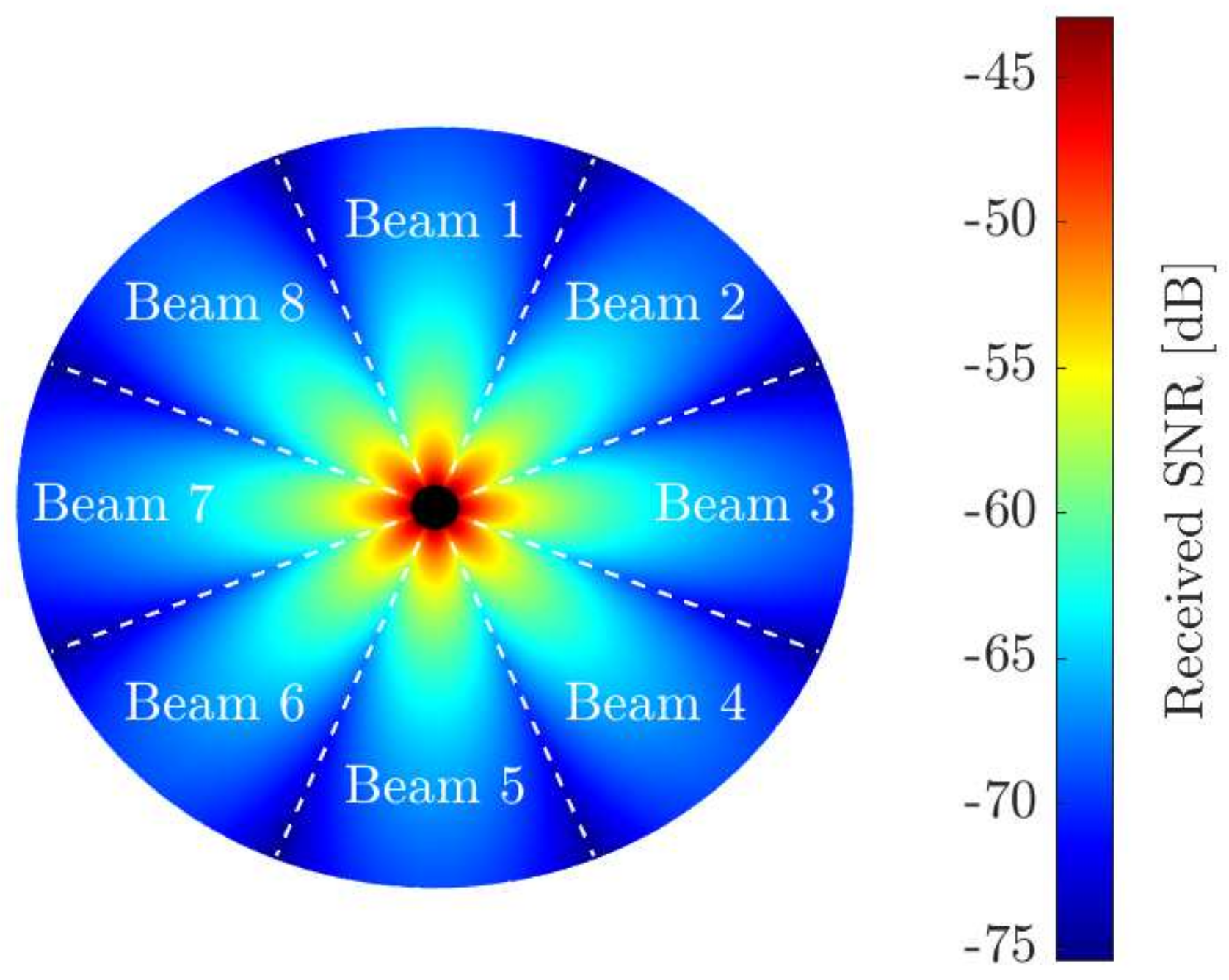
4.1. Single-Antenna CU
4.2. Multiple-Antenna CU
4.3. Multiple-Antenna CNs and CU
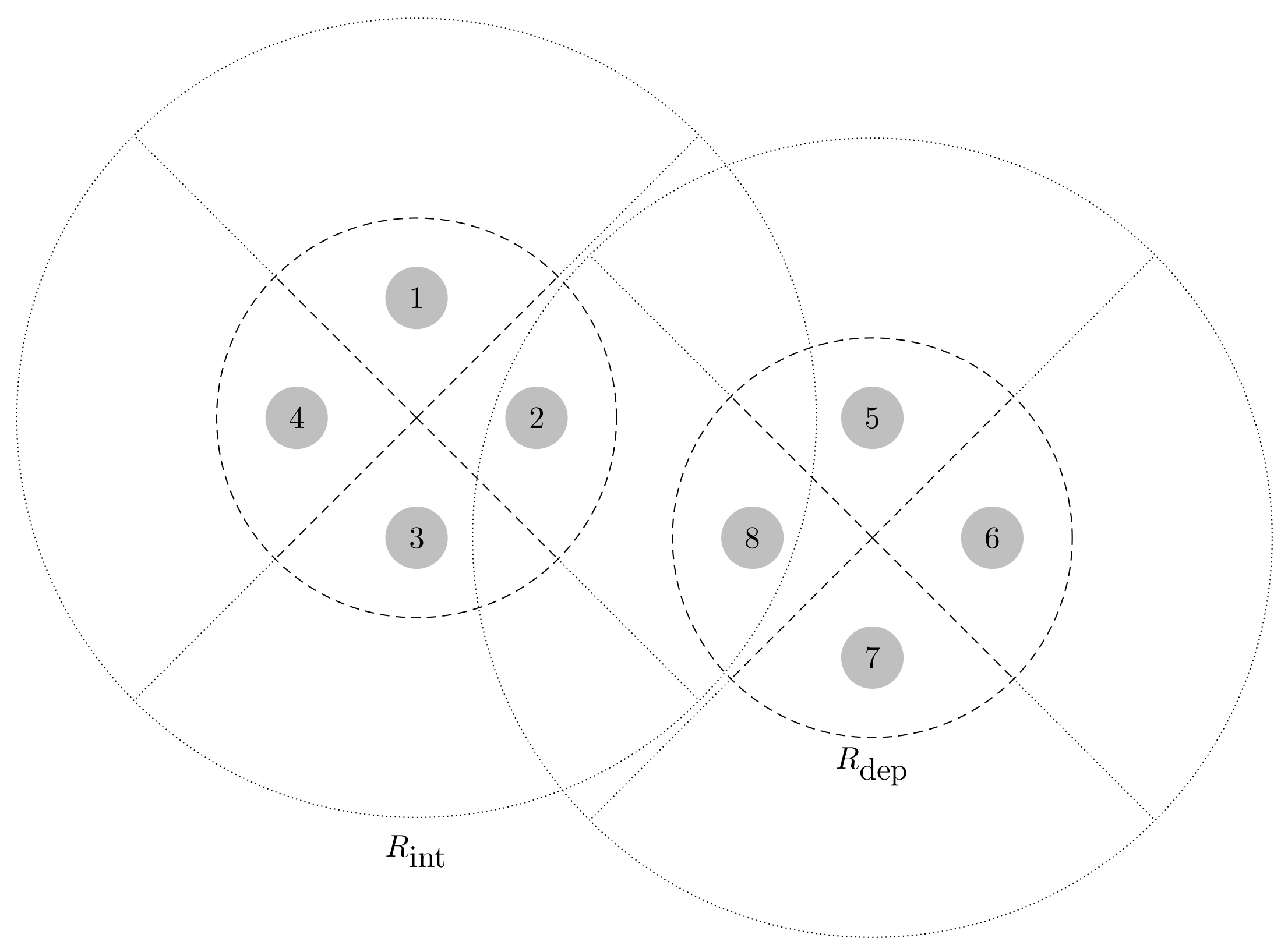
4.3.1. Single-Resource Scenario
4.3.2. Multiple-Resource Scenario
5. Resource Allocation Problem
5.1. Formulation in the Single and Multiple-Resource Setups
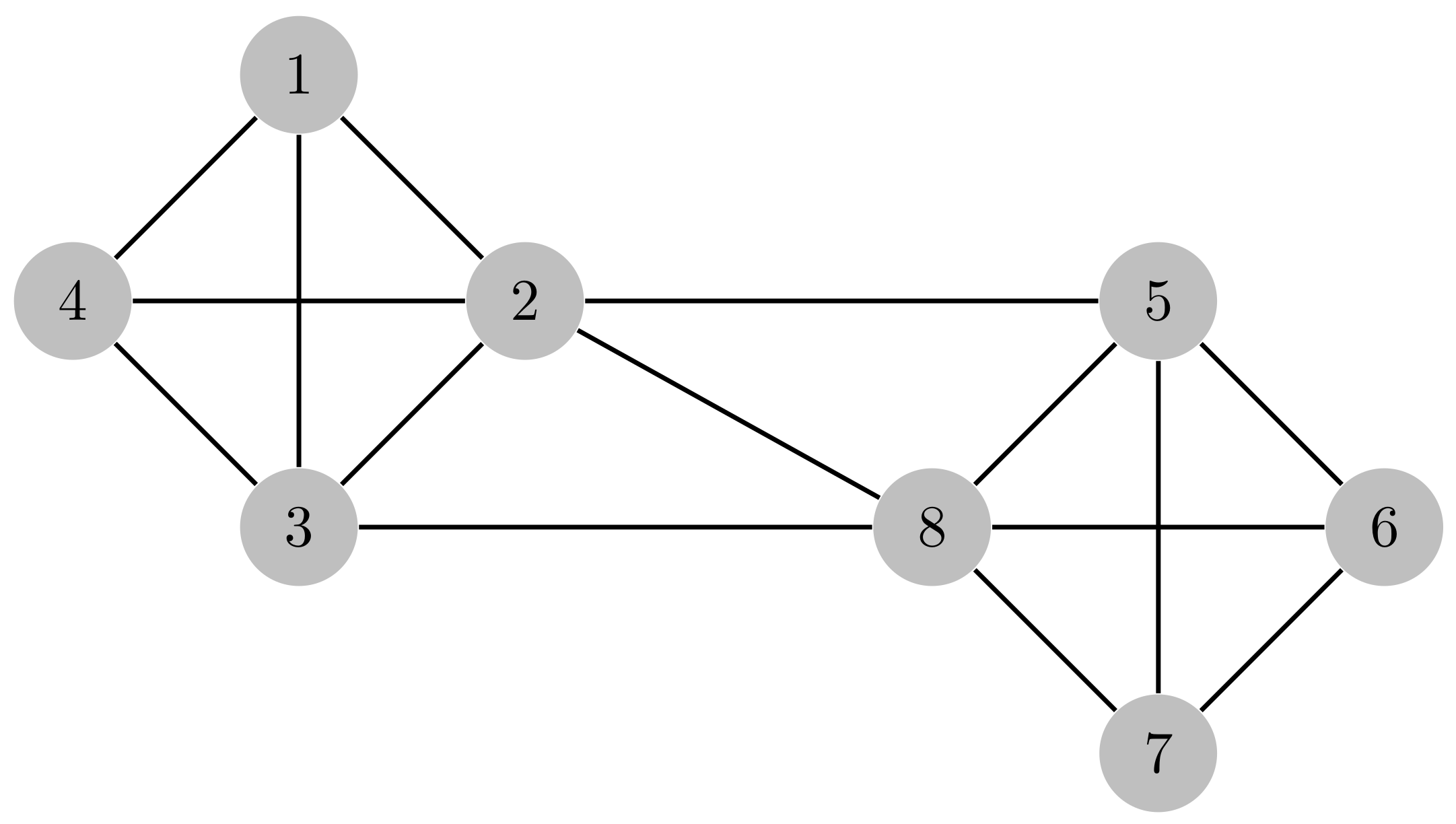
5.2. Solution Based on Graph Coloring
| Algorithm 1 Greedy optimization. | |
| ▹ Compute number of neighbors | |
| ▹ Order by highest degree | |
| ▹ Initialize color vector | |
| ▹ Initialize iteration counter | |
| ▹ Initialize average outage probability | |
| repeat | |
| ▹ Update iteration counter | |
| for do | ▹ Iterate over nodes |
| ▹ Compute color as indicated in Equation (46) | |
| ▹ Update average outage probability | |
| until or | ▹ Stopping criteria |
6. Numerical Results
6.1. Practical Issues
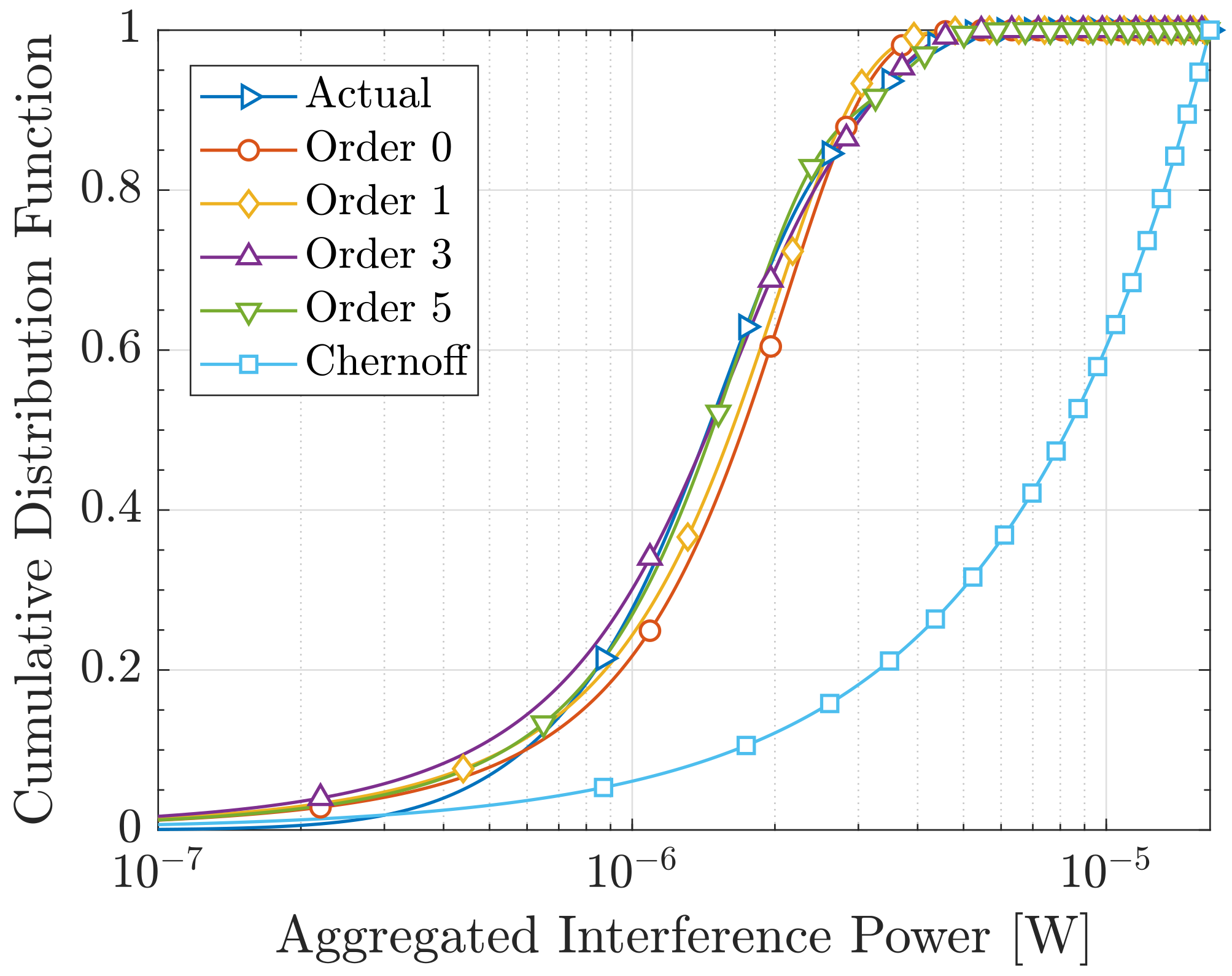
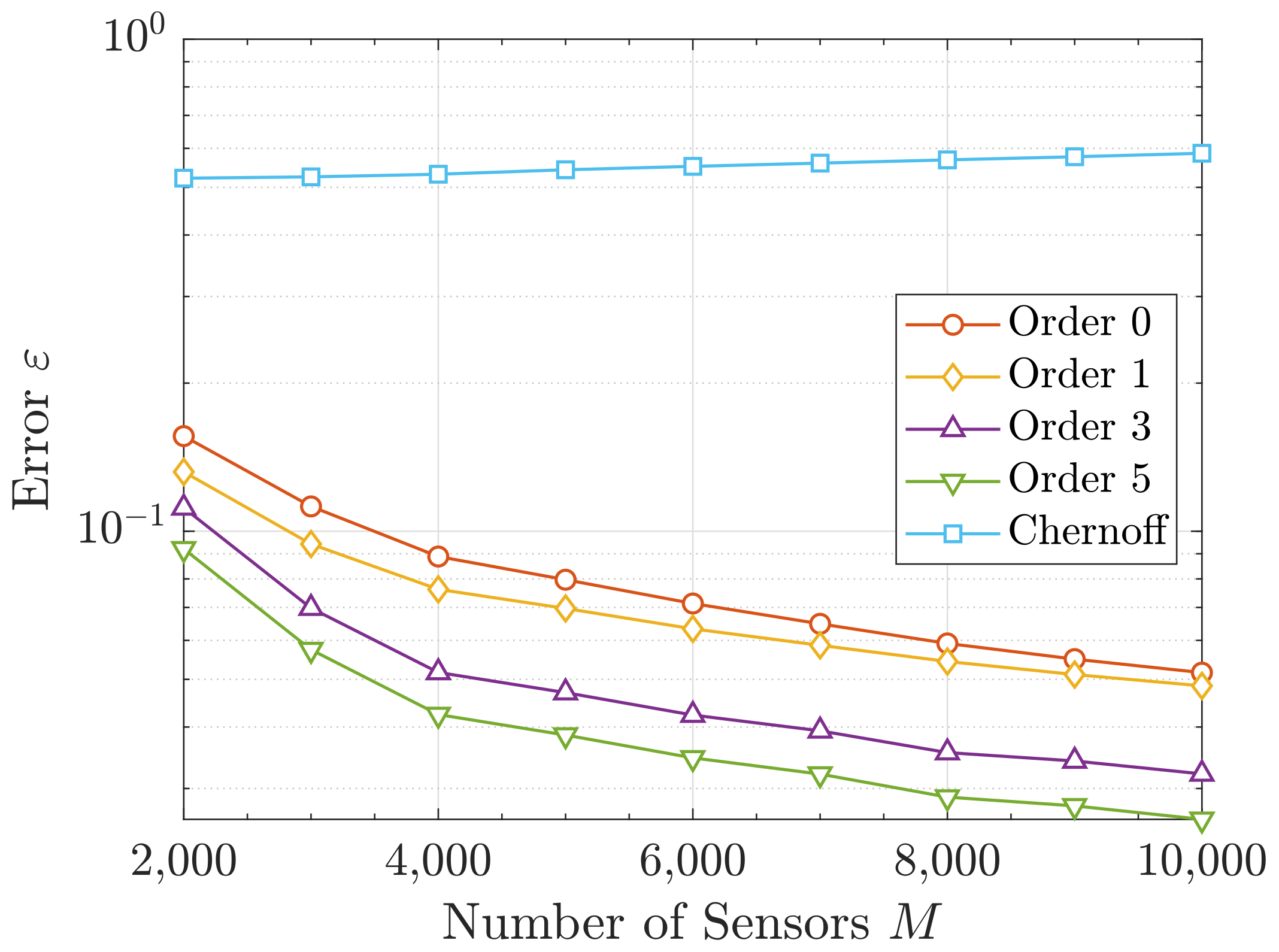
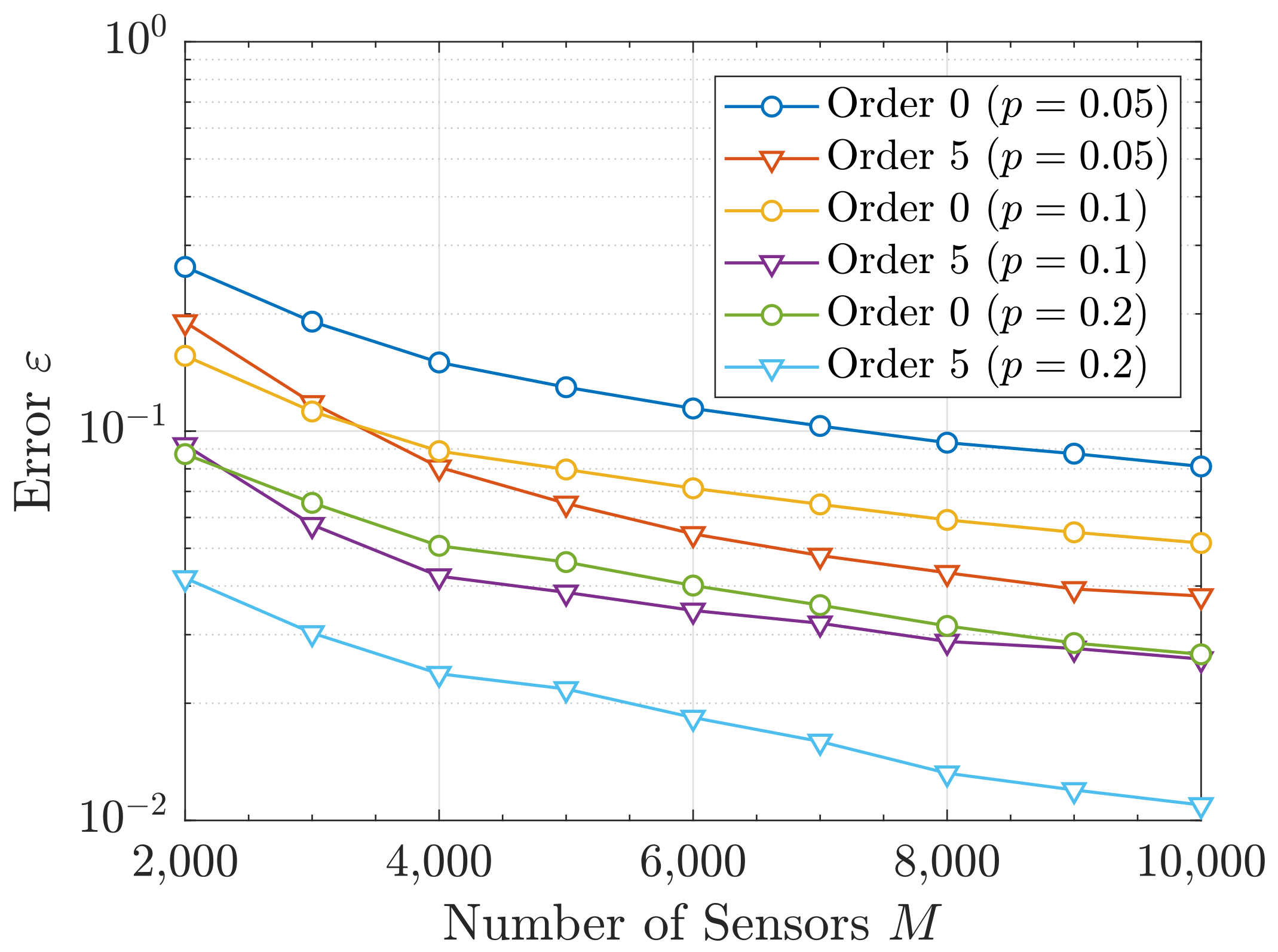
6.2. Aggregated Interference Statistics Approximations
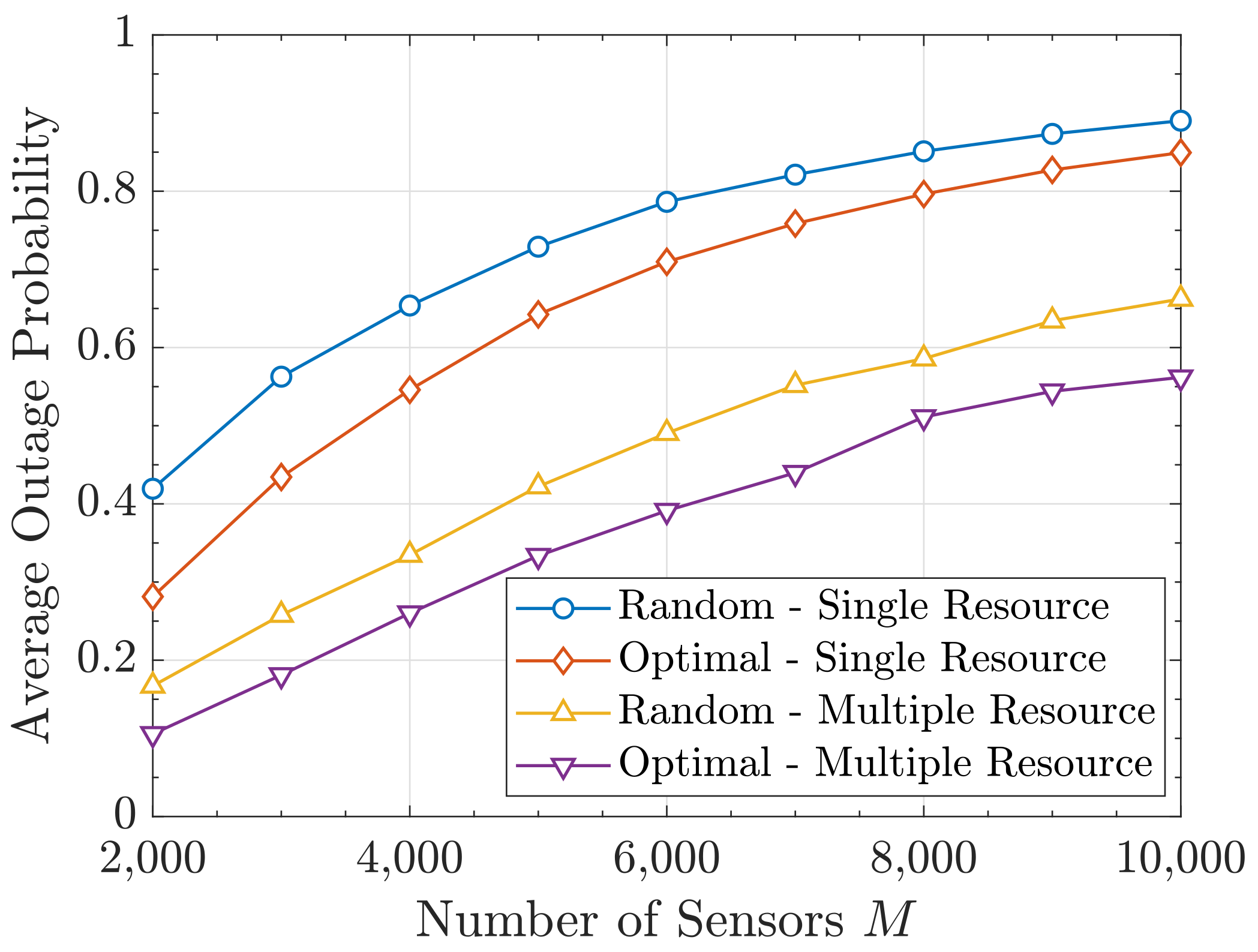
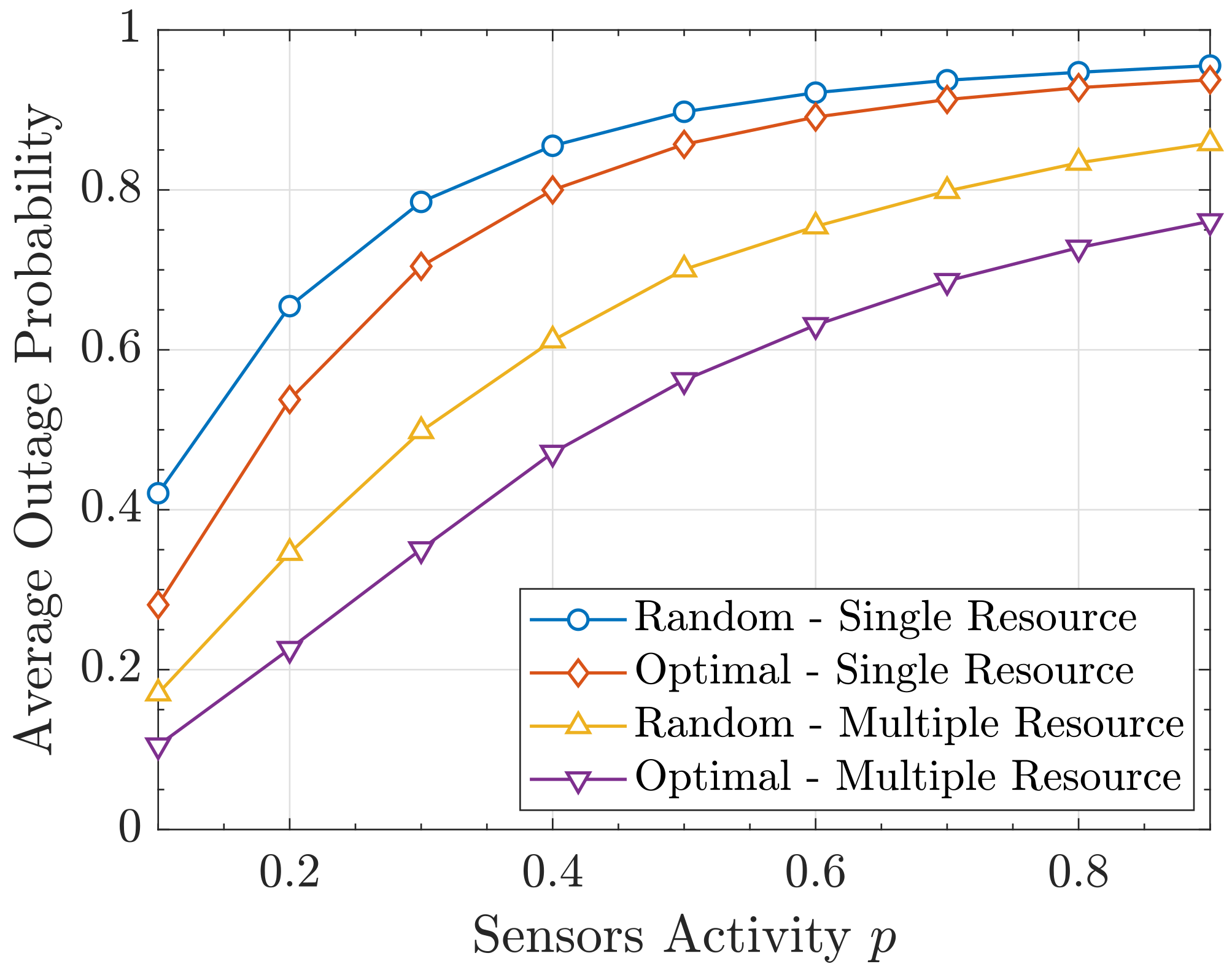
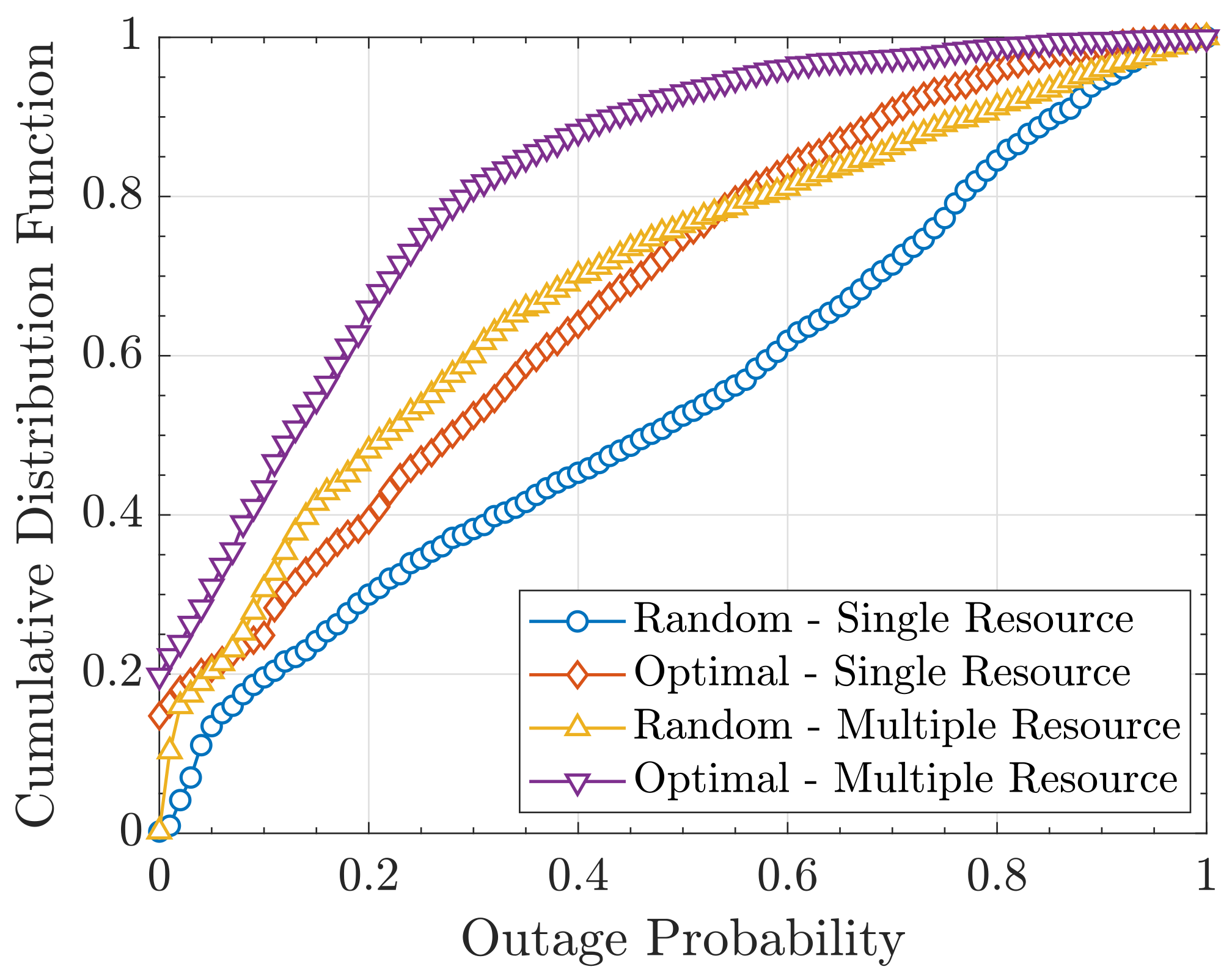
6.3. Resource Allocation
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, H.; Fapojuwo, A.O. A Survey of Enabling Technologies of Low Power and Long Range Machine-to-Machine Communications. IEEE Commun. Surv. Tuts. 2017, 19, 2621–2639. [Google Scholar] [CrossRef]
- Shariatmadari, H.; Ratasuk, R.; Iraji, S.; Laya, A.; Taleb, T.; Jäntti, R.; Ghosh, A. Machine-Type Communications: Current Status and Future Perspectives toward 5G systems. IEEE Commun. Mag. 2015, 53, 10–17. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Yao, J.; Wang, L.; Ming, Z.; Wu, K.; Chen, L. Narrowband Internet of Things: Evolutions, Technologies, and Open Issues. IEEE Internet Things J. 2018, 5, 1449–1462. [Google Scholar] [CrossRef]
- Tehrani, M.N.; Uysal, M.; Yanikomeroglu, H. Device-to-Device Communication in 5G Cellular Networks: Challenges, Solutions, and Future Directions. IEEE Commun. Mag. 2014, 52, 86–92. [Google Scholar] [CrossRef]
- Andrews, J.G.; Buzzi, S.; Choi, W.; Hanly, S.V.; Lozano, A.; Soong, A.C.K.; Zhang, J.C. What Will 5G Be? IEEE J. Sel. Areas Commun. 2014, 32, 1065–1082. [Google Scholar] [CrossRef]
- Xiong, X.; Zheng, K.; Xu, R.; Xiang, W.; Chatzimisios, P. Low Power Wide Area Machine-to-Machine Networks: Key Techniques and Prototype. IEEE Commun. Mag. 2015, 53, 64–71. [Google Scholar] [CrossRef]
- Agiwal, M.; Roy, A.; Saxena, N. Next Generation 5G Wireless Networks: A Comprehensive Survey. IEEE Commun. Surv. Tuts. 2016, 18, 1617–1655. [Google Scholar] [CrossRef]
- Yang, W.; Wang, M.; Zhang, J.; Zou, J.; Hua, M.; Xia, T.; You, X. Narrowband Wireless Access for Low-Power Massive Internet of Things: A Bandwidth Perspective. IEEE Wirel. Commun. 2017, 24, 138–145. [Google Scholar] [CrossRef]
- Nokia. LTE Evolution for IoT Connectivity; White Paper; Nokia: Espoo, Finland, 2016. [Google Scholar]
- Elsaadany, M.; Ali, A.; Hamouda, W. Cellular LTE-A Technologies for the Future Internet-of-Things: Physical Layer Features and Challenges. IEEE Commun. Surv. Tuts. 2017, 19, 2544–2572. [Google Scholar] [CrossRef]
- Gazis, V. A Survey of Standards for Machine-to-Machine and the Internet of Things. IEEE Commun. Surv. Tuts. 2017, 19, 482–511. [Google Scholar] [CrossRef]
- Dawy, Z.; Saad, W.; Ghosh, A.; Andrews, J.G.; Yaacoub, E. Toward Massive Machine Type Cellular Communications. IEEE Wirel. Commun. 2017, 24, 120–128. [Google Scholar] [CrossRef]
- Ali, A.; Hamouda, W.; Uysal, M. Next Generation M2M Cellular Networks: Challenges and Practical Considerations. IEEE Commun. Mag. 2015, 53, 18–24. [Google Scholar] [CrossRef] [Green Version]
- Bockelmann, C.; Pratas, N.; Nikopour, H.; Au, K.; Svensson, T.; Stefanovic, C.; Popovski, P.; Dekorsy, A. Massive Machine-Type Communications in 5G: Physical and MAC-Layer solutions. IEEE Commun. Mag. 2016, 54, 59–65. [Google Scholar] [CrossRef] [Green Version]
- Ericsson. 5G Radio Access: Capabilities and Technologies; White Paper; Ericsson: Stockholm, Sweden, 2016. [Google Scholar]
- Chen, S.; Ma, R.; Chen, H.; Zhang, H.; Meng, W.; Liu, J. Machine-to-Machine Communications in Ultra-Dense Networks—A Survey. IEEE Commun. Surv. Tuts. 2017, 19, 1478–1503. [Google Scholar] [CrossRef]
- 3GPP. Cellular System Support for Ultra Low Complexity and Low Throughput Internet of Things; Technical Report 3GPP TR 45.820; 3rd Generation Partnership Project (3GPP): Valbonne, France, 2016. [Google Scholar]
- Tse, D.; Viswanath, P. Fundamentals of Wireless Communication; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Lien, S.Y.; Chen, K.C.; Lin, Y. Toward Ubiquitous Massive Accesses in 3GPP Machine-to-Machine Communications. IEEE Commun. Mag. 2011, 49, 66–74. [Google Scholar] [CrossRef]
- Ghavimi, F.; Chen, H. M2M Communications in 3GPP LTE/LTE-A Networks: Architectures, Service Requirements, Challenges, and Applications. IEEE Commun. Surv. Tuts. 2015, 17, 525–549. [Google Scholar] [CrossRef]
- Hasan, M.; Hossain, E.; Niyato, D. Random Access for Machine-to-Machine Communication in LTE-Advanced Networks: Issues and Approaches. IEEE Commun. Mag. 2013, 51, 86–93. [Google Scholar] [CrossRef]
- Katzela, I.; Naghshineh, M. Channel Assignment Schemes for Cellular Mobile Telecommunication Systems: A Comprehensive Survey. IEEE Commun. Surv. Tuts. 2000, 3, 10–31. [Google Scholar] [CrossRef]
- Rabbachin, A.; Quek, T.Q.S.; Shin, H.; Win, M.Z. Cognitive Network Interference. IEEE J. Sel. Areas Commun. 2011, 29, 480–493. [Google Scholar] [CrossRef]
- Kusaladharma, S.; Tellambura, C. Aggregate Interference Analysis for Underlay Cognitive Radio Networks. IEEE Wirel. Commun. Lett. 2012, 1, 641–644. [Google Scholar] [CrossRef]
- Alexandropoulos, G.C.; Ferrand, P.; Gorce, J.; Papadias, C.B. Advanced Coordinated Beamforming for the Downlink of Future LTE Cellular Networks. IEEE Commun. Mag. 2016, 54, 54–60. [Google Scholar] [CrossRef] [Green Version]
- Alexandropoulos, G.C.; Ferrand, P.; Papadias, C.B. On the Robustness of Coordinated Beamforming to Uncoordinated Interference and CSI Uncertainty. In Proceedings of the 2017 IEEE Wireless Communications and Networking Conference, San Francisco, CA, USA, 19–22 March 2017; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Heath, R.W., Jr.; Wu, T.; Kwon, Y.H.; Soong, A.C.K. Multiuser MIMO in Distributed Antenna Systems with Out-of-Cell Interference. IEEE Trans. Signal Process. 2011, 59, 4885–4899. [Google Scholar] [CrossRef]
- Cardieri, P. Modeling Interference in Wireless Ad Hoc Networks. IEEE Commun. Surv. Tuts. 2010, 12, 551–572. [Google Scholar] [CrossRef]
- ElSawy, H.; Hossain, E.; Haenggi, M. Stochastic Geometry for Modeling, Analysis, and Design of Multi-Tier and Cognitive Cellular Wireless Networks: A Survey. IEEE Commun. Surv. Tuts. 2013, 15, 996–1019. [Google Scholar] [CrossRef]
- Haenggi, M.; Andrews, J.G.; Baccelli, F.; Dousse, O.; Franceschetti, M. Stochastic Geometry and Random Graphs for the Analysis and Design of Wireless Networks. IEEE J. Sel. Areas Commun. 2009, 27, 1029–1046. [Google Scholar] [CrossRef]
- Andrews, J.G.; Ganti, R.K.; Haenggi, M.; Jindal, N.; Weber, S. A Primer on Spatial Modeling and Analysis in Wireless Networks. IEEE Commun. Mag. 2010, 48, 156–163. [Google Scholar] [CrossRef]
- Kwon, T.; Cioffi, J.M. Random Deployment of Data Collectors for Serving Randomly-Located Sensors. IEEE Trans. Wirel. Commun. 2013, 12, 2556–2565. [Google Scholar] [CrossRef] [Green Version]
- Senel, K.; Larsson, E.G. Grant-Free Massive MTC-Enabled Massive MIMO: A Compressive Sensing Approach. IEEE Trans. Commun. 2018, 66, 6164–6175. [Google Scholar] [CrossRef] [Green Version]
- Kela, P.; Lundqvist, H.; Costa, M.; Leppänen, K.; Jäntti, R. Connectionless Access for Massive Machine Type Communications in Ultra-Dense Networks. In Proceedings of the 2017 IEEE International Conference on Communications, Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Oh, C.; Hwang, D.; Lee, T. Joint Access Control and Resource Allocation for Concurrent and Massive Access of M2M Devices. IEEE Trans. Wirel. Commun. 2015, 14, 4182–4192. [Google Scholar] [CrossRef]
- Si, P.; Yang, J.; Chen, S.; Xi, H. Adaptive Massive Access Management for QoS Guarantees in M2M Communications. IEEE Trans. Veh. Technol. 2015, 64, 3152–3166. [Google Scholar] [CrossRef]
- Laya, A.; Alonso, L.; Alonso-Zarate, J. Is the Random Access Channel of LTE and LTE-A Suitable for M2M Communications? A Survey of Alternatives. IEEE Commun. Surv. Tuts. 2014, 16, 4–16. [Google Scholar] [CrossRef] [Green Version]
- Lagen, S.; Muñoz, O.; Pascual-Iserte, A.; Vidal, J.; Agustin, A. Long-Term Provisioning of Radio Resources Based on their Utilization in Dense OFDMA Networks. In Proceedings of the 2016 IEEE 27th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications, Valencia, Spain, 4–7 September 2016; pp. 1–7. [Google Scholar] [CrossRef]
- Salam, T.; Rehman, W.U.; Tao, X. Cooperative Data Aggregation and Dynamic Resource Allocation for Massive Machine Type Communication. IEEE Access 2018, 6, 4145–4158. [Google Scholar] [CrossRef]
- Alcaraz López, O.L.; Alves, H.; Juliano Nardelli, P.H.; Latva-aho, M. Aggregation and Resource Scheduling in Machine-Type Communication Networks: A Stochastic Geometry Approach. IEEE Trans. Wirel. Commun. 2018, 17, 4750–4765. [Google Scholar] [CrossRef] [Green Version]
- Guo, J.; Durrani, S.; Zhou, X.; Yanikomeroglu, H. Massive Machine Type Communication with Data Aggregation and Resource Scheduling. IEEE Trans. Commun. 2017, 65, 4012–4026. [Google Scholar] [CrossRef] [Green Version]
- Xia, N.; Chen, H.; Yang, C. Radio Resource Management in Machine-to-Machine Communications—A Survey. IEEE Commun. Surv. Tuts. 2018, 20, 791–828. [Google Scholar] [CrossRef]
- Liesegang, S.; Muñoz, O.; Pascual-Iserte, A. Interference Statistics Approximations for Data Rate Analysis in Uplink Massive MTC. In Proceedings of the 2018 IEEE Global Conference on Signal and Information Processing, Anaheim, CA, USA, 26–29 November 2018; pp. 176–180. [Google Scholar] [CrossRef]
- Brenn, T.; Anfinsen, S.N. A Revisit of the Gram-Charlier and Edgeworth Series Expansions; Technical Report; UiT The Arctic University of Norway, Department of Physics and Technology: Tromsø, Norway, 2017. [Google Scholar]
- Comtet, L. Advanced Combinatorics: The Art of Finite and Infinite Expansions; Springer: Cham, The Netherlands, 2012. [Google Scholar]
- Smith, P.J. A Recursive Formulation of the Old Problem of Obtaining Moments from Cumulants and Vice Versa. Am. Stat. 1995, 49, 217–218. [Google Scholar]
- Burkardt, J. The Truncated Normal Distribution; Dept. Scientific Computing Website, Florida State University: Tallahassee, FL, USA, 2014. [Google Scholar]
- Zheng, K.; Hu, F.; Wang, W.; Xiang, W.; Dohler, M. Radio Resource Allocation in LTE-Advanced Cellular Networks with M2M Communications. IEEE Commun. Mag. 2012, 50, 184–192. [Google Scholar] [CrossRef] [Green Version]
- Owen, D.B. A Table of Normal Integrals. Commun. Stat. Simul. Comput. 1980, 9, 389–419. [Google Scholar] [CrossRef]
- Balakrishnan, R.; Ranganathan, K. A Textbook of Graph Theory; Springer: New York, NY, USA, 2012. [Google Scholar]
- Cowen, L.; Goddard, W.; Jesurum, C.E. Defective Coloring Revisited. J. Graph Theory 1997, 24, 205–219. [Google Scholar] [CrossRef]
- Grötschel, M.; Lovasz, L.; Schrijver, A. Geometric Algorithms and Combinatorial Optimization; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Ghosh, A.; Ratasuk, R. Essentials of LTE and LTE-A; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Van Trees, H. Optimum Array Processing: Part IV of Detection, Estimation, and Modulation Theory; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- ITU. Guidelines for Evaluation of Radio Interface Technologies for IMT-Advanced; Technical Report ITU-R M.2135-1; International Telecommunication Union (ITU): Geneva, Switzerland, 2009. [Google Scholar]
- Lin, J. Divergence Measures Based on the Shannon Entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef] [Green Version]
| Notation | Description |
|---|---|
| Bernoulli random variable accounting for the activity of sensor j | |
| Probability that sensor j is active and transmitting | |
| SINR of the received signal from sensor i | |
| Received power of the signal from sensor i | |
| Received power of the signal from sensor j at the detector of sensor i | |
| Power of the noise at the detector of the signal from sensor i | |
| Set of sensors interfering to sensor i | |
| Aggregated interference that the signal from sensor i perceives | |
| Outage probability of sensor i | |
| Probability mass function of the aggregated interference | |
| Characteristic function of the aggregated interference | |
| Probability density function of the Gaussian distribution with mean and standard deviation | |
| Mean of the aggregated interference | |
| Standard deviation of the aggregated interference | |
| nth cumulant of the aggregated interference | |
| nth Bell polynomial | |
| nth Hermite polynomial | |
| nth non-centralized order moment of the aggregated interference | |
| Probability density function of the truncated Gaussian distribution with mean and standard deviation , defined between a and b | |
| Probability density function of the standard Gaussian random variable | |
| Cumulative distribution function of the standard Gaussian random variable | |
| Detection threshold | |
| M | Number of sensors |
| P | Transmit power of the sensors |
| N | Number of receive antennas |
| L | Number of spatial beams |
| K | Number of collector nodes |
| R | Number of available orthogonal resources |
| Sensors detected at the beam l of the collector node k | |
| Resources allocated at the beam l of the collector node k | |
| Intra-beam aggregated interference | |
| Inter-beam aggregated interference | |
| Set of sensors interfering to sensor i and detected at the same beam | |
| Set of sensors interfering to sensor i and detected at another beam | |
| Radius determining the deployment of sensors | |
| Radius determining the range of the interference |
| n | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| M | K | N | P | p | R | |
|---|---|---|---|---|---|---|
| 2000 | 10 | 10 | W | 0.1 | 6 | dB |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liesegang, S.; Pascual-Iserte, A.; Muñoz, O. Approximations of the Aggregated Interference Statistics for Outage Analysis in Massive MTC. Sensors 2019, 19, 5448. https://doi.org/10.3390/s19245448
Liesegang S, Pascual-Iserte A, Muñoz O. Approximations of the Aggregated Interference Statistics for Outage Analysis in Massive MTC. Sensors. 2019; 19(24):5448. https://doi.org/10.3390/s19245448
Chicago/Turabian StyleLiesegang, Sergi, Antonio Pascual-Iserte, and Olga Muñoz. 2019. "Approximations of the Aggregated Interference Statistics for Outage Analysis in Massive MTC" Sensors 19, no. 24: 5448. https://doi.org/10.3390/s19245448





