Next Article in Journal
Robust Depth Estimation for Light Field Microscopy
Previous Article in Journal
Influence of Uniaxial Stress on the Shear-Wave Spectrum Propagating in Steel Members
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Sensors
Volume 19
Issue 3
10.3390/s19030498
sensors-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

High-Sensitivity Microwave Sensor Based on an Interdigital-Capacitor-Shaped Defected Ground Structure for Permittivity Characterization

by
Junho Yeo
1,* and
Jong-Ig Lee
2
1
School of Computer and Communication Engineering, Daegu University, 201 Daegudae-ro, Gyeongsan, Gyeongbuk 38453, Korea
2
Department of Electronics Engineering, Dongseo University, San69-1, Jurye-2dong, Sasang-gu, Busan 47011, Korea
*
Author to whom correspondence should be addressed.
Sensors 2019, 19(3), 498; https://doi.org/10.3390/s19030498
Submission received: 14 January 2019 / Revised: 22 January 2019 / Accepted: 23 January 2019 / Published: 25 January 2019
(This article belongs to the Section Physical Sensors)
Browse Figures
Versions Notes

Abstract

:
This study proposes a high-sensitivity microwave sensor based on an interdigital-capacitor-shaped defected ground structure (IDCS-DGS) in a microstrip transmission line for the dielectric characterization of planar materials. The proposed IDCS-DGS was designed by modifying the straight ridge structure of an H-shaped aperture. The proposed sensor was compared with conventional sensors based on a double-ring complementary split ring resonator (CSRR), a single-ring CSRR, and a rotated single-ring CSRR. All the sensors were designed and fabricated on 0.76-mm-thick RF-35 substrate and operated at 1.5 GHz under unloaded conditions. Five different standard dielectric samples with dielectric constants ranging from 2.17 to 10.2 were tested for the sensitivity comparison. The sensitivity of the proposed sensor was measured by the shift in the resonant frequency of the transmission coefficient, and compared with conventional sensors. The experiment results show that the sensitivity of the proposed sensor was two times higher for a low permittivity of 2.17 and it was 1.42 times higher for a high permittivity of 10.2 when compared with the double-ring CSRR-based sensor.

1. Introduction

The response of a material to electromagnetic (EM) waves depends on its permittivity. Therefore, the accurate measurement of the permittivity is crucial for the design of antennas, microwave circuits, and non-destructive monitoring applications [1,2]. In general, permittivity measurement methods can be classified into resonant and non-resonant methods. In non-resonant methods, the permittivity property of the material is derived from changes in the characteristic impedance and wave velocity of EM waves, measured by the reflection and transmission characteristics. These methods require a means of directing the EM wave towards a material under test (MUT) and then collecting what is reflected and transmitted through it. The non-resonant methods include the waveguide and coaxial transmission line method [3,4,5], free space transmission method [6,7], open-ended transmission line method [8,9], and planar transmission line method [10,11].
The resonant methods can be divided into resonator and resonant perturbation methods [1]. In resonant perturbation methods, the MUT is inserted into a resonant structure, which causes a perturbation in the response in the form of a resonant frequency shift and a quality factor change [12,13,14]. However, these methods require a bulky and costly cavity such as a waveguide cavity or a coaxial cavity for the measurement. In resonator methods, the MUT is considered as a part of the resonator, and the permittivity can be deduced from the shift in resonance frequency [2,15,16].
For resonator methods, planar resonators based on split ring resonator (SRR) [16,17,18,19,20] and complementary SRR (CSRR) [2,21,22,23,24,25,26,27] structures have been widely used because of their advantages such as simple geometry, ease of fabrication, and low cost. For CSRR-based permittivity sensors, conventional CSRR structures using double rings or a single ring were etched on the ground plane of a microstrip transmission line and acted as a band stop filter. However, the sensitivity of double-ring and single-ring CSRRs has not been systematically investigated.
This paper presents a high-sensitivity microwave sensor based on an interdigital-capacitor-shaped defected ground structure (IDCS-DGS) for permittivity characterization. The sensitivity of the proposed IDCS-DGS-based sensor is compared with conventional sensors based on a double-ring complementary split ring resonator (DR-CSRR), a single-ring CSRR (SR-CSRR), and a rotated single-ring CSRR (R-SR-CSRR) by measuring the shift in the resonant frequency of the transmission coefficient. All the sensors were designed and fabricated on 0.76-mm-thick RF-35 substrate and operated at 1.5 GHz under unloaded conditions. The operating frequency of 1.5 GHz was chosen because the lowest frequency above 1 GHz found in the literature for permittivity characterization using the CSSR structure ranged from 1.3 GHz to 1.7 GHz [28], and 1.5 GHz was selected for the center frequency of the lowest frequency above 1 GHz. Full-wave simulations were performed using CST Microwave Studio.

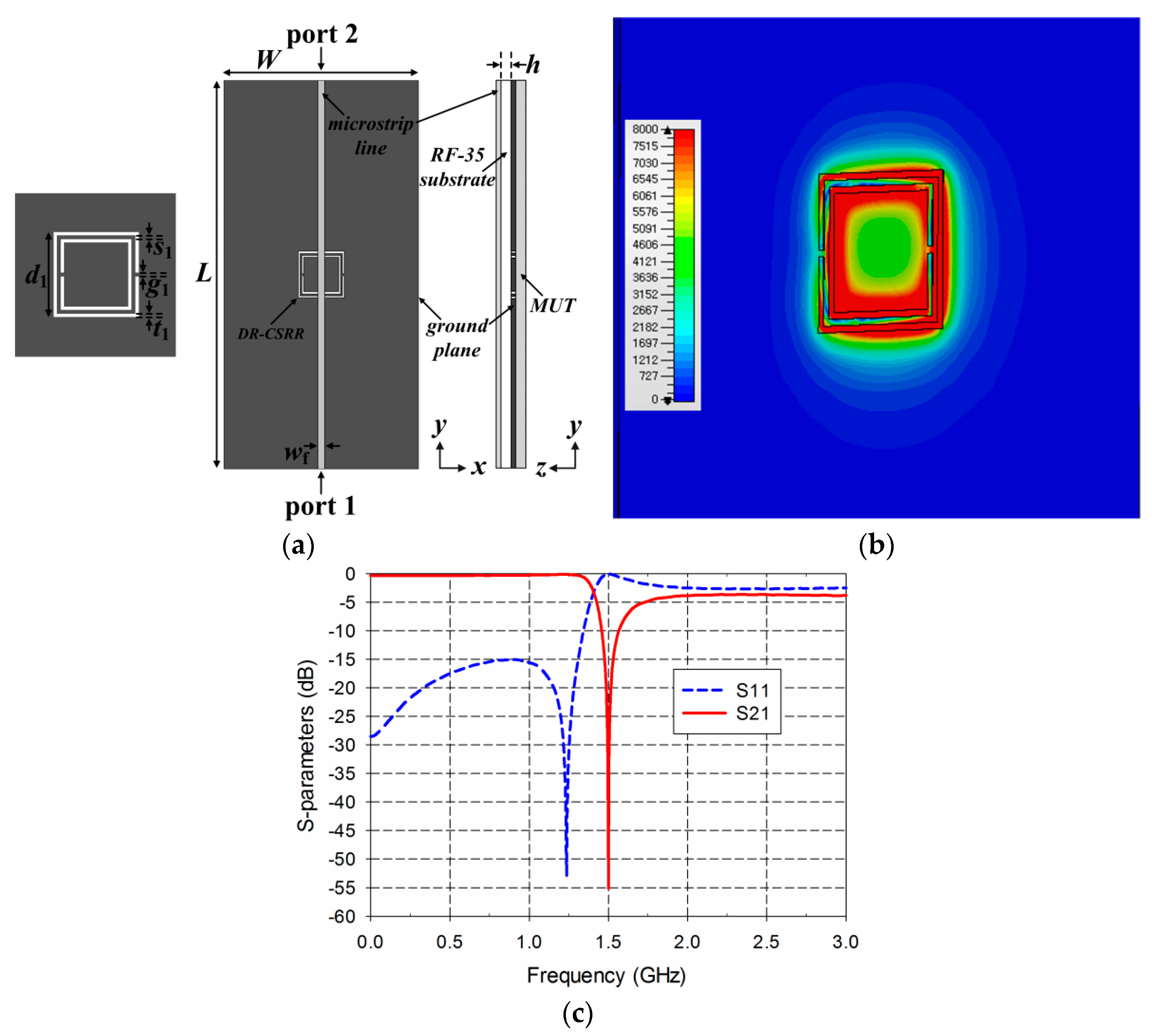
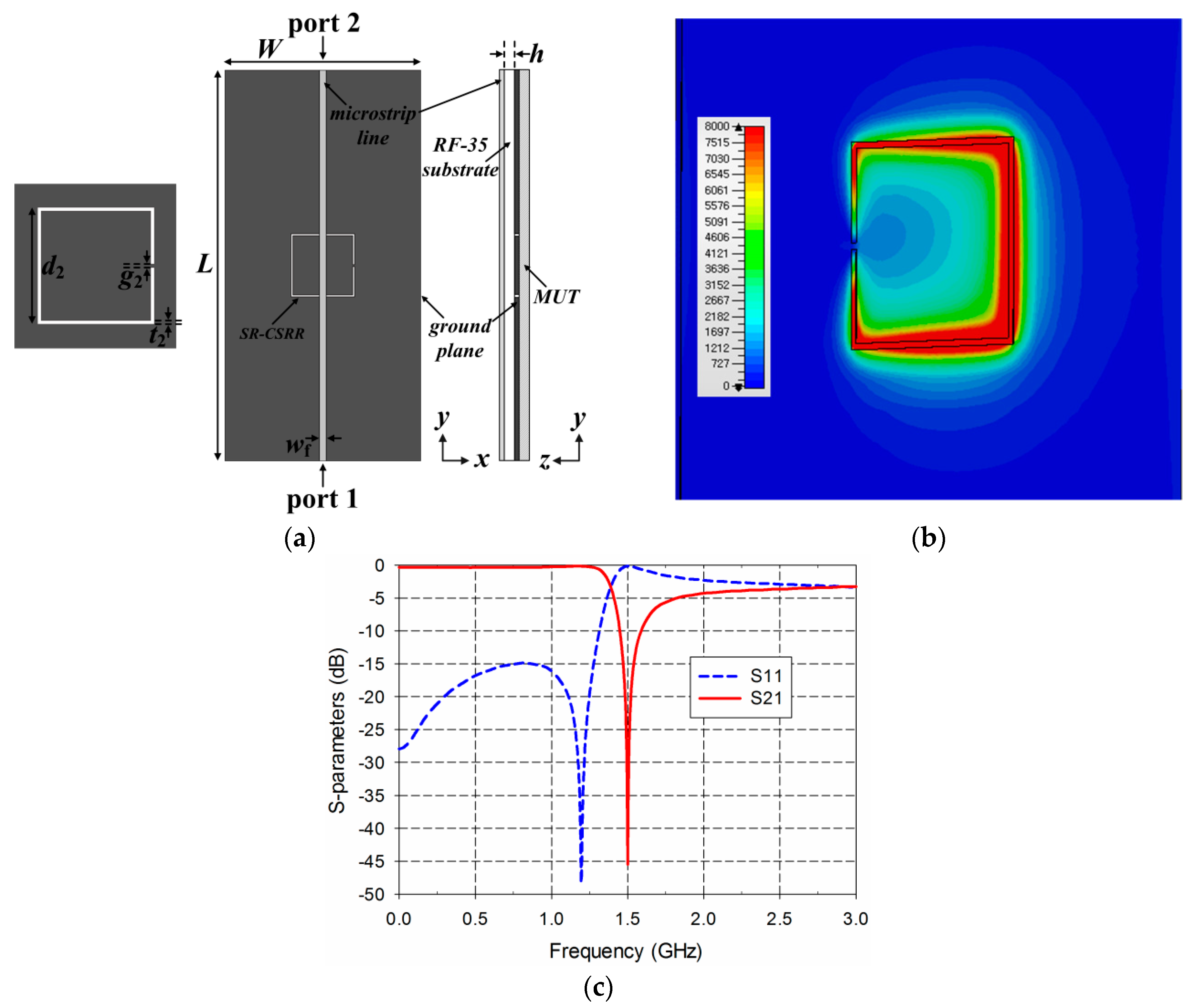
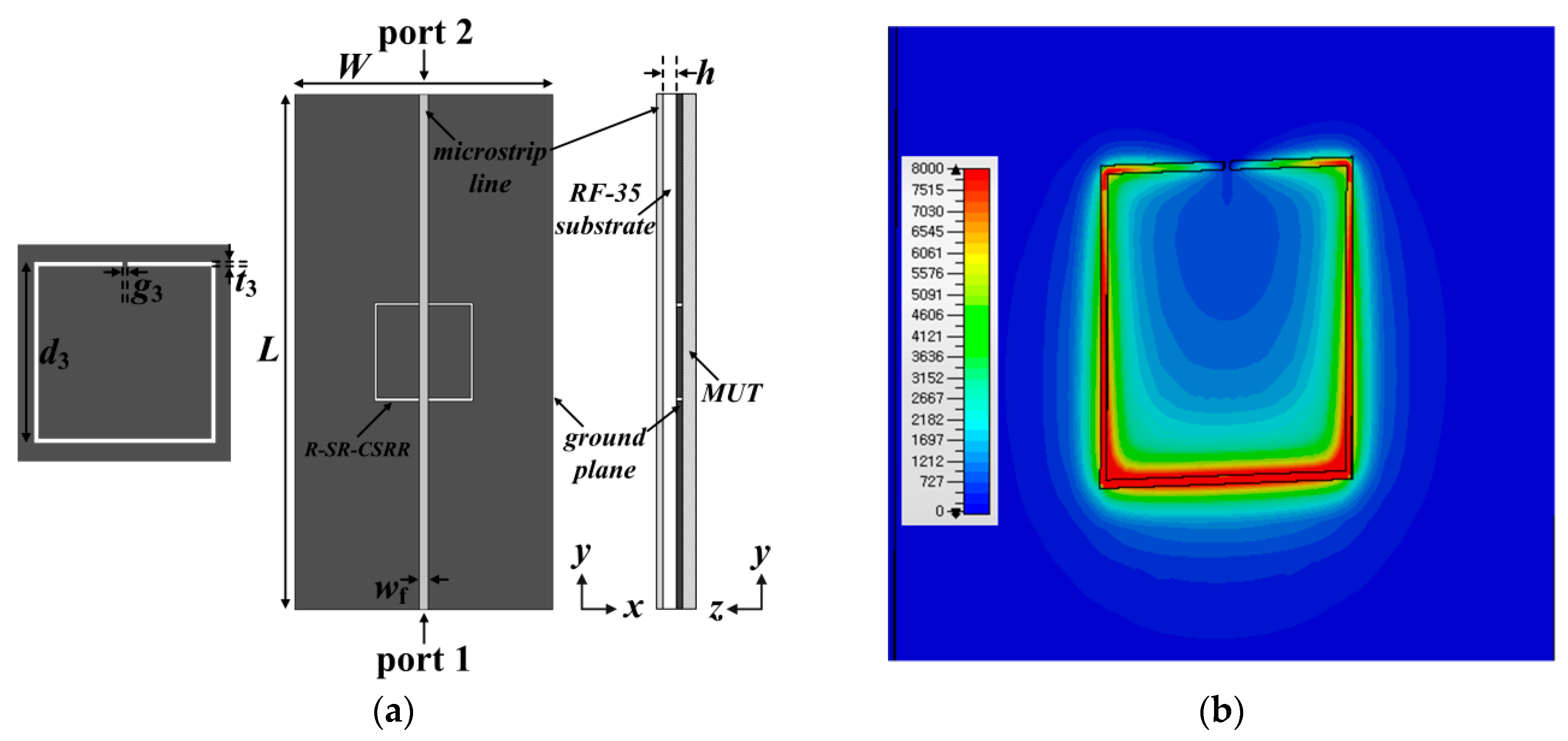
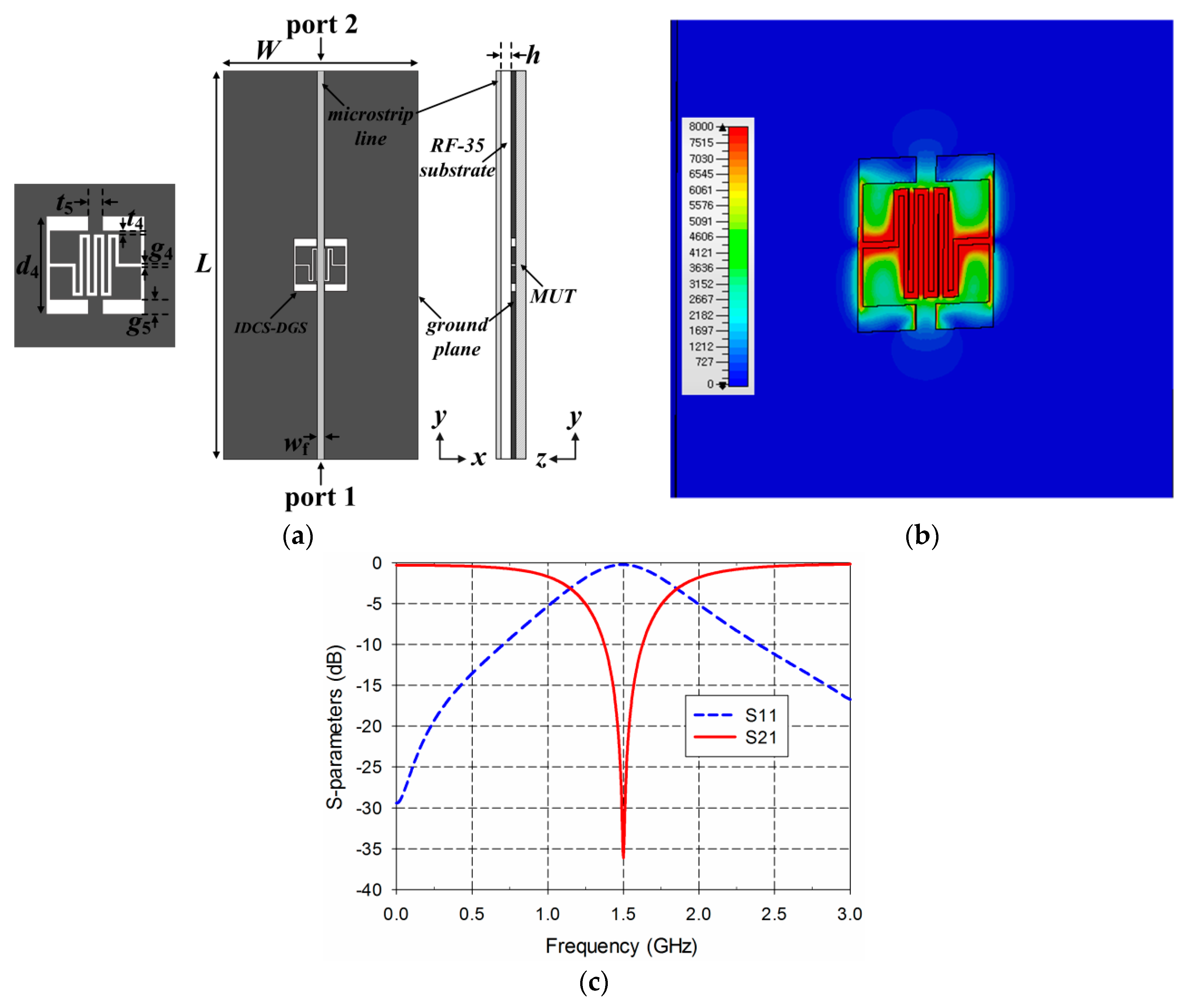
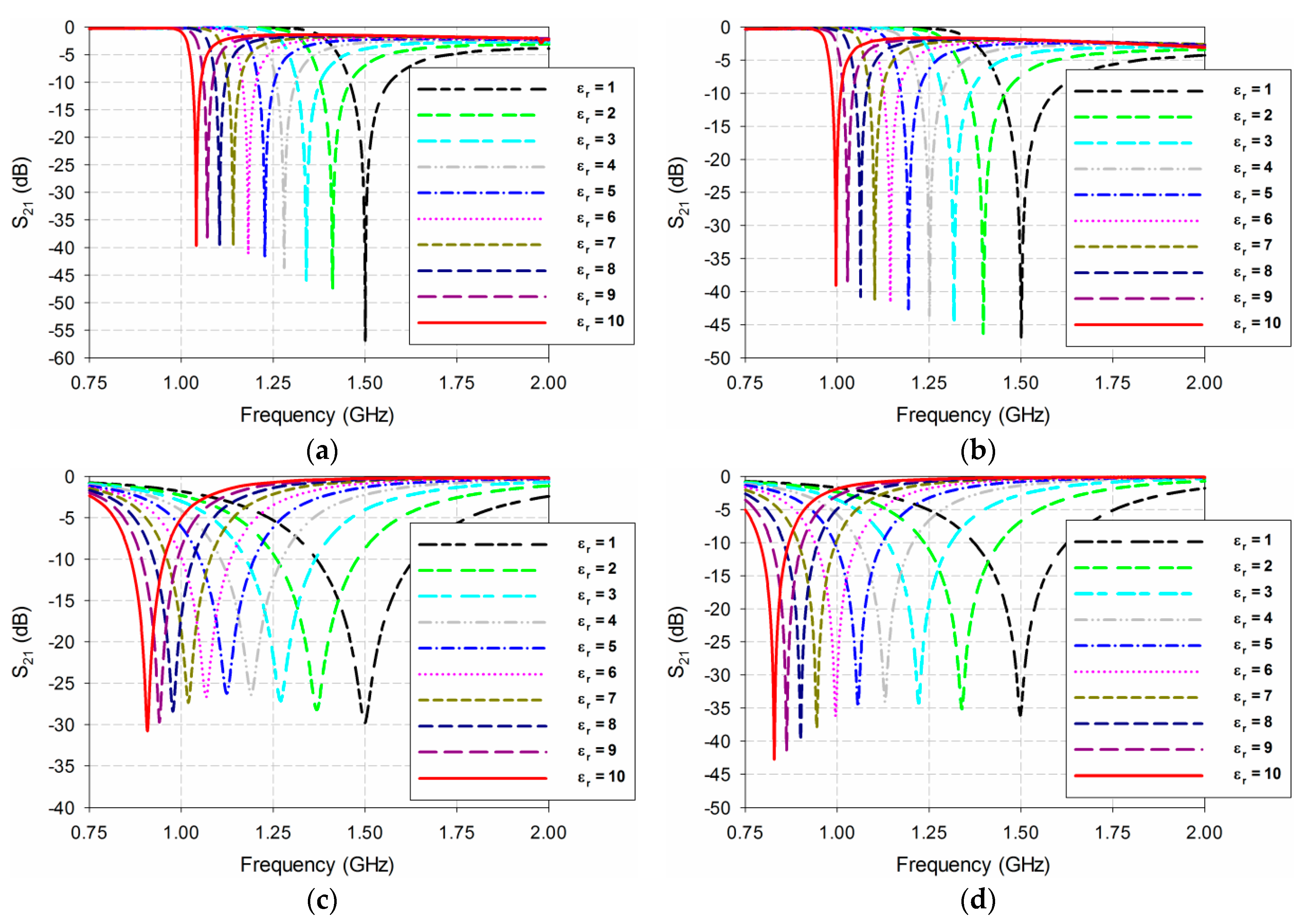
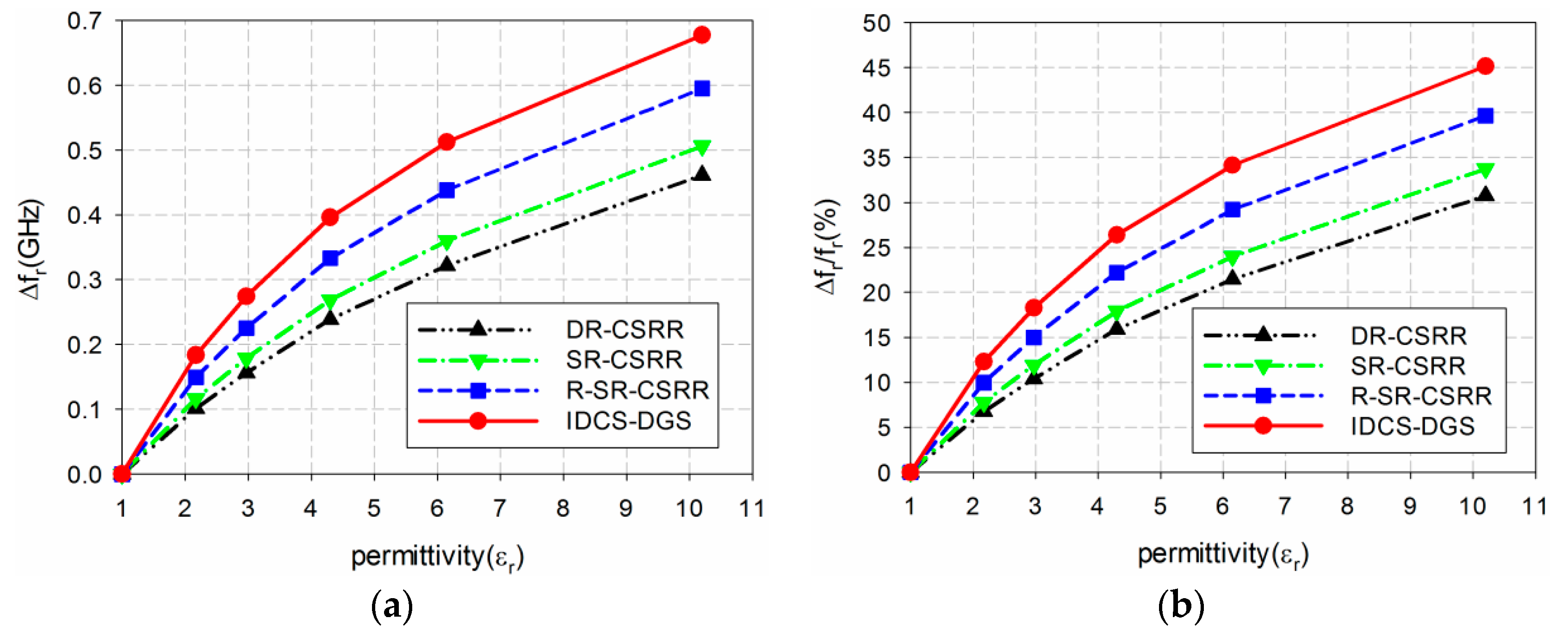
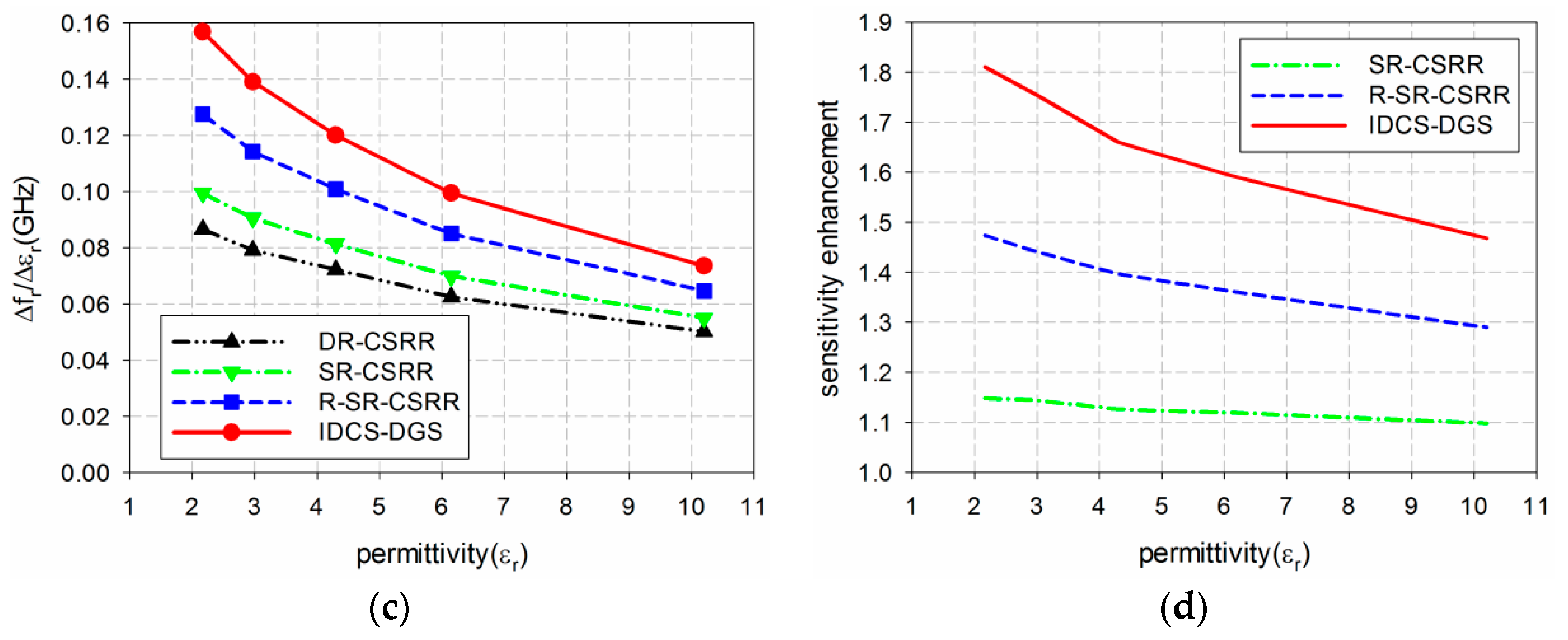
2. Sensor Design and Sensitivity Comparison

Figure 1 shows the four different resonator shapes that were considered for the sensitivity comparison. The dark gray regions corresponded to the conductive parts on the ground plane of a microstrip transmission line, whereas the white regions corresponded to the etched-out parts. The performance of the proposed IDCS-DGS was compared with that of a conventional DR-CSRR, SR-CSRR, and R-SR-CSRR. The four sensors were designed to resonate at 1.5 GHz to measure the dielectric property at a common frequency, because the permittivity of a material is dispersive as a function of frequency. The dimensions of the four resonators were scaled for operating at 1.5 GHz with the same slot width of 0.5 mm. The resonant frequencies of the four sensors were different because the geometric shape and location of each resonator were all different from the viewpoint of microstrip excitation. In fact, the resonant frequency of the DR-CSRR-based sensor was the lowest among the four when the outer dimensions were the same.
Figure 2 shows the structure, electric-field distribution, and S-parameter characteristics of the DR-CSRR-based permittivity sensor. A microstrip line with a width of wf = 1.68 mm was printed on an RF-35 substrate (εr = 3.5, tan δ = 0.0018, h = 0.76 mm) in order to match the 50-ohm characteristic input impedance. The width and length of the ground plane were W = 50 mm and L = 100 mm, respectively. The MUT was placed below the ground plane for loaded conditions, as shown in Figure 2a. The DR-CSRR consisted of two square split ring slots, and its dimensions were selected as t1 = 0.5 mm, g1 = 0.5 mm, s1 = 0.5 mm, and d1 = 11.92 mm to make the transmission coefficient (S21) resonate at 1.5 GHz under unloaded conditions. The reflection coefficient (S11) had a reflection zero at 1.24 GHz and a maximum value at 1.5 GHz. It can be seen that the electric fields were spread over the double-ring slots. The DR-CSRR and SR-CSRR-loaded microstrip lines were considered as a one-dimensional epsilon-negative metamaterial, and the equivalent circuit of them could be modeled as a three-element shunt LC tank [29]. The shunt LC tank circuit consisted of a series LC resonator (L and C1) and a capacitance element (C2) connected in parallel. In this equivalent circuit, there existed two characteristic frequencies—reflection zero frequency and transmission zero frequency. The reflection zero frequency was given by the resonance condition of the whole tank circuit, whereas the transmission zero frequency was given by the resonance condition of the series LC circuits (L and C1). The reflection zero frequency could be removed by adding conducting patches beside the microstrip line to fully cover the aperture of the CSRR or making the aperture structure symmetric along the center of the microstrip line. Therefore, the reflection zero frequency disappeared in the R-SR-CSRR and IDCS-DGS-based sensors because resonator geometries were symmetric along the center of the microstrip line.
Figure 3 shows the structure, electric-field distribution, and S-parameter characteristics of the SR-CSRR-based permittivity sensor. The dimensions of the microstrip line and ground plane were the same as those for the DR-CSRR. The SR-CSRR was the outer square split ring slot of the DR-CSRR, and its dimensions for its S21 resonance at 1.5 GHz were chosen as t2 = 0.5 mm, g2 = 0.5 mm, and d2 = 16.2 mm. In this case, the behaviors of the S-parameters were similar to those of the DR-CSRR-based sensor, and the reflection zero of S11 appeared at 1.19 GHz. To resonate at 1.5 GHz, the outer dimensions of the SR-CSRR became larger compared to the DR-CSRR.
Figure 4 presents the structure, electric-field distribution, and S-parameter characteristics of the R-SR-CSRR-based permittivity sensor. The dimensions of the microstrip line and ground plane were the same as those for the DR-CSRR. The R-SR-CSRR was rotated 90 degrees counter-clockwise compared to the SR-CSRR and looked similar to a C-shaped aperture [30], and the S11 reflection zero frequency disappeared. Its dimensions for S21 resonance at 1.5 GHz were chosen as t3= 0.5 mm, g3 = 0.5 mm, and d3 = 19.1 mm. The electric-field distributions were mainly concentrated along the non-split parts of the R-SR-CSRR. To resonate at 1.5 GHz, the outer dimensions of the R-SR-CSRR were larger compared to the DR-CSRR and SR-CSRR.
Finally, Figure 5 shows the electric-field distribution and S-parameter characteristics of the proposed IDCS-DGS-based permittivity sensor. The dimensions of the microstrip line and ground plane were the same as those for the DR-CSRR. The proposed IDCS-DGS was designed by modifying the straight ridge structure of an H-shaped aperture into an interdigital-capacitor-shaped ridge [31], and its dimensions for S21 resonance at 1.5 GHz were chosen as t4 = 0.5 mm, t5 = 2 mm, g4 = 0.5 mm, g5 = 2 mm, and d4 = 13.63 mm. The geometric parameters of the proposed sensor were optimized for higher sensitivity through a parametric study. Note that the outer dimensions of the IDCS-DGS were reduced compared to the SR-CSRR and R-SR-CSRR. In this case, the S11 reflection zero frequency disappeared, similar to the R-SR-CSRR-based sensor. The electric-field distributions were mainly concentrated on the interdigital capacitor part and this concentration area was more distributed along the microstrip line compared to the other three sensors.
Next, the S21 characteristics of the four permittivity sensors were compared, as shown in Figure 6. The MUT was placed below the ground plane, and its permittivity (εr) was varied from 1 to 10 with a step of 1. In this case, the loss tangent of the MUT was set as 0 like in the lossless case. The width and length of the MUT were the same as those of the ground plane, and its thickness was chosen to be 1.6 mm because the greatest thickness of the substrates available from Taconic, which was used as the MUTs, was around 1.6 mm. For the DR-CSRR-based sensor, the resonance frequency of S21 moved from 1.5 GHz to 1.041 GHz when εr increased from 1 to 10, whereas it shifted from 1.5 GHz to 0.997 GHz for the SR-CSRR-based sensor. The resonant frequency of S21 moved further from 1.5 GHz to 0.908 GHz for the R-SR-CSRR-based sensor. Finally, for the proposed IDCS-DGS-based sensor, the resonance frequency shift was maximized from 1.5 GHz to 0.829 GHz. Table 1 summarizes the resonant frequencies of the S21 responses with different permittivities of the MUT for the four permittivity sensors.
The sensitivity of the four permittivity sensors was analyzed from the results shown in Figure 6 and Table 1. The shift in the resonant frequency (Δfr = fr_unloaded − fr_loaded) of S21 is plotted in Figure 7a. Figure 7b shows the percent relative frequency shift (Δfr/fr_unloaded(%)) of the four permittivity sensors. Next, the sensitivity of the sensors was defined as the ratio of the resonant frequency change to the permittivity change (S = Δfr/Δεr = |(fr_unloaded − fr_loaded)|/|(εr_unloaded − εr_loaded)|) [32], and is plotted in Figure 7c. Figure 7d presents the sensitivity enhancement of the SR-CSRR, R-SR-CSRR, and proposed IDCS-DGS-based sensors compared to the DR-CSRR-based sensor, which is the ratio of the sensitivity of the SR-CSRR, R-SR-CSRR, and proposed IDCS-DGS-based sensors to that of the DR-CSRR-based sensor (S_SR-CSRR,R-SR-CSRR,IDCS-DGS/S_DR-CSRR). When the MUT was loaded below the ground plane, it affected the total capacitance related to the resonators etched on the ground plane and the S21 resonant frequency was a nonlinear function of the resonator related capacitance [20]. It was observed that the sensitivity was not constant as a function of the permittivity, and it became higher for the smaller value of the permittivity. In other words, the sensitivity of the sensors decreased monotonically when the permittivity increased.
For example, when the permittivity of the MUT was εr = 2, the resonant frequency shifts Δfr of the DR-CSRR, SR-CSRR, R-SR-CSRR, and proposed IDCS-DGS-based permittivity sensors were 0.088 GHz, 0.102 GHz, 0.131 GHz, and 0.161 GHz, whereas the percent relative frequency shifts Δfr/fr_unloaded (%) were 5.9%, 6.8%, 8.75%, and 10.8%, respectively. In this case, the sensitivity was the same as the resonant frequency shift because the difference in the permittivity (Δεr) was 1. The sensitivity of the SR-CSRR, R-SR-CSRR, and proposed IDCS-DGS-based sensors increased to 1.16, 1.50, and 1.84 times higher compared to the DR-CSRR-based sensor, as shown in Figure 7d.
However, when the permittivity of the MUT was increased to εr = 10, the resonant frequency shifts Δfr of the DR-CSRR, SR-CSRR, R-SR-CSRR, and proposed IDCS-DGS-based permittivity sensors were 0.459 GHz, 0.503 GHz, 0.592 GHz, and 0.671 GHz, whereas the percent relative frequency shifts Δfr/fr_unloaded (%) were 30.6%, 33.6%, 39.5%, and 44.8%, respectively. The sensitivities of the DR-CSRR, SR-CSRR, R-SR-CSRR, and proposed IDCS-DGS-based sensors were 0.051 GHz, 0.056 GHz, 0.066 GHz, and 0.075 GHz. The sensitivity enhancements of the SR-CSRR, R-SR-CSRR, and proposed IDCS-DGS-based sensors were 1.10, 1.29, and 1.46 compared to the DR-CSRR-based sensor. We can conclude that the sensitivity of the proposed IDCS-DGS-based sensor was moderately higher than that of the conventional DR- and SR-CSRR-based sensors.

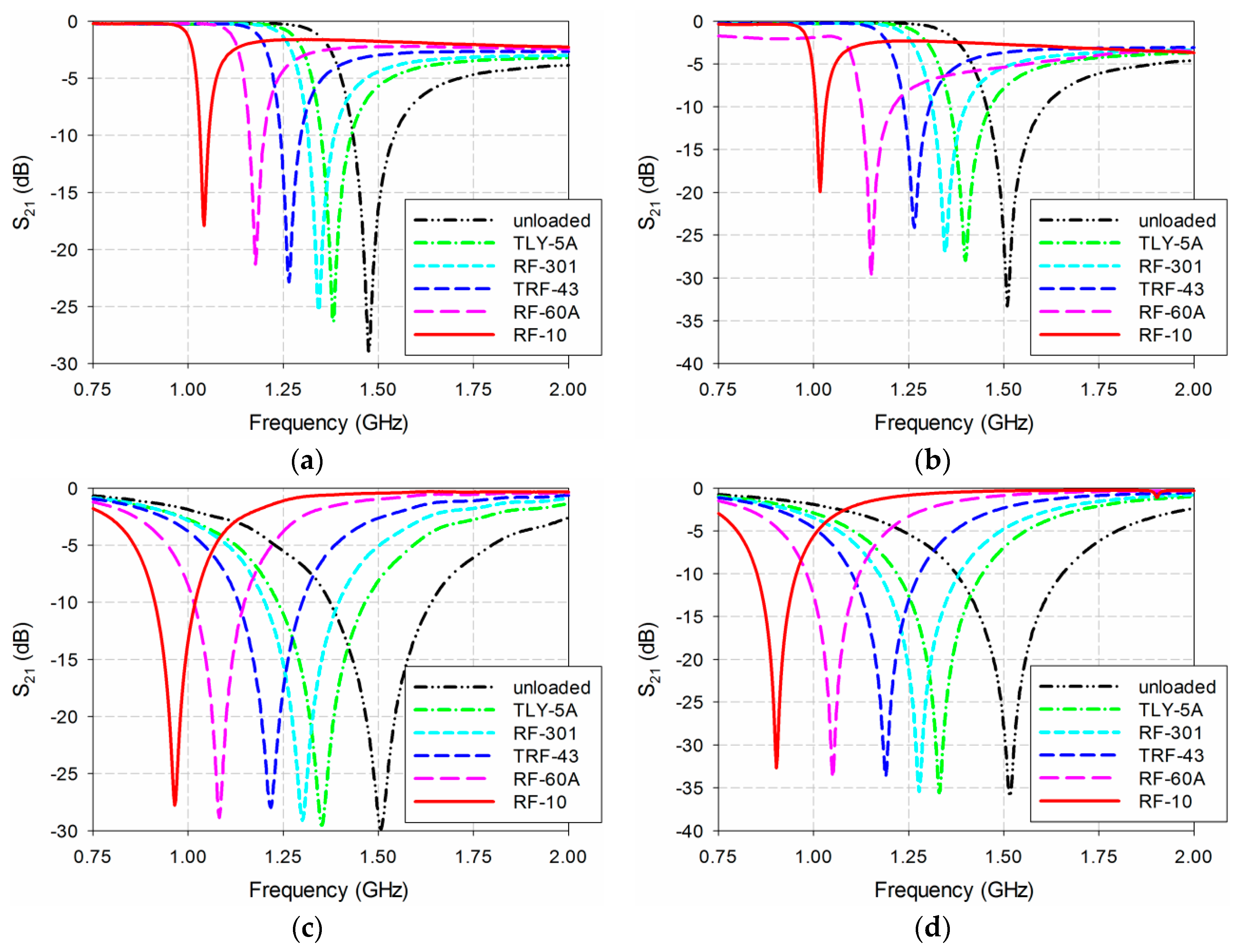
3. Experiment Results and Discussion

Prototypes of the four permittivity sensors described in the previous section were fabricated on an RF-35 substrate (εr = 3.5, tan δ = 0.0018, h = 0.76 mm), as shown in Figure 8. The S-parameter characteristics of the fabricated sensors were measured using an Agilent N5230A network analyzer, and a photograph of the experimental setup is shown in Figure 9. Five different standard dielectric MUTs from Taconic were tested for the sensitivity comparison. The MUTs had permittivity values ranging from 2.17 to 10.2, and their permittivity, loss tangent, and thickness from the data sheet [33] are summarized in Table 2.
The S21 characteristics of the four permittivity sensors were first simulated again with the five MUTs in Table 2 placed below the ground plane, as shown in Figure 10. The length of the MUTs was slightly reduced to 90 mm because there existed two protruding parts in the SMA connectors for soldering in the two ports of the fabricated sensors, as shown in Figure 9b. For the DR-CSRR-based sensor, the resonant frequency of S21 moved from 1.399 GHz for TLY-5A (εr = 2.17) to 1.039 GHz for RF-10 (εr = 10.2). In the case of the SR-CSRR-based sensor, the frequency shifted from 1.384 GHz for TLY-5A to 0.994 GHz for RF-10. For the R-SR-CSRR-based sensor, the resonant frequency of S21 moved from 1.351 GHz for TLY-5A to 0.905 GHz for RF-10, while it shifted from 1.317 GHz to 0.823 GHz for the proposed sensor. Table 3 shows the resonant frequencies of the simulated S21 responses for the four permittivity sensors.
Figure 11 compares the sensitivity of the four permittivity sensors when five MUTs are loaded. When TLY-5A (εr = 2.17) was used as the MUT, the resonant frequency shifts Δfr of the DR-CSRR, SR-CSRR, R-SR-CSRR, and proposed sensors were 0.101 GHz, 0.116 GHz, 0.149 GHz, and 0.183 GHz, and the percent relative frequency shifts Δfr/fr_unloaded (%) were 6.8%, 7.8%, 10.0%, and 12.3%, respectively. The sensitivities of the DR-CSRR, SR-CSRR, R-SR-CSRR, and proposed IDCS-DGS-based sensors were 0.087 GHz, 0.099 GHz, 0.128 GHz, and 0.157 GHz. The sensitivity enhancements of the SR-CSRR, R-SR-CSRR, and proposed IDCS-DGS-based sensors were 1.15, 1.47, and 1.81 compared to the DR-CSRR-based sensor. When RF-10 (εr = 10.2) was used as the MUT, the respective Δfr values were 0.461 GHz, 0.506 GHz, 0.595 GHz, and 0.677 GHz, and the values of Δfr/fr_unloaded (%) were 30.8%, 33.8%, 39.7%, and 45.2%. The sensitivities of the DR-CSRR, SR-CSRR, R-SR-CSRR, and proposed IDCS-DGS-based sensors were 0.050 GHz, 0.055 GHz, 0.065 GHz, and 0.074 GHz. The sensitivity enhancements of the SR-CSRR, R-SR-CSRR, and proposed IDCS-DGS-based sensors were 1.10, 1.29, and 1.47 compared to the DR-CSRR-based sensor. Therefore, the trends of Δfr, Δfr/fr_unloaded (%), sensitivity, and sensitivity enhancement were similar to those of the lossless case in Figure 6, and the only difference was the loss tangent. Since the loss tangent of the MUT mainly influences the magnitude level and quality factor of the S21 characteristics of the sensors [22] and the loss tangent of the MUTs is relatively low—ranging from 0.0009 to 0.0035—, the effect of the loss tangent on the S21 resonant frequencies would be relatively insignificant.
Next, the simulated sensitivity of the four sensors was validated by measuring their S21 characteristics when the five MUTs in Table 2 were placed below the ground plane, as shown in Figure 12. The length of the MUTs was slightly reduced to 90 mm. For the unloaded case, the S21 resonant frequencies of the DR-CSRR, SR-CSRR, R-SR-CSRR, and proposed IDCS-DGS sensors were 1.475 GHz, 1.510 GHz, 1.508 GHz, and 1.518 GHz, respectively, which were close to the simulated resonant frequency of 1.5 GHz. The respective errors compared to the simulated resonant frequency for the unloaded case were 1.7%, 0.7%, 0.5%, and 1.2%, which might have been caused by errors in fabrication and measurement.
For the DR-CSRR-based sensor, the resonant frequency of S21 moved from 1.383 GHz for TLY-5A to 1.043 GHz for RF-10, while it moved from 1.400 GHz for TLY-5A to 1.018 GHz for RF-10 for the SR-CSRR-based sensor. For the R-SR-CSRR-based sensor, the resonant frequency of S21 moved from 1.353 GHz for TLY-5A to 0.965 GHz for RF-10. Finally, the frequency shifted from 1.333 GHz to 0.903 GHz for the proposed IDCS-DGS-based sensor. Table 4 summarizes these results.
The measured sensitivity of the four permittivity sensors is compared in Figure 13a,b. The measured resonant frequency shifts Δfr of the DR-CSRR, SR-CSRR, R-SR-CSRR, and proposed IDCS-DGS sensors for TLY-5A MUT were 0.093 GHz, 0.110 GHz, 0.155 GHz, and 0.185 GHz, while the measured percent relative frequency shifts Δfr/fr_unloaded (%) were 6.2%, 7.3%, 10.3%, and 12.2%, respectively. The measured enhancement in sensitivity for TLY-5A was 5.9%. The sensitivities of the DR-CSRR, SR-CSRR, R-SR-CSRR, and proposed IDCS-DGS-based sensors were 0.079 GHz, 0.094 GHz, 0.133 GHz, and 0.158 GHz. The sensitivity enhancements of the SR-CSRR, R-SR-CSRR, and proposed IDCS-DGS-based sensors were 1.19, 1.68, and 2.00 compared to the DR-CSRR-based sensor. When RF-10 was used as the MUT, the resonant frequency shifts Δfr of the DR-CSRR, SR-CSRR, R-SR-CSRR, and proposed IDCS-DGS sensors were 0.433 GHz, 0.493 GHz, 0.543 GHz, and 0.615 GHz, while the percent relative frequency shifts Δfr/fr_unloaded (%) were 29.8%, 32.6%, 36.0%, and 40.5%, respectively. The sensitivities of the DR-CSRR, SR-CSRR, R-SR-CSRR, and proposed IDCS-DGS-based sensors were 0.047 GHz, 0.054 GHz, 0.059 GHz, and 0.067 GHz. The sensitivity enhancements of the SR-CSRR, R-SR-CSRR, and proposed IDCS-DGS-based sensors were 1.14, 1.25, and 1.42 compared to the DR-CSRR-based sensor.
The differences in the measured and simulated percent relative frequency shift Δfr/fr_unloaded (%) for the low permittivity MUT of TLY-5A were low at 0.1% to 0.5%, but the differences increased to 1.0% to 4.7% for RF-10, which has a high permittivity. The reason for the error in the permittivity value for RF-10 increasing compared to that for TLY-5A could be measurement error such as imperfect contact or a small air gap when the MUT was placed below the ground plane of the sensors. In other words, an air gap between the ground plane and the MUT causes a relatively large error for high permittivity [22].

4. Conclusions

A high-sensitivity planar microwave sensor based on an IDCS-DGS has been designed, fabricated, and tested for permittivity characterization at 1.5 GHz. The sensitivity of the proposed sensor was systematically compared with that of conventional CSRR-based sensors using five MUTs from Taconic. The measured sensitivity of the proposed sensor was two times higher for TLY-5A (εr = 2.17) and 1.42 times higher for RF-10 (εr = 10.2) compared to the conventional DR-CSRR-based sensor. The proposed high-sensitivity microwave sensor is expected to be used for the permittivity characterization of planar solid and microfluidic liquid materials or for wireless sensing of biological samples. It also might be applicable as an environmental sensing unit for chipless radio frequency identification (RFID) sensors for measuring temperature, humidity, and other characteristics.

Author Contributions

J.Y. contributed the idea, simulation, analysis, and the overall research. J.-I.L. contributed to the fabrication and measurement processes.

Funding

This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2018R1D1A1B07046040).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Saeed, K.; Shafique, M.F.; Byrne, M.B.; Hunter, I.C. Planar microwave sensors for complex permittivity characterization of materials and their applications. In Applied Measurement System; Haq, M.Z., Ed.; INTECH: Rijeka, Croatia, 2012. [Google Scholar]
  2. Boybay, M.S.; Ramahi, O.M. Material characterization using complementary split-ring resonators. IEEE Trans. Instrum. Meas. 2012, 61, 3039–3046. [Google Scholar] [CrossRef]
  3. Nicolson, A.; Ross, G. Measurement of the intrinsic properties of materials by time domain techniques. IEEE Trans. Instrum. Meas. 1970, 19, 377–382. [Google Scholar] [CrossRef]
  4. Weir, W. Automatic measurement of complex dielectric constant and permeability at microwave frequencies. Proc. IEEE 1974, 62, 33–36. [Google Scholar] [CrossRef]
  5. Baker-Jarvis, J.; Vanzura, E.; Kissick, W. Improved technique for determining complex permittivity with the transmission/reflection method. IEEE Trans. Microw. Theory Tech. 1990, 38, 1096–1103. [Google Scholar] [CrossRef] [Green Version]
  6. Varadan, V.V.; Hollinger, R.; Ghodgaonkar, D.; Varadan, V.K. Free-space, broadband measurements of high-temperature, complex dielectric properties at microwave frequencies. IEEE Trans. Instrum. Meas. 1991, 40, 842–846. [Google Scholar] [CrossRef]
  7. Akhter, Z.; Akhtar, M.J. Free-Space Time Domain Position Insensitive Technique for Simultaneous Measurement of Complex Permittivity and Thickness of Lossy Dielectric Samples. IEEE Trans. Instrum. Meas. 2016, 65, 2394–2405. [Google Scholar] [CrossRef]
  8. Athey, T.; Stuchly, M.; Stuchly, S. Measurement of radio frequency permittivity of biological tissues with an open ended coaxial line: Part I. IEEE Trans. Microw. Theory Tech. 1982, 30, 82–86. [Google Scholar] [CrossRef]
  9. Grant, J.P.; Clarke, R.N.; Symm, G.T.; Spyrou, N.M. A critical study of the open-ended coaxial line sensor for RF and microwave complex permittivity measurements. J. Phys. E Sci. Instrum. 1989, 22, 757–770. [Google Scholar] [CrossRef]
  10. Raj, A.; Holmes, W.; Judah, S. Wide bandwidth measurement of complex permittivity of liquids using coplanar lines. IEEE Trans. Instrum. Meas. 2001, 50, 905–909. [Google Scholar] [CrossRef]
  11. Hinojosa, J. S-parameter broad-band measurements on-microstrip and fast extraction of the substrate intrinsic properties. IEEE Microw. Wireless Compon. Lett. 2001, 11, 305–307. [Google Scholar] [CrossRef]
  12. Mathew, K.T.; Raveendranath, U. Waveguide cavity perturbation method for measuring complex permittivity of water. Microw. Opt. Technol. Lett. 1993, 6, 104–106. [Google Scholar] [CrossRef]
  13. Raveendranath, U.; Bijukumar, S.; Matthew, K. Broadband coaxial cavity resonator for complex permittivity measurements of liquids. IEEE Trans. Instrum. Meas. 2000, 49, 1305–1312. [Google Scholar] [CrossRef] [Green Version]
  14. Saeed, K.; Pollard, R.D.; Hunter, I.C. Substrate integrated waveguide cavity resonators for complex permittivity characterization of materials. IEEE Trans. Microw. Theory Tech. 2008, 56, 2340–2347. [Google Scholar] [CrossRef]
  15. Fratticcioli, E.; Dionigi, M.; Sorrentino, R. A simple and low-cost measurement system for the complex permittivity characterization of materials. IEEE Trans. Instrum. Meas. 2004, 53, 1071–1077. [Google Scholar] [CrossRef]
  16. Withayachumnankul, W.; Jaruwongrungsee, K.; Adisorn, T.; Fumeaux, C.; Abbott, D. Metamaterial-based microfluidic sensor for dielectric characterization. Sens. Actuators A-Phys. 2013, 189, 233–237. [Google Scholar] [CrossRef] [Green Version]
  17. T, M.S.K.; Ansari, M.A.H.; Jha, A.K.; Akhtar, M.J. Design of SRR-based microwave sensor for characterization of magnetodielectric substrates. IEEE Microw. Compon. Lett. 2017, 27, 524–526. [Google Scholar]
  18. Sha, K.T.M.; Jha, A.K.; Akhtar, M.J. Improved planar resonant RF sensor for retrieval of permittivity and permeability of materials. IEEE Sens. J. 2017, 17, 5479–5486. [Google Scholar]
  19. Velez, P.; Su, L.; Grenier, K.; Mata-Contreras, J.; Dubuc, D.; Martin, F. Microwave microfluidic sensor based on a microstrip splitter/combiner configuration and split ring Resonators (SRRs) for dielectric characterization of liquids. IEEE Sens. J. 2017, 17, 6589–6598. [Google Scholar] [CrossRef]
  20. Ebrahimi, A.; Scott, J.; Ghorbani, K. Differential sensors using microstrip lines loaded with two split ring resonators. IEEE Sens. J. 2018, 18, 5786–5793. [Google Scholar] [CrossRef]
  21. Lee, C.S.; Yang, C.L. Thickness and permittivity measurement in multi-layered dielectric structures using complementary split-ring resonators. IEEE Sens. J. 2014, 14, 695–700. [Google Scholar] [CrossRef]
  22. Lee, C.S.; Yang, C.L. Complementary split-ring resonators for measuring dielectric constants and loss tangents. IEEE Microw. Wireless Compon. Lett. 2014, 24, 563–565. [Google Scholar] [CrossRef]
  23. Ebrahimi, A.; Withayachumnankul, W.; Al-Sarawi, S.; Abbott, D. High-sensitivity metamaterial-inspired sensor for microfluidic dielectric characterization. IEEE Sens. J. 2014, 14, 1345–1351. [Google Scholar] [CrossRef]
  24. Ansari, M.A.H.; Jha, A.K.; Akhtar, M.J. Design and application of the CSRR-based planar sensor for noninvasive measurement of complex permittivity. IEEE Sens. J. 2015, 15, 7181–7189. [Google Scholar] [CrossRef]
  25. Yang, C.L.; Lee, C.S.; Chen, K.W.; Chen, K.Z. Noncontact measurement of complex permittivity and thickness by using planar resonators. IEEE Trans. Microw. Theory Tech. 2016, 64, 247–257. [Google Scholar] [CrossRef]
  26. Su, L.; Mata-Contreras, J.; Naqui, J.; Martín, F. Splitter/combiner microstrip sections loaded with pairs of complementary split ring resonators (CSRRs): Modeling and optimization for differential sensing applications. IEEE Trans. Microw. Theory Tech. 2016, 64, 4362–4370. [Google Scholar] [CrossRef]
  27. Su, L.; Mata-Contreras, J.; Vélez, P.; Fernández-Prieto, A. Analytical method to estimate the complex permittivity of oil samples. Sensors 2018, 18, 984. [Google Scholar] [CrossRef]
  28. Ansari, M.A.H.; Jha, A.K.; Akhter, Z.; Akhtar, M.J. Multi-band RF planar sensor using complementary split ring resonator for testing of dielectric materials. IEEE Sens. J. 2018, 18, 6596–6606. [Google Scholar] [CrossRef]
  29. Li, C.; Li, F. Characterization and modeling of a microstrip line loaded with complementary split-ring resonators (CSRRs) and its application to highpass filters. J. Phys. D Appl. Phys. 2007, 40, 3780–3787. [Google Scholar] [CrossRef]
  30. Shi, X.L.; Hesselink, L.; Thornton, R.L. Ultrahigh light transmission through a C-shaped nanoaperture. Opt. Lett. 2003, 28, 1320–1322. [Google Scholar] [CrossRef]
  31. Yoo, J.G.; Cho, Y.K.; Yeo, J.; Ko, J.H.; Kim, K.C. Design and experiment of miniaturized small resonant aperture using modified ridge structure. IEICE Electron. Express 2017, 14, 1–11. [Google Scholar] [CrossRef]
  32. Salim, A.; Lim, S. Complementary split-ring resonator-loaded microfluidic ethanol chemical sensor. Sensors 2016, 16, 1802. [Google Scholar] [CrossRef] [PubMed]
  33. Taconic PTFE laminates. Available online: http://www.taconic.co.kr/pages/sub02_03.php. (accessed on 14 January 2019).
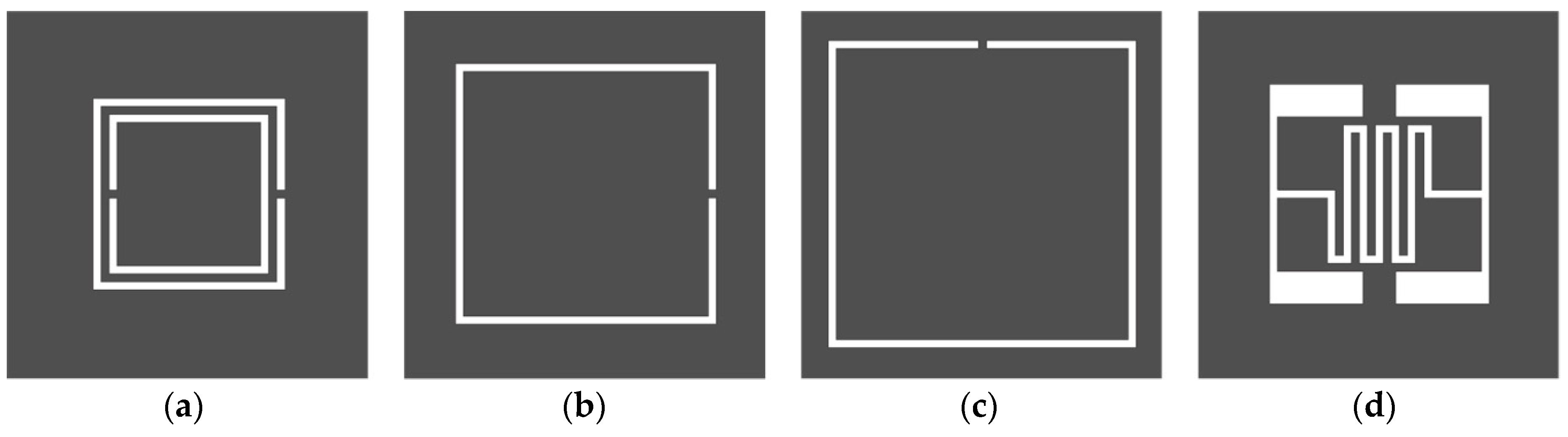
Sensors 19 00498 g001 550
Figure 1. Four different resonator shapes considered for sensitivity comparison: (a) double-ring complementary split ring resonator (DR-CSRR); (b) single-ring complementary split ring resonator (SR-CSRR); (c) rotated single-ring complementary split ring resonator (R-SR-CSRR); (d) interdigital-capacitor-shaped defected ground structure (IDCS-DGS).
Figure 1. Four different resonator shapes considered for sensitivity comparison: (a) double-ring complementary split ring resonator (DR-CSRR); (b) single-ring complementary split ring resonator (SR-CSRR); (c) rotated single-ring complementary split ring resonator (R-SR-CSRR); (d) interdigital-capacitor-shaped defected ground structure (IDCS-DGS).
Sensors 19 00498 g001
Sensors 19 00498 g002 550
Figure 2. DR-CSRR-based permittivity sensor: (a) structure; (b) electric-field distribution at 1.5 GHz; (c) S-parameter characteristics.
Figure 2. DR-CSRR-based permittivity sensor: (a) structure; (b) electric-field distribution at 1.5 GHz; (c) S-parameter characteristics.
Sensors 19 00498 g002
Sensors 19 00498 g003 550
Figure 3. SR-CSRR-based permittivity sensor: (a) structure; (b) electric-field distribution at 1.5 GHz; (c) S-parameter characteristics.
Figure 3. SR-CSRR-based permittivity sensor: (a) structure; (b) electric-field distribution at 1.5 GHz; (c) S-parameter characteristics.
Sensors 19 00498 g003
Sensors 19 00498 g004a 550Sensors 19 00498 g004b 550
Figure 4. R-SR-CSRR-based permittivity sensor: (a) structure; (b) electric-field distribution at 1.5 GHz; (c) S-parameter characteristics.
Figure 4. R-SR-CSRR-based permittivity sensor: (a) structure; (b) electric-field distribution at 1.5 GHz; (c) S-parameter characteristics.
Sensors 19 00498 g004aSensors 19 00498 g004b
Sensors 19 00498 g005 550
Figure 5. Proposed IDCS-DGS-based permittivity sensor: (a) structure; (b) electric-field distribution at 1.5 GHz; (c) S-parameter characteristics.
Figure 5. Proposed IDCS-DGS-based permittivity sensor: (a) structure; (b) electric-field distribution at 1.5 GHz; (c) S-parameter characteristics.
Sensors 19 00498 g005
Sensors 19 00498 g006 550
Figure 6. S21 characteristics of the four permittivity sensors for the varying permittivity of the material under test (MUT): (a) DR-CSRR; (b) SR-CSRR; (c) R-SR-CSRR; (d) proposed IDCS-DGS.
Figure 6. S21 characteristics of the four permittivity sensors for the varying permittivity of the material under test (MUT): (a) DR-CSRR; (b) SR-CSRR; (c) R-SR-CSRR; (d) proposed IDCS-DGS.
Sensors 19 00498 g006
Sensors 19 00498 g007 550
Figure 7. Sensitivity comparison of the four permittivity sensors: (a) frequency shift (Δfr (GHz)); (b) percent relative frequency shift (Δfr/fr (%)); (c) sensitivity(Δfr/Δεr (GHz)); (d) sensitivity enhancement compared to the DR-CSRR-based sensor.
Figure 7. Sensitivity comparison of the four permittivity sensors: (a) frequency shift (Δfr (GHz)); (b) percent relative frequency shift (Δfr/fr (%)); (c) sensitivity(Δfr/Δεr (GHz)); (d) sensitivity enhancement compared to the DR-CSRR-based sensor.
Sensors 19 00498 g007
Sensors 19 00498 g008 550
Figure 8. Photographs of the fabricated permittivity sensors: (a) DR-CSRR; (b) SR-CSRR; (c) R-SR-CSRR; (d) proposed IDCS-DGS.
Figure 8. Photographs of the fabricated permittivity sensors: (a) DR-CSRR; (b) SR-CSRR; (c) R-SR-CSRR; (d) proposed IDCS-DGS.
Sensors 19 00498 g008
Sensors 19 00498 g009 550
Figure 9. Experimental setup: (a) unloaded; (b) loaded.
Figure 9. Experimental setup: (a) unloaded; (b) loaded.
Sensors 19 00498 g009
Sensors 19 00498 g010 550
Figure 10. Simulated S21 characteristics of the four permittivity sensors for MUTs in Table 2: (a) DR-CSRR; (b) SR-CSRR; (c) R-SR-CSRR; (d) proposed IDCS-DGS.
Figure 10. Simulated S21 characteristics of the four permittivity sensors for MUTs in Table 2: (a) DR-CSRR; (b) SR-CSRR; (c) R-SR-CSRR; (d) proposed IDCS-DGS.
Sensors 19 00498 g010
Sensors 19 00498 g011a 550Sensors 19 00498 g011b 550
Figure 11. Simulated sensitivity comparison of the four permittivity sensors: (a) frequency shift (Δfr (GHz)); (b) percent relative frequency shift (Δfr/fr (%)); (c) sensitivity(Δfr/Δεr (GHz)); (d) sensitivity enhancement compared to the DR-CSRR-based sensor.
Figure 11. Simulated sensitivity comparison of the four permittivity sensors: (a) frequency shift (Δfr (GHz)); (b) percent relative frequency shift (Δfr/fr (%)); (c) sensitivity(Δfr/Δεr (GHz)); (d) sensitivity enhancement compared to the DR-CSRR-based sensor.
Sensors 19 00498 g011aSensors 19 00498 g011b
Sensors 19 00498 g012 550
Figure 12. Measured S21 characteristics of the four permittivity sensors for MUTs in Table 2: (a) DR-CSRR; (b) SR-CSRR; (c) R-SR-CSRR; (d) proposed IDCS-DGS.
Figure 12. Measured S21 characteristics of the four permittivity sensors for MUTs in Table 2: (a) DR-CSRR; (b) SR-CSRR; (c) R-SR-CSRR; (d) proposed IDCS-DGS.
Sensors 19 00498 g012
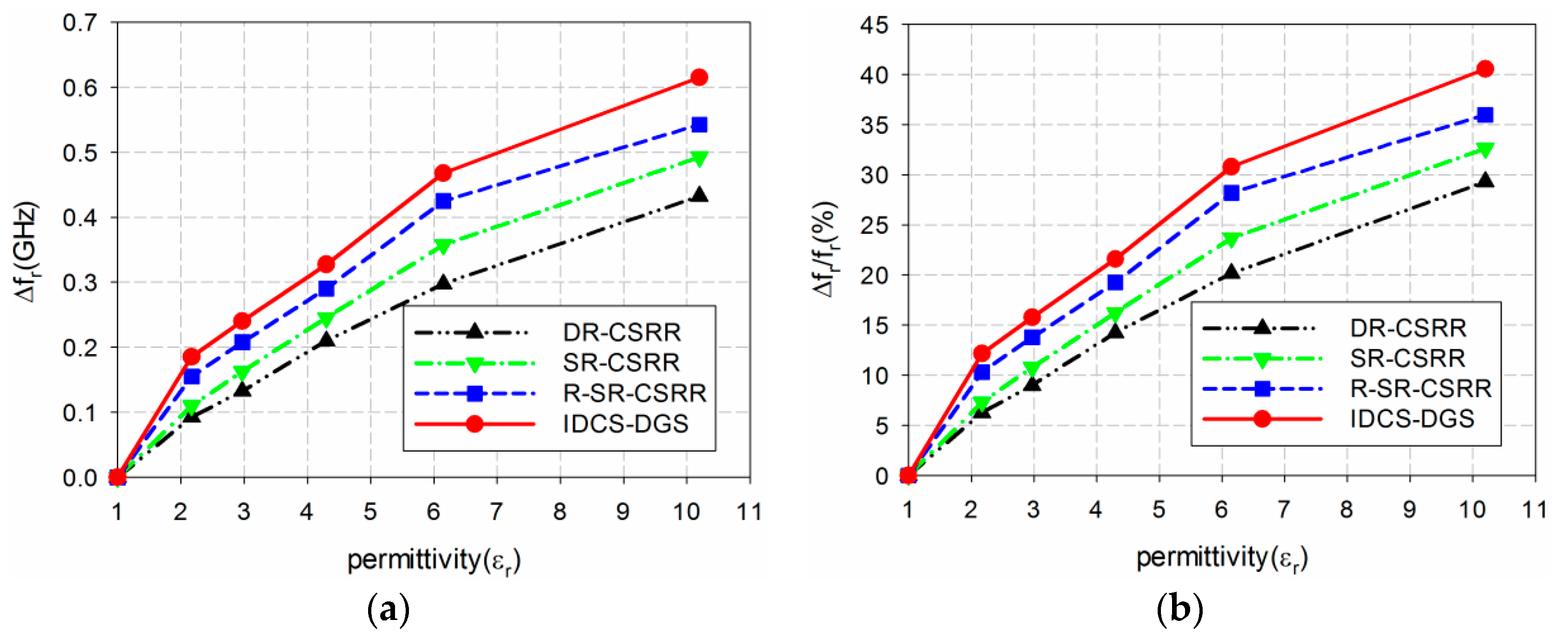
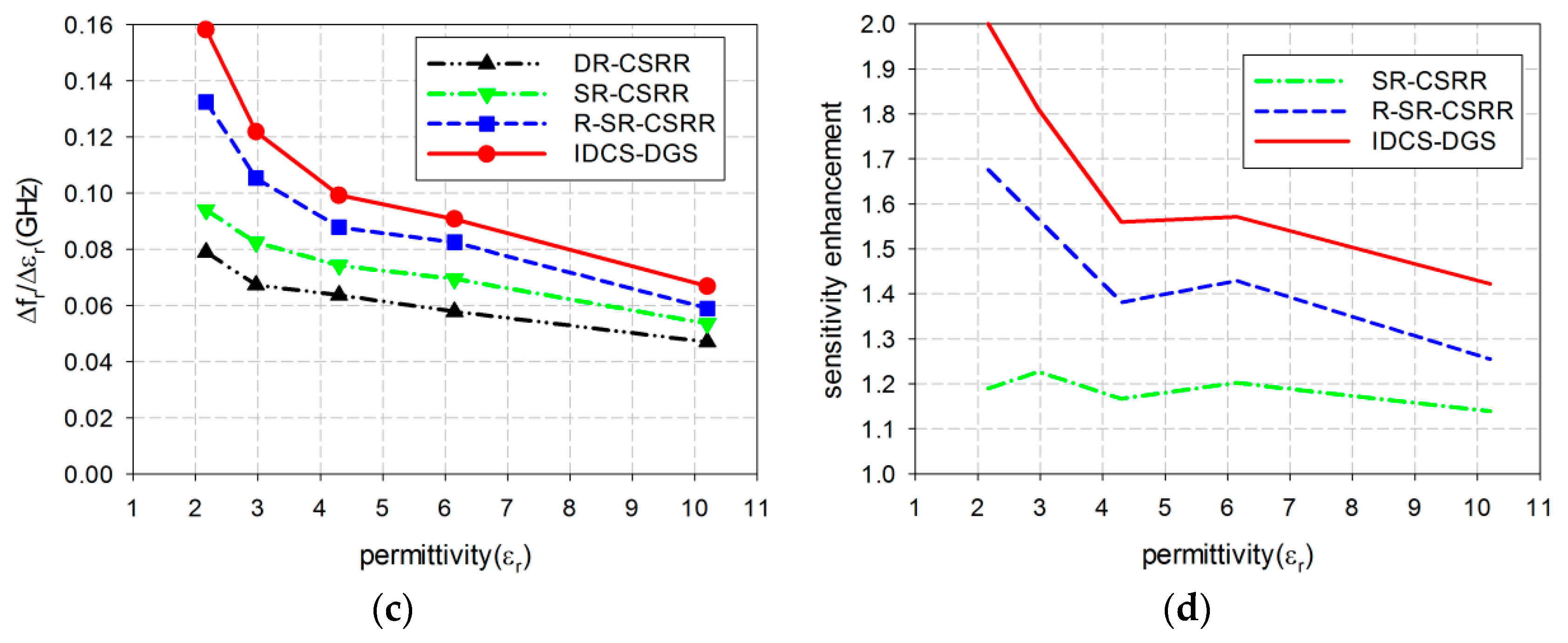
Sensors 19 00498 g013a 550Sensors 19 00498 g013b 550
Figure 13. Measured sensitivity comparison of the four permittivity sensors: (a) frequency shift (Δfr (GHz)); (b) percent relative frequency shift (Δfr/fr (%)); (c) sensitivity (Δfr/Δεr (GHz)); (d) sensitivity enhancement compared to the DR-CSRR-based sensor.
Figure 13. Measured sensitivity comparison of the four permittivity sensors: (a) frequency shift (Δfr (GHz)); (b) percent relative frequency shift (Δfr/fr (%)); (c) sensitivity (Δfr/Δεr (GHz)); (d) sensitivity enhancement compared to the DR-CSRR-based sensor.
Sensors 19 00498 g013aSensors 19 00498 g013b
Table
Table 1. Resonant frequencies of S21 responses for the four permittivity sensors in GHz.
Table 1. Resonant frequencies of S21 responses for the four permittivity sensors in GHz.
Sensor Typeεr = 1εr = 2εr = 3εr = 4εr = 5εr = 6εr = 7εr = 8εr = 9εr = 10
DR-CSSR1.51.4121.3401.2801.2281.1821.1421.1051.0711.041
SR-CSSR1.51.3981.3181.2511.1941.1451.1031.0641.0280.997
R-SR-CSSR1.51.3671.2701.1901.1241.0671.0190.9770.9410.908
Proposed IDCS-DGS1.51.3391.2221.1301.0560.9960.9450.9010.8630.829
Table
Table 2. Permittivity, loss tangent, and thickness of the five MUTs.
Table 2. Permittivity, loss tangent, and thickness of the five MUTs.
No.MUTεrtan δThickness
1TLY-5A2.17 ± 0.020.0009@10 GHz1.58 mm
2RF-3012.97 ± 0.07[email protected] GHz1.52 mm
3TRF-434.3 ± 0.150.0035@10 GHz1.63 mm
4RF-60A6.15 ± 0.150.0028@10 GHz1.52 mm
5RF-1010.2 ± 0.30.0025@10 GHz1.52 mm
Table
Table 3. Simulated resonant frequencies of S21 responses for the four permittivity sensors in GHz.
Table 3. Simulated resonant frequencies of S21 responses for the four permittivity sensors in GHz.
Sensor TypeUnloaded
(εr = 1)		TLY-5A
(εr = 2.17)		RF-301
(εr = 2.97)		TRF-43
(εr = 4.3)		RF-60A
(εr = 6.15)		RF-10
(εr = 10.2)
DR-CSSR1.51.3991.3441.2621.1781.039
SR-CSSR1.51.3841.3221.2321.140.994
R-SR-CSSR1.51.3511.2751.1671.0620.905
Proposed IDCS-DGS1.51.3171.2261.1040.9880.823
Table
Table 4. Measured resonant frequencies of S21 responses for the four permittivity sensors in GHz.
Table 4. Measured resonant frequencies of S21 responses for the four permittivity sensors in GHz.
Sensor TypeUnloaded
(εr = 1)		TLY-5A
(εr = 2.17)		RF-301
(εr = 2.97)		TRF-43
(εr = 4.3)		RF-60A
(εr = 6.15)		RF-10
(εr = 10.2)
DR-CSSR1.4751.3831.3431.2651.1781.043
SR-CSSR1.5101.4001.3481.2651.1531.018
R-SR-CSSR1.5081.3531.3001.2181.0830.965
Proposed IDCS-DGS1.5181.3331.2781.1901.0500.903

Share and Cite

MDPI and ACS Style

Yeo, J.; Lee, J.-I. High-Sensitivity Microwave Sensor Based on an Interdigital-Capacitor-Shaped Defected Ground Structure for Permittivity Characterization. Sensors 2019, 19, 498. https://doi.org/10.3390/s19030498

AMA Style

Yeo J, Lee J-I. High-Sensitivity Microwave Sensor Based on an Interdigital-Capacitor-Shaped Defected Ground Structure for Permittivity Characterization. Sensors. 2019; 19(3):498. https://doi.org/10.3390/s19030498

Chicago/Turabian Style

Yeo, Junho, and Jong-Ig Lee. 2019. "High-Sensitivity Microwave Sensor Based on an Interdigital-Capacitor-Shaped Defected Ground Structure for Permittivity Characterization" Sensors 19, no. 3: 498. https://doi.org/10.3390/s19030498

APA Style

Yeo, J., & Lee, J. -I. (2019). High-Sensitivity Microwave Sensor Based on an Interdigital-Capacitor-Shaped Defected Ground Structure for Permittivity Characterization. Sensors, 19(3), 498. https://doi.org/10.3390/s19030498

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop