Limits of the Effective Medium Theory in Particle Amplified Surface Plasmon Resonance Spectroscopy Biosensors
Abstract
1. Introduction
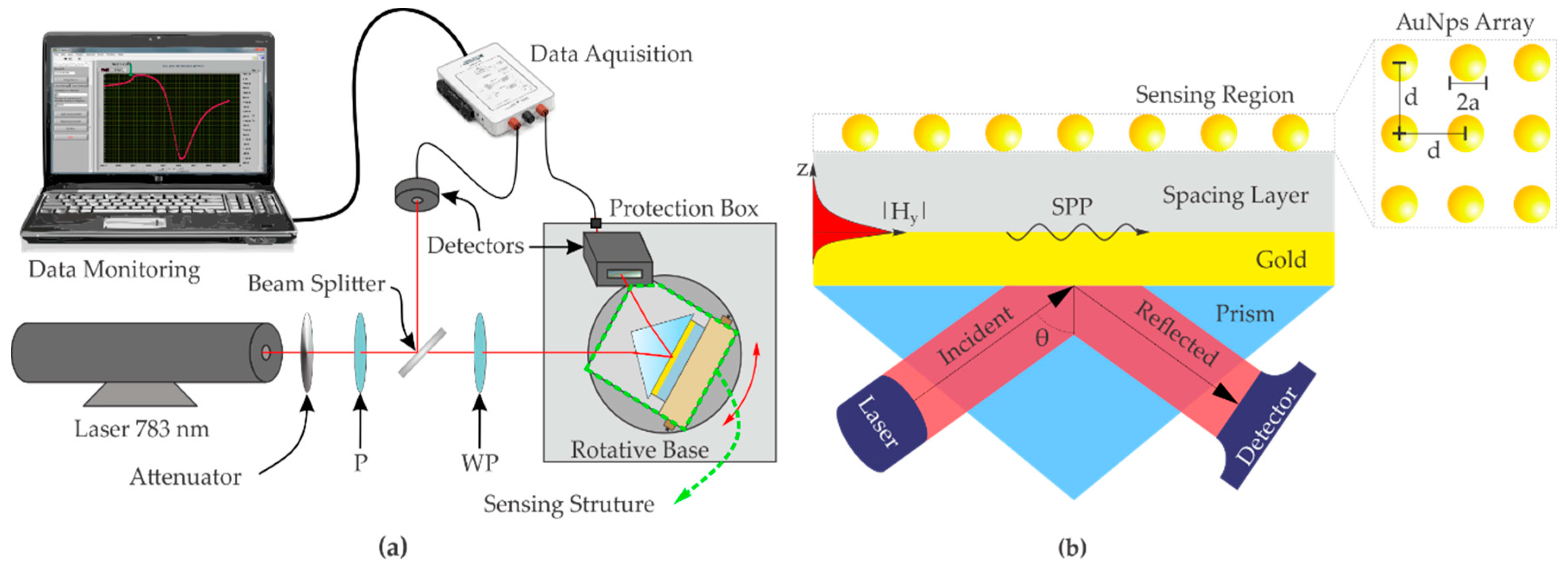
2. Materials and Methods
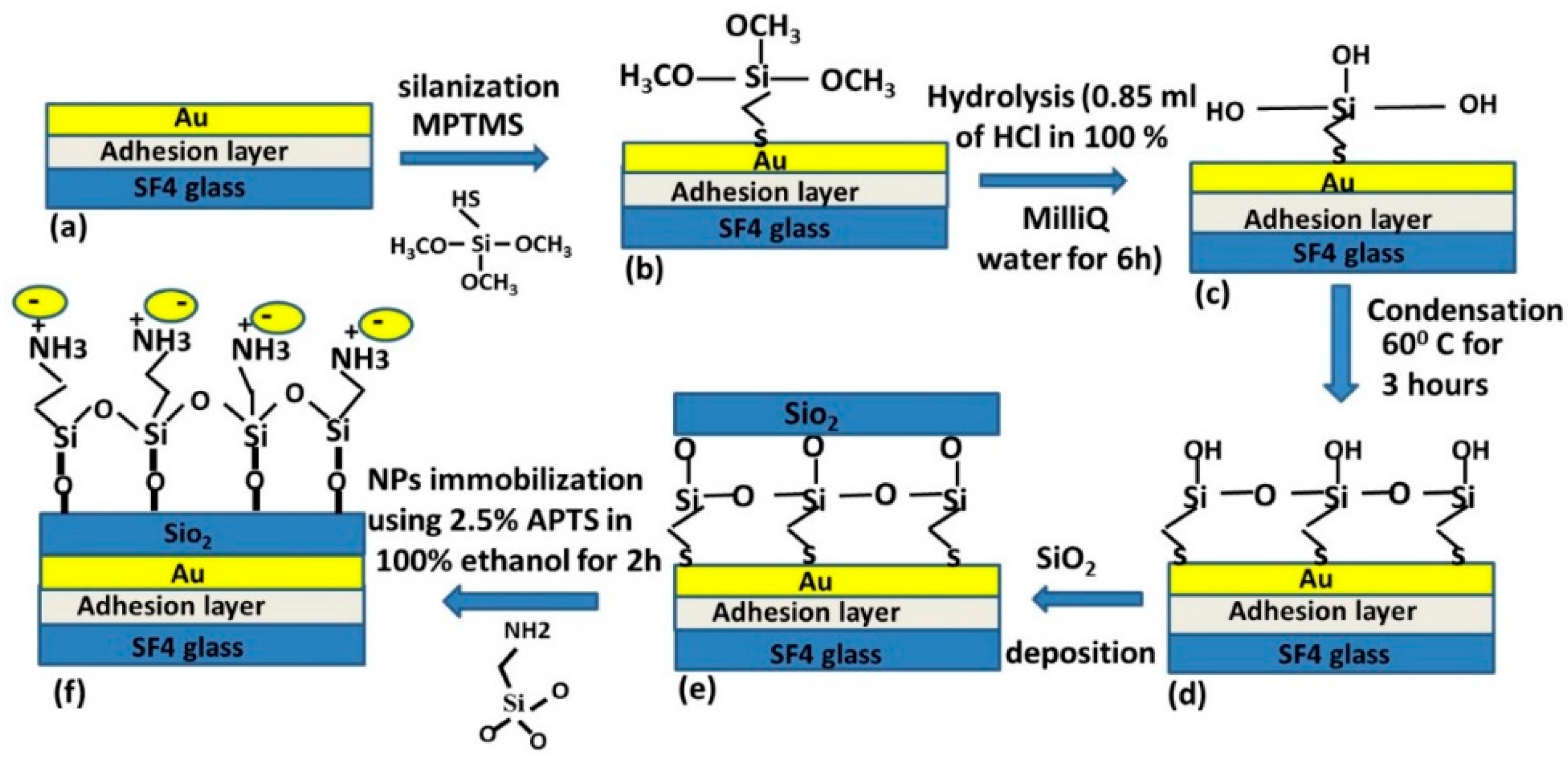
2.1. Fabrication and Working Principle of the Au/SiO2 Sensing Platforms
2.2. Morphological Characterization of the DLWGs and AuNPs Citrate Colloidal Solution
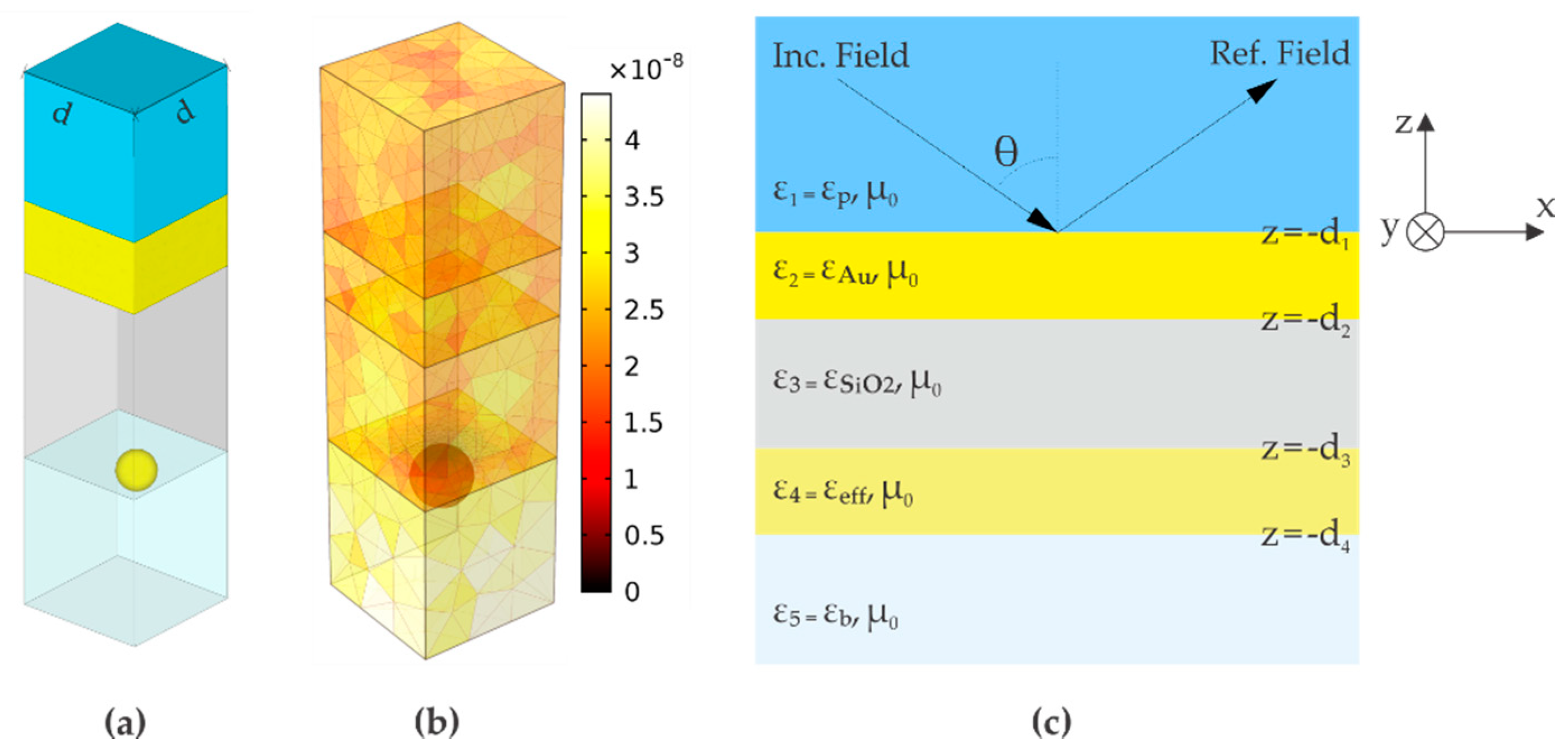
2.3. Theoretical Model
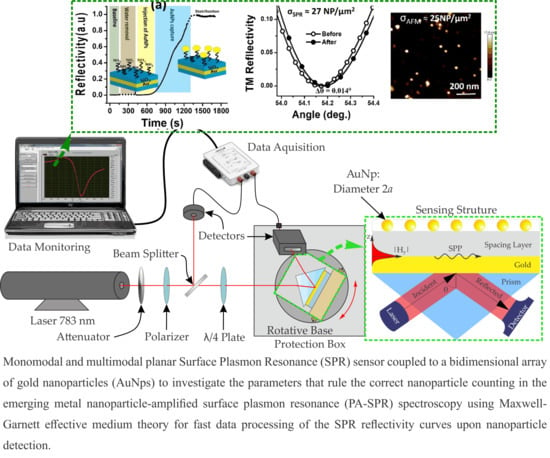
3. Results and Discussion
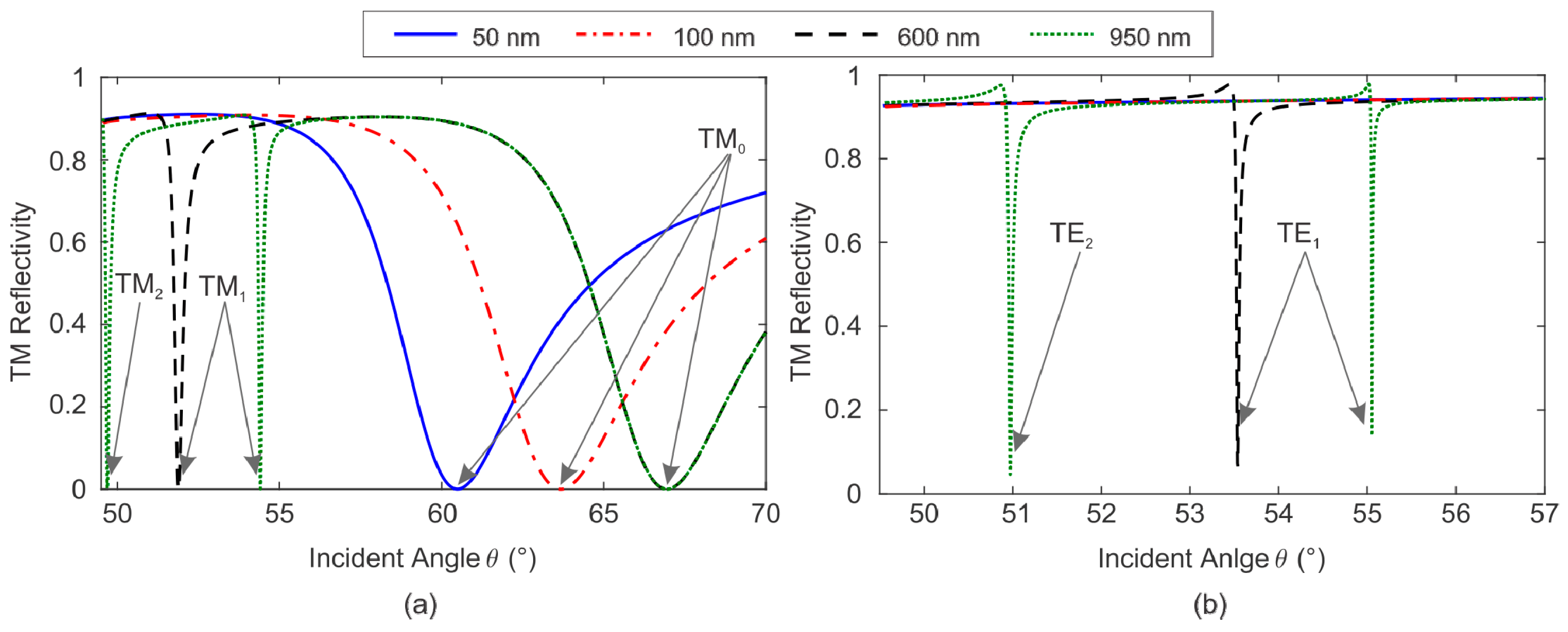
3.1. Modal Analysis
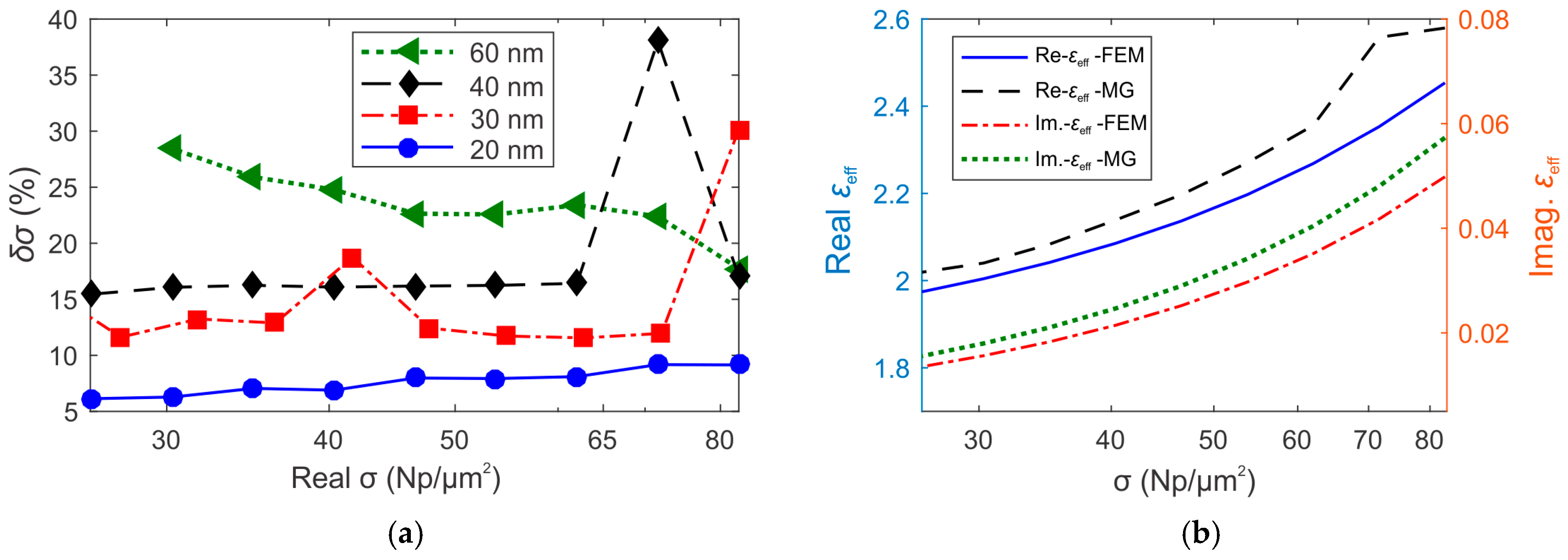
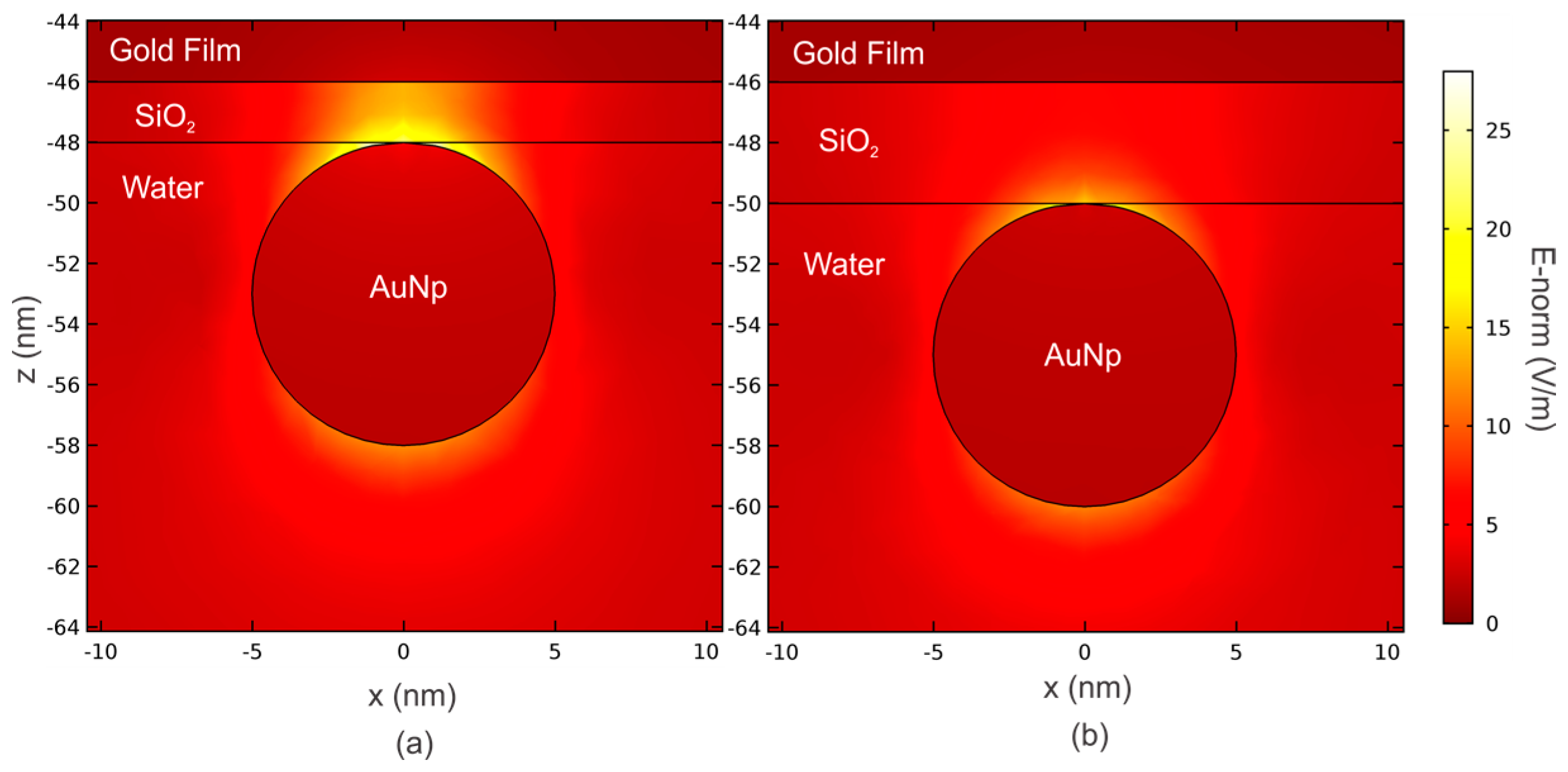
3.2. Parametric Analysis of Models
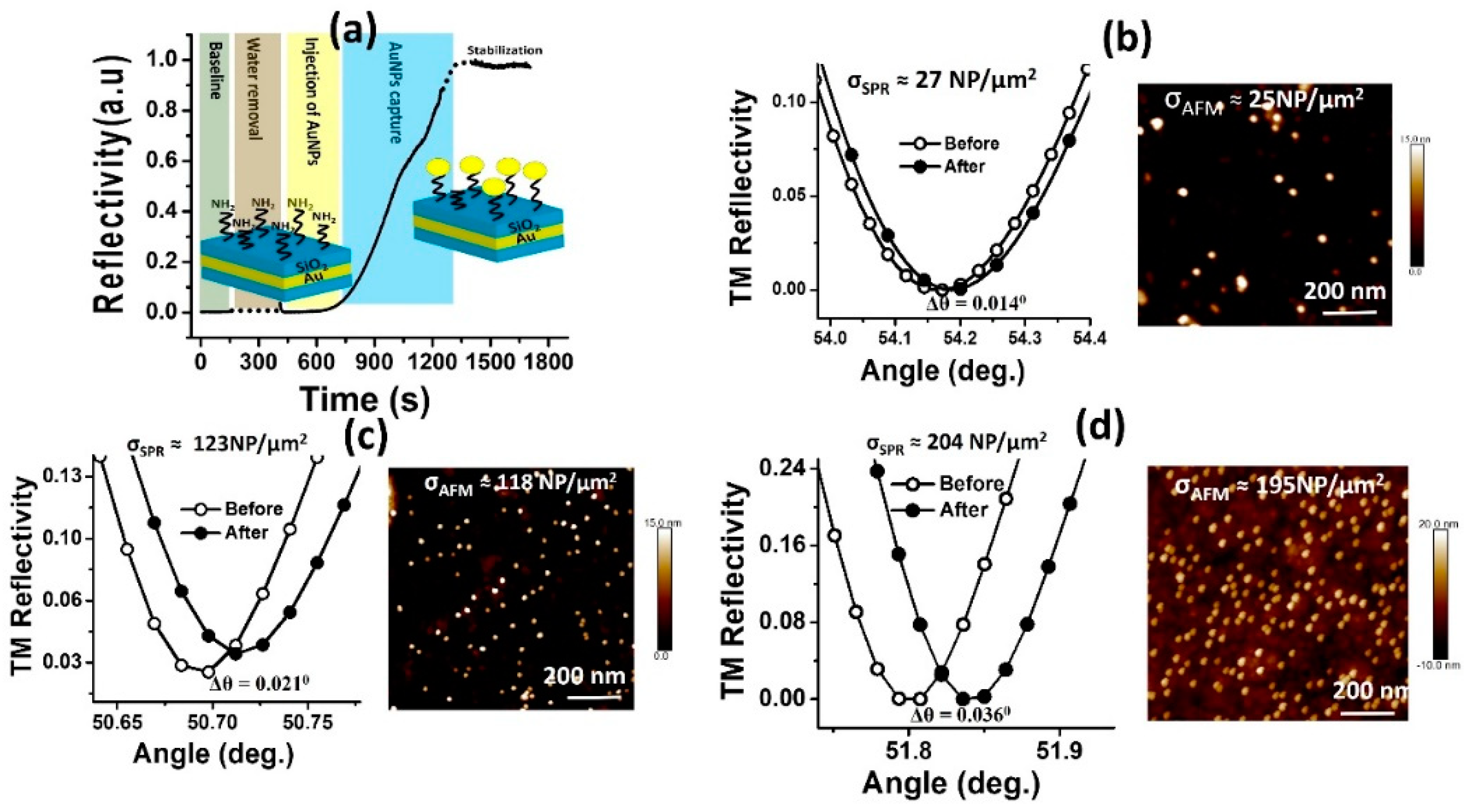
3.3. Experimental SPR AuNPs Counting
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Homola, J. Surface plasmon resonance sensors for detection of chemical and biological species. Chem. Rev. 2008, 108, 462–493. [Google Scholar] [CrossRef] [PubMed]
- Homola, J. Surface Plasmon Resonance Based Sensors. In Springer Series on Chemical Sensors and Biosensors; Wolfbeis, O.S., Ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2006; Volume 4, ISBN 978-3-642-07046-4. [Google Scholar]
- Nenninger, G.G.; Piliarik, M.; Homola, J. Data analysis for optical sensors based on spectroscopy of surface plasmons. J. Meas. Sci. Technol. 2002, 13. [Google Scholar] [CrossRef]
- O’Brien, M.J.; Pérez-Luna, V.H.; Brueck, S.R.J.; López, G.P. A surface plasmon resonance array biosensor based on spectroscopic imaging. Biosens. Bioelectron. 2001, 16, 97–108. [Google Scholar] [CrossRef]
- Ng, S.; Loo, F.; Wu, S.; Kong, S.; Wu, C.; Ho, H. Common-path spectral interferometry with temporal carrier for highly sensitive surface plasmon resonance sensing. Opt. Express 2013, 21, 20268–20273. [Google Scholar] [CrossRef] [PubMed]
- Piliarik, M.; Homola, J. Surface plasmon resonance (SPR) sensors: approaching their limits? Opt. Express 2009, 17, 16505–16517. [Google Scholar] [CrossRef] [PubMed]
- Golden, M.S.; Bjonnes, A.C.; Georgiadis, R.M. Distance- and wavelength-dependent dielectric function of au nanoparticles by angle-resolved surface plasmon resonance imaging. J. Phys. Chem. C 2010, 114, 8837–8843. [Google Scholar] [CrossRef]
- Salamon, Z.; Macleod, H.; Tollin, G. Coupled plasmon-waveguide resonators: a new spectroscopic tool for probing proteolipid film structure and properties. Biophys. J. 1997, 73, 2791–2797. [Google Scholar] [CrossRef]
- Grandidier, J.; Massenot, S.; des Francs, G.C.; Bouhelier, A.; Weeber, J.-C.; Markey, L.; Dereux, A.; Renger, J.; González, M.U.; Quidant, R. Dielectric-loaded surface plasmon polariton waveguides: Figures of merit and mode characterization by image and Fourier plane leakage microscopy. Phys. Rev. B 2008, 78, 245419. [Google Scholar] [CrossRef]
- Lyon, L.A.; Musick, M.D.; Natan, M.J. Colloidal au-enhanced surface plasmon resonance immunosensing. Anal. Chem. 1998, 70, 5177–5183. [Google Scholar] [CrossRef]
- He, L.; Smith, E.A.; Natan, M.J.; Keating, C.D. The distance-dependence of colloidal au-amplified surface plasmon resonance. J. Phys. Chem. B 2004, 108, 10973–10980. [Google Scholar] [CrossRef]
- Špringer, T.; Ermini, M.L.; Špačková, B.; Jabloňků, J.; Homola, J. Enhancing sensitivity of surface plasmon resonance biosensors by functionalized gold nanoparticles: Size matters. Anal. Chem. 2014, 86, 10350–10356. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Tamada, K.; Baba, A.; Knoll, W.; Hara, M. Estimation of dielectric function of biotin-capped gold nanoparticles via signal enhancement on surface plasmon resonance. J. Phys. Chem. B 2006, 110, 15755–15762. [Google Scholar] [CrossRef] [PubMed]
- He, L.; Musick, M.D.; Nicewarner, S.R.; Salinas, F.G.; Benkovic, S.J.; Natan, M.J.; Keating, C.D. Colloidal au-enhanced surface plasmon resonance for ultrasensitive detection of DNA hybridization. J. Am. Chem. Soc. 2000, 122, 9071–9077. [Google Scholar] [CrossRef]
- Scherbahn, V.; Nizamov, S.; Mirsky, V.M. Plasmonic detection and visualization of directed adsorption of charged single nanoparticles to patterned surfaces. Microchimica Acta 2016, 183, 2837–2845. [Google Scholar] [CrossRef] [PubMed]
- Choy, T.C. Effective Medium Theory: Principles and Applications, 2nd ed.; Oxford University Press: Oxford, UK, 2016; ISBN 9780191015182. [Google Scholar]
- Uchiho, Y.; Shimojo, M.; Furuya, K.; Kajikawa, K. Optical response of gold-nanoparticle-amplified surface plasmon resonance spectroscopy. J. Phys. Chem. C 2010, 114, 4816–4824. [Google Scholar] [CrossRef]
- Comsol Multiphysics Modeling Software. Available online: https://www.comsol.com (accessed on 2 November 2018).
- Shiohara, A.; Wang, Y.; Liz-Marzan, L.M. Recent Approaches toward creation of hot spots for SERS detection. J. Photochem. Photobiol. C 2014, 21, 2–25. [Google Scholar] [CrossRef]
- Margheri, G.; Trigari, S.; Sottini, S.; D’Agostino, R.; Del Rosso, T.; Del Rosso, M. The Binding of EGFR to GM1(3) Hosted in Lipid Raft-Like Biomembranes Insighted by Plasmonic Resonance Techniques. J. Sens. 2015, 2015. [Google Scholar] [CrossRef]
- Margheri, F.; Papucci, L.; Schiavone, N.; D’Agostino, R.; Trigari, S.; Serratì, S.; Laurenzana, A.; Biagioni, A.; Luciani, C.; Chillà, A.; Andreucci, E.; Del Rosso, T.; Margheri, G.; Del Rosso, M.; Fibbi, G. Differential uPAR recruitment in caveolar-lipid rafts by GM1 and GM3 gangliosides regulates endothelial progenitor cells angiogenesis. J. Cell. Mol. Med. 2015, 19, 113–123. [Google Scholar] [CrossRef]
- Del Rosso, T.; Sánchez, J.E.H.; Carvalho, R.D.S.; Pandoli, O.; Cremona, M. Accurate and simultaneous measurement of thickness and refractive index of thermally evaporated thin organic films by surface plasmon resonance spectroscopy. Opt. Express 2014, 22, 18914–18923. [Google Scholar] [CrossRef]
- Del Rosso, T.; Zaman, Q.; Cremona, M.; Pandoli, O.; Barreto, A.R.J. SPR sensors for monitoring the degradation processes of Eu(dbm)3(phen) and Alq3 thin films under atmospheric and UVA exposure. Appl. Surf. Sci. 2018, 442, 759–766. [Google Scholar] [CrossRef]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: New York, NY, USA, 2007; ISBN 978-0387-33150-8. [Google Scholar]
- Novotny, L.; Hecht, B. Principles of Nano-Optics, 2nd ed.; Cambridge University Press: New York, NY, USA, 2012; pp. 369–413. ISBN 978-1-107-00546-4. [Google Scholar]
- Turkevich, J.; Stevenson, P.C.; Hillier, J. A study of the nucleation and growth processes in the synthesis of colloidal gold. J. Discuss. Faraday Soc. 1951, 11, 55–75. [Google Scholar] [CrossRef]
- Schaub, A.; Slepicka, P.; Kasparkova, I.; Malinsky, P.; Mackova, A.; Svorcik, V. Gold nanolayer and nanocluster coatings induced by heat treatment and evaporation technique. Nanoscale Res. Lett. 2013, 249. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Robertson, C.S.; Nguyen, A.H.; Kahraman, M.; Wachsmann-Hogiu, S. Thickness of a metallic film, in addition to its roughness, plays a significant role in SERS activity. Sci. Rep. 2015, 11644. [Google Scholar] [CrossRef] [PubMed]
- Del Rosso, T.; Zaman, Q.; Romani, E.C.; Pandoli, O.; Aucelio, R.Q.; Melo de Lima, L.; Cremona, M.; Dmitriev, V.; da Costa, K.Q.; Freire, F.L., Jr.; Maia da Costa, M.E.H. Enhanced stability of plasmonic metal thin films by CVD grown graphene transfer. Thin Solid Films 2017, 644. [Google Scholar] [CrossRef]
- Raether, H. Surface Plasmons on Smooth and Rough Surfaces and on Gratings; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1988; ISBN 978-3-662-15124-2. [Google Scholar]
- Quinten, M. Optical Properties of Nanoparticle Systems: Mie and Beyond; Wiley: Weinheim, Germany, 2011; ISBN 9783527410439. [Google Scholar]
- Capek, I. Noble Metal Nanoparticles: Preparation, Composite Nanostructures, Biodecoration and Collective Properties; Springer: Tokyo, Japan, 2017; ISBN 978-4-431-56556-7. [Google Scholar]
- Zhao, L.; Kelly, K.L.; Schatz, G.C. The extinction spectra of silver nanoparticle arrays: influence of array structure on plasmon resonance wavelength and width. J. Phys. Chem. B 2003, 107, 7343–7350. [Google Scholar] [CrossRef]
- Chew, W. Waves and Fields in Inhomogeneous Media; IEEE Press: Washington, DC, USA, 1996; ISBN 978-0-780-34749-6. [Google Scholar]
- Shalabney, A.; Abdulhalim, I. Electromagnetic fields distribution in multilayer thin film structures and the origin of sensitivity enhancement in surface plasmon resonance sensors. Sens. Actuators A Phys. 2010, 159, 24–32. [Google Scholar] [CrossRef]
- Lahav, A.; Auslender, M.; Abdulhalim, I. Sensitivity enhancement of guided-wave surface-plasmon resonance sensors. Opt. Lett. 2010, 33, 2539–2541. [Google Scholar] [CrossRef]
- Nguyen, H.H.; Park, J.; Kang, S.; Kim, M. Surface plasmon resonance: A versatile technique for biosensor applications. Sensors 2015, 15. [Google Scholar] [CrossRef]
- Pockrand, I. Surface plasma oscillations at silver surfaces with thin transparent and absorbing coatings. Surf. Sci. 1978, 72, 577–588. [Google Scholar] [CrossRef]
- Huang, C.-Z.; Wu, M.-J.; Chen, S.-Y. High Order Gap Modes of Film-Coupled Nanospheres. J. Phys. Chem. C 2015, 119, 13799–13806. [Google Scholar] [CrossRef]
- García, M.A.; Llopis, J.; Paje, S.E. A simple model for evaluating the optical absorption spectrum from small Au-colloids in sol–gel films. Chem. Phys. Lett. 1999, 315, 313–320. [Google Scholar] [CrossRef]
- Del Rosso, T.; Margulis, W.; Fontana, J.; Carvalho, I.C.S. Plasmonics for the Characterization of Metal Organic Films and Nanoparticles. In Nanophotonics, Metal Nanostructures for Photonics; Kassab, L.R.P., de Araujo, C.B., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; ISBN 9780081023785. [Google Scholar]
- Polyanskiy, M.N. Refractive Index Database. Available online: https://refractiveindex.info (accessed on 10 November 2018).
- Laurenzana, A.; Fibbi, G.; Chillá, A.; Margheri, G.; Rosso, T.; Rovida, E.; Rosso, M.; Margheri, F. Lipids rafts: Integrated platforms for vascular organization offering therapeutic opportunities. Cell. Mol. Life Sci. 2015, 72, 1537–1557. [Google Scholar] [CrossRef] [PubMed]







| λ (nm) | Gold | SiO2 | Water | ||
|---|---|---|---|---|---|
| 783 | hAu (nm) | ε =εr + iεi | hSiO2 (nm) | εr | εr |
| 44.57 | −23.91 + i1.72 | 644 | 2.11 | 1.76 [42] | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costa, J.S.; Zaman, Q.; Q. da Costa, K.; Dmitriev, V.; Pandoli, O.; Fontes, G.; Del Rosso, T. Limits of the Effective Medium Theory in Particle Amplified Surface Plasmon Resonance Spectroscopy Biosensors. Sensors 2019, 19, 584. https://doi.org/10.3390/s19030584
Costa JS, Zaman Q, Q. da Costa K, Dmitriev V, Pandoli O, Fontes G, Del Rosso T. Limits of the Effective Medium Theory in Particle Amplified Surface Plasmon Resonance Spectroscopy Biosensors. Sensors. 2019; 19(3):584. https://doi.org/10.3390/s19030584
Chicago/Turabian StyleCosta, Jefferson S., Quaid Zaman, Karlo Q. da Costa, Victor Dmitriev, Omar Pandoli, Giselle Fontes, and Tommaso Del Rosso. 2019. "Limits of the Effective Medium Theory in Particle Amplified Surface Plasmon Resonance Spectroscopy Biosensors" Sensors 19, no. 3: 584. https://doi.org/10.3390/s19030584
APA StyleCosta, J. S., Zaman, Q., Q. da Costa, K., Dmitriev, V., Pandoli, O., Fontes, G., & Del Rosso, T. (2019). Limits of the Effective Medium Theory in Particle Amplified Surface Plasmon Resonance Spectroscopy Biosensors. Sensors, 19(3), 584. https://doi.org/10.3390/s19030584