A Novel Method for Early Gear Pitting Fault Diagnosis Using Stacked SAE and GBRBM
Abstract
:1. Introduction
2. The Proposed Method
2.1. Framework of Proposed Method
2.2. Spare Autoencoder
2.3. Develop the GBRBM based on RBM
3. Experiment Setup and Data Acquisition
4. Results and Discussion
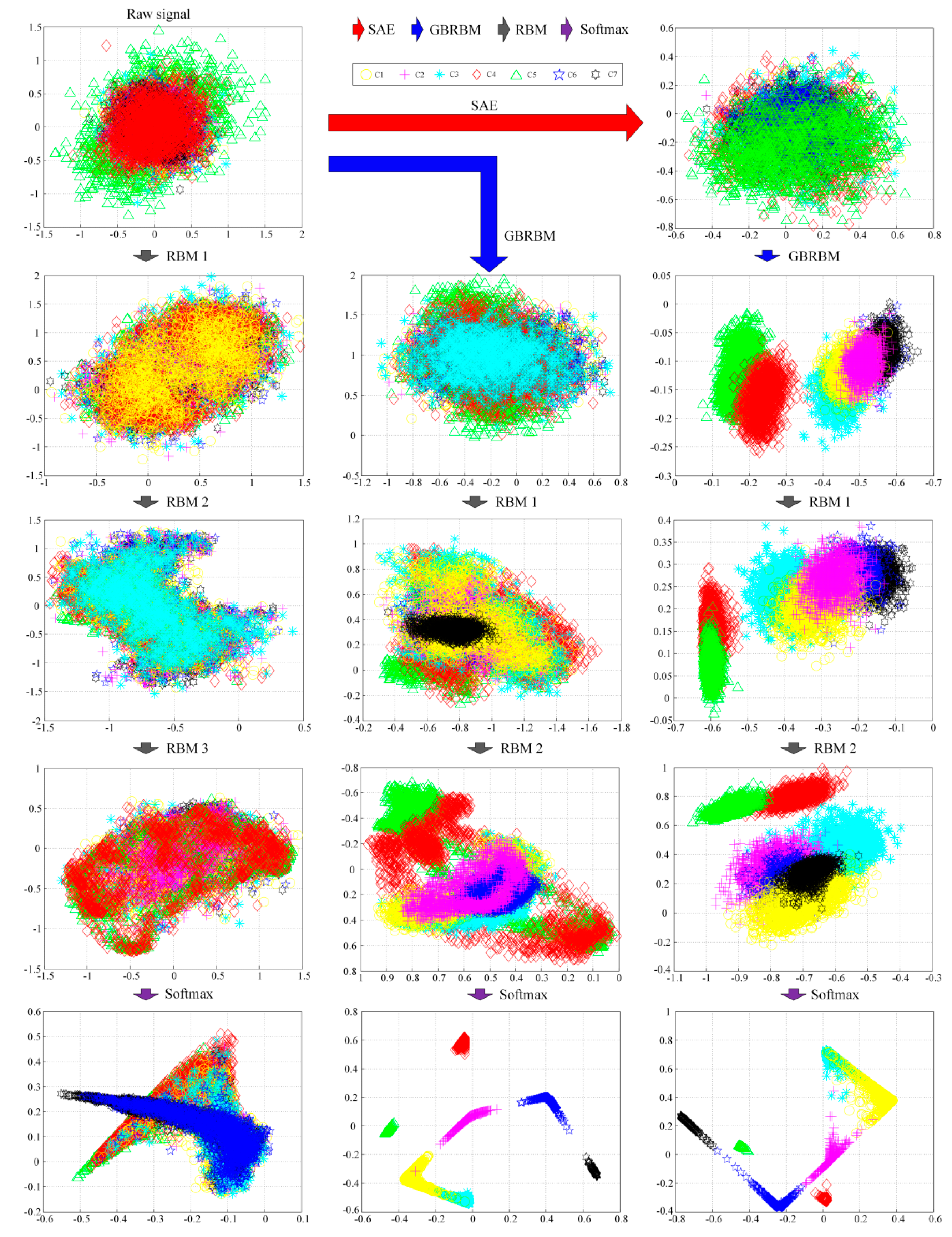
4.1. PCA Data Visualization During the Training Process
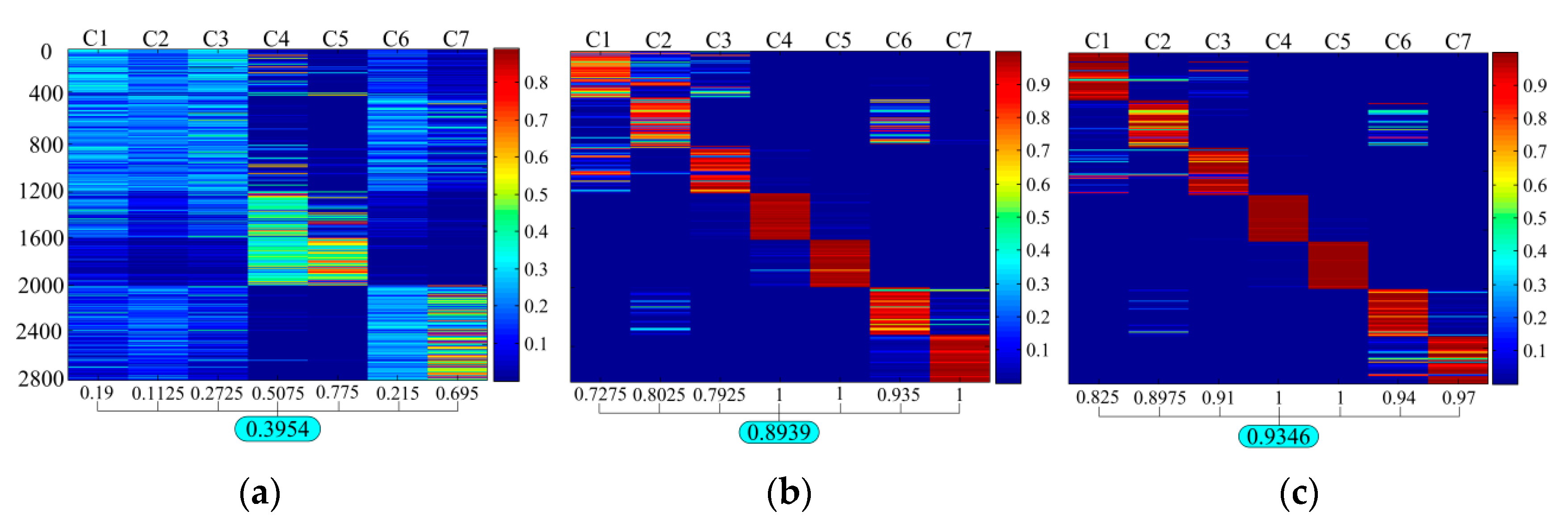
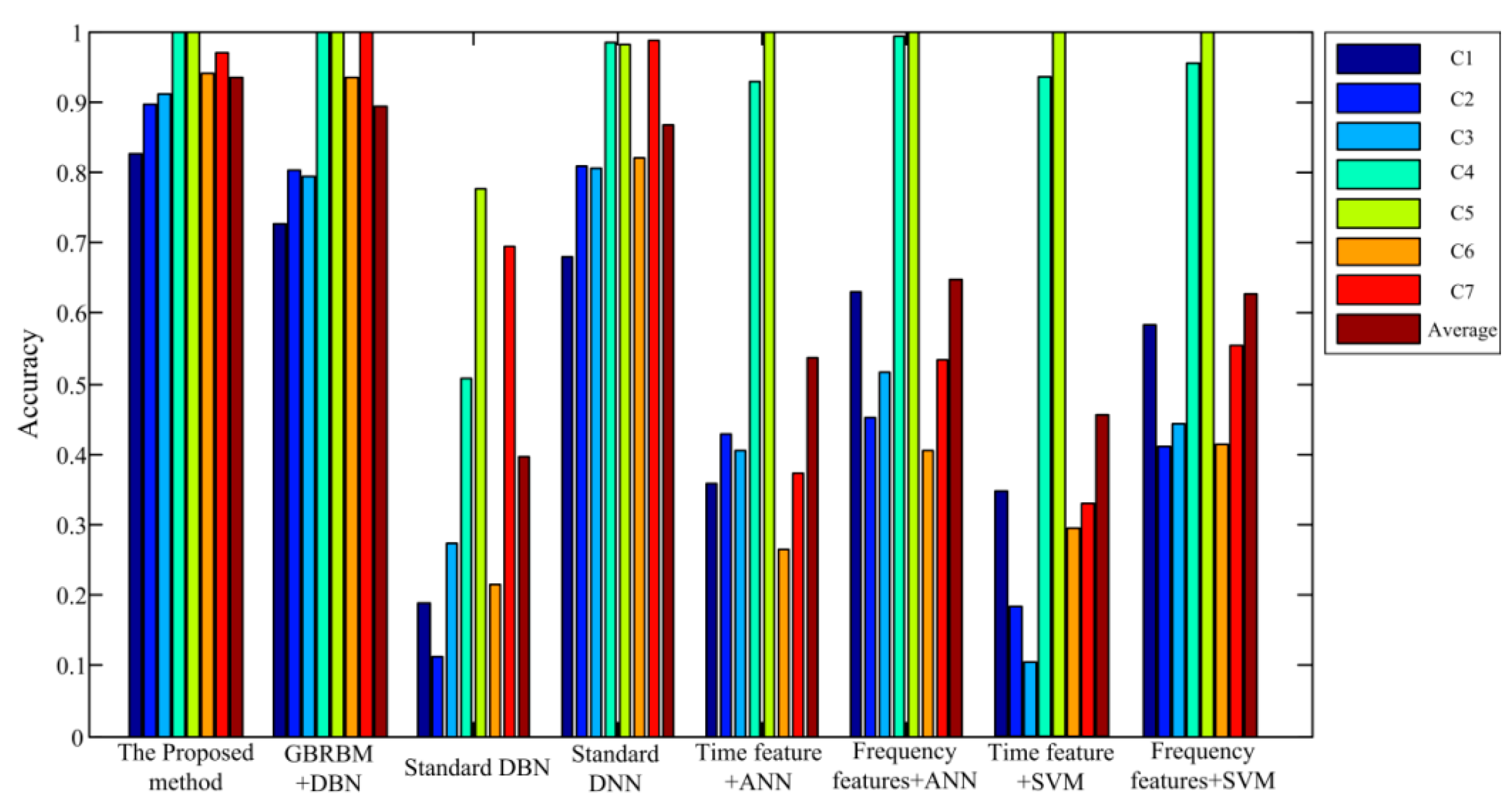
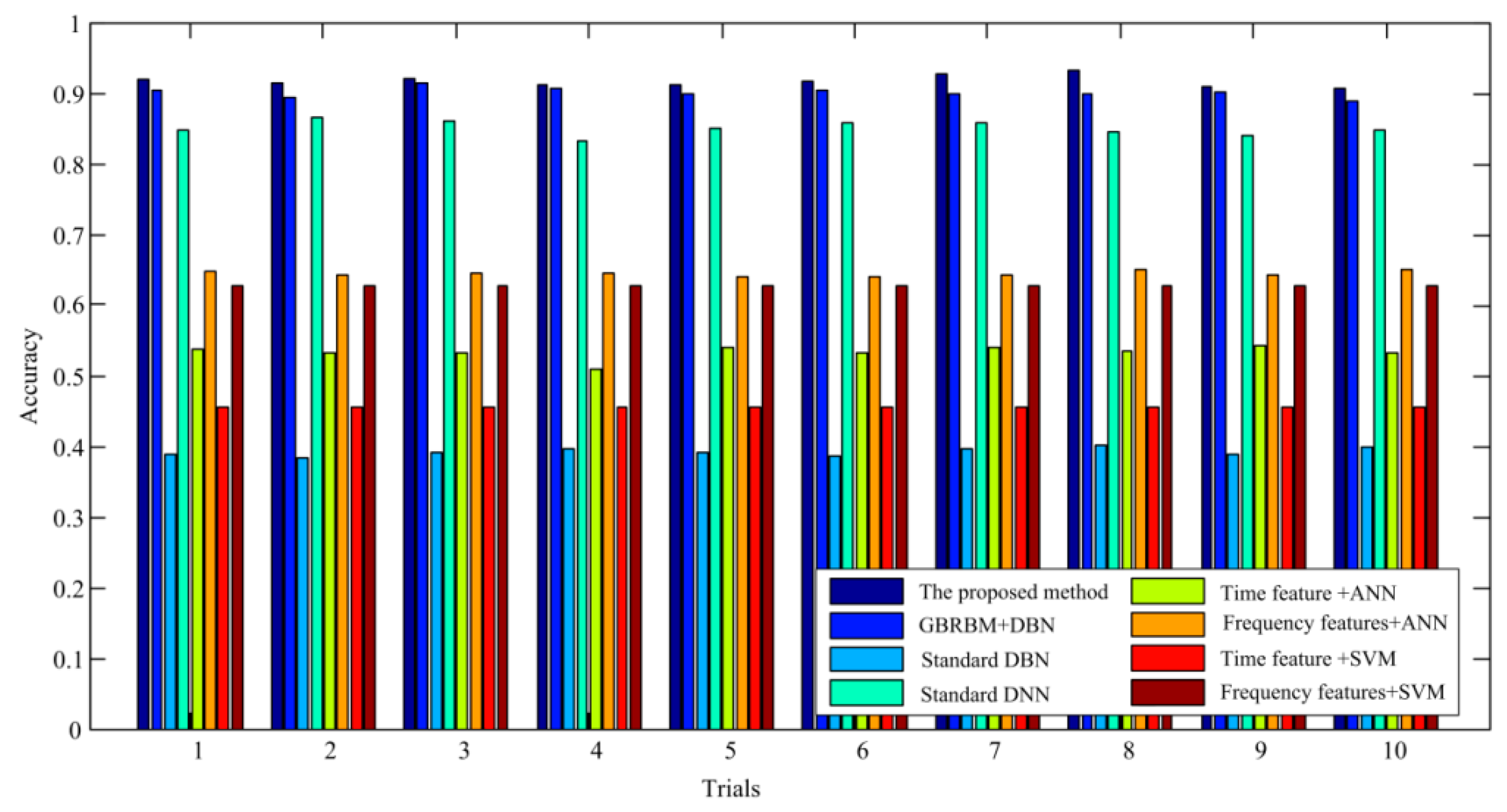
4.2. Diagnostic Results of Proposed Method
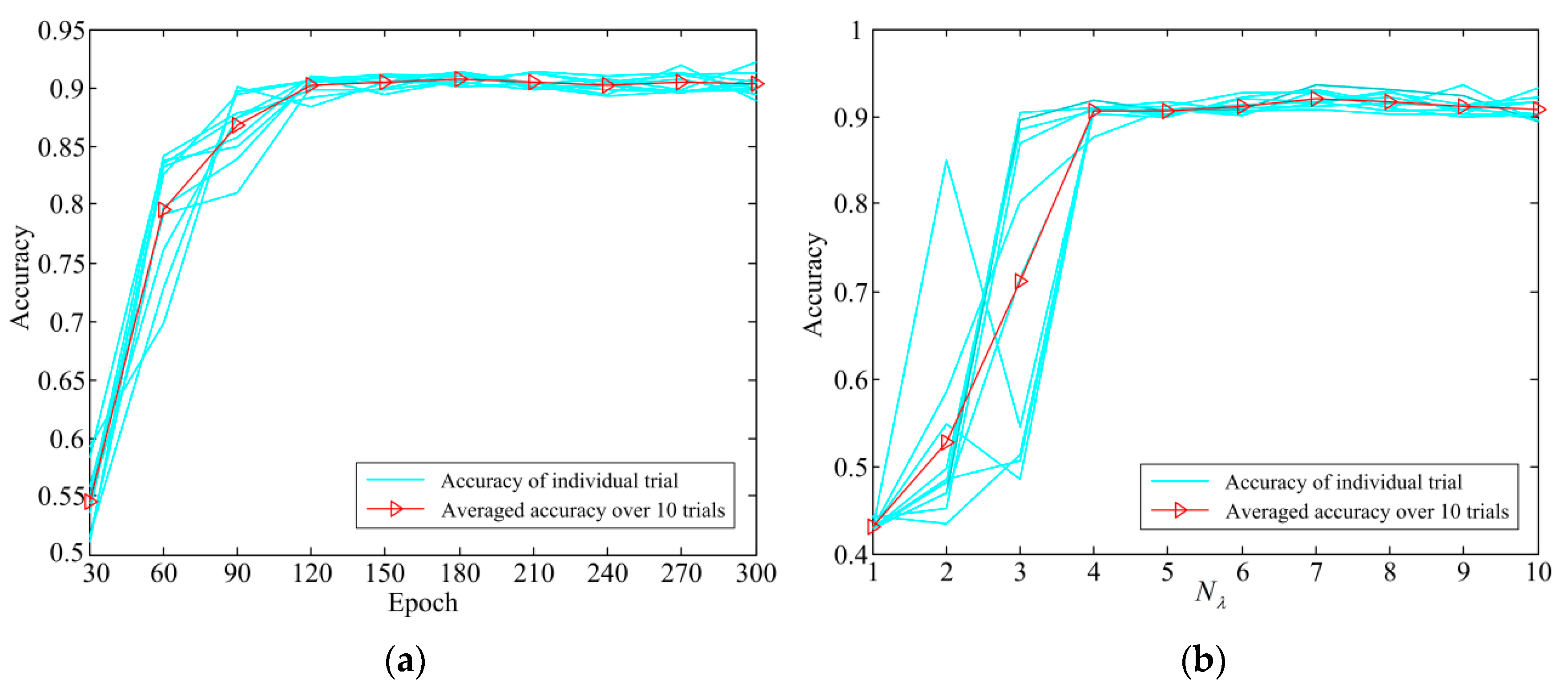
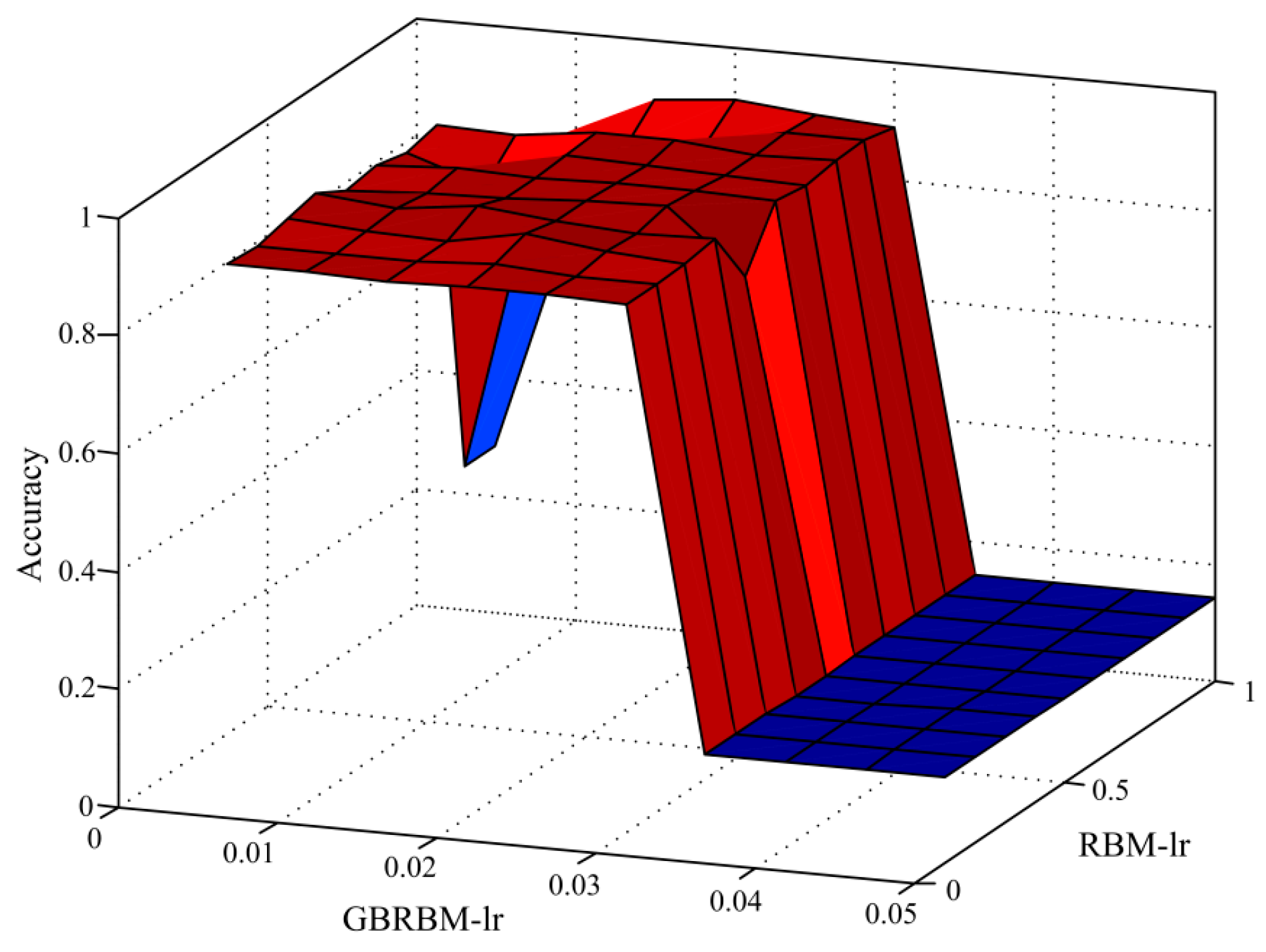
4.3. The Effect of the Parameters on the Diagnostic Accuracy
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Khan, S.; Yairi, T. A review on the application of deep learning in system health management. Mech. Syst. Signal Process. 2018, 107, 241–265. [Google Scholar] [CrossRef]
- Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial intelligence for fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- Soualhi, A.; Medjaher, K.; Zerhouni, N. Bearing Health Monitoring Based on Hilbert-Huang Transform, Support Vector Machine, and Regression. IEEE Trans. Instrum. Meas. 2015, 64, 52–62. [Google Scholar] [CrossRef]
- Mejia-Barron, A.; Valtierra-Rodriguez, M.; Granados-Lieberman, D.; Olivares-Galvan, J.C.; Escarela-Perez, R. The application of EMD-based methods for diagnosis of winding faults in a transformer using transient and steady state currents. Measurement 2018, 117, 371–379. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Pachori, R.; Upadhyay, A.; Acharya, U. Tunable-Q Wavelet Transform Based Multiscale Entropy Measure for Automated Classification of Epileptic EEG Signals. Appl. Sci. 2017, 7, 385. [Google Scholar] [CrossRef]
- Gajjar, S.; Kulahci, M.; Palazoglu, A. Real-time fault detection and diagnosis using sparse principal component analysis. J. Process Control 2018, 67, 112–128. [Google Scholar] [CrossRef]
- Bennacer, L.; Amirat, Y.; Chibani, A.; Mellouk, A.; Ciavaglia, L. Self-Diagnosis Technique for Virtual Private Networks Combining Bayesian Networks and Case-Based Reasoning. IEEE Trans. Autom. Sci. Eng. 2015, 12, 354–366. [Google Scholar] [CrossRef]
- Denœux, T.; Kanjanatarakul, O.; Sriboonchitta, S. EK-NNclus: A clustering procedure based on the evidential K-nearest neighbor rule. Knowl.-Based Syst. 2015, 88, 57–69. [Google Scholar] [CrossRef] [Green Version]
- Ziegier, J.; Gattringer, H.; Mueller, A. Classification of Gait Phases Based on Bilateral EMG Data Using Support Vector Machines. In Proceedings of the 2018 7th IEEE International Conference on Biomedical Robotics and Biomechatronics (Biorob); IEEE: Enschede, The Netherlands, 2018; pp. 978–983. [Google Scholar]
- Ince, T.; Kiranyaz, S.; Eren, L.; Askar, M.; Gabbouj, M. Real-Time Motor Fault Detection by 1-D Convolutional Neural Networks. IEEE Trans. Ind. Electron. 2016, 63, 7067–7075. [Google Scholar] [CrossRef]
- Zhang, R.; Peng, Z.; Wu, L.; Yao, B.; Guan, Y. Fault Diagnosis from Raw Sensor Data Using Deep Neural Networks Considering Temporal Coherence. Sensors 2017, 17, 549. [Google Scholar] [CrossRef]
- Chen, Z.; Li, C.; Sanchez, R.-V. Gearbox Fault Identification and Classification with Convolutional Neural Networks. Shock Vib. 2015, 2015, 1–10. [Google Scholar] [CrossRef]
- Chen, K.; Zhou, X.-C.; Fang, J.-Q.; Zheng, P.; Wang, J. Fault Feature Extraction and Diagnosis of Gearbox Based on EEMD and Deep Briefs Network. Int. J. Rotating Mach. 2017, 2017, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Zhao, X.; Pei, J.; Tang, G. Transformer fault diagnosis using continuous sparse autoencoder. SpringerPlus 2016, 5. [Google Scholar] [CrossRef] [PubMed]
- Tran, V.T.; AlThobiani, F.; Ball, A. An approach to fault diagnosis of reciprocating compressor valves using Teager–Kaiser energy operator and deep belief networks. Expert Syst. Appl. 2014, 41, 4113–4122. [Google Scholar] [CrossRef]
- Han, D.; Zhao, N.; Shi, P. A new fault diagnosis method based on deep belief network and support vector machine with Teager–Kaiser energy operator for bearings. Adv. Mech. Eng. 2017, 9, 168781401774311. [Google Scholar] [CrossRef]
- Shao, H.; Jiang, H.; Wang, F.; Wang, Y. Rolling bearing fault diagnosis using adaptive deep belief network with dual-tree complex wavelet packet. ISA Trans. 2017, 69, 187–201. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Xiang, J.; Zhong, Y.; Tang, H. A data indicator-based deep belief networks to detect multiple faults in axial piston pumps. Mech. Syst. Signal Process. 2018, 112, 154–170. [Google Scholar] [CrossRef]
- Lee, D.; Lee, B.; Woo Shin, J. Fault Detection and Diagnosis with Modelica Language using Deep Belief Network. In Proceedings of the 11th International Modelica Conference, Versailles, France, 21–23 September 2015; pp. 615–623. [Google Scholar]
- Ahmed, H.O.A.; Dennis Wong, M.L.; Nandi, A.K. Effects of deep neural network parameters on classification of bearing faults. In Proceedings of the IECON—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 6329–6334. [Google Scholar]
- Tao, J.; Liu, Y.; Yang, D. Bearing Fault Diagnosis Based on Deep Belief Network and Multisensor Information Fusion. Shock Vib. 2016, 2016, 1–9. [Google Scholar] [CrossRef]
- He, J.; Yang, S.; Gan, C. Unsupervised Fault Diagnosis of a Gear Transmission Chain Using a Deep Belief Network. Sensors 2017, 17, 1564. [Google Scholar] [CrossRef]
- Chen, Z.; Deng, S.; Chen, X.; Li, C.; Sanchez, R.-V.; Qin, H. Deep neural networks-based rolling bearing fault diagnosis. Microelectron. Reliab. 2017, 75, 327–333. [Google Scholar] [CrossRef]
- Deutsch, J.; He, M.; He, D. Remaining Useful Life Prediction of Hybrid Ceramic Bearings Using an Integrated Deep Learning and Particle Filter Approach. Appl. Sci. 2017, 7, 649. [Google Scholar] [CrossRef]
- Geng, Z.; Li, Z.; Han, Y. A new deep belief network based on RBM with glial chains. Inf. Sci. 2018, 463–464, 294–306. [Google Scholar] [CrossRef]
- Ren, H.; Chai, Y.; Qu, J.; Ye, X.; Tang, Q. A novel adaptive fault detection methodology for complex system using deep belief networks and multiple models: A case study on cryogenic propellant loading system. Neurocomputing 2018, 275, 2111–2125. [Google Scholar] [CrossRef]
- Shao, H.; Jiang, H.; Zhang, H.; Duan, W.; Liang, T.; Wu, S. Rolling bearing fault feature learning using improved convolutional deep belief network with compressed sensing. Mech. Syst. Signal Process. 2018, 100, 743–765. [Google Scholar] [CrossRef]
- Jiang, H.; Shao, H.; Chen, X.; Huang, J. A feature fusion deep belief network method for intelligent fault diagnosis of rotating machinery. J. Intell. Fuzzy Syst. 2018, 34, 3513–3521. [Google Scholar] [CrossRef]
- Shao, H.; Jiang, H.; Lin, Y.; Li, X. A novel method for intelligent fault diagnosis of rolling bearings using ensemble deep auto-encoders. Mech. Syst. Signal Process. 2018, 102, 278–297. [Google Scholar] [CrossRef]
- Maurya, S.; Singh, V.; Dixit, S.; Verma, N.K.; Salour, A.; Liu, J. Fusion of Low-level Features with Stacked Autoencoder for Condition based Monitoring of Machines. In Proceedings of the 2018 IEEE International Conference on Prognostics and Health Management (ICPHM), Seattle, WA, USA, 11–13 June 2018; pp. 1–8. [Google Scholar]
- Shao, H.; Jiang, H.; Zhao, H.; Wang, F. A novel deep autoencoder feature learning method for rotating machinery fault diagnosis. Mech. Syst. Signal Process. 2017, 95, 187–204. [Google Scholar] [CrossRef]
- Meng, Z.; Zhan, X.; Li, J.; Pan, Z. An enhancement denoising autoencoder for rolling bearing fault diagnosis. Measurement 2018, 130, 448–454. [Google Scholar] [CrossRef]
- Sohaib, M.; Kim, J.-M. Reliable Fault Diagnosis of Rotary Machine Bearings Using a Stacked Sparse Autoencoder-Based Deep Neural Network. Shock Vib. 2018, 2018, 1–11. [Google Scholar] [CrossRef]
- Saufi, S.R.; bin Ahmad, Z.A.; Leong, M.S.; Lim, M.H. Differential evolution optimization for resilient stacked sparse autoencoder and its applications on bearing fault diagnosis. Meas. Sci. Technol. 2018, 29, 125002. [Google Scholar] [CrossRef]
- Gao, X.; Wang, H.; Gao, H.; Wang, X.; Xu, Z. Fault diagnosis of batch process based on denoising sparse auto encoder. In Proceedings of the 2018 33rd Youth Academic Annual Conference of Chinese Association of Automation (YAC), Nanjing, China, 18–20 May 2018; pp. 764–769. [Google Scholar]
- Mahdi, M.; Genc, V.M.I. Post-fault prediction of transient instabilities using stacked sparse autoencoder. Electr. Power Syst. Res. 2018, 164, 243–252. [Google Scholar] [CrossRef]
- Xu, L.; Cao, M.; Song, B.; Zhang, J.; Liu, Y.; Alsaadi, F.E. Open-circuit fault diagnosis of power rectifier using sparse autoencoder based deep neural network. Neurocomputing 2018, 311, 1–10. [Google Scholar] [CrossRef]
- Amini, S.; Ghaernmaghami, S. Sparse Autoencoders Using Non-smooth Regularization. In Proceedings of the 2018 26th European Signal Processing Conference (EUSIPCO), Rome, Italy, 3–7 September 2018; pp. 2000–2004. [Google Scholar]
- Shao, H.; Jiang, H.; Zhang, X.; Niu, M. Rolling bearing fault diagnosis using an optimization deep belief network. Meas. Sci. Technol. 2015, 26, 115002. [Google Scholar] [CrossRef]
- Jiang, H.; Shao, H.; Chen, X.; Huang, J. Aircraft Fault Diagnosis Based on Deep Belief Network. In Proceedings of the 2017 International Conference on Sensing, Diagnostics, Prognostics, and Control (SDPC), Shanghai, China, 16–18 August 2017; pp. 123–127. [Google Scholar]
- Qin, X.; Zhang, Y.; Mei, W.; Dong, G.; Gao, J.; Wang, P.; Deng, J.; Pan, H. A cable fault recognition method based on a deep belief network. Comput. Electr. Eng. 2018, 71, 452–464. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.-W. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Z.; Cai, X.; Liu, Y.; Zhu, B. A Novel Gaussian–Bernoulli Based Convolutional Deep Belief Networks for Image Feature Extraction. Neural Process. Lett. 2018. [Google Scholar] [CrossRef]
- Cho, K.H.; Raiko, T.; Ilin, A. Gaussian-Bernoulli deep Boltzmann machine. In Proceedings of the 2013 International Joint Conference on Neural Networks (IJCNN), Dallas, TX, USA, 4–9 August 2013; pp. 1–7. [Google Scholar]
- Keronen, S.; Cho, K.; Raiko, T.; Ilin, A.; Palomaki, K. Gaussian-Bernoulli restricted Boltzmann machines and automatic feature extraction for noise robust missing data mask estimation. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 6729–6733. [Google Scholar]
- Lu, W.; Wang, X.; Yang, C.; Zhang, T. A novel feature extraction method using deep neural network for rolling bearing fault diagnosis. In Proceedings of the 27th Chinese Control and Decision Conference (2015 CCDC), Qingdao, China, 23–25 May 2015; pp. 2427–2431. [Google Scholar]
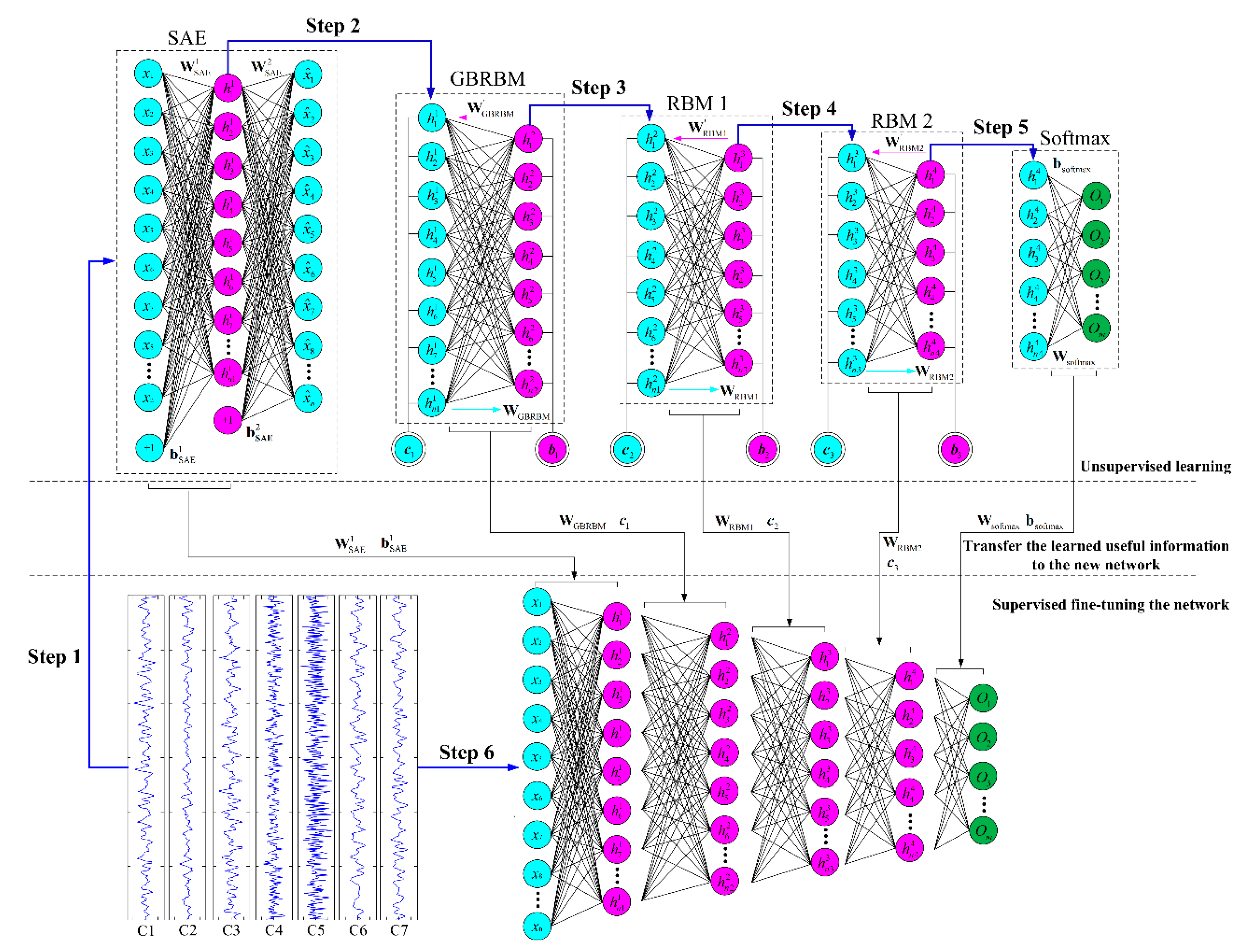


| Overall process: (1) Unsupervised: SAE→GBRBM→RBM(1,2)→Softmax→(2) Supervised: Back propagation | |
| Step 1: SAE training Input: training data x, W and b, λ, β, ƞ1, max-epochs(1) for i to max-epochs(1)
Output: , , Step 2: GBRBM training Input: , max-epochs(2), , , , , ƞ2, α1 for i to max-epochs(2) Output: , , Step 3: RBM1 training Input: , max-epochs(3), , , , ƞ3, α2 for i to max-epochs(3)
Output: , , | Step 4: RBM2 training Input: , max-epochs(4), , , , ƞ4, α3
Step 5: Softmax layer Input: , , Step 6: Back propagation Input: y, max-epochs(5), ƞ5 for i to max-epochs(5)
Output: the trained network Step 7: Test the trained network with test sample |
| Label | Gear Pitting Type | ||
|---|---|---|---|
| 72th Tooth | First Tooth | Second Tooth | |
| C1 | healthy | healthy | healthy |
| C2 | healthy | 10% in middle | healthy |
| C3 | healthy | 30% in middle | healthy |
| C4 | healthy | 50% in middle | healthy |
| C5 | 10% in middle | 50% in middle | healthy |
| C6 | 10% in middle | 50% in middle | 10% in middle |
| C7 | 30% in middle | 50% in middle | 10% in middle |
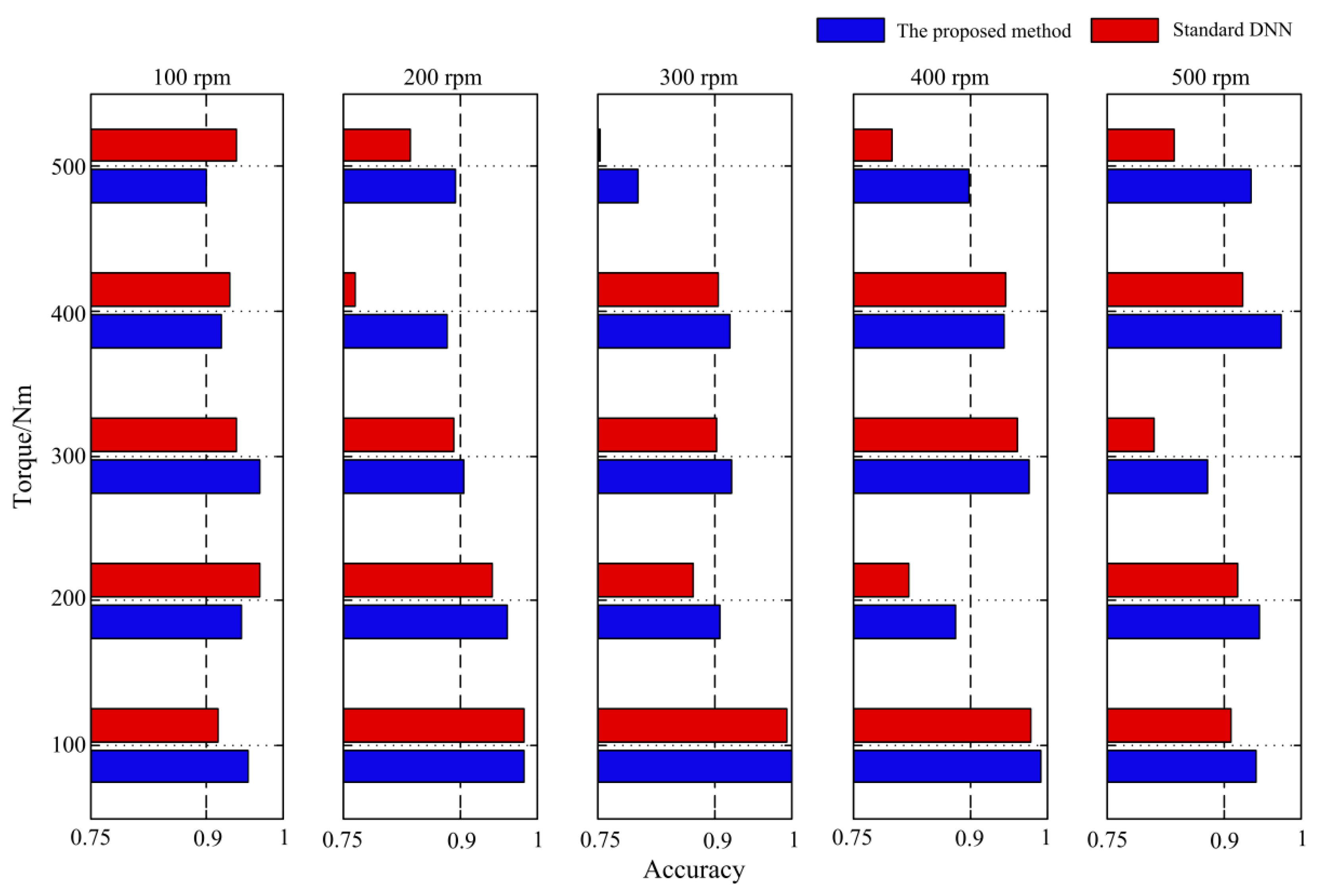
| Speed | Proposed Method | Standard DNN |
|---|---|---|
| 100 rpm | 0.9374 | 0.9372 |
| 200 rpm | 0.9245 | 0.8824 |
| 300 rpm | 0.9091 | 0.8831 |
| 400 rpm | 0.9372 | 0.9003 |
| 500 rpm | 0.9344 | 0.8791 |
| Torque | Proposed Method | Standard DNN |
|---|---|---|
| 100 Nm | 0.9729 | 0.9546 |
| 200 Nm | 0.9279 | 0.9036 |
| 300 Nm | 0.9294 | 0.8997 |
| 400 Nm | 0.9275 | 0.8935 |
| 500 Nm | 0.8848 | 0.8307 |
| Working Condition | Trial 1 | Trial 2 | Trial 3 | Trial 4 | Trial 5 | Row Average | |
|---|---|---|---|---|---|---|---|
| 100 Nm | 100 rpm-100 Nm | 0.9546 | 0.9554 | 0.9621 | 0.9354 | 0.9843 | 0.9584 |
| 200 rpm-100 Nm | 0.9861 | 0.9636 | 0.9736 | 0.9236 | 0.9857 | 0.9665 | |
| 300 rpm-100 Nm | 1 | 0.9986 | 0.9975 | 0.9989 | 0.9961 | 0.9982 | |
| 400 rpm-100 Nm | 0.9954 | 0.9968 | 0.9950 | 0.9921 | 0.9961 | 0.9951 | |
| 500 rpm–100 Nm | 0.9582 | 0.9557 | 0.9446 | 0.9550 | 0.9557 | 0.9539 | |
| Column Average | 0.9789 | 0.9740 | 0.9746 | 0.9610 | 0.9836 | 0.9744 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Li, X.; He, D.; Qu, Y. A Novel Method for Early Gear Pitting Fault Diagnosis Using Stacked SAE and GBRBM. Sensors 2019, 19, 758. https://doi.org/10.3390/s19040758
Li J, Li X, He D, Qu Y. A Novel Method for Early Gear Pitting Fault Diagnosis Using Stacked SAE and GBRBM. Sensors. 2019; 19(4):758. https://doi.org/10.3390/s19040758
Chicago/Turabian StyleLi, Jialin, Xueyi Li, David He, and Yongzhi Qu. 2019. "A Novel Method for Early Gear Pitting Fault Diagnosis Using Stacked SAE and GBRBM" Sensors 19, no. 4: 758. https://doi.org/10.3390/s19040758
APA StyleLi, J., Li, X., He, D., & Qu, Y. (2019). A Novel Method for Early Gear Pitting Fault Diagnosis Using Stacked SAE and GBRBM. Sensors, 19(4), 758. https://doi.org/10.3390/s19040758





