1. Introduction
There are specific requirements for robotic systems working in human environments. Robotic hands play an important role as end-effectors in such robotic systems, and many types of robotic hand have been developed [
1,
2]. In a human environment, interactions between humans and robots cannot be avoided, and thus, the surfaces of robots must be soft to avoid physical damage during these interactions. Considering this, we previously developed a robotic hand with a soft surface by filling a rubber bag with a viscoelastic fluid (
Figure 1) and demonstrated that the hand can grasp a wide variety of fragile objects [
1,
2,
3]. We call this fingertip a fluid fingertip. Owing to the fluid incompressibility, a uniform contact pressure distribution is obtained. Unevenness in an object’s shape can be accommodated by the fluid deformation. These factors are beneficial for delicately grasping fragile objects. In particular, we presented a methodology for grasping (kinugoshi) tofu, which is a highly soft and fragile object, without using any advanced knowledge regarding the fracture stress. We focused on the pressure profile of the filled fluid because this corresponds to the stress. We showed that tofu could be grasped without fracturing at the point where the behavior of the fluid pressure changed [
4]. However, the significance of this point was unclear. In addition, the most important aspect of how to grasp an object using such highly deformable fingertips was not considered. The present study proposes an extended version of our previous grasping strategy for a robotic hand with highly deformable fingertips [
4]. In this study, the following features of the grasping strategy are revealed:
The grasping point corresponds to the point at which the stress inside the object becomes activated over the whole inner area, and deformation begins at the free boundaries. In addition, at this point, invasion of the object body owing to compression at the contact area is almost eliminated, and a substantial grasping pressure or force is transmitted to or exerted on the object.
Fractures and cracks can be avoided.
The threshold for detecting the grasping point is constant regardless of the object.
Information on the deformation and stiffness of the fingertips and target object is unnecessary for detecting the grasping point.
Our previous strategy [
4] began from the state at which the fluid fingertip was in contact with the target object. In actual cases, grasping normally starts from a state where the fingertips and object are sufficiently separated. The new strategy deals with the case in which only fluid pressure monitoring is utilized.
The proposed strategy adopts the following assumptions: the speed of compressing or pushing the target object with the highly deformable fingertips is constant, and the fingertips have high surface friction. The remainder of this paper is organized as follows. The next subsection describes related research.
Section 2 describes the compression test for examining the behavior of the highly deformable fingertips.
Section 3 presents the methodology for detecting the grasping point online.
Section 4 presents experimental results demonstrating the validity of the proposed approach.
3. Methodology for Detecting the Grasping Point
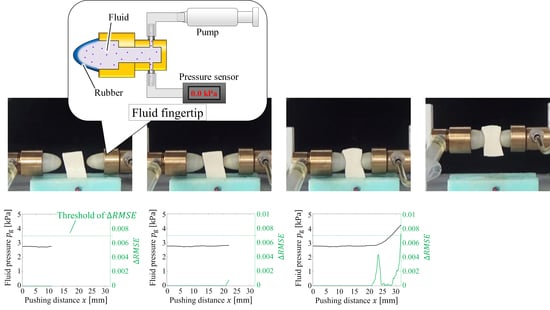
Here, we describe the methodology for detecting the CP online. Because photoelastic imaging can only be applied to photoelastic or transparent materials, using only a pressure sensor to measure the inner fluid pressure is preferable. This is also more cost-effective than using force sensors. Pressure sensors can be connected to the tube, which is connected to the fluid part, to measure the inner fluid pressure, whereas force sensors require installation space and transmission devices. In addition, the pressure information is highly similar to the force information because the fluid fingertip provides a uniform contact pressure, as shown in [
1]. We present a strategy considering the following requirements:
- (1)
The CP can be detected online.
- (2)
CP detection can be conducted by monitoring the fluid pressure only.
- (3)
The threshold for the detection is constant with respect to the type of target object.
- (4)
Advanced knowledge about the stiffness and deformation of the target object is not required.
To detect the CP, we adopted a methodology wherein the point at which the behavior change is detected by comparing the fitting accuracies of different simple and complex regression models, in a manner similar to that in References [
4,
13]. A methodology in which a linear section, indicating a sign of a crack or fracture, is detected by monitoring the fitting accuracy of the linear approximation could be adopted. As shown in
Figure 5, the linear section when compressing tofu is clear, and a methodology based on the linear approximation could be valid. Therefore, we adopted the approach in Reference [
4]. However, Equation (2) represents the ideal case, and the actual pressure behavior is not always completely linear, as suggested by
Figure 3. In such a case, threshold tuning is required, which indicates that the material properties of the target object must be known in advance. In addition, the behavioral change at the CP is not always clear. Hence, we adopted a methodology based on comparing the fitting accuracies of simple and complex models. Before the CP, the data arrangement will be simple, and both the simple and complex models can provide good fitting accuracies. In contrast, if the data arrangement deviates from the original one at the CP, then the fitting accuracy in the simple model will decrease while that in the complex model can be maintained. Hence, the difference in the fitting accuracies of the simple and complex models significantly increases at the CP. By detecting this increase, the CP can be detected. The main benefit of the methodology based on comparing the fitting accuracies of different models is that the threshold for detecting the CP does not have to be changed according to the type of object, and thus, can be constant. The original data arrangement includes a curve, and two- and three-dimensional polynomial functions are then prepared as approximations for the simple and complex models, respectively.
We refer to the point at which the fluid pressure begins to increase as the starting point (SP). The steps of the strategy can be summarized as follows: First, we detect the SP, and subsequently, we detect the CP. The procedure of this strategy is illustrated in
Figure 6.
Let
denote the fluid pressure at time
. Consequently, the SP can be regarded as the point at which
begins to increase. We detected the SP by verifying whether the following condition is satisfied:
Here,
and
denote the average and standard deviation, respectively, of the fluid pressure when the fingertip is unloaded and
is a tuning parameter. The threshold (
) is determined by the system settings and is independent of the target object and pushing speed.
Subsequently, to detect the CP we adopted the methodology mentioned above. The two- and three-dimensional polynomial functions were assumed to represent the simple and complex fitting models, respectively. The regression started from the SP and was performed each time new data were obtained. Let
denote the time for the
time step. The two- and three-dimensional polynomial functions at the
time step are defined as follows:
Here,
are the coefficients of the respective functions. At the
time step, we have a dataset
, where
denotes the obtained fluid pressure value corresponding to the (uniform) contact pressure at the
ith time step. In this case, the coefficients
and
are obtained by solving the following simultaneous linear equations (see the
Appendix A) with little computational effort:
To compare the fitting accuracies of the models, the root mean square error (RMSE) was calculated. Let
and
denote the RMSEs for the two- and three-dimensional polynomial functions, respectively, at the
ith time step. These are defined as follows:
Subsequently, the difference in the fitting accuracies at the
time step,
, is defined as follows:
As shown in
Figure 7, the two- and three-dimensional polynomial functions were selected as the simple and complex models, respectively, in such manner that their fitting accuracies before the CP are close to each other and
is small. Around the CP, the data are rearranged and the curve expressing the behavior from the SP becomes complex. Therefore, the simple model cannot easily express the curve whereas the complex model can. In this case,
becomes large. Hence, by checking whether the value of
exceeds a threshold value (0.007 in this case), the CP can be detected. The two prepared models do not have to describe the data very well, because the purpose is only to detect the change in the data arrangement. The CP detection method requires a simple model that cannot describe the change in the data arrangement very accurately, and a complex model that can achieve this better than the simple model. Therefore, the simple two- and three-dimensional polynomial functions perform well.
4. Experimental Validation
To verify the effectiveness of the proposed strategy, grasping tests were conducted on various objects.
Figure 8 illustrates the experimental setup for the grasping tests. A robotic gripper was utilized, consisting of two opposing linear actuators (oriental motor and DRLM42G-04A2PN-K) with one fluid fingertip attached to each of them. According to the proposed grasping strategy, a pressure sensor (Keyence, AP-12S) was installed on one of the fluid fingertips to monitor the fluid pressure. The gripper was mounted on an automatic vertical positioning stage.
Gelatin, soft tofu, sushi, origami [
21], and potato chips were selected as the target objects. The target objects were placed at the center, between the fingertips. The origin of the pushing distance
was randomly set such that the object was not contacted by both fingertips at the origin. The tests were conducted five times for each target object. All the objects were grasped without sustaining any damage.
Figure 9,
Figure 10,
Figure 11,
Figure 12 and
Figure 13 present images of the grasping tests. When grasping the gelatin, photoelastic imaging was adopted to confirm the absence of cracks and activation of shape deformation around the free boundaries at the detected CP. Although every target was fragile, no fractures were observed in the target objects. Small shape deformations around the free boundaries were observed when each of the objects was grasped. These deformations indicate a substantial transmission of the applied pressure or force during grasping. Hence, the proposed strategy allows fragile objects to be grasped without using any prior knowledge of the fracture stress.
Figure 9,
Figure 10,
Figure 11,
Figure 12 and
Figure 13 indicate that the pressure value at the CP varies with the type of target object, and it is difficult to detect the CP using the same threshold for the pressure value.
Figure 14 illustrates the behaviors of
and
between the SP and CP in the grasping test for each target object. The value of
at the CP varied with the type of object (for example, 0.027 for gelatin and 0.015 for origami). If we attempt to detect the CP by only checking the value of
, the threshold should be defined according to the type of target. This means that we require prior knowledge of the target object. In contrast, the proposed strategy was capable of detecting the appropriate grasping point for each target with a unique threshold for the difference in
. The utilization of the unique threshold indicates that prior knowledge about the type of target is unnecessary. The results validate the effectiveness of the proposed strategy.
To verify the significance of the CP from the viewpoint of grasping stability, we investigated the resistible force when grasping the gelatin object with the fluid fingertips under various degrees of compression. The experimental setup is illustrated in
Figure 15, where a force gauge (IMADA DST-50N) was added to the setup shown in
Figure 8. The object was first grasped with the two opposing fluid fingertips with pushing distances of 12, 14, 16, 18, 20, 22, and 24 mm (Step 1 in
Figure 15). The values of the pushing distance correspond to those in
Figure 4, and the pushing distance of 20 mm corresponds to the CP. Subsequently, a load in the horizontal direction was applied to the side of the object and we increased the value of this load until the object fell. The maximum value of the applicable load was defined as the resistible force and examined. The experiment was conducted three times for each case.
Figure 16 illustrates the results, where the average value and standard deviation are displayed for each pushing distance. Around the CP (the pushing distance of 20 mm), the resistible force converged to a high value. Moreover, the standard deviation of the resistible force converged to a small value around the CP. The grasping was maintained even when a disturbing force was applied, indicating stable grasping. Therefore, a high resistible force indicates highly stable grasping and the stability of the grasping maximized around the CP. Additionally, the applied force was substantially transmitted to the object at the CP. The reason for the convergence of the resistible force is that the invasion into the object body almost stopped and the contact area became almost constant. When the pushing distance
was less than the CP, the resistible force was small, and it varied or fluctuated. This indicates that grasping at this pushing distance is more unstable than that at the CP. The results indicate that the CP is the most preferable grasping point from the viewpoint of stable grasping.
5. Conclusions
This study proposes a novel strategy for delicately grasping fragile objects using fluid fingertips. While pushing a target object at a constant speed, the fluid pressure behavior changes at the CP. This strategy advocates grasping at the CP because fractures of the target object can be avoided, while a substantial force or pressure can be transmitted to the target object by the fluid fingertips. Subsequently, we present a method for detecting the CP by comparing the fitting accuracies of fitting models. The features of this method are as follows: (1) online detection can be achieved, (2) only information on the fluid pressure is required, and (3) the threshold for the detection is constant with respect to the type of target object. The proposed method does not require advanced knowledge on the stiffness and deformation of the target object. The validity of the proposed approach is verified through several experiments.
The fluid pressure of the fingertips corresponds to the contact pressure, and thus, it includes object state information such as stiffness or viscosity. Therefore, the monitoring and regulation of the fluid pressure can provide the tuning of the fingertip stiffness according to the object state, leading to sophisticated grasping or manipulation strategies with the identification of unknown parameters, such as stiffness or viscosity, of an unknown target object. One example is the proposed strategy, in which the parameter or characteristic related with fracture was identified for delicate grasping. With the identification, the proposed strategy provided soft-contact impact with the target object along with enough fingertip stiffness for supporting the object weight via the tuning of the fingertip stiffness by the fluid pressure control. Our future work may involve the development of other types of grasping or manipulation strategies utilizing the fluid pressure control.