Compact Acoustic Rainbow Trapping in a Bioinspired Spiral Array of Graded Locally Resonant Metamaterials
Abstract
:1. Introduction
2. Numerical Simulation
2.1. Numerical Model
2.2. Dispersion Analysis
2.3. Spatial–Spectral Analysis
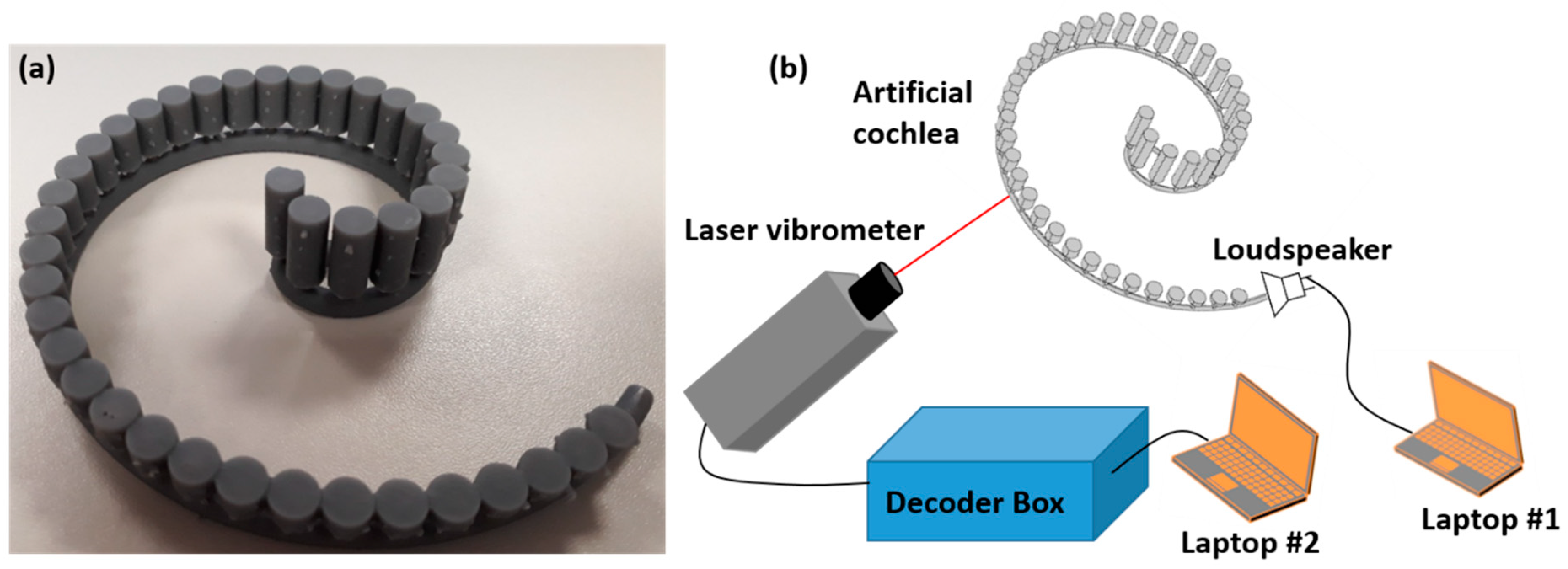
3. Experiments
3.1. Experimental Setup
3.2. Experimental Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Suhaimi, S.A.; Azemi, S.N.; Jack, S.P. Structural health monitoring system using 3d frequency selective surface. In Proceedings of the 2016 IEEE Asia-Pacific Conference on Applied Electromagnetics (APACE), Melaka, Malaysia, 11–13 December 2016; pp. 145–149. [Google Scholar]
- Sang-Dong, J.; Byung-Woo, K.; Jaehwan, K. Frequency selective surface based passive wireless sensor for structural health monitoring. Smart Mater. Struct. 2013, 22, 025002. [Google Scholar]
- Sung, G.H.; Sowerby, K.W.; Neve, M.J.; Williamson, A.G. A frequency-selective wall for interference reduction in wireless indoor environments. IEEE Antennas Propag. Mag. 2006, 48, 29–37. [Google Scholar] [CrossRef]
- Zhao, L.; Yang, J.; Wang, K.W.; Semperlotti, F. An application of impediography to the high sensitivity and high resolution identification of structural damage. Smart Mater. Struct. 2015, 24, 065044. [Google Scholar] [CrossRef] [Green Version]
- Zhao, J.; Zhang, Q.; Wang, R.; Chen, Y. Incident-Insensitive Frequency Selective Surface using degradable material for bio-medical application. In Proceedings of the 2014 Asia-Pacific Microwave Conference, Sendai, Japan, 4–7 November 2014; pp. 537–539. [Google Scholar]
- Seman, F.C.; Cahill, R.; Fusco, V.F.; Goussetis, G. Design of a salisbury screen absorber using frequency selective surfaces to improve bandwidth and angular stability performance. IET Microw. Antennas Propag. 2011, 5, 149–156. [Google Scholar] [CrossRef]
- Tsakmakidis, K.L.; Boardman, A.D.; Hess, O. ‘Trapped rainbow’ storage of light in metamaterials. Nature 2007, 450, 397. [Google Scholar] [CrossRef] [PubMed]
- Gan, Q.; Ding, Y.J.; Bartoli, F.J. “rainbow’’ trapping and releasing at telecommunication wavelengths. Phys. Rev. Lett. 2009, 102, 056801. [Google Scholar] [CrossRef] [PubMed]
- Williams, C.R.; Andrews, S.R.; Maier, S.A.; Fernández-Domínguez, A.I.; Martín-Moreno, L.; García-Vidal, F.J. Highly confined guiding of terahertz surface plasmon polaritons on structured metal surfaces. Nat. Photonics 2008, 2, 175. [Google Scholar] [CrossRef]
- Gan, Q.; Gao, Y.; Wagner, K.; Vezenov, D.; Ding, Y.J.; Bartoli, F.J. Experimental verification of the rainbow trapping effect in adiabatic plasmonic gratings. Proc. Natl. Acad. Sci. USA 2011, 108, 5169. [Google Scholar] [CrossRef] [PubMed]
- Jang, M.S.; Atwater, H. Plasmonic rainbow trapping structures for light localization and spectrum splitting. Phys. Rev. Lett. 2011, 107, 207401. [Google Scholar] [CrossRef] [PubMed]
- Kats, M.A.; Woolf, D.; Blanchard, R.; Yu, N.; Capasso, F. Spoof plasmon analogue of metal-insulator-metal waveguides. Opt. Express 2011, 19, 14860–14870. [Google Scholar] [CrossRef]
- Chen, L.; Wang, G.P.; Gan, Q.; Bartoli, F.J. Trapping of surface-plasmon polaritons in a graded bragg structure: Frequency-dependent spatially separated localization of the visible spectrum modes. Phys. Rev. B 2009, 80, 161106. [Google Scholar] [CrossRef]
- He, S.; He, Y.; Jin, Y. Revealing the truth about ‘trapped rainbow’ storage of light in metamaterials. Sci. Rep. 2012, 2, 583. [Google Scholar] [CrossRef] [PubMed]
- Noda, S.; Chutinan, A.; Imada, M. Trapping and emission of photons by a single defect in a photonic bandgap structure. Nature 2000, 407, 608. [Google Scholar] [CrossRef] [PubMed]
- Julsgaard, B.; Sherson, J.; Cirac, J.I.; Fiurášek, J.; Polzik, E.S. Experimental demonstration of quantum memory for light. Nature 2004, 432, 482. [Google Scholar] [CrossRef] [PubMed]
- Xia, F.; Sekaric, L.; Vlasov, Y. Ultracompact optical buffers on a silicon chip. Nat. Photonics 2006, 1, 65. [Google Scholar] [CrossRef]
- Yanik, M.F.; Fan, S. Dynamic photon storage. Nat. Phys. 2007, 3, 372. [Google Scholar] [CrossRef]
- Fiore, V.; Yang, Y.; Kuzyk, M.C.; Barbour, R.; Tian, L.; Wang, H. Storing optical information as a mechanical excitation in a silica optomechanical resonator. Phys. Rev. Lett. 2011, 107, 133601. [Google Scholar] [CrossRef]
- Zhu, J.; Chen, Y.; Zhu, X.; Garcia-Vidal, F.J.; Yin, X.; Zhang, W.; Zhang, X. Acoustic rainbow trapping. Sci. Rep. 2013, 3, 1728. [Google Scholar] [CrossRef]
- Senesi, M.; Ruzzene, M. A frequency selective acoustic transducer for directional lamb wave sensing. J. Acoust. Soc. Am. 2011, 130, 1899–1907. [Google Scholar] [CrossRef]
- Baravelli, E.; Senesi, M.; Ruzzene, M.; Marchi, L.D.; Speciale, N. Double-channel, frequency-steered acoustic transducer with 2-d imaging capabilities. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 1430–1441. [Google Scholar] [CrossRef]
- Kusano, Y.; Segovia-Fernandez, J.; Sonmezoglu, S.; Amirtharajah, R.; Horsley, D.A. Frequency selective mems microphone based on a bioinspired spiral-shaped acoustic resonator. In Proceedings of the 2017 19th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Kaohsiung, Taiwan, 18–22 June 2017; pp. 71–74. [Google Scholar]
- Tanaka, K.; Abe, M.; Ando, S. A novel mechanical cochlea “fishbone” with dual sensor/actuator characteristics. IEEE/ASME Trans. Mechatron. 1998, 3, 98–105. [Google Scholar] [CrossRef]
- Xu, T.; Bachman, M.; Zeng, F.-G.; Li, G.-P. Polymeric micro-cantilever array for auditory front-end processing. Sens. Actuators A Phys. 2004, 114, 176–182. [Google Scholar] [CrossRef]
- Chen, F.; Cohen, H.I.; Bifano, T.G.; Castle, J.; Fortin, J.; Kapusta, C.; Mountain, D.C.; Zosuls, A.; Hubbard, A.E. A hydromechanical biomimetic cochlea: Experiments and models. J. Acoust. Soc. Am. 2006, 119, 394–405. [Google Scholar] [CrossRef] [PubMed]
- Wittbrodt, M.J.; Steele, C.R.; Puria, S. Developing a physical model of the human cochlea using microfabrication methods. Audiol. Neurotol. 2006, 11, 104–112. [Google Scholar] [CrossRef] [PubMed]
- Shintaku, H.; Nakagawa, T.; Kitagawa, D.; Tanujaya, H.; Kawano, S.; Ito, J. Development of piezoelectric acoustic sensor with frequency selectivity for artificial cochlea. Sens. Actuators A Phys. 2010, 158, 183–192. [Google Scholar] [CrossRef]
- Foucaud, S.; Michon, G.; Gourinat, Y.; Pelat, A.; Gautier, F. Artificial cochlea and acoustic black hole travelling waves observation: Model and experimental results. J. Sound Vib. 2014, 333, 3428–3439. [Google Scholar] [CrossRef] [Green Version]
- White, R.D.; Grosh, K. Microengineered hydromechanical cochlear model. Proc. Natl. Acad. Sci. USA 2005, 102, 1296. [Google Scholar] [CrossRef]
- Atturo, F.; Schart-Morén, N.; Larsson, S.; Rask-Andersen, H.; Li, H. The human cochlear aqueduct and accessory canals: A micro-ct analysis using a 3d reconstruction paradigm. Otol. Neurotol. 2018, 39, e429–e435. [Google Scholar] [CrossRef]
- Pietsch, M.; Aguirre Dávila, L.; Erfurt, P.; Avci, E.; Lenarz, T.; Kral, A. Spiral form of the human cochlea results from spatial constraints. Sci. Rep. 2017, 7, 7500. [Google Scholar] [CrossRef]
- Kwon, B.J.; Jo, C.; Park, K.C.; Oh, I.-K. Wave propagation characteristics of acoustic metamaterials with helmholtz resonators. Korean Sci. 2013, 23. [Google Scholar] [CrossRef]
- Liu, B.; Yang, L. Transmission of low-frequency acoustic waves in seawater piping systems with periodical and adjustable helmholtz resonator. J. Mar. Sci. Eng. 2017, 5, 56. [Google Scholar]
- Yamamoto, T. Acoustic metamaterial plate embedded with helmholtz resonators for extraordinary sound transmission loss. J. Appl. Phys. 2018, 123, 215110. [Google Scholar] [CrossRef]
- Yang, X.; Yin, J.; Yu, G.; Peng, L.; Wang, N. Acoustic superlens using helmholtz-resonator-based metamaterials. Appl. Phys. Lett. 2015, 107, 193505. [Google Scholar] [CrossRef]
- Yu, X.; Lu, Z.; Cui, F.; Cheng, L.; Cui, Y. Tunable acoustic metamaterial with an array of resonators actuated by dielectric elastomer. Extreme Mech. Lett. 2017, 12, 37–40. [Google Scholar] [CrossRef] [Green Version]
- Casarini, C.; Windmill, J.F.C.; Jackson, J.C. 3D printed small-scale acoustic metamaterials based on helmholtz resonators with tuned overtones. In Proceedings of the 2017 IEEE SENSORS, Glasgow, UK, 29 October–1 November 2017; pp. 1–3. [Google Scholar]
- Dubois, M.; Shi, C.; Wang, Y.; Zhang, X. A thin and conformal metasurface for illusion acoustics of rapidly changing profiles. Appl. Phys. Lett. 2017, 110, 151902. [Google Scholar] [CrossRef]
- Faure, C.; Richoux, O.; Félix, S.; Pagneux, V. Experiments on metasurface carpet cloaking for audible acoustics. Appl. Phys. Lett. 2016, 108, 064103. [Google Scholar] [CrossRef]
- Groby, J.P.; Lagarrigue, C.; Brouard, B.; Dazel, O.; Tournat, V.; Nennig, B. Enhancing the absorption properties of acoustic porous plates by periodically embedding helmholtz resonators. J. Acoust. Soc. Am. 2015, 137, 273–280. [Google Scholar] [CrossRef]
- Jiménez, N.; Huang, W.; Romero-García, V.; Pagneux, V.; Groby, J.P. Ultra-thin metamaterial for perfect and quasi-omnidirectional sound absorption. Appl. Phys. Lett. 2016, 109, 121902. [Google Scholar] [CrossRef] [Green Version]
- Fang, N.; Xi, D.; Xu, J.; Ambati, M.; Srituravanich, W.; Sun, C.; Zhang, X. Ultrasonic metamaterials with negative modulus. Nat. Mater. 2006, 5, 452. [Google Scholar] [CrossRef] [PubMed]
- Elford, D.P.; Chalmers, L.; Kusmartsev, F.V.; Swallowe, G.M. Matryoshka locally resonant sonic crystal. J. Acoust. Soc. Am. 2011, 130, 2746–2755. [Google Scholar] [CrossRef] [PubMed]
- Comsol Multiphysics Version 5.3-Structural and Acoustics Module.
- Jiménez, N.; Romero-García, V.; Pagneux, V.; Groby, J.-P. Rainbow-trapping absorbers: Broadband, perfect and asymmetric sound absorption by subwavelength panels for transmission problems. Sci. Rep. 2017, 7, 13595. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vanhille, C. Two-dimensional numerical simulations of ultrasound in liquids with gas bubble agglomerates: Examples of bubbly-liquid-type acoustic metamaterials (blamms). Sensors 2017, 17, 173. [Google Scholar] [CrossRef] [PubMed]
- Decker, C. Kinetic study and new applications of uv radiation curing. Macromol. Rapid Commun. 2003, 23, 1067–1093. [Google Scholar] [CrossRef]
- Ni, X.; Wu, Y.; Chen, Z.-G.; Zheng, L.-Y.; Xu, Y.-L.; Nayar, P.; Liu, X.-P.; Lu, M.-H.; Chen, Y.-F. Acoustic rainbow trapping by coiling up space. Sci. Rep. 2014, 4, 7038. [Google Scholar] [CrossRef] [PubMed] [Green Version]





© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, L.; Zhou, S. Compact Acoustic Rainbow Trapping in a Bioinspired Spiral Array of Graded Locally Resonant Metamaterials. Sensors 2019, 19, 788. https://doi.org/10.3390/s19040788
Zhao L, Zhou S. Compact Acoustic Rainbow Trapping in a Bioinspired Spiral Array of Graded Locally Resonant Metamaterials. Sensors. 2019; 19(4):788. https://doi.org/10.3390/s19040788
Chicago/Turabian StyleZhao, Liuxian, and Shengxi Zhou. 2019. "Compact Acoustic Rainbow Trapping in a Bioinspired Spiral Array of Graded Locally Resonant Metamaterials" Sensors 19, no. 4: 788. https://doi.org/10.3390/s19040788
APA StyleZhao, L., & Zhou, S. (2019). Compact Acoustic Rainbow Trapping in a Bioinspired Spiral Array of Graded Locally Resonant Metamaterials. Sensors, 19(4), 788. https://doi.org/10.3390/s19040788




