A Three-Dimensional Hough Transform-Based Track-Before-Detect Technique for Detecting Extended Targets in Strong Clutter Backgrounds
Abstract
:1. Introduction
2. Models
2.1. Preliminaries
2.2. Problem Statement
3. Hough Transform Based TBD Algorithm for Extended Targets
3.1. Introduction of the 3DHT-ET-TBD
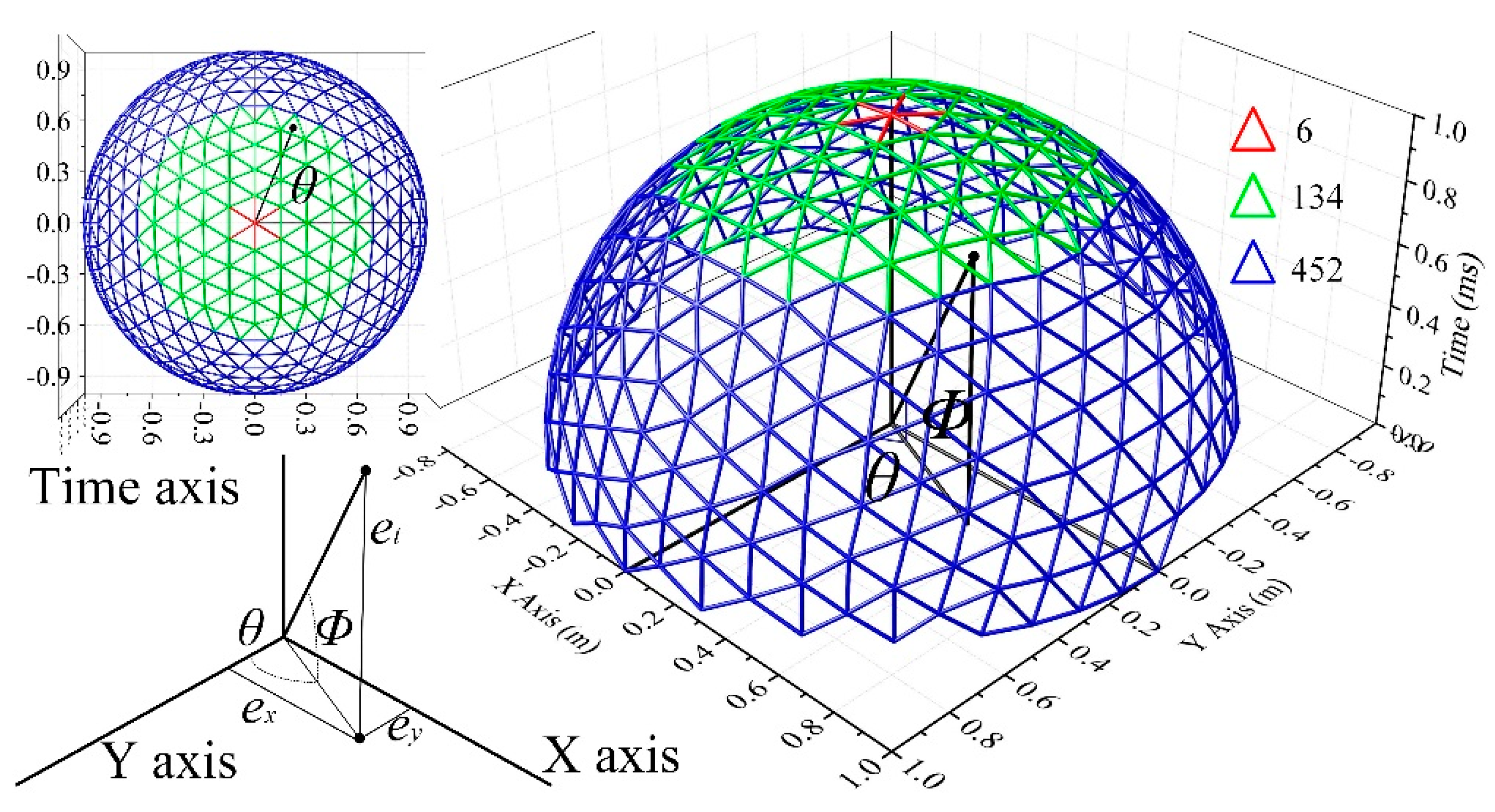
3.2. Parameter Space Discretization
3.3. Iterative Line Detection and Post-Processing
4. Simulation Results
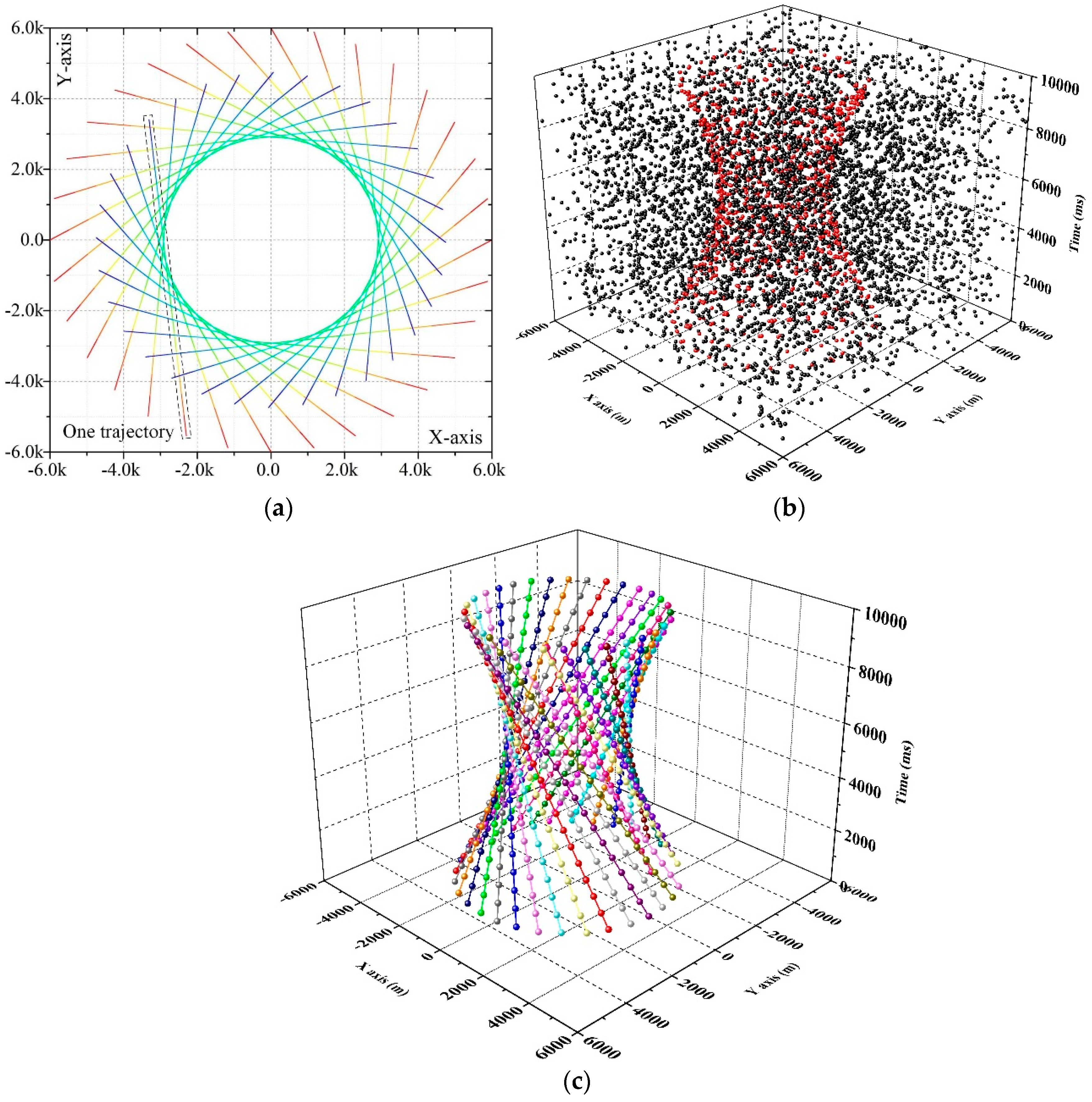
4.1. Synthetic Data
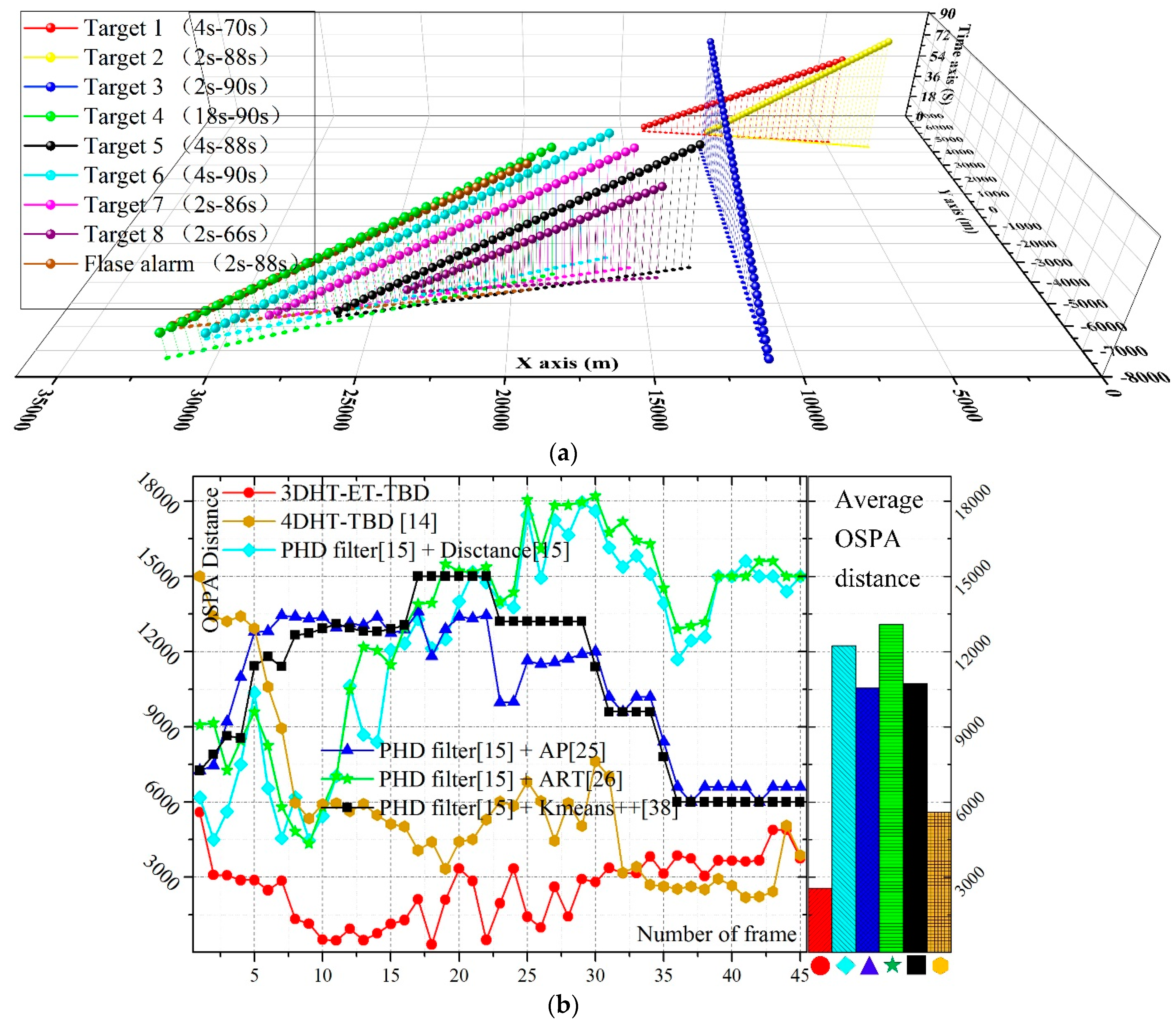
4.2. Real Data
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wei, L.; Zhang, X.; Fan, L. A TBD Algorithm Based on Improved Randomized Hough Transform for Dim Target Detection. In Proceedings of the 2010 2nd International Conference on Signal Processing Systems, Dalian, China, 5–7 July 2010. [Google Scholar]
- Errasti-Alcala, B.; Braca, P. Track before Detect Algorithm for Tracking Extended Targets Applied to Real-World Data of X-Band Marine Radar. In Proceedings of the 2014 17th International Conference on Fusion, Salamanca, Spain, 7–10 July 2014. [Google Scholar]
- Errasti-Alcala, B.; Fuscaldo, W.; Braca, P.; Vivone, G. Realistic Extended Target Model for Track before Detect in Maritime Surveillance. In Proceedings of the 2015 OCEANS—Genova, Genoa, Italy, 18–21 May 2015. [Google Scholar]
- Boers, Y.; Driessen, H.; Torstensson, J.; Trieb, M.; Karlsson, R.; Gustafsson, F. Track-before-Detect Algorithm for Tracking Extended Targets. IEE Proc. Radar Sonar Navig. 2006, 153, 345–351. [Google Scholar] [CrossRef]
- Wei, Y.; Morelande, M.R.; Lingjiang, K.; Jianyu, Y. An Efficient Multi-Frame Track-before-Detect Algorithm for Multi-Target Tracking. IEEE J. Sel. Top. Signal Process. 2013, 7, 421–434. [Google Scholar]
- Emanuele, G.; Lops, M.; Venturino, L. A Novel Dynamic Programming Algorithm for Track-Before-Detect in Radar Systems. IEEE Trans. Signal Process. 2013, 61, 2608–2619. [Google Scholar]
- Arnold, J.; Shaw, S.W.; Pasternack, H.E.N.R.I. Efficient Target Tracking using Dynamic Programming. IEEE Trans. Aerosp. Electron. Syst. 1993, 29, 44–56. [Google Scholar] [CrossRef]
- Richards, G.A. Application of the Hough Transform as a track-before-detect method. In Proceedings of the IEE Colloquium on Target Tracking and Data Fusion, Malvern, UK, 6–7 November 1996. [Google Scholar]
- Moyer, L.R.; Spak, J.; Lamanna, P. A Multi-Dimensional Hough Transform-Based Track-Before-Detect Technique for Detecting Weak Targets in Strong Clutter Backgrounds. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 3062–3068. [Google Scholar] [CrossRef]
- Yan, B.; Xu, L.; Li, M.; Yan, J.Z. A Track-Before-Detect Algorithm Based on Dynamic Programming for Multi-Extended-Targets Detection. IET Signal Process. 2017, 11, 674–686. [Google Scholar] [CrossRef]
- Lin, L.; Guohong, W.; Xiangyu, Z.; Hongbo, Y. The track initiation algorithm based on Hough Transform and space accumulation. In Proceedings of the 2016 IEEE 13th International Conference on Signal Processing (ICSP), Chengdu, China, 6–10 November 2016; pp. 1466–1470. [Google Scholar]
- Alexiev, K.M.; Bojilov, L.V. A Hough Transform track initiation algorithm for multiple passive sensors. In Proceedings of the Third International Conference on Information Fusion, Paris, France, 10–13 July 2000; pp. TUB2/11–TUB2/16. [Google Scholar]
- Mukhopadhyay, P.; Chaudhuri, B.B. A survey of Hough Transform. Pattern Recognit. 2015, 48, 993–1010. [Google Scholar] [CrossRef]
- Sobhani, B.; Zwick, T.; Chiani, M. Target TOA association with the Hough Transform in UWB radars. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 743–754. [Google Scholar] [CrossRef]
- Granstrom, K.; Lundquist, C.; Orguner, O. Extended Target Tracking Using a Gaussian-Mixture PHD Filter. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 3268–3286. [Google Scholar] [CrossRef]
- Granstrom, K.; Orguner, U. On Spawning and Combination of Extended/Group Targets Modeled with Random Matrices. IEEE Trans. Signal Process. 2013, 61, 678–692. [Google Scholar] [CrossRef]
- Beard, M.; Reuter, S.; Granström, K.; Vo, B.T.; Vo, B.N.; Scheel, A. Multiple Extended Target Tracking with Labeled Random Finite Sets. IEEE Trans. Signal Process. 2016, 64, 1638–1653. [Google Scholar] [CrossRef]
- Mahler, R. Multi target Bayes Filtering via First-Order Multitarget Moments. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1152–1178. [Google Scholar] [CrossRef]
- Mahler, R. PHD Filters for Nonstandard Targets, I: Extended targets. In Proceedings of the 12th International Conference on Information Fusion, Seattle, WA, USA, 6–9 July 2009. [Google Scholar]
- Gilholm, K.; Godsill, S.; Maskell, S. Poisson Models for Extended Target and Group Tracking. Int. Soc. Opt. Photonics 2005, 5913, 59130R. [Google Scholar]
- Koch, J.W. Bayesian Approach to Extended Object and Cluster Tracking using Random Matrices. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 1042–1059. [Google Scholar] [CrossRef]
- Musicki, D.; Evans, R. Joint Integrated Probabilistic Data Association: JIPDA. IEEE Trans. Aerosp. Electron. Syst. 2004, 40, 1093–1099. [Google Scholar] [CrossRef]
- Musicki, D.; La Scala, B.F.; Evans, R.J. Integrated Track Splitting Filter—Efficient Multi-scan Single Target Tracking in Clutter. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 1409–1425. [Google Scholar]
- Puranik, S.; Tugnait, J.K. Tracking of Multiple Maneuvering Targets using Multiscan JPDA and IMM Filtering. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 23–35. [Google Scholar] [CrossRef]
- Zhang, T.; Wu, R. Affinity Propagation Clustering of Measurements for Multiple Extended Target Tracking. Sensors 2015, 15, 22646–22659. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Ji, H. A Robust and Fast Partitioning Algorithm for Extended Target Tracking using a Gaussian Inverse Wishart PHD Filter. Knowl.-Based Syst. 2016, 95, 125–141. [Google Scholar] [CrossRef]
- Dalitz, C.; Schramke, T.; Jeltsch, M. Iterative Hough Transform for Line Detection in 3D Point Clouds. IEEE Trans. Image Process. 2017, 7, 184–196. [Google Scholar] [CrossRef] [Green Version]
- Duda, R.O.; Hart, P.E. Use of the Hough Transformation to Detect Lines and Curves in Pictures. Commun. ACM 1972, 15, 11–15. [Google Scholar] [CrossRef]
- Ji, J.; Chen, G.; Sun, L. A Novel Hough Transform Method for Line Detection by Enhancing Accumulator Array. Pattern Recognit. Lett. 2011, 32, 1503–1510. [Google Scholar] [CrossRef]
- Xia, D.; Cha, H.; Xiao, C.; Lin, J. A New Hough Transform Applied in Track Initiation. In Proceedings of the IEEE International Conference on Consumer Electronics, Communications and Networks, XianNing China, 16–18 April 2011. [Google Scholar]
- Zhang, Y.; Su, X.; Ma, P. Multi-Hough Transform Track Initiation for Detecting Target with Constant Acceleration. In Proceedings of the IEEE Computer Society International Symposium on Information Science and Engieering, Shanghai, China, 20–22 December 2008. [Google Scholar]
- Yan, B.; Xu, L.P.; Yang, Y.; Li, C. Improved Plot Fusion Method for Dynamic Programming Based Track Before Detect Algorithm. AEU Int. J. Electron. Commun. 2017, 74, 31–43. [Google Scholar] [CrossRef]
- Yan, B.; Xu, L.P.; Yan, J.Z.H.; Li, C. An Efficient Extended Target Detection Method Based on Region Growing and Contour Tracking Algorithm. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2017, 232, 825–836. [Google Scholar] [CrossRef]
- Li, T. Single-Road-Constrained Positioning Based on Deterministic Trajectory Geometry. IEEE Commun. Lett. 2019, 23, 80–83. [Google Scholar] [CrossRef]
- Olson, C.F. Constrained Hough Transforms for Curve Detection. Comput. Vis. Image Underst. 1999, 73, 329–345. [Google Scholar] [CrossRef] [Green Version]
- Roberts, K.S. A New Representation for a Line. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Ann Arbor, MI, USA, 5–9 June 1988. [Google Scholar]
- Nadarajah, N.; Tharmarasa, R.; McDonald, M.; Kirubarajan, T. IMM Forward Filtering and Backward Smoothing for Maneuvering Target Tracking. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2673–2678. [Google Scholar] [CrossRef]
- Arthur, D.; Vassilvitskii, S. K-means++: The advantages of careful seeding. In Proceedings of the ACM-SIAM Symposium on Discrete Algorithms, Philadelphia, PA, USA, 7–9 January 2007; pp. 1027–1035. [Google Scholar]




| Measurement Rate γ | Measurement Noise (m) | Number of Clutter Per Square (1/m2) | |
|---|---|---|---|
| Scenario 1 | 4 | 10 | 6 × 10−7 |
| Scenario 2 | 4 | 50 | 6 × 10−7 |
| Scenario 3 | 4 | 100 | 6 × 10−7 |
| Scenario 4 | 4 | 50 | 1.2 × 10−6 |
| Scenario 5 | 4 | 50 | 1.8 × 10−6 |
| Scenario 6 | 2 | 10 | 6 × 10−7 |
| Scenario 7 | 2 | 50 | 6 × 10−7 |
| Scenario 8 | 2 | 100 | 6 × 10−7 |
| Scenario 9 | 2 | 50 | 1.2 × 10−6 |
| Scenario 10 | 2 | 50 | 1.8 × 10−6 |
| 3DHT-ET-TBD | 4DHT-TBD [14] | PHDF [15] + Distance [15] | PHDF [15] + AP [25] | PHDF [15] + ART [26] | PHDF [15] + Kmeans++ [38] | |
|---|---|---|---|---|---|---|
| Scenario 1 | 993.8 | 1791.0 | 1755.3 | 1529 | 1797.6 | 1976.5 |
| Scenario 2 | 1530.8 | 2765.4 | 2467.6 | 1811.3 | 5725.1 | 2604.6 |
| Scenario 3 | 2963.1 | 6450.5 | 6132.1 | 6029 | 6890.3 | 3956.7 |
| Scenario 4 | 1327 | 2782.2 | 3188.4 | 1536.3 | 5108.9 | 2664.3 |
| Scenario 5 | 1600.3 | 2820.9 | 4408.2 | 1628.5 | 4468.7 | 2924.1 |
| Scenario 6 | 1232.3 | 2806.1 | 1540.3 | 2828.7 | 1156.2 | 5018.8 |
| Scenario 7 | 2152.6 | 3747.7 | 3105.4 | 3571.2 | 6212.2 | 5183.4 |
| Scenario 8 | 4303.5 | 6634.1 | 6063.6 | 4396.7 | 4665.5 | 4160 |
| Scenario 9 | 2101.1 | 3155.8 | 4874.6 | 3279.5 | 3784.3 | 3017.4 |
| Scenario 10 | 2336.5 | 3572.5 | 4861.1 | 3204.5 | 3929.1 | 3499 |
| Measurement Rate γ | Probability of Detection and Survival | Covariance of Systematic Error | Covariance of Measuring Error (m,°) | Number of Clutter Per Squre (1/m2) | |
|---|---|---|---|---|---|
| Scenario 1 | 4 | (0.99,0.99) | 10 | (20, 1.17) | 6 × 10−7 |
| Scenario 5 | 4 | (0.99,0.99) | 50 | (20, 1.17) | 1.8 × 10−6 |
| Scenario 8 | 2 | (0.99,0.99) | 100 | (20, 1.17) | 6 × 10−7 |
| Real data | 4 | (0.99,0.99) | 50 | (20, 1.17) | 6 × 10−7 |
| Parameters in the 3DHT-ET-TBD | Parameter Values Used in the 4DHT | ||
|---|---|---|---|
| Number of bins in X axis Nx | 100 | Number of bins in X axis Nx | 100 |
| Width of bins in X axis (m) | 160 | Width of bins in X axis (m) | 160 |
| Number of bins in Y axis Ny | 100 | Number of bins in Y axis Ny | 100 |
| Width of bins in Y axis (m) | 160 | Width of bins in Y axis (m) | 160 |
| Minimum vote count | 30 | Minimum vote count | 30 |
| Threshold of points d in Equation (16) | 160 | Threshold of points d in Equation (16) | 160 |
| Length of sliding window | 7 | Length of sliding window | 7 |
| Number of bins in 3D direction Nd | 541 | Number of bins in velocity Nv | 60 |
| Width of bins in velocity (m/s) | 15 | ||
| Number of bins in course Nc | 90 | ||
| Width of bins in course (°) | 4 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, B.; Xu, N.; Zhao, W.-B.; Xu, L.-P. A Three-Dimensional Hough Transform-Based Track-Before-Detect Technique for Detecting Extended Targets in Strong Clutter Backgrounds. Sensors 2019, 19, 881. https://doi.org/10.3390/s19040881
Yan B, Xu N, Zhao W-B, Xu L-P. A Three-Dimensional Hough Transform-Based Track-Before-Detect Technique for Detecting Extended Targets in Strong Clutter Backgrounds. Sensors. 2019; 19(4):881. https://doi.org/10.3390/s19040881
Chicago/Turabian StyleYan, Bo, Na Xu, Wen-Bo Zhao, and Lu-Ping Xu. 2019. "A Three-Dimensional Hough Transform-Based Track-Before-Detect Technique for Detecting Extended Targets in Strong Clutter Backgrounds" Sensors 19, no. 4: 881. https://doi.org/10.3390/s19040881
APA StyleYan, B., Xu, N., Zhao, W.-B., & Xu, L.-P. (2019). A Three-Dimensional Hough Transform-Based Track-Before-Detect Technique for Detecting Extended Targets in Strong Clutter Backgrounds. Sensors, 19(4), 881. https://doi.org/10.3390/s19040881




