Detection of Induced GNSS Spoofing Using S-Curve-Bias
Abstract
:1. Introduction
2. Signal Model
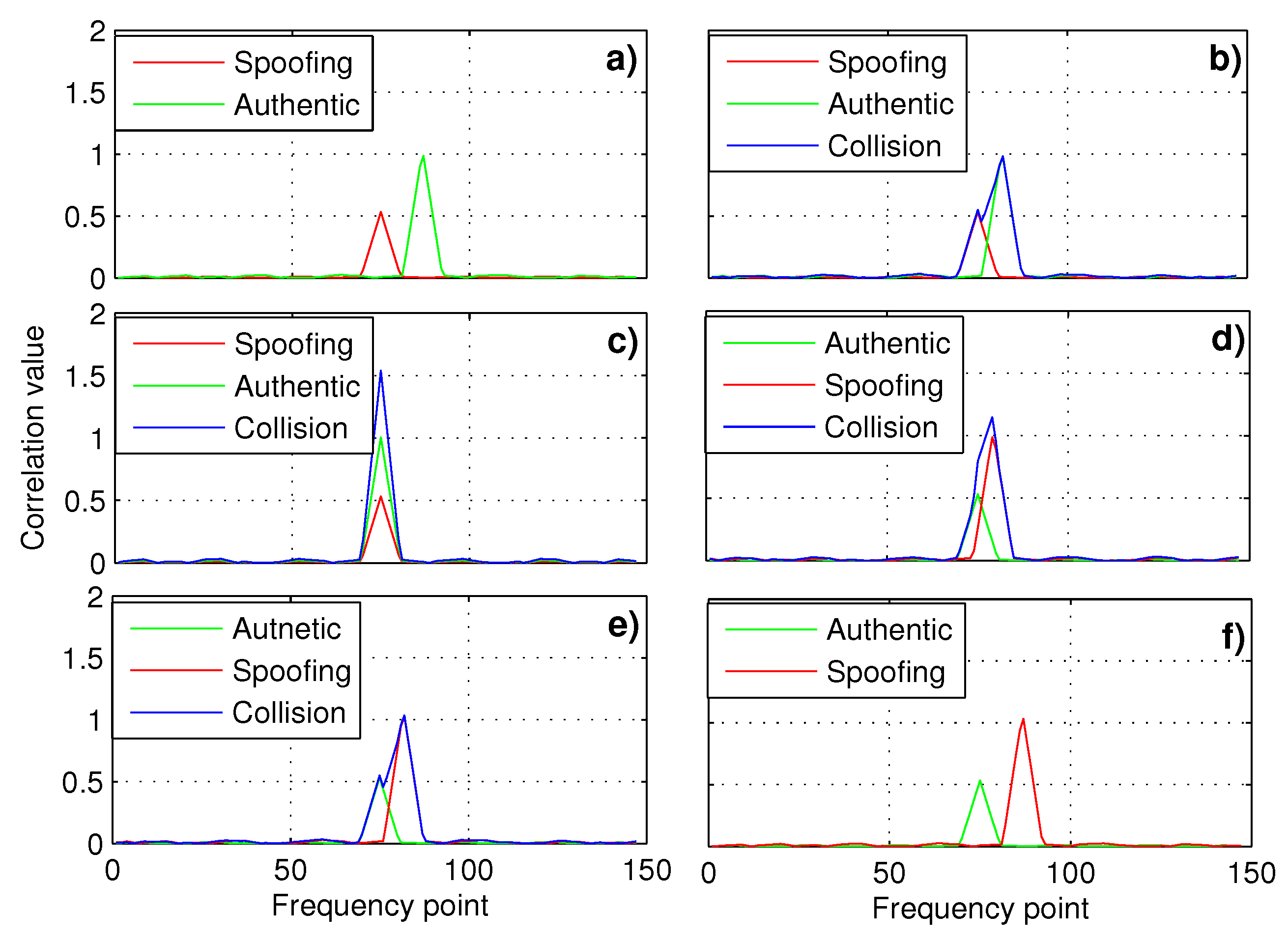
3. Detection of Induced Spoofing
3.1. The Proposed Method
3.2. Probability Analysis
4. Experiments
4.1. Introduction of TEXBAT Data Sets
4.2. Ratio Test Detection Method
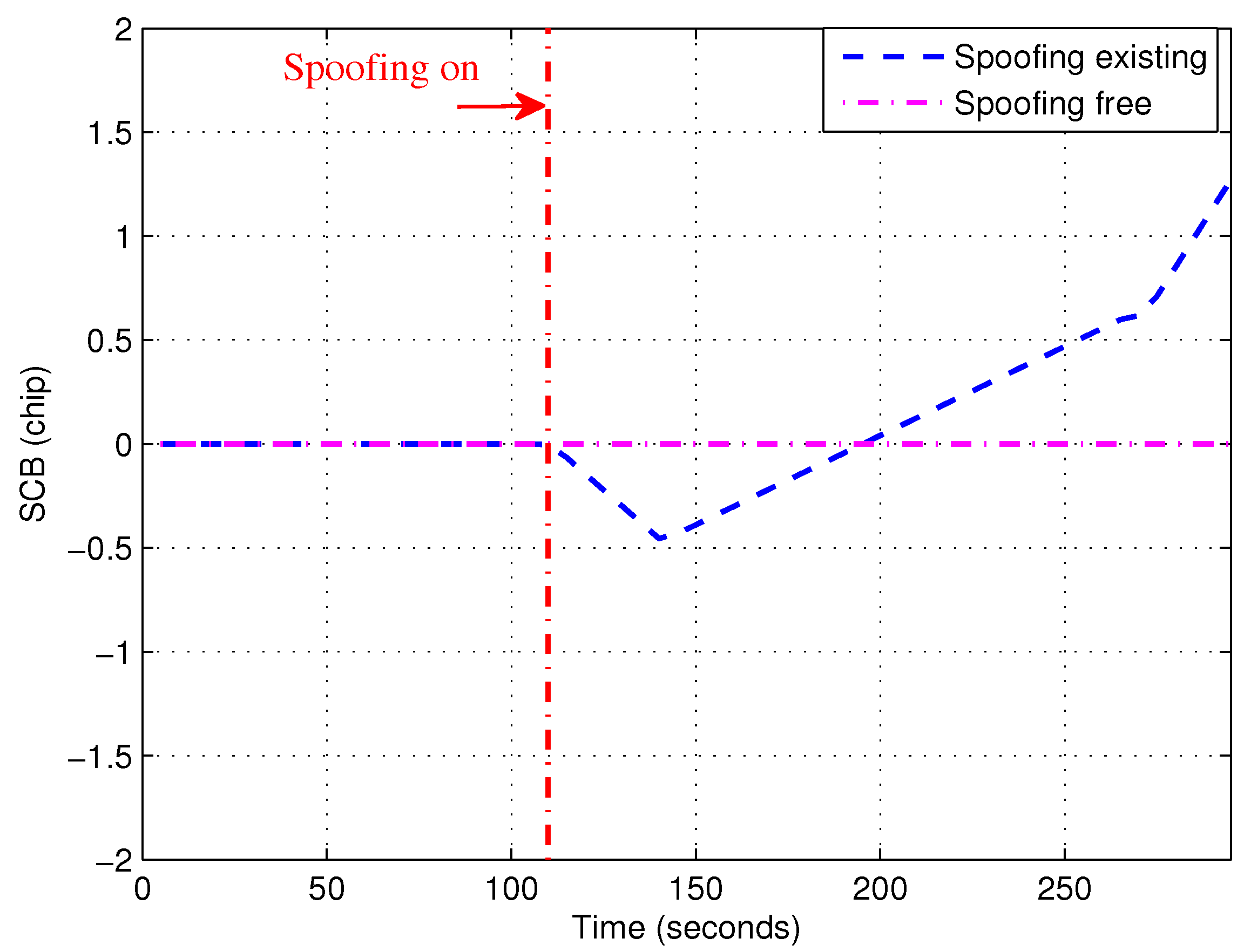
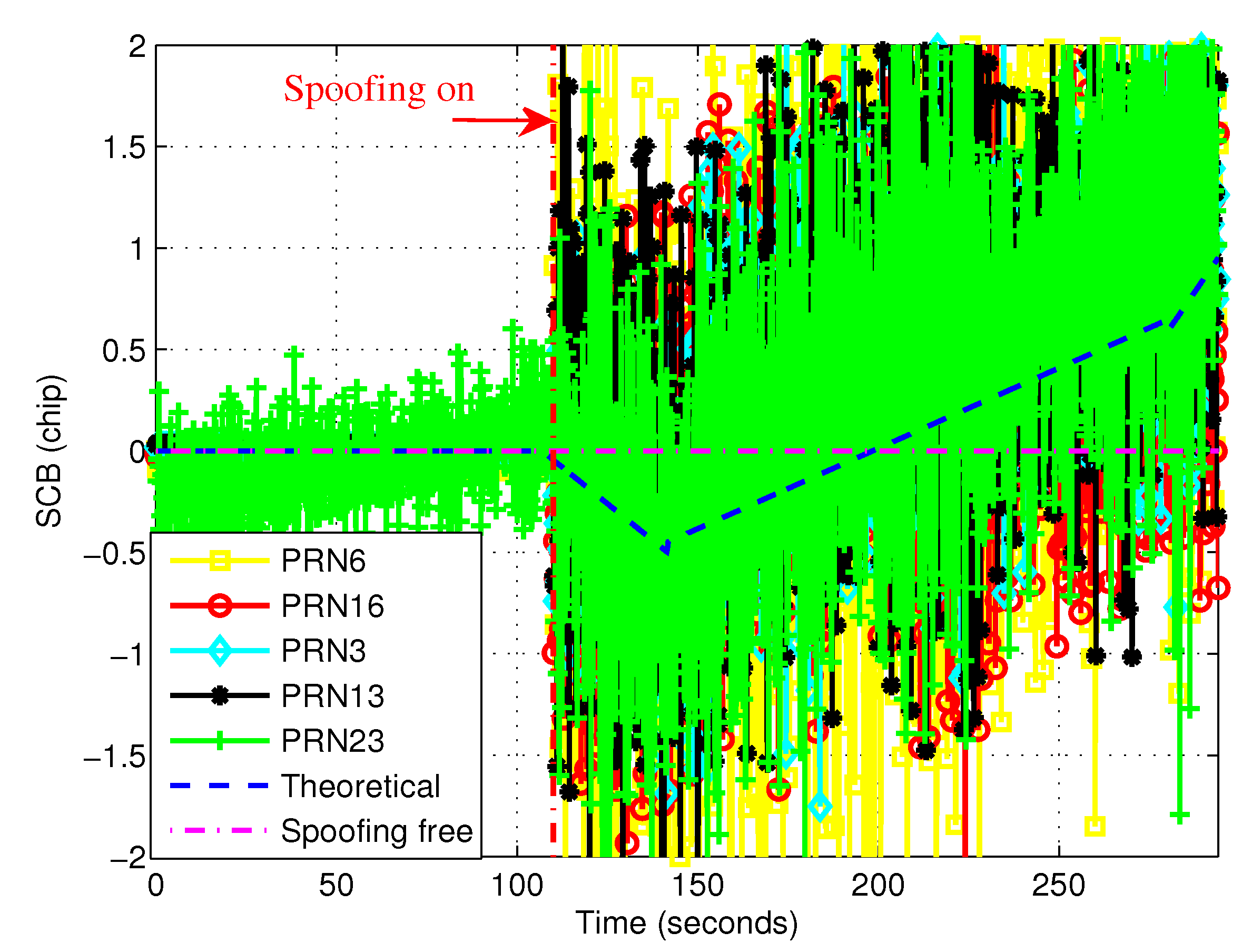
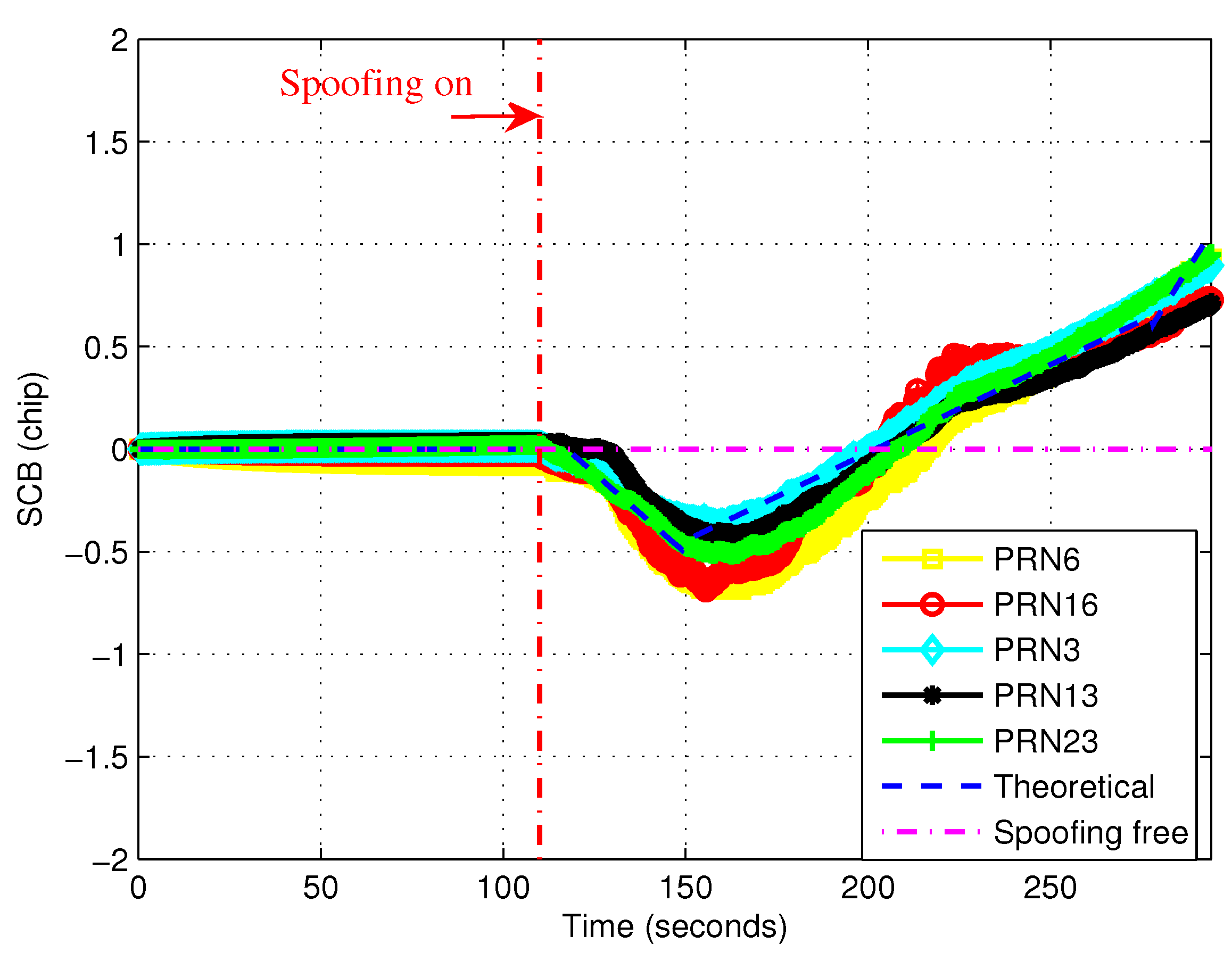
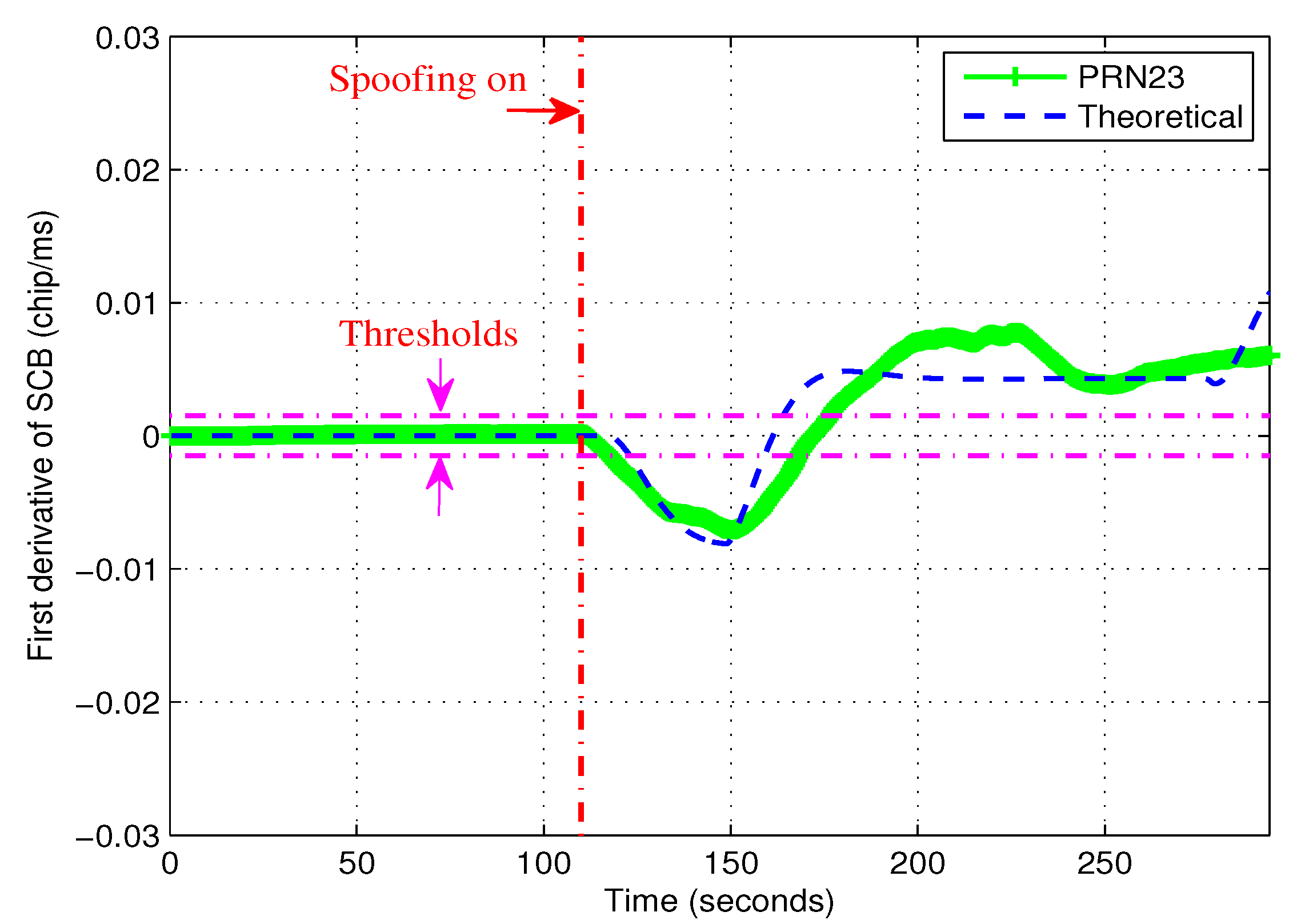
4.3. Results of the Proposed Method
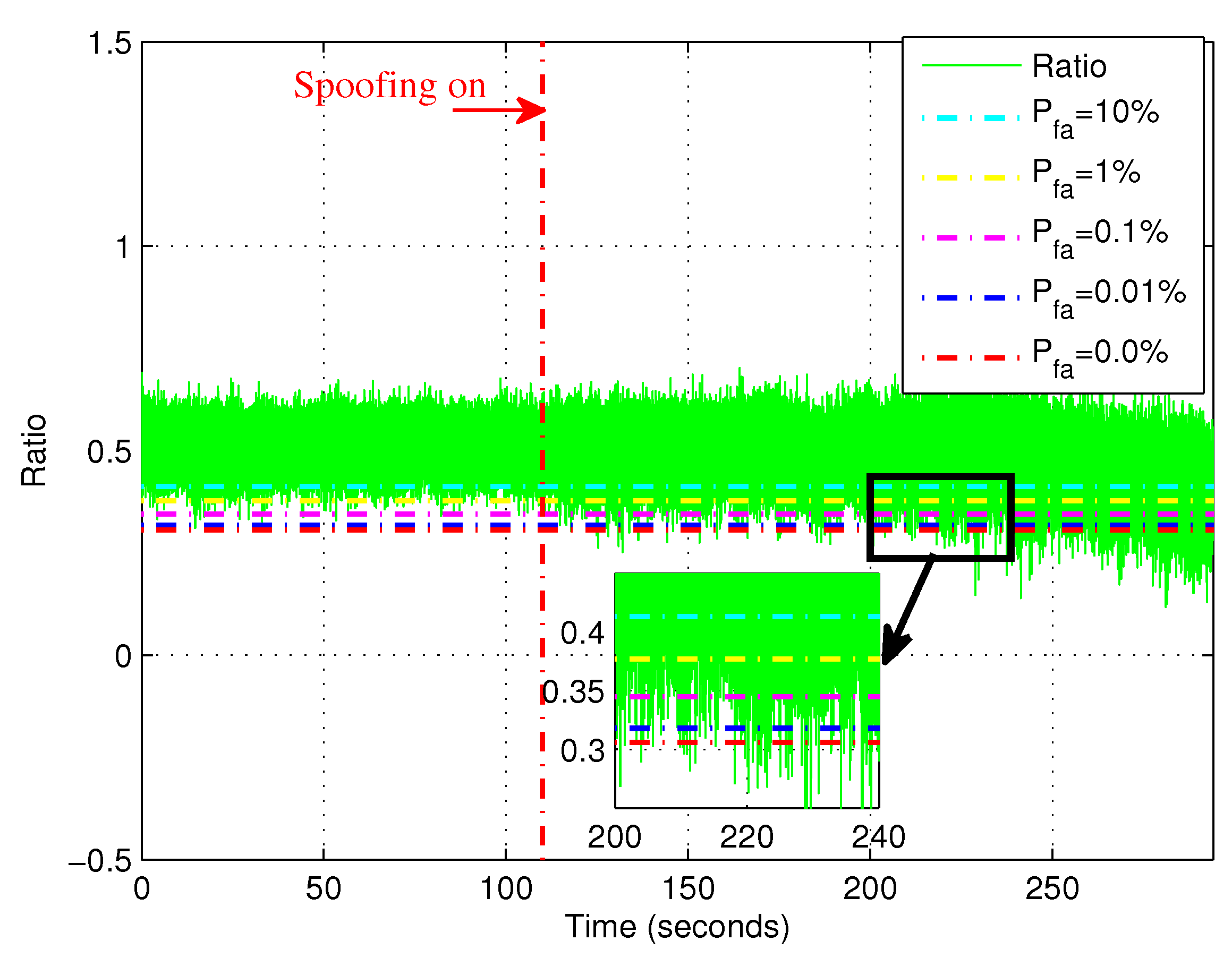
4.4. Results of Ratio Method
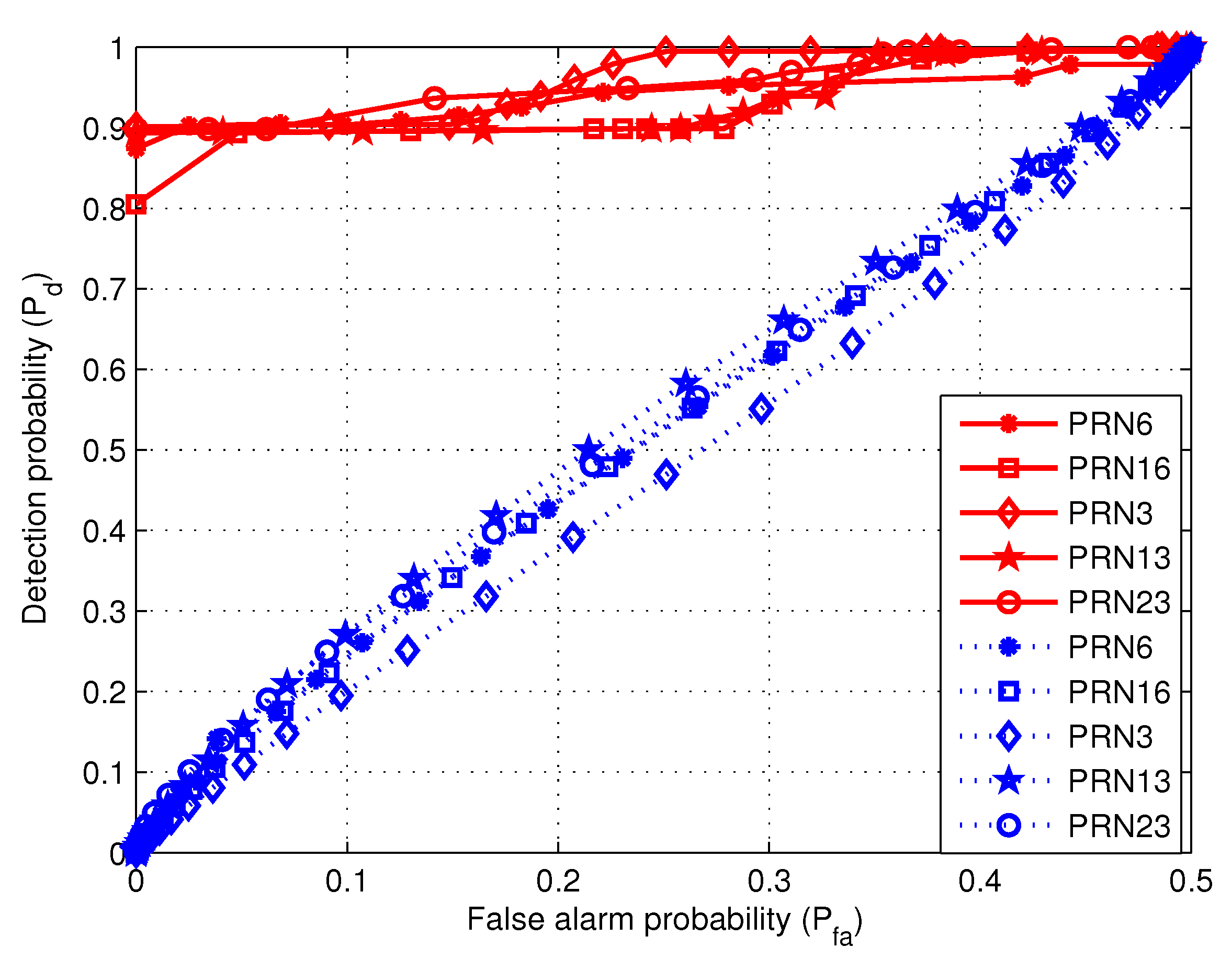
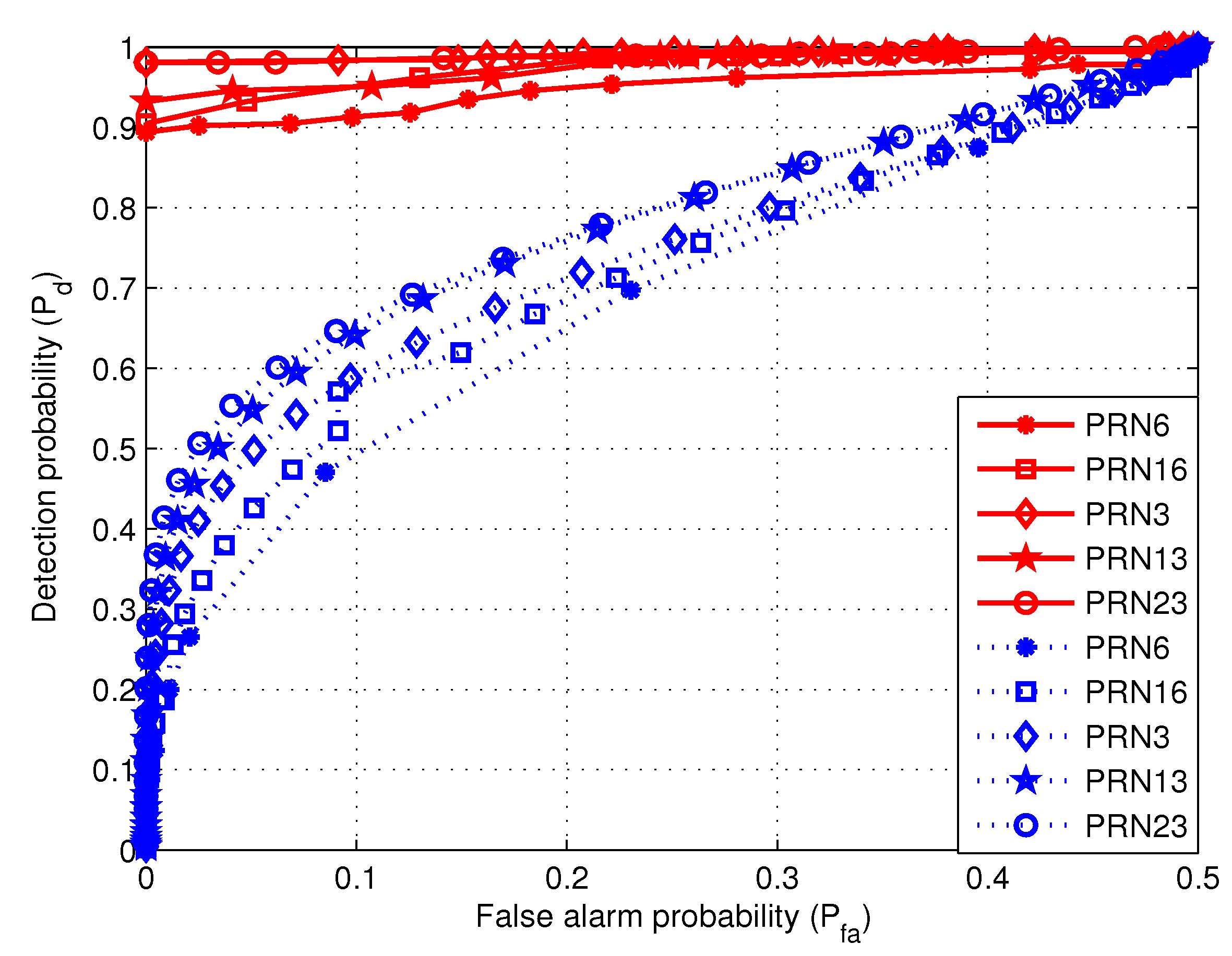
4.5. Comparison of Two Methods
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- European GNSS Agency. GNSS Market Report; Technical Report; GSA: Prague, Czech Republic, 2017.
- Amin, M.G.; Closas, P.; Broumandan, A.; Volakis, J.L. Vulnerabilities, threats, and authentication in satellite-based navigation systems [scanning the issue]. Proc. IEEE 2016, 104, 1169–1173. [Google Scholar] [CrossRef]
- Ali, K.; Manfredini, E.G.; Dovis, F. Vestigial signal defense through signal quality monitoring techniques based on joint use of two metrics. In Proceedings of the IEEE/ION PLANS, Monterey, CA, USA, 5–8 May 2014; pp. 1240–1247. [Google Scholar]
- Bhatti, J.; Humphreys, T.E. Hostile control of ships via false GPS signals: Demonstration and detection. Navigation 2017, 64, 51–66. [Google Scholar] [CrossRef]
- Shepard, D.P.; Humphreys, T.E.; Fansler, A.A. Evaluation of smart grid and civilian UAV vulnerability to GPS spoofing attacks. In Proceedings of the ION GNSS Meeting, Nashville, TN, USA, 19–22 September 2012; pp. 19–21. [Google Scholar]
- Psiaki, M.L.; Humphreys, T.E.; Stauffer, B. Attackers can spoof navigation signals without our knowledge. Heres how to fight back GPS lies. IEEE Spectr. 2016, 53, 26–53. [Google Scholar] [CrossRef]
- Humphreys, T.E.; Ledvina, B.M.; Psiaki, M.L.; O’Hanlon, B.W.; Kintner, P.M. Assessing the spoofing threat: Development of a portable GPS civilian spoofer. In Proceedings of the ION GNSS Meeting, Savannah, GA, USA, 16–19 September 2008; pp. 16–19. [Google Scholar]
- Humphreys, T.E.; Shepard, D.P.; Bhatti, J.A.; Wesson, K.D. A testbed for developing and evaluating GNSS signal authentication techniques. In Proceedings of the CERGAL, Dresden, Germany, 8–9 July 2014. [Google Scholar]
- Jafarnia-Jahromi, A.; Broumandan, A.; Nielsen, J.; Lachapelle, G. GPS vulnerability to spoofing threats and a review of antispoofing techniques. Int. J. Navig. Obs. 2012, 2012, 1–16. [Google Scholar] [CrossRef]
- Montgomery, P.Y.; Humphreys, T.E.; Ledvina, B.M. A multiantenna defense: Receiver-autonomous GPS spoofing detection. Inside GNSS 2009, 4, 40–46. [Google Scholar]
- McDowell, C.E. GPS Spoofer and Repeater Mitigation System Using Digital Spatial Nulling. U.S. Patent 7,250,903 B1, 31 July 2007. [Google Scholar]
- Wang, J.; Zhou, M.; Li, H.; Cui, X.; Lu, M. On the requirements of GNSS intermediate spoofing. In Proceedings of China Satellite Navigation Conference (CSNC); Lecture Notes in Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2014; Volume 303, pp. 543–552. [Google Scholar]
- Ioannides, R.; Pany, T.; Gibbons, G. Known vulnerabilities of global navigation satellite systems, status, and potential mitigation techniques. Proc. IEEE 2016, 104, 1174–1194. [Google Scholar] [CrossRef]
- Psiaki, M.L.; Humphreys, T.E. GNSS spoofing and detection. Proc. IEEE 2016, 104, 1258–1270. [Google Scholar] [CrossRef]
- Montgomery, P.Y.; Humphreys, T.E.; Ledvina, B.M. Receiver autonomous spoofing detection: Experimental results of a multi-antenna receiver defense against a portable civil GPS spoofer. In Proceedings of the ION GNSS Meeting, Anaheim, CA, USA, 26–28 January 2009; pp. 124–130. [Google Scholar]
- Jafarnia-Jahromi, A.; Broumandan, A.; Nielsen, J.; Lachapelle, G. GPS spoofer countermeasure effectiveness based on signal strength, noise power and C/N0 observables. Int. J. Satell. Commun. Netw. 2012, 30, 181–191. [Google Scholar] [CrossRef]
- Borio, D.; Gioia, C. A sum-of-squares approach to GNSS spoofing detection. IEEE Trans. Aerosp. Electr. Syst. 2016, 52, 1756–1768. [Google Scholar] [CrossRef]
- Moshavi, S. Multi-user detection for DS-CDMA communications. IEEE Commun. Mag. 1996, 34, 124–136. [Google Scholar] [CrossRef]
- Dehghanian, V.; Nielsen, J.; Lachapelle, G. GNSS spoofing detection based on receiver C/N0 estimates. In Proceedings of the ION GNSS Meeting, Nashville, TN, USA, 17–21 September 2012; pp. 2878–2884. [Google Scholar]
- Gamba, M.T.; Truong, M.D.; Motella, B.; Falletti, E.; Ta, T.H. Hypothesis testing methods to detect spoofing attacks: A test against the TEXBAT datasets. GPS Solut. 2017, 21, 577–589. [Google Scholar] [CrossRef]
- Jafarnia-Jahromi, A.; Lin, T.; Broumandan, A.; Nielsen, J.; Lachapelle, G. Detection and mitigation of spoofing attack on a vector based tracking GPS receiver. In Proceedings of the ION GNSS Meeting, Portland, OR, USA, 19–23 September 2011; pp. 790–800. [Google Scholar]
- Yuan, D.; Li, H.; Wang, F.; Lu, M. A GNSS acquisition method with the capability of spoofing detection and mitigation. Chin. J. Electron. 2018, 27, 213–222. [Google Scholar] [CrossRef]
- Lo, S.C.; Enge, P.K. Authenticating aviation augmentation system broadcasts. In Proceedings of the IEEE/ION PLANS, Indian Wells, CA, USA, 4–6 May 2010; pp. 708–717. [Google Scholar]
- Fantino, M.; Molino, A.; Mulassano, P.; Nicola, M.; Rao, M. Signal quality monitoring: correlation mask based on ratio test metrics for multipath detection. In Proceedings of the IGNSS, Surfers Paradise, QLD, Australia, 1–3 December 2009. [Google Scholar]
- Wesson, K.D.; Rothlisberger, M.; Humphreys, T.E. Practical cryptographic civil GPS signal authentication. Navigation 2012, 59, 177–193. [Google Scholar] [CrossRef]
- Broumandan, A.; Jafarnia-Jahromi, A.; Lachapelle, G. Spoofing detection, classification and cancelation (SDCC) receiver architecture for a moving GNSS receiver. GPS Solut. 2014, 19, 1–13. [Google Scholar] [CrossRef]
- Closas, P.; Arribas, J.; Fernández-Prades, C. Spoofing detection by a reduced acquisition process. In Proceedings of the Precise Time and Time Interval Systems and Applications Meeting (ION PTTI 2016), Monterey, CA, USA, 25–28 January 2016. [Google Scholar]
- Wang, F.; Li, H.; Lu, M. GNSS spoofing detection and mitigation based on maximum likelihood estimation. Sensors 2017, 17, 1532. [Google Scholar] [CrossRef] [PubMed]
- Pini, M.; Fantino, M.; Cavaleri, A.; Ugazio, S.; Lo Presti, L. Signal quality monitoring applied to spoofing detection. In Proceedings of the ION GNSS Meeting, Portland, OR, USA, 20–23 September 2001; pp. 1888–1896. [Google Scholar]
- Phelts, P.; Akos, D.; Enge, P. Robust signal quality monitoring and detection of evil waverforms. In Proceedings of the ION GNSS+ Meeting, Salt Lake City, UT, USA, 19–22 September 2000; pp. 1180–1190. [Google Scholar]
- Mitelman, A.M. Signal Quality Monitoring for GPS Augmentation System. Ph.D. Thesis, Stanford University, Stanford, CA, USA, January 2005. [Google Scholar]
- Phelts, R.E. Multicorrelator Techniques for Robust Mitigation of Threats to GPS Signal Quality. Ph.D. Thesis, Stanford University, Stanford, CA, USA, October 2001. [Google Scholar]
- Cavaleri, A.; Motella, B.; Pini, M.; Fantino, M. Detection of spoofed GPS signals at code and carrier tracking level. In Proceedings of the NAVITEC’10, ESA/ESTEC, Noordwijk, The Netherlands, 8–10 December 2010; pp. 2875–2884. [Google Scholar]
- Manfredini, E.G.; Dovis, F.; Motella, B. Validation of a signal quality monitoring technique over a set of spoofed scenarios. In Proceedings of the NAVITEC’14, ESA/ESTEC, Noordwijk, The Netherlands, 3–5 December 2014; pp. 1–7. [Google Scholar]
- Jafarnia-Jahromi, A.; Broumandan, A.; Daneshmand, S.; Lachapelle, G.; Ioannides, R.T. Galileo signal authenticity verification using signal quality monitoring methods. In Proceedings of the ICL-GNSS, Barcelona, Spain, 28–30 June 2016; pp. 1–8. [Google Scholar]
- Yang, Y.; Li, H.; Lu, M. Performance assessment of signal quality monitoring based GNSS spoofing detection techniques. In Proceedings of the CSNC 2015, Xi’an, China, 13–15 May 2015; pp. 783–793. [Google Scholar]
- Soellner, M.; Kurzhals, C.; Hechenblaikner, G.; Rapisarda, M.; Burger, T.; Erker, S.; Furthner, J.; Grunert, U.; Meurer, M.; Tholert, S. GNSS offline signal quality assessment. In Proceedings of the ION GNSS+ Meeting, Fairfax, VA, USA, 16–19 September 2007; pp. 164–182. [Google Scholar]
- Humphreys, T.E.; Bhatti, J.A.; Shepard, D.P.; Wesson, K.D. The Texas spoofing test battery: Toward a standard for evaluating GNSS signal authentication techniques. In Proceedings of the ION GNSS+ Meeting, Nashville, TN, USA, 17–21 September 2012; pp. 3569–3583. [Google Scholar]
- Laboratory, T.R. Texas Spoofing Test Battery (TEXBAT). Available online: http://radionavlab.ae.utexas.edu/texbat (accessed on 22 February 2019).
- Closas, P.; Fernández-Prades, C. A statistical multipath detector for antenna array based GNSS receivers. IEEE Trans. Wirel. Commun. 2011, 10, 916–929. [Google Scholar] [CrossRef]
- Jia, Q.; Wu, R.; Wang, W.; Lu, D.; Wang, L.; Li, J. Multipath interference mitigation in GNSS via WRELAX. GPS Solut. 2017, 21, 487–498. [Google Scholar] [CrossRef]
- Humphreys, T.E. Texbat Data Sets 7 and 8. 2015. Available online: http://radionavlab.ae.utexas.edu/ datastore/texbat/texbat_ds7_and_ds8.pdf (accessed on 22 February 2019).



| False Alarm Probability (%) | Detection Threshold | |
|---|---|---|
| 1 | 10 | 1.421 × |
| 2 | 1 | 1.476 × |
| 3 | 0.1 | 1.480 × |
| 4 | 0.01 | 1.485 × |
| 5 | 0 | 1.495 × |
| False Alarm Probability (%) | Detection Threshold | |
|---|---|---|
| 1 | 10 | 0.455 |
| 2 | 1 | 0.413 |
| 3 | 0.1 | 0.379 |
| 4 | 0.01 | 0.342 |
| 5 | 0 | 0.315 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Li, N.; Wu, R.; Closas, P. Detection of Induced GNSS Spoofing Using S-Curve-Bias. Sensors 2019, 19, 922. https://doi.org/10.3390/s19040922
Wang W, Li N, Wu R, Closas P. Detection of Induced GNSS Spoofing Using S-Curve-Bias. Sensors. 2019; 19(4):922. https://doi.org/10.3390/s19040922
Chicago/Turabian StyleWang, Wenyi, Na Li, Renbiao Wu, and Pau Closas. 2019. "Detection of Induced GNSS Spoofing Using S-Curve-Bias" Sensors 19, no. 4: 922. https://doi.org/10.3390/s19040922
APA StyleWang, W., Li, N., Wu, R., & Closas, P. (2019). Detection of Induced GNSS Spoofing Using S-Curve-Bias. Sensors, 19(4), 922. https://doi.org/10.3390/s19040922





