1. Introduction
Object detection and classification in remote sensing images are hot research topics in earth observation applications. With the development of object detection and classification techniques, a lot of convolutional neural network (CNN)-based methods [
1,
2,
3,
4,
5,
6,
7] are adopted in real-time processing systems, such as spaceborne and airborne systems. However, considering the huge volume of remote sensing images and the high requirements for storage and computing resources, deploying these successful CNN models in real-time processing systems is a challenging task [
8,
9]. To accomplish this task, many researchers adopt a high-performance device as the implementation platform for CNNs. Despite the amazing performance of CNN’s implementation, graphics processing units (GPUs) and central processing units (CPUs) are not very suitable for being loaded in remote sensing systems, as the high power consumption far exceeds the constraints. The field-programmable gate arrays (FPGAs) or application-specific integrated circuits (ASICs) spend less power and provide better performance per watt consumption than GPUs. While the on-chip resources of these platforms are limited, designers still prefer to adopt these platforms in remote sensing applications. However, most state-of-the-art CNN models have the characteristics of intensive complexities and dense calculations, which hinder their deployments in these low-power devices. Therefore, facing the constrains of remote sensing real-time processing platforms, we must provide optimization strategies and corresponding hardware designs to make it possible for CNN-based methods to be implemented in real-time processing platforms.
Recently, there have been a lot of studies on reducing the model complexities of CNNs, and several previous works [
10,
11,
12] proved that convolutional and fully connected operations have a high consumption of computing and storage resources. To reduce these requirements, state-of-the-art methods can be roughly divided into two categories: (1) network structure compression; (2) quantization of CNNs. Both category methods are friendly to hardware implementation.
Extensive studies in the first category are dedicated to the exploration of compact network architectures, which exploit efficient computations. Iandola et al. [
13] proposed an efficient macro-architecture, called Fire Module, which used 1×1 size to replace most 3×3 size of convolution kernels to reduce the parameters of CNNs. This strategies have been evaluated on AlexNet [
14], and the results showed that the parameters are reduced by 50 times. Howard et al. [
15] exploited a similar method to simplify the model using Depth-wise Separable Convolution, which had nearly the same accuracy as VGG-16 [
16], with a 32× smaller model size and 27× less computing consumption. Zhang et al. [
17] proposed Channel Shuffle for Group Convolutions, which generalized the group convolution and depth-wise separable convolution in a novel form. Maintaining a comparable accuracy, ShuffleNet provided 13× speeds up over AlexNet on an ARM-based mobile device. Some other researchers attempted to eliminate weight redundancies within CNNs. Liu et al. [
18] proposed Sparse Convolutional Neural Networks (SCNN) to reduce the inherent redundancy. The evaluation result on the PASCAL VOC2007 [
19] dataset showed that although SCNN had approximately 2% accuracy degradation, it gained a faster server speed. Denil et al. [
20] found that it is feasible to accurately predict up to 95% of weights, with a few determined values for each feature map in several deep learning models. In a similar vein, Wang et al. [
21] proposed an improved oriented response network (IORN) using average active rotating filters (A-ARFs). While gaining great performance in oriented prediction, the weights are also compressed 4 to 8 times.
In the second category, researchers are exploring another way, which is to quantize the models, converting the floating-point precision into lower bit-width fixed-point numerical representation. This type of methods aims at increasing the computation efficiency via approximate multiplications and additions. Gupta et al. [
22] proved that it was feasible to train models with 16-bit fixed-point representation, while the degradation of classification accuracy was negligible. Gysel et al. [
23] proposed an approximation framework in Caffe [
24] using dynamic fixed-point (DFP) quantization and argued that DFP had a more stable accuracy than static fixed-point (SFP). Courbariaux et al. [
25] applied a similar approach for classification in three distinct formats: floating-point, fixed-point, and DFP. The results showed that DFP seemed well suited to training deep neural networks. Miyashita et al. [
26] proposed logarithmic data representation, which enables CNNs to be encoded to 3 bits with negligible loss in classification performance. Zhou et al. [
27] presented an efficient method to convert any pre-trained full-precision CNNs models into a hardware-friendly format, constrained to be either a power of two or zero. Using this method [
24], floating-point multiplications can be performed using low-precision multiplications or simple shift operations. Some extreme trends are to represent CNNs with one or two bits. Courbariaux et al. [
28] proposed Binary Neural Networks (BNN), where the weights are constrained to only two possible values (e.g., −1 or 1). Li et al. [
29] proposed Ternary Weight Networks (TWN) on the basis of BNN, where the weights have one more alternative value 0. BNN and TWN had great benefits to power-hungry components of the digital implementation, converting multiply-accumulate operations into simple accumulations. Moreover, BNN and TWN require 32× or 16× less memory storage than the floating-point models, respectively. Rastegari et al. [
30] proposed XNOR-Net, in which activations, as well as weights of BNN were binarized. Experiments showed that while the network provided a 58× speed up and enabled complex models to be deployed on CPU in real time, it still had a significant degradation of classification accuracy on ImageNet.
Consequently, the prior category of approaches is more focused on designing compact network architectures to achieve a high computational efficiency, which has great improvements in some baseline architectures. With the inherent redundancy, it is easy to obtain a high compression ratio of over-parameterized architectures. Notably, these approaches are owned by CNN model designers rather than hardware engineers and have the non-essential contributions to hardware optimization. Instead, a more meaningful challenge for hardware design is to quantize the CNNs that have already gained a trade-off between model complexity and accuracy degradation. While many quantization approaches obtain efficiency improvements to custom hardware, there are still some shortcomings. The approaches that only consider weights quantization [
31] mainly focus on memory consumption and less on computational efficiency. Lower bit-depth approximation in BNN, TWN, and XNOR-Net is indeed a hardware-friendly quantization scheme. While converting the floating-point multiplications and additions into shift and count operations is efficient, the substantial accuracy degradation is unacceptable for massive models. With a distinct scaling factor for each layer, DFP successfully optimizes the word length into 6-bit; however, it requires strict dynamic ranges to ensure the correctness of the results. Besides, Jacob et al. [
32] proposed a generic quantization method, which is evaluated on several benchmarks and achieves a satisfying performance. However, applying this method in hardware design has a high computing resources requirement.
In this paper, a hybrid-type inference method for CNN implementation in FPGA was proposed, which enables a CNN-based remote sensing image classification network to be successfully deployed in FPGA with limited power and resource budgets. This paper’s contributions can be summarized as follows.
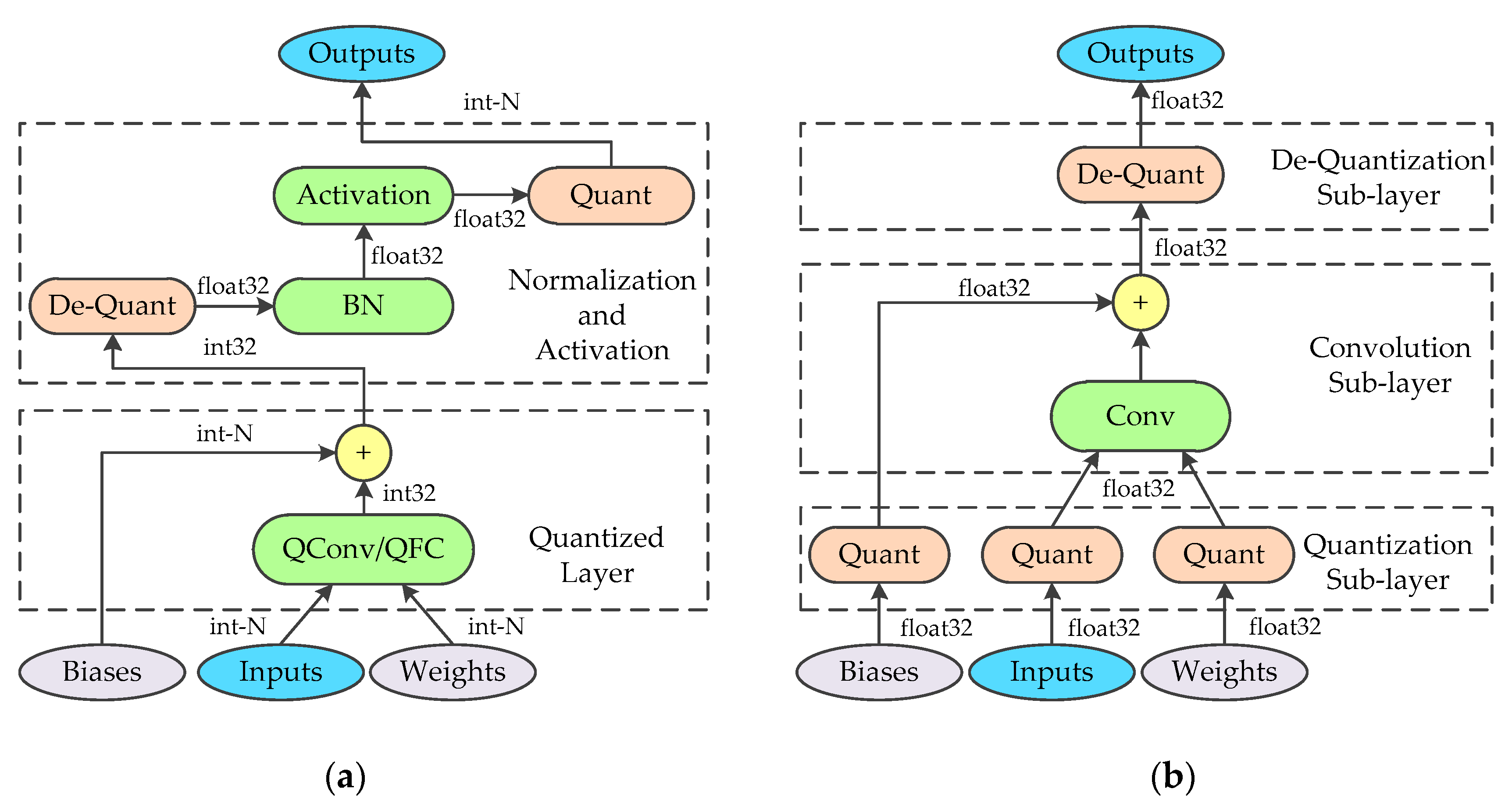
A symmetric quantization scheme-based hybrid-type inference method is proposed for CNNs. In this method, both feature maps and parameters are quantized into a low bit-depth signed integer. Meanwhile, integer/floating mixed calculations are adopted to efficiently obtain the outputs.
A training approach for quantized layers is proposed, which reproduces the same hybrid-type algorithm to simulate the behavior of inference. Using this approach, the degradation of model accuracy is reduced when applying the proposed inference method.
Based on our previous work [
33], a hardware architecture is designed to apply the hybrid-type inference in FPGA. In this architecture, a processing engine (PE) for quantized convolutional and fully connected layers is presented. Besides, a fused-layer PE is proposed for state-of-the-art CNNs equipped with Batch-Normalization and LeakyRelu.
The hybrid-type inference method and training approach are evaluated in five distinct bit-widths on GPU. The results on MSTAR [
34] show that the 8-bit hybrid-type obtains a trade-off between optimized bit-width and accuracy degradation. The 8-bit quantized model is implemented in FPGA. The results show that this hardware implementation achieves significant improvements in memory and logical resource consumption.