Adaptive Image Rendering Using a Nonlinear Mapping-Function-Based Retinex Model
Abstract
:1. Introduction
2. Related Work
3. The Proposed Method
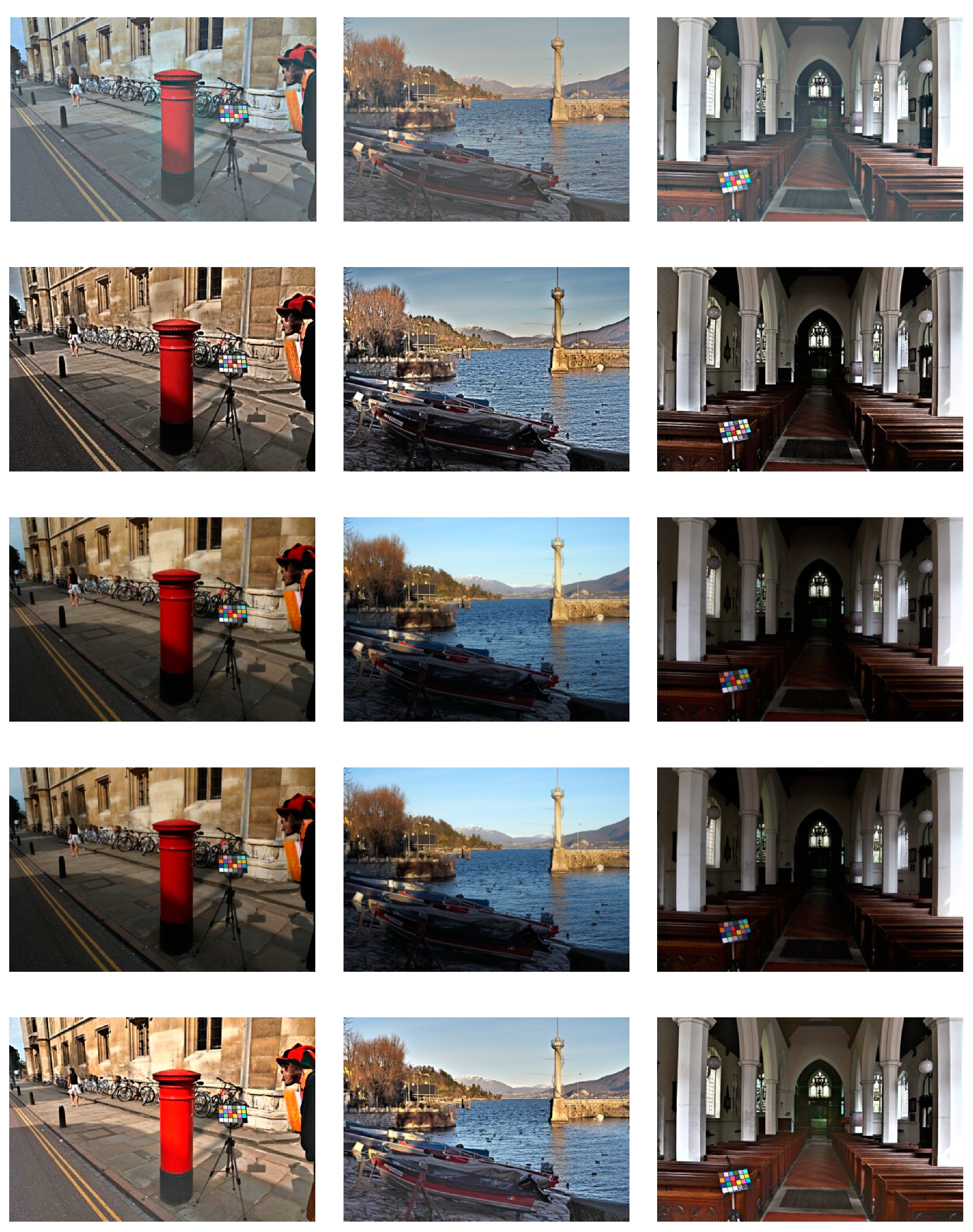
4. Experimental Results
4.1. Experimental Setup
4.2. Analyses of Experimental Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xie, S.J.; Lu, Y.; Yoon, S.; Yang, J.; Park, D.S. Intensity variation normalization for finger vein recognition using guided filter based singe scale retinex. Sensors 2015, 15, 7. [Google Scholar] [CrossRef] [PubMed]
- Chien, J.-C.; Chen, Y.-S.; Lee, J.-D. Improving night time driving safety using vision-based classification techniques. Sensors 2017, 17, 10. [Google Scholar] [CrossRef] [PubMed]
- Ochoa-Villegas, A.M.; Nolazco-Flores, J.A.; Barron-Cano, O.; Kakadiaris, I.A. Addressing the illuminance challenge in two-dimensional face recognition: A survey. IET Comput. Vis. 2015, 9, 978–992. [Google Scholar] [CrossRef]
- Celik, T. Spatial entropy-based global and local image contrast enhancement. IEEE Trans. Image Process. 2014, 23, 5298–5309. [Google Scholar] [CrossRef] [PubMed]
- Ogata, M.; Tsuchiya, T.; Kubozono, T.; Ueda, K. Dynamic range compression based on illuminance compensation. IEEE Trans. Consum. Electron. 2001, 47, 548–558. [Google Scholar] [CrossRef]
- Land, E.; McCann, J. Lightness and retinex theory. J. Opt. Soc. Am. 1971, 61, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Provenzi, E.; Fierro, M.; Rizzi, A.; Carli, L.D.; Gadia, D.; Marini, D. Random spray retinex: A new retinex implementation to investigate the local properties of the model. IEEE Trans. Image Process. 2007, 16, 162–171. [Google Scholar] [CrossRef] [PubMed]
- Banic, N.; Loncaric, S. Light random spray retinex: exploiting the noisy illumination estimation. IEEE Signal Process. Lett. 2013, 20, 1240–1243. [Google Scholar] [CrossRef]
- Simone, G.; Audino, G.; Farup, I.; Albregtsen, F.; Rizzi, A. Termite retinex: a new implementation based on a colony of intelligent agents. J. Electron. Imaging 2014, 23, 1. [Google Scholar] [CrossRef]
- Lecca, M.; Rizzi, A.; Serapioni, R.P. GRASS: A gradient-based random sampling scheme for Milano retinex. IEEE Trans. Image Process. 2017, 26, 2767–2780. [Google Scholar] [CrossRef] [PubMed]
- Jobson, D.J.; Woodell, G.A. Properties and performance of a center/surround retinex. IEEE Trans. Image Process. 1997, 6, 451–462. [Google Scholar] [CrossRef] [PubMed]
- Jobson, D.J.; Rahman, Z.; Woodell, G.A. A multi-scale retinex for bridging the gap between color images and the human observation of scenes. IEEE Trans. Image Process. 1997, 6, 965–976. [Google Scholar] [CrossRef] [PubMed]
- Dou, Z.; Gao, K.; Zhang, B.; Yu, X.; Han, L.; Zhu, Z. Realistic image rendition using a variable exponent functional model for retinex. Sensors 2016, 16, 6. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, T.; Kuwahara, Y.; Kurosawa, T. An adaptive multi-scale retinex algorithm realizing high color quality and high-speed processing. J. Imaging Sci. Tech. 2005, 49, 486–497. [Google Scholar]
- Kim, K.; Bae, J.; Kim, J. Natural HDR image tone mapping based on retinex. IEEE Trans. Consum. Electron. 2011, 57, 1807–1814. [Google Scholar] [CrossRef]
- Kimmel, R.; Elad, M.; Sobel, I. A variational framework for retinex. Int. J. Comput. Vis. 2003, 52, 7–23. [Google Scholar] [CrossRef]
- Zosso, D.; Tran, G.; Osher, S.J. Non-local retinex-A unifying framework and beyond. SIAM J. Imaging Sci. 2015, 8, 787–826. [Google Scholar] [CrossRef]
- Park, S.; Yu, S.; Moon, B.; Ko, S.; Paik, J. Low-light image enhancement using variational optimization-based retinex model. IEEE Trans. Consum. Electron. 2017, 63, 178–184. [Google Scholar] [CrossRef]
- Lore, K.G.; Akintayo, A.; Sarkar, S. LLNet: A deep autoencoder approach to natural low-light image enhancement. Pattern Recognit. 2017, 61, 650–662. [Google Scholar] [CrossRef] [Green Version]
- Baslamisli, A.S.; Le, H.-A.; Gevers, T. CNN based learning using reflection and retinex models for intrinsic image decomposition. In Proceedings of the IEEE International Conference Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18‒23 June 2018; pp. 6674–6683. [Google Scholar]
- Lee, C.H.; Shih, J.-L.; Lien, C.-C.; Han, C.-C. Adaptive multiscale retinex for image contrast enhancement. In Proceedings of the International Conference on Signal Image Technology and Internet Based System, Kyoto, Japan, 2–5 December 2013; Volume 13, pp. 43–50. [Google Scholar]
- Shin, Y.; Jeong, S.; Lee, S. Efficient naturalness restoration for non-uniform illuminance images. IET Image Process. 2015, 9, 662–671. [Google Scholar] [CrossRef]
- Ciurea, F.; Funt, B.V. Tuning retinex parameters. J. Electron. Imaging 2004, 13, 1. [Google Scholar] [CrossRef]
- Seglen, P.O. The skewness of science. J. Am. Soc. Inform. Sci. 1992, 43, 628–638. [Google Scholar] [CrossRef]
- Peli, E. Contrast in complex images. J. Opt. Soc. Am. A 1990, 7, 2032–2040. [Google Scholar] [CrossRef] [PubMed]
- Recommendation ITU-R, BT.500-13 Methodology for the subjective assessment of the quality of television pictures. ITU-R BT.500-13. 2012. Available online: https://www.itu.int/rec/R-REC-BT.500-13-201201-I/en (accessed on 25 February 2019).








| Image | Low-Light Image | MSR [12] | AMSR | RSR [7] | LRSR [8] | Proposed Method |
|---|---|---|---|---|---|---|
| A1 | 49.15 | 107.10 | 125.08 | 57.14 | 57.91 | 108.80 |
| A2 | 93.48 | 123.61 | 161.08 | 61.18 | 61.44 | 135.53 |
| A3 | 64.40 | 80.68 | 106.13 | 51.77 | 51.75 | 87.24 |
| A4 | 39.58 | 43.28 | 47.31 | 25.19 | 25.20 | 52.65 |
| A5 | 64.89 | 145.21 | 195.21 | 86.61 | 86.13 | 156.65 |
| A6 | 74.37 | 104.75 | 130.80 | 75.50 | 75.50 | 121.39 |
| A7 | 81.59 | 139.97 | 168.05 | 90.83 | 90.81 | 147.96 |
| A8 | 47.61 | 131.13 | 174.43 | 66.30 | 66.50 | 132.10 |
| A9 | 50.94 | 86.63 | 122.18 | 47.76 | 47.72 | 91.02 |
| A10 | 23.59 | 127.66 | 140.02 | 60.76 | 59.63 | 139.79 |
| A11 | 20.25 | 53.63 | 63.24 | 22.01 | 22.06 | 59.34 |
| A12 | 40.53 | 71.90 | 92.44 | 40.59 | 40.55 | 79.46 |
| A13 | 46.69 | 114.50 | 150.67 | 66.90 | 66.52 | 116.76 |
| A14 | 50.07 | 156.64 | 171.69 | 70.32 | 70.50 | 158.31 |
| A15 | 44.55 | 86.26 | 109.51 | 48.20 | 48.16 | 88.11 |
| A16 | 74.68 | 174.04 | 201.31 | 80.90 | 80.90 | 182.31 |
| A17 | 102.04 | 150.07 | 198.70 | 102.34 | 102.32 | 162.68 |
| A18 | 58.23 | 91.08 | 121.71 | 58.23 | 58.24 | 101.36 |
| A19 | 26.10 | 72.53 | 92.45 | 35.39 | 35.39 | 72.83 |
| A20 | 22.39 | 72.34 | 88.95 | 51.13 | 51.41 | 77.18 |
| B1 | 18.10 | 34.02 | 62.89 | 18.10 | 18.10 | 54.72 |
| B2 | 37.21 | 64.25 | 85.68 | 37.21 | 37.21 | 171.48 |
| B3 | 72.29 | 92.70 | 157.57 | 72.33 | 72.38 | 159.09 |
| B4 | 43.39 | 57.35 | 102.68 | 43.39 | 43.39 | 101.91 |
| B5 | 42.18 | 53.55 | 78.27 | 42.18 | 42.18 | 93.28 |
| B6 | 30.44 | 45.33 | 62.39 | 30.47 | 30.49 | 84.21 |
| B7 | 32.34 | 37.73 | 74.18 | 32.94 | 32.94 | 64.44 |
| B8 | 29.93 | 34.14 | 61.00 | 29.93 | 29.93 | 55.09 |
| B9 | 17.82 | 22.19 | 51.64 | 17.91 | 17.91 | 34.55 |
| B10 | 23.73 | 26.08 | 53.05 | 23.73 | 23.73 | 46.56 |
| B11 | 57.31 | 85.71 | 103.21 | 57.51 | 57.40 | 92.46 |
| B12 | 70.76 | 85.56 | 107.85 | 75.56 | 75.46 | 102.88 |
| B13 | 7.16 | 26.70 | 18.09 | 7.23 | 7.23 | 28.90 |
| B14 | 7.29 | 15.96 | 19.41 | 11.15 | 11.16 | 15.58 |
| B15 | 38.22 | 83.06 | 132.15 | 46.55 | 46.58 | 87.75 |
| B16 | 31.78 | 54.21 | 80.94 | 32.77 | 32.78 | 63.38 |
| B17 | 29.58 | 47.03 | 58.78 | 31.14 | 31.05 | 50.82 |
| B18 | 89.18 | 132.21 | 163.30 | 89.18 | 89.18 | 147.28 |
| B19 | 93.72 | 144.15 | 165.91 | 93.72 | 93.74 | 172.37 |
| B20 | 10.54 | 48.49 | 38.88 | 10.54 | 10.54 | 54.72 |
| Average | 45.80 | 81.97 | 107.28 | 49.33 | 49.31 | 97.58 |
| Image | MSR | AMSR | RSR | LRSR | Proposed Method |
|---|---|---|---|---|---|
| A1 | 6.231 | 3.584 | 11.255 | 11.771 | 3.109 |
| A2 | 6.257 | 3.560 | 11.155 | 11.673 | 3.097 |
| A3 | 6.254 | 3.520 | 11.210 | 11.687 | 3.043 |
| A4 | 6.179 | 3.502 | 11.232 | 11.691 | 3.050 |
| A5 | 7.641 | 4.076 | 12.738 | 13.252 | 3.571 |
| A6 | 7.108 | 4.352 | 12.756 | 13.208 | 3.650 |
| A7 | 6.241 | 3.588 | 11.206 | 11.642 | 3.099 |
| A8 | 7.583 | 4.172 | 12.688 | 13.316 | 3.586 |
| A9 | 6.135 | 3.601 | 11.094 | 11.581 | 3.147 |
| A10 | 6.306 | 3.841 | 11.122 | 11.658 | 3.709 |
| A11 | 7.114 | 3.213 | 10.767 | 11.098 | 2.751 |
| A12 | 5.962 | 3.185 | 10.704 | 11.141 | 2.761 |
| A13 | 5.895 | 3.175 | 10.578 | 11.230 | 2.907 |
| A14 | 5.992 | 3.299 | 10.910 | 11.453 | 2.856 |
| A15 | 6.245 | 3.195 | 10.716 | 11.283 | 2.871 |
| A16 | 5.929 | 3.246 | 10.922 | 11.102 | 2.765 |
| A17 | 5.909 | 3.380 | 10.611 | 10.845 | 2.870 |
| A18 | 5.653 | 3.111 | 10.468 | 11.011 | 2.728 |
| A19 | 5.952 | 3.158 | 10.513 | 10.982 | 2.748 |
| A20 | 5.952 | 3.132 | 10.472 | 10.982 | 2.742 |
| B1 | 6.999 | 3.813 | 10.976 | 11.311 | 3.311 |
| B2 | 5.978 | 3.718 | 10.888 | 11.347 | 3.489 |
| B3 | 6.120 | 3.710 | 10.870 | 11.375 | 3.262 |
| B4 | 6.017 | 3.835 | 10.791 | 11.293 | 3.221 |
| B5 | 5.955 | 3.781 | 10.904 | 11.332 | 3.252 |
| B6 | 6.007 | 3.747 | 10.838 | 11.277 | 3.267 |
| B7 | 6.052 | 3.681 | 10.794 | 11.322 | 3.292 |
| B8 | 6.019 | 3.694 | 10.890 | 11.290 | 3.196 |
| B9 | 6.917 | 3.825 | 10.885 | 11.390 | 3.363 |
| B10 | 6.916 | 3.783 | 10.913 | 11.376 | 3.181 |
| B11 | 6.041 | 3.677 | 10.754 | 11.330 | 3.138 |
| B12 | 6.003 | 3.598 | 10.553 | 11.075 | 3.251 |
| B13 | 8.147 | 3.791 | 11.963 | 12.308 | 3.462 |
| B14 | 5.954 | 3.373 | 10.608 | 11.015 | 2.989 |
| B15 | 5.910 | 3.588 | 10.636 | 11.019 | 3.129 |
| B16 | 6.062 | 3.612 | 10.584 | 10.995 | 3.254 |
| B17 | 5.935 | 3.923 | 10.629 | 10.970 | 3.099 |
| B18 | 5.894 | 3.523 | 10.583 | 10.980 | 3.126 |
| B19 | 5.894 | 3.597 | 10.537 | 10.953 | 3.252 |
| B20 | 6.984 | 3.850 | 11.277 | 11.679 | 3.378 |
| Average | 6.309 | 3.600 | 11.000 | 11.456 | 3.149 |
| Image | MSR | AMSR | RSR | LRSR | Proposed | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Avg. | Std. | Avg. | Std. | Avg. | Std. | Avg. | Std. | Avg. | Std. | |
| A1 | 5.556 | 2.672 | 4.556 | 2.076 | 5.444 | 1.824 | 5.611 | 1.857 | 6.833 | 2.256 |
| A2 | 5.444 | 2.289 | 4.556 | 1.774 | 5.944 | 1.359 | 6.278 | 1.236 | 5.667 | 2.220 |
| A3 | 4.778 | 2.269 | 5.167 | 2.269 | 5.111 | 1.431 | 5.111 | 1.023 | 7.167 | 1.833 |
| A4 | 5.000 | 2.238 | 3.444 | 1.749 | 5.611 | 1.241 | 5.722 | 1.229 | 6.556 | 1.562 |
| A5 | 5.889 | 1.609 | 3.889 | 1.813 | 4.500 | 1.200 | 4.667 | 1.071 | 6.333 | 2.012 |
| A6 | 7.444 | 1.744 | 4.444 | 1.946 | 5.500 | 1.161 | 5.611 | 1.152 | 7.389 | 1.396 |
| A7 | 4.944 | 2.159 | 4.778 | 2.128 | 5.111 | 0.805 | 5.167 | 0.768 | 5.556 | 2.308 |
| A8 | 6.667 | 1.952 | 3.278 | 1.905 | 5.722 | 1.382 | 5.667 | 1.236 | 6.668 | 1.749 |
| A9 | 4.056 | 1.359 | 4.111 | 1.830 | 5.611 | 1.241 | 5.833 | 1.400 | 6.556 | 1.851 |
| A10 | 6.556 | 2.617 | 3.772 | 1.744 | 6.056 | 1.265 | 6.111 | 1.284 | 6.778 | 2.632 |
| A11 | 4.550 | 2.523 | 3.350 | 2.207 | 5.650 | 1.565 | 5.850 | 1.531 | 6.250 | 2.268 |
| A12 | 5.100 | 2.245 | 4.650 | 2.207 | 5.050 | 1.432 | 4.550 | 1.191 | 7.450 | 1.638 |
| A13 | 6.900 | 1.744 | 4.300 | 1.780 | 6.800 | 1.240 | 5.800 | 1.673 | 8.250 | 1.446 |
| A14 | 7.200 | 1.473 | 3.850 | 1.309 | 6.450 | 1.572 | 4.600 | 1.875 | 7.250 | 2.221 |
| A15 | 5.850 | 2.033 | 4.450 | 1.872 | 5.350 | 1.089 | 4.750 | 1.293 | 6.500 | 2.115 |
| A16 | 7.200 | 1.795 | 4.300 | 1.559 | 5.350 | 0.998 | 5.100 | 1.210 | 7.000 | 1.864 |
| A17 | 5.300 | 2.003 | 4.500 | 1.821 | 5.600 | 1.392 | 5.050 | 1.146 | 6.150 | 2.300 |
| A18 | 5.700 | 1.809 | 4.200 | 1.542 | 5.150 | 1.424 | 5.000 | 1.487 | 5.950 | 2.502 |
| A19 | 6.800 | 1.436 | 4.000 | 1.589 | 5.950 | 1.432 | 5.850 | 1.599 | 7.500 | 2.103 |
| A20 | 6.400 | 1.501 | 3.700 | 1.525 | 7.600 | 1.392 | 7.000 | 1.451 | 8.250 | 1.585 |
| B1 | 7.113 | 0.816 | 3.111 | 0.994 | 4.444 | 1.066 | 4.333 | 0.943 | 7.333 | 0.943 |
| B2 | 5.556 | 2.061 | 5.111 | 0.875 | 4.556 | 0.685 | 4.667 | 0.667 | 7.111 | 1.286 |
| B3 | 7.111 | 1.728 | 5.889 | 1.286 | 5.333 | 0.471 | 5.222 | 0.629 | 7.667 | 0.943 |
| B4 | 5.667 | 2.000 | 5.556 | 1.423 | 5.111 | 0.314 | 5.111 | 0.314 | 6.556 | 1.707 |
| B5 | 6.778 | 1.750 | 5.889 | 1.100 | 4.889 | 0.737 | 4.989 | 0.750 | 7.778 | 1.685 |
| B6 | 3.667 | 1.633 | 5.556 | 0.956 | 4.778 | 0.629 | 4.987 | 0.692 | 7.111 | 0.567 |
| B7 | 7.556 | 1.257 | 3.889 | 1.523 | 5.222 | 0.786 | 5.111 | 0.567 | 7.000 | 0.943 |
| B8 | 7.333 | 1.826 | 5.444 | 1.257 | 4.889 | 0.567 | 4.889 | 0.567 | 7.444 | 0.685 |
| B9 | 7.556 | 1.872 | 3.889 | 1.286 | 5.000 | 0.667 | 4.889 | 0.567 | 7.778 | 1.771 |
| B10 | 7.000 | 0.943 | 4.889 | 1.100 | 4.778 | 1.100 | 4.889 | 0.567 | 7.111 | 1.523 |
| B11 | 4.350 | 1.981 | 5.600 | 2.062 | 5.350 | 1.424 | 5.050 | 1.050 | 6.200 | 2.215 |
| B12 | 4.300 | 1.809 | 4.100 | 1.651 | 5.050 | 0.887 | 4.800 | 1.105 | 5.050 | 2.434 |
| B13 | 4.800 | 2.546 | 4.750 | 1.333 | 5.000 | 0.918 | 4.600 | 0.940 | 5.200 | 2.419 |
| B14 | 5.950 | 1.986 | 2.850 | 1.663 | 5.600 | 2.393 | 4.850 | 2.110 | 5.250 | 2.468 |
| B15 | 5.900 | 2.222 | 3.150 | 1.531 | 6.050 | 1.761 | 5.750 | 1.482 | 6.600 | 2.113 |
| B16 | 5.250 | 2.268 | 3.250 | 1.517 | 5.900 | 1.586 | 5.500 | 1.318 | 5.100 | 2.553 |
| B17 | 4.450 | 2.188 | 3.250 | 1.618 | 5.350 | 1.268 | 4.900 | 1.410 | 5.900 | 2.382 |
| B18 | 5.400 | 2.010 | 5.300 | 2.452 | 5.150 | 1.040 | 5.000 | 1.206 | 5.600 | 2.415 |
| B19 | 5.150 | 2.110 | 5.300 | 1.525 | 5.050 | 1.050 | 4.800 | 0.951 | 5.350 | 2.397 |
| B20 | 4.750 | 2.149 | 5.200 | 2.215 | 5.150 | 0.875 | 5.000 | 0.649 | 6.150 | 2.412 |
| Average | 5.824 | 1.916 | 4.382 | 1.650 | 5.405 | 1.116 | 5.217 | 1.125 | 6.634 | 1.891 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oh, J.; Hong, M.-C. Adaptive Image Rendering Using a Nonlinear Mapping-Function-Based Retinex Model. Sensors 2019, 19, 969. https://doi.org/10.3390/s19040969
Oh J, Hong M-C. Adaptive Image Rendering Using a Nonlinear Mapping-Function-Based Retinex Model. Sensors. 2019; 19(4):969. https://doi.org/10.3390/s19040969
Chicago/Turabian StyleOh, JongGeun, and Min-Cheol Hong. 2019. "Adaptive Image Rendering Using a Nonlinear Mapping-Function-Based Retinex Model" Sensors 19, no. 4: 969. https://doi.org/10.3390/s19040969
APA StyleOh, J., & Hong, M. -C. (2019). Adaptive Image Rendering Using a Nonlinear Mapping-Function-Based Retinex Model. Sensors, 19(4), 969. https://doi.org/10.3390/s19040969




