Distributed Fusion of Sensor Data in a Constrained Wireless Network
Abstract
:1. Introduction
2. System Overview
2.1. Overview
2.2. Prerequisite: Occupancy Inference based on HMMs
- (1)
- State transition probability matrix: . The transition probabilities describe how space occupancy changes over time. Because we assume only two possible states, two transition probabilities need to be specified, namely and .
- (2)
- Emission probability matrix: . The observed symbols are sensor readings monitoring the hidden states, such as, for example, ultrasound or PIR sensors providing measurements. Our mathematical approach is very suitable to combine data from sensors with different reliabilities. Yet, in the examples that we give in this work, we use one type of sensor, namely ultrasound (USR) sensors. Typically, sensor measurements are continuous-valued variables, such as a time-of-flight distance. However, for simplification in the calculations, we map each continuous observation to a binary value . The emission probabilities are a metric of the quality of the sensor modality used and thus are directly linked to the successful detection rate (SDR) and the false alarm rate (FAR). The SDR is the probability of obtaining a sensor reading given that a person is present, while the FAR is the probability of obtaining a sensor reading given that a person is absent. Accordingly, the emission probability matrix is defined as follows:
- (3)
- : Initial state probability vector. The initial state distribution specifies the occupancy probability at the initial time step , prior to any observation. Yet, in our application, the influence of the initial state rapidly vanishes.
2.3. Dynamic Transition Probabilities
2.4. State Estimation in HMMs
2.5. Decision Rule
2.6. Communication Strategy
2.7. Data Fusion
| Algorithm 1: Distributed hidden Markov model (HMM) Algorithm with Sub-Optimal Retroactive Reconstruction |
| 1: Initialization: 2: while new data exist do 3: Calculate the likelihood ratio: 4: if do 5: send 6: end if 7: if received do 8: Trace back to 9: Retroactively calculate according to 10: Update 11: end if 12: Estimate state according to decision rule 13: end while |
| Algorithm 2: Distributed HMM Algorithm with Correction Term Fusion |
| 1: Initialization: 2: while new data exist do 3: Calculate the likelihood ratio: 4: if do 5: send 6: end if 7: if received do 8: Calculate according to 10: Update 11: end if 12: Estimate state according to decision rule 13: end while |
| Algorithm 3: Distributed HMM Algorithm with Weighted Averaging Fusion |
| 1: Initialization: 2: while new data exist do 3: Calculate the likelihood ratio: 4: if do 5: send 6: end if 7: if received do 8: Calculate according to 10: Update 11: end if 12: Estimate state according to decision rule 13: end while |
3. Proof of Concept
3.1. Implementation Details
3.2. Data Log
3.3. Study Design
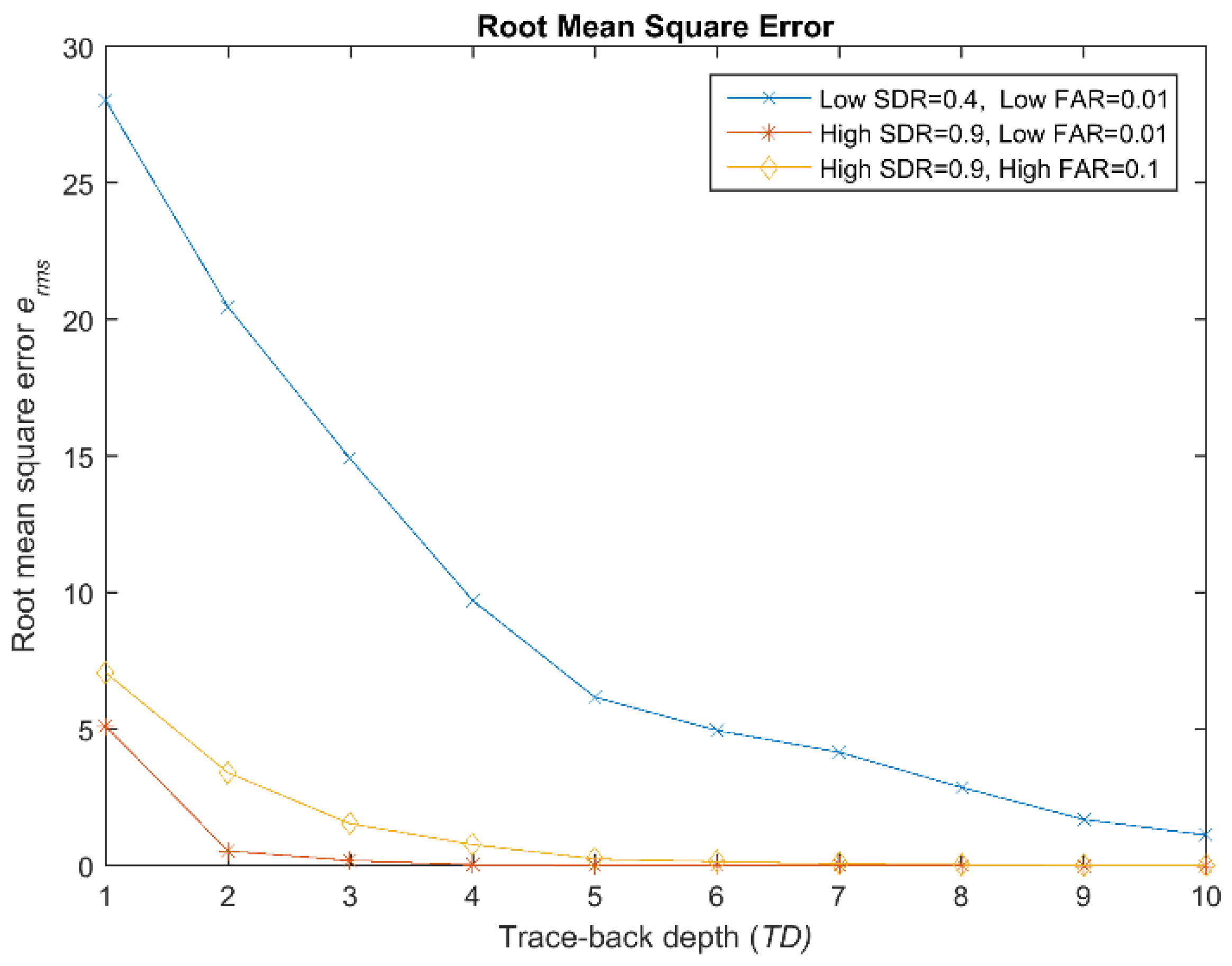
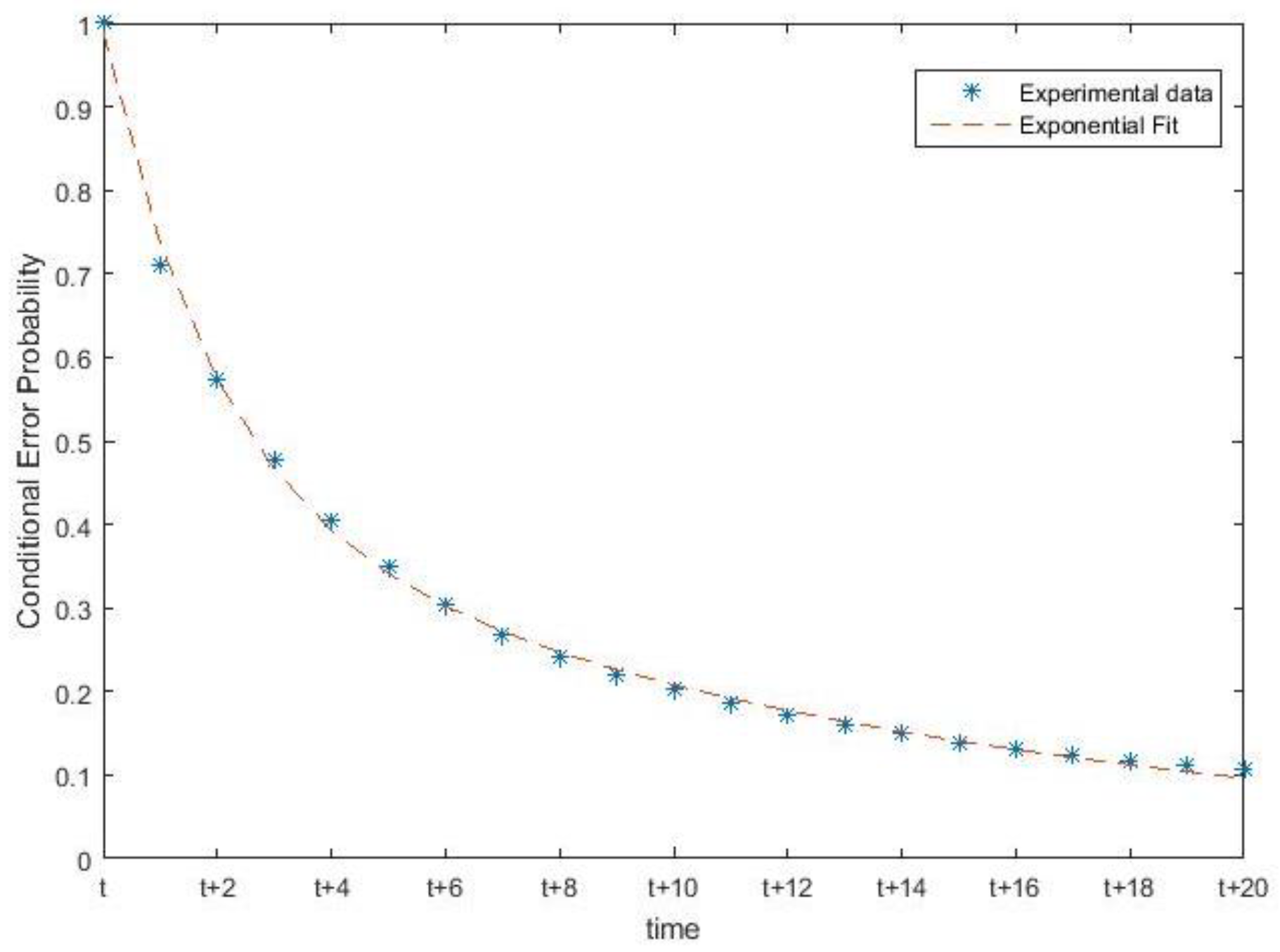
3.4. Experimental Results
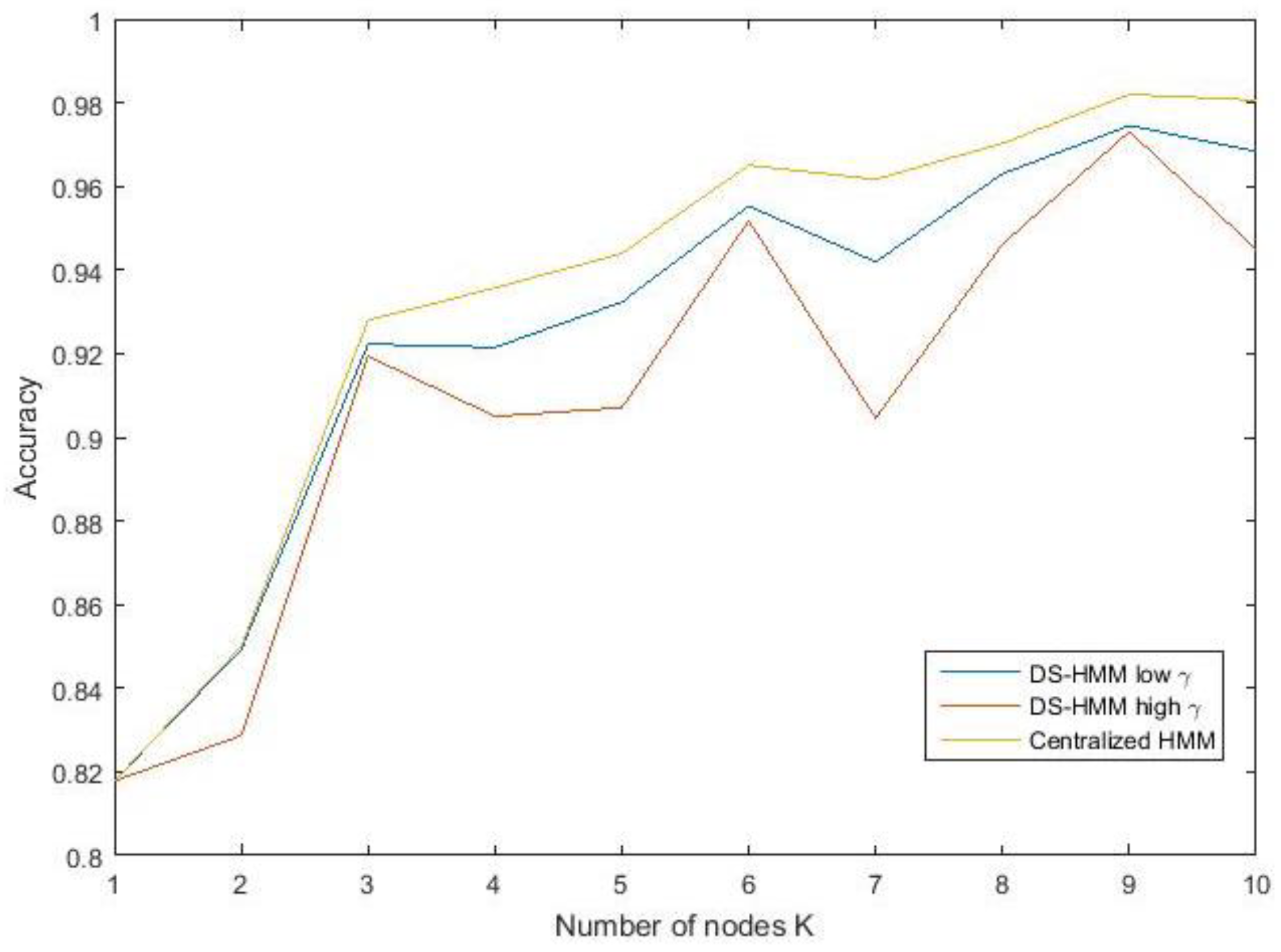
3.5. Scalability
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kamthe, A.; Jiang, L.; Dudys, M.; Cerpa, A. SCOPES: Smart Cameras Object Position Estimation System; Springer: Berlin/Heidelberg, Germany, 2009; pp. 279–295. [Google Scholar]
- Erickson, V.L.; Lin, Y.; Kamthe, A.; Brahme, R.; Surana, A.; Cerpa, A.E.; Sohn, M.D.; Narayanan, S. Energy efficient building environment control strategies using real-time occupancy measurements. In Proceedings of the First ACM Workshop on Embedded Sensing Systems for Energy-Efficiency in Buildings―BuildSys ’09, Berkeley, CA, USA, 3 November 2009; p. 19. [Google Scholar]
- Zhen, Z.-N.; Jia, Q.-S.; Song, C.; Guan, X. An Indoor Localization Algorithm for Lighting Control using RFID. In Proceedings of the 2008 IEEE Energy Conference, Atlanta, GA, USA, 17–18 November 2008; pp. 1–6. [Google Scholar]
- Pan, J.; Jain, R.; Paul, S.; Vu, T.; Saifullah, A.; Sha, M. An Internet of Things Framework for Smart Energy in Buildings: Designs, Prototype, and Experiments. IEEE Internet Things J. 2015, 2, 527–537. [Google Scholar] [CrossRef]
- Dodier, R.H.; Henze, G.P.; Tiller, D.K.; Guo, X. Building occupancy detection through sensor belief networks. Energy Build. 2006, 38, 1033–1043. [Google Scholar] [CrossRef]
- Nguyen, T.A.; Nguyen, T.A.; Aiello, M. Beyond Indoor Presence Monitoring with Simple Sensors. In Proceedings of the International Conference on Pervasive and Embedded Computing and Communication Systems (PECCS), Rome, Italy, 24–26 February 2012; pp. 5–14. [Google Scholar]
- Huang, Q.; Mao, C. Occupancy Estimation in Smart Building Using Hybrid CO2/Light Wireless Sensor Network. J. Appl. Sci. Arts 2017, 1, 5. [Google Scholar]
- Papatsimpa, C.; Linnartz, J.-P.M.G. Improved Presence Detection for Occupancy Control in Multisensory Environments. In Proceedings of the 2017 IEEE International Conference on Computer and Information Technology (CIT), Helsinki, Finland, 21–23 August 2017; pp. 75–80. [Google Scholar]
- Ericsson, A.B. More than 50 Billion Connected Devices―Taking Connected Devices to Mass Market and Profitability; Technical Report; Ericsson: Stockholm, Sweden, 2020. [Google Scholar]
- Shebli, F.; Dayoub, I.; M’foubat, A.O.; Rivenq, A.; Rouvaen, J.M. Minimizing energy consumption within wireless sensors networks using optimal transmission range between nodes. In Proceedings of the 2007 IEEE International Conference on Signal Processing and Communications, Dubai, United Arab Emirates, 24–27 November 2007; pp. 105–108. [Google Scholar]
- Sendra, S.; Lloret, J.; Garcia, M.; Toledo, J.F. Power Saving and Energy Optimization Techniques for Wireless Sensor Neworks (Invited Paper). J. Commun. 2011, 6, 439–458. [Google Scholar] [CrossRef]
- Papatsimpa, C.; Linnartz, J.P.M.G. Propagating sensor uncertainty to better infer office occupancy in smart building control. Energy Build. 2018, 179, 73–82. [Google Scholar] [CrossRef]
- Rabiner, L.R. A tutorial on hidden Markov models and selected applications in speech recognition. Proc. IEEE 1989, 77, 257–286. [Google Scholar] [CrossRef] [Green Version]
- Papatsimpa, C.; Linnartz, J.-P. Using Dynamic Occupancy Patterns for Improved Presence Detection in Intelligent Buildings. In Proceedings of the 2018 9th IFIP International Conference on New Technologies, Mobility and Security (NTMS), Paris, France, 26–28 February 2018; pp. 1–5. [Google Scholar]
- ANSI/ASHRAE/IESNA Addenda a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, r, s, t, u, v, x, and ak to ANSI/ASHRAE/IESNA Standard 90.1-2004; American Society of Heating and Air-Conditioning Engineers (ASHAE): Atlanta, GA, USA, 2006.
- Liggins, M.E.; Chong, Ch.; Kadar, I.; Alford, M.G.; Vannicola, V.; Thomopoulos, S. Distributed Fusion Architectures and Algorithms for Target Tracking. Proc. IEEE 1997, 85, 95–107. [Google Scholar] [CrossRef] [Green Version]
- Le, C.A.; Huynh, V.-N.; Shimazu, A. An Evidential Reasoning Approach to Weighted Combination of Classifiers for Word Sense Disambiguation; Springer: Berlin/Heidelberg, Germany, 2005; pp. 516–525. [Google Scholar]
- Nassif, N. A robust CO2-based demand-controlled ventilation control strategy for multi-zone HVAC systems. Energy Build. 2012, 45, 72–81. [Google Scholar] [CrossRef]
- Kelly, B.; Hollosi, D.; Cousin, P.; Leal, S.; Iglár, B.; Cavallaro, A. Application of Acoustic Sensing Technology for Improving Building Energy Efficiency. Procedia Comput. Sci. 2014, 32, 661–664. [Google Scholar] [CrossRef] [Green Version]
- Huang, Q.; Ge, Z.; Lu, C. Occupancy Estimation in Smart Buildings using Audio-Processing Techniques. arXiv, 2016; arXiv:1602.08507. [Google Scholar]





| References | Sensing Modality | Processing Algorithm | Cost | Intrusive | Occupancy Detection Performance | Communication Requirements | Centralized (Cloud) or Decentralized EDGE |
|---|---|---|---|---|---|---|---|
| [3,4] | RFID | SVM Regression models | Low | Yes | High accuracy | Constant connection | Centralized |
| [2] | Image Camera | Multivariate Gaussian Model | High | Yes | High accuracy | Constant connection | Centralized |
| [18] | CO2 | Threshold on sensor reading | Low | No | Accuracy varies by case | Constant connection | Centralized |
| [19,20] | Acoustic recognition | PCA/LDA Gaussian Mixture Model and HMMs | Low | No | Varying with environment, failure when people keep silent | Constant connection | Centralized |
| [6,7] | Hybrid | Threshold on sensor reading | Low | No | Improved accuracy with sensor collaboration | Constant connection | Centralized |
| [8,12] | USR Radar | Centralized HMM | High accuracy | Constant connection | Centralized | ||
| This work | USR, but can support any type | HMM | Low | No | High accuracy | Sparse transmissions | Can be decentralized |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papatsimpa, C.; Linnartz, J.-P. Distributed Fusion of Sensor Data in a Constrained Wireless Network. Sensors 2019, 19, 1006. https://doi.org/10.3390/s19051006
Papatsimpa C, Linnartz J-P. Distributed Fusion of Sensor Data in a Constrained Wireless Network. Sensors. 2019; 19(5):1006. https://doi.org/10.3390/s19051006
Chicago/Turabian StylePapatsimpa, Charikleia, and Jean-Paul Linnartz. 2019. "Distributed Fusion of Sensor Data in a Constrained Wireless Network" Sensors 19, no. 5: 1006. https://doi.org/10.3390/s19051006
APA StylePapatsimpa, C., & Linnartz, J.-P. (2019). Distributed Fusion of Sensor Data in a Constrained Wireless Network. Sensors, 19(5), 1006. https://doi.org/10.3390/s19051006






