An Intelligent Fault Diagnosis Method for Reciprocating Compressors Based on LMD and SDAE
Abstract
:1. Introduction
2. Theoretical Background
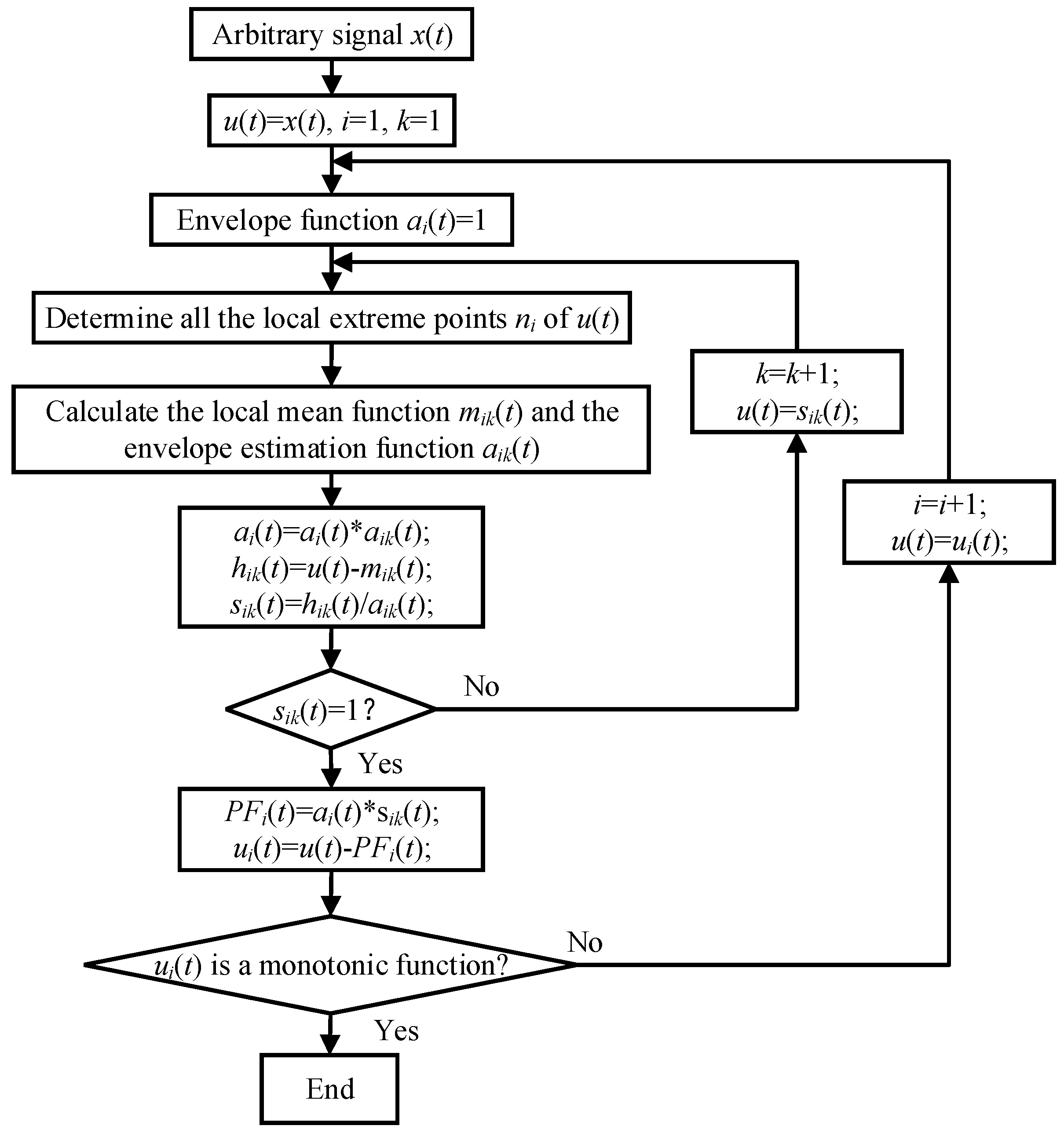
2.1. Local Mean Decomposition
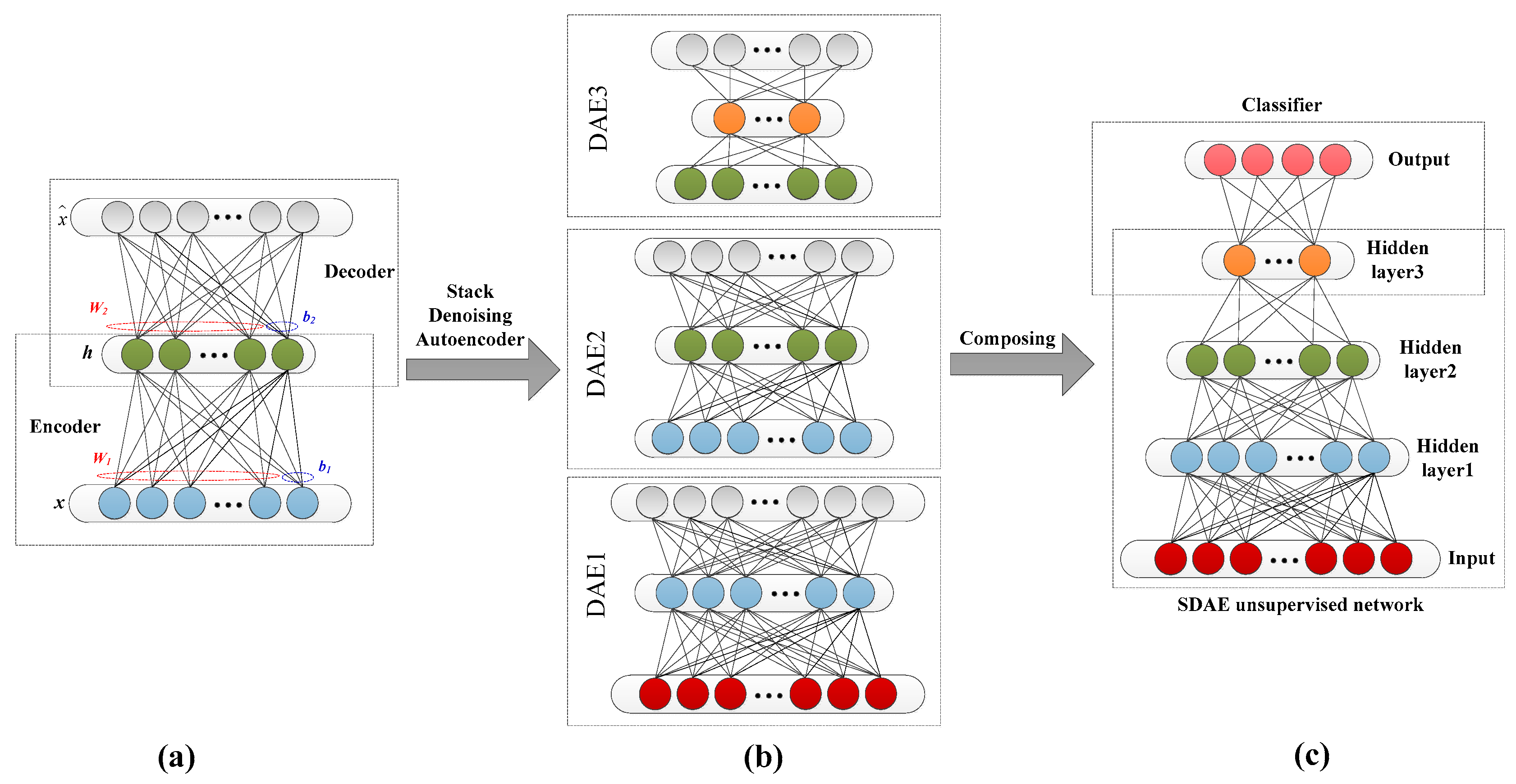
2.2. Stack Denoising Autoencoder
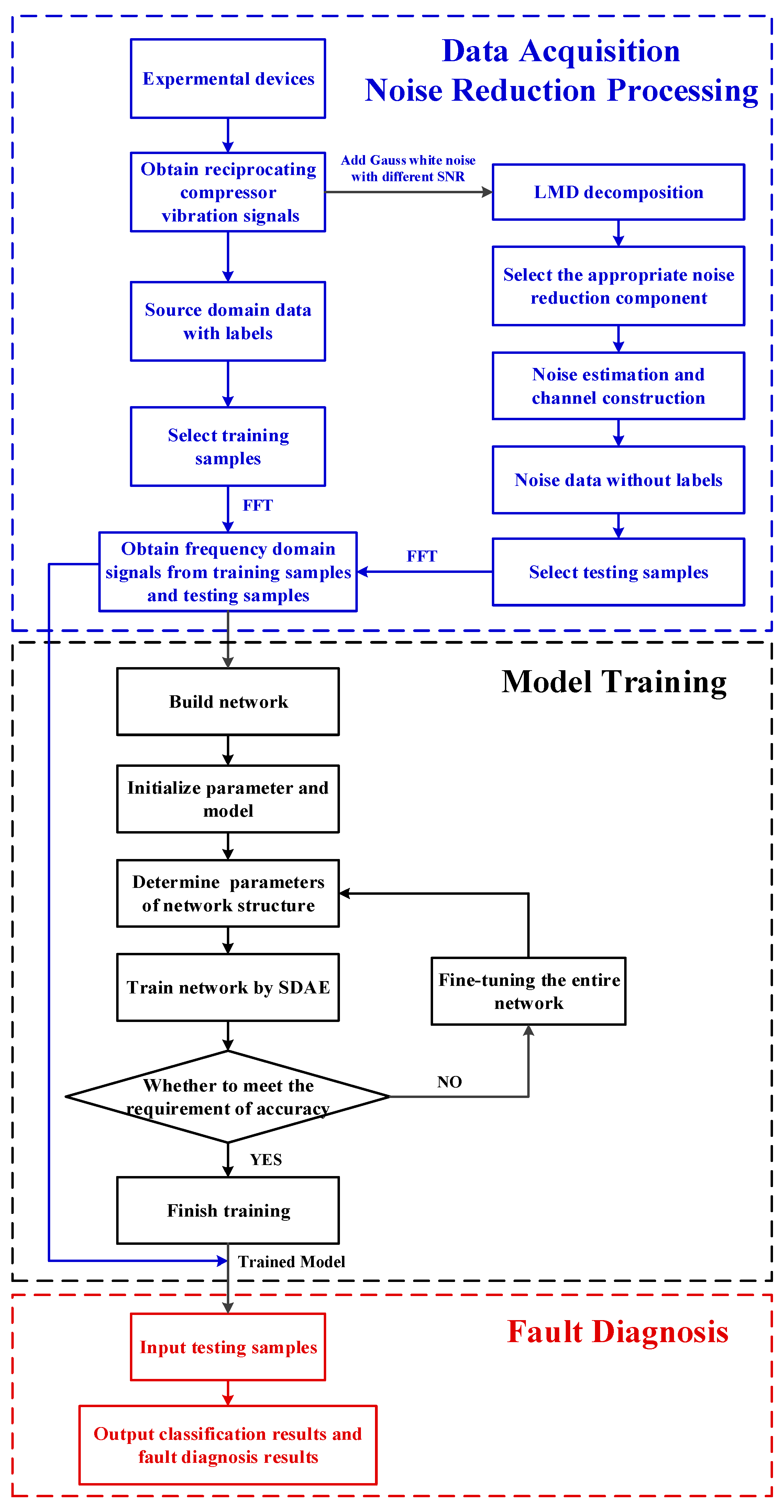
3. The Proposed Method
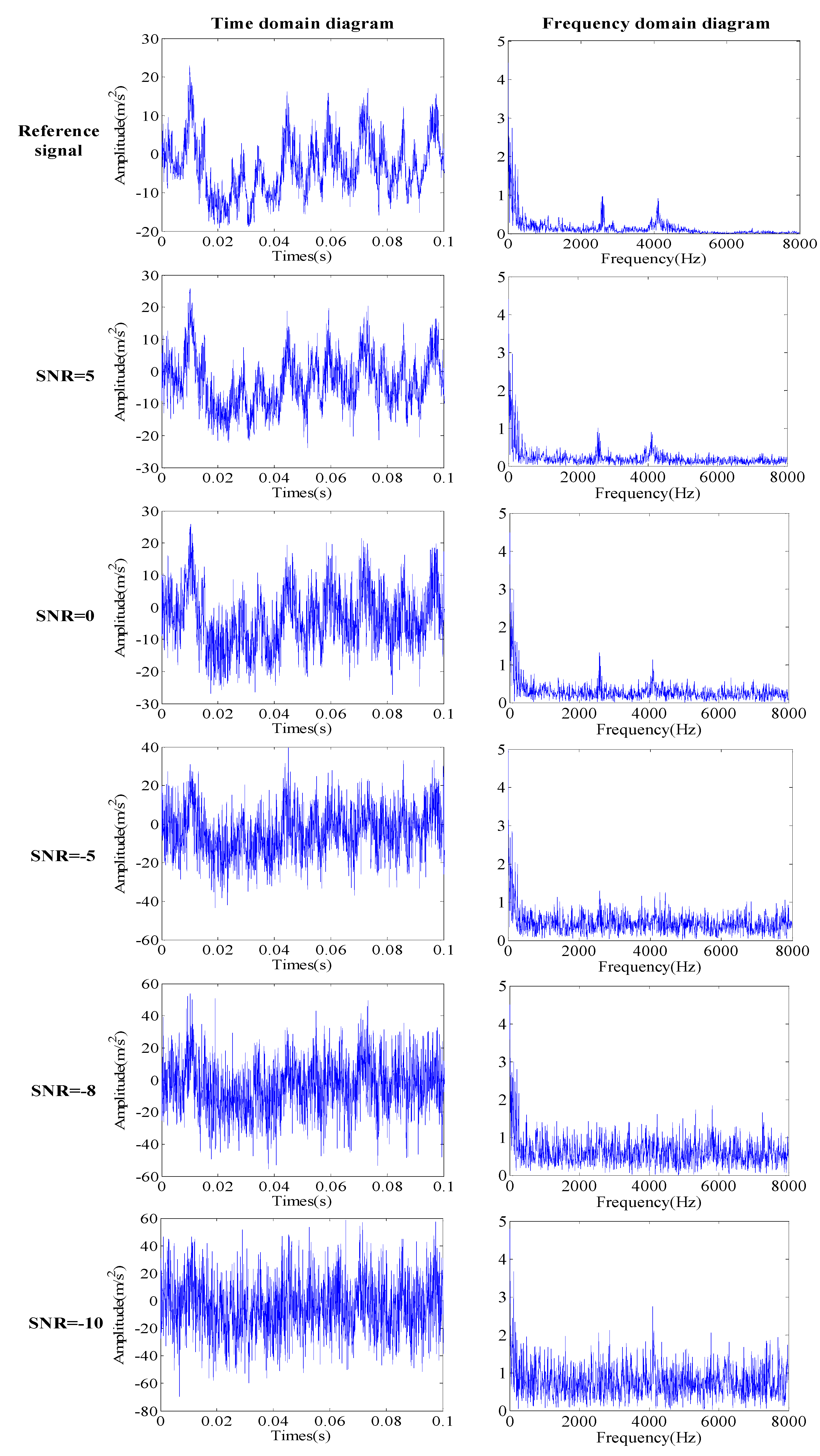
4. Experimental Studies
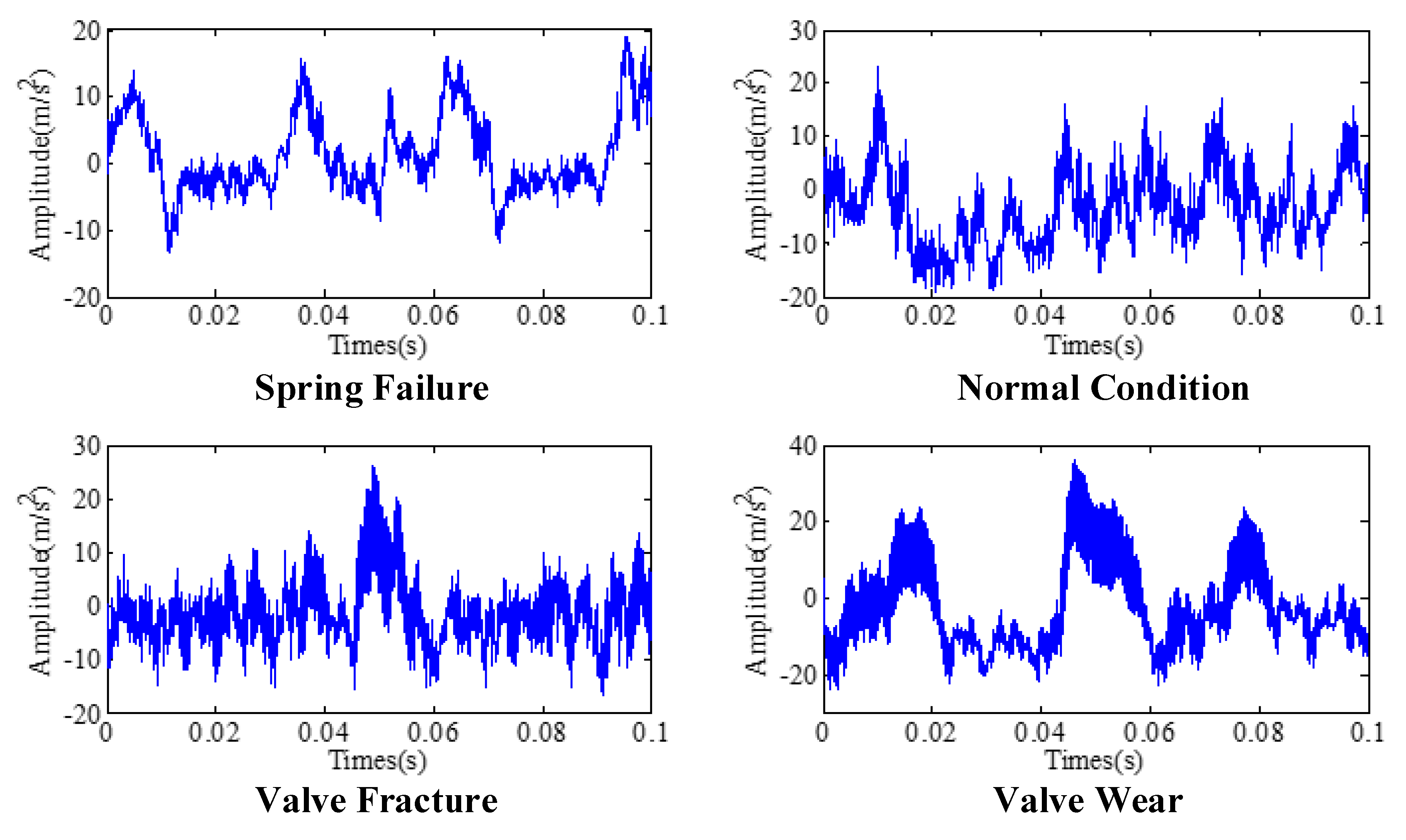
4.1. Data Description
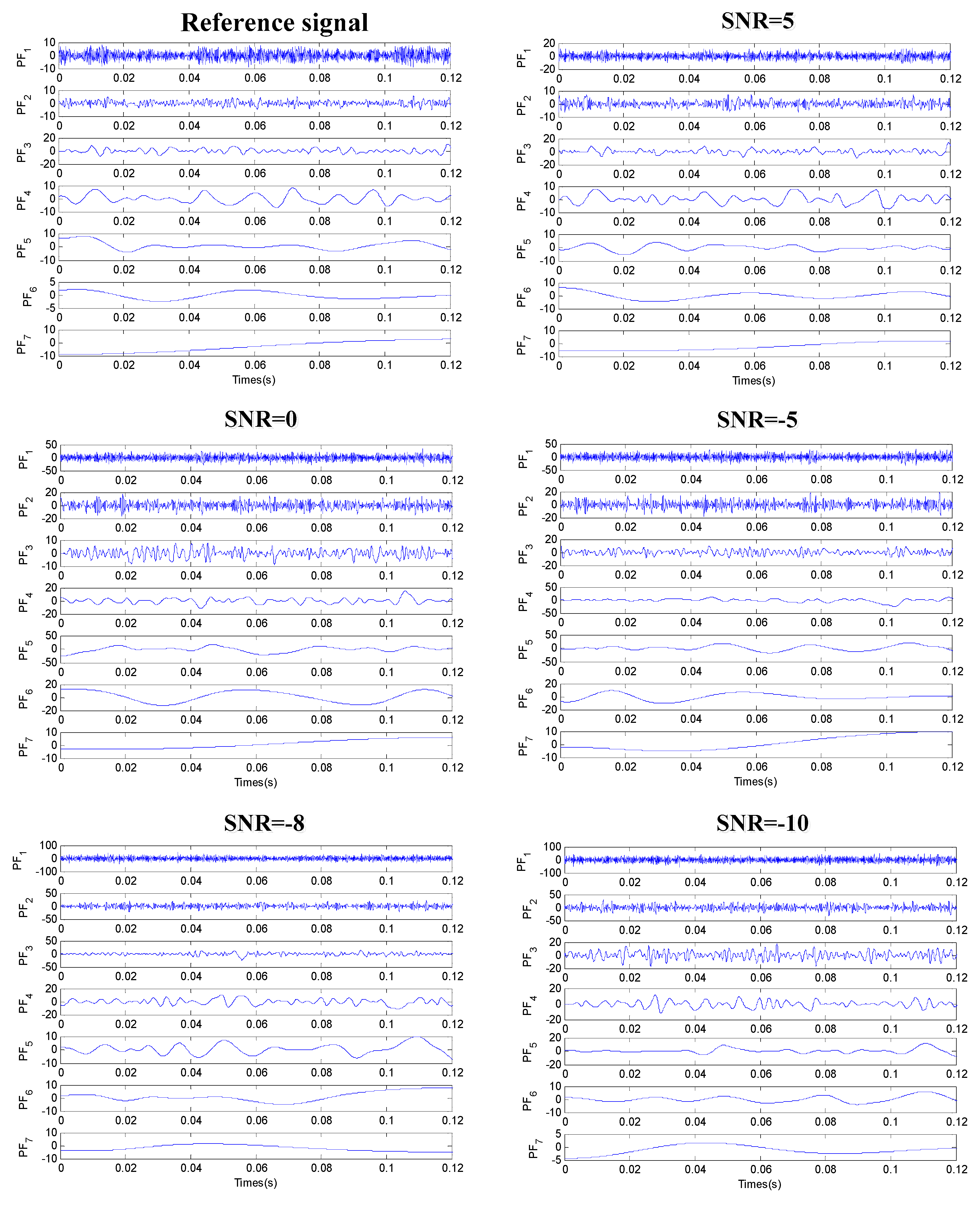
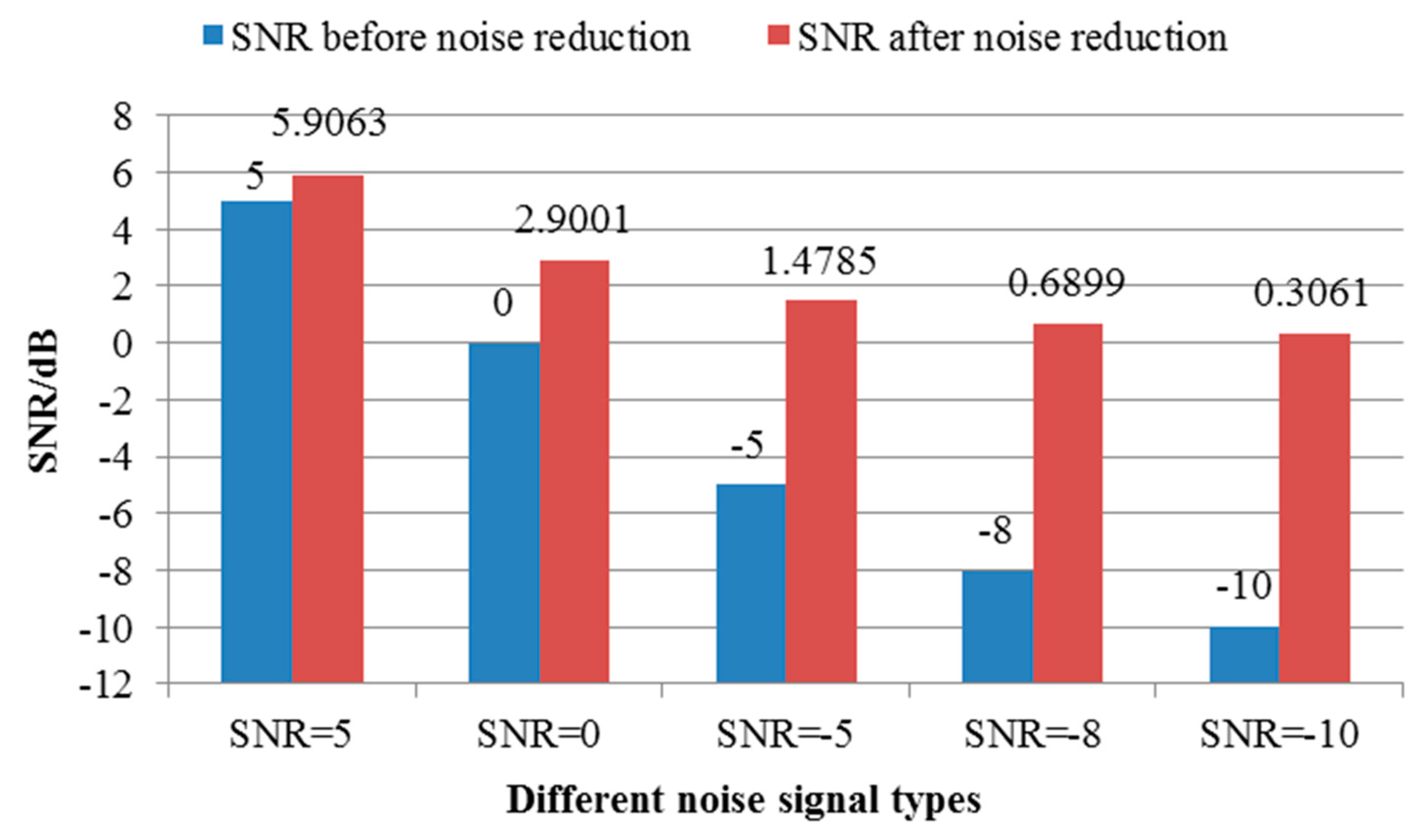
4.2. Fault Diagnosis Using the Proposed Method
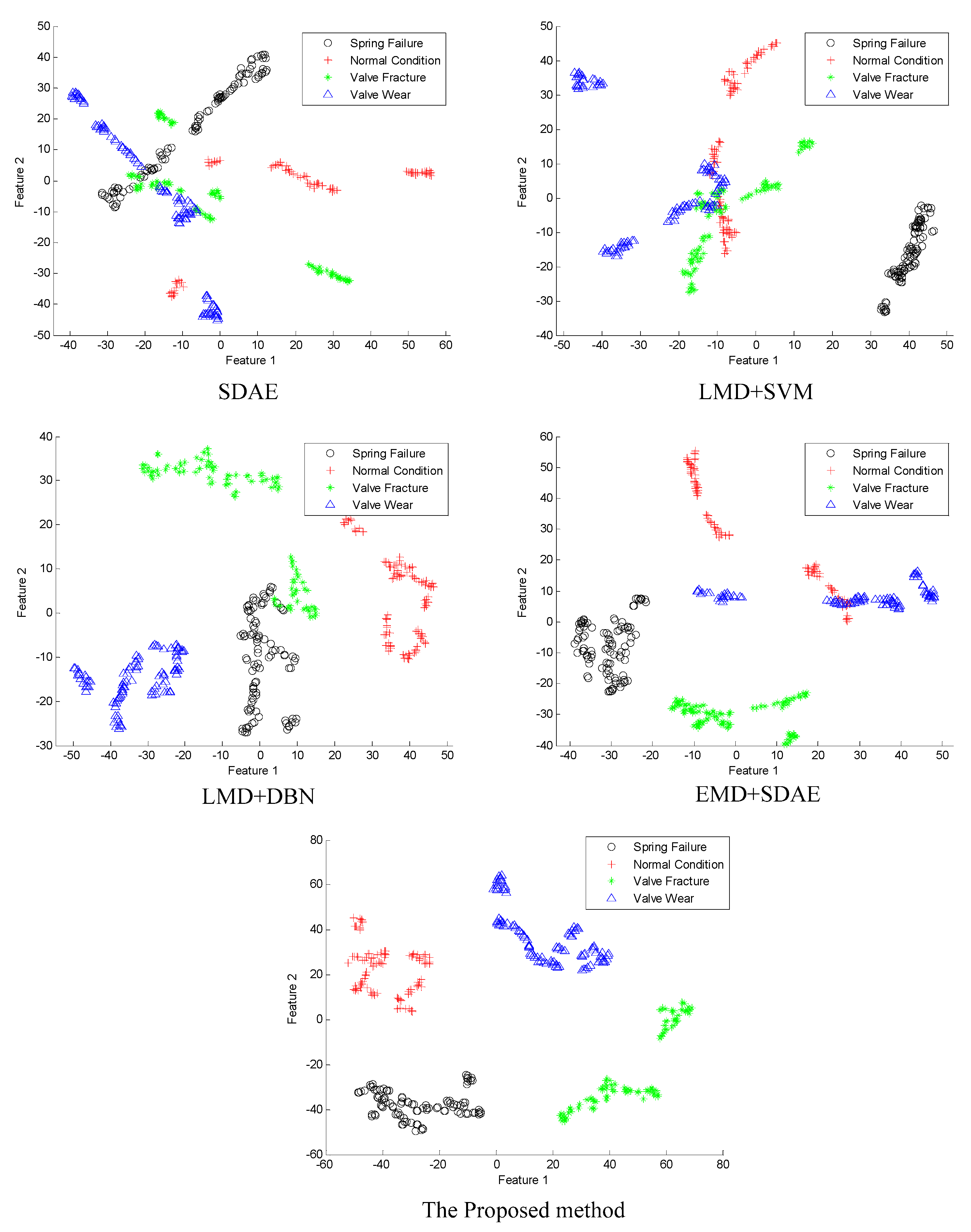
4.3. Comparison and Analysis of Traditional Methods
5. Conclusions
- (1)
- The proposed method reduces the overlapping of the system signal and the noise signal by decomposition and reconstruction. Therefore, the proposed method has strong noise reduction effect and the obtained de-noised signal has a high SNR.
- (2)
- The proposed method utilizes the massive data to fully explore the information of vibration signals, and learn the high-dimensional deep features. Therefore, the proposed method has good learning ability and the necessary generalization abilities.
- (3)
- The features of the de-noised signal are automatically extracted by the proposed method, which reduced the subjectivity of artificial features extraction. Therefore, the proposed method has a better feature extraction effect and higher diagnosis accuracy, which proves the effectiveness of the proposed method in adaptive feature learning.
- (4)
- The proposed method has great application prospects in the fault diagnosis of industrial reciprocating compressors based on the experimental results of this study. Especially, this method has good effect of adaptive feature extraction under low SNR, and the accuracy of the classification diagnosis is higher than that of traditional fault diagnosis methods, which proves the robustness of the proposed method.
Author Contributions
Funding
Conflicts of Interest
References
- Ma, J.; Jiang, Z.N.; Gao, J.J. Feature extraction method based on chaotic fractal theory and its application in fault diagnosis of gas valves. J. Vib. Shock 2012, 31, 26–30. [Google Scholar]
- Chen, J.L.; Zhang, L.B.; Duan, L.X.; Hu, C. Diagnosis of reciprocating compressor piston-cylinder liner wear fault based on lifting scheme packet. J. China Univ. Pet. (Ed. Nat. Sci.) 2011, 35, 130–134. [Google Scholar]
- Tang, Y.F.; Liu, S.L. Time-frequency feature extraction from multiple impulse source signal of reciprocating compressor based on local frequency. J. Vibroeng. 2013, 15, 574–587. [Google Scholar]
- Kocyigit, N.; Bulgurcu, H.; Lin, C.X. Fault diagnosis of a vapor compression refrigeration system with hermetic reciprocating compressor based on p-h diagram. Int. J. Refrig. 2014, 45, 44–54. [Google Scholar] [CrossRef]
- Cui, H.X.; Zhang, L.B.; Kang, R.Y.; Lan, X.Y. Research on fault diagnosis for reciprocating compressor valve using information entropy and SVM method. J. Loss Prev. Process Ind. 2009, 22, 864–867. [Google Scholar] [CrossRef]
- Niu, Q.; Wang, L. Working condition recognition of screw compressor using wavelets theory. In Proceedings of the World Congress on Intelligent Control & Automation, Chongqing, China, 25–27 June 2008; pp. 3643–3647. [Google Scholar]
- Wang, L.; Ma, L.; Huang, Y. The Application of Lifting Wavelet Transform in the Fault Diagnosis of Reciprocating Air Compressor. In Proceedings of the International Conference on Intelligent System Design and Engineering Application, Hunan, China, 13–14 October 2010; pp. 574–576. [Google Scholar]
- Cao, Y.J.; Zang, S.S.; Ge, B. Analyzing the Acoustic Signal of Compressor Surge by Using Fast Fourier Transform and Wavelet Transform. Energy Technol. 2010, 31, 125–128. [Google Scholar]
- Wang, J.D.; Dai, M.; Du, Y.J.; Yang, S.S. Fault Feature Extraction from Reciprocating Compressor Valve Based on EMD and Information Entropy. Compress. Technol. 2013, 4, 37–39. [Google Scholar]
- Li, Y.J.; Tse, P.W.; Yang, X.; Yang, J.G. EMD-based fault diagnosis for abnormal clearance between contacting components in a diesel engine. Mech. Syst. Signal Process. 2010, 24, 193–210. [Google Scholar] [CrossRef]
- Zhao, H.Y.; Xu, M.Q.; Wang, J.D. Fault feature extraction based on multifractal and singular value decomposition for reciprocating compressors. J. Vib. Shock 2013, 32, 105–109. [Google Scholar]
- Tang, S.L.; Dong, L.Y.; Wang, Z.M.; Zhu, L.N.; Zhang, J.J. A Diagnosis Method for Typical Fault in Reciprocating Compressor Based on Principal Components Analysis and Support Vector Machine. Compress. Technol. 2016, 3, 23–28. [Google Scholar]
- Gao, X.Z.; Wang, X.; Zenger, K. Motor fault diagnosis using negative selection algorithm. Neural Comput. Appl. 2014, 25, 55–65. [Google Scholar] [CrossRef]
- Alzghoul, A.; Backe, B.; Löfstrand, M.; Byström, A.; Liljedahl, B. Comparing a knowledge-based and a data-driven method in querying data streams for system fault detection: A hydraulic drive system application. Comput. Ind. 2014, 65, 1126–1135. [Google Scholar] [CrossRef]
- Fernández-Francos, D.; Martínez-Rego, D.; Fontenla-Romero, O.; Alonso-Betanzos, A. Automatic bearing fault diagnosis based on one-class ν-SVM. Comput. Ind. Eng. 2013, 64, 357–365. [Google Scholar] [CrossRef]
- Liu, Z.W.; Chen, X.F.; He, Z.J.; Shen, Z.J. LMD Method and Multi-Class RWSVM of Fault Diagnosis for Rotating Machinery Using Condition Monitoring Information. Sensors 2013, 13, 8679–8694. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Selak, L.; Butala, P.; Sluga, A. Condition monitoring and fault diagnostics for hydropower plants. Comput. Ind. 2014, 65, 924–936. [Google Scholar] [CrossRef]
- Smith, J.S. The local mean decomposition and its application to EEG perception data. J. R. Soc. Interface 2005, 2, 443–454. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, L.; Liu, Z.W.; Miao, Q.; Zhang, X. Complete ensemble local mean decomposition with adaptive noise and its application to fault diagnosis for rolling bearings. Mech. Syst. Signal Process. 2018, 106, 24–39. [Google Scholar] [CrossRef]
- Li, Y.B.; Xu, M.Q.; Zhao, H.Y.; Wei, Y.; Huang, W.H. A new rotating machinery fault diagnosis method based on improved local mean decomposition. Dig. Signal Process. 2015, 46, 201–214. [Google Scholar] [CrossRef]
- Cai, J.H.; Chen, Q.Y. Bearing Fault Diagnosis Method Based on Local Mean Decomposition and Wigner Higher Moment Spectrum. Exp. Tech. 2016, 40, 1–10. [Google Scholar] [CrossRef]
- Chen, G.J.; Zou, L.Q.; Zhao, H.Y.; Li, Y.Q. An improved local mean decomposition method and its application for fault diagnosis of reciprocating compressor. J. Vibroeng. 2016, 18, 1474–1485. [Google Scholar]
- Zhao, H.Y.; Wang, J.D.; Xing, J.J.; Gao, Y.Q. A feature extraction method based on LMD and MSE and its application for fault diagnosis of reciprocating compressor. J. Vibroeng. 2015, 55, 3515–3526. [Google Scholar]
- Li, Y.B.; Xu, M.Q.; Wei, Y.; Huang, W.H. Application of CBSR and LMD in reciprocating compressor fault diagnosis. J. Vibroeng. 2015, 17, 203–215. [Google Scholar]
- Zhang, W.; Peng, G.L.; Li, C.H.; Chen, Y.H.; Zhang, Z.J. A New Deep Learning Model for Fault Diagnosis with Good Anti-Noise and Domain Adaptation Ability on Raw Vibration Signals. Sensors 2017, 17, 425. [Google Scholar] [CrossRef] [PubMed]
- Janssens, O.; Slavkovikj, V.; Vervisch, B.; Stockman, K.; Loccufier, M.; Verstockt, S.; Walle, R.V.D.; Hoeckea, S.V. Convolutional Neural Network Based Fault Detection for Rotating Machinery. J. Sound Vib. 2016, 377, 331–345. [Google Scholar] [CrossRef]
- Eren, L.; Ince, T.; Kiranyaz, S. A Generic Intelligent Bearing Fault Diagnosis System Using Compact Adaptive 1D CNN Classifier. J. Signal Process. Syst. 2019, 91, 179–189. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.Y.; Gao, L.; Zhang, Y.Y. A New Convolutional Neural Network Based Data-Driven Fault Diagnosis Method. IEEE Trans. Ind. Electron. 2018, 65, 5990–5998. [Google Scholar] [CrossRef]
- Jing, L.Y.; Wang, T.Y.; Zhao, M.; Wang, P. An Adaptive Multi-Sensor Data Fusion Method Based on Deep Convolutional Neural Networks for Fault Diagnosis of Planetary Gearbox. Sensors 2017, 17, 414. [Google Scholar] [CrossRef] [PubMed]
- Gan, M.; Wang, C.; Zhu, C.A. Construction of hierarchical diagnosis network based on deep learning and its application in the fault pattern recognition of rolling element bearings. Mech. Syst. Signal Process. 2016, 72–73, 92–104. [Google Scholar] [CrossRef]
- Gao, Z.; Ma, C.; Song, D.; Liu, Y. Deep quantum inspired neural network with application to aircraft fuel system fault diagnosis. Neurocomputing 2017, 238, 13–23. [Google Scholar] [CrossRef]
- Hu, J.Q.; Zhang, L.B.; Cai, A.S.; Wang, Y. An intelligent fault diagnosis system for process plant using a functional HAZOP and DBN integrated methodology. Eng. Appl. Artif. Intell. 2015, 45, 119–135. [Google Scholar] [CrossRef]
- He, J.; Yang, S.X.; Gan, C.B. Unsupervised Fault Diagnosis of a Gear Transmission Chain Using a Deep Belief Network. Sensors 2017, 17, 1564. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Cao, M.Y.; Song, B.Y.; Zhang, J.S.; Liu, Y.R.; Alsaadi, F.E. Open-Circuit Fault Diagnosis of Power Rectifier using Sparse Autoencoder based Deep Neural Network. Neurocomputing 2018, 311, 1–10. [Google Scholar] [CrossRef]
- Lu, C.; Wang, Z.Y.; Qin, W.L.; Ma, J. Fault diagnosis of rotary machinery components using a stacked denoising autoencoder-based health state identification. Signal Process. 2017, 130, 377–388. [Google Scholar] [CrossRef]
- Sohaib, M.; Kim, C.H.; Kim, J.M. A Hybrid Feature Model and Deep-Learning-Based Bearing Fault Diagnosis. Sensors 2017, 17, 2876. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Zhang, W.; Ding, Q. A robust intelligent fault diagnosis method for rolling element bearings based on deep distance metric learning. Neurocomputing 2018, 310, 77–95. [Google Scholar] [CrossRef]
- Xia, M.; Li, T.; Liu, L.Z.; Xu, L.; Silva, C.W.D. Intelligent fault diagnosis approach with unsupervised feature learning by stacked denoising autoencoder. IET Sci. Meas. Technol. 2017, 11, 687–695. [Google Scholar] [CrossRef]
- Zhang, C.G.; Jiang, J.Q. Study on Sparse De-noising Auto-Encoder Neural Network. J. Inn. Mong. Univ. Natl. (Nat. Sci.) 2016, 31, 21–25. [Google Scholar]
- Zhu, Y.Q.; Huang, S.X.; Yang, T.Q.; Sun, J.X. Fault diagnosis based on stacked denoising autoencoder. Manuf. Autom. 2017, 39, 152–156. [Google Scholar]
- Wang, L.H.; Xie, Y.Y.; Zhang, Y.H.; Zhao, X.P.; Zhou, Z.X. A Fault Diagnosis Method for Asynchronous Motor Using Deep Learning. J. Xi’an Jiaotong Univ. 2017, 51, 128–134. [Google Scholar]




| Datasets | Training Datasets | Testing Datasets | Label | ||
|---|---|---|---|---|---|
| Number of Samples | Length of Samples | Number of Samples | Length of Samples | ||
| SF | 2400 | 2048 | 800 | 2048 | 1 |
| NL | 2400 | 2048 | 800 | 2048 | 2 |
| VF | 2400 | 2048 | 800 | 2048 | 3 |
| VW | 2400 | 2048 | 800 | 2048 | 4 |
| Signal Type | PF1 | PF2 | PF3 | PF4 | PF5 | PF6 | PF7 |
|---|---|---|---|---|---|---|---|
| Reference signal | 0.4022 | 0.2807 | 0.4055 | 0.4760 | 0.3716 | 0.2540 | 0.3551 |
| SNR = 5 | 0.2652 | 0.2007 | 0.4591 | 0.4759 | 0.3117 | 0.4504 | 0.3816 |
| SNR = 0 | 0.1364 | 0.1195 | 0.0635 | 0.3442 | 0.5348 | 0.4334 | 0.2269 |
| SNR = −5 | 0.1416 | 0.0047 | 0.0905 | 0.2285 | 0.6616 | 0.4186 | 0.2204 |
| SNR = −8 | 0.0900 | 0.1516 | 0.0950 | 0.3605 | 0.4939 | 0.1637 | 0.0423 |
| SNR = −10 | 0.0962 | 0.1345 | 0.0871 | 0.1815 | 0.5480 | 0.4221 | 0.2025 |
| Signal Type | Network Structure | Opts. Numepochs | Opts. Batchsize | Learning Rate | Feature Dimension |
|---|---|---|---|---|---|
| Reference signal | 1024-500-250-50 | 50 | 10 | 1 | 50 |
| SNR = 5 | 1024-500-250-50 | 40 | 20 | 1 | 50 |
| SNR = 0 | 1024-500-250-50 | 80 | 50 | 1 | 50 |
| SNR = −5 | 1024-500-250-50 | 100 | 100 | 1 | 50 |
| SNR = −8 | 1024-500-250-50 | 240 | 100 | 1 | 50 |
| SNR = −10 | 1024-500-250-50 | 350 | 100 | 1 | 50 |
| SNR (dB) | SDAE | LMD+SVM | LMD+DBN | EMD+SDAE | The Proposed Method |
|---|---|---|---|---|---|
| ∞ | 100% | 100% | 100% | 100% | 100% |
| 5 | 100% | 98.63% | 100% | 99.66% | 99.84% |
| 0 | 98.28% | 92.44% | 96.47% | 98.44% | 99.09% |
| −5 | 68.91% | 85.47% | 94.84% | 95.59% | 97.75% |
| −8 | 48.47% | 80.06% | 93.72% | 92.44% | 97.22% |
| −10 | 42.56% | 73.97% | 87.69% | 84.97% | 92.72% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Duan, L.; Yuan, Z.; Wang, N.; Zhao, J. An Intelligent Fault Diagnosis Method for Reciprocating Compressors Based on LMD and SDAE. Sensors 2019, 19, 1041. https://doi.org/10.3390/s19051041
Liu Y, Duan L, Yuan Z, Wang N, Zhao J. An Intelligent Fault Diagnosis Method for Reciprocating Compressors Based on LMD and SDAE. Sensors. 2019; 19(5):1041. https://doi.org/10.3390/s19051041
Chicago/Turabian StyleLiu, Yang, Lixiang Duan, Zhuang Yuan, Ning Wang, and Jianping Zhao. 2019. "An Intelligent Fault Diagnosis Method for Reciprocating Compressors Based on LMD and SDAE" Sensors 19, no. 5: 1041. https://doi.org/10.3390/s19051041
APA StyleLiu, Y., Duan, L., Yuan, Z., Wang, N., & Zhao, J. (2019). An Intelligent Fault Diagnosis Method for Reciprocating Compressors Based on LMD and SDAE. Sensors, 19(5), 1041. https://doi.org/10.3390/s19051041





