Bearing Fault Diagnosis Method Based on Deep Convolutional Neural Network and Random Forest Ensemble Learning
Abstract
:1. Introduction
- (1)
- The important and representative features containing enough fault information are manually extracted and selected from raw data, which depend heavily on prior knowledge and diagnostic expertise of signal processing techniques. In addition, the feature extraction and selection processes for different diagnostic problems are case sensitive, thus they are also time-consuming and laborious.
- (2)
- (1)
- In many practical fault diagnosis applications, the training data and testing data are collected under different operational conditions, thus they are drawn from the different feature distribution [23]. It is well known that the extracted high-level features in CNN models are specific for particular dataset or task, while the low-level features in the hidden layers are universal and similar for different but related distribution datasets or tasks [24,25,26]. That is to say, low-level features extracted from training data in source domain are also applicable to test data in target domain. The generalization ability of the CNN-based fault diagnosis methods only taking high-level features into account would be poor. Therefore, low-level features in the hidden layers should be combined to obtain the better accuracy and generalization performance.
- (2)
- Bearing health conditions with the same fault types under different damage sizes need to be classified in some practical applications. Since there are still some accurate details and local characteristics existing in low-level features which are not well preserved in high-level features [25,26], the classifier should make full use of multi-level features for accurate and complex fault diagnosis tasks.
- (3)
- The extracted features in each layer are another abstract representation of raw data, thus the features in all layers can directly impact the diagnosis results.
- (4)
- Sometimes, the extracted low-level features already contain enough fault information used for effective fault classification, there is no need to extract high-level features, which will cost more time and computer memory.
2. Literature Review
2.1. Data-Driven Fault Diagnosis
2.2. Deep Learning and CNN
2.3. Ensemble Learning
3. Theoretical Background
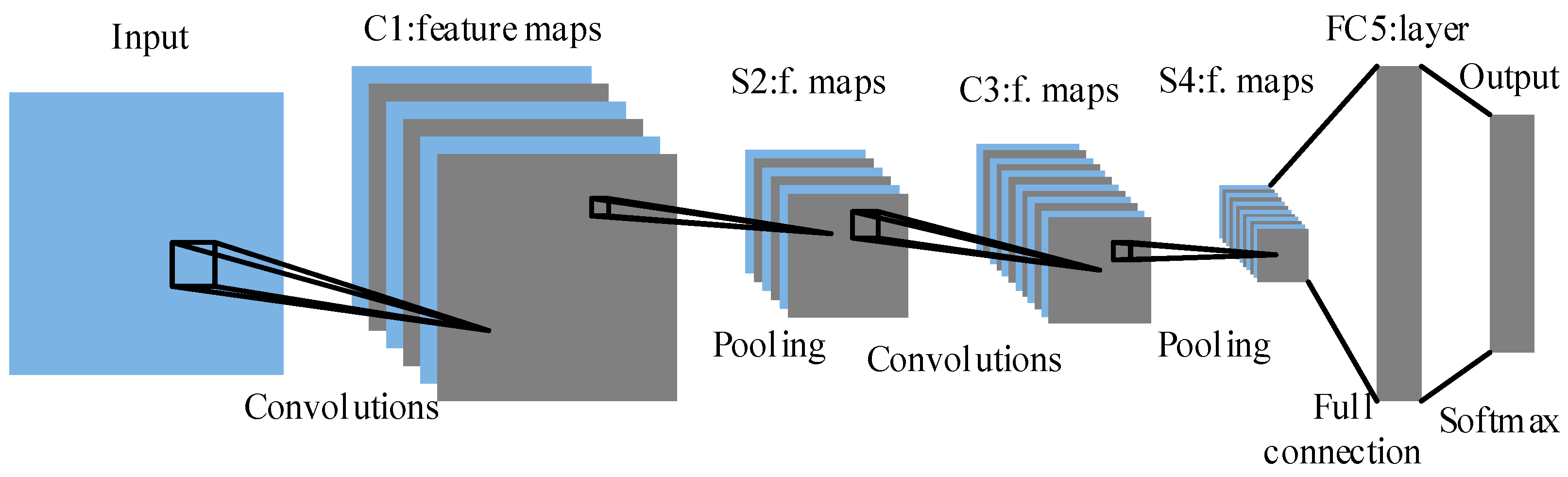
3.1. CNN
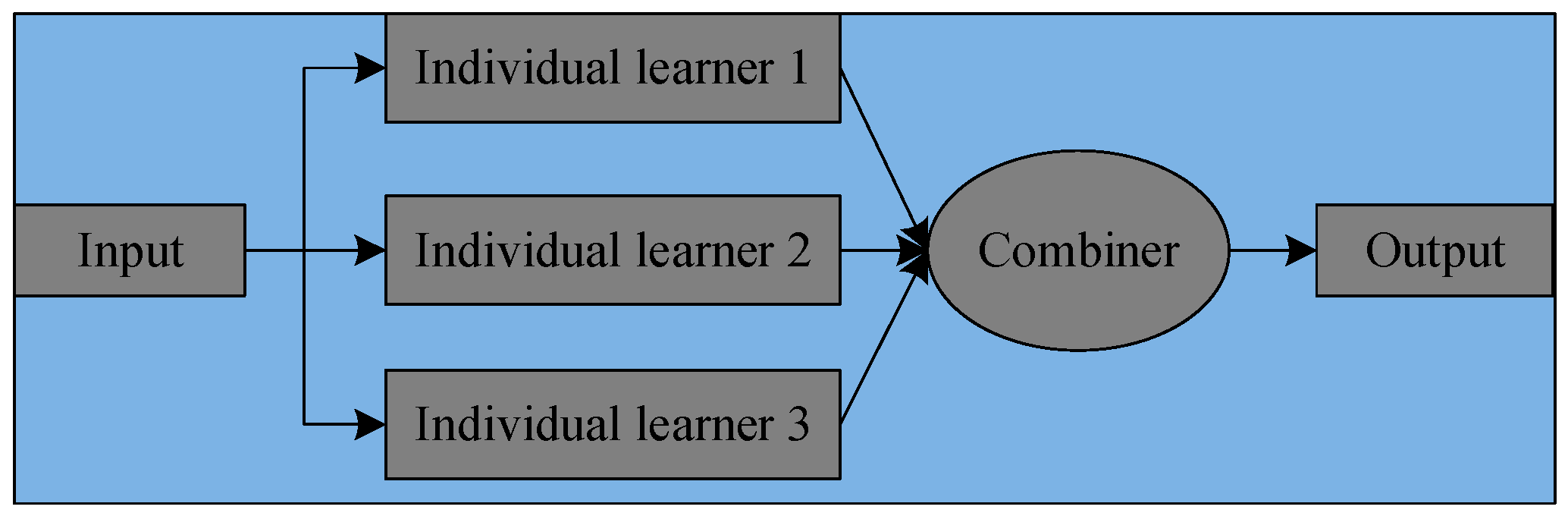
3.2. Ensemble Learning and RF
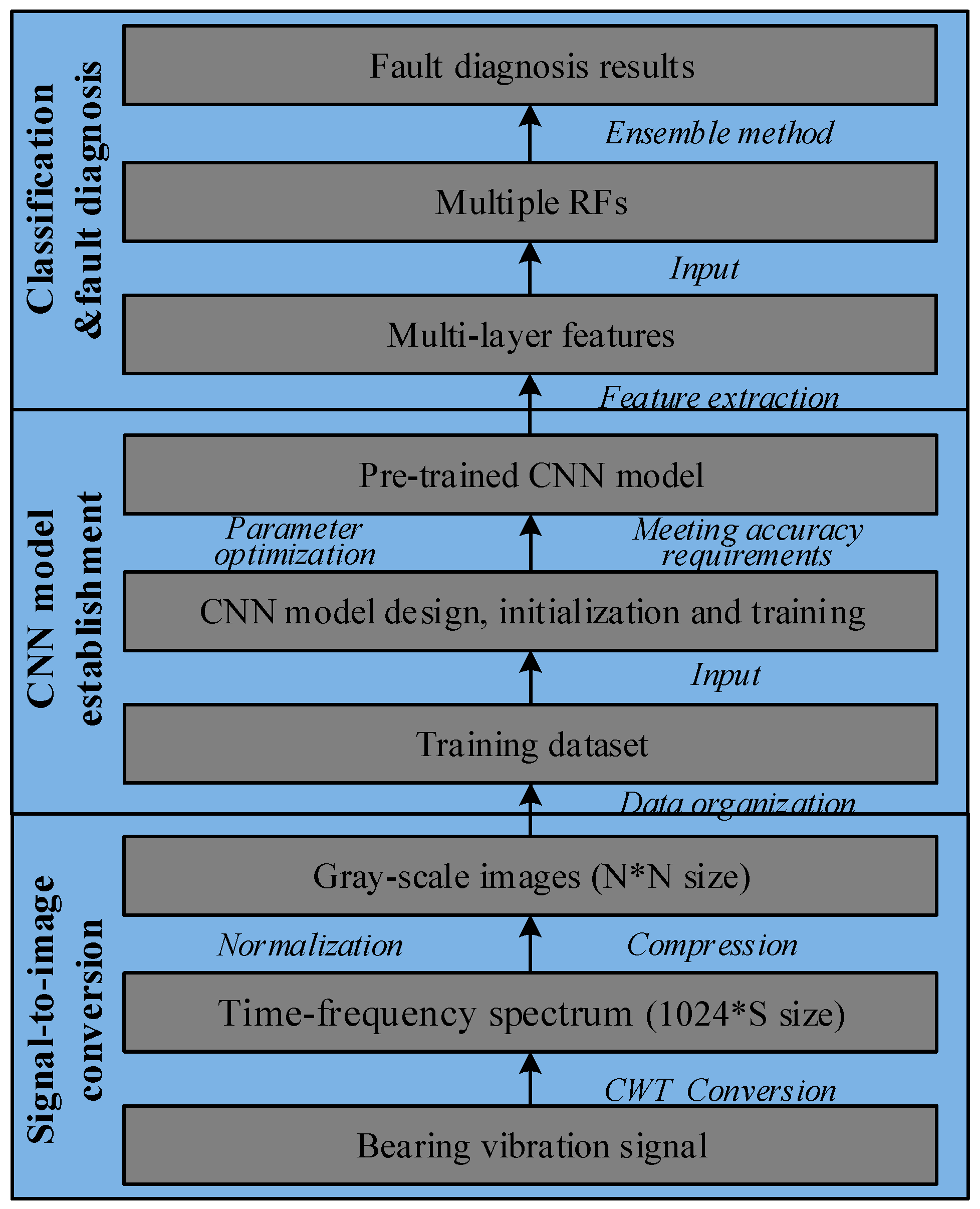
4. Proposed Method
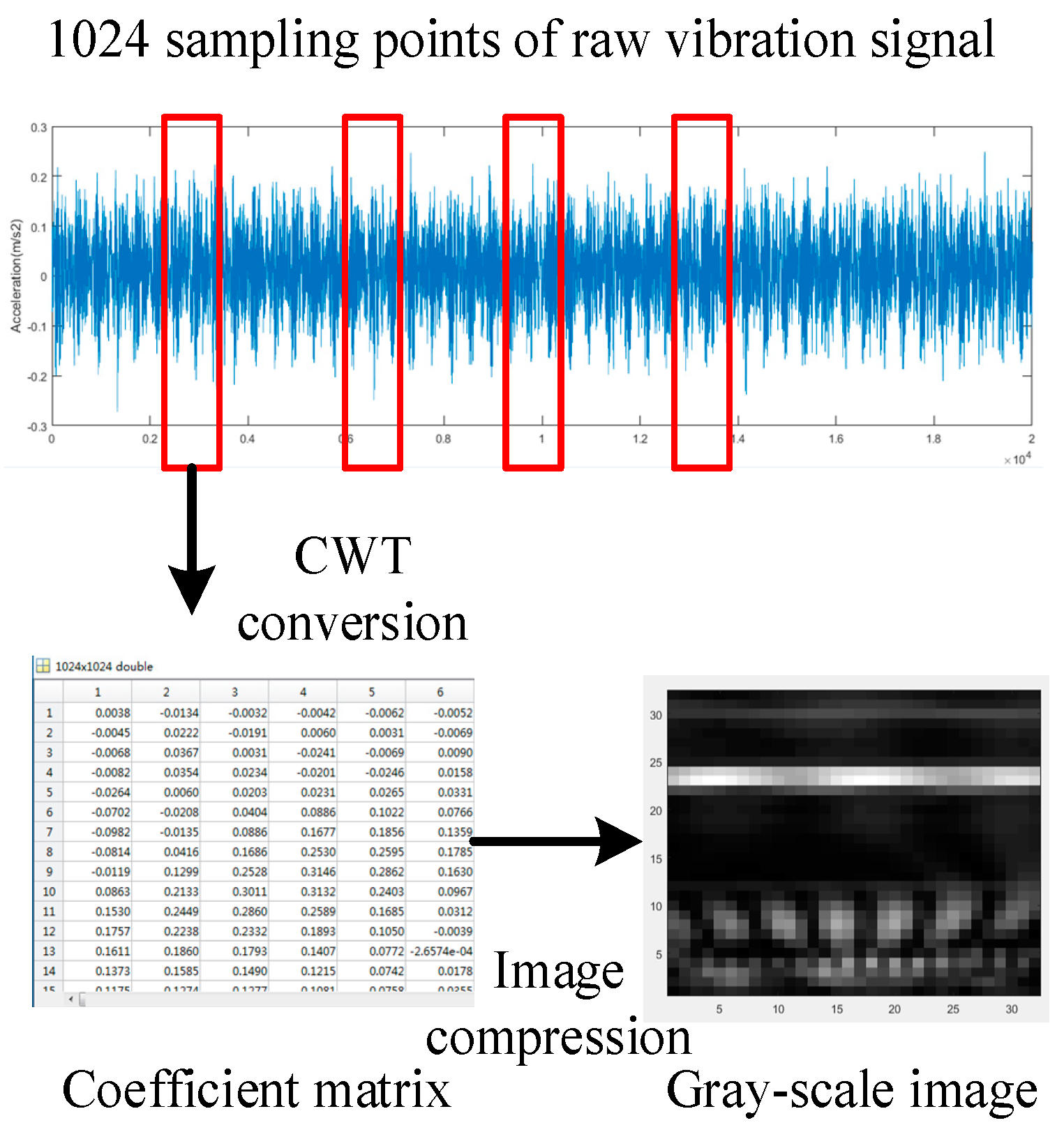
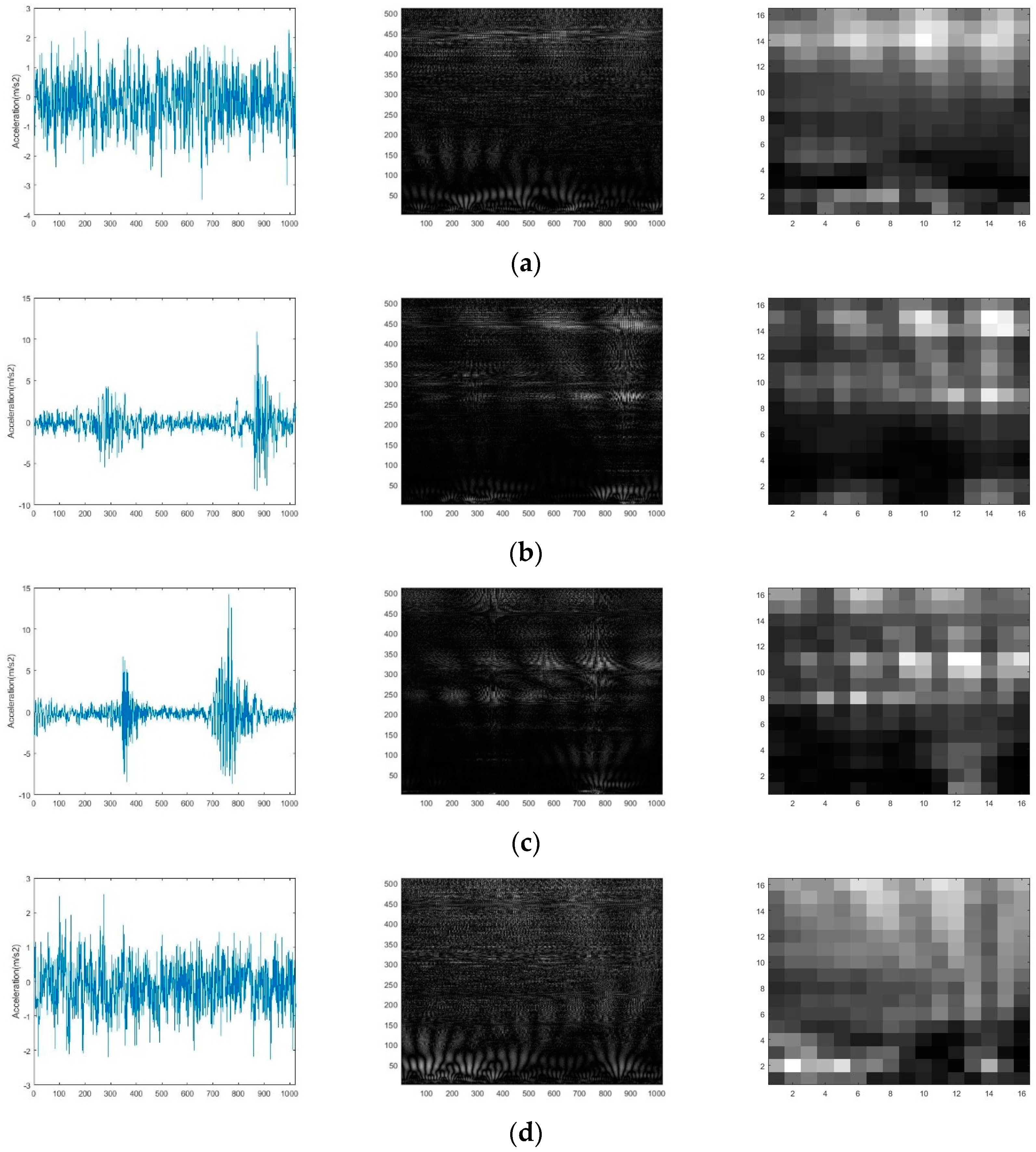
4.1. Signal-to-Image Conversion Based on CWT
4.2. Design of the Proposed CNN
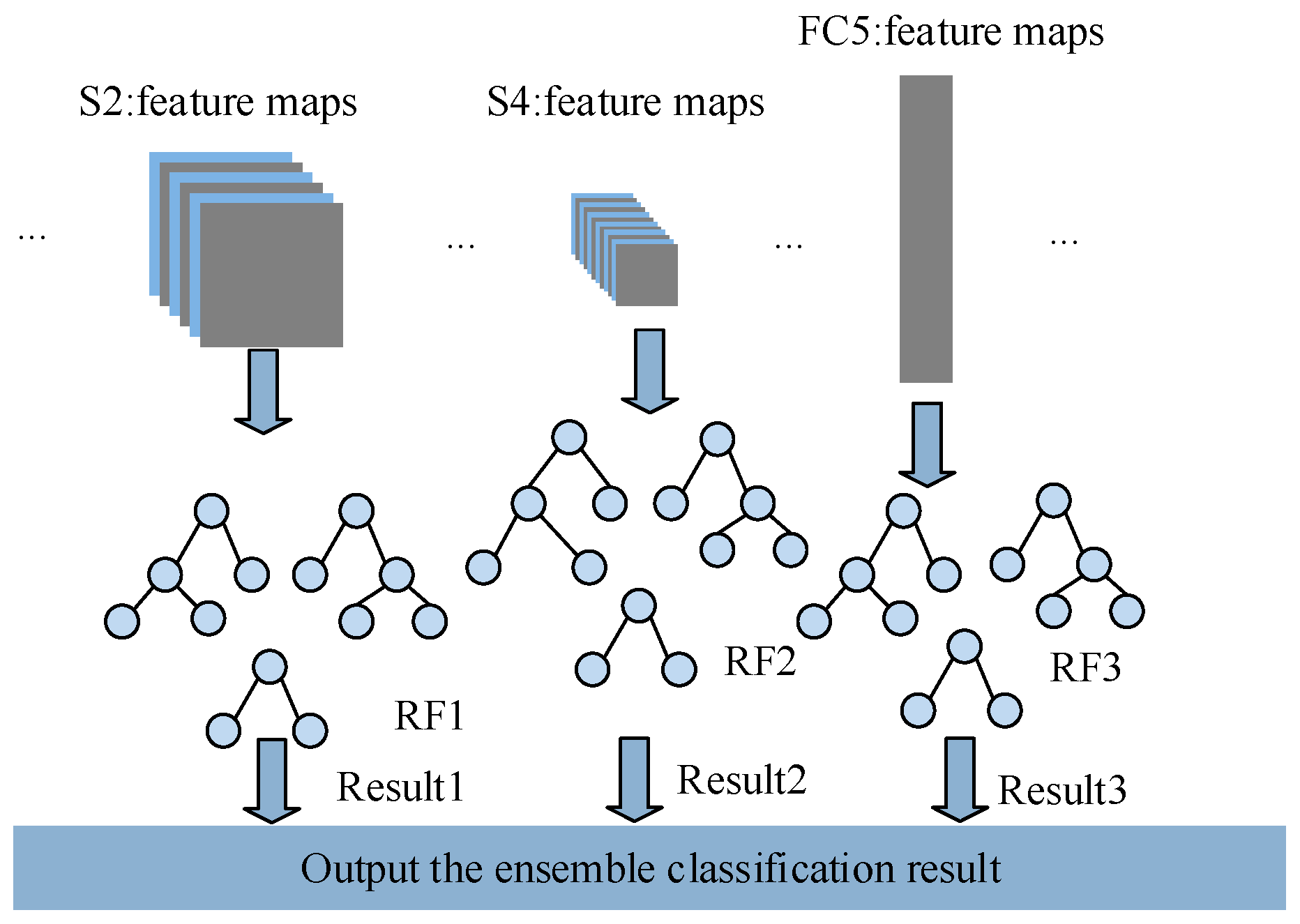
4.3. Ensemble Classification
| Algorithm 1 General Procedure of the Proposed Method |
| Input: Given the bearing dataset composed of vibration signal samples, the architecture and hyper-parameters of the proposed CNN and the RF classifier Output: The diagnostic results, and the testing accuracy and efficiency Step 1: Generate the training dataset and the test dataset 1.1: Obtain the spectrums of vibration signal samples for training and samples for testing using the signal-to-image conversion method. 1.2: Use the spectrums to generate the training dataset and the test dataset . Step 2: Construct and train the CNN for multi-level features extraction 2.1 Construct the CNN and initialize the parameters (weight vectors and bias) of the CNN randomly. 2.2 Train the CNN on the training dataset , calculate the outputs of layers in the CNN using Equations (1)–(4). 2.3 Calculate the outputs of the output layer and the loss function of softmax classifier using Equations (9) and (10). 2.4 Optimize the parameters through minimizing the Equation (10) using the mini-batch stochastic gradient descent method. 2.5 Repeat (2.2)–(2.4) until meeting the training requirements, and finish the training process of the CNN. 2.6 Extract the features , , in layer S2, S4 and FC5 from the trained CNN, and donates the output feature map of th level. Step 3: Use multi-level features to train multiple RF classifiers 3.1 Use the extracted features , , to train the classifiers RF1, RF2, RF3, respectively. 3.2 Output the diagnostic results of three RF classifiers separately. Step 4: Output the final result using the ensemble method Aggregate the outputs of three RF classifiers with the winner-take-all ensemble strategy to output the final diagnostic result. Step 5: Validate the performance of the proposed method Validate the performance of the proposed method on test dataset and output the testing accuracy and efficiency of the proposed method |
5. Experimental Results
5.1. Case Study 1: Bearing Fault Diagnosis for Reliance Electric Motor
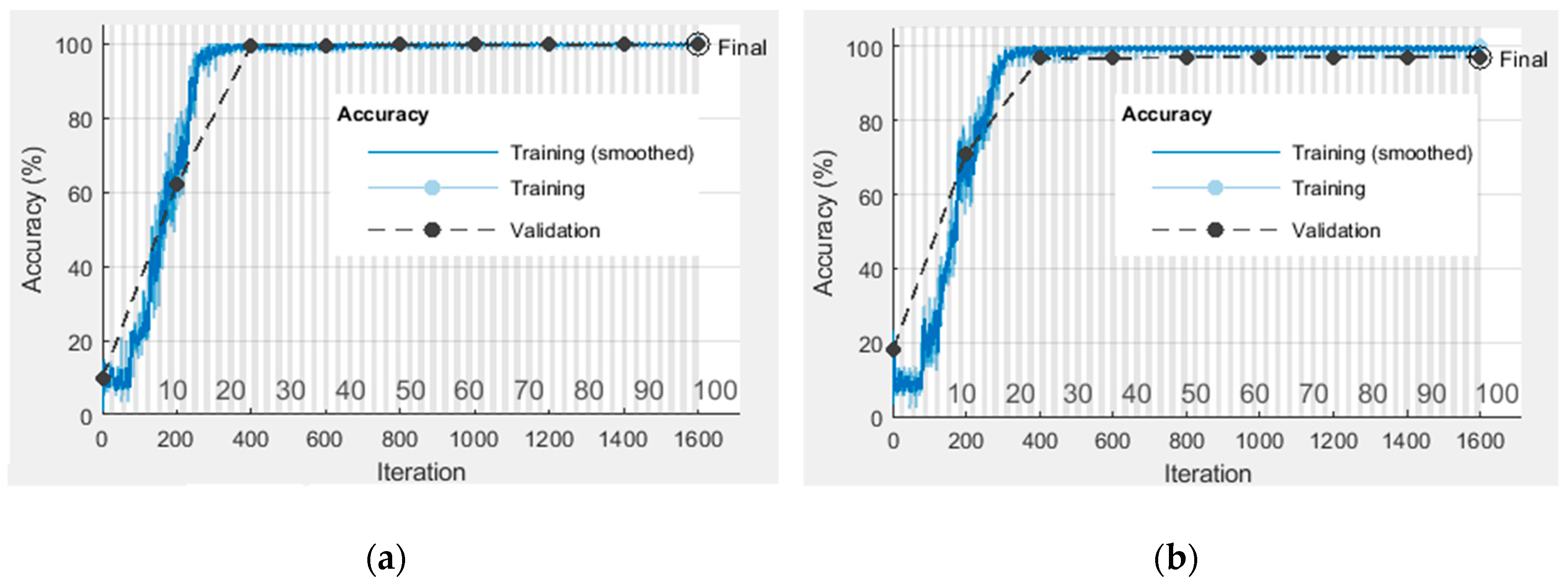
5.1.1. Experimental Setup and Dataset
5.1.2. Results and Discussion
5.1.3. Comparison with Other Methods
5.2. Case Study 2: Bearing Fault Diagnosis for BaoSteel Rolling Mill
5.2.1. Experimental Setup and Dataset
5.2.2. Results and Discussion
5.2.3. Comparison with Other Methods
6. Conclusions and Future Work
- (1)
- Presenting a novel signal-to-image conversion method based on CWT. The time-frequency spectra obtained from CWT not only fully capture the non-stationary signal characteristics and contain abundant fault information, but also can be regarded as two-dimensional gray-scale images, which are suitable as the input of CNN.
- (2)
- Implementing an automatic feature extractor using CNN. An improved CNN model with optimized configuration is constructed and pre-trained in a supervised manner. The pre-trained model has the ability of extracting sensitive and representative multi-level features automatically from gray-scale images. The extracted multi-level features contain both local and global fault information and can contribute different knowledge to diagnosis results.
- (3)
- Applying the winner-take-all ensemble strategy of multiple RF classifiers to improve the accuracy and generalization performance of the fault diagnosis method. The multi-level features, especially the low-level features in hidden layers, are used for classifying faults independently in this paper. The extracted features in each layer are fed into a RF classifier and each RF classifier separately outputs the diagnostic result. The outputs of all classifiers are combined by the winner-take-all ensemble strategy to generate more accurate diagnostic result.
- (4)
- The proposed method is validated by two bearing datasets from public website and BaoSteel MRO Management System. The former achieves higher diagnostic accuracy at 99.73% than the latter at 97.38%. In particular, the different feature distribution of training and test dataset has almost no effect on the classification accuracy, which indicates the strong generalization ability. The experimental results prove the availability and superiority of the proposed method.
Author Contributions
Funding
Conflicts of Interest
References
- Jiang, W.; Xie, C.H.; Zhuang, M.Y.; Shou, Y.H.; Tang, Y.C. Sensor Data Fusion with Z-Numbers and Its Application in Fault Diagnosis. Sensors 2016, 16, 1509. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.N.; Yang, B.Y.; Zio, E.; Chen, X.F. Artificial intelligence for fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- Li, C.; Sánchez, R.; Zurita, G.; Cerrada, M.; Cabrera, D. Fault Diagnosis for Rotating Machinery Using Vibration Measurement Deep Statistical Feature Learning. Sensors 2016, 16, 895. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Yan, C.; Wen, J. Intelligent Bearing Fault Diagnosis Method Combining Compressed Data Acquisition and Deep Learning. IEEE Trans. Instrum. Meas. 2018, 23, 101–110. [Google Scholar] [CrossRef]
- Lu, S.; He, Q.; Yuan, T.; Kong, F. Online Fault Diagnosis of Motor Bearing via Stochastic-Resonance-Based Adaptive Filter in an Embedded System. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 1111–1122. [Google Scholar] [CrossRef]
- Cai, B.; Zhao, Y.; Liu, H.; Xie, M. A Data-Driven Fault Diagnosis Methodology in Three-Phase Inverters for PMSM Drive Systems. IEEE Trans. Power Electron. 2016, 32, 5590–5600. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.; Gao, L.; Zhang, Y. A New Convolutional Neural Network Based Data-Driven Fault Diagnosis Method. IEEE Trans. Ind. Electron. 2018, 65, 5990–5998. [Google Scholar] [CrossRef]
- Flores-Fuentes, W.; Sergiyenko, O.; Gonzalez-Navarro, F.F.; Rivas-López, M.; Rodríguez-Quiñonez, J.C.; Hernández-Balbuena, D.; Tyrsa, V.; Lindner, L. Multivariate outlier mining and regression feedback for 3D measurement improvement in opto-mechanical system. Opt. Quantum Electron. 2016, 48, 403. [Google Scholar] [CrossRef]
- Lei, Y.; He, Z.; Zi, Y. EEMD method and WNN for fault diagnosis of locomotive roller bearings. Expert Syst. Appl. 2011, 38, 7334–7341. [Google Scholar] [CrossRef]
- Lin, L.; Ji, H. Signal feature extraction based on an improved EMD method. Measurement 2009, 42, 796–803. [Google Scholar] [CrossRef]
- Ngaopitakkul, A.; Bunjongjit, S. An application of a discrete wavelet transform and a back-propagation neural network algorithm for fault diagnosis on single-circuit transmission line. Int. J. Syst. Sci. 2013, 44, 1745–1761. [Google Scholar] [CrossRef]
- Sun, W.; Chen, J.; Li, J. Decision tree and PCA-based fault diagnosis of rotating machinery. Noise Vib. Worldw. 2007, 21, 1300–1317. [Google Scholar] [CrossRef]
- Jin, X.; Zhao, M.; Chow, T.W.S.; Pecht, M. Motor Bearing Fault Diagnosis Using Trace Ratio Linear Discriminant Analysis. IEEE Trans. Ind. Electron. 2013, 61, 2441–2451. [Google Scholar] [CrossRef]
- Yang, Y.; Yu, D.; Cheng, J. A fault diagnosis approach for roller bearing based on IMF envelope spectrum and SVM. Measurement 2007, 40, 943–950. [Google Scholar] [CrossRef]
- Pandya, D.H.; Upadhyay, S.H.; Harsha, S.P. Fault diagnosis of rolling element bearing with intrinsic mode function of acoustic emission data using APF-KNN. Expert Syst. Appl. 2013, 40, 4137–4145. [Google Scholar] [CrossRef]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Shao, H.; Jiang, H.; Zhang, X.; Niu, M. Rolling bearing fault diagnosis using an optimization deep belief network. Meas. Sci. Technol. 2015, 26, 11500. [Google Scholar] [CrossRef]
- He, M.; He, D. Deep Learning Based Approach for Bearing Fault Diagnosis. IEEE Trans. Ind. Appl. 2017, 53, 3057–3065. [Google Scholar] [CrossRef]
- Qi, Y.; Shen, C.; Wang, D.; Shi, J.; Jiang, X.; Zhu, Z. Stacked Sparse Autoencoder-Based Deep Network for Fault Diagnosis of Rotating Machinery. IEEE Access 2017, 5, 15066–15079. [Google Scholar] [CrossRef]
- Shao, H.; Jiang, H.; Liu, X.; Wu, S. Intelligent fault diagnosis of rolling bearing using deep wavelet auto-encoder with extreme learning machine. Knowl.-Based Syst. 2018, 140, 1–14. [Google Scholar]
- Xia, M.; Li, T.; Xu, L.; Liu, L.; Silva, C.W. Fault Diagnosis for Rotating Machinery Using Multiple Sensors and Convolutional Neural Networks. IEEE/ASME Trans. Mechatron. 2018, 23, 101–110. [Google Scholar] [CrossRef]
- Lee, K.B.; Cheon, S.; Chang, O.K. A Convolutional Neural Network for Fault Classification and Diagnosis in Semiconductor Manufacturing Processes. IEEE Trans. Semicond. Manuf. 2017, 30, 135–142. [Google Scholar] [CrossRef]
- Wen, L.; Gao, L.; Li, X. A New Deep Transfer Learning Based on Sparse Auto-Encoder for Fault Diagnosis. IEEE Trans. Syst. Man Cybern. Syst. 2017, 99, 1–9. [Google Scholar] [CrossRef]
- Li, H.; Chen, J.; Lu, H.; Chi, Z. CNN for saliency detection with low-level feature integration. Neurocomputing 2017, 226, 212–220. [Google Scholar] [CrossRef]
- Ding, X.; He, Q. Energy-Fluctuated Multiscale Feature Learning with Deep ConvNet for Intelligent Spindle Bearing Fault Diagnosis. IEEE Trans. Instrum. Meas. 2017, 66, 1926–1935. [Google Scholar] [CrossRef]
- Zeiler, M.D.; Fergus, R. Visualizing and Understanding Convolutional Networks. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 818–833. [Google Scholar]
- Sun, Y.; Wang, X.; Tang, X. Deep Learning Face Representation from Predicting 10,000 Classes. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1891–1898. [Google Scholar]
- Lee, J.; Nam, J. Multi-Level and Multi-Scale Feature Aggregation Using Pre-trained Convolutional Neural Networks for Music Auto-tagging. IEEE Signal Process. Lett. 2017, 24, 1208–1212. [Google Scholar] [CrossRef]
- Sermanet, P.; Lecun, Y. Traffic sign recognition with multi-scale Convolutional Networks. In Proceedings of the International Joint Conference on Neural Networks, San Jose, CA, USA, 31 July–5 August 2011; pp. 2809–2813. [Google Scholar]
- Zheng, J.; Pan, H.; Cheng, J. Rolling bearing fault detection and diagnosis based on composite multiscale fuzzy entropy and ensemble support vector machines. Mech. Syst. Signal Process. 2017, 85, 746–759. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, B.; Chen, X. Intelligent fault diagnosis of roller bearings with multivariable ensemble-based incremental support vector machine. Knowl.-Based Syst. 2015, 89, 56–85. [Google Scholar] [CrossRef]
- Shao, H.; Jiang, H.; Lin, Y.; Li, X. A novel method for intelligent fault diagnosis of rolling bearings using ensemble deep auto-encoders. Mech. Syst. Signal Process. 2018, 102, 278–297. [Google Scholar] [CrossRef]
- Li, X.; Ding, Q.; Sun, J.Q. Remaining useful life estimation in prognostics using deep convolution neural networks. Reliab. Eng. Syst. Saf. 2018, 172, 1–11. [Google Scholar] [CrossRef]
- Do, V.T.; Chong, U.P. Signal Model-Based Fault Detection and Diagnosis for Induction Motors Using Features of Vibration Signal in Two-Dimension Domain. Stroj. Vestn. 2011, 57, 655–666. [Google Scholar] [CrossRef]
- Chohra, A.; Kanaoui, N.; Amarger, V. A Soft Computing Based Approach Using Signal-To-Image Conversion for Computer Aided Medical Diagnosis. Inf. Process. Secur. Syst. 2005, 365–374. [Google Scholar] [CrossRef]
- Flores-Fuentes, W.; Rodríguez-Quiñonez, J.C.; Hernandez-Balbuena, D.; Rivas-López, M.; Sergiyenko, O.; Gonzalez-Navarro, F.F.; Rivera-Castillo, J. Machine vision supported by artificial intelligence. In Proceedings of the IEEE International Symposium on Industrial Electronics, Istanbul, Turkey, 1–4 June 2014. [Google Scholar]
- Wang, G.; Sun, J.; Ma, J.; Xu, K.; Gu, J. Sentiment classification: The contribution of ensemble learning. Decis. Support Syst. 2014, 57, 77–93. [Google Scholar] [CrossRef]
- Guo, C.; Yang, Y.; Pan, H.; Li, T.; Jin, W. Fault analysis of High Speed Train with DBN hierarchical ensemble. In Proceedings of the International Joint Conference on Neural Networks, Vancouver, BC, Canada, 24–29 July 2016. [Google Scholar]
- Wang, Z.; Lai, C.; Chen, X.; Yang, B.; Zhao, S.; Bai, X. Flood hazard risk assessment model based on random forest. J. Hydrol. 2015, 527, 1130–1141. [Google Scholar] [CrossRef]
- Santur, Y.; Karaköse, M.; Akin, E. Random forest based diagnosis approach for rail fault inspection in railways. In Proceedings of the National Conference on Electrical, Electronics and Biomedical Engineering, Bursa, Turkey, 1–3 December 2016. [Google Scholar]
- Qian, Q.; Jin, R.; Yi, J.; Zhang, L.; Zhu, S. Efficient distance metric learning by adaptive sampling and mini-batch stochastic gradient descent (SGD). Mach. Learn. 2013, 99, 353–372. [Google Scholar] [CrossRef]
- Safavian, S.R.; Landgrebe, D. A survey of decision tree classifier methodology. IEEE Trans. Syst. Man Cybern. 2002, 21, 660–674. [Google Scholar] [CrossRef]
- Lécun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Huang, S.J.; Hsieh, C.T. High-impedance fault detection utilizing a Morlet wavelet transform approach. IEEE Trans. Power Deliv. 1999, 14, 1401–1410. [Google Scholar] [CrossRef]
- Lin, J.; Qu, L. Feature extraction based on morlet wavelet and its application for mechanical fault diagnosis. J. Sound Vib. 2000, 234, 135–148. [Google Scholar] [CrossRef]
- Peng, Z.K.; Chu, F.L. Application of the wavelet transform in machine condition monitoring and fault diagnostics: A review with bibliography. Mech. Syst. Signal Process. 2004, 18, 199–221. [Google Scholar] [CrossRef]
- Verstraete, D.; Ferrada, A.; Droguett, E.L.; Meruane, V.; Modarres, M. Deep Learning Enabled Fault Diagnosis Using Time-Frequency Image Analysis of Rolling Element Bearings. Shock Vib. 2017, 2017, 1–17. [Google Scholar] [CrossRef]
- MathWorks. Available online: http://cn.mathworks.com/help/images/ref/imresize.html (accessed on 12 December 2018).
- Loparo, K. Case Western Reserve University Bearing Data Centre Website. 2012. Available online: http://csegroups.case.edu/bearingdatacenter/pages/download-data-file (accessed on 12 December 2018).
- Van der Maaten, L.; Hinton, G.; Maaten, L.D. Visualizing data using t-SNE. J. Mach. Learn. Res. 2017, 9, 2579–2605. [Google Scholar]

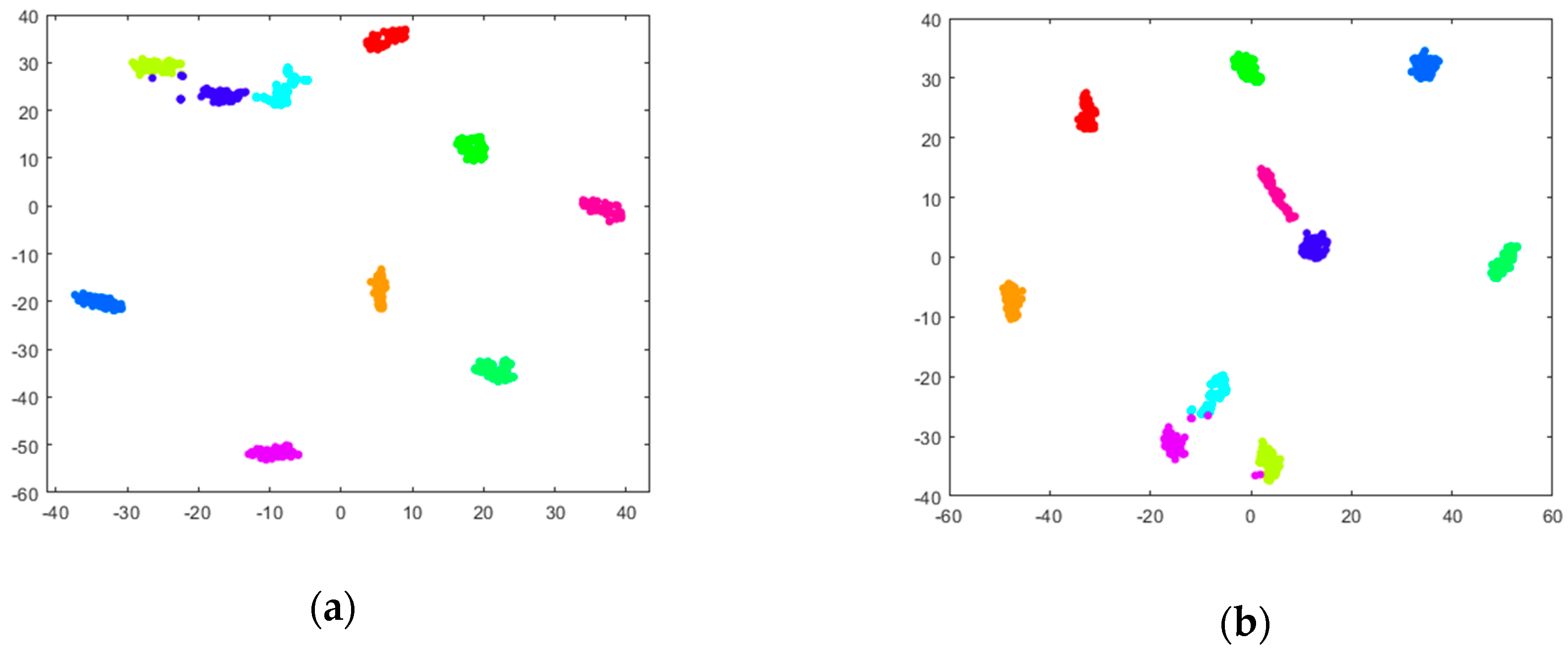
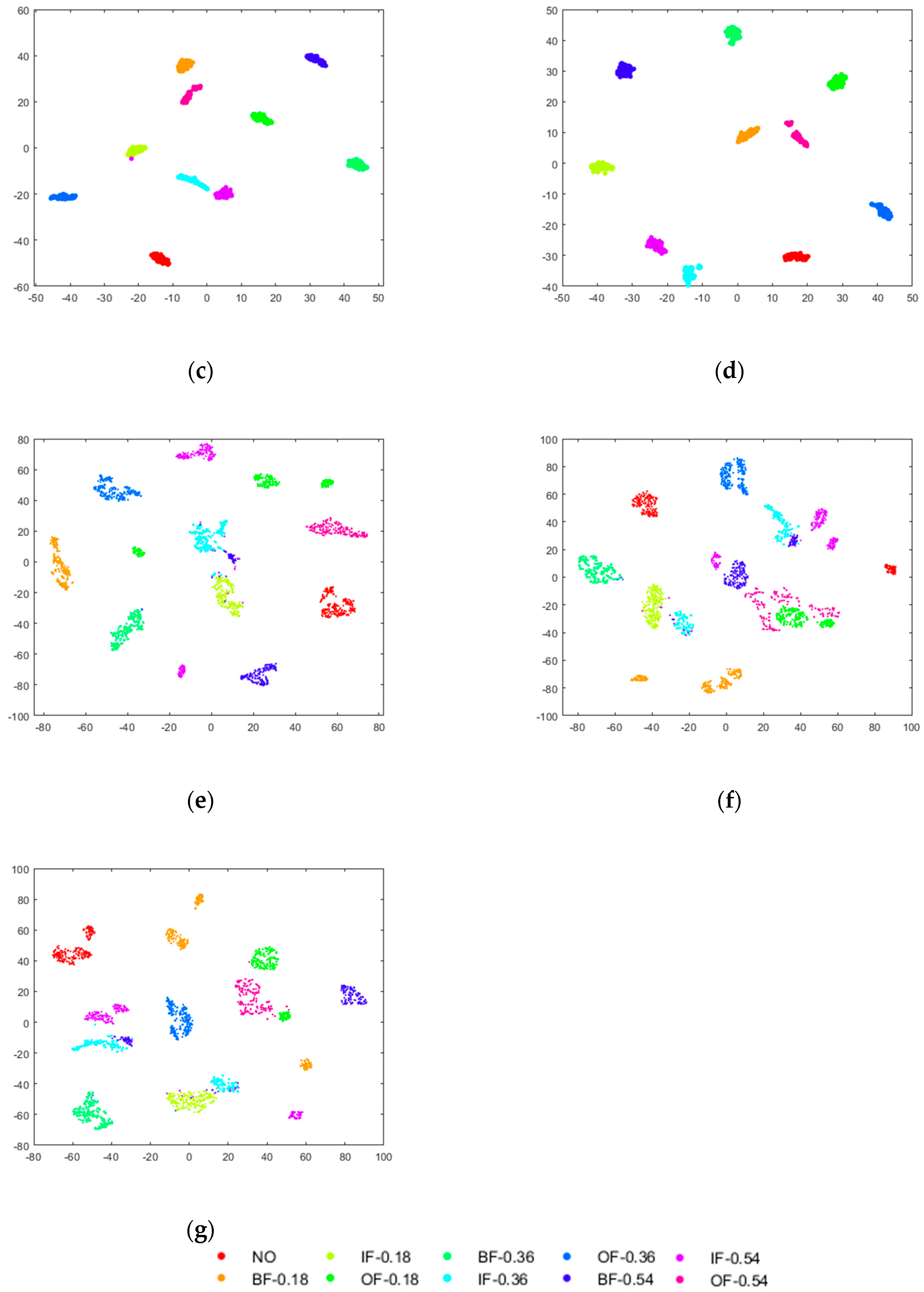
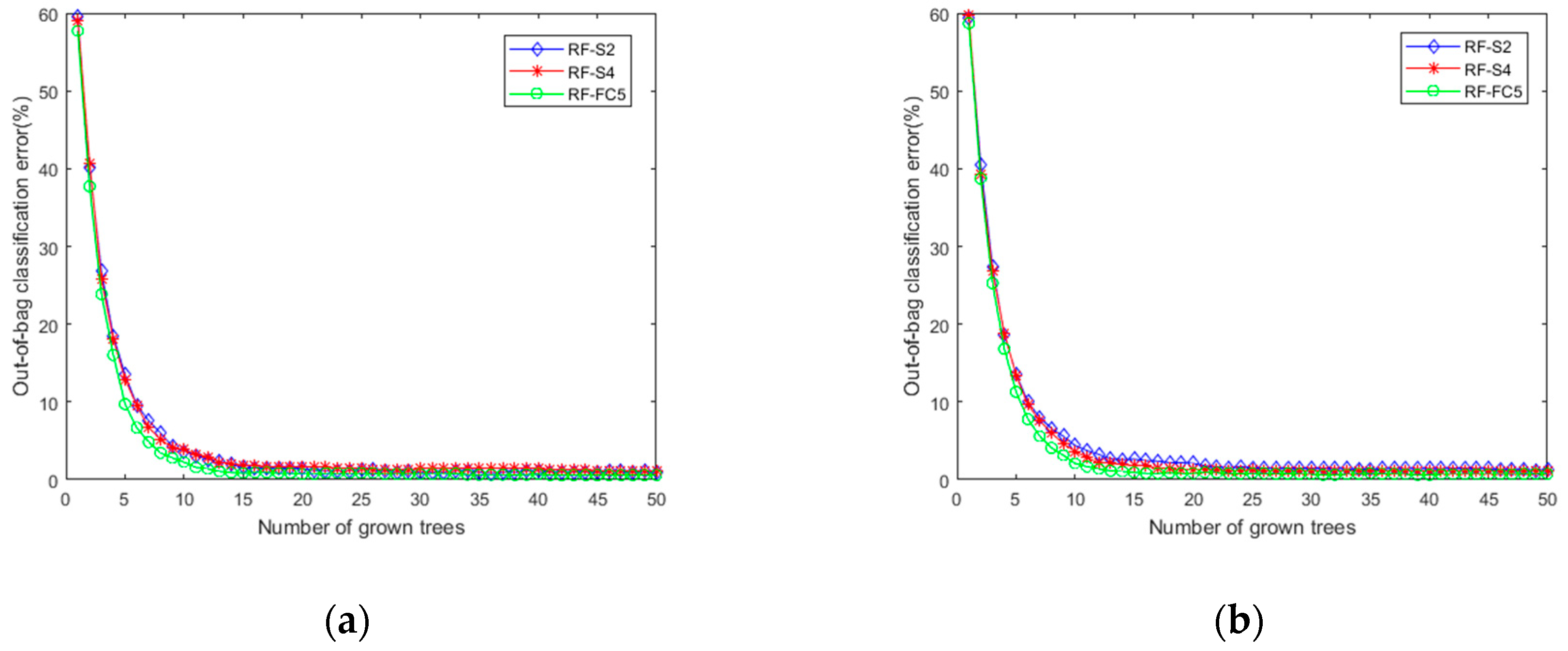
| Health Condition Type | Class Label | Dataset I Number of Training (Loads: 0–3)/Testing (Loads: 0–3) Samples | Dataset II Number of Training (Loads: 0–2)/Testing (Loads:3) samples |
|---|---|---|---|
| NO | 1 | 200/200 | 150/50 |
| IF-0.18 | 2 | 200/200 | 150/50 |
| BF-0.18 | 3 | 200/200 | 150/50 |
| OF-0.18 | 4 | 200/200 | 150/50 |
| IF-0.36 | 5 | 200/200 | 150/50 |
| BF-0.36 | 6 | 200/200 | 150/50 |
| OF-0.36 | 7 | 200/200 | 150/50 |
| IF-0.54 | 8 | 200/200 | 150/50 |
| BF-0.54 | 9 | 200/200 | 150/50 |
| OF-0.54 | 10 | 200/200 | 150/50 |
| Layer Name | Configuration | Kernel/Pooling Size |
|---|---|---|
| Input | 32 × 32 | |
| C1 | 6@28 × 28 | 6@5 × 5 |
| S2 | 6@14 × 14 | 2 × 2 |
| C3 | 12@12 × 12 | 12@3 × 3 |
| S4 | 12@6 × 6 | 2 × 2 |
| FC5 | 240 | |
| Output | 10 |
| Methods | Accuracy for Dataset I (%) | Standard Deviation (%) | Accuracy for Dataset II (%) | Standard Deviation (%) |
|---|---|---|---|---|
| CNN + Softmax | 99.66 | 0.101 | 97.04 | 0.45 |
| CNN + RF1 | 99.46 | 0.243 | 98.26 | 0.542 |
| CNN + RF2 | 99.73 | 0.109 | 99.08 | 0.379 |
| CNN + RF3 | 99.66 | 0.128 | 95.02 | 0.447 |
| Proposed method | 99.73 | 0.109 | 99.08 | 0.379 |
| Methods | Accuracy for Dataset I (%) | Computation Time for Dataset I (s) | Accuracy for Dataset II (%) | Computation Time for Dataset II (s) |
|---|---|---|---|---|
| BPNN | 85.1 | 18.57 | 69.8 | 13.56 |
| SVM | 87.45 | 12.91 | 74.5 | 9.12 |
| DBN | 89.46 | 146.94 | 86.55 | 109.42 |
| DAE | 93.1 | 139.03 | 89.4 | 103.89 |
| CNN | 99.66 | 144.75 | 97.04 | 107.58 |
| Proposed method | 99.73 | 152.71 | 99.08 | 114.57 |
| Layer Name | Configuration | Kernel/Pooling Size |
|---|---|---|
| Input | 16 × 16 | |
| C1 | 32@16 × 16 | 32@3 × 3 |
| S2 | 32@8 × 8 | 2 × 2 |
| C3 | 64@8 × 8 | 64@3 × 3 |
| S4 | 64@4 × 4 | 2 × 2 |
| FC5 | 128 | |
| Output | 4 |
| Methods | Accuracy (%) | Standard Deviation (%) |
|---|---|---|
| CNN + Softmax | 96.67 | 0.122 |
| CNN + RF1 | 96.32 | 0.28 |
| CNN + RF2 | 96.12 | 0.193 |
| CNN + RF3 | 97.38 | 0.131 |
| Proposed method | 97.38 | 0.131 |
| Methods | Accuracy (%) | Computation Time (s) |
|---|---|---|
| BPNN | 83.1 | 20.66 |
| SVM | 86.22 | 14.95 |
| DBN | 87.91 | 151.23 |
| DAE | 90.01 | 142.77 |
| CNN | 96.67 | 150.12 |
| Proposed method | 97.38 | 161.43 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, G.; Liu, M.; Jiang, Z.; Söffker, D.; Shen, W. Bearing Fault Diagnosis Method Based on Deep Convolutional Neural Network and Random Forest Ensemble Learning. Sensors 2019, 19, 1088. https://doi.org/10.3390/s19051088
Xu G, Liu M, Jiang Z, Söffker D, Shen W. Bearing Fault Diagnosis Method Based on Deep Convolutional Neural Network and Random Forest Ensemble Learning. Sensors. 2019; 19(5):1088. https://doi.org/10.3390/s19051088
Chicago/Turabian StyleXu, Gaowei, Min Liu, Zhuofu Jiang, Dirk Söffker, and Weiming Shen. 2019. "Bearing Fault Diagnosis Method Based on Deep Convolutional Neural Network and Random Forest Ensemble Learning" Sensors 19, no. 5: 1088. https://doi.org/10.3390/s19051088
APA StyleXu, G., Liu, M., Jiang, Z., Söffker, D., & Shen, W. (2019). Bearing Fault Diagnosis Method Based on Deep Convolutional Neural Network and Random Forest Ensemble Learning. Sensors, 19(5), 1088. https://doi.org/10.3390/s19051088







