Research on Optical Fiber Sensor Based on Underwater Deformation Measurement
Abstract
:1. Introduction
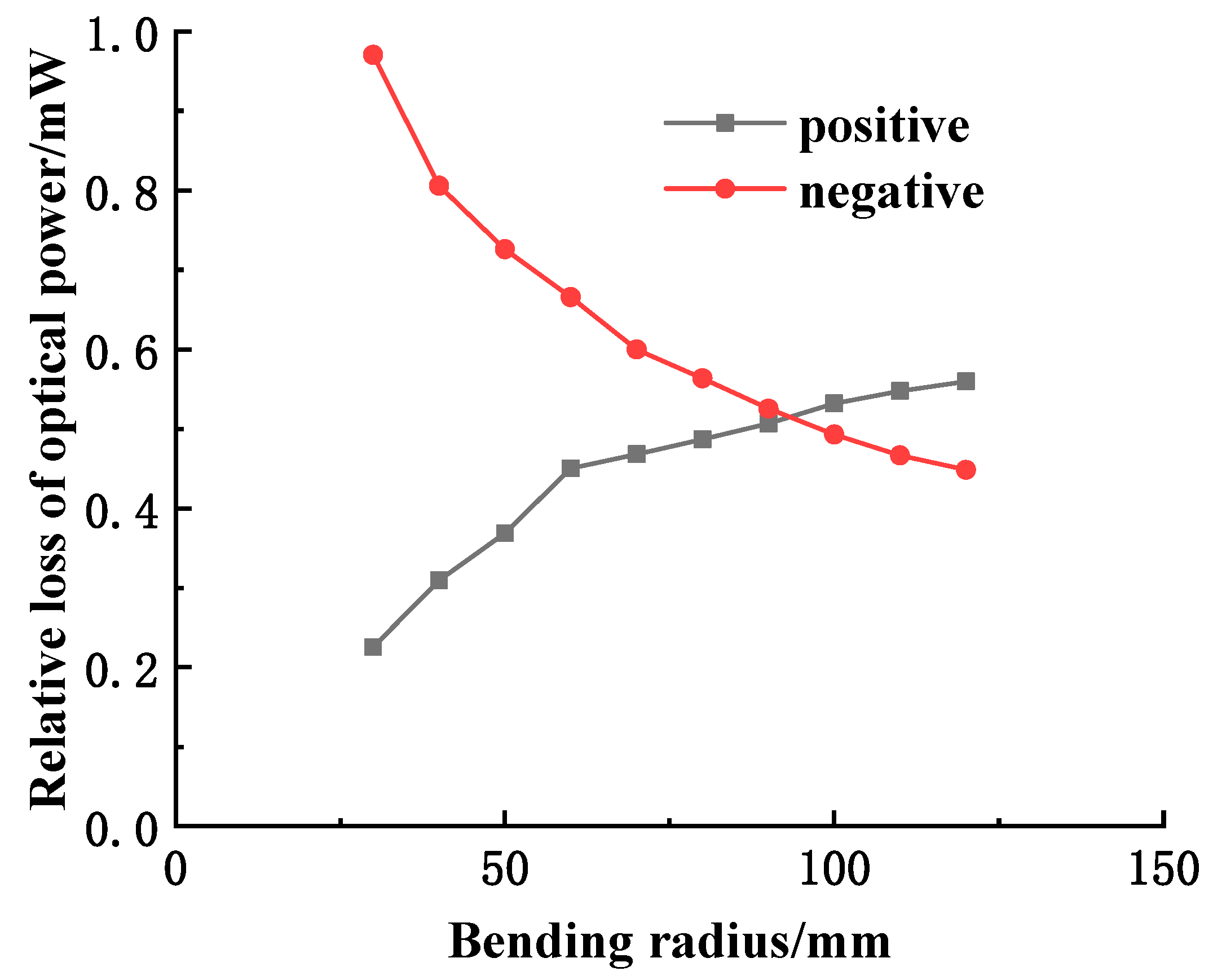
2. Optical Power Loss in Bending of the Fiber Sensitive Region
2.1. Transmission Power of the Optical Fiber Sensitive Region during Bending
2.1.1. Positive Bending
2.1.2. Negative Bending
2.2. Transmission Power of the Optical Fiber Sensitive Region during Bending
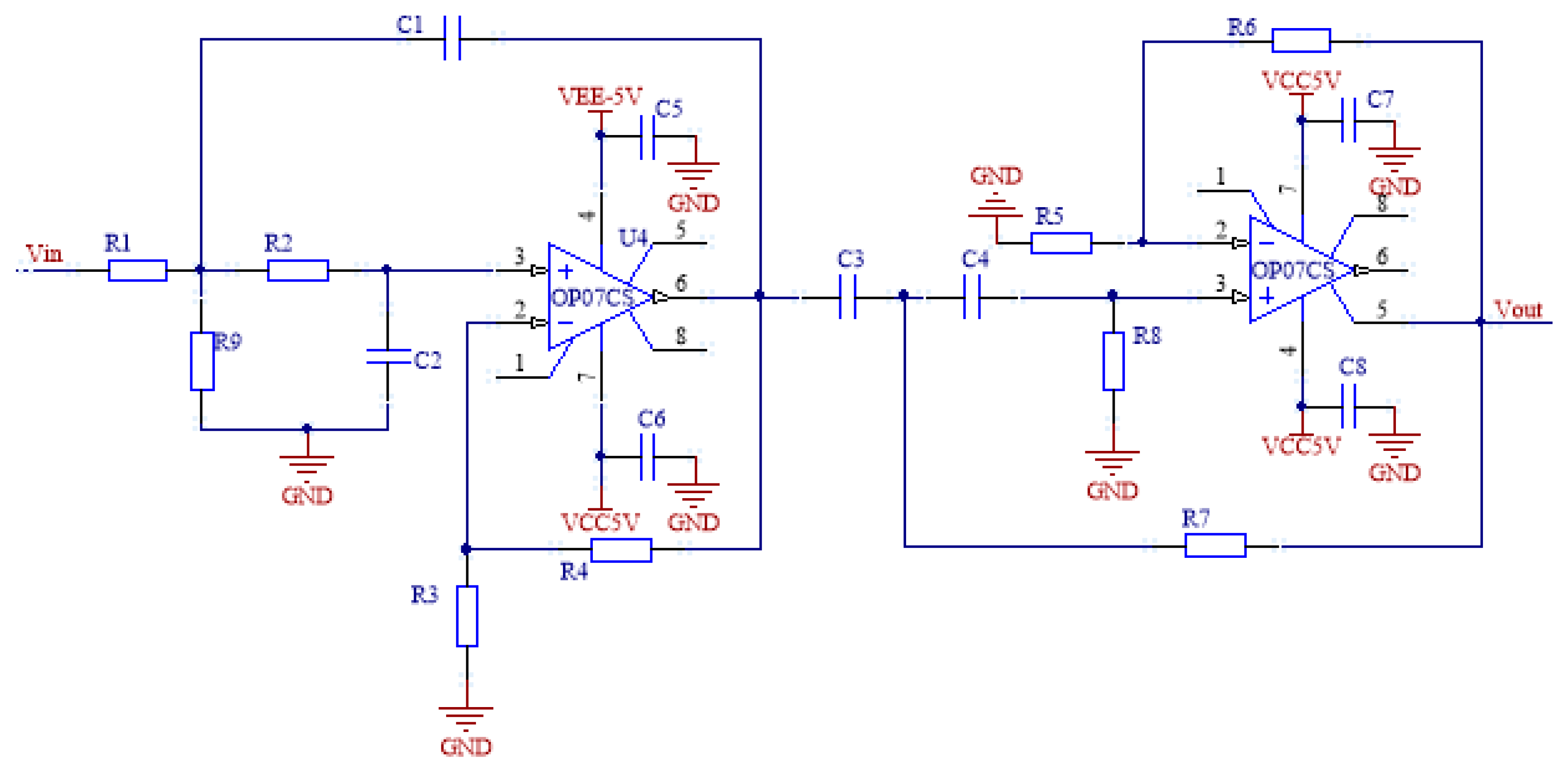
3. Sensor Signal Conditioning Circuit
3.1. Amplifying Circuit
3.2. Filter Circuit
3.3. Summing Circuit
4. Sensor Characteristics Analysis
4.1. Linear Measurement Range Analysis
4.1.1. A Sensitive Region
4.1.2. Two Sensitive Regions
4.2. Underwater Measurement Accuracy Analysis
4.2.1. Underwater Simple Beam Measurement
4.2.2. Underwater Dynamic Curvature Measurement
4.2.3. Measurement of Underwater Static Curvature
5. Conclusions
- The accuracy of the model of bending power relative loss and bending radius is verified by measuring the optical power loss in the sensitive region of the fiber, and the characteristics of positive and negative bending are explained effectively.
- The sensor conditioning circuit can effectively amplify and filter the weak voltage signal, and can simultaneously measure the curvature of different bending degrees with a good application range.
- After adding a second sensitive region on one fiber, the output voltage of the fiber curvature sensor will decrease while the sensitivity will decrease, but the linear measurement range remains basically unchanged.
- When the sensor is applied underwater, its linear measurement range can be defined as 8.3–50 m−1, which is improved compared with the linear measurement range of 0–16.67 m−1 of the existing products.
Author Contributions
Funding
Conflicts of Interest
References
- Shiming, L.; Ping, R.; Hongnian, M. Development and Countermeasures of Marine Underwater Engineering Technology. Ocean Sci. 1997, 16, 49–53. [Google Scholar]
- Zhang, Q.; Liu, N.; Kong, W.X.; Pang, Y.C. Discussion on underwater deformation and leakage detection method for seismic shell equipment. Ship Sci. Technol. 2017, 39, 44–47. [Google Scholar]
- Kocak, D.M.; Dalgleish, F.R.; Caimi, F.M.; Schechner, Y.Y. A Focus on Recent Developments and Trends in Underwater Imaging. Mar. Technol. Soc. J. 2008, 42, 52–67. [Google Scholar] [CrossRef]
- Shen, Y. GPS Underwater Topographic survey without Tide Gauge. Geotich. Investig. Surv. 2002, 28, 37–40. [Google Scholar]
- Liu, S.; Tian, J. Review on the Development of Underwater Topographic Measurement Technology. Water Transp. Eng. 2008, 1, 11–15. [Google Scholar]
- Liu, Y. Discussion on GPS Measurement Technology and Its Application in Measurement Engineering; Heilongjiang Xilin Iron and Steel Group Co., Ltd. Equipment Engineering Department: Yichun, China, 2007. [Google Scholar]
- Liu, J. Principle and Method of GPS Satellite Navigation and Positioning; Science Press: Beijing, China, 2003. [Google Scholar]
- Yang, Q. Fiber Optic Sensor and Its Application. J. Sens. 1999, 4, 36–38. [Google Scholar]
- Liu, A.M.; Yu, Z.F.; Li, J.S. Automatic Monitoring Technology for Surface Settlement of Underwater Foundation. Appl. Mech. Mater. 2013, 401–403, 992–996. [Google Scholar] [CrossRef]
- Zhou, M.; Yang, P. Establishment and Application of Deformation Monitoring System for Underwater Engineering Construction. Railw. Technol. Innov. 2012, 3, 101–103. [Google Scholar]
- Di, H.; Liu, R. Research Progress in Measurement of Curvature by Optical Fiber Sensing Technology. J. Sens. Microsyst. 2011, 30, 5–7. [Google Scholar]
- Liu, R.; Liu, P.; Fu, Z. Study on the Mechanism of Curvature Sensing Fiber Curvature Sensor. Acta Opt. Sin. 2007, 27, 807–812. [Google Scholar]
- Di, H.; Fu, Y.; Liu, R. A Mezzanine Research System for Curvature Fiber Sensors. Photoelectron. Laser 2010, 21, 1597–1601. [Google Scholar]
- Kuang, K.S.C.; Well, J.C.; Scully, P.J. An evaluation of a novel plastic optical fib re sensor f or axi al strain and bend measurements. Meas. Sci. Technol. 2002, 13, 1523–1534. [Google Scholar] [CrossRef]
- Fu, Y.; Di, H. Study on Simultaneous Measurement of Torsion and Bending Moment Using Curvature Fiber Sensor; Institute of Robotics, Harbin Institute of Technology: Harbin, China, 2005. [Google Scholar]
- Wang, Y.; Chen, J.; Rao, Y. Long period fiber grating sensors measuring bend-curvature and determining benddirection simultaneously. J. Optoelectron. Laser 2005, 16, 1139–1143. [Google Scholar]
- Kovacevic, M.; Djordjevich, A.; Nikezic, D. Mont e Carlo simulation of curvature gauges by ray tracing. Meas. Sci. Technol. 2004, 15, 1756–1761. [Google Scholar]
- Cui, G.L.; Che, X.L. Small Signal Acquisition System Based on STC12C5A60S2 and AD620. Electron. Des. Eng. 2012, 20, 112–114. [Google Scholar]
- Liu, S.-L. Introduction of strumentation amplifier AD620 applied in precision data acguisition of high level switching power supply. World Power Supply 2005, 1, 59–62. [Google Scholar]
- Chen, G.R. Development of digitally-controlled DC current source based on single-chip microcomputer. Mod. Electron. Tech. 2013, 8, 153–156. [Google Scholar]
- Dan, H.; Gang, Z.; Jiming, S. Design and Implementation of a Practical Photoelectric Detection Circuit. Instrum. Technol. Sens. 2010, 11, 79–81. [Google Scholar]
- Tong, S.; Hua, C. The Basis of Analog Electronic Technology, 4th ed.; Higher Education Press: Beijing, China, 2006; pp. 361–370. [Google Scholar]
- Michalski, S.E.; Andrews, K.M.; Mieczkowski, D. Method and Apparatus for Low Power Offset Correction of Amplified Sensor Signals. U.S. Patent 4816752, 28 March 1989. [Google Scholar]






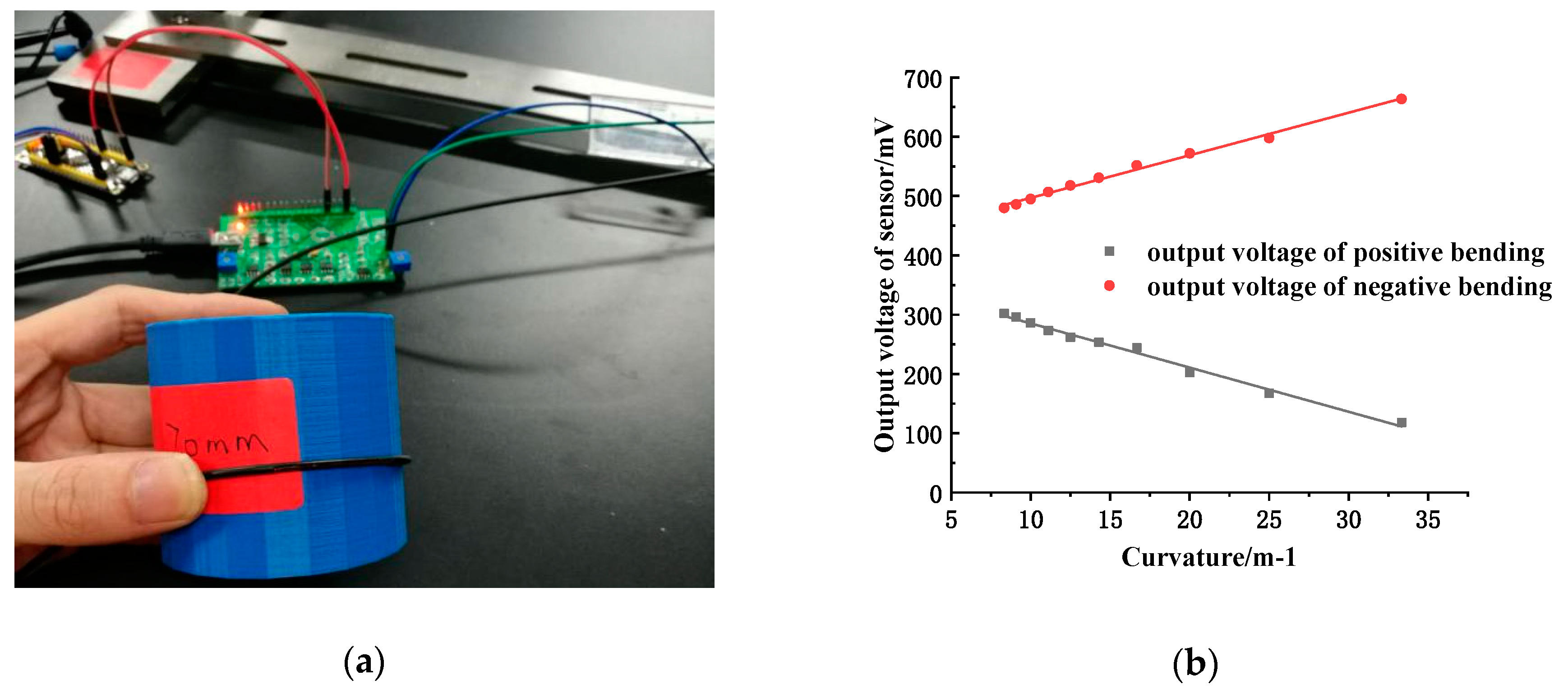






| Bending Radius(mm) | Theoretical Curvature(m−1) | Forward Output Voltage (mV) | Measuring Curvature (mm) | Backward Output Voltage (mV) | Measuring Curvature (mm) |
|---|---|---|---|---|---|
| 120 | 8.33 | 298 | 8.26 | 484 | 8.32 |
| 100 | 10.00 | 284 | 10.11 | 486 | 10.26 |
| 80 | 12.50 | 262 | 13.09 | 519 | 12.93 |
| 60 | 16.67 | 241 | 15.91 | 549 | 17.27 |
| 40 | 25.00 | 174 | 24.92 | 602 | 24.73 |
| 20 | 50.00 | 165 | 49.52 | 782 | 49.56 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Cao, C.; Huang, Y.; Zhang, Y.; Ge, Y. Research on Optical Fiber Sensor Based on Underwater Deformation Measurement. Sensors 2019, 19, 1115. https://doi.org/10.3390/s19051115
Chen J, Cao C, Huang Y, Zhang Y, Ge Y. Research on Optical Fiber Sensor Based on Underwater Deformation Measurement. Sensors. 2019; 19(5):1115. https://doi.org/10.3390/s19051115
Chicago/Turabian StyleChen, Jiawang, Chen Cao, Yue Huang, Yonglei Zhang, and Yongqiang Ge. 2019. "Research on Optical Fiber Sensor Based on Underwater Deformation Measurement" Sensors 19, no. 5: 1115. https://doi.org/10.3390/s19051115
APA StyleChen, J., Cao, C., Huang, Y., Zhang, Y., & Ge, Y. (2019). Research on Optical Fiber Sensor Based on Underwater Deformation Measurement. Sensors, 19(5), 1115. https://doi.org/10.3390/s19051115







