Comparative Study of Different Methods in Vibration-Based Terrain Classification for Wheeled Robots with Shock Absorbers
Abstract
1. Introduction
- A large body of comparative experiments are conducted to demonstrate the performance of the existing feature-engineering and feature-learning classification methods.
- According to the long short-term memory (LSTM) network, we propose a one-dimensional convolutional LSTM (1DCL)-based VTC method to learn both spatial and temporal characteristics of the dampened vibration signals.
- In feature-engineering approaches, the combination of power spectral density (PSD) and random forest (RF) achieves the highest accuracy of 69.88%.
- The conventional feature-learning approaches outperforms the feature-engineering ones slightly by about 2%, though they are computationally intensive.
- The proposed 1DCL-based VTC method outperforms the conventional methods in an accuracy of 80.18%, which exceeds the second method (LSTM) by 8.23%.
2. Related Work
3. Feature-Engineering Approaches
3.1. Vibration Feature Extraction
- (1)
- Zero crossing rate (ZCR). The ZCR counts the number of times that the signal crosses the zero axis, which is an approximate estimation of the frequency of .
- (2)
- Mean. The mean expresses the average roughness of ground surface.
- (3)
- Standard deviation. Intuitively, the standard deviation is greater with a rougher ground surface.
- (4)
- Norm. Usually the -norm is used which reflects the energy of .
- (5)
- Autocorrelation. The autocorrelation r is a measure of the non-randomness as defined bywhere r gets larger with the dependence of successive vibration values.
- (6)
- Maximum. Find the maximum of the degree of bump.
- (7)
- Minimum. Find the minimum of the degree of bump.
- (8)
- Skewness. The skewness describes the asymmetry of the distribution about its mean, calculated as
- (9)
- Excess kurtosis. The excess kurtosis reflects the degree of deviation from the Gaussian distribution as defined by
3.2. Classifiers
4. Feature-Learning Approaches
4.1. Overview of CNN and LSTM
4.1.1. Convolutional Neural Network
4.1.2. Long Short-Term Memory
4.2. Proposed 1DCL
5. Experiment and Results Analysis
5.1. Experiment Setup
5.2. Experiment Results and Analysis
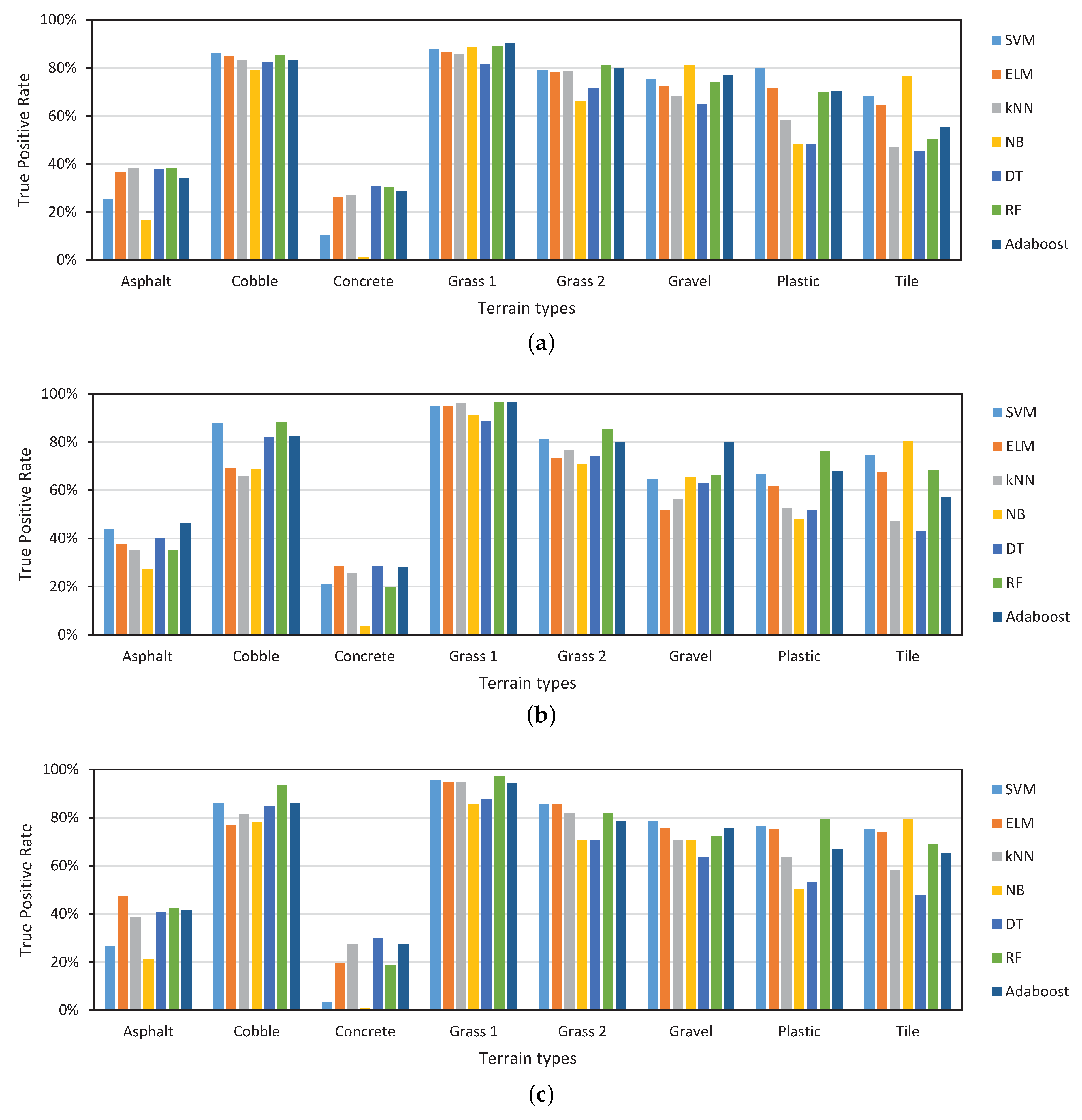
5.2.1. Analysis of Performance of Feature-Engineering Approaches
5.2.2. Analysis of Performance of Feature-Learning Approaches
- 1D-CNN. A one-dimensional convolutional neural network with alternating convolutional and pooling layers learns spatial features of a segment, and is followed by two fully connected layers and a SoftMax layer.
- LSTM. A single layer LSTM model directly handles 200 points length segments with 10 LSTM cells in series, which helps to learn temporal dynamics.
- 1DCL. The proposed model is a spatiotemporal architecture.
- 1DCL-FC. A variant of our 1DCL that we use a fully connected layer to replace the convolutional layer.
- 1DCL-3Conv. Another variant of our 1DCL model that we consider increasing the number of convolutional layers to learn better spatial features. Here, we build two normal convolutional layers and a convolutional layer for a total of 3 convolutional layers.
5.2.3. Comparison of Classification Time
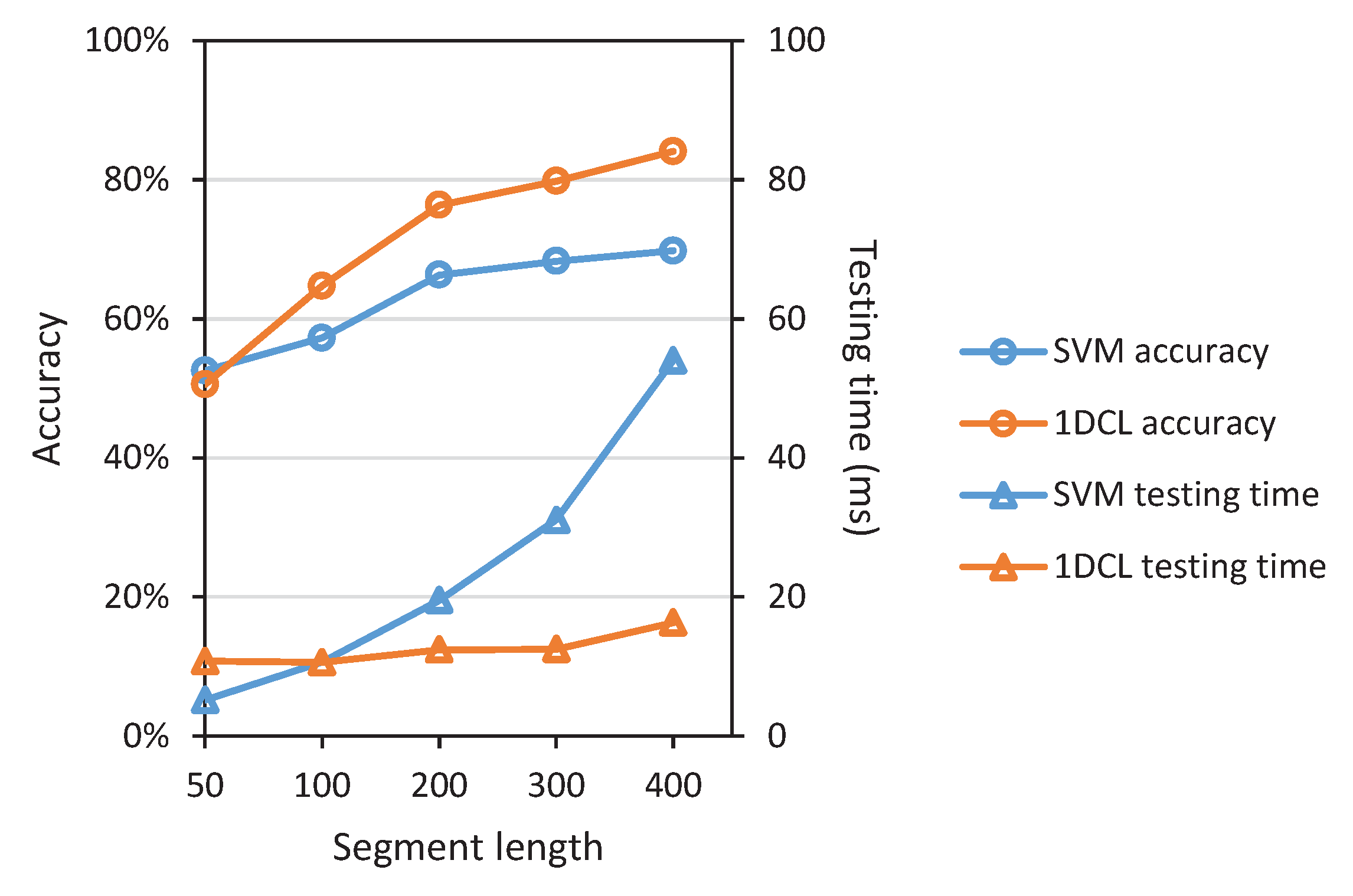
5.2.4. Comparison of Varying Segment Length
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lozano-Perez, T. Autonomous Robot Vehicles; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- García-Sánchez, J.; Tavera-Mosqueda, S.; Silva-Ortigoza, R.; Hernández-Guzmán, V.; Sandoval-Gutiérrez, J.; Marcelino-Aranda, M.; Taud, H.; Marciano-Melchor, M. Robust Switched Tracking Control for Wheeled Mobile Robots Considering the Actuators and Drivers. Sensors 2018, 18, 4316. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, R.; Iagnemma, K. Slippage estimation and compensation for planetary exploration rovers. State of the art and future challenges. J. Field Robot. 2018, 35, 564–577. [Google Scholar] [CrossRef]
- Helmick, D.; Angelova, A.; Matthies, L. Terrain adaptive navigation for planetary rovers. J. Field Robot. 2009, 26, 391–410. [Google Scholar] [CrossRef]
- Iagnemma, K.; Dubowsky, S. Traction control of wheeled robotic vehicles in rough terrain with application to planetary rovers. Int. J. Robot. Res. 2004, 23, 1029–1040. [Google Scholar] [CrossRef]
- Chen, Y.; Li, X.; Wiet, C.; Wang, J. Energy management and driving strategy for in-wheel motor electric ground vehicles with terrain profile preview. IEEE Trans. Ind. Inform. 2014, 10, 1938–1947. [Google Scholar] [CrossRef]
- Manjanna, S.; Dudek, G. Autonomous gait selection for energy efficient walking. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 5155–5162. [Google Scholar]
- Zhao, X.; Dou, L.; Su, Z.; Liu, N. Study of the Navigation Method for a Snake Robot Based on the Kinematics Model with MEMS IMU. Sensors 2018, 18, 879. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Luo, K.; Ma, C.; Liu, Q.; Jin, B. Superpixel Segmentation Based Synthetic Classifications with Clear Boundary Information for a Legged Robot. Sensors 2018, 18, 2808. [Google Scholar] [CrossRef] [PubMed]
- Khan, Y.N.; Komma, P.; Zell, A. High resolution visual terrain classification for outdoor robots. In Proceedings of the 2011 IEEE International Conference on Computer Vision Workshops (ICCV Workshops), Barcelona, Spain, 6–13 November 2011; pp. 1014–1021. [Google Scholar]
- Filitchkin, P.; Byl, K. Feature-based terrain classification for littledog. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Algarve, Portugal, 7–12 October 2012; pp. 1387–1392. [Google Scholar]
- Anantrasirichai, N.; Burn, J.; Bull, D. Terrain classification from body-mounted cameras during human locomotion. IEEE Trans. Cybern. 2015, 45, 2249–2260. [Google Scholar] [CrossRef] [PubMed]
- Ozkul, M.C.; Saranli, A.; Yazicioglu, Y. Acoustic surface perception from naturally occurring step sounds of a dexterous hexapod robot. Mech. Syst. Signal Process. 2013, 40, 178–193. [Google Scholar] [CrossRef]
- Christie, J.; Kottege, N. Acoustics based terrain classification for legged robots. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 3596–3603. [Google Scholar]
- Valada, A.; Burgard, W. Deep spatiotemporal models for robust proprioceptive terrain classification. Int. J. Robot. Res. 2017, 36, 1521–1539. [Google Scholar] [CrossRef]
- Wu, X.A.; Huh, T.M.; Mukherjee, R.; Cutkosky, M. Integrated Ground Reaction Force Sensing and Terrain Classification for Small Legged Robots. IEEE Robot. Autom. Lett. 2016, 1, 1125–1132. [Google Scholar] [CrossRef]
- Walas, K. Terrain classification and negotiation with a walking robot. J. Intell. Robot. Syst. 2015, 78, 401–423. [Google Scholar] [CrossRef]
- Hoffmann, M.; Štěpánová, K.; Reinstein, M. The effect of motor action and different sensory modalities on terrain classification in a quadruped robot running with multiple gaits. Robot. Auton. Syst. 2014, 62, 1790–1798. [Google Scholar] [CrossRef]
- Weiss, C.; Tamimi, H.; Zell, A. A combination of vision- and vibration-based terrain classification. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 2204–2209. [Google Scholar]
- Otte, S.; Weiss, C.; Scherer, T.; Zell, A. Recurrent Neural Networks for fast and robust vibration-based ground classification on mobile robots. In Proceedings of the IEEE International Conference on Robotics and Automation, Stockholm, Sweden, 6–20 May 2016; pp. 5603–5608. [Google Scholar]
- Bermudez, F.L.G.; Julian, R.C.; Haldane, D.W.; Abbeel, P.; Fearing, R.S. Performance analysis and terrain classification for a legged robot over rough terrain. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Algarve, Portugal, 7–12 October 2012; pp. 513–519. [Google Scholar]
- Libby, J.; Stentz, A.J. Using sound to classify vehicle-terrain interactions in outdoor environments. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, St. Paul, MN, USA, 14–18 May 2012; pp. 3559–3566. [Google Scholar]
- Hoepflinger, M.A.; Remy, C.D.; Hutter, M.; Spinello, L.; Siegwart, R. Haptic terrain classification for legged robots. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, Alaska, 3–8 May 2010; pp. 2828–2833. [Google Scholar]
- Kurban, T.; Beşdok, E. A comparison of RBF neural network training algorithms for inertial sensor based terrain classification. Sensors 2009, 9, 6312–6329. [Google Scholar] [CrossRef] [PubMed]
- Khan, Y.N.; Masselli, A.; Zell, A. Visual terrain classification by flying robots. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation (ICRA), St. Paul, MN, USA, 14–18 May 2012; pp. 498–503. [Google Scholar]
- Yin, J.; Yang, J.; Zhang, Q. Assessment of GF-3 polarimetric sar data for physical scattering mechanism analysis and terrain classification. Sensors 2017, 17, 2785. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.; Rangarajan, A.; Ranka, S. An Efficient Deep Representation Based Framework for Large-Scale Terrain Classification. In Proceedings of the 2018 24th International Conference on Pattern Recognition (ICPR), Beijing, China, 20–24 August 2018; pp. 940–945. [Google Scholar]
- Gonzalez, R.; Iagnemma, K. DeepTerramechanics: Terrain Classification and Slip Estimation for Ground Robots via Deep Learning. arXiv, 2018; arXiv:1806.07379. [Google Scholar]
- Lu, L.; Ordonez, C.; Collins, E.G.; DuPont, E.M. Terrain surface classification for autonomous ground vehicles using a 2D laser stripe-based structured light sensor. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 11–15 October 2009; pp. 2174–2181. [Google Scholar]
- Rankin, A.; Huertas, A.; Matthies, L.; Bajracharya, M.; Assad, C.; Brennan, S.; Bellutta, P.; Sherwin, G.W. Unmanned ground vehicle perception using thermal infrared cameras. Unmanned Systems Technology XIII. Int. Soc. Opt. Photonics 2011, 8045, 804503. [Google Scholar]
- Zhou, S.; Xi, J.; McDaniel, M.W.; Nishihata, T.; Salesses, P.; Iagnemma, K. Self-supervised learning to visually detect terrain surfaces for autonomous robots operating in forested terrain. J. Field Robot. 2012, 29, 277–297. [Google Scholar] [CrossRef]
- McDaniel, M.W.; Nishihata, T.; Brooks, C.A.; Salesses, P.; Iagnemma, K. Terrain classification and identification of tree stems using ground-based LiDAR. J. Field Robot. 2012, 29, 891–910. [Google Scholar] [CrossRef]
- Brooks, C.A.; Iagnemma, K. Vibration-based terrain classification for planetary exploration rovers. IEEE Trans. Robot. 2005, 21, 1185–1191. [Google Scholar] [CrossRef]
- Weiss, C.; Frohlich, H.; Zell, A. Vibration-based terrain classification using support vector machines. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 4429–4434. [Google Scholar]
- Chen, Z.; Li, C.; Sanchez, R.V. Gearbox fault identification and classification with convolutional neural networks. Shock Vib. 2015, 2015. [Google Scholar] [CrossRef]
- Ince, T.; Kiranyaz, S.; Eren, L.; Askar, M.; Gabbouj, M. Real-Time Motor Fault Detection by 1-D Convolutional Neural Networks. IEEE Trans. Ind. Electron. 2016, 63, 7067–7075. [Google Scholar] [CrossRef]
- Abdeljaber, O.; Avci, O.; Kiranyaz, S.; Gabbouj, M.; Inman, D.J. Real-time vibration-based structural damage detection using one-dimensional convolutional neural networks. J. Sound Vib. 2017, 388, 154–170. [Google Scholar] [CrossRef]
- Wang, S.; Kodagoda, S.; Shi, L.; Dai, X. Two-Stage Road Terrain Identification Approach for Land Vehicles Using Feature-Based and Markov Random Field Algorithm. IEEE Intell. Syst. 2018, 33, 29–39. [Google Scholar] [CrossRef]
- Otsu, K.; Ono, M.; Fuchs, T.J.; Baldwin, I.; Kubota, T. Autonomous terrain classification with co-and self-training approach. IEEE Robot. Autom. Lett. 2016, 1, 814–819. [Google Scholar] [CrossRef]
- Dutta, A.; Dasgupta, P. Ensemble learning with weak classifiers for fast and reliable unknown terrain classification using mobile robots. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 2933–2944. [Google Scholar] [CrossRef]
- Zhao, K.; Dong, M.; Gu, L. A New Terrain Classification Framework Using Proprioceptive Sensors for Mobile Robots. Math. Probl. Eng. 2017, 2017, 3938502. [Google Scholar] [CrossRef]
- Vicente, A.; Liu, J.; Yang, G.Z. Surface classification based on vibration on omni-wheel mobile base. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 916–921. [Google Scholar]
- Janssens, O.; Slavkovikj, V.; Vervisch, B.; Stockman, K.; Loccufier, M.; Verstockt, S.; Van de Walle, R.; Van Hoecke, S. Convolutional neural network based fault detection for rotating machinery. J. Sound Vib. 2016, 377, 331–345. [Google Scholar] [CrossRef]
- Weiss, C.; Fechner, N.; Stark, M.; Zell, A. Comparison of Different Approaches to Vibration-Based Terrain Classification; EMCR: Freiburg, Germany, 19–21 September 2007. [Google Scholar]
- Komma, P.; Weiss, C.; Zell, A. Adaptive bayesian filtering for vibration-based terrain classification. In Proceedings of the IEEE International Conference on Robotics and Automation, ICRA’09, Kobe, Japan, 12–17 May 2009; pp. 3307–3313. [Google Scholar]
- Zou, Y.; Chen, W.; Xie, L.; Wu, X. Comparison of different approaches to visual terrain classification for outdoor mobile robots. Pattern Recognit. Lett. 2014, 38, 54–62. [Google Scholar] [CrossRef]
- Bouguelia, M.R.; Gonzalez, R.; Iagnemma, K.; Byttner, S. Unsupervised classification of slip events for planetary exploration rovers. J. Terramech. 2017, 73, 95–106. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: a library for support vector machines. ACM Trans. Intell. Syst. Technol. (TIST) 2011, 2, 27. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Nguyen, B.P.; Tay, W.L.; Chui, C.K. Robust biometric recognition from palm depth images for gloved hands. IEEE Trans. Hum.-Mach. Syst. 2015, 45, 799–804. [Google Scholar] [CrossRef]
- Domingos, P.; Pazzani, M. On the optimality of the simple Bayesian classifier under zero-one loss. Mach. Learn. 1997, 29, 103–130. [Google Scholar] [CrossRef]
- Breiman, L. Classification and Regression Trees; Routledge: London, UK, 2017. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J.Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Lin, M.; Chen, Q.; Yan, S. Network in network. arXiv, 2013; arXiv:1312.4400. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–8 December 2012; pp. 1097–1105. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–8 December 2012; pp. 2951–2959. [Google Scholar]
- Yang, Y.; Liu, X. A re-examination of text categorization methods. In Proceedings of the 22nd International Conference on Research and Development in Information Retrieval, Berkeley, CA, USA, 15–19 August 1999. [Google Scholar]






| Features | Metrics | Classifiers | ||||||
|---|---|---|---|---|---|---|---|---|
| SVM | ELM | kNN | NB | DT | RF | Adaboost | ||
| Time-domain | Accuracy | 65.30% | 65.95% | 61.53% | 57.96% | 58.39% | 65.89% | 66.07% |
| F1-score | 0.6438 | 0.6497 | 0.6065 | 0.5617 | 0.5803 | 0.6475 | 0.6465 | |
| FFT-based | Accuracy | 67.99% | 62.96% | 57.75% | 57.67% | 59.62% | 68.07% | 68.12% |
| F1-score | 0.6674 | 0.6068 | 0.5695 | 0.5612 | 0.5898 | 0.6679 | 0.6717 | |
| PSD-based | Accuracy | 67.52% | 69.84% | 65.69% | 58.37% | 60.26% | 69.88% | 67.91% |
| F1-score | 0.6622 | 0.6853 | 0.6454 | 0.5595 | 0.5999 | 0.6897 | 0.6699 | |
| Metrics | Networks | ||||
|---|---|---|---|---|---|
| CNN | LSTM | 1DCL | 1DCL-FC | 1DCL-3Conv | |
| Accuracy | 70.17% | 71.95% | 80.18% | 67.94% | 72.93% |
| F1-score | 0.6893 | 0.7030 | 0.7878 | 0.6622 | 0.7159 |
| Classifiers | Training Time (s) | Testing Time (ms) | ||||
|---|---|---|---|---|---|---|
| T | FFT | PSD | T | FFT | PSD | |
| SVM | 15.43 | 188.9 | 90.20 | 18.78 | 235.2 | 115.4 |
| ELM | 0.5709 | 1.401 | 0.5674 | 19.93 | 27.20 | 21.72 |
| kNN | 0.01219 | 0.01956 | 0.01423 | 8.298 | 69.40 | 36.63 |
| NB | 0.03499 | 0.01702 | 1.225 | 4.144 | 1.779 | |
| DT | 0.01089 | 0.1596 | 0.08480 | 0.1409 | 0.4181 | 0.3472 |
| RF | 1.5371 | 22.80 | 11.81 | 16.35 | 10.71 | 9.431 |
| Adaboost | 6.911 | 173.1 | 82.26 | 81.54 | 96.39 | 82.07 |
| CNN | 251.8 | 7.110 | ||||
| LSTM | 746.5 | 13.18 | ||||
| 1DCL | 1295 | 15.22 | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mei, M.; Chang, J.; Li, Y.; Li, Z.; Li, X.; Lv, W. Comparative Study of Different Methods in Vibration-Based Terrain Classification for Wheeled Robots with Shock Absorbers. Sensors 2019, 19, 1137. https://doi.org/10.3390/s19051137
Mei M, Chang J, Li Y, Li Z, Li X, Lv W. Comparative Study of Different Methods in Vibration-Based Terrain Classification for Wheeled Robots with Shock Absorbers. Sensors. 2019; 19(5):1137. https://doi.org/10.3390/s19051137
Chicago/Turabian StyleMei, Mingliang, Ji Chang, Yuling Li, Zerui Li, Xiaochuan Li, and Wenjun Lv. 2019. "Comparative Study of Different Methods in Vibration-Based Terrain Classification for Wheeled Robots with Shock Absorbers" Sensors 19, no. 5: 1137. https://doi.org/10.3390/s19051137
APA StyleMei, M., Chang, J., Li, Y., Li, Z., Li, X., & Lv, W. (2019). Comparative Study of Different Methods in Vibration-Based Terrain Classification for Wheeled Robots with Shock Absorbers. Sensors, 19(5), 1137. https://doi.org/10.3390/s19051137





