Calculation Method for Phenotypic Traits Based on the 3D Reconstruction of Maize Canopies
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Treatments and Measurement of Phenotypic Traits
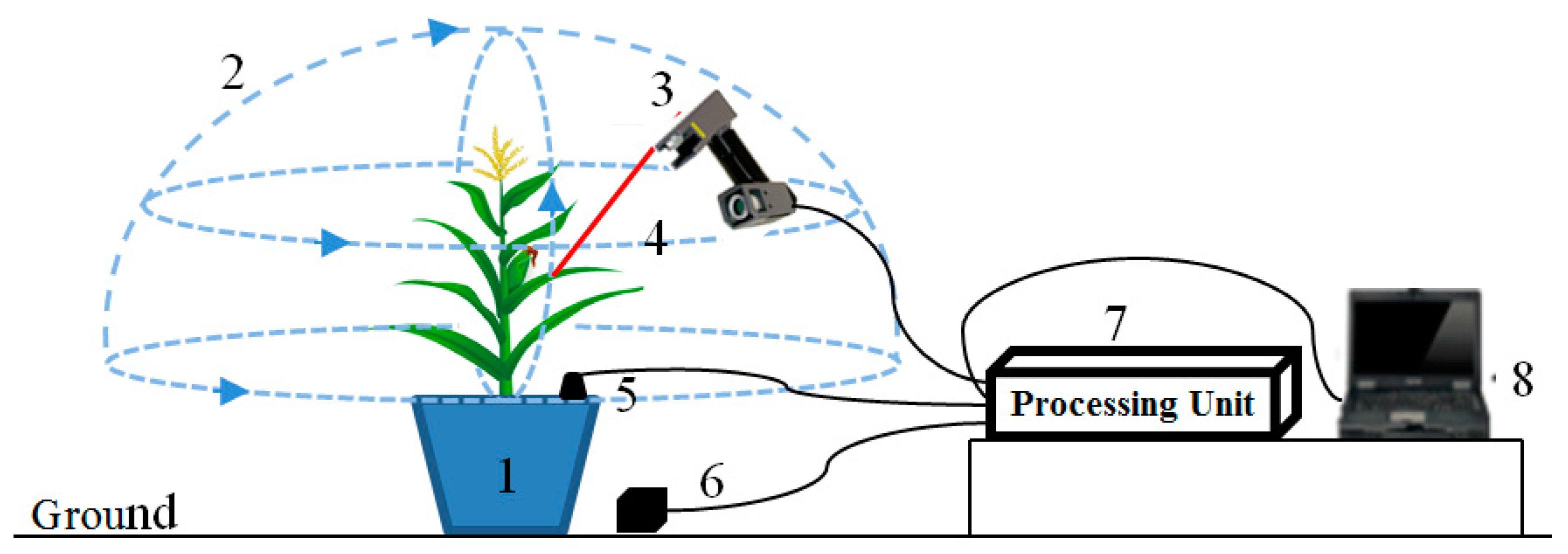
2.2. Data Acquisition Device
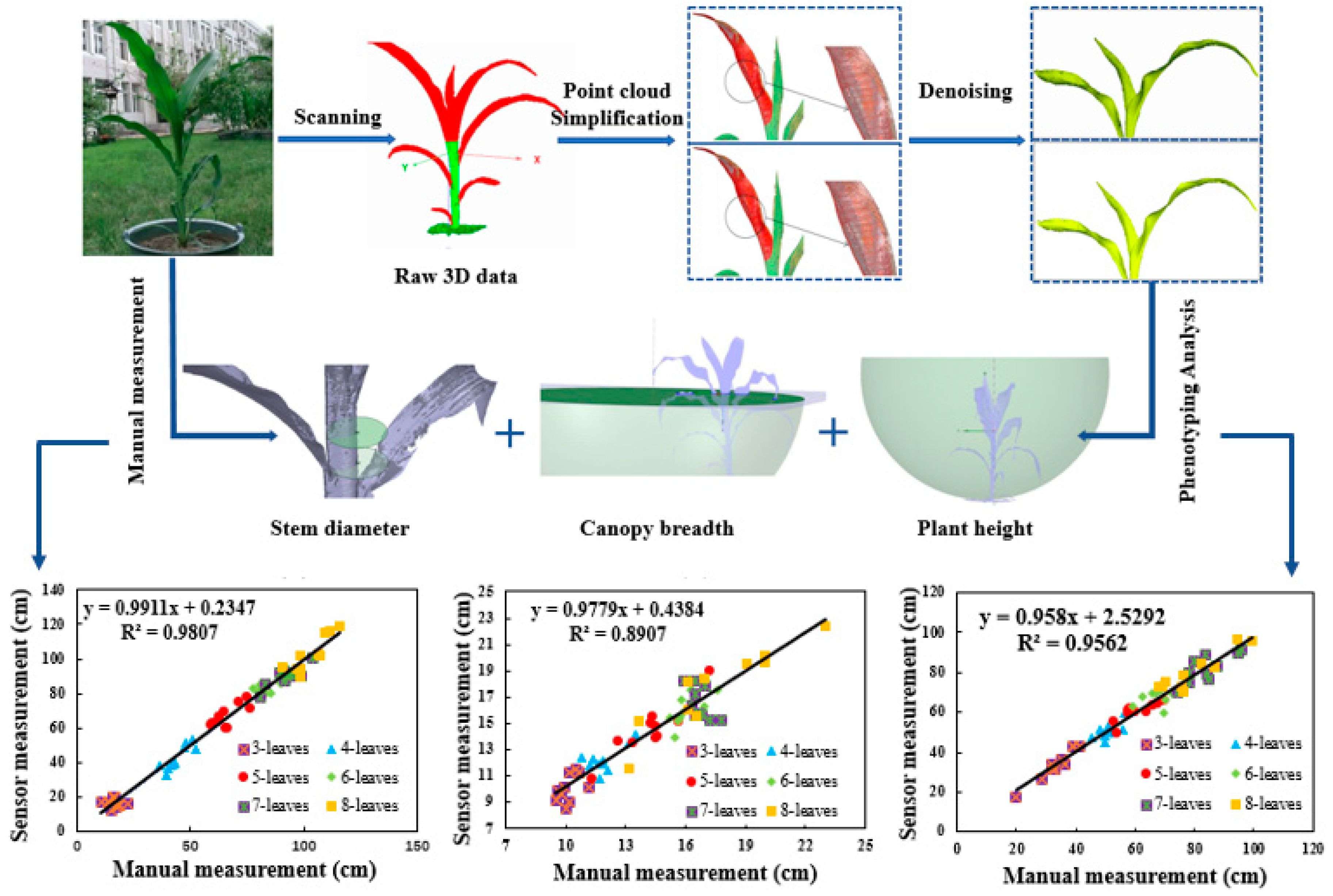
2.3. Overall Process Flow for Calculating Phenotypic Traits
2.4. Pre-Processing of the Raw 3D Point Cloud
2.4.1. Simplification Algorithm for Raw Data
2.4.2. Denoising Algorithm for Raw Data
2.5. Calculation Method for Phenotypic Traits
2.5.1. Calculation Method for Plant Height
2.5.2. Calculation Method for Stem Diameter
2.5.3. Calculation Method for Canopy Breadth
3. Results
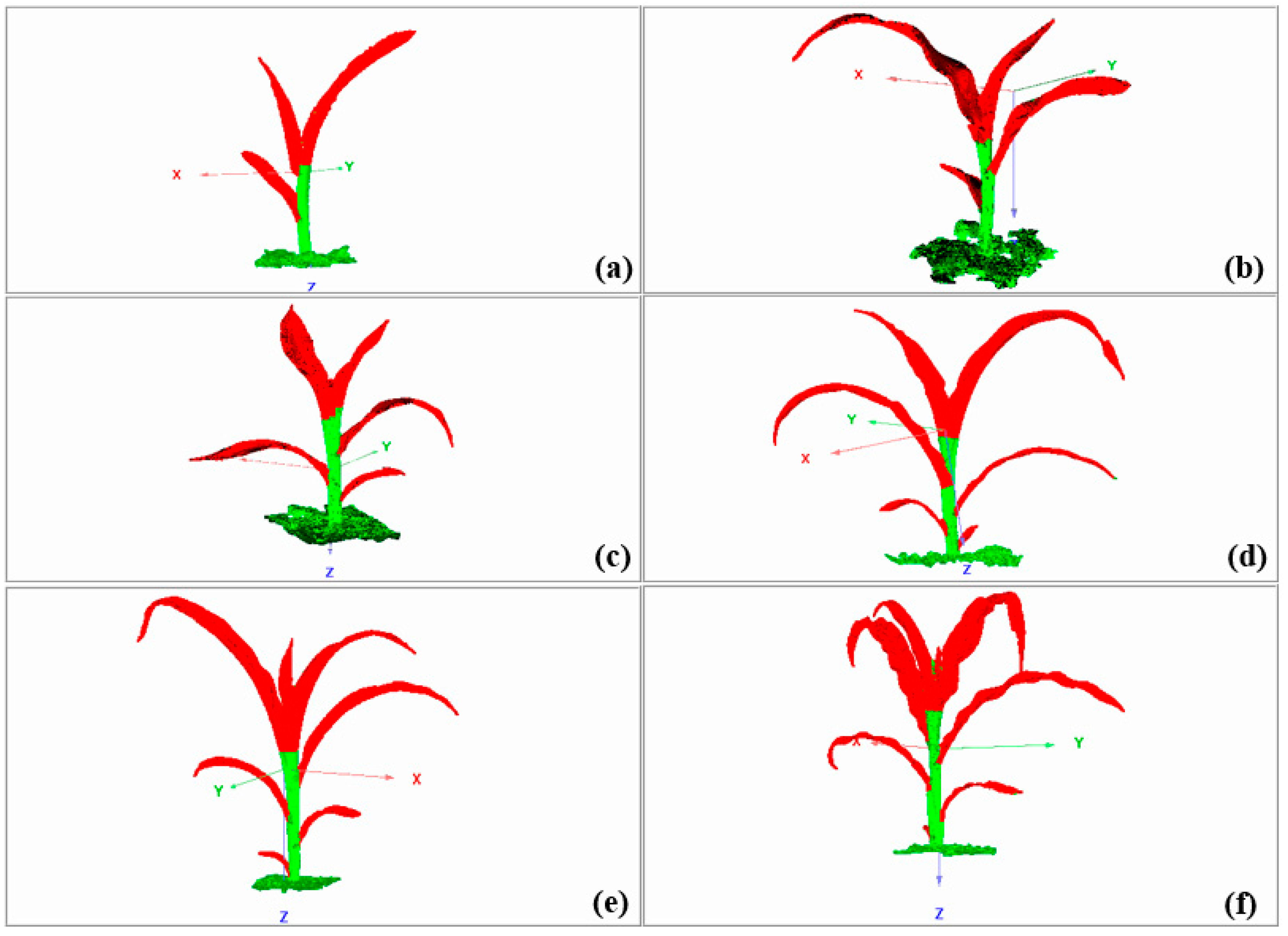
3.1. Acquisition of Raw Data
3.2. Simplification Effect of Raw Data
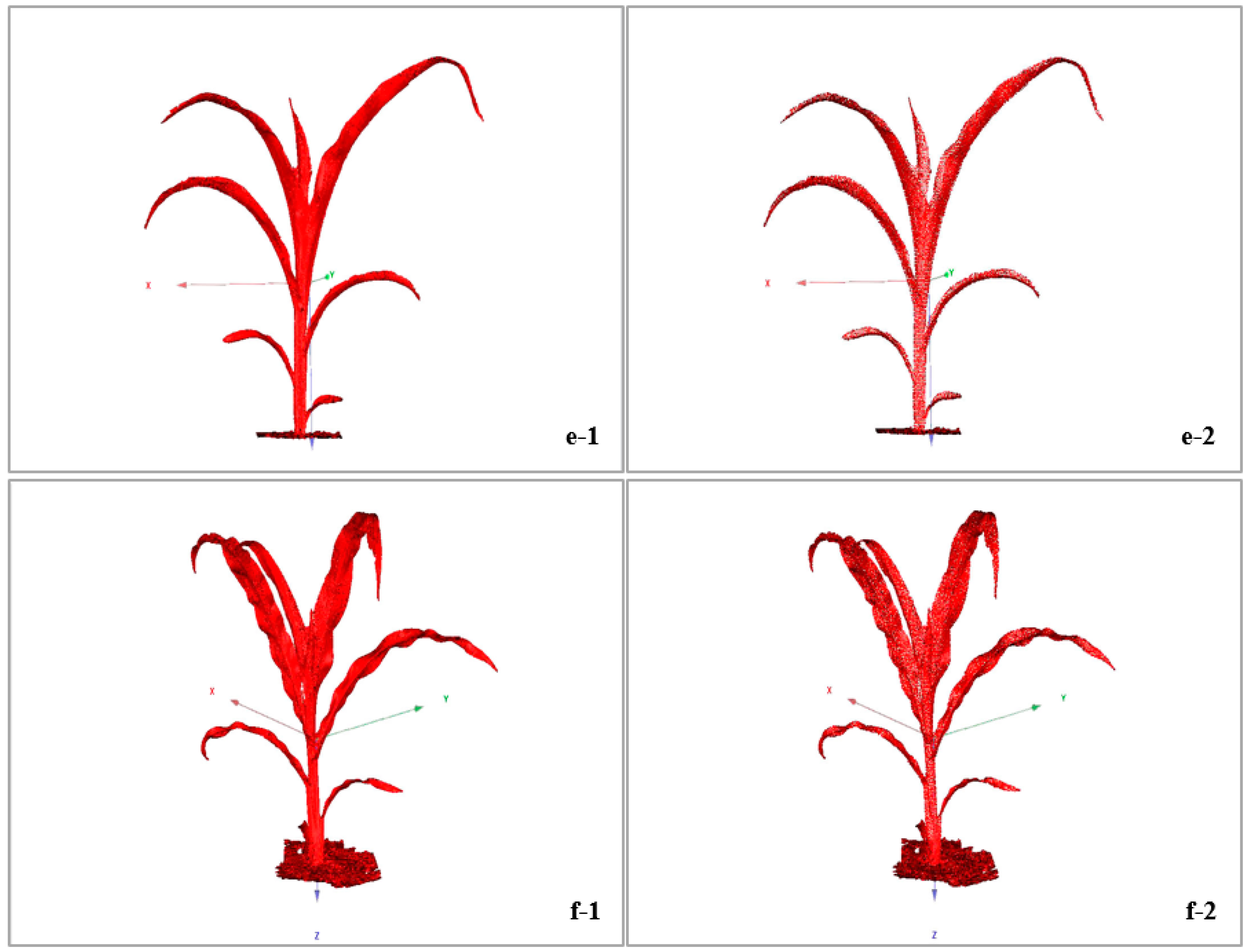
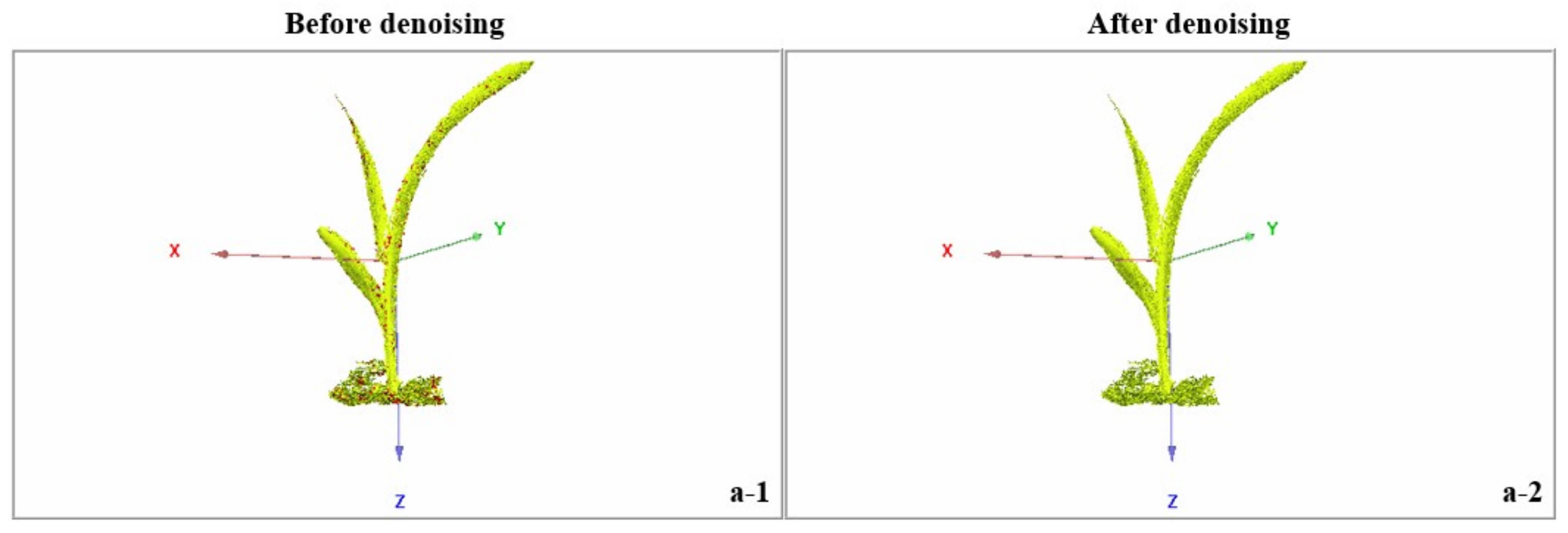
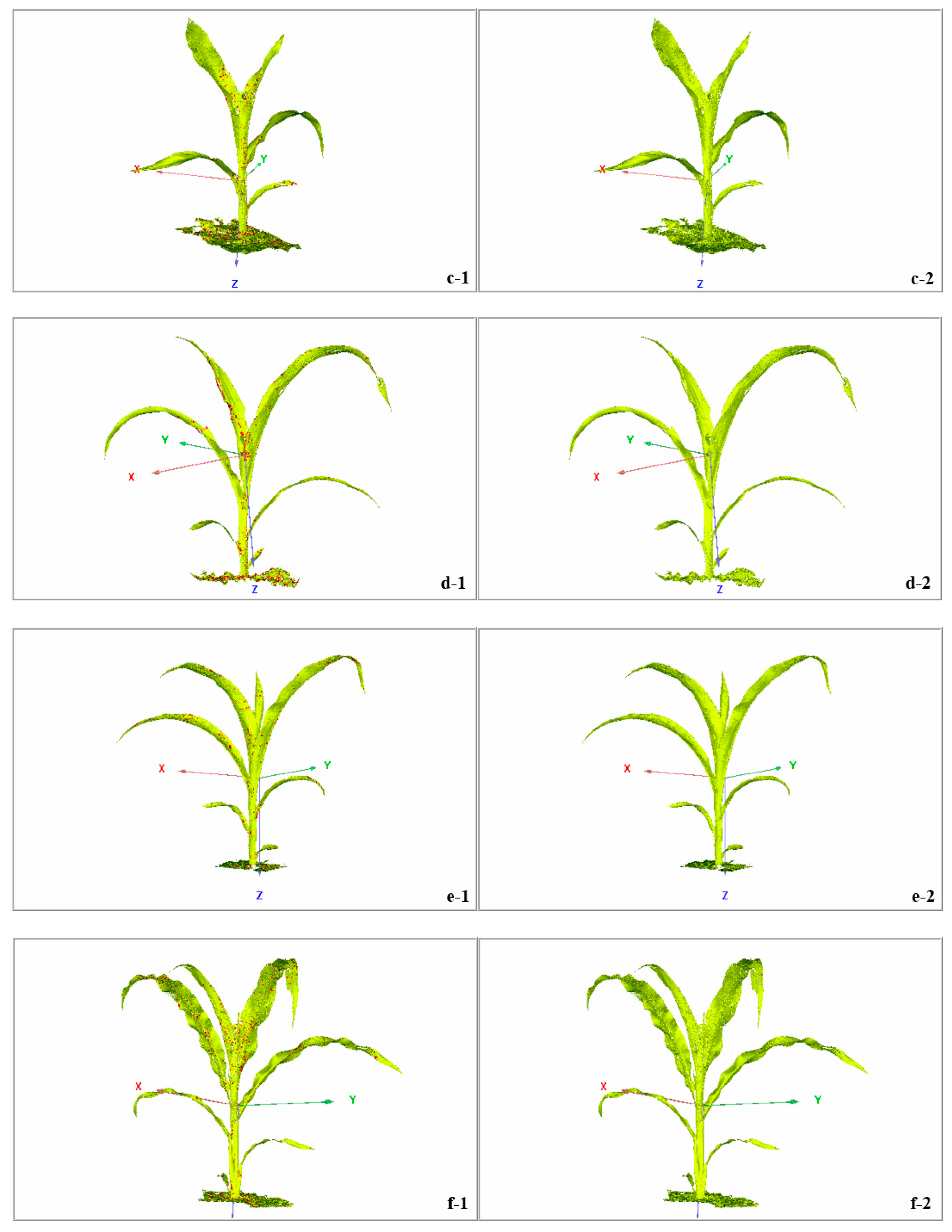
3.3. Denoising Effect of Raw Data
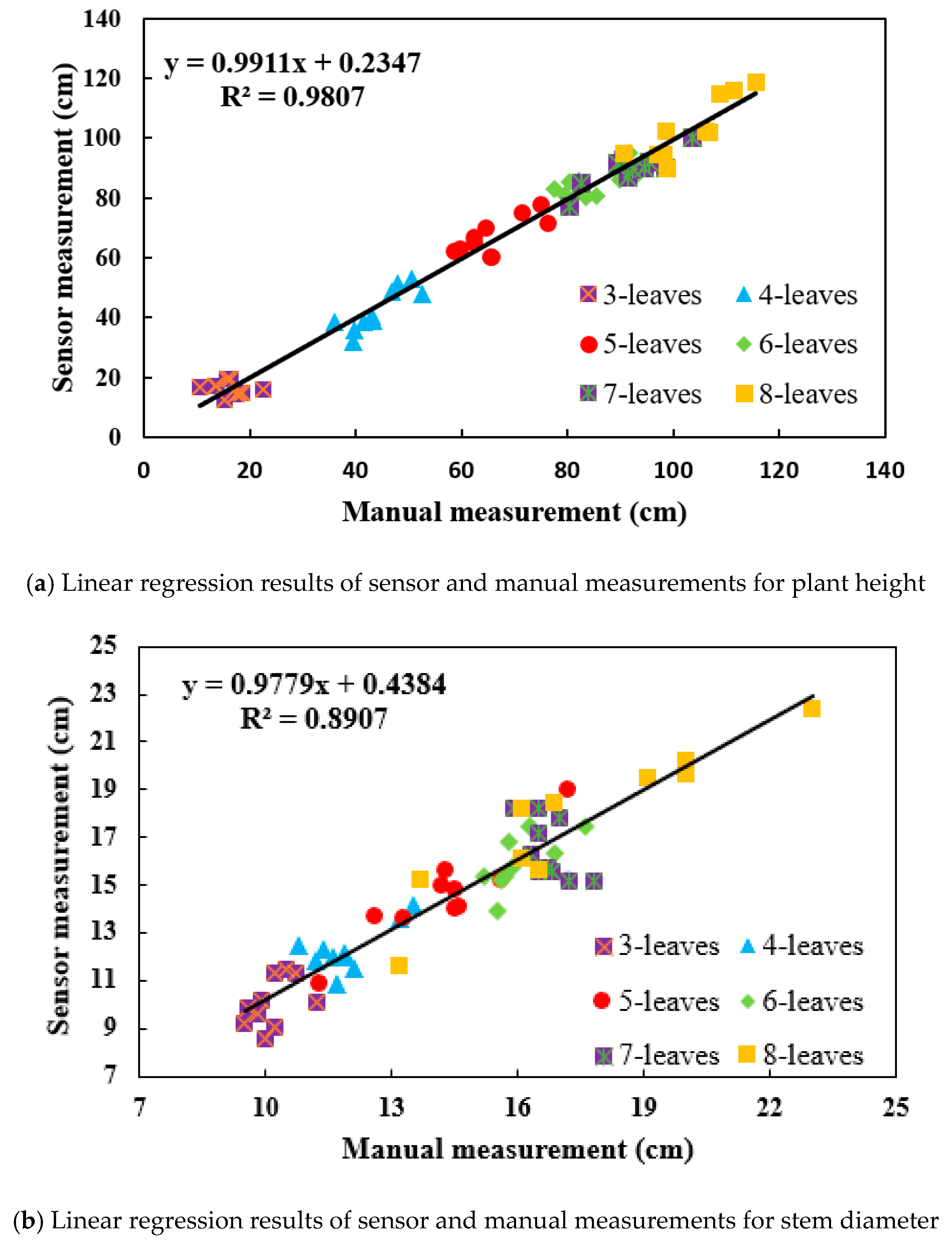
3.4. Effectiveness of the Calculation Method for Phenotypic Traits
4. Discussion
4.1. Analysis andComparison of the Experimental Results
4.2. Advantages and Limitations of the Acquisition System
4.3. Future Work
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hölker, A.C.; Schipprack, W.; Utz, H.F.; Molenaar, W.S.; Melchinger, A.E. Progress for testcross performance within the flint heterotic pool of a public maize breeding program since the onset of hybrid breeding. Euphytica 2019, 215, 50. [Google Scholar] [CrossRef]
- Sserumaga, J.P.; Makumbi, D.; Warburton, M.L.; Opiyo, S.O.; Asea, G.; Muwonge, A.; Kasozi, C. Genetic diversity among tropical provitamin a maize inbred lines and implications for a biofortification program. Cereal Res. Commun. 2019, 47, 134–144. [Google Scholar] [CrossRef]
- Sarker, A.; Muehlbauer, F.J. Improving cultivation of lentil International Center for Agricultural Research in the Dry Areas (ICARDA), India. In Achieving Sustainable Cultivation of Grain Legumes; Burleigh Dodds Science Publishing: London, UK, 2018; Volume 2, pp. 93–104. [Google Scholar]
- Su, Y.; Wu, F.; Ao, Z.; Jin, S.; Qin, F.; Liu, B.; Guo, Q. Evaluating maize phenotype dynamics under drought stress using terrestrial lidar. Plant Methods 2019, 15, 11. [Google Scholar] [CrossRef] [PubMed]
- Xin, Y.; Tao, F. Optimizing genotype-environment-management interactions to enhance productivity and eco-efficiency for wheat-maize rotation in the North China Plain. Sci. Total Environ. 2019, 654, 480–492. [Google Scholar] [CrossRef] [PubMed]
- Biddick, M.; Burns, K.C. Phenotypic trait matching predicts the topology of an insular plant–bird pollination network. Integr. Zool. 2018, 13, 339–347. [Google Scholar] [CrossRef] [PubMed]
- Santangelo, J.S.; Thompson, K.A.; Johnson, M.T. Herbivores and plant defences affect selection on plant reproductive traits more strongly than pollinators. J. Evol. Biol. 2019, 32, 4–18. [Google Scholar] [CrossRef] [PubMed]
- Bolger, A.M.; Poorter, H.; Dumschott, K.; Bolger, M.E.; Arend, D.; Osorio, S.; Usadel, B. Computational aspects underlying genome to phenome analysis in plants. Plant J. 2019, 97, 182–198. [Google Scholar] [CrossRef]
- Guan, H.; Liu, M.; Ma, X.; Yu, S. Three-dimensional reconstruction of soybean canopies using multisource imaging for phenotyping analysis. Remote Sens. 2018, 10, 1206. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, P.; Zhang, X.; Zheng, Q.; Chen, M.; Ge, F.; Zheng, Y. Multi-locus genome-wide association study reveals the genetic architecture of salk lodging resistance-related traits in maize. Front. Plant Sci. 2018, 9, 611. [Google Scholar] [CrossRef]
- Bao, Y.; Tang, L.; Srinivasan, S.; Schnable, P.S. Field-based architectural traits characterisation of maize plant using time-of-flight 3D imaging. Biosyst. Eng. 2019, 178, 86–101. [Google Scholar] [CrossRef]
- Liu, W.G.; Hussain, S.; Liu, T.; Zou, J.L.; Ren, M.L.; Zhou, T.; Yang, F.; Yang, W.Y. Shade stress decreases stem strength of soybean through restraining lignin biosynthesis. J. Integr. Agric. 2019, 18, 43–53. [Google Scholar] [CrossRef]
- Wang, J.; Kang, S.; Du, T.; Tong, L.; Ding, R.; Li, S. Estimating the upper and lower limits of kernel weight under different water regimes in hybrid maize seed production. Agric. Water Manag. 2019, 213, 128–134. [Google Scholar] [CrossRef]
- Zhu, B.; Liu, F.; Zhu, J.; Guo, Y.; Ma, Y. Three-dimensional quantifications of plant growth dynamics in field-grown plants based on machine vision method. Trans. Chin. Soc. Agric. Mach. 2018, 49, 256–262. [Google Scholar]
- Sun, S.; Li, C.; Paterson, A.H. In-field high-throughput phenotyping of cotton plant height using LiDAR. Remote Sens. 2017, 9, 377. [Google Scholar] [CrossRef]
- Sheng, Y.; Song, L. Agricultural production and food consumption in China: A long-term projection. China Econ. Rev. 2019, 53, 15–29. [Google Scholar] [CrossRef]
- Han, S.; Miedaner, T.; Utz, H.F.; Schipprack, W.; Schrag, T.A.; Melchinger, A.E. Genomic prediction and gwas of gibberella ear rot resistance traits in dent and flint lines of a public maize breeding program. Euphytica 2018, 214, 6. [Google Scholar] [CrossRef]
- Pajares, G. Overview and current status of remote sensing applications based on Unmanned aerial vehicles (UAVs) photogramm. Eng. Remote Sens. 2015, 81, 281–330. [Google Scholar]
- Grosskinsky, D.K.; Svensgaard, J.; Christensen, S.; Roitsch, T. Plant phenomics and the need for physiological phenotyping across scales to narrow the genotype-to-phenotype knowledge gap. J. Exp. Bot. 2015, 66, 5429–5440. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, N. Imaging technologies for plant high-throughput phenotyping: A review. Front. Agric. Sci. Eng. 2018, 5, 406–419. [Google Scholar] [CrossRef]
- Dreccer, M.F.; Molero, G.; Rivera-Amado, C.; John-Bejai, C.; Wilson, Z. Yielding to the image: How phenotyping reproductive growth can assist crop improvement and production. Plant Sci. 2018. [Google Scholar] [CrossRef]
- Qiu, R.; Wei, S.; Zhang, M.; Sun, H.; Li, H.; Liu, G. Sensors for measuring plant phenotyping: A review. Int. J. Agric. Biol. Eng. 2018, 11, 1–17. [Google Scholar] [CrossRef]
- Frasson, R.P.D.M.; Krajewski, W.F. Three-dimensional digital model of a maize plant. Agric. For. Meteorol. 2010, 150, 488. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, C.; Yang, G.; Yu, H.; Zhao, X.; Xu, B.; Niu, Q. Review of field-based phenotyping by unmanned aerial vehicle remote sensing platform. Trans. Chin. Soc. Agric. Eng. (Trans. Csae) 2016, 32, 98–106. [Google Scholar]
- Schmidt, D.; Kahlen, K. Towards More Realistic Leaf Shapes in functional-structural plant models. Symmetry 2018, 10, 278. [Google Scholar] [CrossRef]
- Li, H. 3D Reconstruction of maize leaves based on virtual visual technology. Bull. Sci. Technol. 2016, 32, 96–101. [Google Scholar]
- Guo, W.; Fukatsu, T.; Ninomiya, S. Automated characterization of flowering dynamics in rice using field-acquired time-series RGB images. Plant Methods 2015, 11, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Bendig, J.; Bolten, A.; Bennertz, S.; Broscheit, J.; Eichfuss, S.; Bareth, G. Estimating biomass of barley using crop surface models (CSMs) derived from UAV-Based RGB Imaging. Remote Sens. 2014, 6, 10395–10412. [Google Scholar] [CrossRef]
- Ma, X.; Feng, J.; Guan, H.; Liu, G. Prediction of Chlorophyll Content in Different Light Areas of Apple Tree Canopies based on the Color Characteristics of 3D Reconstruction. Remote Sens. 2018, 10, 429. [Google Scholar] [CrossRef]
- Vicari, M.B.; Pisek, J.; Disney, M. New estimates of leaf angle distribution from terrestrial LiDAR: Comparison with measured and modelled estimates from nine broadleaf tree species. Agric. For. Meteorol. 2019, 264, 322–333. [Google Scholar] [CrossRef]
- Wu, Z.; Ni, M.; Hu, Z.; Wang, J.; Li, Q.; Wu, G. Mapping invasive plant with UAV-derived 3D mesh model in mountain area-A case study in Shenzhen Coast, China. Int. J. Appl. Earth Obs. Geoinf. 2019, 77, 129–139. [Google Scholar] [CrossRef]
- Sankaran, S.; Khot, L.R.; Carter, A.H. Field-based crop phenotyping: Multispectral aerial imaging for evaluation of winter wheat emergence and spring stand. Comput. Electron. Agric. 2015, 118, 372–379. [Google Scholar] [CrossRef]
- Campbell, Z.C.; Acosta-Gamboa, L.M.; Nepal, N.; Lorence, A. Engineering plants for tomorrow: How high-throughput phenotyping is contributing to the development of better crops. Phytochem. Rev. 2018, 17, 1329–1343. [Google Scholar] [CrossRef]
- Zhou, J.; Fu, X.; Schumacher, L.; Zhou, J. Evaluating Geometric Measurement Accuracy Based on 3D Reconstruction of Automated Imagery in a Greenhouse. Sensors 2018, 18, 2270. [Google Scholar] [CrossRef] [PubMed]
- Thomas, S.; Behmann, J.; Steier, A.; Kraska, T.; Muller, O.; Rascher, U.; Mahlein, A.K. Quantitative assessment of disease severity and rating of barley cultivars based on hyperspectral imaging in a non-invasive, automated phenotyping platform. Plant Methods 2018, 14, 45. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Chen, H.; Zhou, J.; Fu, X.; Ye, H.; Nguyen, H.T. Development of an automated phenotyping platform for quantifying soybean dynamic responses to salinity stress in greenhouse environment. Comput. Electron. Agric. 2018, 151, 319–330. [Google Scholar] [CrossRef]
- Jay, S.; Rabatel, G.; Hadoux, X.; Moura, D.; Gorretta, N. In-field crop row phenotyping from 3D modeling performed using Structure from Motion. Comput. Electron. Agric. 2015, 110, 70–77. [Google Scholar] [CrossRef]
- Mir, R.R.; Reynolds, M.; Pinto, F.; Khan, M.A.; Bhat, M.A. High-throughput Phenotyping for Crop Improvement in The Genomics Era. Plant Sci. 2019. [Google Scholar] [CrossRef]
- Khanna, R.; Schmid, L.; Walter, A.; Nieto, J.; Siegwart, R.; Liebisch, F. A spatio temporal spectral framework for plant stress phenotyping. Plant Methods 2019, 15, 13. [Google Scholar] [CrossRef]
- Hosoi, F.; Kenji, O. Estimating vertical plant area density profile and growth parameters of a wheat canopy at different growth stages using three-dimensional portable lidar imaging. Isprs J. Photogramm. Remote Sens. 2009, 64, 151–158. [Google Scholar] [CrossRef]
- Xia, C.; Shi, Y.; Yin, W. Obtaining and denoising method of three-dimensional point cloud data of plants based on TOF depth sensor. Trans. Chin. Soc. Agric. Eng. (Trans. Csae) 2018, 34, 168–174. [Google Scholar]
- Xue, A.; Ju, S.; He, W.; Chen, W. Study on algorithms for local outlier detection. Chin. J. Comput. 2007, 30, 1455–1463. [Google Scholar]
- Zhang, L.; Cheng, X.; Tan, K. Automatically sphere target extracting and parameter fitting based on intensity image. Geotech. Investig. Surv. 2014, 12, 65–69. [Google Scholar]
- Busemeyer, L.; Mentrup, D.; Möller, K.; Wunder, E.; Alheit, K.; Hahn, V.; Rahe, F. BreedVision-A multi-sensor platform for non-destructive field-based phenotyping in plant breeding. Sensors 2013, 13, 2830–2847. [Google Scholar] [CrossRef] [PubMed]
- Ruckelshausen, A.; Biber, P.; Dorna, M.; Gremmes, H.; Klose, R.; Linz, A.; Weiss, U. BoniRob: An autonomous field robot platform for individual plant phenotyping. Precis. Agric. 2009, 9, 841–847. [Google Scholar]
- Ralph, K.; Jaime, P.; Arno, R. Usability study of 3D time-of flight cameras for automatic plant phenotyping. Bornimer Agrartech. Ber. 2009, 69, 93–105. [Google Scholar]
- Paulus, S.; Dupuis, J.; Mahlein, A.K.; Kuhlmann, H. Surface feature-based classification of plant organs from 3D laser scanned point clouds for plant phenotyping. Bmc Bioinform. 2013, 14, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Paulus, S.; Schumann, H.; Kuhlmann, H.; Léon, J. High-precision laser scanning system for capturing 3D plant architecture and analyzing growth of cereal plants. Biosyst. Eng. 2014, 121, 1–11. [Google Scholar] [CrossRef]
- Paulus, S.; Dupuis, J.; Riedel, S.; Kuhlmann, H. Automated analysis of barley organs using 3D laser scanning: An approach for high throughput phenotyping. Sensors 2014, 14, 12670–12686. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, J. Cylindrical fitting method of laser scanner point cloud data. Sci. Surv. Mapp. 2018, 43, 83–87. [Google Scholar]
- Jackson, T.; Shenkin, A.; Wellpott, A.; Calders, K.; Origo, N.; Disney, M.; Fourcaud, T. Finite element analysis of trees in the wind based on terrestrial laser scanning data. Agric. For. Meteorol. 2019, 265, 137–144. [Google Scholar] [CrossRef]
- Moritani, R.; Kanai, S.; Date, H.; Watanabe, M.; Nakano, T.; Yamauchi, Y. Cylinder-based Efficient and Robust Registration and Model Fitting of Laser-scanned Point Clouds for As-built Modeling of Piping Systems. Proc. Cad 2019, 16, 396–412. [Google Scholar] [CrossRef]
- Guo, C.; Zong, Z.; Zhang, X.; Liu, G. Apple tree canopy geometric parameters acquirement based on 3D point clouds. Trans. Chin. Soc. Agric. Eng. 2017, 33, 175–181. [Google Scholar]
- Feng, J.; Ma, X.; Guan, H.; Zhu, K.; Yu, S. Calculation method of soybean plant height based on depth information. Acta Optica Sinica. pp. 1–18. Available online: http://kns.cnki.net/kcms/detail/31.1252.O4. 20190225.0920.030.html (accessed on 1 March 2019).
- Nieves-Chinchilla, J.; Martínez, R.; Farjas, M.; Tubio-Pardavila, R.; Cruz, D.; Gallego, M. Reverse engineering techniques to optimize facility location of satellite ground stations on building roofs. Autom. Constr. 2018, 90, 156–165. [Google Scholar] [CrossRef]
- Azzari, G.; Goulden, M.; Rusu, R. Rapid characterization of vegetation structure with a Microsoft Kinect sensor. Sensors 2013, 13, 2384–2398. [Google Scholar] [CrossRef] [PubMed]
- Xia, C.; Wang, L.; Chung, B.; Lee, J. In situ 3D segmentation of individual plant leaves using a RGB-D camera for agricultural automation. Sensors 2015, 15, 20463–20479. [Google Scholar] [CrossRef] [PubMed]
- Rueda-Ayala, V.P.; Peña, J.M.; Höglind, M.; Bengochea-Guevara, J.M.; Andújar, D. Comparing UAV-Based technologies and RGB-D reconstruction methods for plant height and biomass monitoring on grass ley. Sensors 2019, 19, 535. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Zhang, L.; Dong, H.; Alelaiwi, A.; Saddik, A.E. Evaluating and improving the depth accuracy of Kinect for Windows v2. Ieee Sens. J. 2015, 15, 4275–4285. [Google Scholar] [CrossRef]
- Ma, X.; Liu, G.; Feng, J.; Zhou, W. Multi-source image registration for canopy organ of apple trees in mature period. Trans. Chin. Soc. Agric. Mach. 2014, 45, 82–88. [Google Scholar]
- Zhou, W.; Liu, G.; Ma, X.; Feng, J. Study on multi-image registration of apple tree at different growth stages. Acta Opt. Sin. 2014, 34, 177–183. [Google Scholar]
- Fukuda, T.; Ji, Y.; Umeda, K. Accurate range image generation using sensor fusion of TOF and Stereo-based Measurement. In Proceedings of the 12th France-Japan and 10th Europe-Asia Congress on Mechatronics, Tsu, Japan, 10–12 September 2018; pp. 67–70. [Google Scholar]
- Hu, C.; Pan, Z.; Li, P. A 3D point cloud filtering method for leaves based on manifold distance and normal estimation. Remote Sens. 2019, 11, 198. [Google Scholar] [CrossRef]
- Itakura, K.; Hosoi, F. Estimation of Leaf Inclination Angle in Three-Dimensional Plant Images Obtained from Lidar. Remote Sens. 2019, 11, 344. [Google Scholar] [CrossRef]
- Roosjen, P.P.J.; Brede, B.; Suomalainen, J.M.; Bartholomeus, H.M.; Kooistra, L.; Clevers, J.G. Improved estimation of leaf area index and leaf chlorophyll content of a potato crop using multi-angle spectral data—Potential of unmanned aerial vehicle imagery. Int. J. Appl. Earth Obs. Geoinf. 2018, 66, 14–26. [Google Scholar] [CrossRef]
- Zheng, H.; Cheng, T.; Li, D.; Zhou, X.; Yao, X.; Tian, Y.; Cao, W.; Zhu, Y. Evaluation of RGB, color-Infrared and multispectral images acquired from unmanned aerial systems for the estimation of nitrogen accumulation in rice. Remote Sens. 2018, 10, 824. [Google Scholar] [CrossRef]
- Zou, X.; Ttus, M.M.; Tammeorg, P.; Torres, C.L.; Takala, T.; Pisek, J.; Torres, C.L.; Takala, T.; Pisek, J.; Pellikka, P. Photographic measurement of leaf angles ind fiel crops. Agric. For. Meteorol. 2014, 184, 137–146. [Google Scholar] [CrossRef]
- Aminifard, M.H.; Bayat, H.; Khayyat, M. Individual modelling of leaf area in cress and radish using leaf dimensions and weight. J. Hortic. Postharvest Res. 2019, 2, 83–94. [Google Scholar]
- Dong, T.; Liu, J.; Shang, J.; Qian, B.; Ma, B.; Kovacs, J.M.; Shi, Y. Assessment of red-edge vegetation indices for crop leaf area index estimation. Remote Sens. Environ. 2019, 222, 133–143. [Google Scholar] [CrossRef]
- Larrinaga, A.; Brotons, L. Greenness Indices from a Low-Cost UAV Imagery as Tools for Monitoring Post-Fire Forest Recovery. Drones 2019, 3, 6. [Google Scholar] [CrossRef]
- Sanz, R.; Llorens, J.; EscolÀ, A.; Arnó, J.; Planas, S.; Román, C.; Rosell-Polo, J.R. LIDAR and non-LIDAR-based canopy parameters to estimate the leaf area in fruit trees and vineyard. Agric. For. Meteorol. 2018, 260–261, 229–239. [Google Scholar] [CrossRef]











| 3-Leaves | 4-Leaves | 5-Leaves | 6-Leaves | 7-Leaves | 8-Leaves | |
|---|---|---|---|---|---|---|
| Raw data | 10,256 | 19,587 | 26,120 | 30,015 | 39,542 | 43,957 |
| After simplification | 7401 | 14,521 | 19,854 | 23,025 | 29,525 | 32,019 |
| rate (%) | 27.8 | 25.9 | 24.0 | 23.3 | 25.3 | 27.1 |
| Maximum Error/mm | Average Error/mm | |
|---|---|---|
| Laplace filtering | 19.74 | 2.54 |
| Bilateral filtering algorithm | 15.57 | 1.57 |
| Sensors | Plant Height | Stem Diameter | Canopy Breadth |
|---|---|---|---|
| FastSCAN | R2 = 0.9807 | R2 = 0.8907 | R2 = 0.9562 |
| Kinect v2.0 | R2 = 0.9858 | R2 = 0.6973 | R2 = 0.8854 |
| Sensors | Distance of Point-to-Point | Advantages | Limitations |
|---|---|---|---|
| Stereo vision system | Various resolutions | Low cost Suitable for unmanned aerial vehicles (UAV) | Heavy computation Sensitive to strong light |
| Lidar/laser sensor (e.g., Trimble TX8) | 7.5 mm at 30 m | Long measurement range High resolution | High cost Limited information on occlusions and shadows |
| Range camera (e.g., Kinect v 2.0) | >4.0 mm at more than 4 m | Low cost High frame rate | Sensitive to strong light Low resolution |
| Hand held laser scanner (e.g., FastSCAN) | 0.178 mm in the range of 200 mm | High resolution High accuracy for 3D model | Short measurement range Hand held |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Zhu, K.; Guan, H.; Feng, J.; Yu, S.; Liu, G. Calculation Method for Phenotypic Traits Based on the 3D Reconstruction of Maize Canopies. Sensors 2019, 19, 1201. https://doi.org/10.3390/s19051201
Ma X, Zhu K, Guan H, Feng J, Yu S, Liu G. Calculation Method for Phenotypic Traits Based on the 3D Reconstruction of Maize Canopies. Sensors. 2019; 19(5):1201. https://doi.org/10.3390/s19051201
Chicago/Turabian StyleMa, Xiaodan, Kexin Zhu, Haiou Guan, Jiarui Feng, Song Yu, and Gang Liu. 2019. "Calculation Method for Phenotypic Traits Based on the 3D Reconstruction of Maize Canopies" Sensors 19, no. 5: 1201. https://doi.org/10.3390/s19051201
APA StyleMa, X., Zhu, K., Guan, H., Feng, J., Yu, S., & Liu, G. (2019). Calculation Method for Phenotypic Traits Based on the 3D Reconstruction of Maize Canopies. Sensors, 19(5), 1201. https://doi.org/10.3390/s19051201





