Quasi-static Analysis Based on an Equivalent Circuit Model for a CMOS Terahertz Plasmon Detector in the Subthreshold Region
Abstract
:1. Introduction
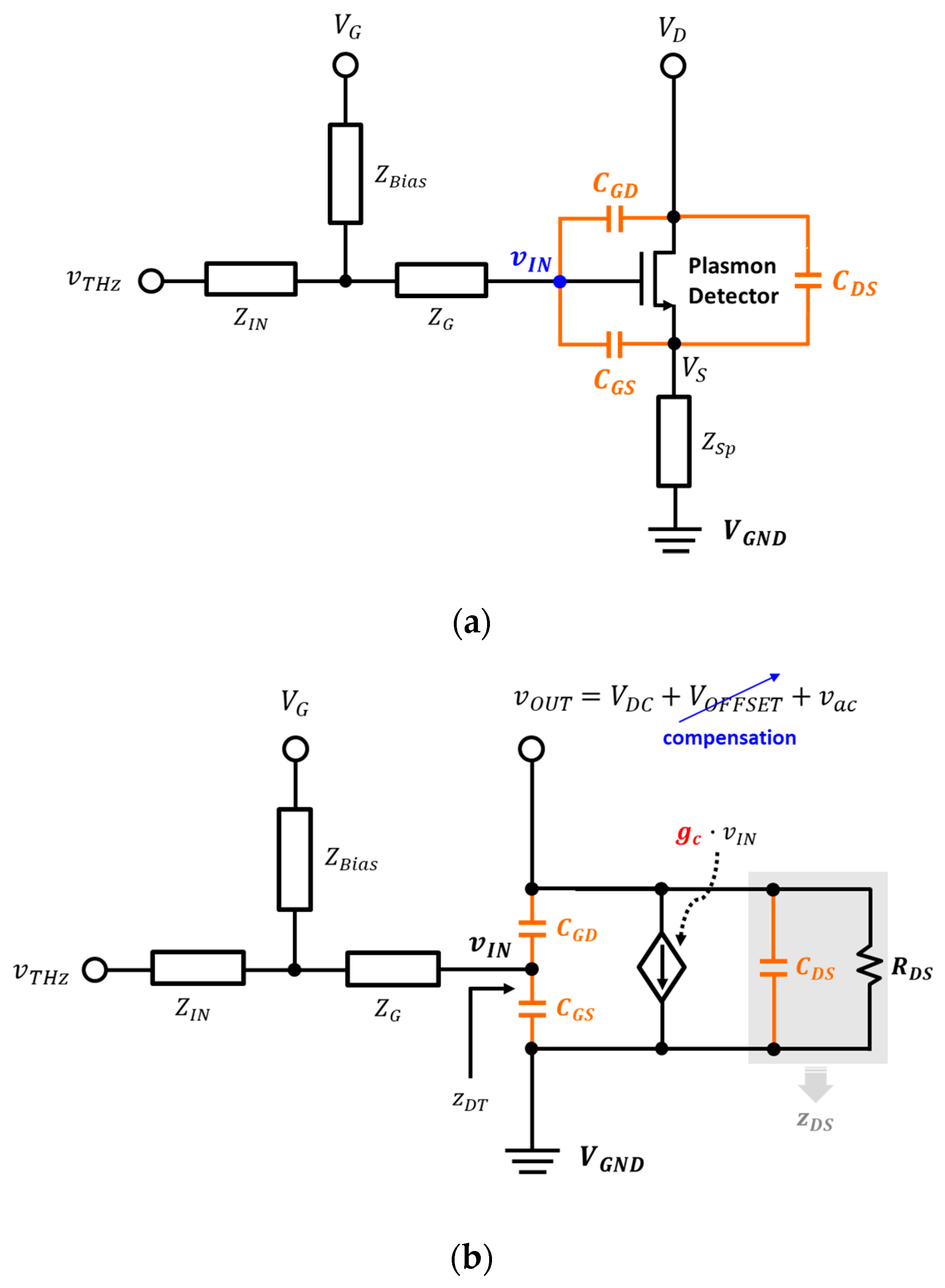
2. Quasi-Static Analysis Using the Proposed Equivalent Circuit Model
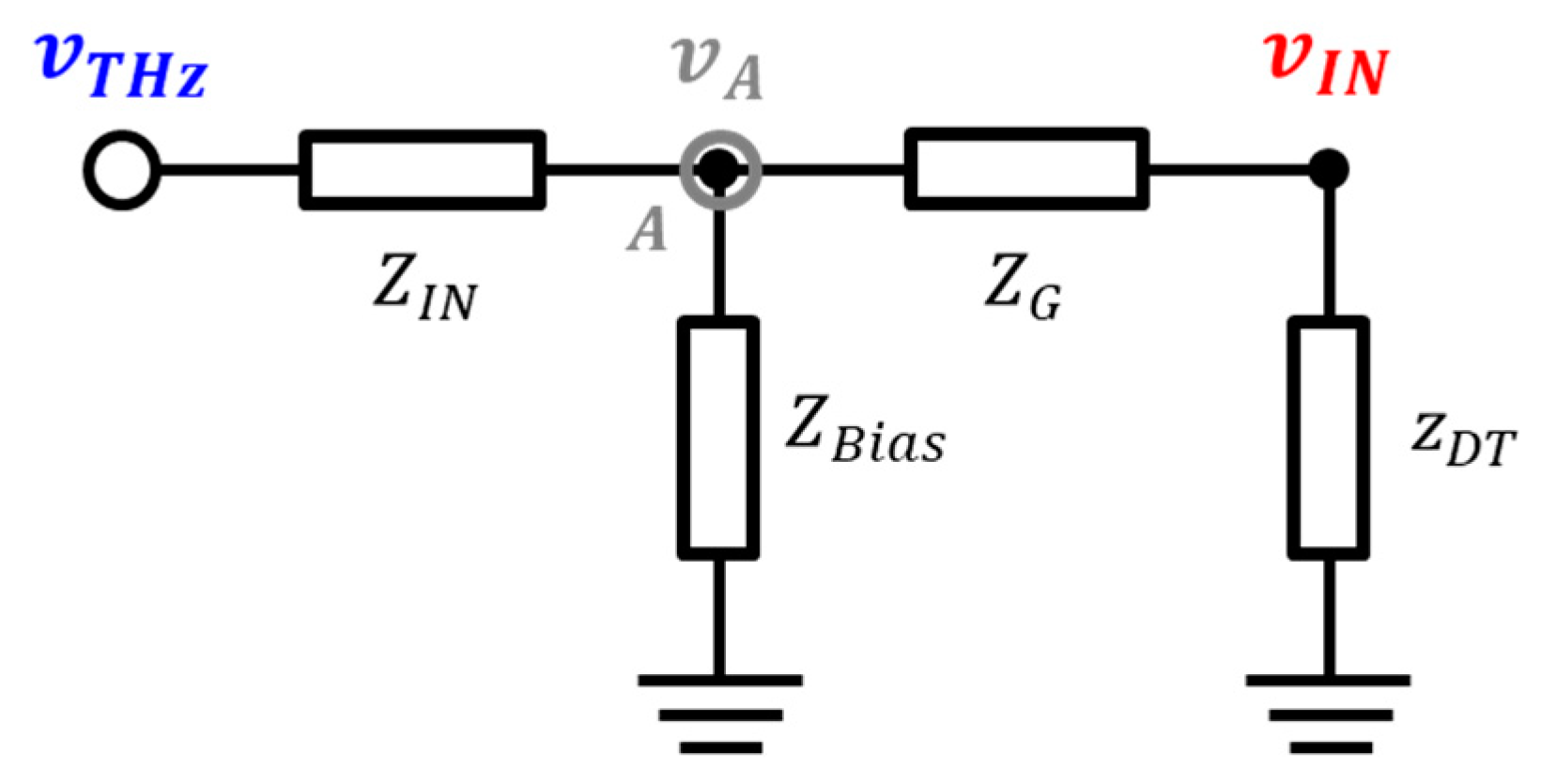
2.1. Analysis Using a Superposition Method
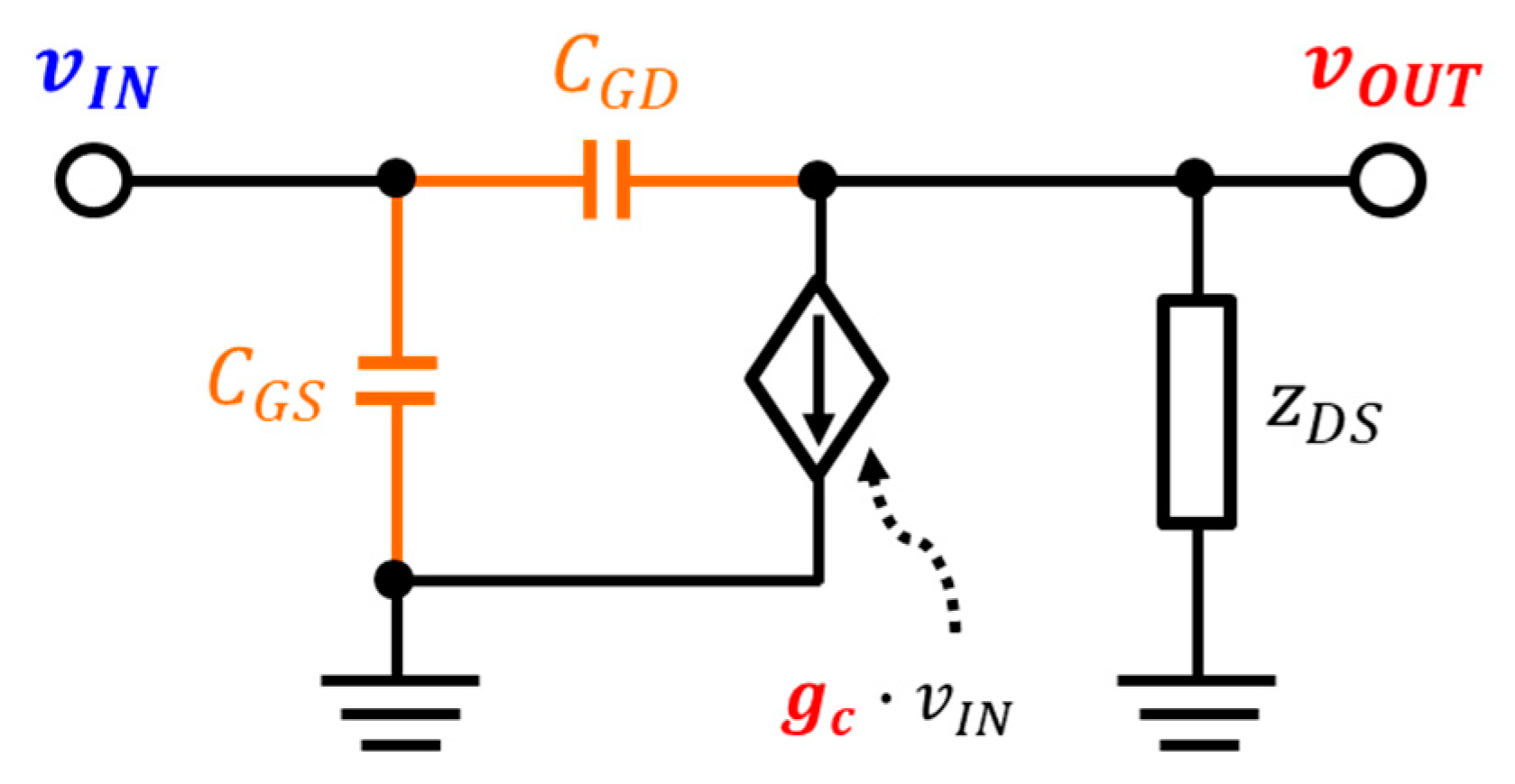
2.2. Analysis Using a Small-Signal Method at The Subthreshold Region
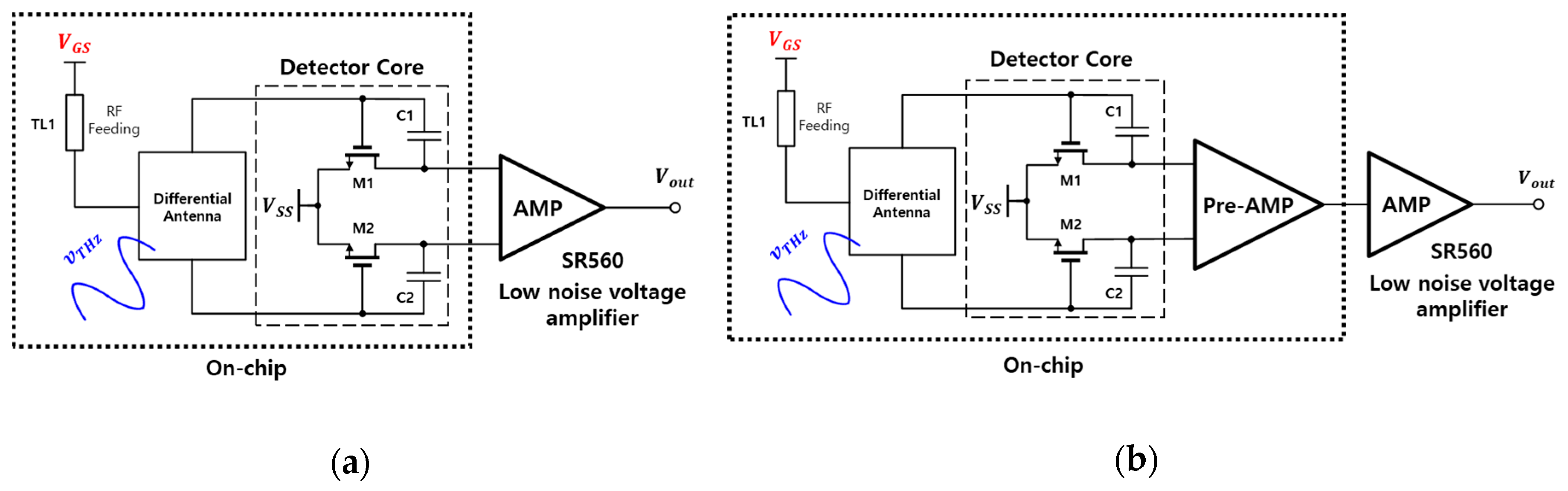
3. Two Plasmon Detectors
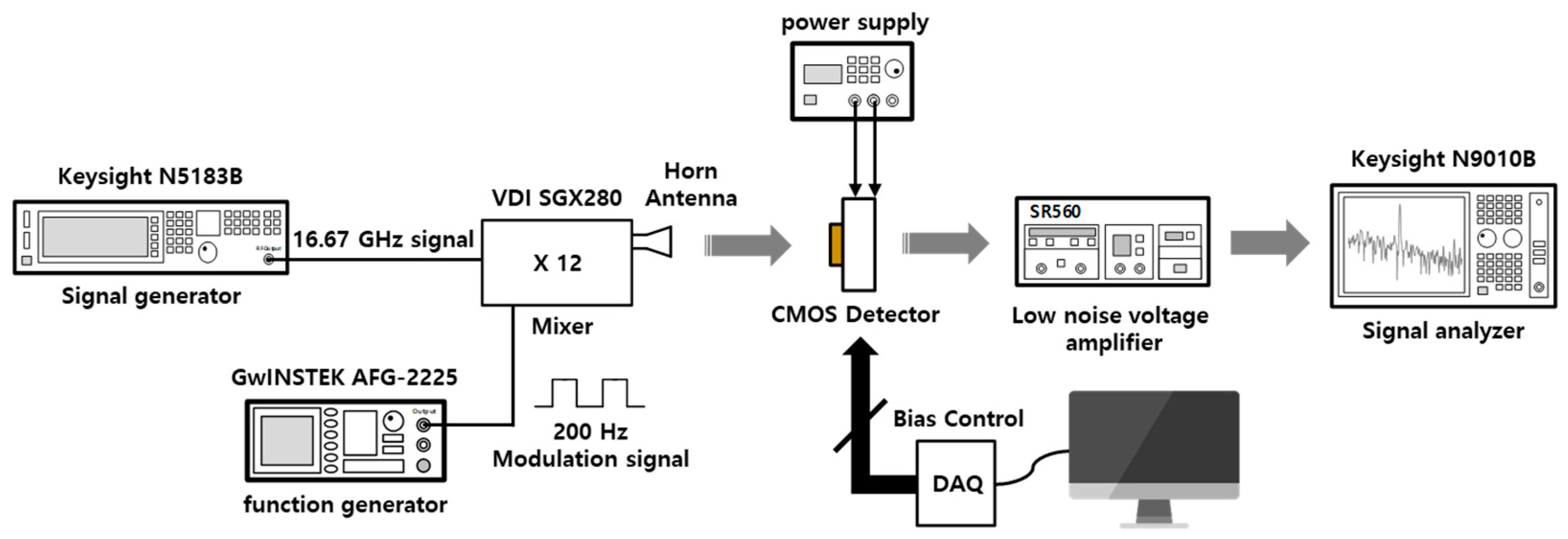
4. Measurement Results and Discussion
4.1. Measurement Setup
4.2. Performance Comparison Between two THz Detectors
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Lee, Y.-S. Principle of Terahertz Science and Technology; Springer: New York, NY, USA, 2009; pp. 7–10. [Google Scholar]
- Siegel, P.H. Terahertz technology. IEEE Trans. Microw. Theory Tech. 2002, 50, 910–928. [Google Scholar] [CrossRef]
- Pawar, A.Y.; Sonawane, D.D.; Erande, K.B.; Derle, D.V. Terahertz technology and its applications. Drug Invent. Today 2013, 5, 157–163. [Google Scholar] [CrossRef]
- Yang, X.; Zhao, X.; Yang, K.; Liu, Y.; Liu, Y.; Fu, W.; Luo, Y. Biomedical applications of terahertz spectroscopy and imaging. Trends Biotechnol. 2016, 34, 810–824. [Google Scholar] [CrossRef] [PubMed]
- Carranza, I.E.; Grant, J.P.; Gough, J.; Cumming, D. Terahertz metamaterial absorbers implemented in CMOS technology for imaging applications: Scaling to large format focal plane arrays. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 4700508. [Google Scholar]
- Escorcia, I.; Grant, J.; Gough, J.; Cumming, D. Uncooled CMOS terahertz imager using a metamaterial absorber and pn diode. Opt. Lett. 2016, 41, 3261–3264. [Google Scholar] [CrossRef] [PubMed]
- Bhan, R.K.; Saxena, R.S.; Jalwania, C.R.; Lomash, S.K. Uncooled infrared microbolometer arrays and their characterisation techniques. Def. Sci. J. 2009, 59, 580–589. [Google Scholar] [CrossRef]
- Han, S.-P.; Ko, H.K.; Park, J.-W.; Kim, N.; Yoon, Y.-J.; Shin, J.-H.; Kim, D.Y.; Lee, D.H.; Park, K.H. InGaAs schottky barrier diode array detector for a real-time compact terahertz line scanner. Opt. Exp. 2013, 21, 25874–25882. [Google Scholar] [CrossRef]
- Pfeiffer, U.R.; Öjefors, E. Terahertz imaging with CMOS/BiCMOS process technologies. In Proceedings of the 36th IEEE European Solid State Circuits Conference, Seville, Spain, 13–17 September 2010; pp. 52–60. [Google Scholar]
- Otsuji, T. Trends in the research of modern terahertz detectors: Plasmon detectors. IEEE Trans. Terahertz Sci. Technol. 2015, 5, 1110–1120. [Google Scholar]
- Otsuji, T.; Shur, M. Terahertz plasmonics: Good results and great expectations. IEEE Microw. Mag. 2014, 15, 43–50. [Google Scholar] [CrossRef]
- Schuster, E.; Coquillat, D.; Videlier, H.; Sakowicz, M.; Teppe, F.; Dussopt, L.; Giffard, B.; Skotnicki, T.; Knap, W. Broadband terahertz imaging with highly sensitive silicon CMOS detectors. Opt. Express 2011, 19, 7821–7832. [Google Scholar] [CrossRef] [PubMed]
- Rogalski, A.; Sizov, F. Terahertz detectors and focal plane arrays. Opto-Electron. Rev. 2011, 19, 346–404. [Google Scholar] [CrossRef] [Green Version]
- Dyakonov, M.; Shur, M. Detection, mixing, and frequency multiplication of terahertz radiation by two-dimensional electronic fluid. IEEE Trans. Electron Devices 1996, 43, 380–387. [Google Scholar] [CrossRef]
- Knap, W.; Dyakonov, M.; Coquillat, D.; Teppe, F.; Dyakonova, N.; Lusakowski, J.; Karpierz, K.; Sakowicz, M.; Valusis, G.; Seliuta, D.; et al. Field effect transistors for terahertz detection: Physics and first imaging applications. J. Infrared Millim. Terahertz Waves 2009, 30, 1319–1337. [Google Scholar] [CrossRef]
- Knap, W.; Teppe, F.; Meziani, Y.; Dyakonova, N.; Lusakowski, J.; Boeuf, F.; Skotnicki, T.; Maude, D.; Rumyantsev, S.; Shur, M.S. Plasma wave detection of sub-terahertz and terahertz radiation by silicon field-effect transistors. Appl. Phys. Lett. 2004, 85, 675–677. [Google Scholar] [CrossRef]
- Lisauskas, A.; Pfeiffer, U.; Öjefors, E.; Bolìvar, P.H.; Glaab, D.; Roskos, H.G. Rational design of high-responsivity detectors of terahertz radiation based on distributed self-mixing in silicon field-effect transistors. J. Appl. Phys. 2009, 105, 114511. [Google Scholar] [CrossRef]
- Maas, S.A. A GaAs MESFET mixer with very low intermodulation. IEEE Trans. Microw. Theory Tech. 1987, 35, 425–429. [Google Scholar] [CrossRef]
- Öjefors, E.; Lisauskas, A.; Glaab, D.; Roskos, H.G.; Pfeiffer, U.R. Terahertz imaging detectors in CMOS technology. J. Infrared Millim. Terahertz Waves 2009, 30, 1269–1280. [Google Scholar] [CrossRef]
- Öjefors, E.; Pfeiffer, U.R.; Lisauskas, A.; Roskos, H.G. A 0.65 THz focal-plane array in a quarter-micron CMOS process technology. IEEE J. Solid-State Circuits 2009, 44, 1968–1976. [Google Scholar] [CrossRef]
- Khatib, M.; Perenzoni, M. A low-noise direct incremental A/D converter for FET-based THz imaging detectors. Sensors 2018, 18, 1867. [Google Scholar] [CrossRef]
- Chai, S.; Lim, S.; Kim, C.-Y.; Hong, S. Matching condition of direct THz-signal detection from on-chip resonating antennas with CMOS transistors in non-resonant plasma wave mode. J. Infrared Millim. Terahertz Waves 2018, 39, 521–534. [Google Scholar] [CrossRef]
- Yang, J.-R.; Lee, W.-J.; Han, S.-T. Signal-conditioning block of a 1 × 200 CMOS detector array for a terahertz real-time imaging system. Sensors 2016, 16, 319. [Google Scholar] [CrossRef] [PubMed]
- Aizin, G.R.; Dyer, G.C. Transmission line theory of collective plasma excitations in periodic two-dimensional electron systems: Finite plasmonic crystals and tamm states. Phys. Rev. B 2012, 86, 235316-1–235316-11. [Google Scholar] [CrossRef]
- Pfeiffer, U.R.; Öjefors, E. A 600-GHz CMOS Focal-Plane Array for Terahertz Imaging Applications. In Proceedings of the ESSCIRC 2008—34th European Solid-State Circuits Conference, Edinburgh, UK, 15–19 September 2008. [Google Scholar]
- Razavi, B. Design of Analog CMOS Integrated Circuits, 2nd ed.; McGraw-Hill: New York, NY, USA, 2017; pp. 23–28. [Google Scholar]
- Yang, J.-R.; Han, S.-T.; Baek, D. Differential CMOS Sub-Treahertz Detector with Subthreshold Amplifier. Sensors 2017, 17, 69. [Google Scholar] [CrossRef]
- Hadi, R.A.; Sherry, H.; Grzyb, J.; Zhao, Y.; Förster, W.; Keller, H.M.; Cathelin, A.; Kaiser, A.; Pfeiffer, U.R. A 1k-pixel video camera for 0.7–1.1 terahertz imaging applications in 65-nm CMOS. IEEE J. Solid-State Circuits 2012, 47, 2999–3012. [Google Scholar] [CrossRef]
- Boukhayma, A.; Dupret, A.; Rostaing, J.P.; Enz, C. A low-noise CMOS THz imager based on source modulation and an in-pixel high-Q passive switched-capacitor N-path filter. Sensors 2016, 16, 325. [Google Scholar] [CrossRef]
- Károlyi, G.; Gergelyi, D.; Földesy, P. Sub-THz sensor array with embedded signal processing in 90 nm CMOS technology. IEEE Sens. J. 2013, 14, 2432–2441. [Google Scholar] [CrossRef]



| Ref. | Freq. [GHz] | CMOS Technology | Responsivity 1 [KV/W] | NEP [pW/] | |
|---|---|---|---|---|---|
| [20] | 650 | 0.25 µm | 80 | 300 | |
| [28] | 856 | 65 nm | 140 | 100 | |
| [29] | 270 | 0.13 μm | 300 | 18.7 | |
| [30] | 365 | 90 nm | 1200 | 200 | |
| This work | without preamplifier | 200 | 0.25 μm | 202 | 130 |
| including preamplifier | 200 | 0.25 μm | 482 | 39.3 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Son, J.-H.; Yang, J.-R. Quasi-static Analysis Based on an Equivalent Circuit Model for a CMOS Terahertz Plasmon Detector in the Subthreshold Region. Sensors 2019, 19, 1508. https://doi.org/10.3390/s19071508
Son J-H, Yang J-R. Quasi-static Analysis Based on an Equivalent Circuit Model for a CMOS Terahertz Plasmon Detector in the Subthreshold Region. Sensors. 2019; 19(7):1508. https://doi.org/10.3390/s19071508
Chicago/Turabian StyleSon, Ju-Hee, and Jong-Ryul Yang. 2019. "Quasi-static Analysis Based on an Equivalent Circuit Model for a CMOS Terahertz Plasmon Detector in the Subthreshold Region" Sensors 19, no. 7: 1508. https://doi.org/10.3390/s19071508
APA StyleSon, J. -H., & Yang, J. -R. (2019). Quasi-static Analysis Based on an Equivalent Circuit Model for a CMOS Terahertz Plasmon Detector in the Subthreshold Region. Sensors, 19(7), 1508. https://doi.org/10.3390/s19071508






