An Fiber Bragg Grating-Based Monitoring System for Slope Deformation Studies in Geotechnical Centrifuges
Abstract
:1. Introduction
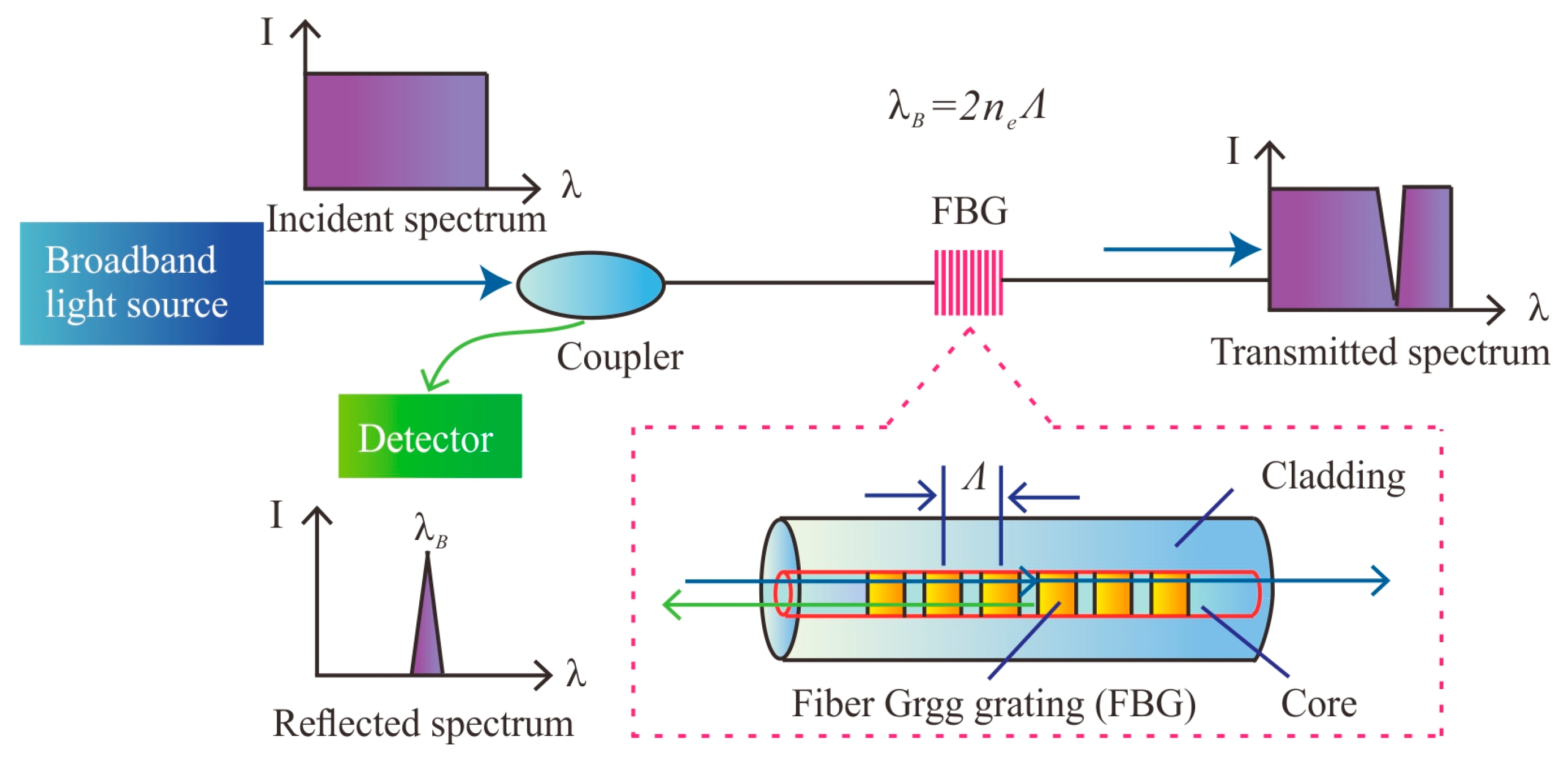
2. FBG-Based Sensors: Principle and Design
2.1. Working Principle
2.2. Sensor Design
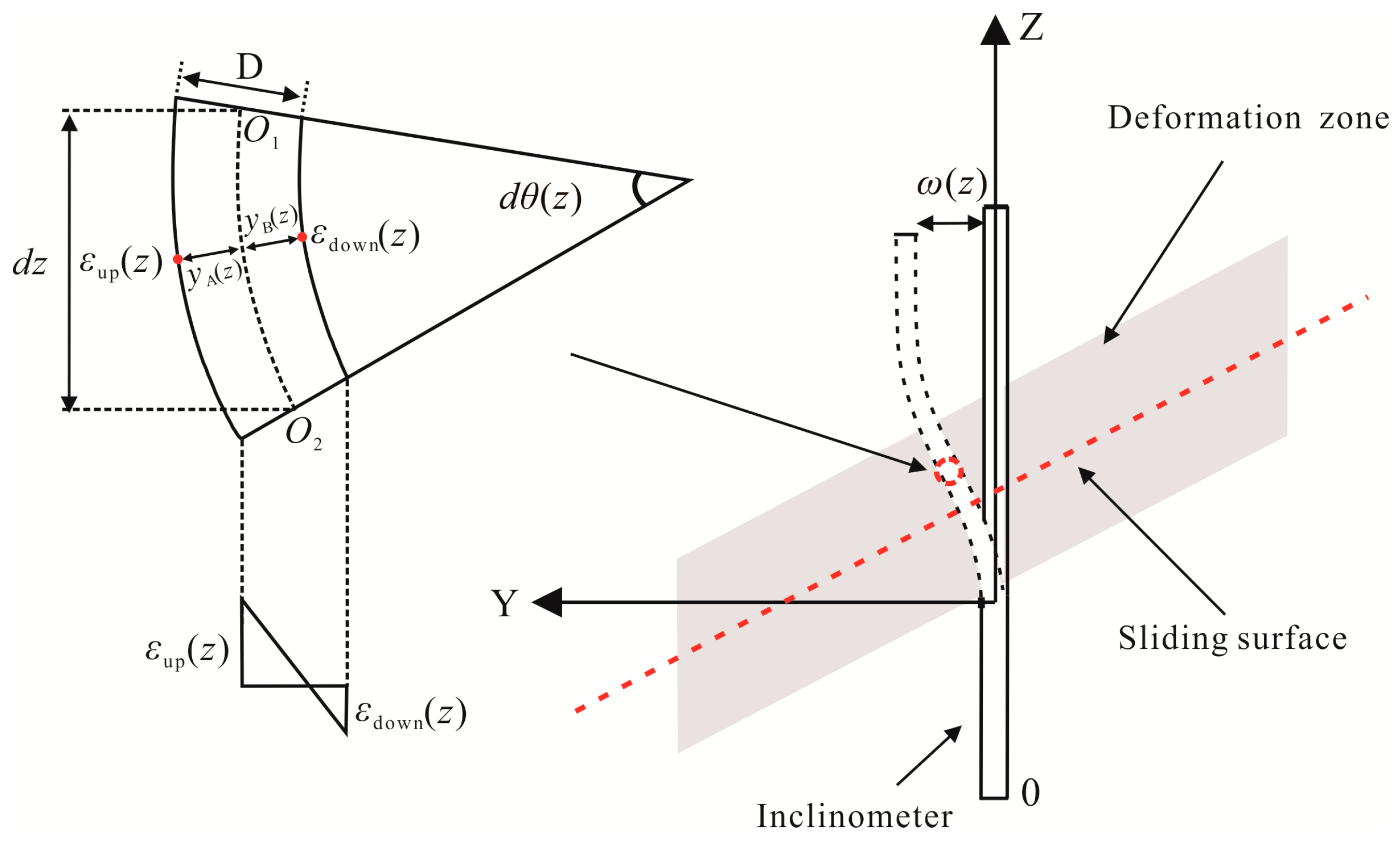
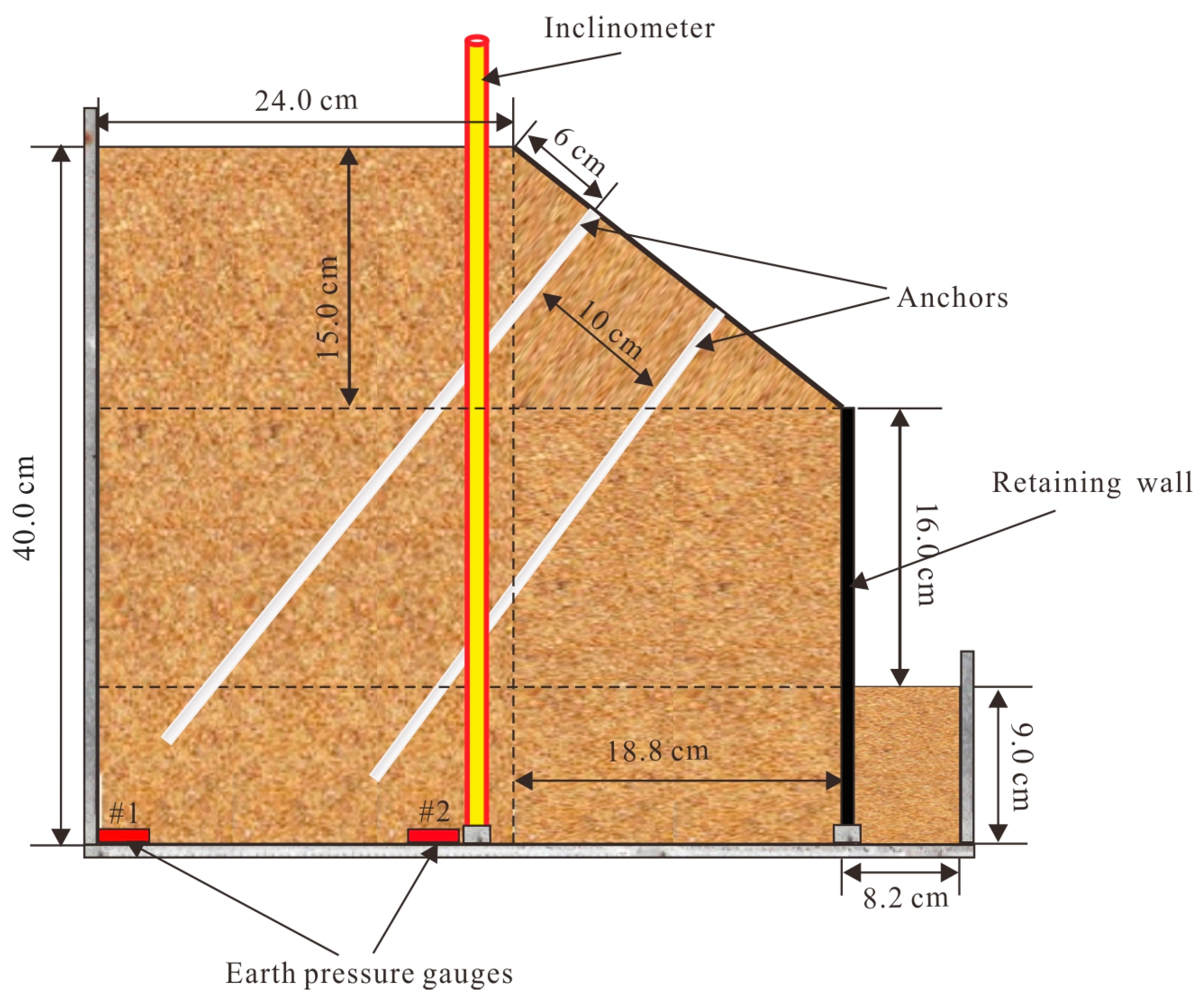
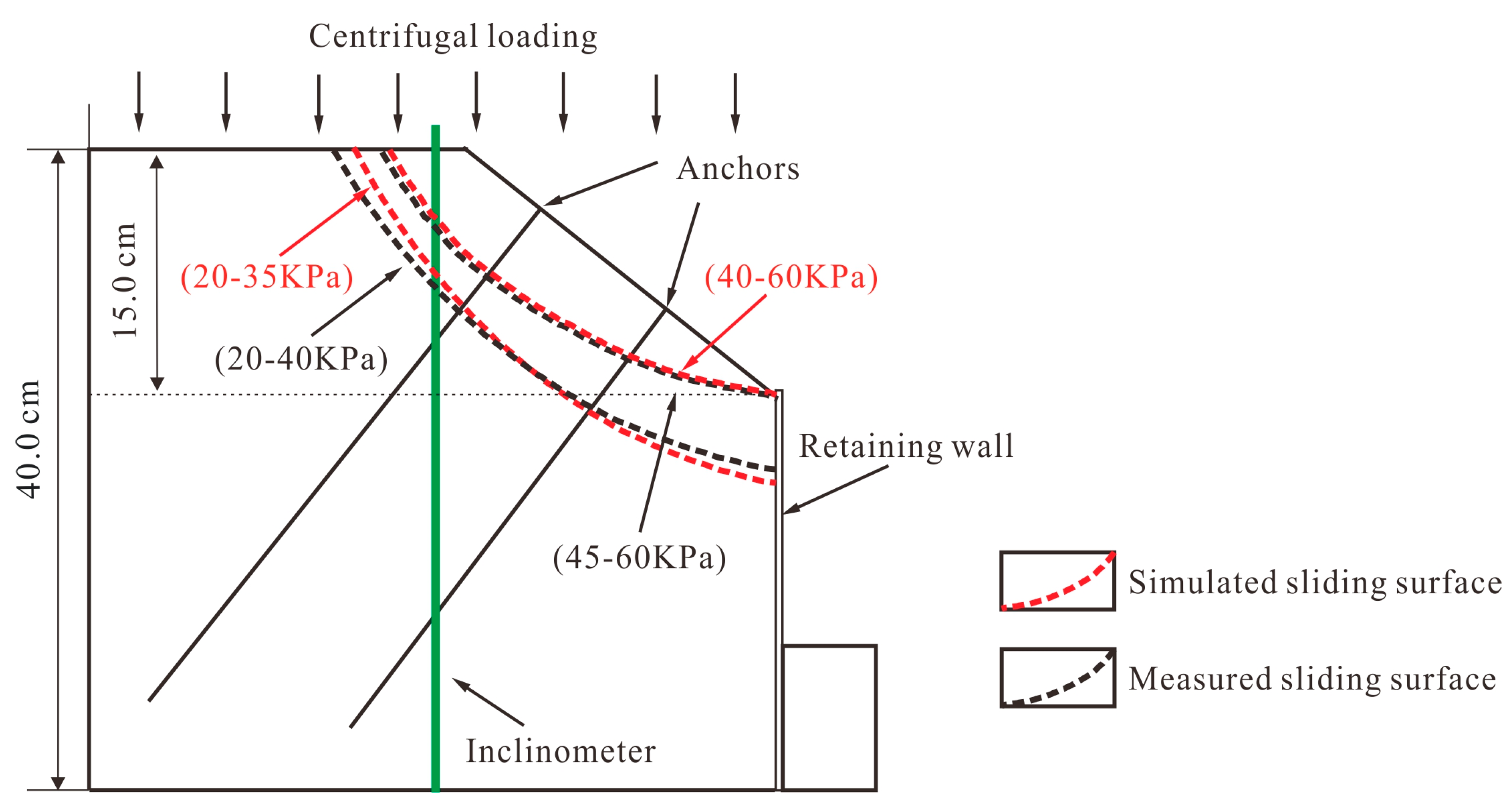
2.2.1. Anchors and Inclinometers
2.2.2. Earth Pressure Gauge and Retaining Wall
3. Laboratory Calibration
3.1. Calibration of the FBGs
3.2. Calibration of Earth Pressure Gauges and Anchors
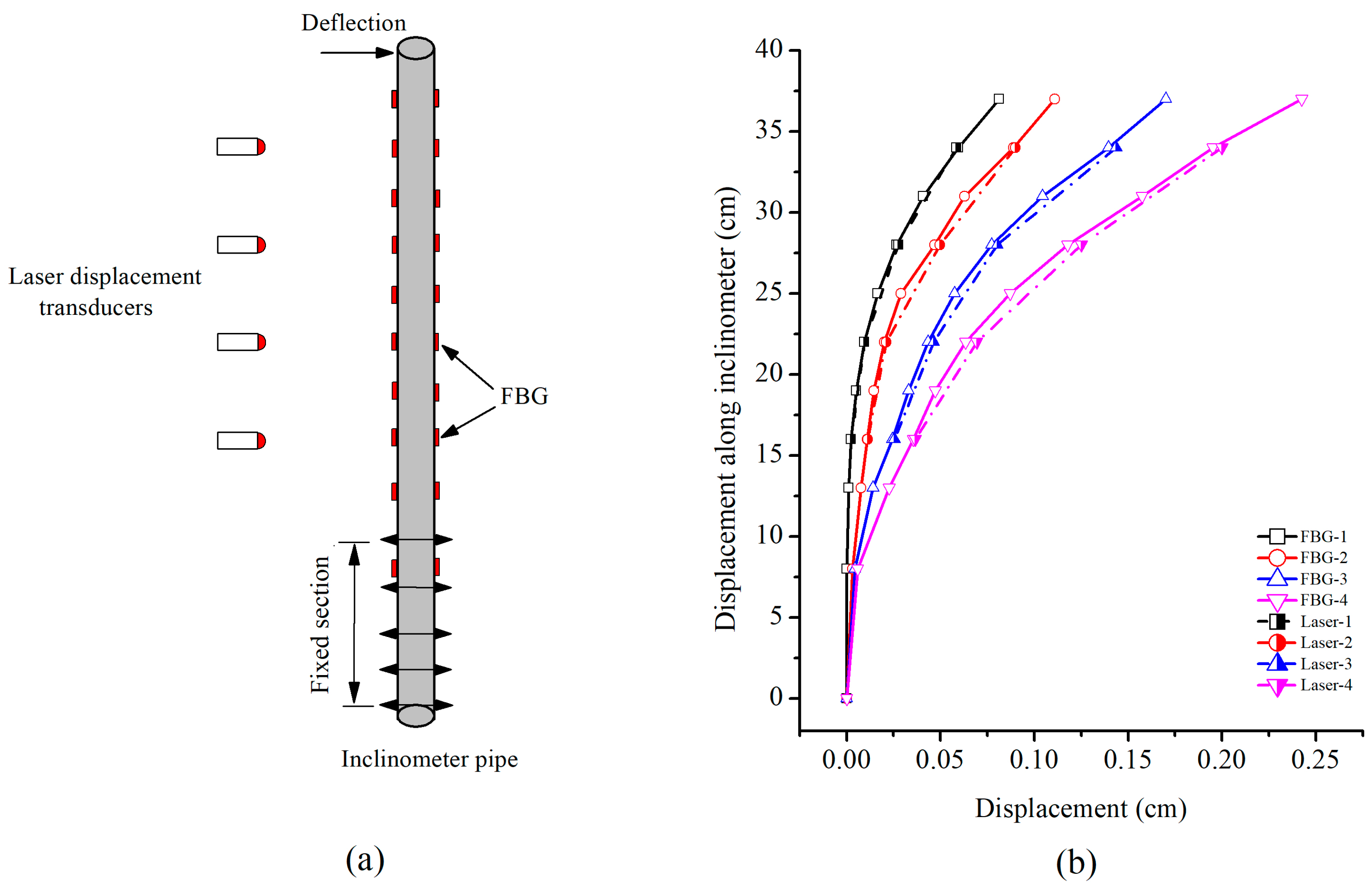
3.3. Calibration of Inclinometer Pipe
4. Centrifuge Model Test
5. Test Result and Analysis
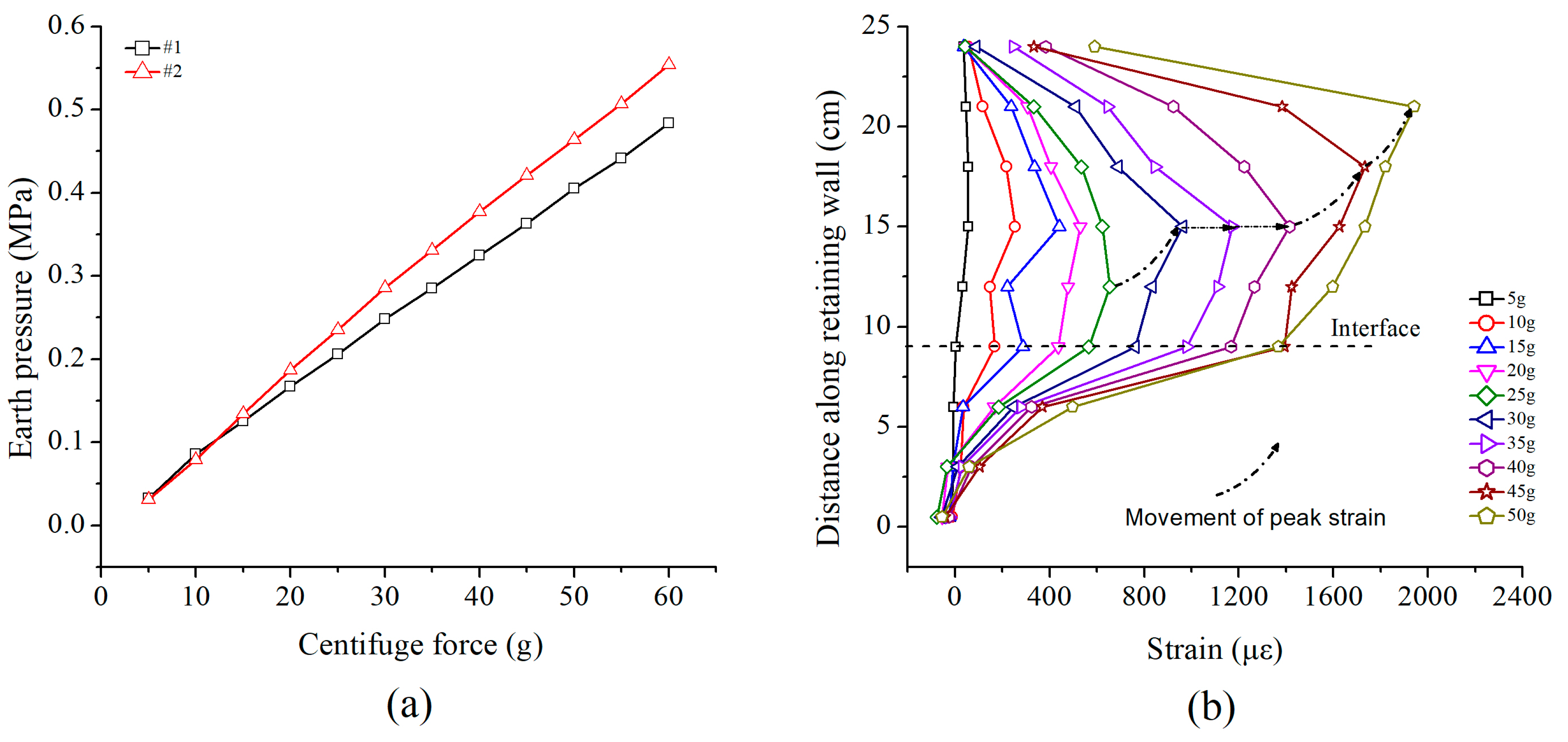
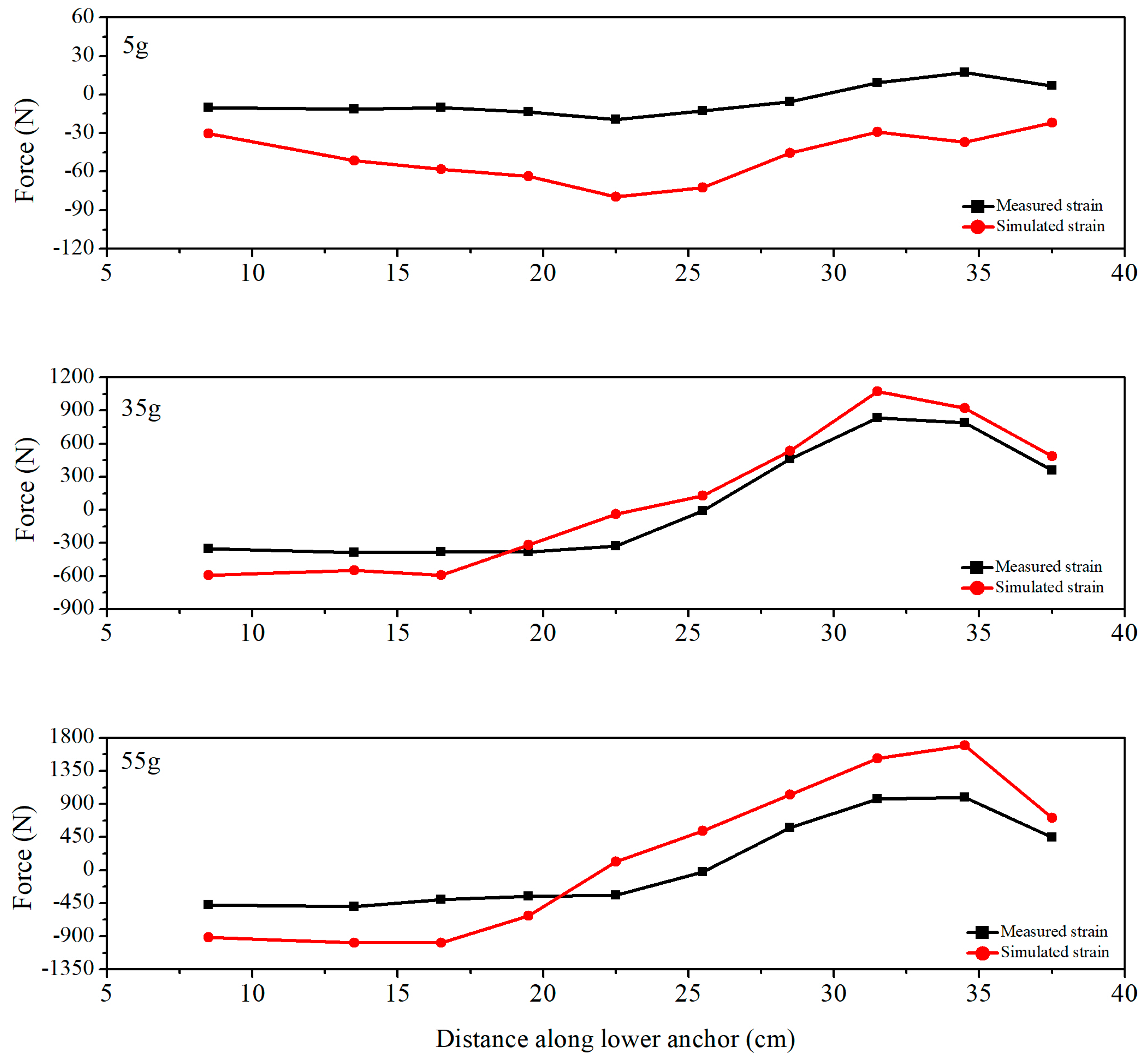
5.1. Anchors Test Result
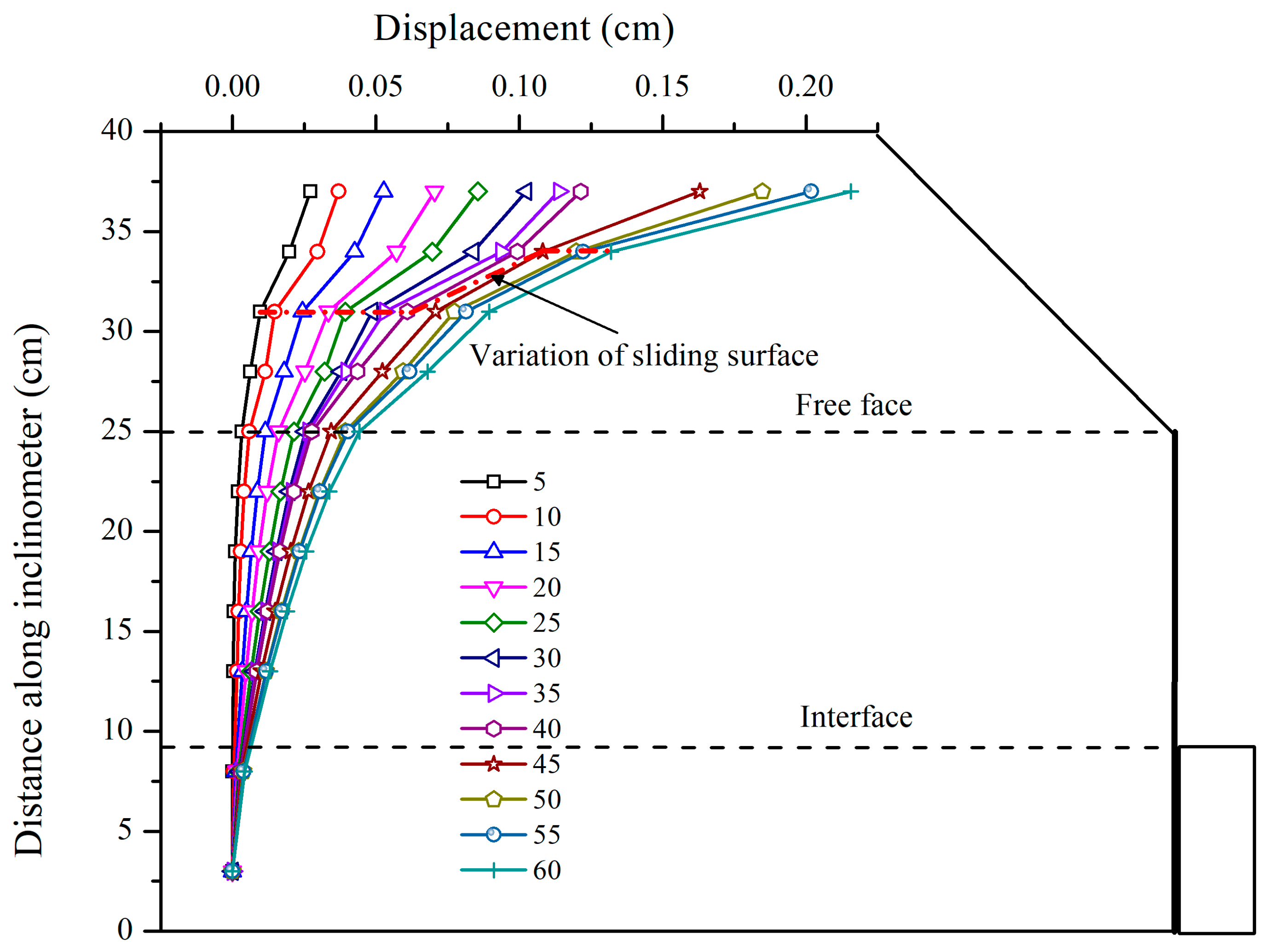
5.2. Inclinometers Test Result
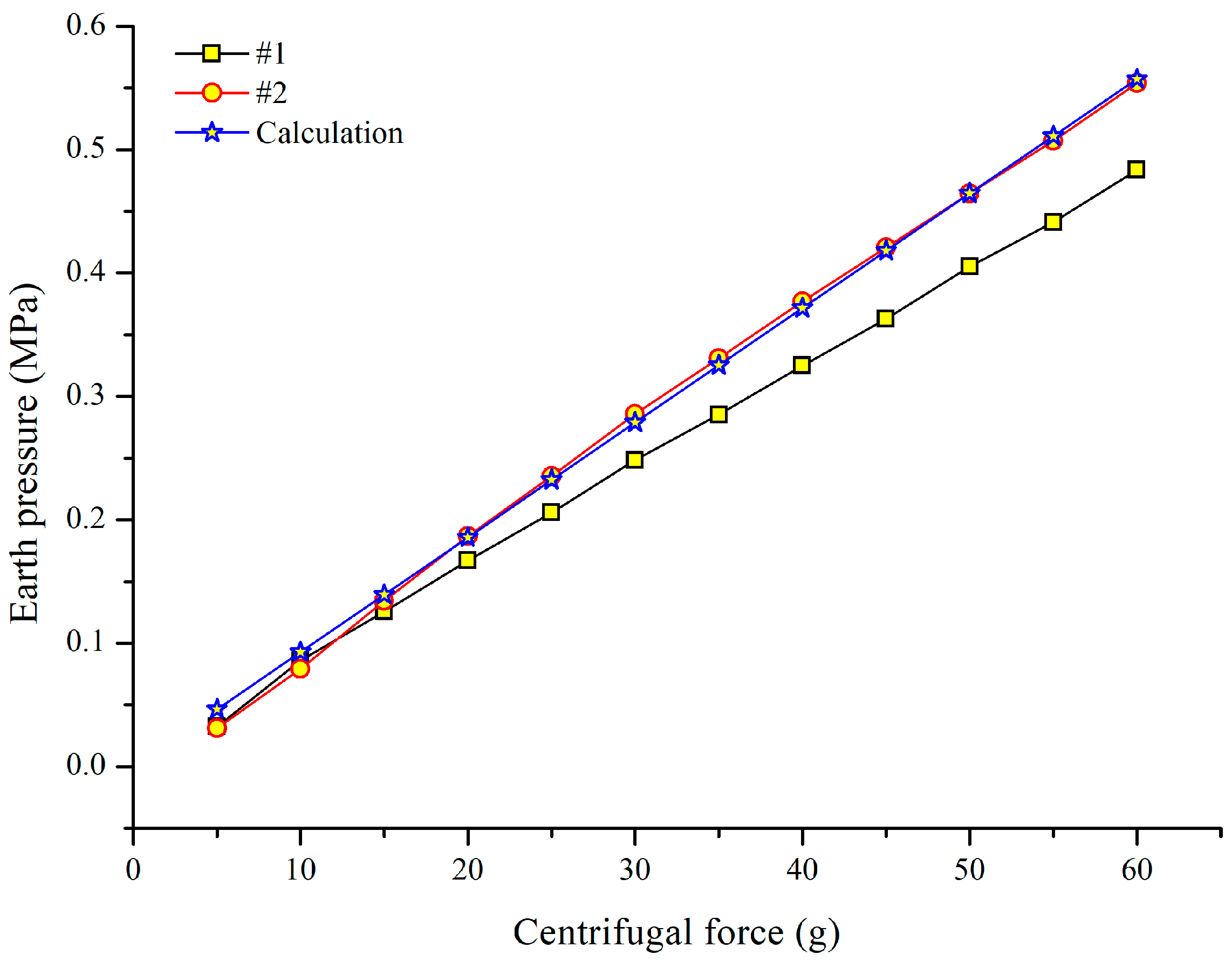
5.3. Retaining Wall and Earth Pressure Test Result
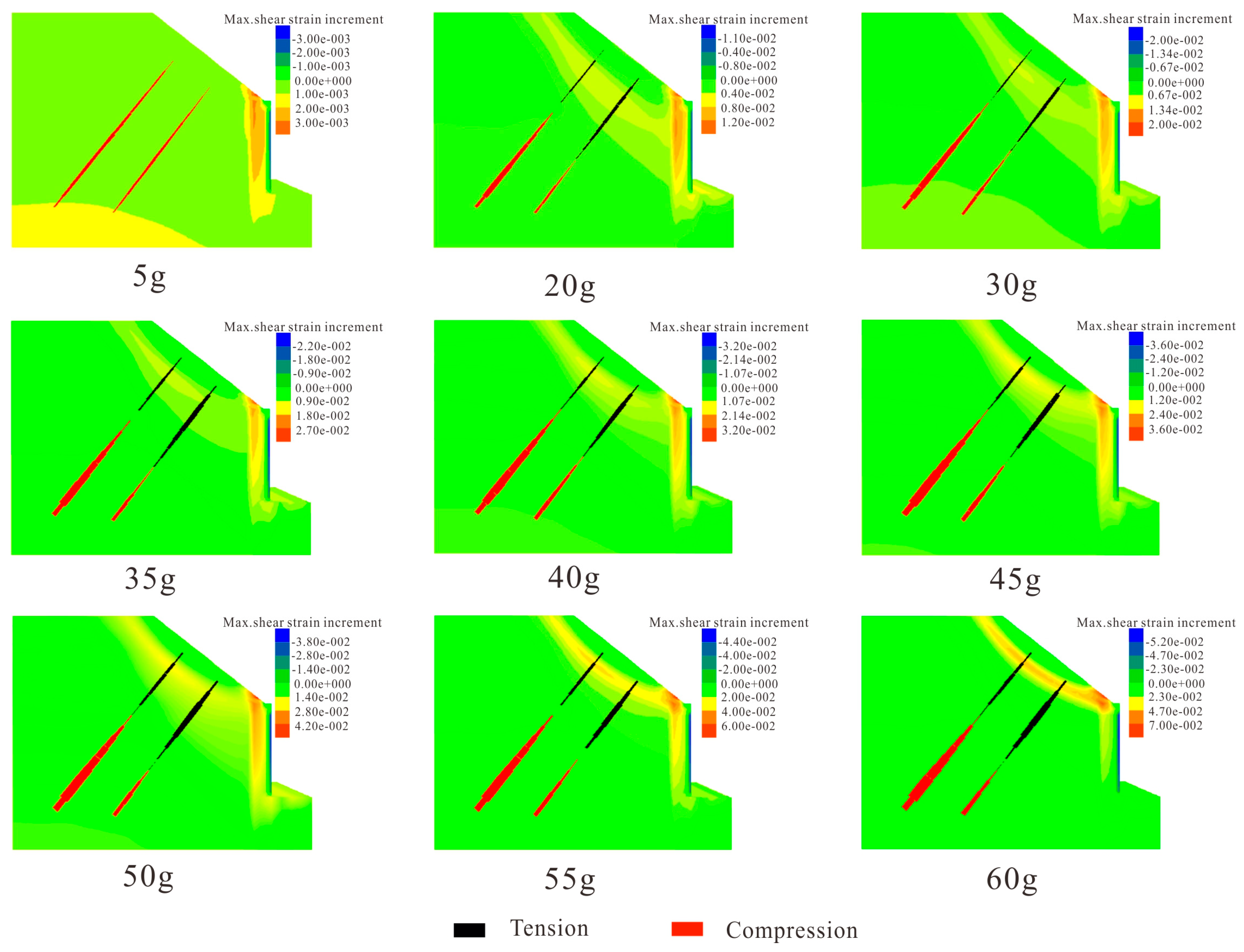
6. Discussion
7. Conclusions
- (1).
- An FBG-based monitoring system was developed. Compared to conventional sensors, the proposed system has the unique advantages of low weight, small volume, immunity to electromagnetic interference and quasi-distributed sensing, which makes it especially attractive for centrifugal tests.
- (2).
- According to the laboratory calibration test, the FBG monitoring system can monitor the multi-parameter information of the slope, including the stress (the earth pressure and anchor force), the displacement (inclinometer pipe deformation) and strain (retaining wall bending) of the model slope with high accuracy.
- (3).
- The stress state of the anchors, the strain distribution of the retaining wall together with the displacement of the inclinometer pipe depict the failure mode of the model slope, and change when increasing the centrifugal force. Furthermore, we have found that the critical centrifugal force for the transition of the sliding surface is 45 g.
- (4).
- The maximum displacement occurred at the crest of the slope, therefore the maximum deformation starting at the crest of the slope will reach the toe area gradually. Considering that the lower anchor exerts its resistance force later than the upper one, we conclude that the slope exhibits thrust load-caused deformation pattern.
- (5).
- Based on the developed FBG monitoring system, multi-parameter information of centrifugal slope can be obtained and further comprehensive analysis on evolution mechanism and stability evaluation can be carried out.
Author Contributions
Funding
Conflicts of Interest
References
- Luo, F.Y.; Zhang, G.; Liu, Y.; Ma, C. Centrifuge modeling of the geotextile reinforced slope subject to drawdown. Geotext. Geomembr. 2018, 46, 11–21. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Wang, T.; Wu, S.R.; Tang, H.M.; Liang, C.Y. Seismic performance of loess-mudstone slope in Tianshui—Centrifuge model tests and numerical analysis. Eng. Geol. 2017, 222, 225–235. [Google Scholar] [CrossRef]
- Weng, M.C.; Chen, T.C.; Tsai, S.J. Modeling scale effects on consequent slope deformation by centrifuge model tests and the discrete element method. Landslides 2017, 13, 981–993. [Google Scholar] [CrossRef]
- Fern, E.J.; De Lange, D.A.; Zwanenburg, C.; Teunissen, J.A.M.; Rohe, A.; Soga, K. Experimental and numerical investigations of dyke failures involving soft materials. Eng. Geol. 2016, 219, 130–139. [Google Scholar] [CrossRef]
- White, D.J.; Take, W.A.; Bolton, M.D. Soil Deformation Measurement Using Particle Image Velocimetry (PIV) and Photogrammetry. Géotechnique 2003, 53, 619–631. [Google Scholar] [CrossRef]
- Kruse, G.A.M.; Bezuijen, A. The use of CT scans to evaluate soil models. In Proceedings of the International Conference Centrifuge 98, Tokyo, Japan, 23–25 September 1998; pp. 79–84. [Google Scholar]
- Acosta, E.A.; Tibana, S.; de Almeida, M.D.S.S.; Saboya, F., Jr. Centrifuge modeling of hydroplaning in submarine slopes. Ocean Eng. 2017, 129, 451–458. [Google Scholar] [CrossRef]
- Zhang, G.; Hu, Y.; Zhang, J.M. New image analysis-based displacement-measurement system for geotechnical centrifuge modeling tests. Measurement 2009, 42, 87–96. [Google Scholar] [CrossRef]
- Hansen, C.; Pak, R.Y. Centrifuge Characterization of Buried, Explosive-Induced Soil Ejecta Kinematics and Crater Morphology. J. Dyn. Behav. Mater. 2016, 2, 306–325. [Google Scholar] [CrossRef] [Green Version]
- Sommers, A.N.; Viswanadham, B.V.S. Centrifuge model tests on the behavior of strip footing on geotextile-reinforced slopes. Geotext. Geomembr. 2009, 27, 497–505. [Google Scholar] [CrossRef]
- Ng, C.W.; Shi, J.; Hong, Y. Three-dimensional centrifuge modelling of basement excavation effects on an existing tunnel in dry sand. Can. Geotech. J. 2013, 50, 874–888. [Google Scholar] [CrossRef]
- Elshafie, M.Z.E.B.; Choy, C.K.C.; Mair, R.J. Centrifuge modeling of deep excavations and their interaction with adjacent buildings. Geotech. Test. J. 2013, 36, 637–648. [Google Scholar] [CrossRef]
- Zhu, H.H.; Shi, B.; Zhang, C.C. FBG-Based Monitoring of Geohazards: Current Status and Trends. Sensors 2017, 17, 452. [Google Scholar] [CrossRef]
- Bao, X.Y.; Chen, L. Recent progress in distributed fiber optic sensors. Sensors 2012, 12, 8601–8639. [Google Scholar] [CrossRef]
- Damiano, E.; Avolio, B.; Minardo, A.; Olivares, L.; Picarelli, L.; Zeni, L. A laboratory study on the use of optical fibers for early detection of pre-failure slope movements in shallow granular soil deposits. Geotech. Test. J. 2017, 40, 529–541. [Google Scholar] [CrossRef]
- Habel, W.R.; Krebber, K. Fiber-optic sensor applications in civil and geotechnical engineering. Photonic Sens. 2011, 1, 268–280. [Google Scholar] [CrossRef] [Green Version]
- Dou, Z.W.; Li, H. The Slope Disaster Early Warning System of Fiber Bragg Grating Anchor Bar Sensor Based On RFID. Appl. Math. Inf. Sci. 2013, 7, 1–4. [Google Scholar] [CrossRef]
- Correia, R.; Li, J.; Staines, S.; Chehura, E.; James, S.W.; Kutner, J.; Dewhurst, P.; Ferreira, P.; Tatam, R.P. Fibre Bragg grating based effective soil pressure sensor for geotechnical applications. Proc. SPIE 2009, 7503, 75030F. [Google Scholar]
- Zhu, H.H.; Shi, B.; Yan, J.F.; Zhang, J.; Wang, J. Investigation of the evolutionary process of a reinforced model slope using a fiber-optic monitoring network. Eng. Geol. 2015, 186, 34–43. [Google Scholar] [CrossRef]
- Hong, C.Y.; Zhang, Y.F.; Zhang, M.X.; Leung, L.M.G.; Liu, L.Q. Application of FBG sensors for geotechnical health monitoring, a review of sensor design, implementation methods and packaging techniques. Sens. Actuators A-Phys. 2016, 244, 184–197. [Google Scholar] [CrossRef]
- Zhang, D.; Xu, Q.; Bezuijen, A.; Zheng, G.; Wang, H.X. Internal deformation monitoring for centrifuge slope model with embedded FBG arrays. Landslides 2016, 14, 407–417. [Google Scholar] [CrossRef] [Green Version]
- Weng, X.L.; Chen, J.; Wang, J. Fiber Bragg grating-based performance monitoring of piles fiber in a geotechnical centrifugal model test. Adv. Mater. Sci. Eng. 2014, 659276. [Google Scholar] [CrossRef]
- Guo, Y.X.; Fu, J.J.; Li, L.Q.; Li, X. Fiber Bragg grating sensor-based monitoring strategy for slope deformation in centrifugal model test. Sens. Rev. 2018, 39, 71–77. [Google Scholar] [CrossRef]
- Sun, Y.J.; Zhang, D.; Shi, B.; Tong, H.J.; Wei, G.Q.; Wang, X. Distributed acquisition, characterization and process analysis of multi-field information in slopes. Eng. Geol. 2014, 182, 49–62. [Google Scholar] [CrossRef]
- Hill, K.O.; Fujii, Y.; Johnson, D.C.; Kawasaki, B.S. Photosensitivity in optical fiber waveguides: Application to reflection filter fabrication. Appl. Phys. Lett. 2008, 32, 647–649. [Google Scholar] [CrossRef]
- Huang, X.F.; Sheng, D.R.; Cen, K.F.; Zhou, H. Low-cost relative humidity sensor based on thermoplastic polyimide-coated fiber Bragg grating. Sens. Actuators B Chem. 2007, 127, 518–524. [Google Scholar] [CrossRef]
- Wei, G.Q.; Shi, B.; Jia, J.X.; Hu, S.; Li, K.; Zhang, D. Application of distributed optical fiber sensing to testing inner force of prefabricated piles. Chin. J. Geotech. Eng. 2009, 31, 911–916. (In Chinese) [Google Scholar]
- Sun, Y.J.; Shi, B.; Zhang, D.; Tong, H.J. Internal Deformation Monitoring of Slope Based on BOTDR. J. Sens. 2016, 2016, 9496285. [Google Scholar] [CrossRef]
- Zhang, Q.H.; Wang, Y.; Sun, Y.Y.; Gao, L.; Zhang, Z.L.; Zhang, W.Y.; Zhao, P.C.; Yue, Y. Using custom fiber Bragg grating-based sensors to monitor artificial landslides. Sensors 2016, 16, 1417. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Hu, Y.; Wang, L.P. Behaviour and mechanism of failure process of soil slopes. Environ. Earth Sci. 2015, 73, 1701–1713. [Google Scholar] [CrossRef]
- Li, L.Q.; Ju, N.P.; Guo, Y.X. Effectiveness of Fiber Bragg Grating monitoring in the centrifugal model test of soil slope under rainfall conditions. J. Mt. Sci. 2017, 5, 130–141. [Google Scholar] [CrossRef]
- Schofield, A.N. Cambridge Geotechnical Centrifuge Operations. Geotechnique 1980, 30, 227–268. [Google Scholar] [CrossRef]






| Unit Weight Γ (kN/m3) | Elastic Modulus E (MPa) | Poisson’s Ratio | Friction Angle Φ (°) | Cohesion C (kPa) |
|---|---|---|---|---|
| 19.8 | 58 | 0.3 | 25.4 | 5.2 |
| Material | Bulk Modulus K (MPa) | Shear Modulus G (MPa) |
|---|---|---|
| Plexiglass | 870 | 430 |
| Material | Elastic Modulus E (GPa) | Tensile Strength (MPa) |
|---|---|---|
| Steel | 95 | 600 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Shi, B.; Zeni, L.; Minardo, A.; Zhu, H.; Jia, L. An Fiber Bragg Grating-Based Monitoring System for Slope Deformation Studies in Geotechnical Centrifuges. Sensors 2019, 19, 1591. https://doi.org/10.3390/s19071591
Zhang L, Shi B, Zeni L, Minardo A, Zhu H, Jia L. An Fiber Bragg Grating-Based Monitoring System for Slope Deformation Studies in Geotechnical Centrifuges. Sensors. 2019; 19(7):1591. https://doi.org/10.3390/s19071591
Chicago/Turabian StyleZhang, Lei, Bin Shi, Luigi Zeni, Aldo Minardo, Honghu Zhu, and Lixiang Jia. 2019. "An Fiber Bragg Grating-Based Monitoring System for Slope Deformation Studies in Geotechnical Centrifuges" Sensors 19, no. 7: 1591. https://doi.org/10.3390/s19071591
APA StyleZhang, L., Shi, B., Zeni, L., Minardo, A., Zhu, H., & Jia, L. (2019). An Fiber Bragg Grating-Based Monitoring System for Slope Deformation Studies in Geotechnical Centrifuges. Sensors, 19(7), 1591. https://doi.org/10.3390/s19071591









