The Synthesis Model of Flat-Electrode Hemispherical Resonator Gyro
Abstract
1. Introduction
2. Motion Equations of Hemispherical Shell Resonator
2.1. Motion Equations of Ideal Hemispherical Shell Resonator
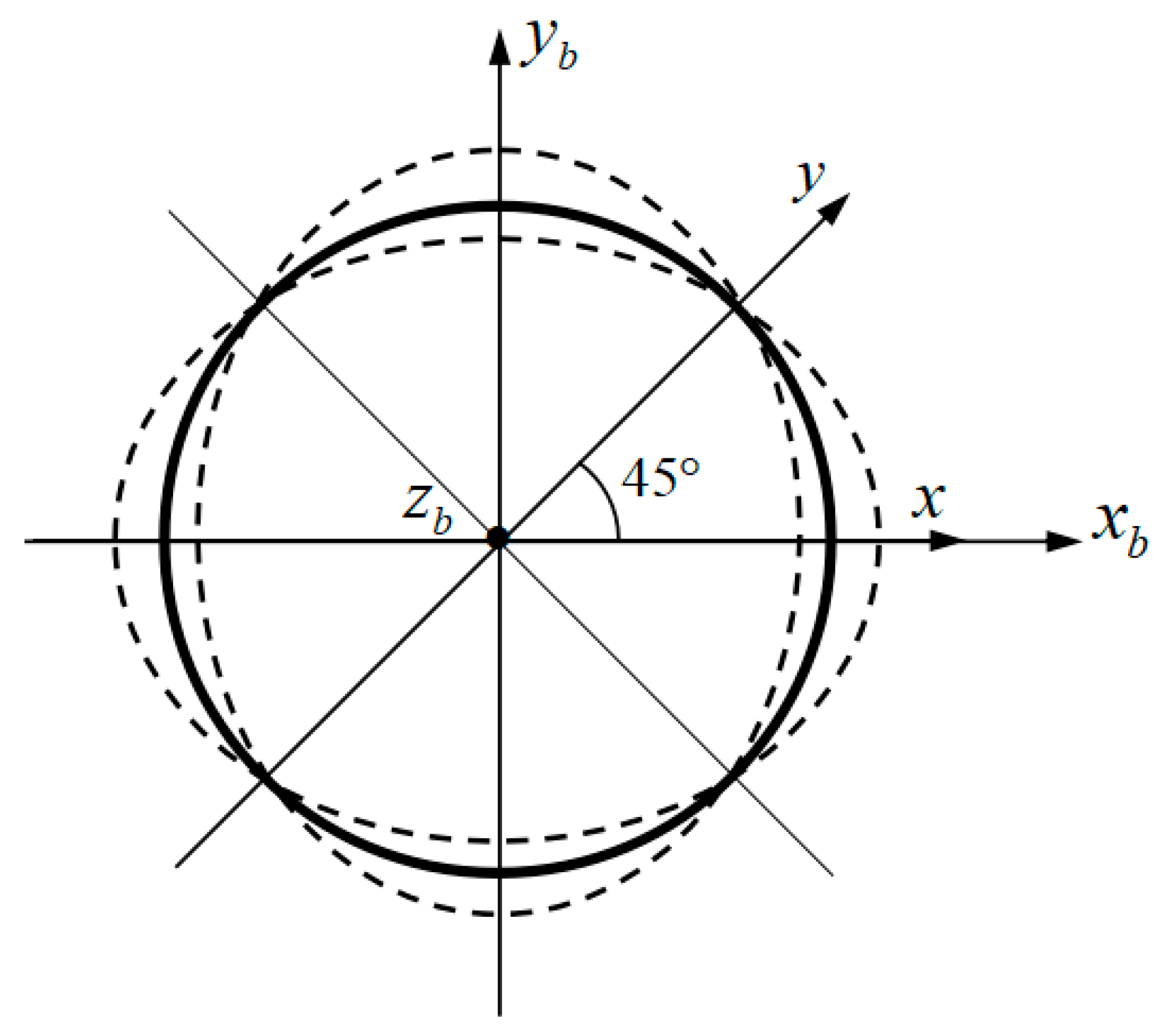
- Orthogonal Curvilinear Coordinate System : Origin is located on , axis is perpendicular to , axes , lie in , and axes , , are orthogonal to each other.
- Middle Surface Coordinate System : Origin is located on , axes , , are parallel to the tangential directions of axes , , , respectively.
- Shell Coordinate System : Origin is located at the centre of the circular opening of shell, axis is coincident with the shell symmetry axis, axes , lie in the circular opening mentioned above, and axes , , are orthogonal to each other and fixed with the shell.
- Rotation Coordinate System : Origin P is located at the centre of the circular opening of shell, axes , , are parallel to axes , , .
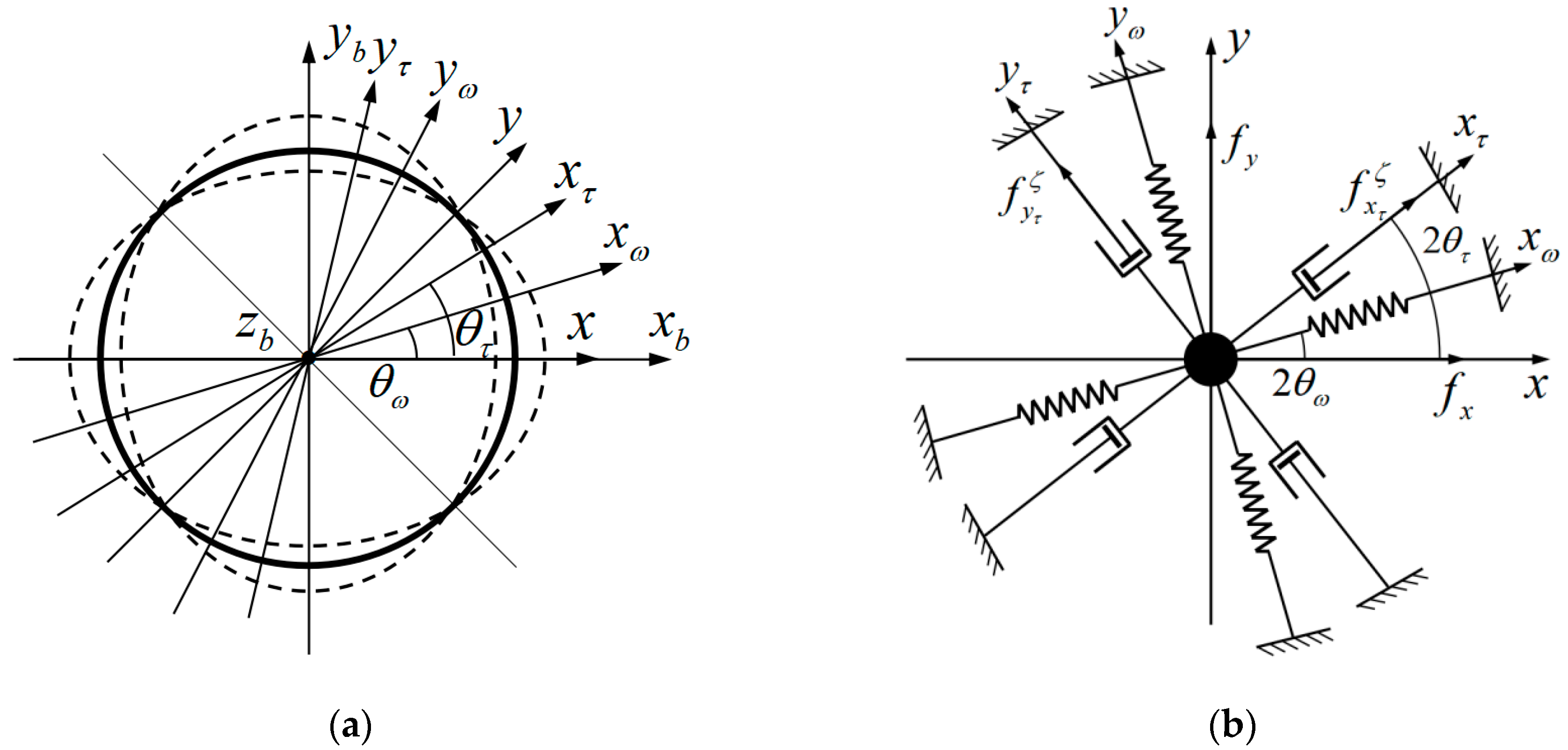
2.2. Effects of Inherent Frequency Axis and Inherent Damping Axis
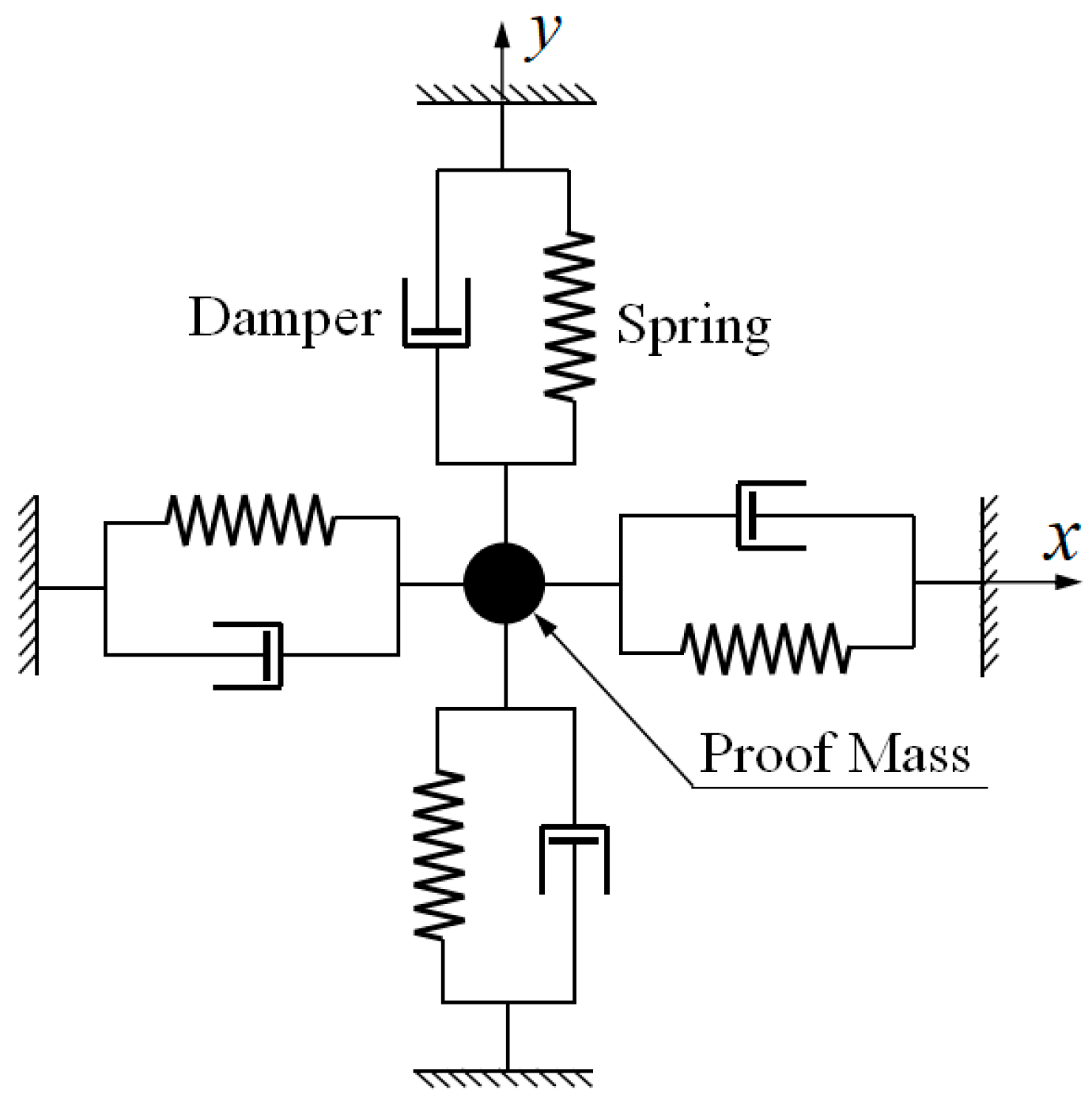
2.3. Effects of External Control Force
3. Excitation and Detection Models
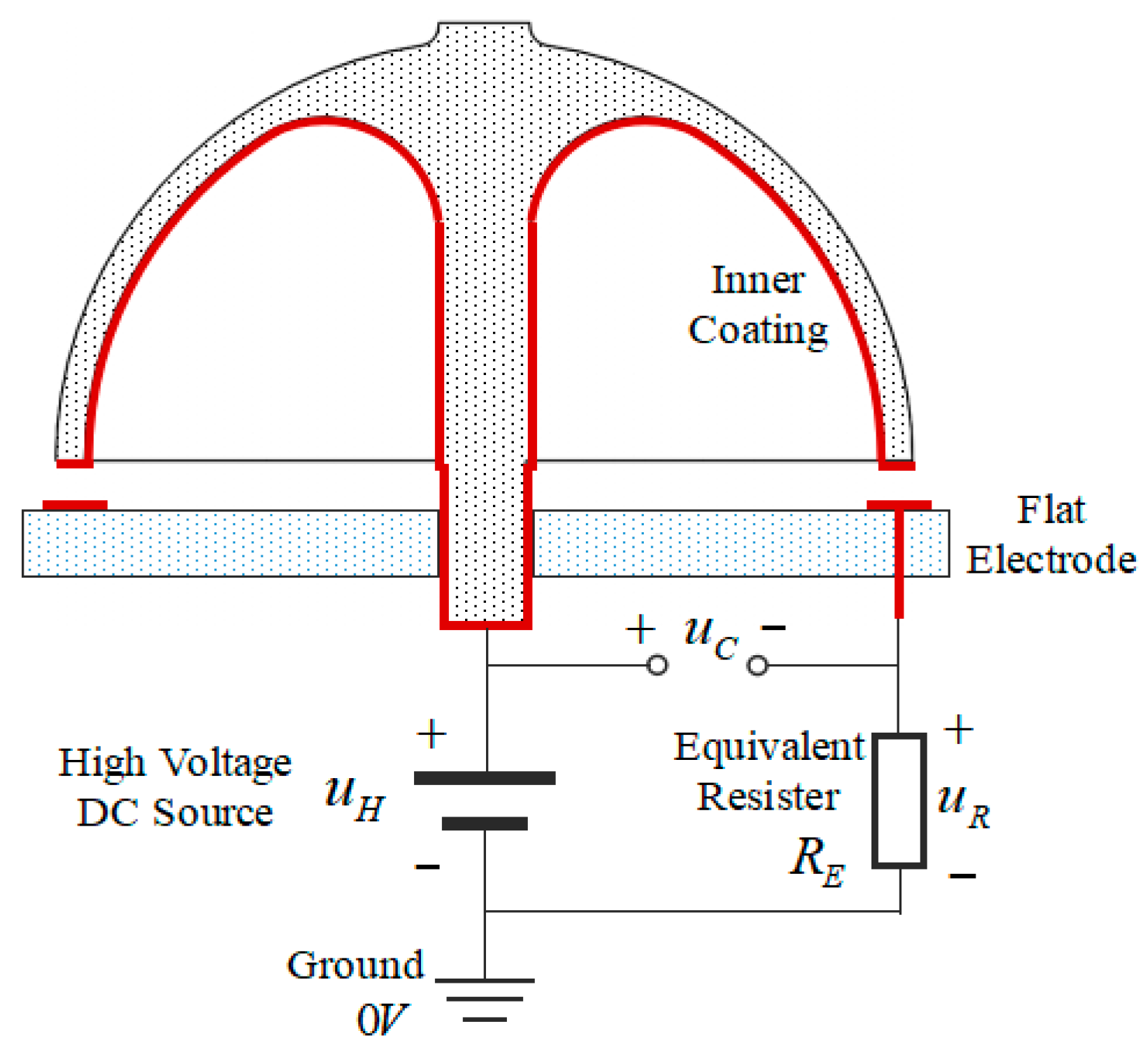
3.1. Capacitor Structure
3.2. Capacitor Model
3.3. Excitation Model
3.4. Detection Model
4. Identification of Assemble Errors and Parameters
4.1. Approximate Identification Model
4.2. Identification Method of Assemble Errors and Parameters
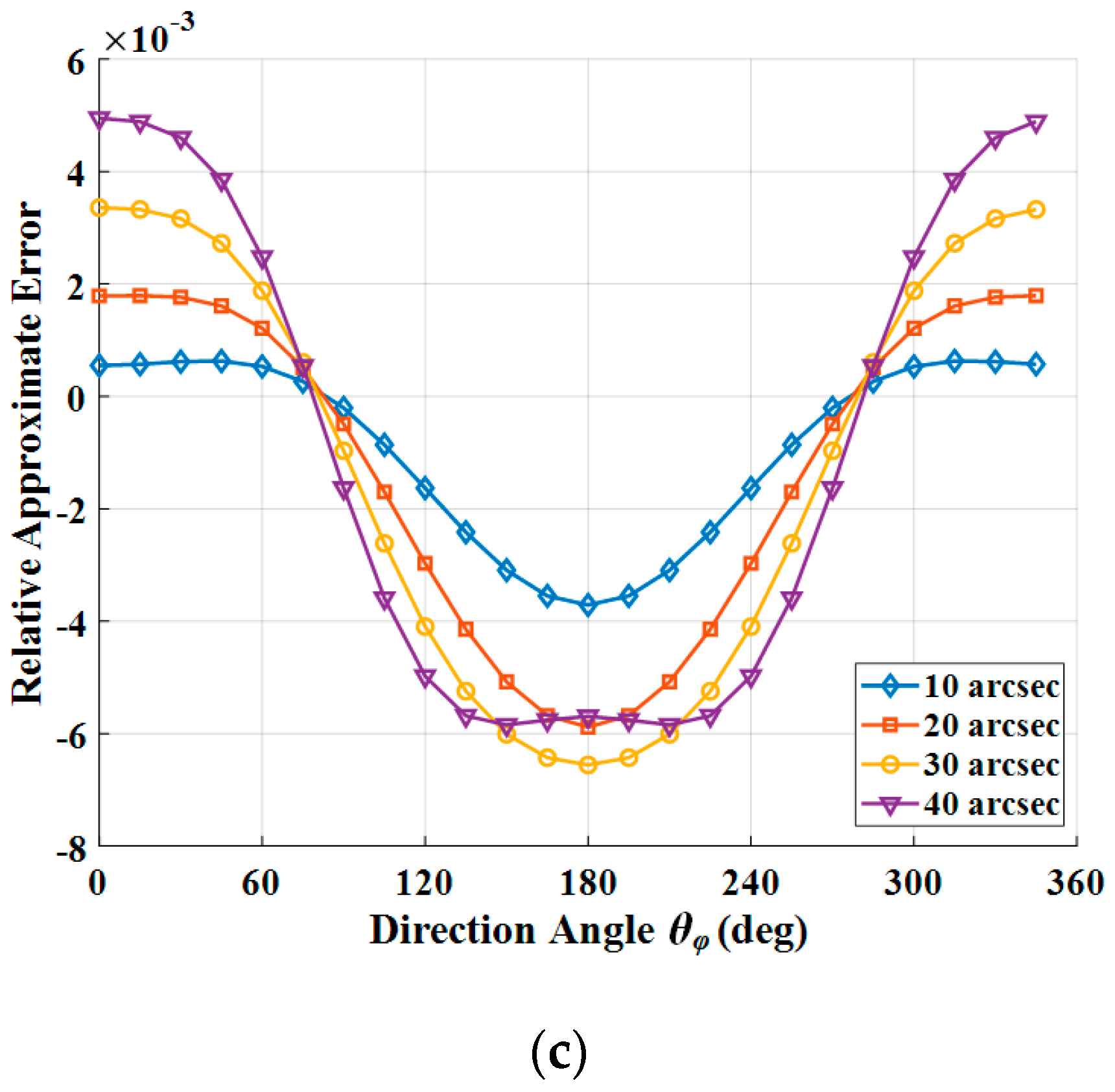
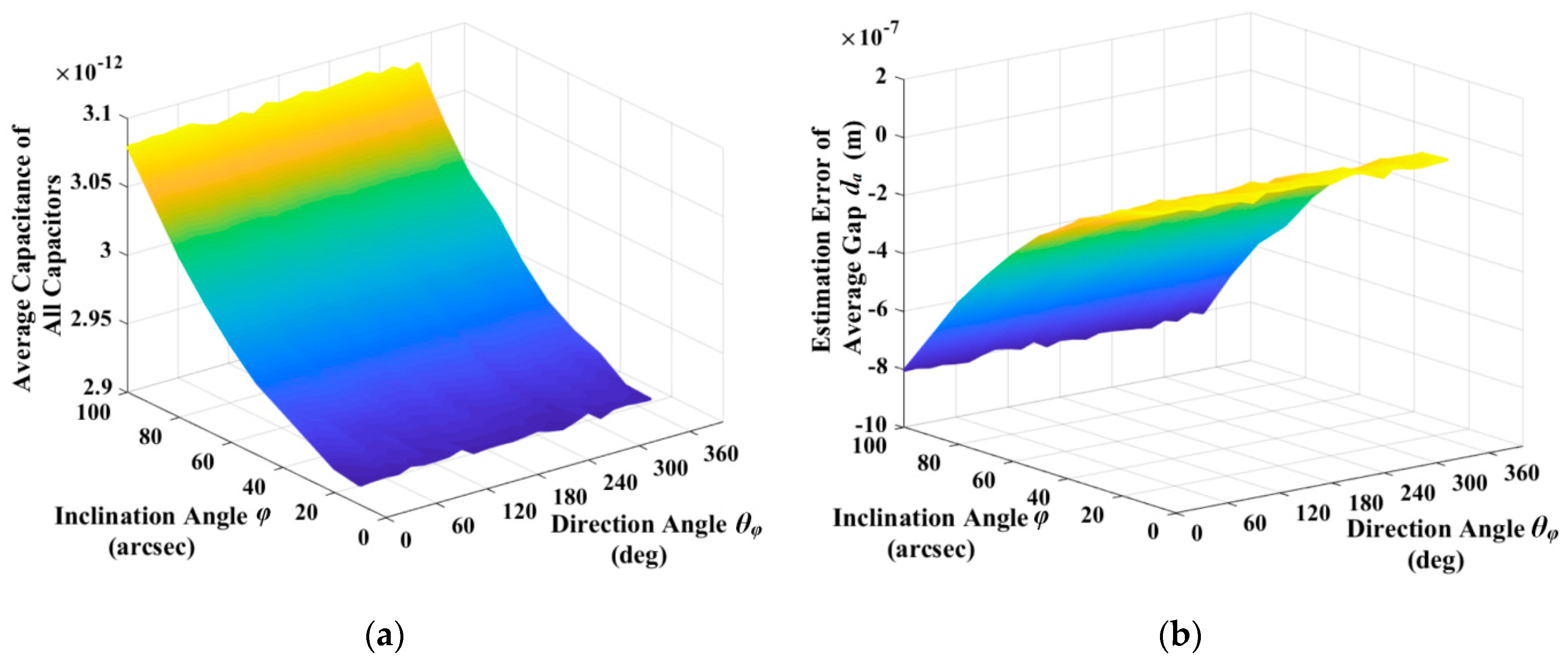
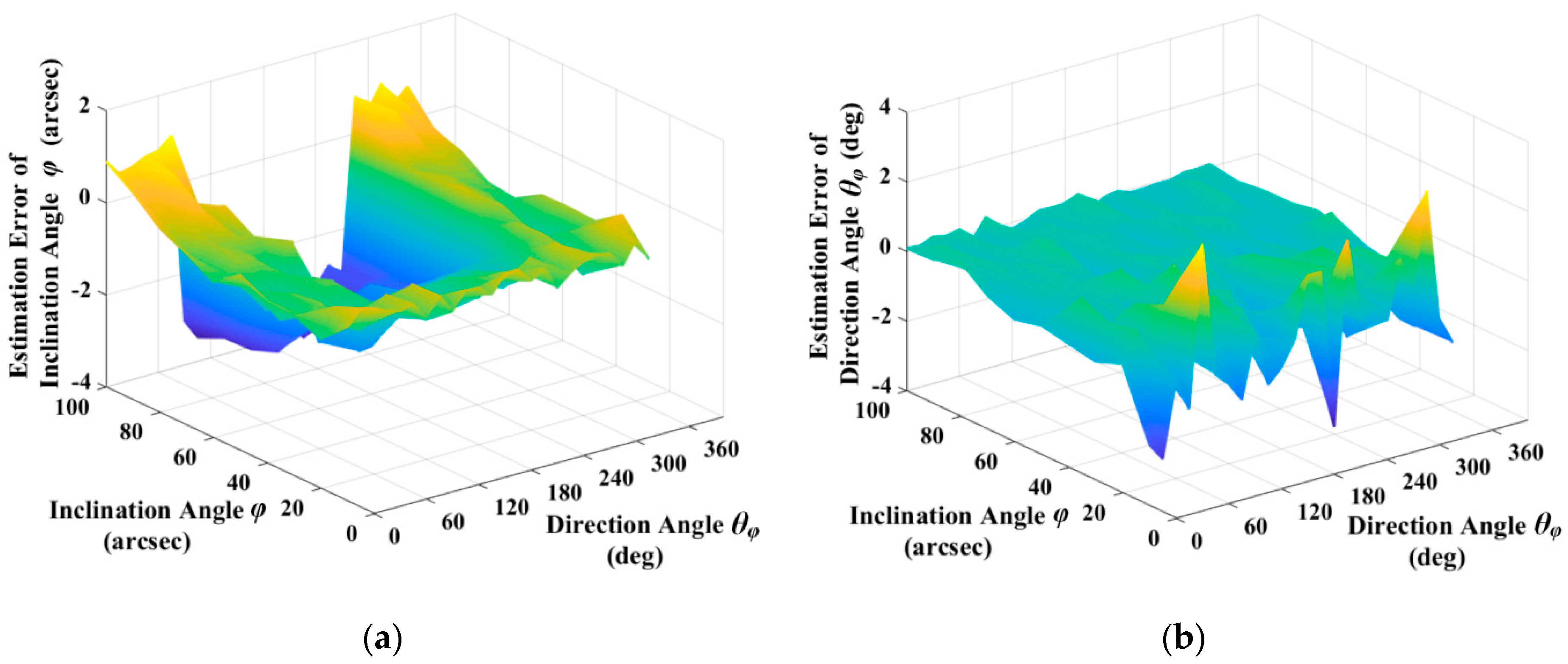
4.3. Analysis of Simulation Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rozelle, D. The Hemispherical Resonator Gyro: From Wineglass to the Planets. In Proceedings of the 19th AAS/AIAA Space Flight Mechanics Meeting, Savannah, Georgia, 8–12 February 2009; pp. 1157–1178. [Google Scholar]
- Delhaye, F.; Girault, J.P. SpaceNaute®: HRG Technological Breakthrough for Advanced Space Launcher Inertial Reference System. In Proceedings of the 2018 25th Saint Petersburg International Conference on Integrated Navigation Systems, St. Petersburg, Russia, 28–30 May 2018; pp. 1–5. [Google Scholar]
- Girard, O.; Caron, J.M.; Berthier, P. HRG Technology: A Promising Gyrometer Space Equipment. In Proceedings of the 6th International ESA Conference on Guidance, Navigation and Control Systems, Loutraki, Greece, 17–20 October 2005; Volume 606. [Google Scholar]
- Burrough, E.L.; Lee, A.Y. In-flight Characterization of Cassini Inertial Reference Units. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit 2007, Hilton Head, SC, USA, 20–23 August 2007; Volume 6340. [Google Scholar]
- Brown, T.S. In-Flight Performance of the Cassini Hemispherical Quartz Resonator Gyro Inertial Reference Units. In Proceedings of the AIAA Guidance, Navigation, and Control (GNC) Conference 2013, Boston, MA, USA, 19–22 August 2013; Volume 4630. [Google Scholar]
- Jeanroy, A.; Grosset, G.; Goudon, J.C.; Delhaye, F. HRG by Sagem From Laboratory to Mass Production. In Proceedings of the 2016 IEEE International Symposium on Inertial Sensors and Systems 2016, Laguna Beach, CA, USA, 22–25 February 2016; pp. 1–4. [Google Scholar]
- Vandebeuque, P. Gyroscopic Sensor and Method for Manufacturing Such a Sensor. U.S. Patent 9,068,833, 30 June 2015. [Google Scholar]
- Jeanroy, A.; Leger, P. Gyroscopic Sensor and Rotation Measurement Apparatus Constituting an Application Thereof. U.S. Patent 6,474,161, 5 November 2002. [Google Scholar]
- Jeanroy, A. Gyroscopic Sensor. U.S. Patent 6,662,656, 16 December 2003. [Google Scholar]
- Lynch, D.D. Bell Gyro and Improved Means for Operating Same. U.S. Patent 3,656,354, 18 April 1972. [Google Scholar]
- Matthews, A.; Varty, G.T. Method and Apparatus for Generating Driving Signals for a Vibratory Rotation Sensor. U.S. Patent 6,079,270, 27 June 2000. [Google Scholar]
- Loper, E.J., Jr.; Lynch, D.D. Sonic Vibrating Bell Gyro. U.S. Patent 4,157,041, 5 June 1979. [Google Scholar]
- Delhaye, F. HRG by SAFRAN: The Game-Changing Technology. In Proceedings of the 2018 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL) 2018, Moltrasio, Italy, 26–29 March 2018; pp. 1–4. [Google Scholar]
- Lynch, D.D. Vibratory Gyro Analysis by the Method of Averaging. In Proceedings of the 2nd St. Petersburg Conference on Gyroscopic Technology and Navigation, St. Petersburg, Russia, 24–25 May 1995; pp. 26–34. [Google Scholar]
- IEEE Standard Specification Format Guide and Test Procedure for Coriolis Vibratory Gyros. Available online: https://ieeexplore.ieee.org/servlet/opac?punumber=9606 (accessed on 8 April 2019).
- Apostolyuk, V. Coriolis Vibratory Gyroscopes Theory and Design, 1st ed.; Springer International Publishing: New York, NY, USA, 2016. [Google Scholar]
- Shatalov, M.Y.; Joubert, S.V.; Coetzee, C.E.; Fedotov, I.A. Free Vibration of Rotating Hollow Spheres Containing Acoustic Media. J. Sound Vib. 2009, 322, 1038–1047. [Google Scholar] [CrossRef]
- Gao, S. Analysis and Design of Hemispherical Resonator Gyro. Ph.D. Thesis, Harbin Engineering University, Harbin, China, June 2008. (In Chinese). [Google Scholar]
- Li, W. Measurement Method and Error Mechanism Analysis of Hemispherical Resonator Gyro. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, November 2013. (In Chinese). [Google Scholar]
- Zhao, H.; Ren, S.; Li, W. Establishment of Dynamics Equation of HRG Resonator and Calculation of Natural Frequency. J. Harbin Inst. Technol. 2010, 42, 1702–1706. (In Chinese) [Google Scholar]
- Yu, B.; Fang, Z.; Jiang, C. Finite Element Analysis Based on Optimized HRG Resonator. Piezoelectr. Acoustoopt. 2015, 37, 561–564. (In Chinese) [Google Scholar]
- Li, W. Measurement Error Analysis of Hemisphere Resonant Gyro. Master’s Thesis, Chongqing University, Chongqing, China, May 2010. (In Chinese). [Google Scholar]
- Shen, B. Satellite Attitude Determination Based on HRG and Star Sensor. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, September 2010. (In Chinese). [Google Scholar]
- Wang, X. Error Modeling Compensation and Forces to Rebalannce Control Methods Study for Hemispherical Resonator Gyro. Ph.D. Thesis, National University of Defense Technology, Hunan, China, September 2012. (In Chinese). [Google Scholar]
- Wang, X.; Wu, W.; Luo, B.; Fang, Z.; Li, Y.; Jiang, Q. Force to Rebalance Control of HRG and Suppression of Its Errors on the Basis of FPGA. Sensors 2011, 11, 11761–11773. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Yun, S.W.; Rhim, J. Design and Verification of a Digital Controller for a 2-Piece Hemispherical Resonator Gyroscope. Sensors 2016, 16, 555. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Lin, J.; Cao, M. Theory of Plates and Shells, 1st ed.; Zhejiang University Press: Zhejiang, China, 1987. (In Chinese) [Google Scholar]
- Matveev, V.A.; Lipatnikov, V.I.; Alekin, A.V.; Basarab, M.A.; Kravchenko, V.F. Solid State Wave Gyro (Translated essays), 1st ed.; National Defense Industry Press: Beijing, China, 2009. (In Chinese) [Google Scholar]
- Qin, Y. Inertial Navigation, 2nd ed.; Science Press: Beijing, China, 2014. (In Chinese) [Google Scholar]
- Ji, W.; Fang, T.; Chen, S. Mechanical Vibration, 1st ed.; Science Press: Beijing, China, 1985. (In Chinese) [Google Scholar]
- Bao, W.; Bai, Q.; Lu, H. Vibration Mechanics Foundation and the Application of MATLAB, 1st ed.; Tsinghua University Press: Beijing, China, 2015. (In Chinese) [Google Scholar]
- Fan, S. Axisymmetric Shell Resonator Gyroscopes, 1st ed.; National Defense Industry Press: Beijing, China, 2013. (In Chinese) [Google Scholar]
- Saukoski, M. System and Circuit Design for a Capacitive MEMS Gyroscope. Ph.D. Thesis, Helsinki University of Technology, Espoo, Finland, April 2008. [Google Scholar]
- Lei, T.; Peng, H.; Ding, Q.; Jiang, L.; Fang, Z. Modeling and Analysis of Slight Vibration Capacitance of HRG. Piezoelectr. Acoustoopt. 2010, 33, 34–37. (In Chinese) [Google Scholar]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]

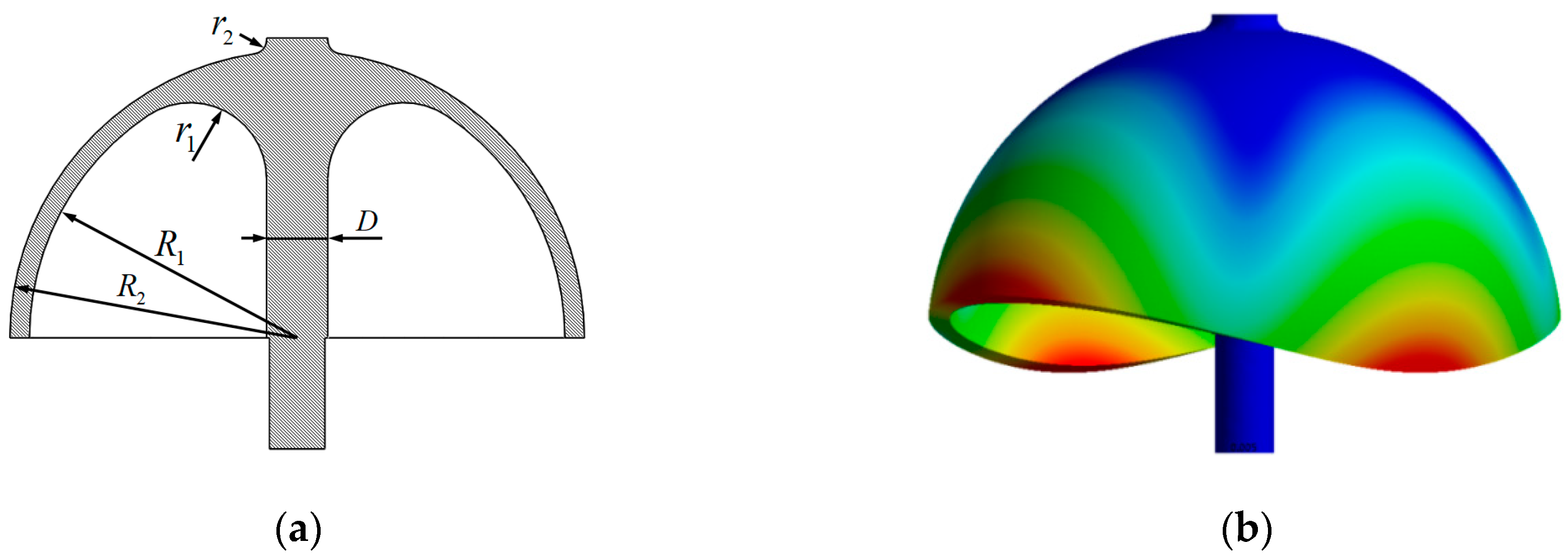






| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Density ρ | 2.2 × 103 kg/m3 | Inner radius of hemispherical shell R1 | 9.65 × 10−3 m |
| Yong’s Modulus E | 7.67 × 1010 Pa | Outer radius of hemispherical shell R2 | 10.35 × 10−3 m |
| Poisson’s Ratio μ | 0.17 | Inner corner radius r1 | 2.75 × 10−3 m |
| Diameter of stem D | 2.2 × 10−3 m | Outer corner radius r2 | 0.5 × 10−3 m |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| R1 | 9.65 × 10−3 m | λ1 | 1.8782 × 10−12 F |
| R2 | 10.35 × 10−3 m | λ2 | 0.0799 |
| da | 10 × 10−6 m | λ3 | 2.9856 × 104 |
| de | 0.4 × 10−3 m | λ4 | 4.3715 × 10−12 F |
| φ | 0″ to 100″, interval 10″ | θφ | 0° to 345°, interval 15° |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Z.; Yi, G.; Huo, Y.; Qi, Z.; Xu, Z. The Synthesis Model of Flat-Electrode Hemispherical Resonator Gyro. Sensors 2019, 19, 1690. https://doi.org/10.3390/s19071690
Wei Z, Yi G, Huo Y, Qi Z, Xu Z. The Synthesis Model of Flat-Electrode Hemispherical Resonator Gyro. Sensors. 2019; 19(7):1690. https://doi.org/10.3390/s19071690
Chicago/Turabian StyleWei, Zhennan, Guoxing Yi, Yan Huo, Ziyang Qi, and Zeyuan Xu. 2019. "The Synthesis Model of Flat-Electrode Hemispherical Resonator Gyro" Sensors 19, no. 7: 1690. https://doi.org/10.3390/s19071690
APA StyleWei, Z., Yi, G., Huo, Y., Qi, Z., & Xu, Z. (2019). The Synthesis Model of Flat-Electrode Hemispherical Resonator Gyro. Sensors, 19(7), 1690. https://doi.org/10.3390/s19071690





