Simulation of Radiation Damage for Silicon Drift Detector
Abstract
:1. Introduction
2. Radiation Damage
3. Simulation and Validation
3.1. Simuation Model
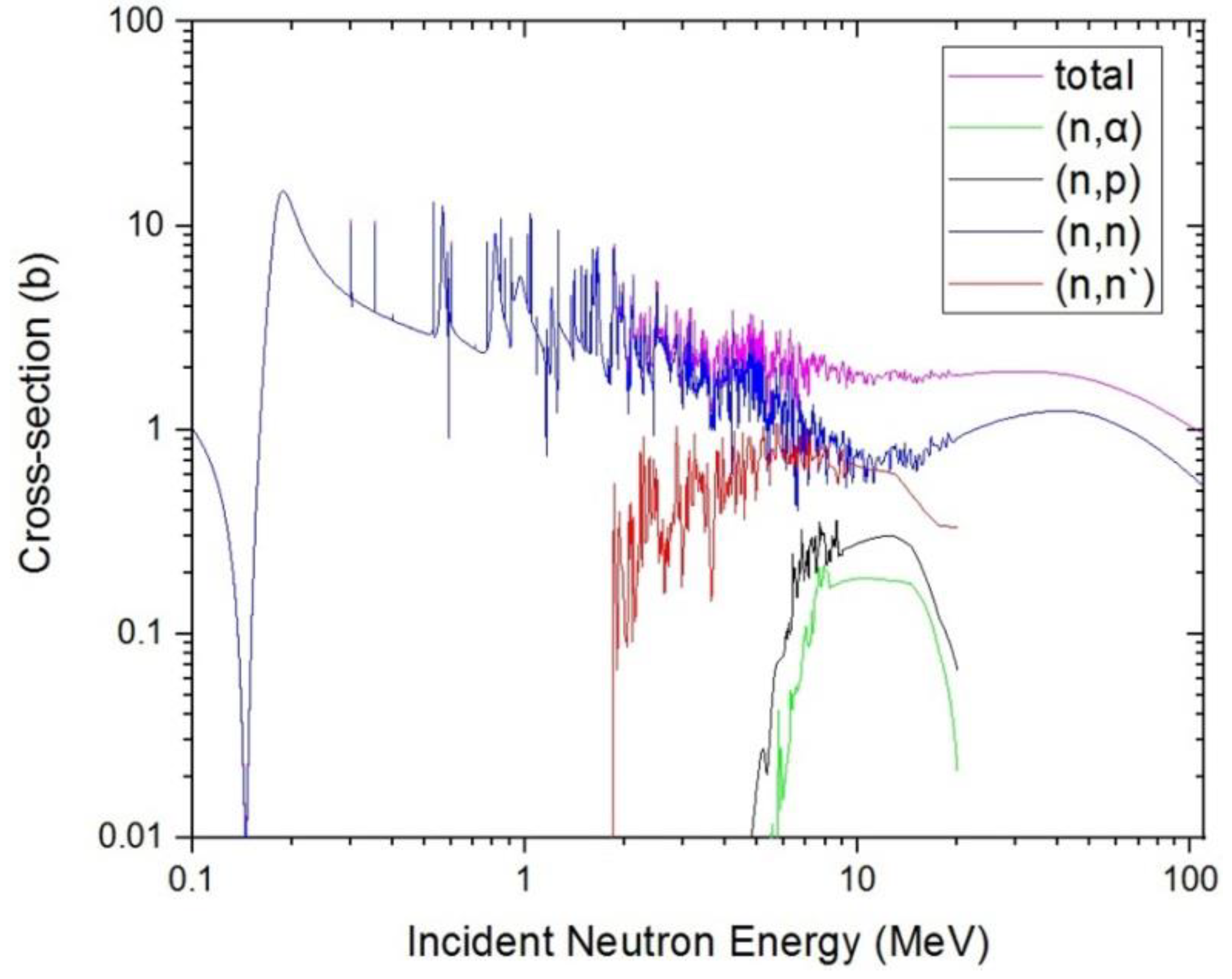
3.2. Radiation Damage Caused by Neutrons in SDD
3.2.1. Displacement Damage
- Track structure
- PKA spatial distribution
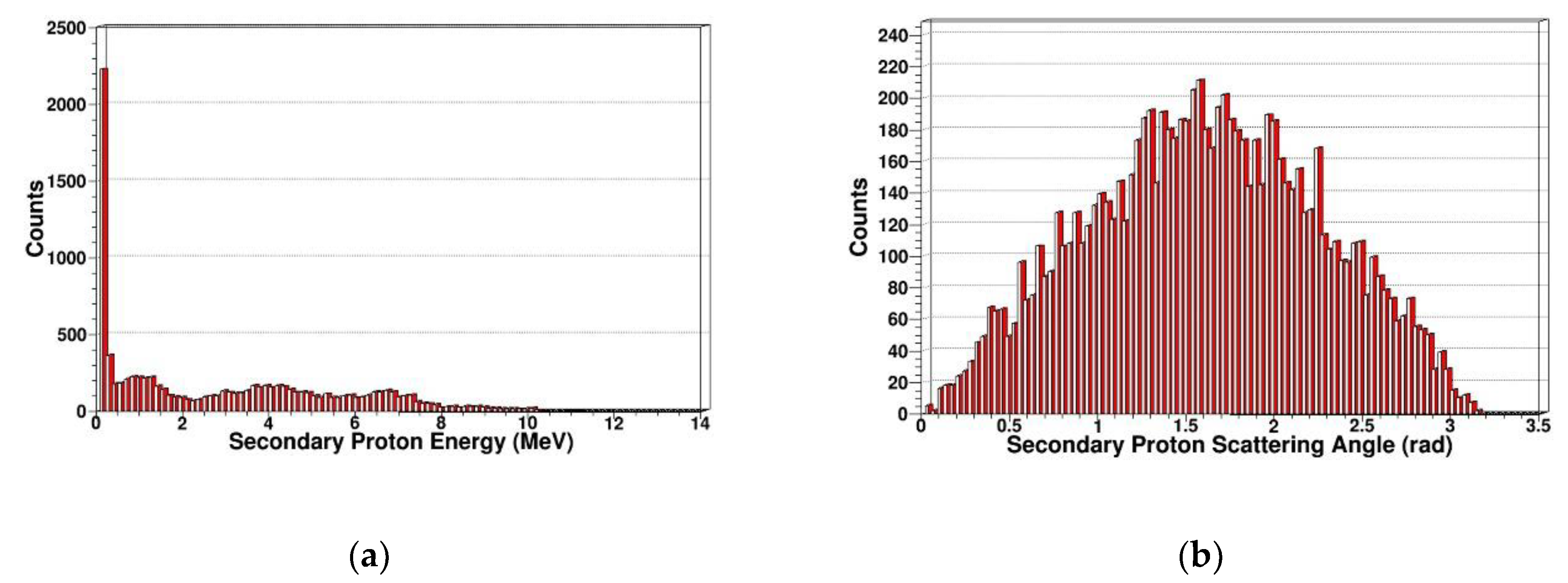
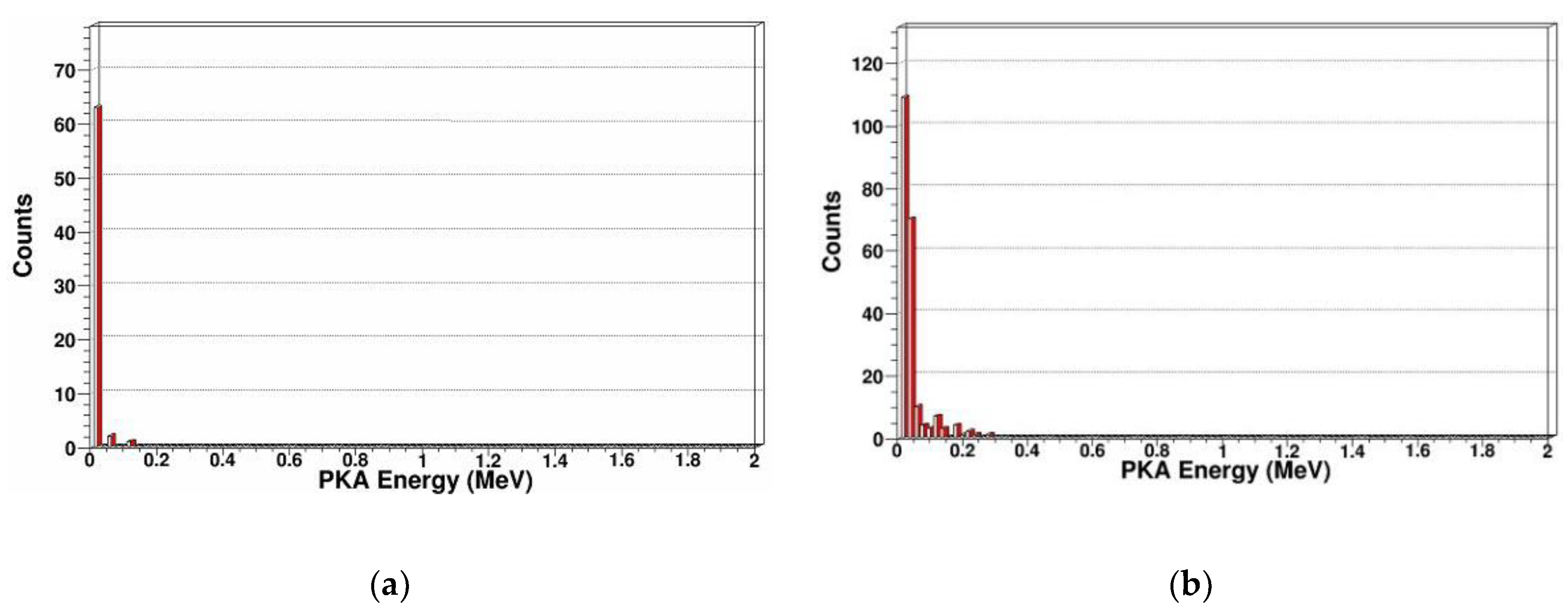
- PKA energy spectrum
- PKA scatting angle
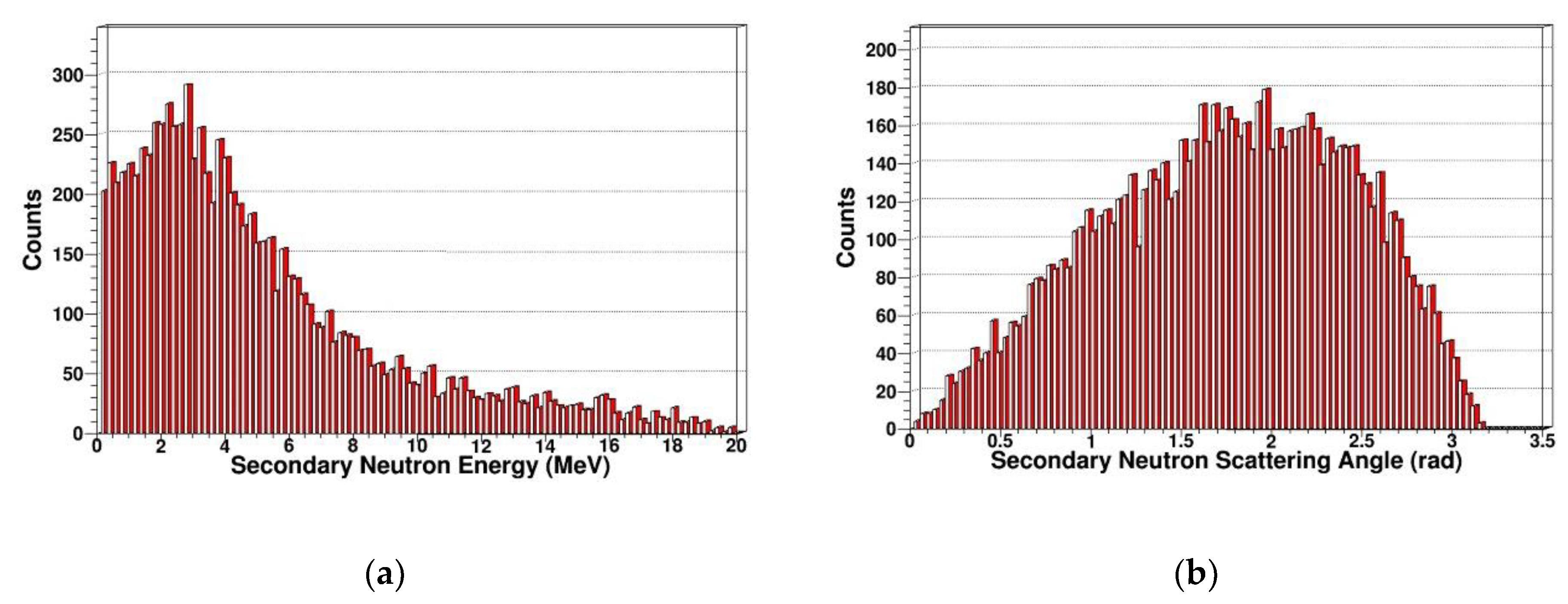
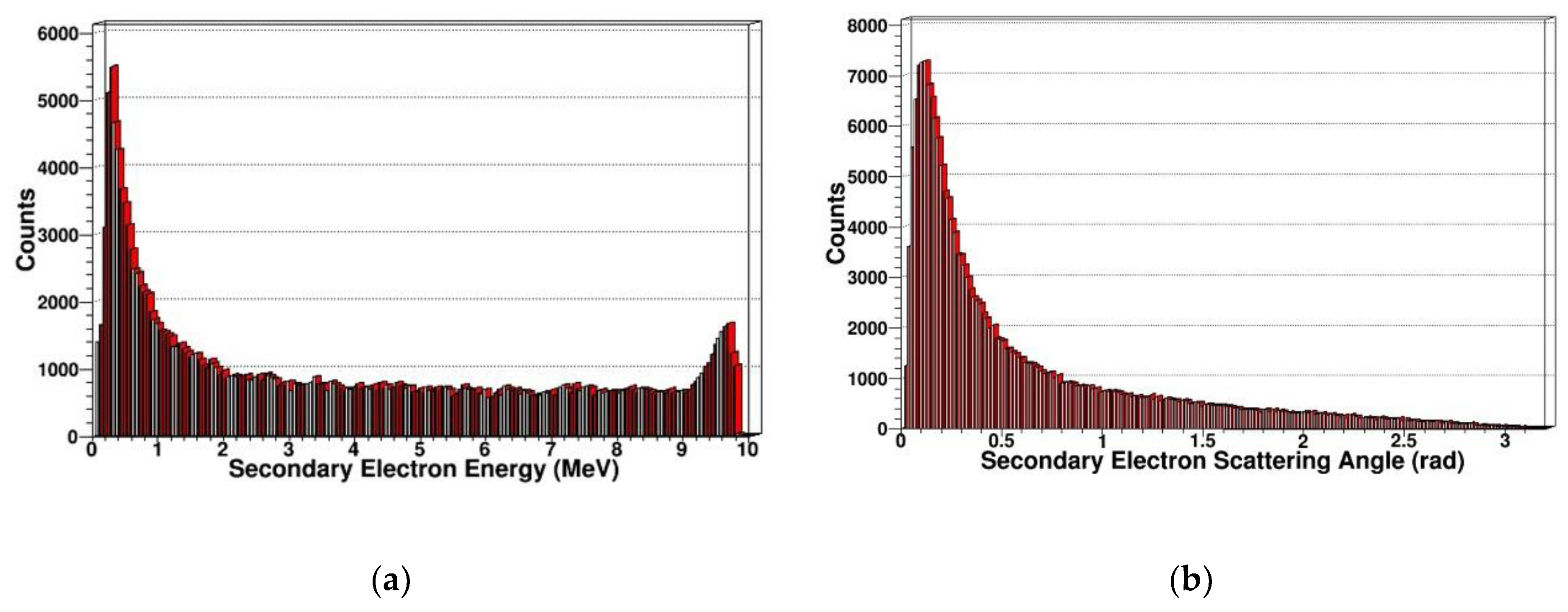
- Secondary knock-on atom
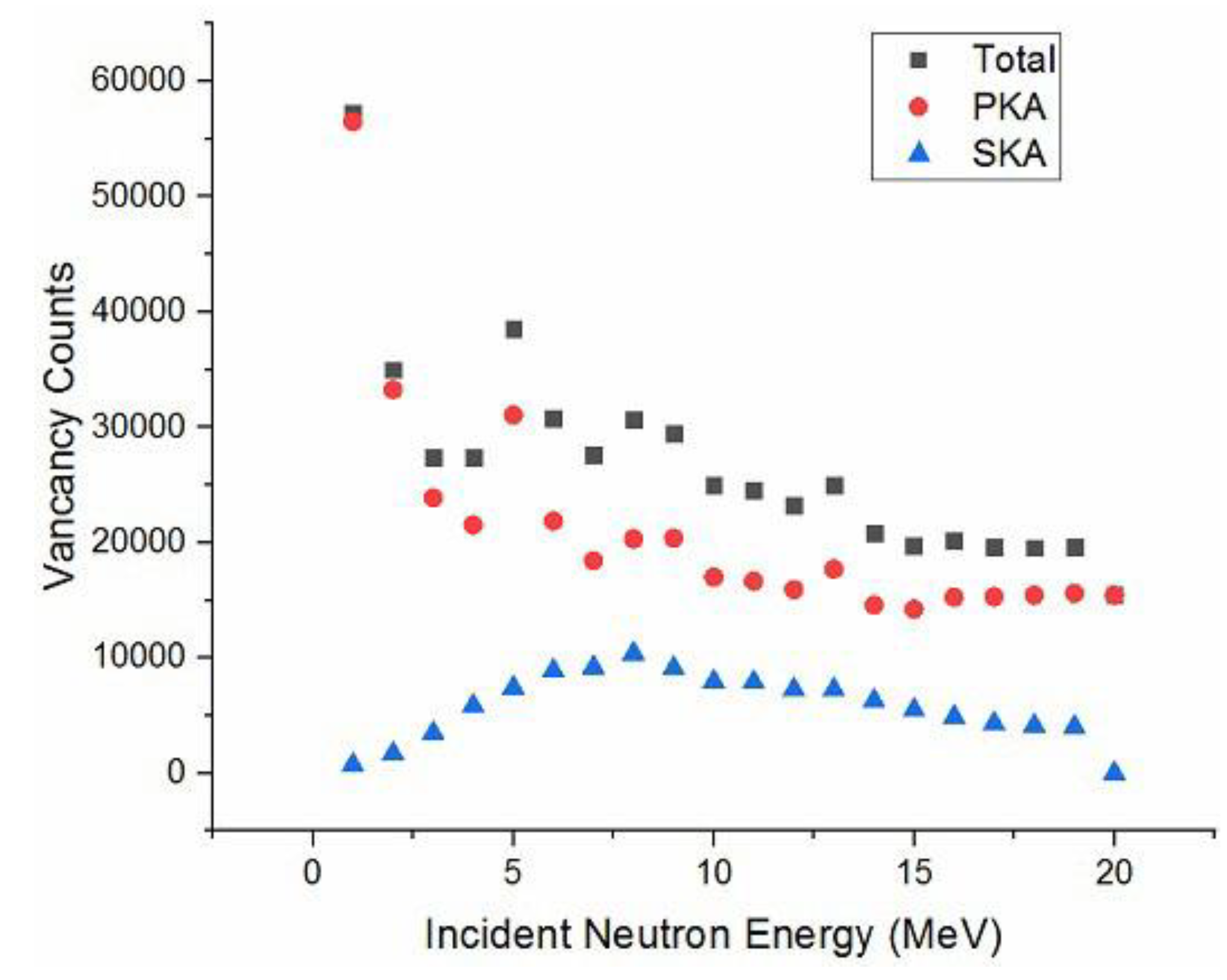
3.2.2. Vacancy Defect
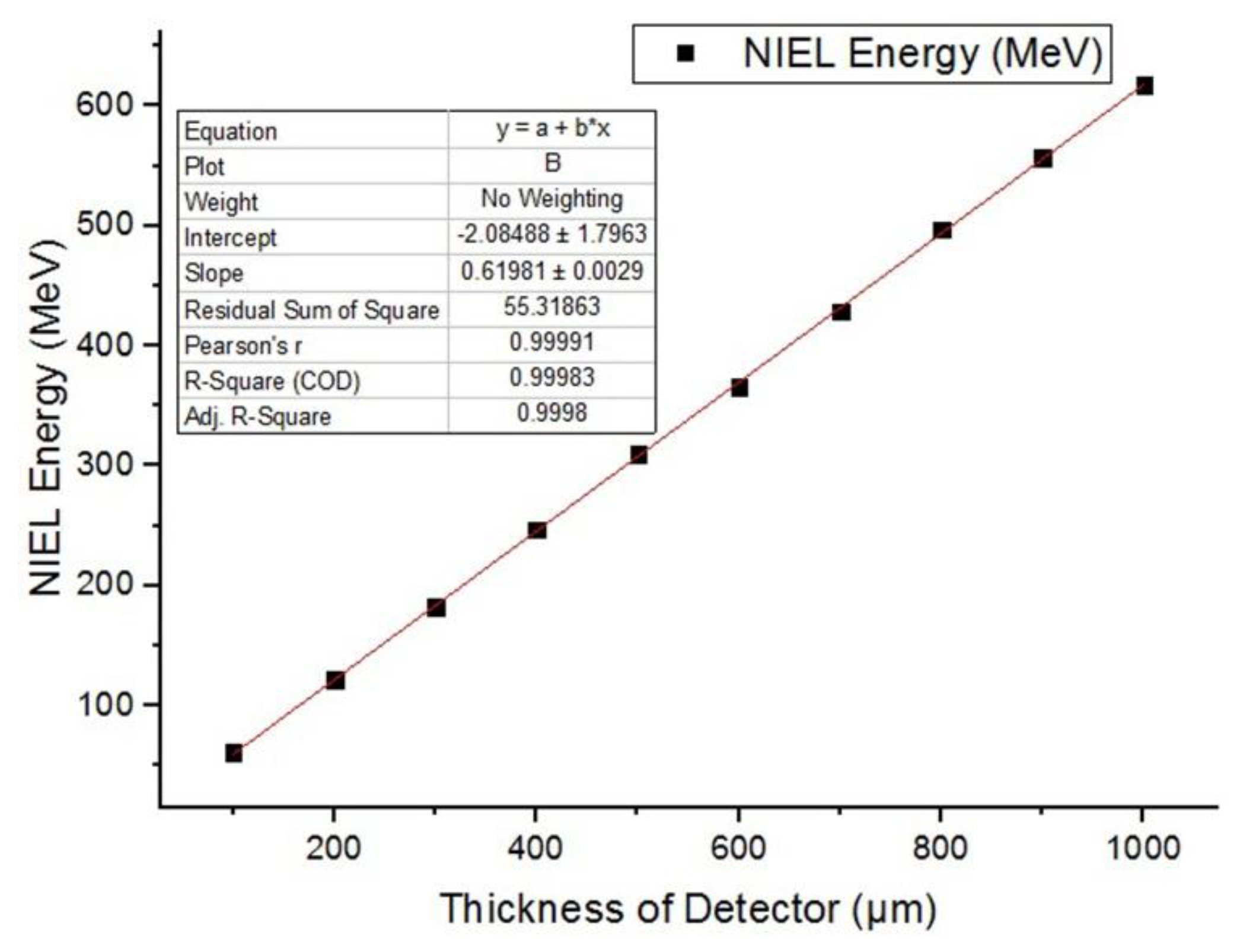
3.2.3. Relationship between NIEL, IEL, and Thickness of SDD
3.3. Radiation Damage Caused by Gammas in SDD
3.3.1. Displacement Damage
- Track structure
- Primary knock-on atom
- Secondary knock-on atom
3.3.2. Relationship between IEL and Thickness of SDD
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pines, D.J. ARPA/DARPA space programs. XNAV Ind. Day 2004, 8, 1–15. [Google Scholar]
- Deng, N.Q.; Zhao, B.S.; Sheng, L.Z. System of space voice communication based on X-ray. Acta Phys. Sin. 2007, 3, 3–4. [Google Scholar]
- Nasa Space Technology Roadmaps. 2015. Available online: https://www.nasa.gov/offices/oct/home/roadmaps/index.html (accessed on 15 February 2019).
- Gatti, E.; Rehak, P. Semiconductor drift chamber-An application of a novel charge transport scheme. Nucl. Instrum. Methods Phys. Res. 1984, 225, 608–614. [Google Scholar] [CrossRef]
- Nomerotski, A. Silicon detectors for tracking and vertexing. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2009, 598, 33–40. [Google Scholar] [CrossRef]
- Evangelista, Y.; Ambro, F.; Feroci, M. Characterization of a novel pixelated silicon drift detector (PixDD) for high-throughput X-ray astrophysics. J. Instrum. 2018, 13, P09011. [Google Scholar] [CrossRef]
- Butt, A.D.; Fiorini, C.; Beretta, M. Application of silicon drift detectors for the readout of a CdWO4 scintillating crystal. IEEE Trans. Nucl. Sci. 2018, 65, 1040–1046. [Google Scholar] [CrossRef]
- Shanmugam, M.; Acharya, Y.B.; Vadawale, S.V. Experimental characterization of silicon drift detector for X-ray spectrometry: Comparison with theoretical estimation. Measurement. 2016, 91, 66–72. [Google Scholar] [CrossRef]
- Monte, E.D.; Rachevski, A.; Zampa, G. Measurement of the effect of non ionizing energy losses on the leakage current of silicon drift detector prototypes for the LOFT satellite. J. Instrum. 2014, 9, P07016. [Google Scholar] [CrossRef]
- Monte, E.D.; Evangelista, Y.; Bozzo, E. The effect of the displacement damage on the charge collection efficiency in silicon drift detectors for the LOFT satellite. J. Instrum. 2015, 10, P05002. [Google Scholar] [CrossRef]
- Harper, R.S.; Buttar, C.M.; Allport, P.P. Evolution of silicon microstrip detector currents during proton irradiation at the CERN PS. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2002, 479, 548–554. [Google Scholar] [CrossRef] [Green Version]
- Kramberger, G.; Cindro, V.; Mandic, I. Effective trapping time of electrons and holes in different silicon materials irradiated with neutrons, protons and pions. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2002, 481, 297–305. [Google Scholar] [CrossRef] [Green Version]
- Hayashi, K.; Park, I.; Dotsu, K. Radiation effects on the silicon semiconductor detectors for the ASTRO-H mission. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2013, 699, 225–229. [Google Scholar] [CrossRef]
- Pandey, S.U.; Vikelis, G.; Humanic, T.J. Studies of ionizing radiation effects on silicon drift detectors. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1995, 361, 457–460. [Google Scholar] [CrossRef]
- Kraner, H.W.; Li, Z.; Posnecker, K.U. Fast neutron damage in silicon detectors. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1989, 279, 226–271. [Google Scholar] [CrossRef]
- Li, Z.; Chen, W.; Dou, L. Study of the long term stability of the effective concentration of ionized space charges Neff of neutron irradiated silicon detectors fabricated by various thermal oxidation processes. IEEE Trans. Nucl. Sci. 1992, 39, 219–223. [Google Scholar] [CrossRef]
- Mueller, G.P.; Wilsey, N.D. The structure of displacement cascades in silicon. IEEE Trans. Nucl. Sci. 1982, 29, 1493–1497. [Google Scholar] [CrossRef]
- Donegani, E.M.; Fretwurst, E. Study of point- and cluster-defects in radiation-damaged silicon. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2018, 898, 15–23. [Google Scholar] [CrossRef] [Green Version]
- Borodin, V.A. Molecular dynamics simulation of annealing of post-ballistic cascade remnants in silicon. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2012, 282, 33–37. [Google Scholar] [CrossRef]
- Ruzin, A.; Casse, G.; Glaser, A. Comparison of radiation damage in silicon induced by proton and neutron irradiation. IEEE Trans. Nucl. Sci. 1999, 46, 1310–1313. [Google Scholar] [CrossRef] [Green Version]
- Saha, U.; Devan, K. The computation of displacement damage cross section of silicon, carbon and silicon carbide for high energy application. Mater. Today Proc. 2018, 5, 16501–16508. [Google Scholar] [CrossRef]
- Moll, M.; Feick, H.; Fretwurst, E. Comparison of defects produced by fast neutrons and 60Co-gammas in high-resistivity silicon detectors using deep-level transient spectroscopy. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1997, 388, 335–339. [Google Scholar] [CrossRef]
- Raine, M.; Jay, A.; Richard, N. Simulation of single particle displacement damage in silicon-Part I; Global approach and primary interaction simulation. IEEE Trans. Nucl. Sci. 2017, 1, 133–140. [Google Scholar] [CrossRef]
- GEANT4, a Simulation Toolkit. Available online: http://www.geant4.org/geant4 (accessed on 1 February 2018).
- Lazanu, I.; Lazanu, S. Silicon detectors: From radiation hard devices operating beyond LHC conditions to characterization of primary fourfold coordinated vacancy defects. Rom. Rep. Phys. 2005, 57, 342–348. [Google Scholar]
- Robinson, M.T.; Torrens, I.M. Computer simulation of atomic-displacement cascades in solids in the binary-collision approximation. Phys. Rev. B 1974, 9, 5008–5024. [Google Scholar] [CrossRef]












© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Zhu, T.; Yao, J.; Ouyang, X. Simulation of Radiation Damage for Silicon Drift Detector. Sensors 2019, 19, 1767. https://doi.org/10.3390/s19081767
Liu Y, Zhu T, Yao J, Ouyang X. Simulation of Radiation Damage for Silicon Drift Detector. Sensors. 2019; 19(8):1767. https://doi.org/10.3390/s19081767
Chicago/Turabian StyleLiu, Yang, Tengfei Zhu, Jianxi Yao, and Xiaoping Ouyang. 2019. "Simulation of Radiation Damage for Silicon Drift Detector" Sensors 19, no. 8: 1767. https://doi.org/10.3390/s19081767
APA StyleLiu, Y., Zhu, T., Yao, J., & Ouyang, X. (2019). Simulation of Radiation Damage for Silicon Drift Detector. Sensors, 19(8), 1767. https://doi.org/10.3390/s19081767





