Concrete Crack Detection and Monitoring Using a Capacitive Dense Sensor Array
Abstract
:1. Introduction
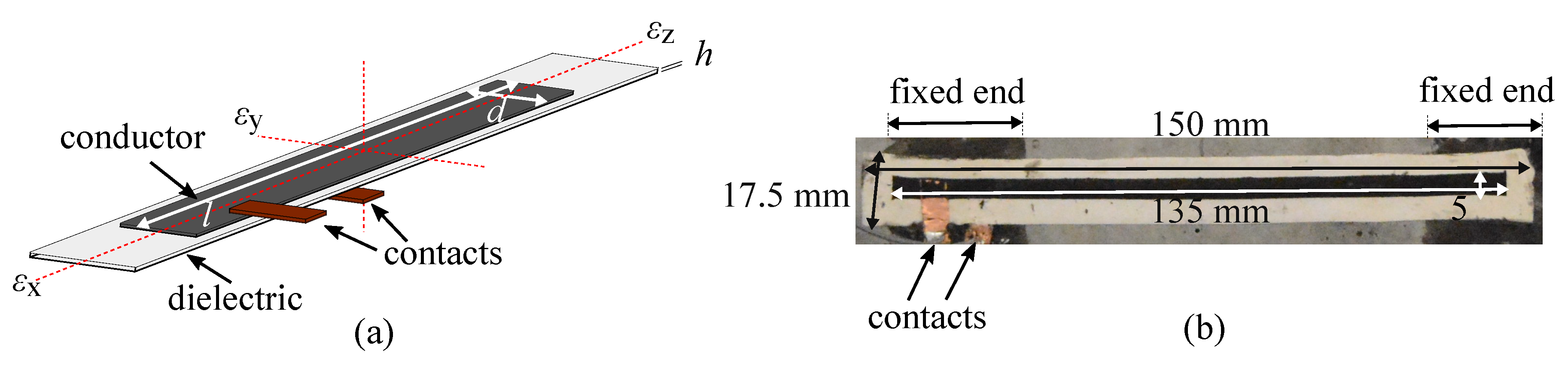
2. Soft Elastomeric Capacitor Technology
2.1. Sensor Fabrication
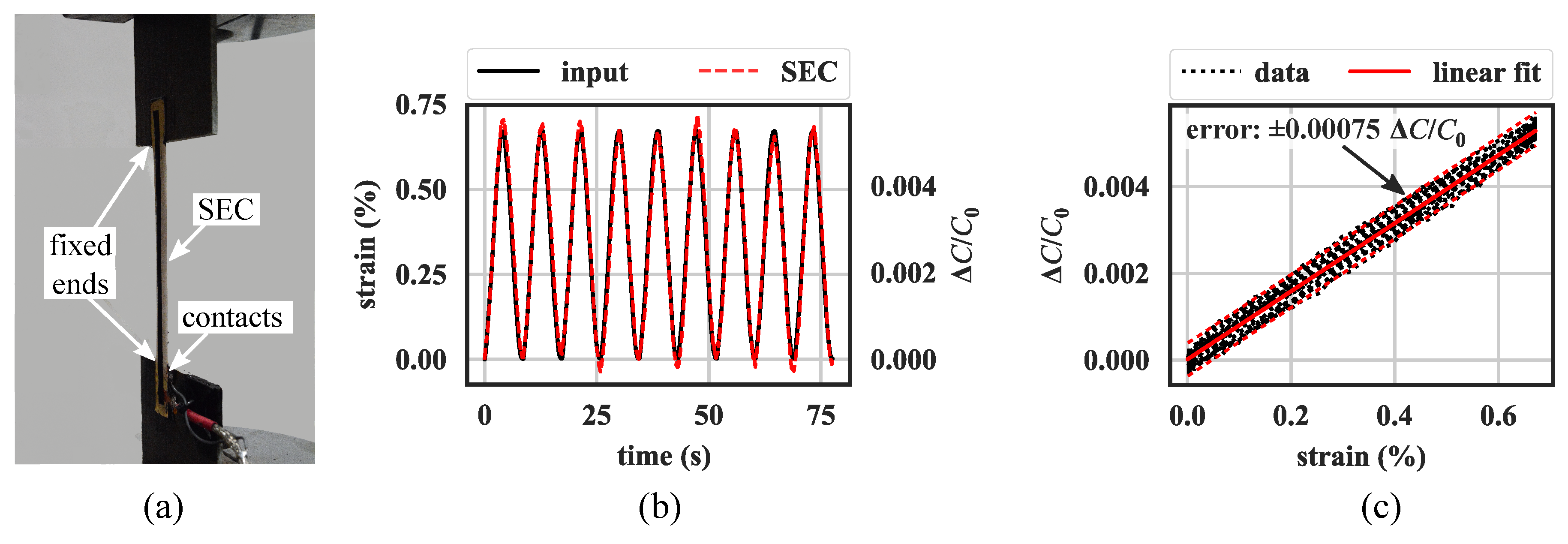
2.2. Sensor Response Characterization
2.3. Small-Scale Prototyping Test
3. Verification on Full-Scale Post-Tensioned Concrete Beam
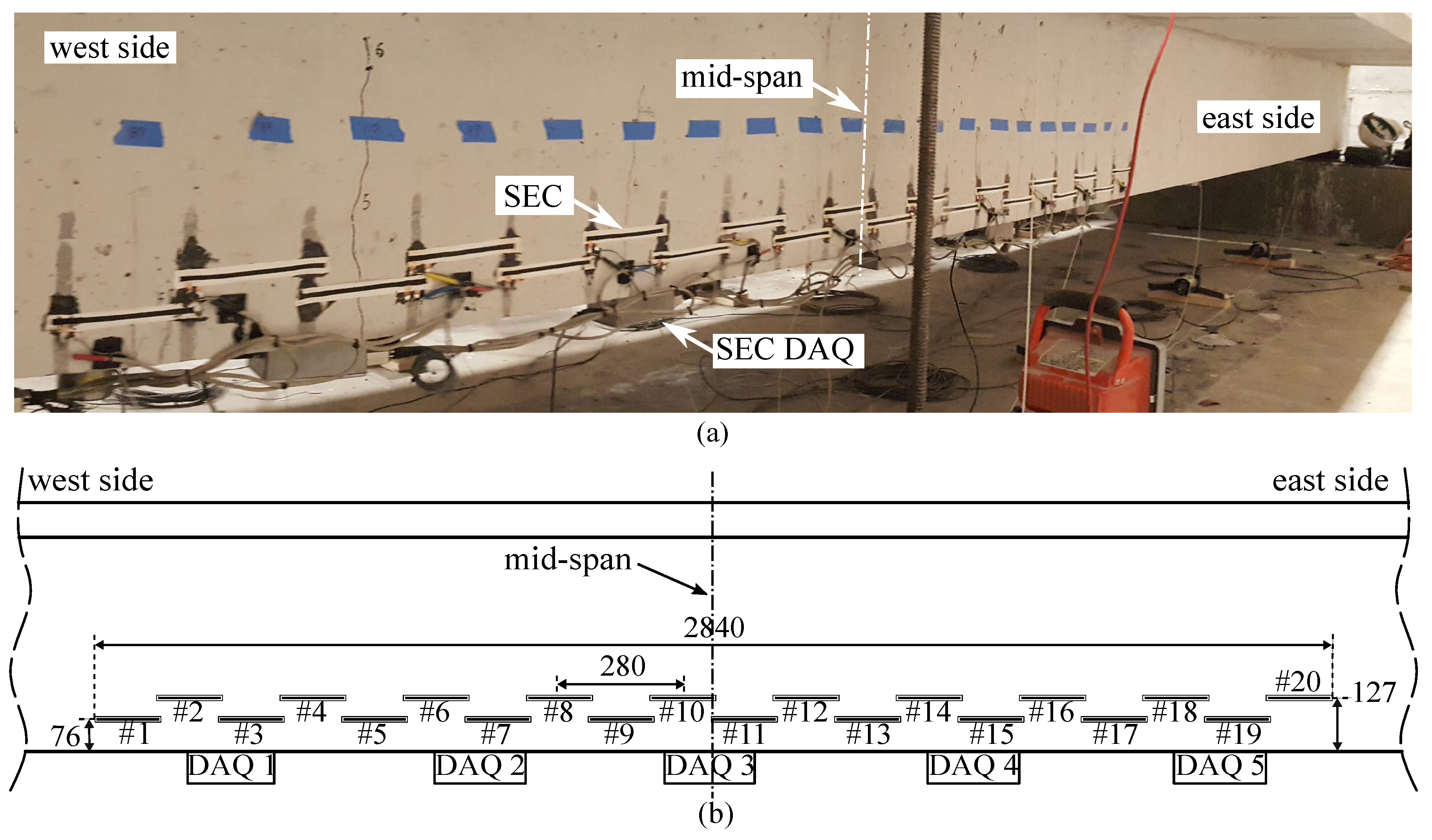
3.1. Experimental Structural System
Dense Sensor Network Instrumentation Strategy
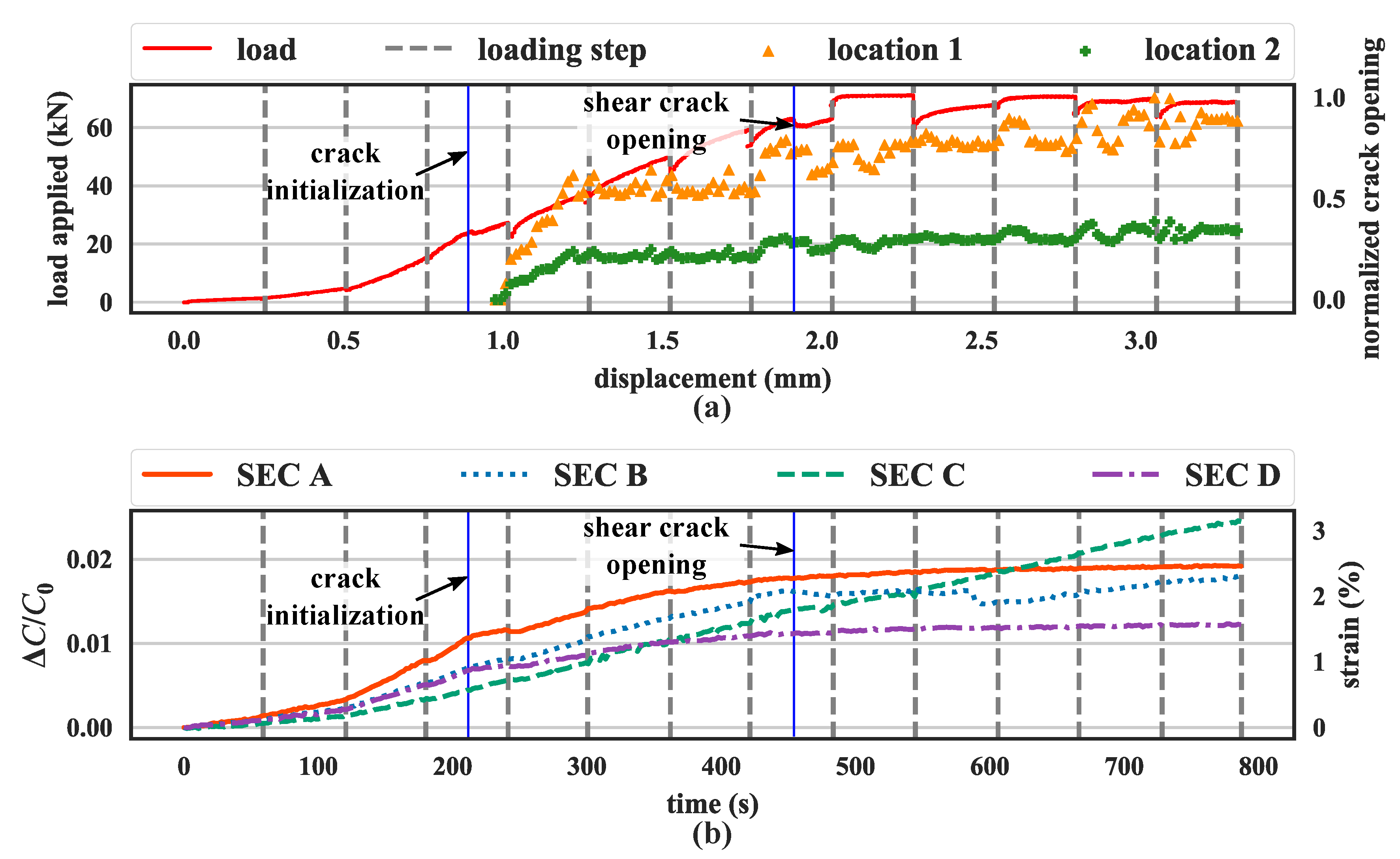
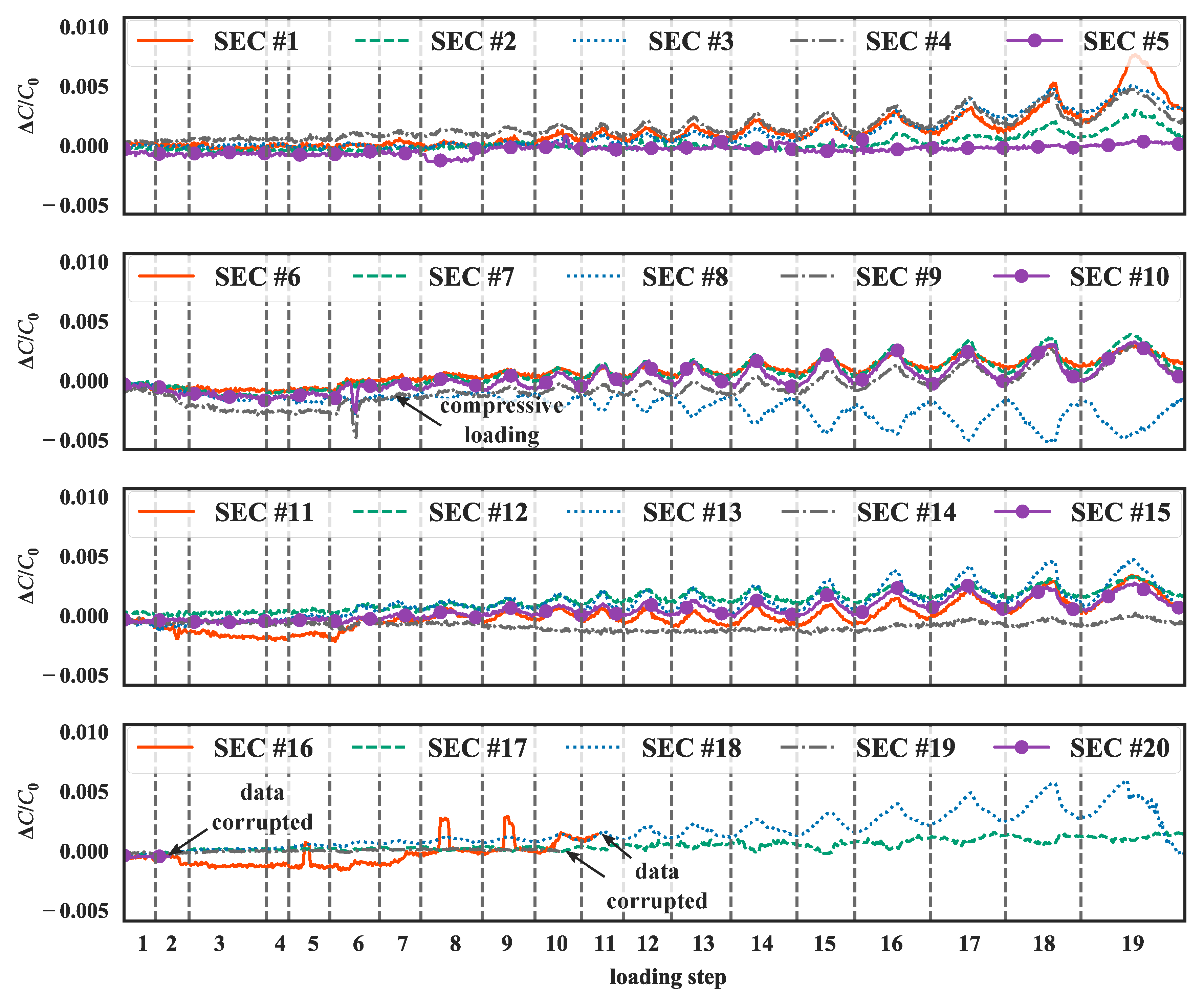
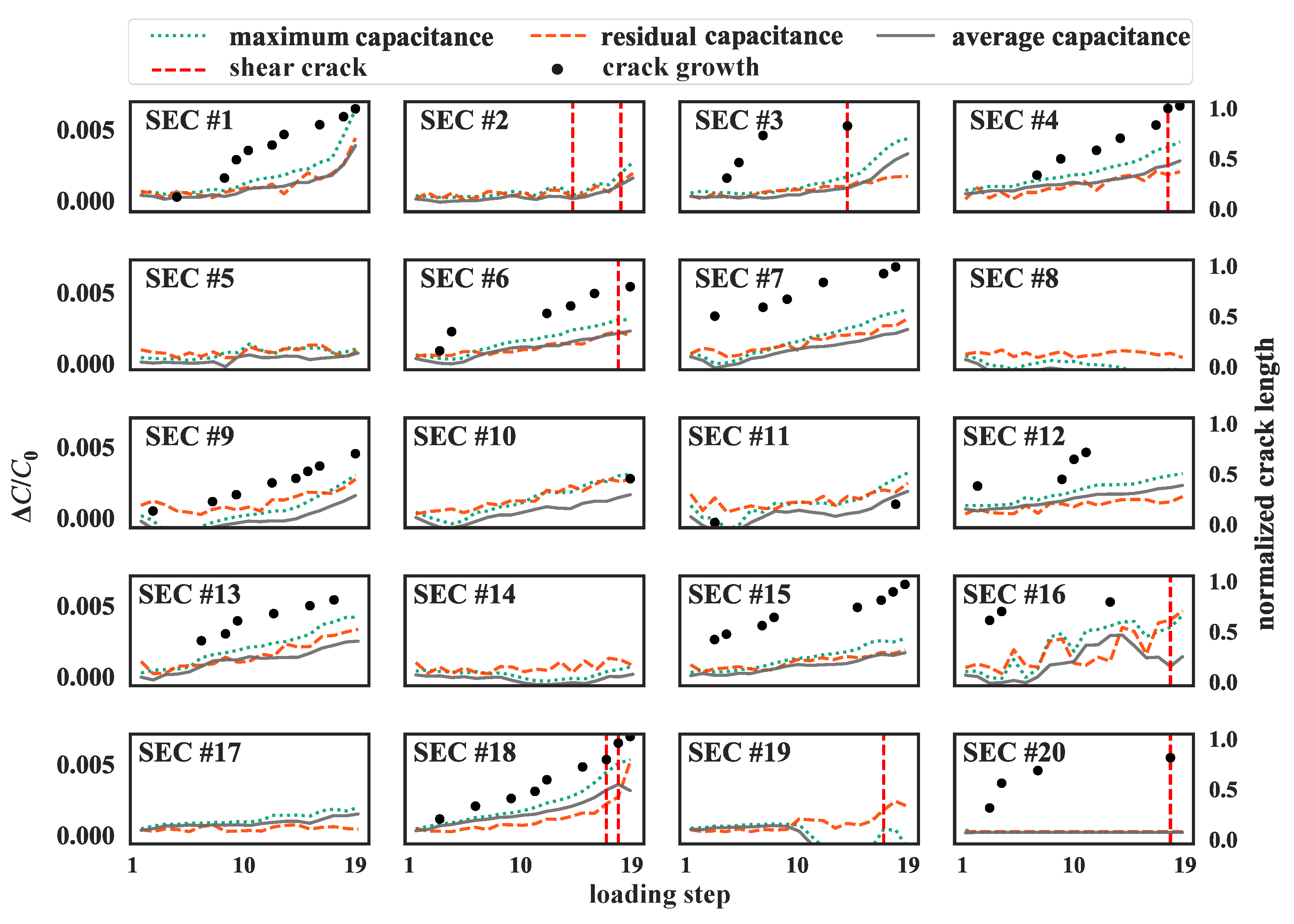
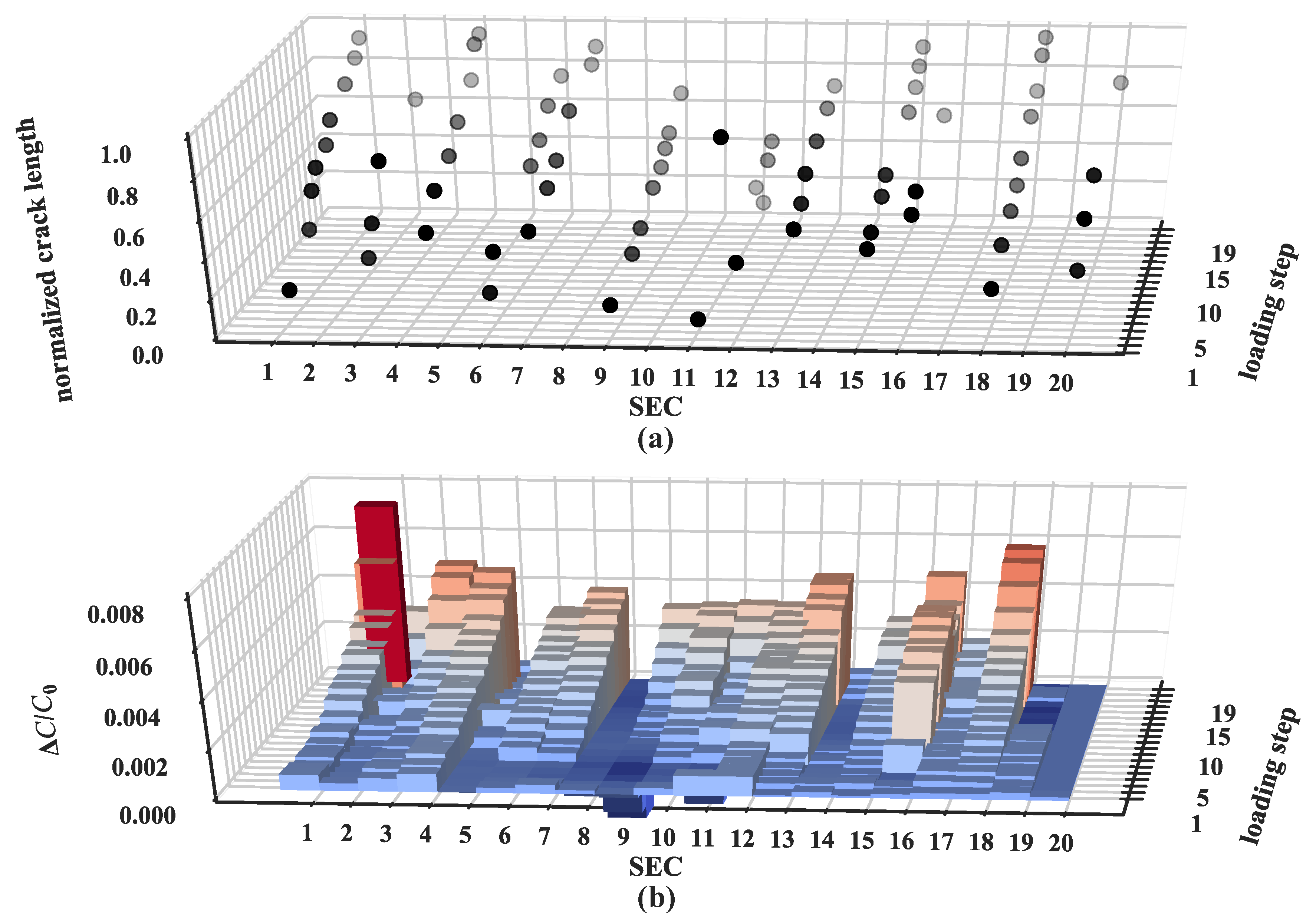
3.2. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tang, S.; Yao, Y.; Andrade, C.; Li, Z. Recent Durability Studies on Concrete Structure. Cem. Concr. Res. 2015, 78, 143–154. [Google Scholar] [CrossRef]
- Zhang, J.K.; Yan, W.; Cui, D.M. Concrete Condition Assessment Using Impact-Echo Method and Extreme Learning Machines. Sensors 2016, 16, 447. [Google Scholar] [CrossRef]
- Hwang, E.; Kim, G.; Choe, G.; Yoon, M.; Gucunski, N.; Nam, J. Evaluation of Concrete Degradation Depending on Heating Conditions by Ultrasonic Pulse Velocity. Constr. Build. Mater. 2018, 171, 511–520. [Google Scholar] [CrossRef]
- ElBatanouny, M.K.; Ziehl, P.H.; Larosche, A.; Mangual, J.; Matta, F.; Nanni, A. Acoustic Emission Monitoring for Assessment of Prestressed Concrete Beams. Constr. Build. Mater. 2014, 58, 46–53. [Google Scholar] [CrossRef]
- Eisenmann, D.; Margetan, F.J.; Koester, L.; Clayton, D. Inspection of a Large Concrete Block Containing Embedded Defects Using Ground Penetrating Radar. AIP Conf. Proc. 2016, 1706. [Google Scholar] [CrossRef]
- Gribniak, V.; Arnautov, A.K.; Kaklauskas, G.; Tamulenas, V.; Timinskas, E.; Sokolov, A. Investigation on Application of Basalt Materials as Reinforcement for Flexural Elements of Concrete Bridges. Balt. J. Road Bridge Eng. 2015, 10, 201–206. [Google Scholar] [CrossRef]
- Park, H.; Shin, Y.; Choi, S.; Kim, Y. An Integrative Structural Health Monitoring System for the Local/Global Responses of a Large-Scale Irregular Building under Construction. Sensors 2013, 13, 9085–9103. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Xu, Y.; Zhang, T. A Wireless Monitoring System for Cracks on the Surface of Reactor Containment Buildings. Sensors 2016, 16, 883. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Tian, Z.; Ziehl, P.; ElBatanouny, M. Crack Detection and Evaluation in Grout Structures with Passive/Active Methods. J. Mater. Civ. Eng. 2016, 28, 04015168. [Google Scholar] [CrossRef]
- Han, B.; Yu, X.; Ou, J. Self-Sensing Concrete in Smart Structures; Butterworth-Heinemann: Oxford, UK, 2014. [Google Scholar] [CrossRef]
- Glisic, B. Fibre Optic Methods for Structural Health Monitoring; John Wiley and Sons: Chichester, UK, 2007. [Google Scholar] [CrossRef]
- Barrias, A.; Casas, J.; Villalba, S. A Review of Distributed Optical Fiber Sensors for Civil Engineering Applications. Sensors 2016, 16, 748. [Google Scholar] [CrossRef]
- Barrias, A.; Casas, J.; Villalba, S. Embedded Distributed Optical Fiber Sensors in Reinforced Concrete Structures—A Case Study. Sensors 2018, 18, 980. [Google Scholar] [CrossRef] [PubMed]
- Tung, S.T.; Yao, Y.; Glisic, B. Sensing Sheet: The Sensitivity of Thin-Film Full-Bridge Strain Sensors for Crack Detection and Characterization. Meas. Sci. Technol. 2014, 25, 075602. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, S.; Li, X.; Zhang, X.; Yang, G.; Qiu, M. Crack Width Monitoring of Concrete Structures Based on Smart Film. Smart Mater. Struct. 2014, 23, 045031. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, B.; Xia, K.; Li, X.; Yan, G.; Zhang, K. Smart Film for Crack Monitoring of Concrete Bridges. Struct. Health Monit. 2010, 10, 275–289. [Google Scholar] [CrossRef]
- Hallaji, M.; Seppänen, A.; Pour-Ghaz, M. Electrical Impedance Tomography-Based Sensing Skin for Quantitative Imaging of Damage in Concrete. Smart Mater. Struct. 2014, 23, 085001. [Google Scholar] [CrossRef]
- Gupta, S.; Gonzalez, J.G.; Loh, K.J. Self-Sensing Concrete Enabled by Nano-Engineered Cement-Aggregate Interfaces. Struct. Health Monit. 2016, 16, 309–323. [Google Scholar] [CrossRef]
- Downey, A.; D’Alessandro, A.; Ubertini, F.; Laflamme, S. Automated Crack Detection in Conductive Smart-Concrete Structures Using a Resistor Mesh Model. Meas. Sci. Technol. 2018, 29, 035107. [Google Scholar] [CrossRef]
- Schumacher, T.; Thostenson, E.T. Development of Structural Carbon Nanotube-Based Sensing Composites for Concrete Structures. J. Intell. Mater. Syst. Struct. 2013, 25, 1331–1339. [Google Scholar] [CrossRef]
- Downey, A.; Laflamme, S.; Ubertini, F. Experimental wind tunnel study of a smart sensing skin for condition evaluation of a wind turbine blade. Smart Mater. Struct. 2017. [Google Scholar] [CrossRef]
- Downey, A.; Pisello, A.L.; Fortunati, E.; Fabiani, C.; Luzi, F.; Torre, L.; Ubertini, F.; Laflamme, S. Durability Assessment of Soft Elastomeric Capacitor Skin for SHM of Wind Turbine Blades. Proc. SPIE 2018, 10599, 105991J. [Google Scholar] [CrossRef]
- Laflamme, S.; Kollosche, M.; Connor, J.J.; Kofod, G. Robust Flexible Capacitive Surface Sensor for Structural Health Monitoring Applications. J. Eng. Mech. 2013, 139, 879–885. [Google Scholar] [CrossRef] [Green Version]
- Kong, X.; Li, J.; Collins, W.; Bennett, C.; Laflamme, S.; Jo, H. Sensing Distortion-Induced Fatigue Cracks in Steel Bridges with Capacitive Skin Sensor Arrays. Smart Mater. Struct. 2018, 27, 115008. [Google Scholar] [CrossRef]
- Harrey, P.; Ramsey, B.; Evans, P.; Harrison, D. Capacitive-type Humidity Sensors Fabricated Using the Offset Lithographic Printing Process. Sens. Actuators B Chem. 2002, 87, 226–232. [Google Scholar] [CrossRef]
- Yan, J.; Austin Downey, A.C.S.L.; Chen, A. Detection and Monitoring of Cracks in Reinforced Concrete Using an Elastic Sensing Skin. Struct. Congr. 2019. preprint. [Google Scholar]
- Gerber, M.; Weaver, C.; Aygun, L.; Verma, N.; Sturm, J.; Glišić, B. Strain Transfer for Optimal Performance of Sensing Sheet. Sensors 2018, 18, 1907. [Google Scholar] [CrossRef] [PubMed]





© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, J.; Downey, A.; Cancelli, A.; Laflamme, S.; Chen, A.; Li, J.; Ubertini, F. Concrete Crack Detection and Monitoring Using a Capacitive Dense Sensor Array. Sensors 2019, 19, 1843. https://doi.org/10.3390/s19081843
Yan J, Downey A, Cancelli A, Laflamme S, Chen A, Li J, Ubertini F. Concrete Crack Detection and Monitoring Using a Capacitive Dense Sensor Array. Sensors. 2019; 19(8):1843. https://doi.org/10.3390/s19081843
Chicago/Turabian StyleYan, Jin, Austin Downey, Alessandro Cancelli, Simon Laflamme, An Chen, Jian Li, and Filippo Ubertini. 2019. "Concrete Crack Detection and Monitoring Using a Capacitive Dense Sensor Array" Sensors 19, no. 8: 1843. https://doi.org/10.3390/s19081843
APA StyleYan, J., Downey, A., Cancelli, A., Laflamme, S., Chen, A., Li, J., & Ubertini, F. (2019). Concrete Crack Detection and Monitoring Using a Capacitive Dense Sensor Array. Sensors, 19(8), 1843. https://doi.org/10.3390/s19081843







