Computationally Efficient Sources Location Method for Nested Array via Massive Virtual Difference Co-Array
Abstract
:1. Introduction
- (a)
- We extract the DFT method for the DOA estimation problem by constructing a massive virtual difference co-array with nested array. Besides, it is applicable to any sparse arrays which can generate a large virtual ULA, e.g., coprime arrays.
- (b)
- The proposed method remarkably reduces the computational complexity since it applies FFT to obtain initial estimates and searches for fine estimates over a small refined region. Besides, it can avoid the process of eigenvalue decomposition (EVD) and has no need to know the number of sources in advance, which are all inevitable in the existing SS methods and CS methods.
- (c)
- The proposed algorithm can utilize the full DOFs offered by the virtual array and hence increase the number of resolvable sources and improves estimation performance. Since the DFT method works well especially with large number of sensors, the proposed method can obtain pretty high accuracy by using massive virtual difference co-arrays generated by nested array.
2. Signal Model of Nested Array
3. Proposed Method for Direction of Arrival (DOA) Estimation
3.1. Vectorization of the Covariance Matrix
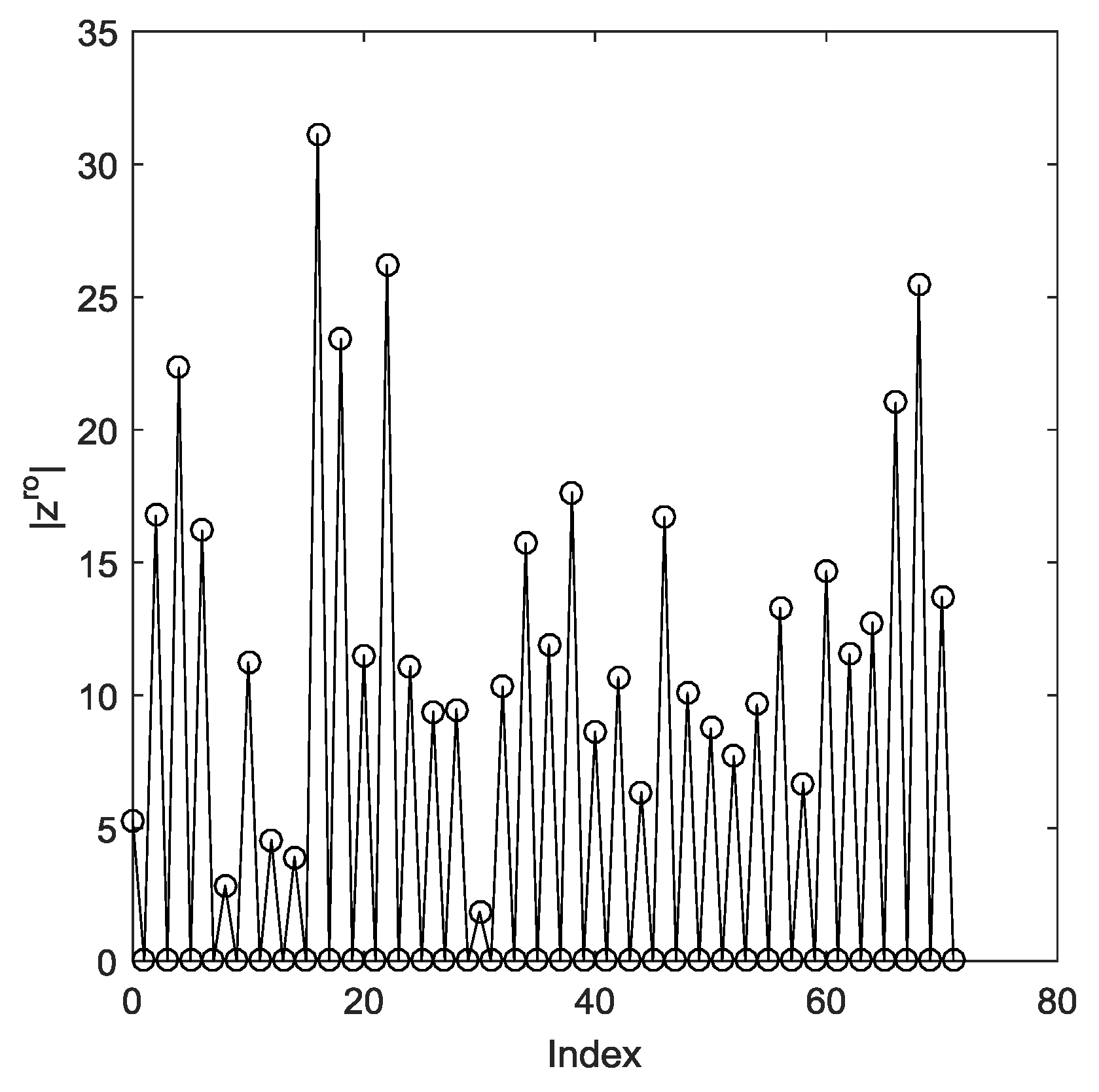
3.2. Coarse Initial Estimation
3.3. Fine Estimation
3.4. Detailed Steps
- Step 1
- Compute the covariance matrix and get the observation vector in (5);
- Step 2
- Compute the DFT of and search the spectrum of for values to obtain ;
- Step 3
- Compute and search over to obtain the optimal phase shifter ;
- Step 4
- Compute fine DOA estimates according to (16).
4. Performance Analysis
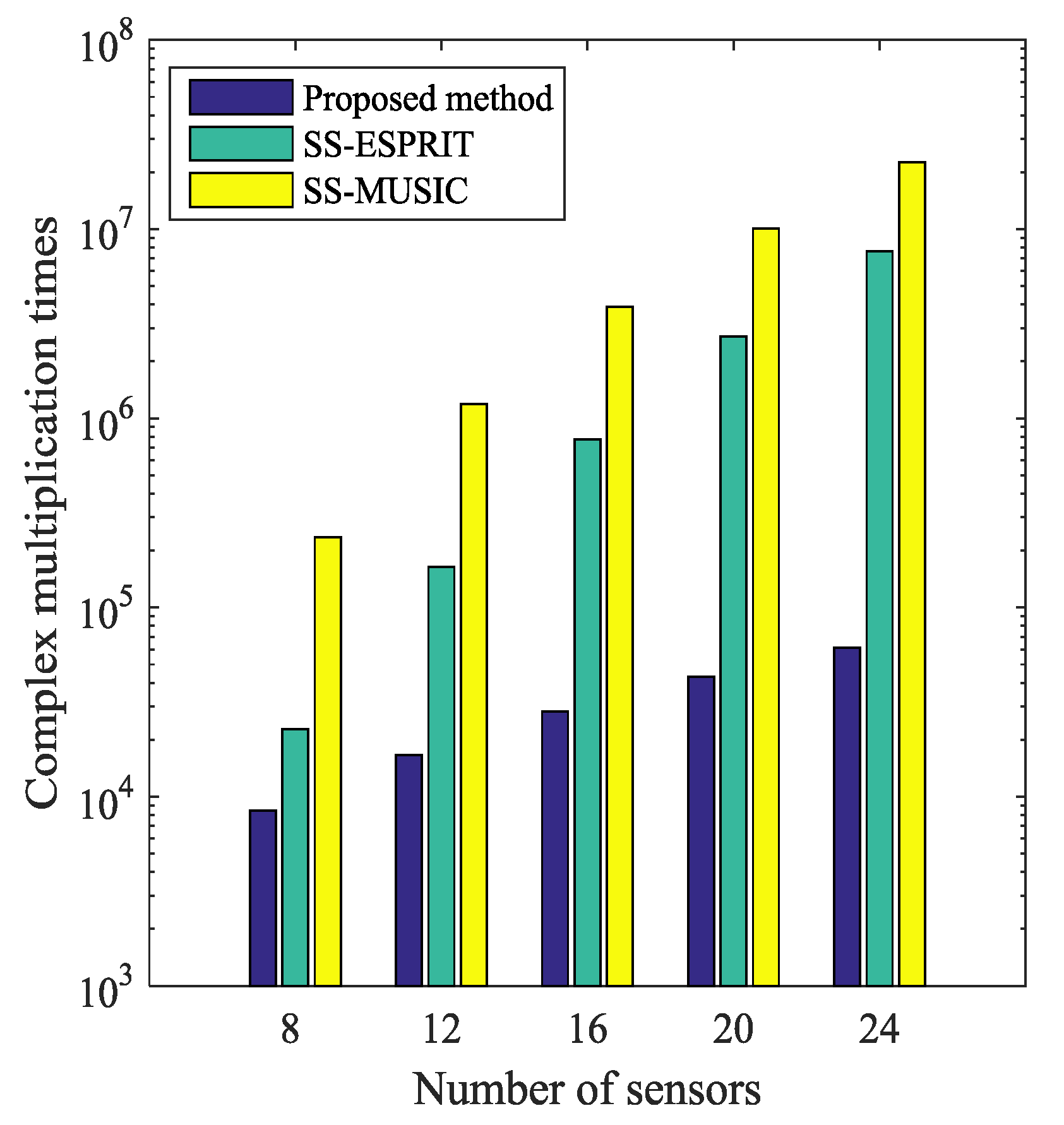
4.1. Computational Complexity
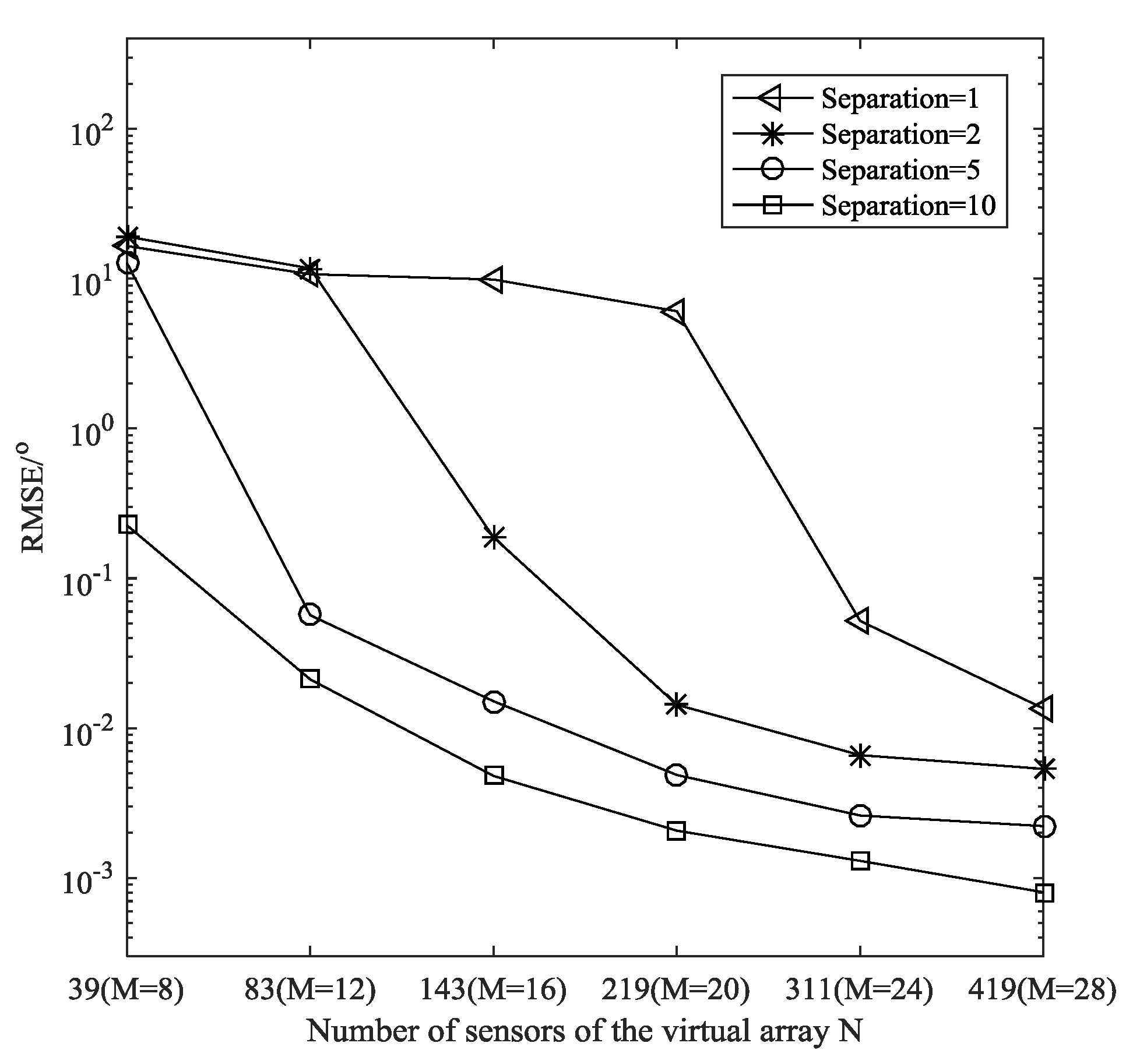
4.2. Resolution and DOF
4.3. Advantages
- The proposed method outperforms SS-ESPRIT and SS-MUSIC [25] for distant sources DOA estimation with nested arrays as it involves the full aperture of the virtual ULA and a phase rotation operation is applied for fine estimation.
- The proposed method is computationally efficient since it applies DFT (FFT) and searches for peaks over a small sector. Besides, it can avoid performing EVD operation, which is time-consuming and inevitable in SS methods.
- The proposed algorithm has no need to know the number of sources in advance, which is practical and attractive in the realistic scenario.
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Krim, H.; Viberg, M. Two decades of array signal processing research: The parametric approach. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Amin, M.G.; Wang, X.; Zhang, Y.D.; Ahmad, F.; Aboutanios, E. Sparse arrays and sampling for interference mitigation and DOA estimation in GNSS. Proc. IEEE 2016, 104, 1302–1317. [Google Scholar] [CrossRef]
- Talisa, S.H.; O’Haver, K.W.; Comberiate, T.M.; Sharp, M.D.; Somerlock, O.F. Benefits of digital phased array radars. Proc. IEEE 2016, 104, 530–543. [Google Scholar] [CrossRef]
- Wu, Q.H.; Ding, G.R.; Wang, J.L.; Yao, Y. Spatial-temporal opportunity detection for spectrum-heterogeneous cognitive radio networks: Two-dimensional sensing. IEEE Trans. Wirel. Commun. 2013, 12, 516–526. [Google Scholar] [CrossRef]
- Wu, Q.H.; Ding, G.R.; Xu, Y.H.; Feng, S.; Du, Z.Y.; Wang, J.L.; Long, K.P. Cognitive internet of things: A new paradigm beyond connection. IEEE Internet Things J. 2014, 1, 129–143. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Shi, J.; Chen, H.; Guizani, M.; Qiu, P.L. A cooperation strategy based on Nash bargaining solution in cooperative relay networks. IEEE Trans. Veh. Technol. 2008, 57, 2570–2577. [Google Scholar] [CrossRef]
- Zhu, G.X.; Zhong, C.J.; Suraweera, H.A.; Karagiannidis, G.K.; Zhang, Z.Y.; Tsiftsis, T.A. Wireless information and power transfer in relay systems with multiple antennas and interference. IEEE Trans. Commun. 2015, 63, 1400–1418. [Google Scholar] [CrossRef]
- Zhang, X.F.; Cao, X.; Xu, D.Z. Novel blind carrier frequency offset estimation for OFDM system with multiple antennas. IEEE Trans. Wirel. Commun. 2010, 9, 881–885. [Google Scholar] [CrossRef]
- Schmidt, R.O. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1990, 37, 984–995. [Google Scholar] [CrossRef]
- Stoica, P.; Nehorai, A. Performance study of conditional and unconditional direction-of-arrival estimation. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1783–1795. [Google Scholar] [CrossRef]
- Chambers, C.; Tozer, T.; Sharman, K.; Durrani, T. Temporal and spatial sampling influence on the estimates of superimposed narrowband signals: When less can mean more. IEEE Trans. Signal Process. 1996, 44, 3085–3098. [Google Scholar] [CrossRef]
- Vaidyanathan, P.P.; Pal, P. Direct-MUSIC on sparse arrays. In Proceedings of the IEEE International Conference on Signal Processing and Communications, Bangalore, India, 22–25 July 2012; pp. 1–5. [Google Scholar]
- Hoctor, R.T.; Kassam, S.A. The unifying role of the coarray in aperture synthesis for coherent and incoherent imaging. Proc. IEEE 1990, 78, 735–752. [Google Scholar] [CrossRef]
- Moffet, A. Minimum-redundancy linear arrays. IEEE Trans. Antennas Propag. 1968, 16, 172–175. [Google Scholar] [CrossRef] [Green Version]
- Vaidyanathan, P.P.; Pal, P. Sparse sensing with co-prime samplers and arrays. IEEE Trans. Signal Process. 2011, 59, 573–586. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P.P. Coprime sampling and the MUSIC algorithm. In Proceedings of the IEEE Digital Signal Processing Workshop and IEEE Signal Processing Education Workshop, Sedona, AZ, USA, 4–7 January 2011; pp. 289–294. [Google Scholar]
- Qin, S.; Zhang, Y.D.; Amin, M.G. Generalized coprime array configurations for direction-of-arrival estimation. IEEE Trans. Signal Process. 2015, 63, 1377–1389. [Google Scholar] [CrossRef]
- Shi, J.P.; Hu, G.P.; Zhang, X.F.; Sun, F.G.; Zhou, H. Sparsity-based two-dimensional DOA estimation for coprime array: From sum-difference co-array viewpoint. IEEE Trans. Signal Process. 2017, 65, 5591–5604. [Google Scholar] [CrossRef]
- Zheng, W.; Zhang, X.F.; Zhai, H. Generalized coprime planar array geometry for 2-D DOA estimation. IEEE Commun. Lett. 2017, 21, 1075–1078. [Google Scholar] [CrossRef]
- Li, J.F.; Zhang, X.F. Direction of arrival estimation of quasi-stationary signals using unfolded coprime array. IEEE Access 2017, 5, 6538–6545. [Google Scholar] [CrossRef]
- Zheng, W.; Zhang, X.F.; Gong, P.; Zhai, H. DOA estimation for coprime linear arrays: An Ambiguity-Free Method Involving Full DOFs. IEEE Commun. Lett. 2017, 22, 562–565. [Google Scholar] [CrossRef]
- Zhou, C.W.; Gu, Y.J.; He, S.B.; Shi, Z.G. A robust and efficient algorithm for coprime array adaptive beamforming. IEEE Trans. Veh. Technol. 2018, 67, 1099–1112. [Google Scholar] [CrossRef]
- Shi, Z.G.; Zhou, C.W.; Gu, Y.J.; Goodman, N.A.; Qu, F.Z. Source estimation using coprime array: A sparse reconstruction perspective. IEEE Sens. J. 2017, 17, 755–765. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P.P. Nested arrays: A novel approach to array processing with enhanced degrees of freedom. IEEE Trans. Signal Process. 2010, 58, 4167–4181. [Google Scholar] [CrossRef]
- Zheng, W.; Zhang, X.F.; Shi, J.P. Sparse Extension array geometry for DOA estimation with nested MIMO radar. IEEE Access 2017, 5, 9580–9586. [Google Scholar] [CrossRef]
- Liu, C.L.; Vaidyanathan, P.P. Super nested arrays: Linear sparse arrays with reduced mutual coupling—Part I: Fundamentals. IEEE Trans. Signal Process. 2016, 64, 3997–4012. [Google Scholar] [CrossRef]
- Liu, C.L.; Vaidyanathan, P.P. Super nested arrays: Linear sparse arrays with reduced mutual coupling—Part II: High-order extensions. IEEE Trans. Signal Process. 2016, 64, 4203–4217. [Google Scholar] [CrossRef]
- Liu, J.Y.; Zhang, Y.M.; Lu, Y.L.; Ren, S.W.; Cao, S. Augmented nested arrays with enhanced DOF and reduced mutual coupling. IEEE Trans. Signal Process. 2017, 65, 5549–5563. [Google Scholar] [CrossRef]
- Shi, J.P.; Hu, G.P.; Zhang, X.F.; Zhou, H. Generalized Nested Array: Optimization for Degrees of Freedom and Mutual Coupling. IEEE Commun. Lett. 2018, 22, 1208–1211. [Google Scholar] [CrossRef]
- Huang, H.; Liao, B.; Wang, X.; Guo, X.; Huang, J. A New Nested Array Configuration with Increased Degrees of Freedom. IEEE Access 2018, 6, 1490–1497. [Google Scholar] [CrossRef]
- Shan, T.J.; Wax, M.; Kailath, T. On spatial smoothing for direction-of-arrival estimation of coherent signals. IEEE Trans. Acoust. Speech Signal Process. 1985, 33, 806–811. [Google Scholar] [CrossRef]
- Stoica, P.; Arye, N. MUSIC, maximum likelihood, and Cramer-Rao bound. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 720–741. [Google Scholar] [CrossRef]
- Ziskind, I.; Wax, M. Maximum likelihood localization of multiple sources by alternating projection. IEEE Trans. Acoust. Speech Signal Process. 1988, 36, 1553–1560. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Amin, M.G.; Himed, B. Sparsity-based DOA estimation using co-prime arrays. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 3967–3971. [Google Scholar]
- Candes, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressive sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Baraniuk, R.G. Compressive sensing. IEEE Signal Process. Mag. 2007, 24, 118–121. [Google Scholar] [CrossRef]
- Sun, F.; Wu, Q.; Sun, Y.; Ding, G.; Lan, P. An iterative approach for sparse direction-of-arrival estimation in co-prime arrays with off-grid targets. Digit. Signal Process. 2017, 61, 35–42. [Google Scholar] [CrossRef]
- Cao, R.Z.; Liu, B.Y.; Gao, F.F.; Zhang, X.F. A low-complex one-snapshot DOA estimation algorithm with massive ULA. IEEE Commun. Lett. 2017, 21, 1071–1074. [Google Scholar] [CrossRef]
- Zhang, X.F.; Xu, L.Y.; Xu, D.Z. Direction of departure (DOD) and direction of arrival (DOA) estimation in MIMO radar with reduced-dimension MUSIC. IEEE Commun. Lett. 2010, 14, 1161–1163. [Google Scholar] [CrossRef]
- Ma, W.K.; Hsieh, T.H.; Chi, C.Y. DOA estimation of quasi-stationary signals via Khatri-Rao subspace. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 May 2009; pp. 2165–2168. [Google Scholar]
- Larsson, E.G.; Edfors, O.; Tufvesson, F.; Marzetta, T.L. Massive MIMO for next generation wireless systems. IEEE Commun. Mag. 2014, 52, 186–195. [Google Scholar] [CrossRef] [Green Version]
- Swindlehurst, A.L.; Kailath, T. Passive direction-of-arrival and range estimation for near-field sources. In Proceedings of the Fourth Annual ASSP Workshop on Spectrum Estimation Modeling, Minneapolis, MN, USA, 3–5 August 1988; pp. 123–128. [Google Scholar]
- He, J.; Swamy, M.N.S.; Ahmad, M.O. Efficient application of music algorithm under the coexistence of far-field and near-field sources. IEEE Trans. Signal Process. 2012, 60, 2066–2070. [Google Scholar] [CrossRef]
- Xie, J.; Tao, H.; Rao, X.; Su, J. Passive localization of noncircular sources in the near-field. In Proceedings of the 16th International Radar Symposium (IRS), Dresden, Germany, 24–26 June 2015; IEEE: Piscataway, NJ, USA, 2015. [Google Scholar]
- Wang, M.; Nehorai, A. Coarrays, MUSIC, and the Cramér—Rao Bound. IEEE Trans. Signal Process. 2017, 65, 933–946. [Google Scholar] [CrossRef]
- Zhou, C.W.; Gu, Y.J.; Fan, X.; Shi, Z.G.; Mao, G.Q.; Zhang, Y.D. Direction-of-arrival estimation for coprime array via virtual array interpolation. IEEE Trans. Signal Process. 2018, 66, 5956–5971. [Google Scholar] [CrossRef]
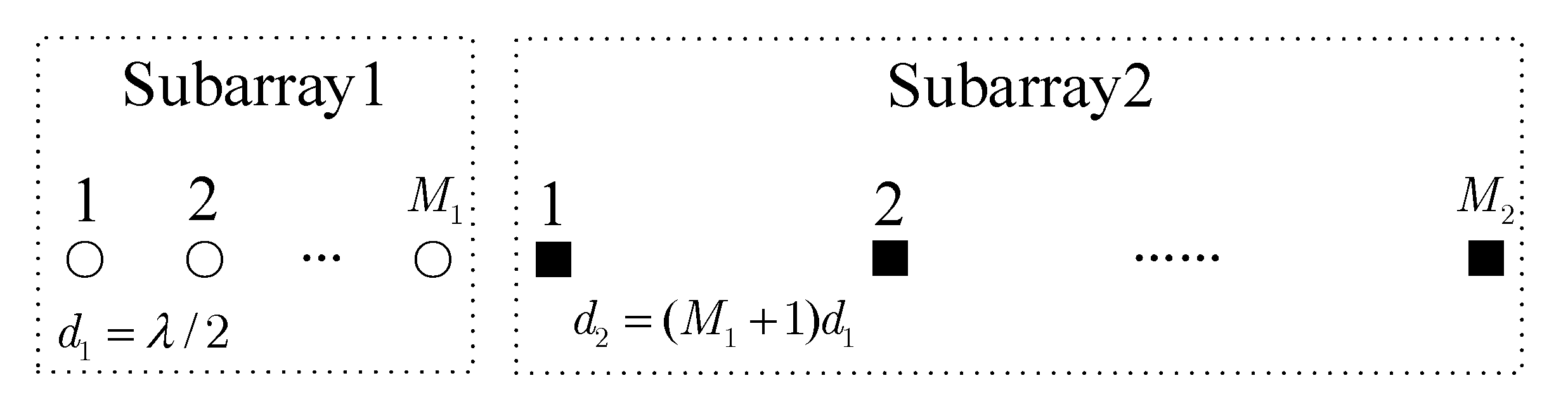





| Method | Complexity |
|---|---|
| Proposed | |
| SS-ESPRIT | |
| SS-MUSIC |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, W.; Wang, Y.; Zhang, X.; Li, J. Computationally Efficient Sources Location Method for Nested Array via Massive Virtual Difference Co-Array. Sensors 2019, 19, 1961. https://doi.org/10.3390/s19091961
Wu W, Wang Y, Zhang X, Li J. Computationally Efficient Sources Location Method for Nested Array via Massive Virtual Difference Co-Array. Sensors. 2019; 19(9):1961. https://doi.org/10.3390/s19091961
Chicago/Turabian StyleWu, Wei, Yunfei Wang, Xiaofei Zhang, and Jianfeng Li. 2019. "Computationally Efficient Sources Location Method for Nested Array via Massive Virtual Difference Co-Array" Sensors 19, no. 9: 1961. https://doi.org/10.3390/s19091961




