Focusing Sensor Design for Open Electrical Impedance Tomography Based on Shape Conformal Transformation †
Abstract
:1. Introduction
2. Materials and Methods
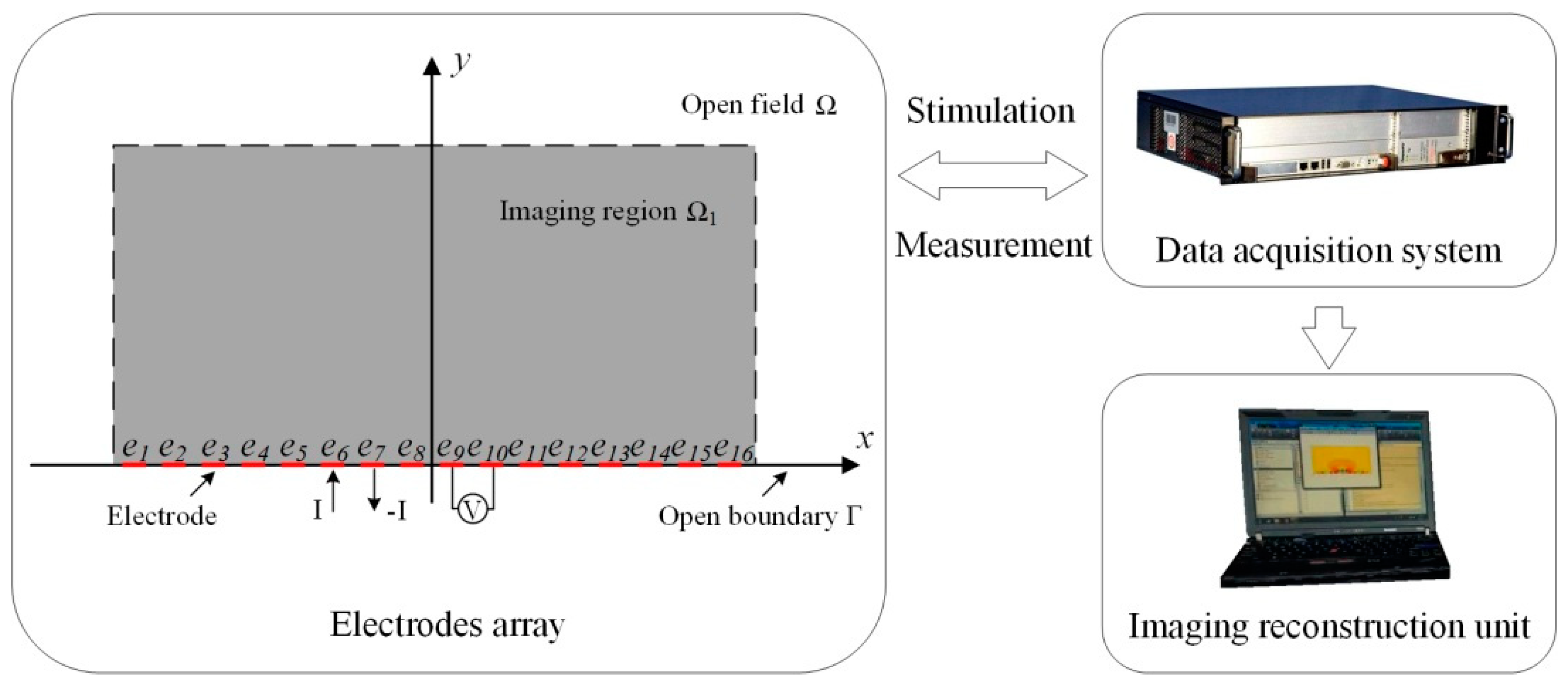
2.1. Principle of OEIT
- (1)
- The boundary voltage measurement data is collected by the electrodes placed on the boundary of the open field.
- (2)
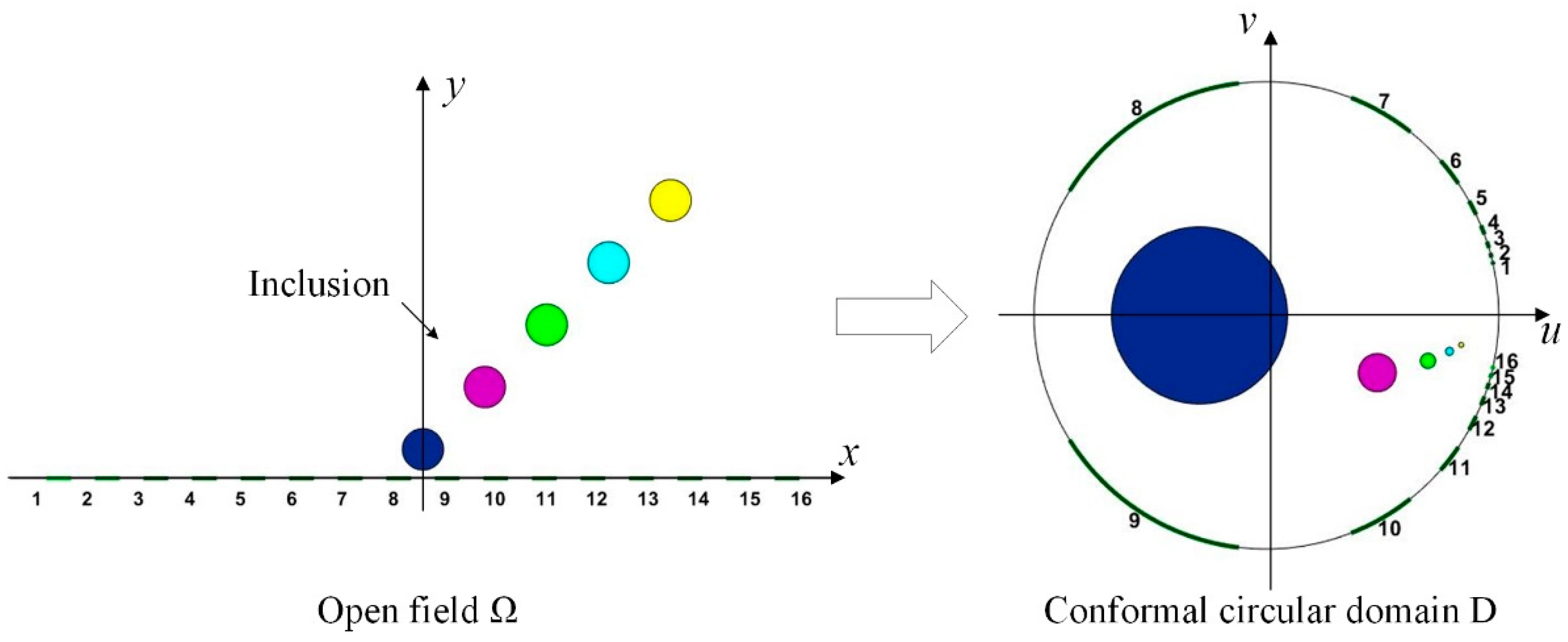
- The reconstructed image is obtained in the conformal circular domain according to the boundary voltage measurement.
- (3)
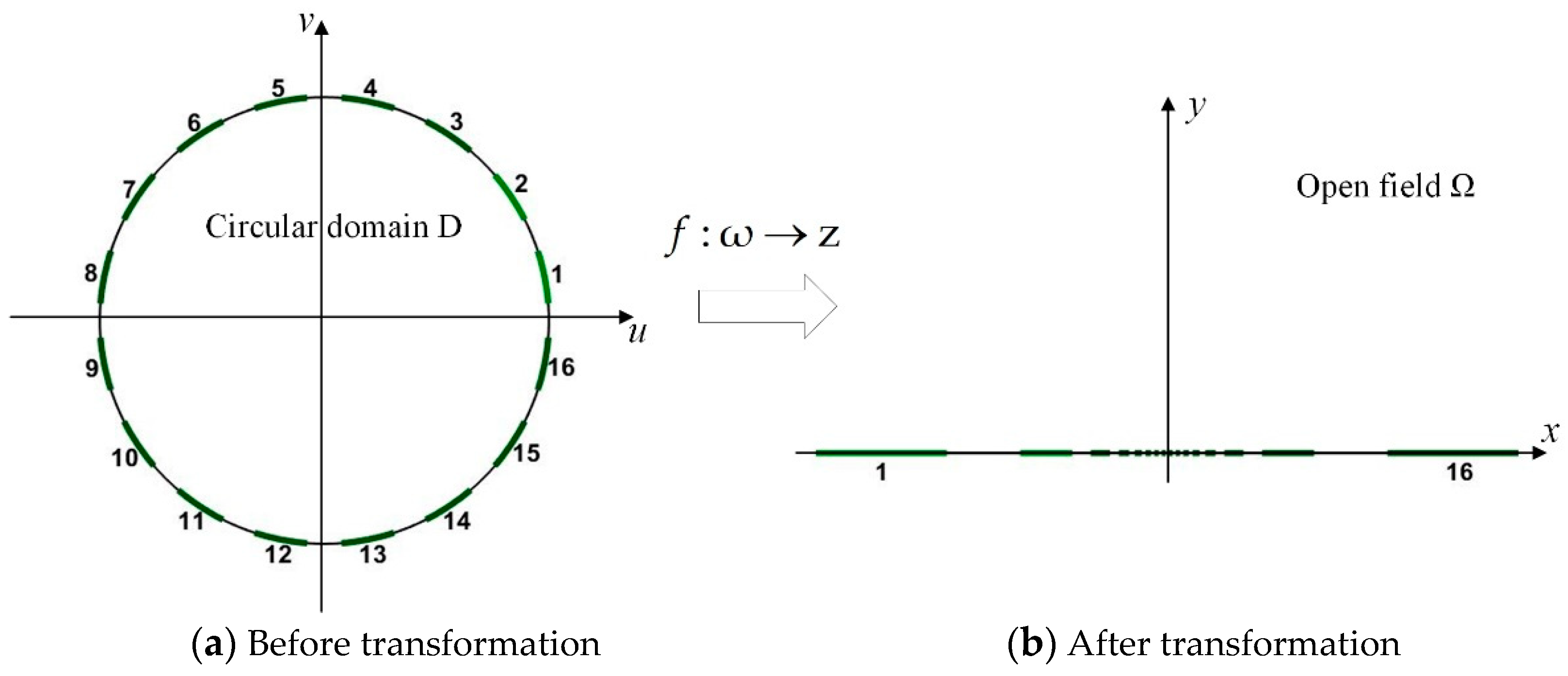
- The conductivity distribution image of the open field is mapped from the conformal circular domain by the mapping relation [18].
2.2. Focusing Sensor Design
2.3. Forward Problem Solutions
2.4. Inverse Problem Solutions
3. Results
3.1. Numerical Simulation
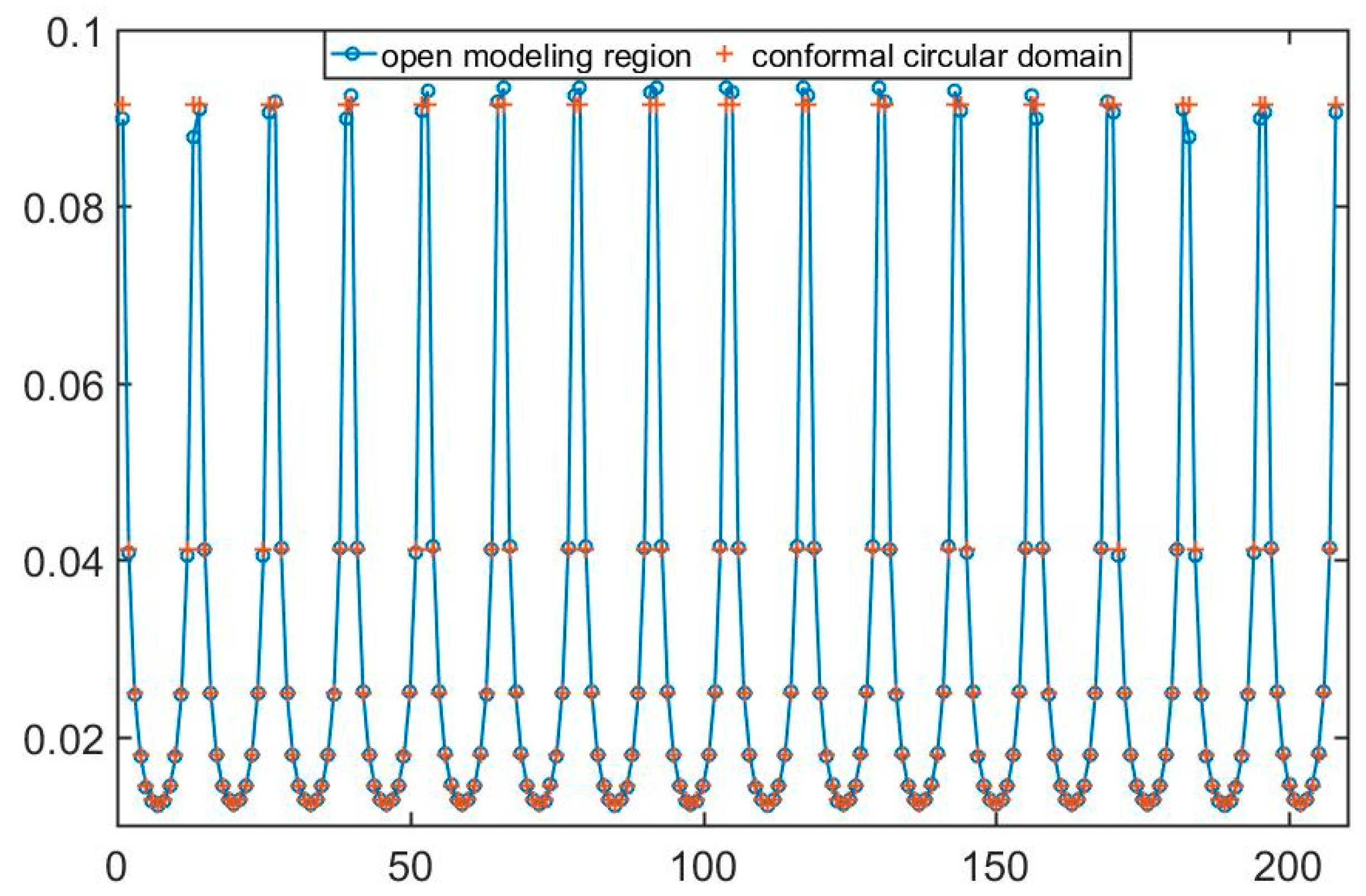
3.1.1. Boundary Measurement Consistency in Transformation Domain
3.1.2. Quantitative Index
- Resolution (RES) measures the ratio of the number of pixels in inclusions to the total number of pixels, as shown in (7). In the reconstructed images, the reconstructed inclusions are segmented from the reconstructed images by using a threshold of 75% maximum pixel amplitudes [31]. The total number of pixels represents the area of the region of interest for imaging. In this article, RES is used to measure the relative resolution of the focusing sensor and conventional uniform sensor. A smaller RES means the reconstructed image has high resolution for a similar inclusion:where Aq is the number of pixels in inclusions, An is the total number of pixels of the image region.
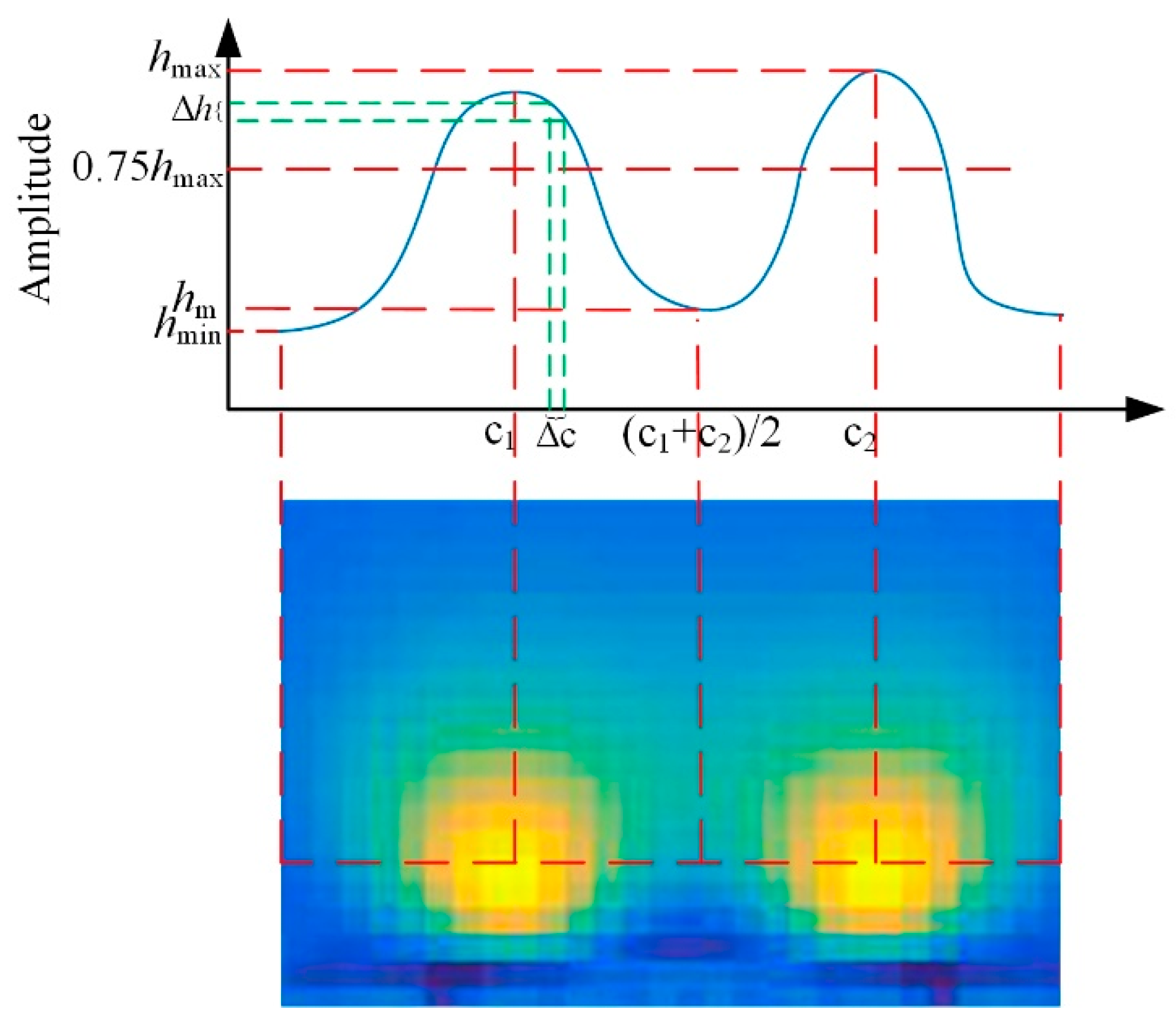
- Resolution ability (Ra) is defined as the measurement ability of distinguish between multiple inclusions. Figure 7 illustrates the schematic diagram of Ra with two inclusions as an example. The bottom row shows the reconstructed image, while the top row plots the amplitude across a row through the center of the multiple simulation inclusions. Ra compares the relationship between the amplitude at the midpoint of the centers of the two inclusions and the 75% maximum pixel amplitudes to measure whether the two inclusions can be clearly distinguished in the reconstructed image. The definition of Ra is shown in (8):where hm is the amplitude value at the midpoint of the centers of the two inclusions, hmax and hmin is the maximum and minimum value of the amplitude across the row through the center of the multiple simulation inclusions. For a certain reconstructed image, a Ra greater than 0 indicates that multiple inclusions can be distinguished; a Ra closer to 1 indicates a stronger ability to distinguish inclusions; while a Ra less than 0 indicates that multiple inclusions cannot be distinguished.
- Average gradient (Ag) is defined to measure the steepness of the multiple reconstructed inclusions boundary. As shown in Figure 7, Ag calculates the mean of the absolute value of gradient of the reconstructed pixels between the centers of the multiple simulation inclusions. The definition of Ag is shown in (9):where . Δc is the length between adjacent pixels. A large Ag means a large relative steepness of the reconstructed inclusion boundary.
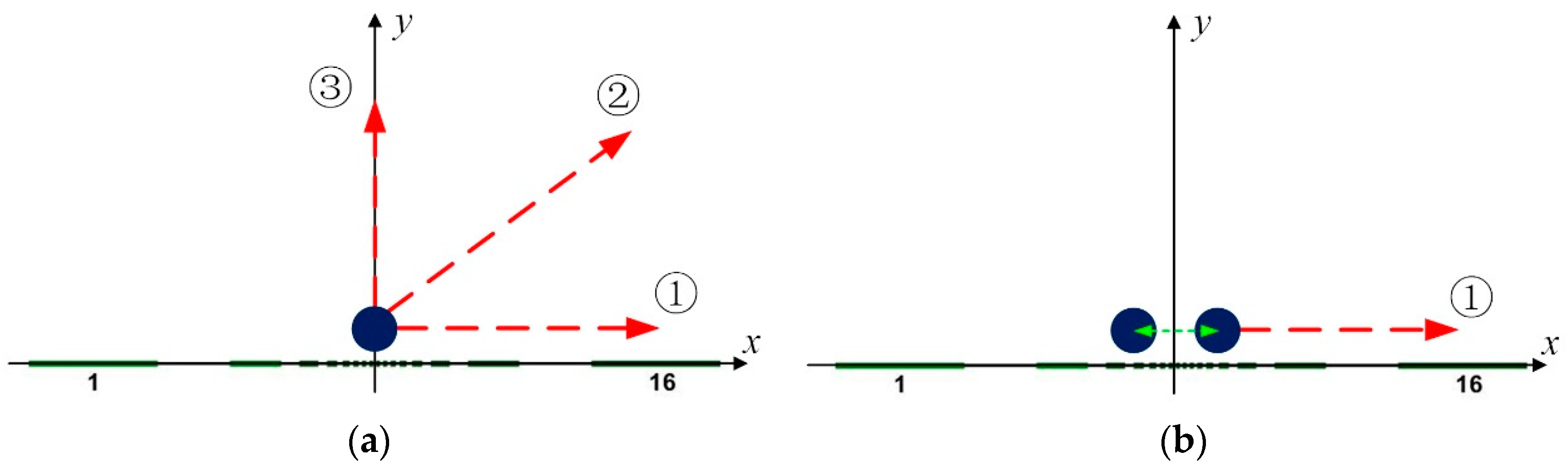
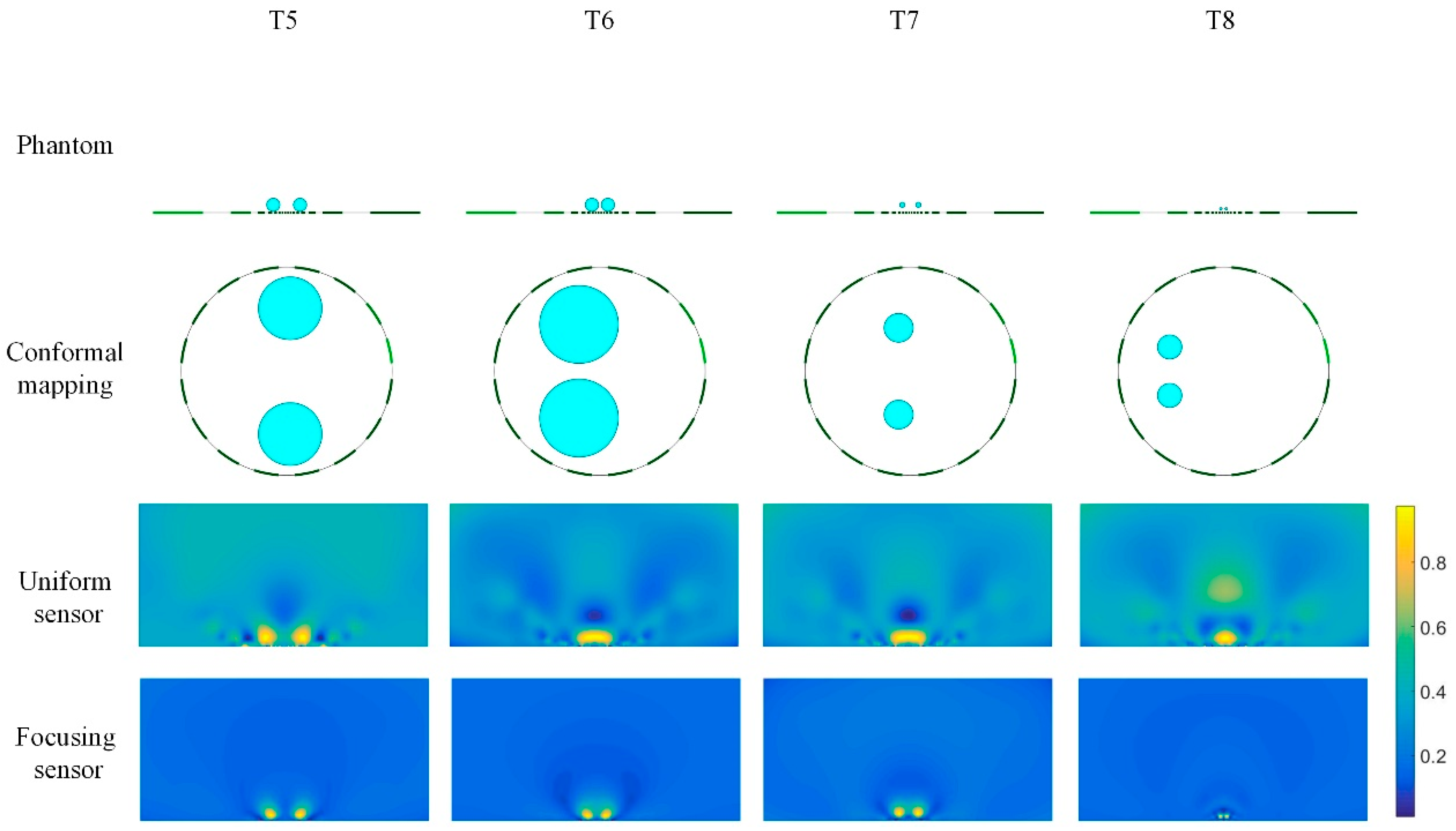
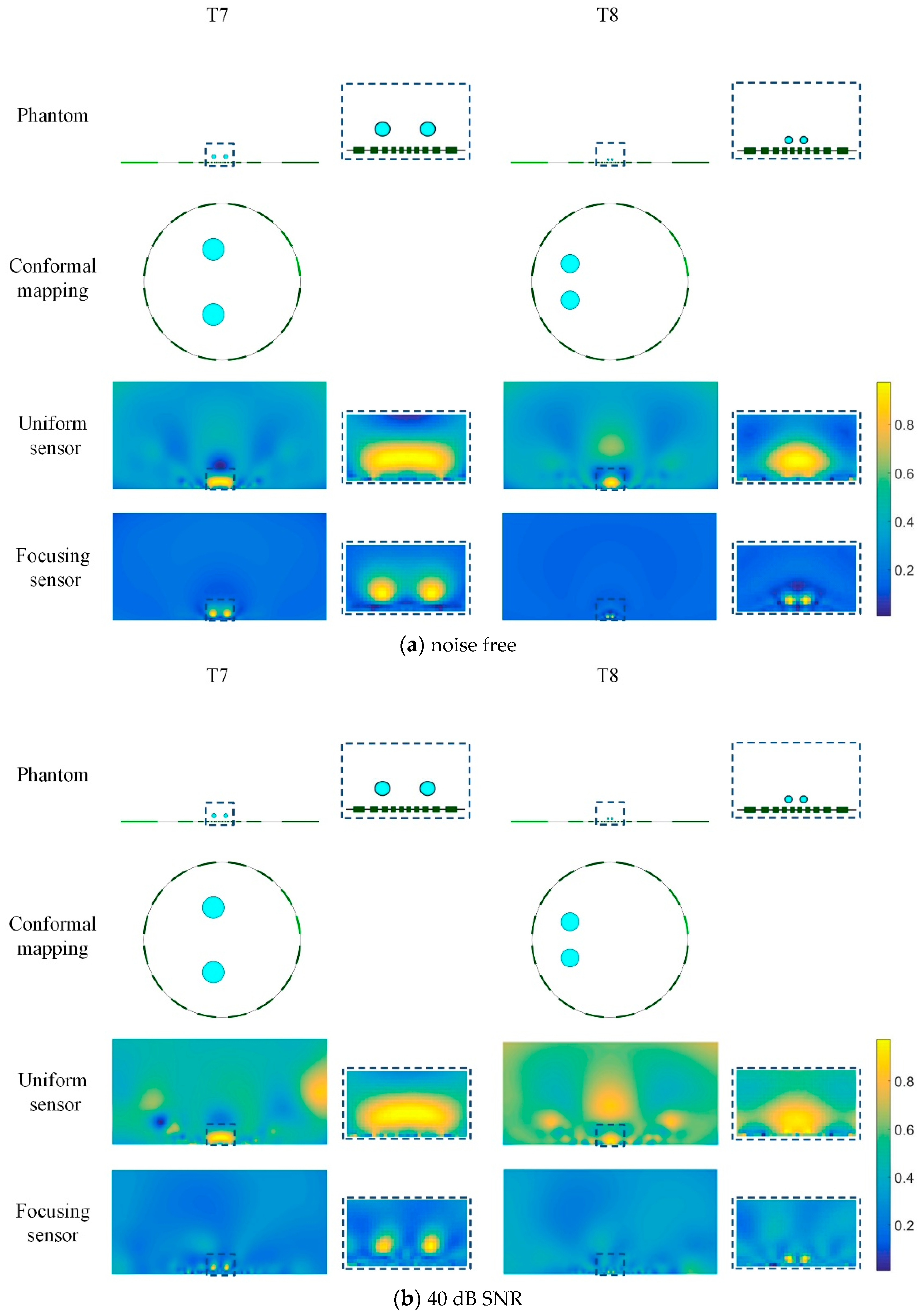
3.1.3. Reconstruction Analyses of Multiple Positions
3.1.4. Reconstruction Results Combining the Focusing Sensor and Uniform Sensor
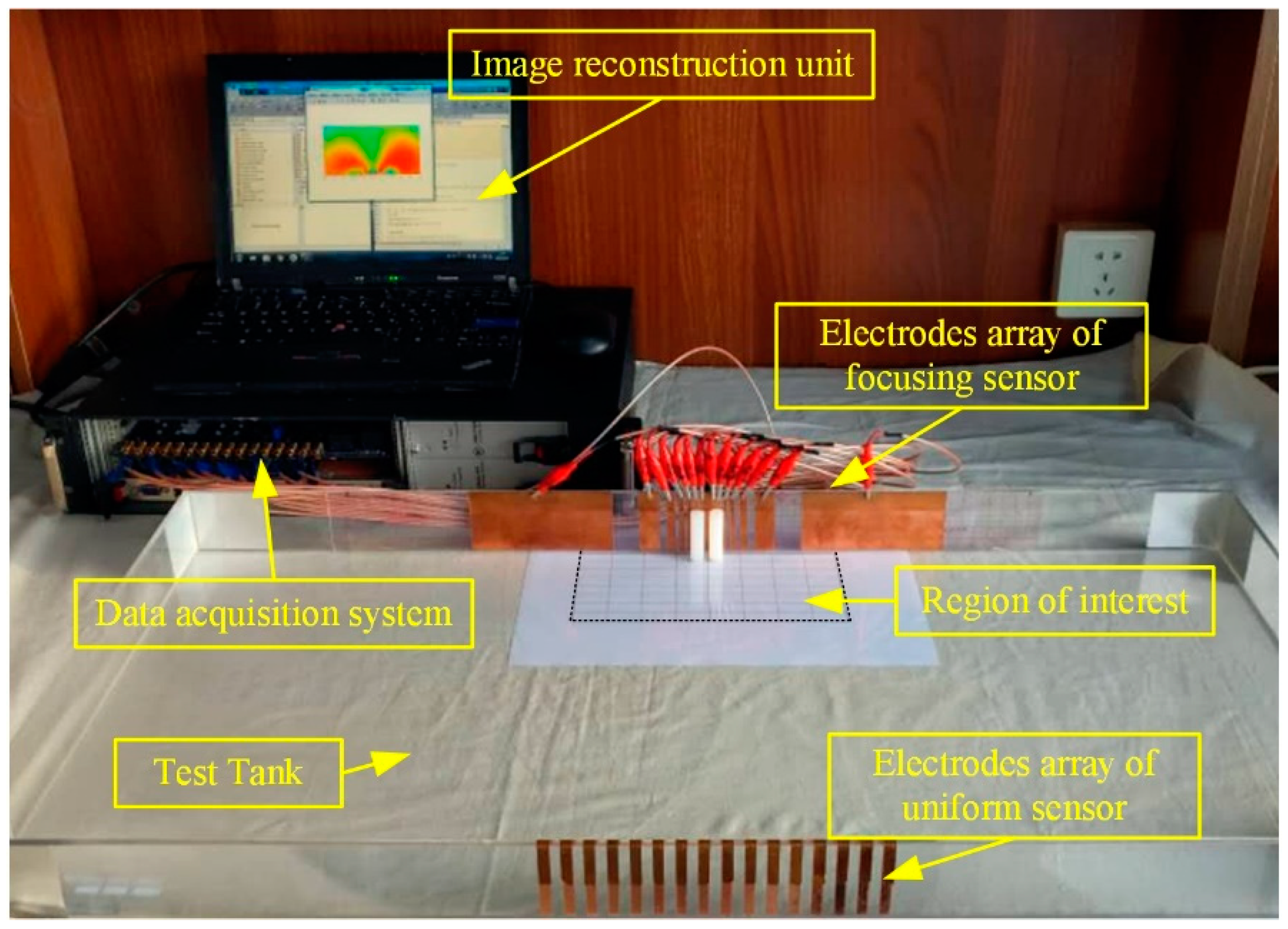
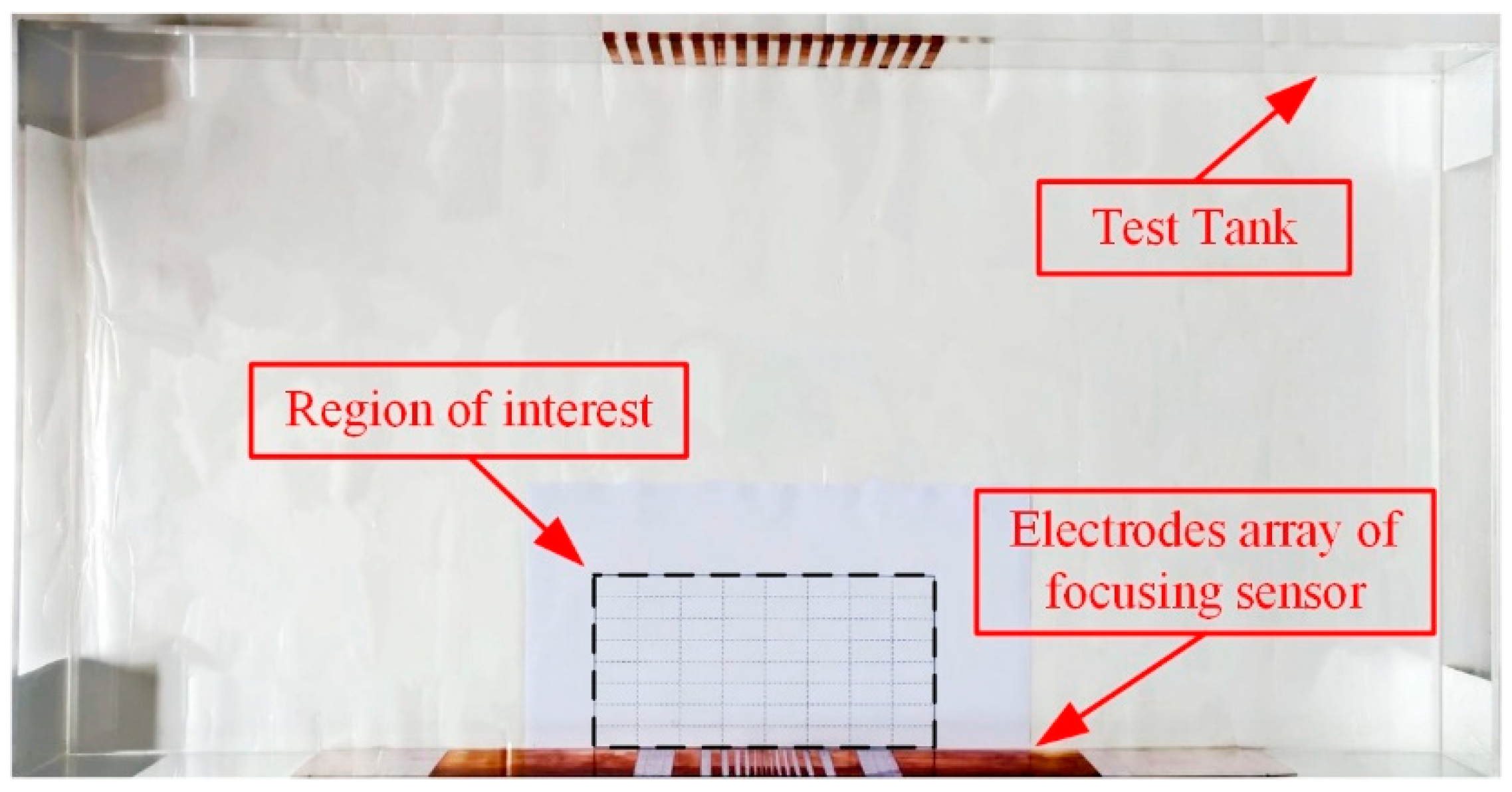
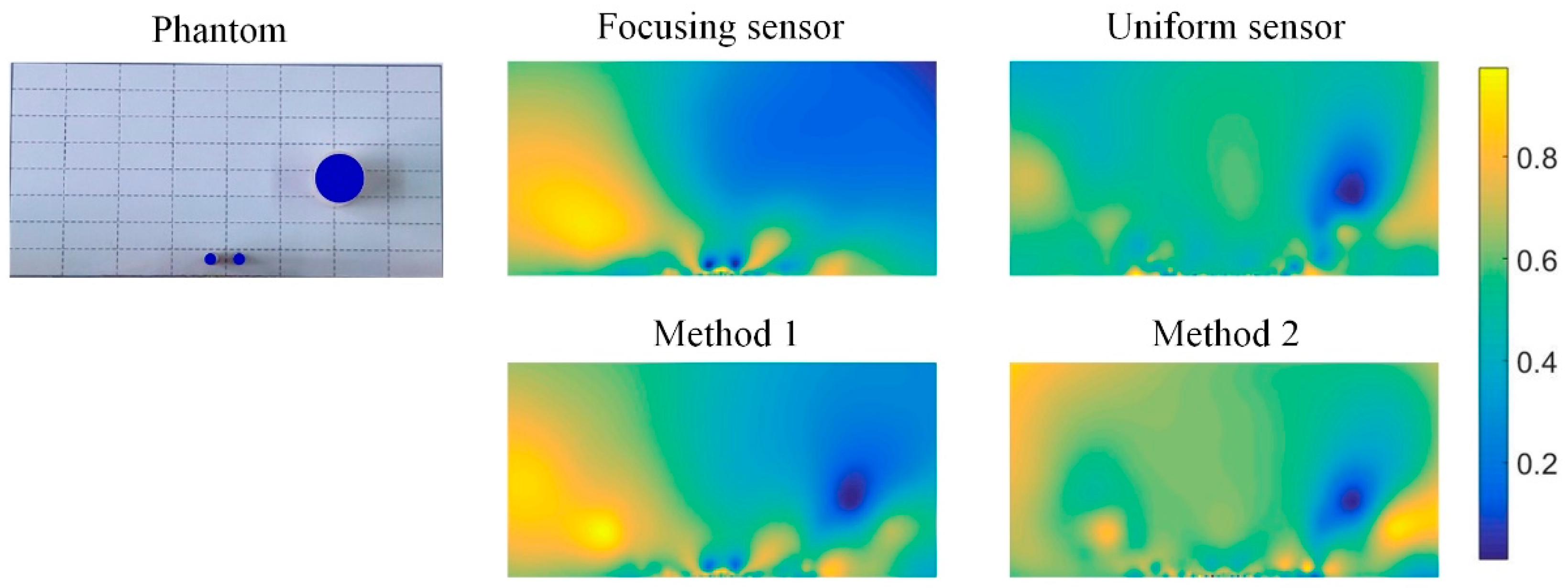
3.2. Experimental Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Holder, D.S. Electrical Impedance Tomography: Methods, History and Applications; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Yao, J.F.; Takei, M. Application of process tomography to multiphase flow measurement in industrial and biomedical fields—A review. IEEE Sens. J. 2017, 17, 8196–8205. [Google Scholar] [CrossRef]
- Xu, Z.F.; Yao, J.F.; Wang, Z.; Liu, Y.L.; Wang, H.; Chen, B.; Wu, H.T. Development of a portable electrical impedance tomography system for biomedical applications. IEEE Sens. J. 2018, 8, 8117–8124. [Google Scholar] [CrossRef]
- Ren, S.J.; Sun, K.; Liu, D.; Dong, F. A statistical shape constrained reconstruction framework for electrical impedance tomography. IEEE Trans. Med. Imag. 2019, in press. [Google Scholar] [CrossRef]
- Liu, D.; Kolehmainen, V.; Siltanen, S.; Laukkanen, A.M.; Seppanen, A. Estimation of conductivity changes in a region of interest with electrical impedance tomography. Inverse Probl. Imag. 2015, 9, 211–229. [Google Scholar] [CrossRef]
- Liu, D.; Khambampati, A.K.; Du, J. A parametric level set method for electrical impedance tomography. IEEE Trans. Med. Imag. 2018, 37, 451–460. [Google Scholar] [CrossRef] [PubMed]
- Youssef, A.M.; Elkaliouby, H.; Zabramawi, Y.A. Sinkhole detection using electrical resistivity tomography in Saudi Arabia. J. Geophys. Eng. 2012, 9, 655–663. [Google Scholar] [CrossRef]
- Church, P.; Mcfee, J.E.; Gagnon, S.; Wort, P. Electrical impedance tomographic imaging of buried landmines. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2407–2420. [Google Scholar] [CrossRef]
- Baltopoulos, A.; Polydorides, N.; Pambaguian, L.; Vavouliotis, A.; Kostopoulos, V. Damage identification in carbon fiber reinforced polymer plates using electrical resistance tomography mapping. J. Compos. Mater. 2013, 47, 3285–3301. [Google Scholar] [CrossRef]
- Allen, S.; Allen, L.R. Electrical impedance tomography-based sensing skin for quantitative imaging of damage in concrete. Smart Mater. Struct. 2014, 23, 085001. [Google Scholar]
- Mueller, J.L.; Isaacson, D.; Newell, J.C. Reconstruction of conductivity changes due to ventilation and perfusion from EIT data collected on a rectangular electrode array. Physiol. Meas. 2001, 22, 97–106. [Google Scholar] [CrossRef]
- Borsic, A.; Halter, R.; Wan, Y.; Hartov, A.; Paulsen, K.D. Electrical impedance tomography reconstruction for three-dimensional imaging of the prostate. Physiol. Meas. 2010, 31, S1-16. [Google Scholar] [CrossRef]
- Cherepenin, V.A.; Gulyaev, Y.V.; Korjenevsky, A.V.; Sapetsky, S.A.; Tuykin, T.S. An electrical impedance tomography system for gynecological application GIT with a tiny electrode array. Physiol. Meas. 2012, 33, 849–862. [Google Scholar]
- Aristovich, K.Y.; Santos, G.S.D.; Packham, B.C.; Holder, D.S. A method for reconstructing tomographic images of evoked neural activity with electrical impedance tomography using intracranial planar arrays. Physiol. Meas. 2014, 35, 1095–1109. [Google Scholar] [CrossRef] [PubMed]
- Murphy, E.K.; Mahara, A.; Halter, R.J. A novel regularization technique for microendoscopic electrical impedance tomography. IEEE Trans. Med. Imag. 2016, 35, 1593–1603. [Google Scholar] [CrossRef]
- Perez, H.; Pidcock, M.; Sebu, C. A three-dimensional image reconstruction algorithm for electrical impedance tomography using planar electrode arrays. Inverse Probl. Sci. Eng. 2017, 25, 471–491. [Google Scholar] [CrossRef]
- Liu, J.; Xiong, H.; Lin, L.; Li, G. Evaluation of measurement and stimulation patterns in open electrical impedance tomography with scanning electrode. Med. Biol. Eng. Comput. 2015, 53, 589–597. [Google Scholar] [CrossRef]
- Wang, Y.; Ren, S.J.; Dong, F. A transformation-domain image reconstruction method for open electrical impedance tomography based on conformal mapping. IEEE Sens. J. 2018, 19, 1873–1883. [Google Scholar] [CrossRef]
- Baber, C.C.; Brown, B.H.; Freeston, I.L. Imaging spatial distributions of resistivity using applied potential tomography. Electron. Lett. 1983, 19, 93–95. [Google Scholar]
- Vauhkonen, P.J.; Vauhkonen, M.; Savolainen, T.; Kaipio, J.P. Three-dimensional electrical impedance tomography based on the complete electrode model. IEEE Trans. Bio-Med. Eng. 1999, 46, 1150–1160. [Google Scholar] [CrossRef]
- Ahlfors, L.V. Complex Analysis, 3rd ed.; McGraw-Hill Book Company: New York, NY, USA, 1953. [Google Scholar]
- Kober, H. Dictionary of Conformal Representations, 2nd ed.; Dover Publications: New York, NY, USA, 1957. [Google Scholar]
- Adler, A.; Lionheart, W.R. Uses and abuses of EIDORS: An extensible software base for EIT. Physiol. Meas. 2006, 27, 25–42. [Google Scholar] [CrossRef] [PubMed]
- Ren, S.J.; Wang, Y.; Liang, G.H.; Dong, F. A robust inclusion boundary reconstructor for electrical impedance tomography with geometric constraints. IEEE Trans. Instrum. Meas. 2019, 68, 762–773. [Google Scholar] [CrossRef]
- Ren, S.J.; Soleimani, M.; Dong, F. Inclusion boundary reconstruction and sensitivity analysis in electrical impedance tomography. Inverse Probl. Sci. Eng. 2018, 26, 1037–1061. [Google Scholar] [CrossRef]
- Woo, E.J.; Hua, P.; Webster, J.G. Finite-element method in electrical impedance tomography. Med. Biol. Eng. Comput. 1994, 32, 530–536. [Google Scholar] [CrossRef] [PubMed]
- Chittenden, C.T.; Soleimani, M. Planar array capacitive imaging sensor design optimization. IEEE Sens. J. 2017, 17, 8059–8071. [Google Scholar] [CrossRef]
- Vauhkonen, M.; Vadasz, D.; Karjalainen, P.A.; Somersalo, E.; Kaipio, J.P. Tikhonov regularization and prior information in electrical impedance tomography. IEEE Trans. Med. Imag. 1998, 17, 285–293. [Google Scholar] [CrossRef]
- Borsic, A.; Graham, B.M.; Adler, A.; Lionheart, W.R.B. In vivo impedance imaging with total variation regularization. IEEE Trans. Med. Imag. 2010, 29, 44–54. [Google Scholar] [CrossRef]
- Brandstatter, B. Jacobian calculation for electrical impedance tomography based on the reciprocity principle. IEEE Trans. Magn. 2003, 39, 1309–1312. [Google Scholar] [CrossRef]
- Adler, A.; Arnold, J.H.; Bayford, R.; Borsic, A.; Brown, B.; Dixon, P.; Faes, T.J.C.; Frerichs, I.; Gagon, H.; Garber, Y.; et al. GREIT: A unified approach to 2D linear EIT reconstruction of lung images. Physiol. Meas. 2009, 30, 35–55. [Google Scholar] [CrossRef]
- Yang, W.Q.; Peng, L.H. Image reconstruction algorithms for electrical capacitance tomography. Meas. Sci. Technol. 2003, 14, R1–R13. [Google Scholar] [CrossRef]
- Tan, C.; Liu, S.W.; Jia, J.B.; Dong, F. A Wideband Electrical Impedance Tomography System Based on Sensitive Bioimpedance Spectrum Bandwidth. IEEE Trans. Instrum. Meas. 2019, in press. [Google Scholar] [CrossRef]






| T5 | T6 | T7 | T8 | |||||
|---|---|---|---|---|---|---|---|---|
| Uniform | Focusing | Uniform | Focusing | Uniform | Focusing | Uniform | Focusing | |
| Ra | 0.642 | 0.813 | −0.132 | 0.611 | −0.149 | 0.545 | −0.217 | 0.498 |
| Ag | 4.531 | 6.045 | 0.728 | 12.145 | 0.538 | 14.266 | 0.911 | 28.644 |
| RE | 0.132 | 0.143 | 0.177 | 0.101 | 0.233 | 0.131 | 0.250 | 0.089 |
| CC | 0.855 | 0.872 | 0.780 | 0.842 | 0.750 | 0.851 | 0.714 | 0.887 |
| Noise Free | 40 dB SNR | |||||||
|---|---|---|---|---|---|---|---|---|
| T7 | T8 | T7 | T8 | |||||
| Uniform | Focusing | Uniform | Focusing | Uniform | Focusing | Uniform | Focusing | |
| Ra | −0.149 | 0.545 | −0.217 | 0.498 | −0.161 | 0.441 | −0.117 | 0.312 |
| Ag | 0.538 | 14.266 | 0.911 | 28.644 | 0.507 | 13.889 | 0.912 | 28.627 |
| RE | 0.233 | 0.131 | 0.250 | 0.089 | 0.251 | 0.142 | 0.370 | 0.136 |
| CC | 0.750 | 0.851 | 0.714 | 0.887 | 0.678 | 0.788 | 0.623 | 0.811 |
| Electrode Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| (16) | (15) | (14) | (13) | (12) | (11) | (10) | (9) | |
| Length (mm) | 110 | 15.5 | 6.0 | 3.5 | 2.6 | 2.0 | 1.7 | 1.5 |
| E1 | E2 | E3 | E4 | |||||
|---|---|---|---|---|---|---|---|---|
| Uniform | Focusing | Uniform | Focusing | Uniform | Focusing | Uniform | Focusing | |
| RE | 0.314 | 0.150 | 0.238 | 0.093 | 0.271 | 0.164 | 0.325 | 0.137 |
| CC | 0.681 | 0.879 | 0.713 | 0.895 | 0.737 | 0.828 | 0.632 | 0.841 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Ren, S.; Dong, F. Focusing Sensor Design for Open Electrical Impedance Tomography Based on Shape Conformal Transformation. Sensors 2019, 19, 2060. https://doi.org/10.3390/s19092060
Wang Y, Ren S, Dong F. Focusing Sensor Design for Open Electrical Impedance Tomography Based on Shape Conformal Transformation. Sensors. 2019; 19(9):2060. https://doi.org/10.3390/s19092060
Chicago/Turabian StyleWang, Yu, Shangjie Ren, and Feng Dong. 2019. "Focusing Sensor Design for Open Electrical Impedance Tomography Based on Shape Conformal Transformation" Sensors 19, no. 9: 2060. https://doi.org/10.3390/s19092060
APA StyleWang, Y., Ren, S., & Dong, F. (2019). Focusing Sensor Design for Open Electrical Impedance Tomography Based on Shape Conformal Transformation. Sensors, 19(9), 2060. https://doi.org/10.3390/s19092060





