Flying Small Target Detection for Anti-UAV Based on a Gaussian Mixture Model in a Compressive Sensing Domain
Abstract
:1. Introduction
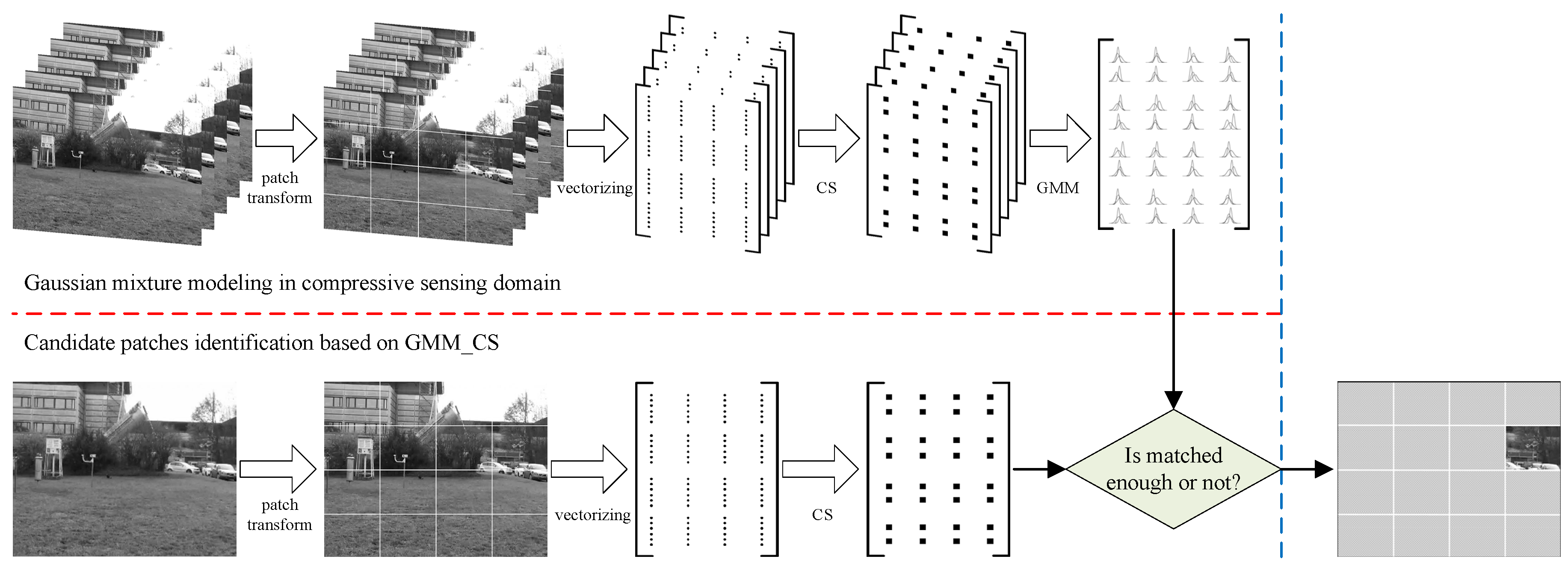
2. Gaussian Mixture Modeling in a Compressive Sensing Domain
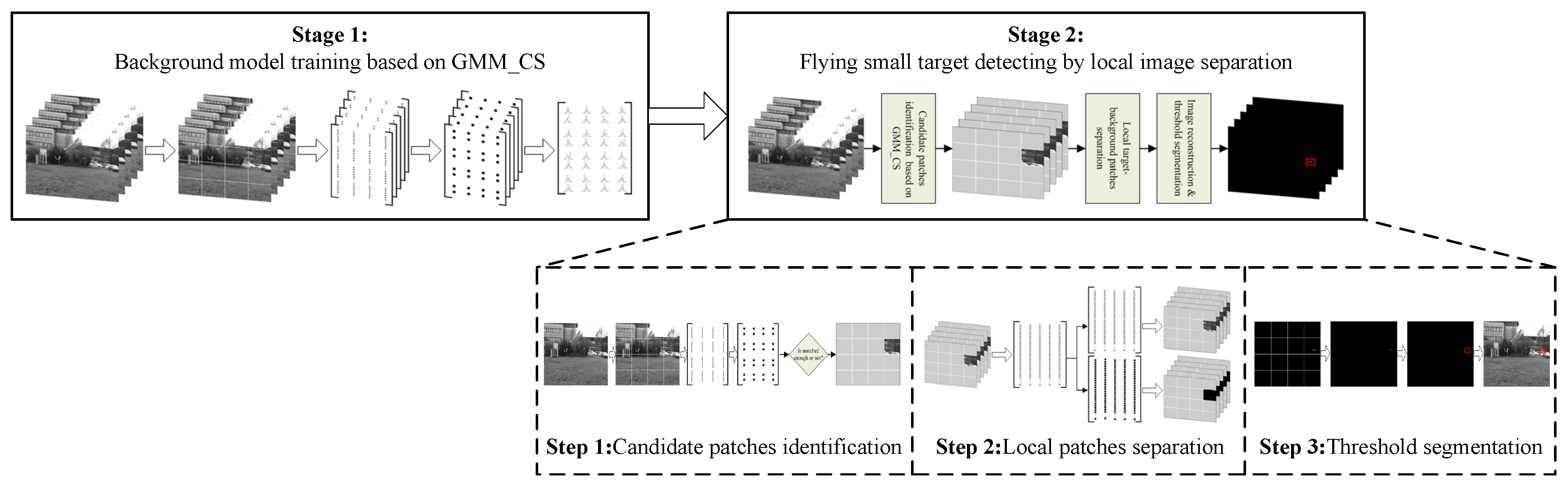
3. Approach to Flying Small Target Detection by Local Image Separation
3.1. Candidate Patches Identification Based on GMM_CS
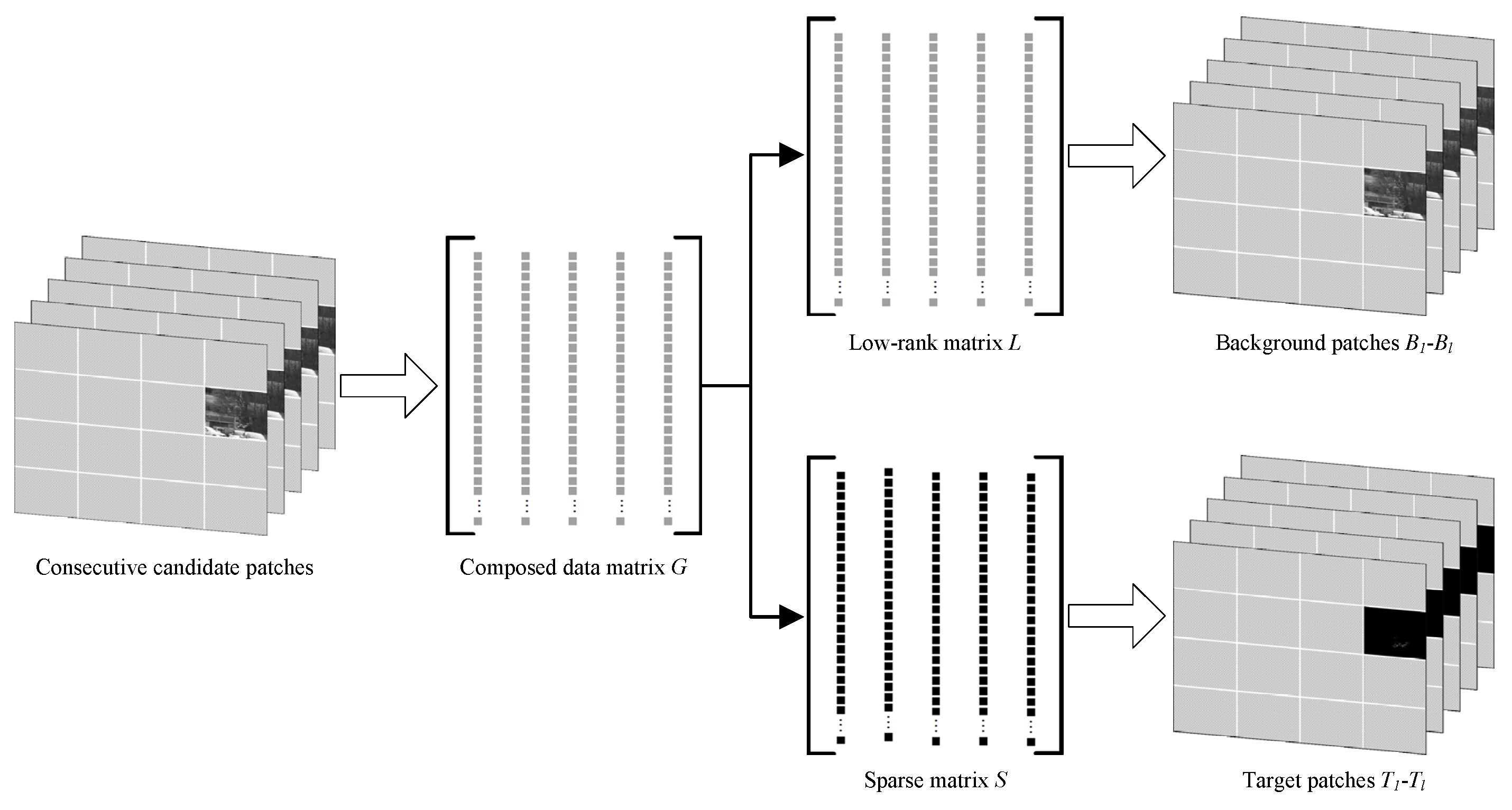
3.2. Local Target-Background Patches Separation
3.3. Comprehensive Scheme and Algorithm Implementation
| Algorithm 1 Approach to flying small target detection based on GMM_CS. |
| Input: Flying small target image sequence |
| Output: Detection results of each image in sequence |
|
4. Experimental Results and Analysis
4.1. Experiment Setting and Evaluation Metrics
4.2. Performance Evaluation and Comparative Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, T.; Qin, R.; Chen, Y.; Snoussi, H.; Choi, C. A reinforcement learning approach for UAV target searching and tracking. Multimedia Tools Appl. 2019, 78, 4347–4364. [Google Scholar] [CrossRef]
- Ganti, S.R.; Kim, Y. Implementation of detection and tracking mechanism for small UAS. In Proceedings of the 2016 International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016; pp. 1254–1260. [Google Scholar]
- Mian, A.S. Realtime visual tracking of aircrafts. In Proceedings of the Digital Image Computing: Techniques and Applications (DICTA’08), Canberra, ACT, Australia, 1–3 December 2008; pp. 351–356. [Google Scholar]
- Farlik, J.; Kratky, M.; Casar, J.; Stary, V. Radar cross section and detection of small unmanned aerial vehicles. In Proceedings of the 2016 17th International Conference on Mechatronics-Mechatronika (ME), Prague, Czech Republic, 7–9 December 2016; pp. 1–7. [Google Scholar]
- Hoffmann, F.; Ritchie, M.; Fioranelli, F.; Charlish, A.; Griffiths, H. Micro-Doppler based detection and tracking of UAVs with multistatic radar. In Proceedings of the 2016 IEEE Radar Conference (RadarConf), Philadelphia, PA, USA, 2–6 May 2016; pp. 1–6. [Google Scholar]
- Tapsall, T.B. Using crowd sourcing to combat potentially illegal or dangerous UAV operations. In Unmanned/ Unattended Sensors and Sensor Networks XII; International Society for Optics and Photonics: Edinburgh, UK, 2016; Volume 9986, p. 998605. [Google Scholar]
- Shi, X.; Yang, C.; Xie, W.; Chao, L.; Shi, Z.; Chen, J. Anti-Drone System with Multiple Surveillance Technologies: Architecture, Implementation, and Challenges. IEEE Commun. Mag. 2018, 56, 68–74. [Google Scholar] [CrossRef]
- Sosnowski, T.; Bieszczad, G.; Madura, H.; Kastek, M. Thermovision system for flying objects detection. In Proceedings of the 2018 Baltic URSI Symposium (URSI), Poznan, Poland, 15–17 May 2018; pp. 141–144. [Google Scholar]
- Hwang, K.; Har, D. Identifying Small Drones Using Infrared Polarization Filters. TECHART J. Arts Imaging Sci. 2016, 3, 50–54. [Google Scholar] [CrossRef]
- Li, J.; Ye, D.H.; Chung, T.; Kolsch, M.; Wachs, J.; Bouman, C. Multi-target detection and tracking from a single camera in Unmanned Aerial Vehicles (UAVs). In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Daejeon, South Korea, 9–14 October 2016; pp. 4992–4997. [Google Scholar]
- Rozantsev, A.; Lepetit, V.; Fua, P. Flying objects detection from a single moving camera. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR2015), Boston, MA, USA, 7–12 June 2015; pp. 4128–4136. [Google Scholar]
- Rozantsev, A.; Lepetit, V.; Fua, P. Detecting Flying Objects using a Single Moving Camera. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 879–892. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Cao, Y.; Ding, M.; Zhuang, L.; Wang, Z. Spatial and Temporal Context Information Fusion Based Flying Objects Detection for Autonomous Sense and Avoid. In Proceedings of the 2018 International Conference on Unmanned Aircraft Systems (ICUAS), Dallas, TX, USA, 12–15 June 2018; pp. 569–578. [Google Scholar]
- Du, L.; Gao, C.; Feng, Q.; Wang, C.; Liu, J. Small UAV Detection in Videos from a Single Moving Camera. In Proceedings of the CCF Chinese Conference on Computer Vision, Tianjin, China, 11–14 October 2017; Springer: Singapore, 2017; pp. 187–197. [Google Scholar]
- Wu, P.F.; Xiao, F.; Sha, C.; Huang, H.P.; Wang, R.C.; Xiong, N.X. Node Scheduling Strategies for Achieving Full-View Area Coverage in Camera Sensor Networks. Sensors 2017, 17, 1303. [Google Scholar] [CrossRef]
- Han, R.; Yang, W.; Zhang, L. Achieving Crossed Strong Barrier Coverage in Wireless Sensor Network. Sensors 2018, 18, 534. [Google Scholar] [CrossRef] [PubMed]
- Rossi, P.S.; Ciuonzo, D.; Kansanen, K.; Ekman, T. On energy detection for MIMO decision fusion in wireless sensor networks over NLOS fading. IEEE Commun. Lett. 2015, 19, 303–306. [Google Scholar] [CrossRef]
- Rossi, P.S.; Ciuonzo, D.; Kansanen, K.; Ekman, T. Performance analysis of energy detection for MIMO decision fusion in wireless sensor networks over arbitrary fading channels. IEEE Trans. Wirel. Commun. 2016, 15, 7794–7806. [Google Scholar] [CrossRef]
- Rossi, P.S.; Ciuonzo, D.; Ekman, T. HMM-based decision fusion in wireless sensor networks with noncoherent multiple access. IEEE Commun. Lett. 2015, 19, 871–874. [Google Scholar] [CrossRef]
- Stein, D.W. Detection of random signals in Gaussian mixture noise. IEEE Trans. Inf. Theory 1995, 41, 1788–1801. [Google Scholar] [CrossRef]
- Zhuang, X.; Huang, J.; Potamianos, G.; Hasegawa-Johnson, M. Acoustic fall detection using Gaussian mixture models and GMM supervectors. In Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; pp. 69–72. [Google Scholar]
- Wang, T.; Qiao, M.; Chen, J.; Wang, C.; Zhang, W.; Snoussi, H. Abnormal global and local event detection in compressive sensing domain. AIP Adv. 2018, 8, 055224. [Google Scholar] [CrossRef]
- Stauffer, C.; Grimson, W.E.L. Adaptive Background Mixture Models for Real-Time Tracking. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR1999), Fort Collins, CO, USA, 23–25 June 1999; Volume 2, pp. 246–252. [Google Scholar]
- Kozick, R.J.; Sadler, B.M. Maximum-likelihood array processing in non-Gaussian noise with Gaussian mixtures. IEEE Trans. Signal Process. 2000, 48, 3520–3535. [Google Scholar]
- Cevher, V.; Sankaranarayanan, A.; Duarte, M.F.; Reddy, D.; Baraniuk, R.G.; Chellappa, R. Compressive Sensing for Background Subtraction; Springer: Berlin/Heidelberg, Germany, 2008; pp. 155–168. [Google Scholar]
- Fornasier, M.; Rauhut, H. Compressive sensing. In Handbook of Mathematical Methods in Imaging; Springer: New York, NY, USA, 2011; pp. 187–228. [Google Scholar]
- Liu, Y.; Pados, D.A. Compressed-Sensed-Domain L1-PCA Video Surveillance. IEEE Trans. Multimedia 2016, 18, 351–363. [Google Scholar] [CrossRef]
- Lu, C.; Shi, J.; Jia, J. Online Robust Dictionary Learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition(CVPR2013), Portland, OR, USA, 23–28 June 2013; pp. 415–422. [Google Scholar]
- Baraniuk, R.G. A lecture on compressive sensing. IEEE Signal Process. Mag. 2007, 24, 118–121. [Google Scholar] [CrossRef]
- Candès, E.J. The restricted isometry property and its implications for compressed sensing. C. R. Math. 2008, 346, 589–592. [Google Scholar] [CrossRef]
- Candès, E.J.; Tao, T. Decoding by linear programming. IEEE Trans. Inf. Theory 2005, 51, 4203–4215. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Li, H.; Li, T.; Gao, F. Infrared small target detection in compressive domain. Electron. Lett. 2014, 50, 510–512. [Google Scholar] [CrossRef]
- Wang, C.; Qin, S. Background Modeling of Infrared Image in Dynamic Scene with Gaussian Mixture Model in Compressed Sensing Domain. Acta Autom. Sin. 2018, 44, 1212–1226. [Google Scholar]
- Wang, T.; Qiao, M.; Lin, Z.; Li, C.; Snoussi, H.; Liu, Z.; Choi, C. Generative Neural Networks for Anomaly Detection in Crowded Scenes. IEEE Trans. Inf. Forensics Secur. 2019, 14, 1390–1399. [Google Scholar] [CrossRef]
- Gan, L. Block Compressed Sensing of Natural Images. In Proceedings of the International Conference on Digital Signal Processing, Cardiff, UK, 1–4 July 2007; pp. 403–406. [Google Scholar]
- Cho, T.S.; Butman, M.; Avidan, S.; Freeman, W.T. The patch transform and its applications to image editing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR2008), Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Candès, E.J.; Li, X.; Ma, Y.; Wright, J. Robust principal component analysis? J. ACM 2011, 58, 1–39. [Google Scholar] [CrossRef]
- Chen, C.; Li, S.; Qin, H.; Hao, A. Robust salient motion detection in non-stationary videos via novel integrated strategies of spatio-temporal coherency clues and low-rank analysis. Pattern Recognit. 2016, 52, 410–432. [Google Scholar] [CrossRef]
- Wright, J.; Ganesh, A.; Rao, S.; Ma, Y. Robust Principal Component Analysis: Exact Recovery of Corrupted Low-Rank Matrices via Convex Optimization. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 7–10 December 2009; pp. 2080–2088. [Google Scholar]
- Wang, C.; Qin, S. Approach for moving small target detection in infrared image sequence based on reinforcement learning. J. Electron. Imaging 2016, 25, 053032. [Google Scholar] [CrossRef]
- Waters, A.E.; Sankaranarayanan, A.C.; Baraniuk, R. SpaRCS: Recovering low-rank and sparse matrices from compressive measurements. In Proceedings of the Advances in Neural Information Processing Systems, Granada, Spain, 12–14 December 2011; pp. 1089–1097. [Google Scholar]
- Lee, K.; Bresler, Y. ADMiRA: Atomic decomposition for minimum rank approximation. IEEE Trans. Inf. Theory 2010, 56, 4402–4416. [Google Scholar] [CrossRef]
- Needell, D.; Tropp, J.A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples. Appl. Comput. Harmon. Anal. 2009, 26, 301–321. [Google Scholar] [CrossRef] [Green Version]
- Berg, A.; Ahlberg, J.; Felsberg, M. A thermal Object Tracking benchmark. In Proceedings of the IEEE International Conference on Advanced Video and Signal Based Surveillance, Karlsruhe, Germany, 25–28 August 2015; pp. 1–6. [Google Scholar]
- Kaewtrakulpong, P.; Bowden, R. An Improved Adaptive Background Mixture Model for Real-time Tracking with Shadow Detection. In Video Based Surveillance Systems; Remagnino, P., Jones, G.A., Paragios, N., Regazzoni, C.S., Eds.; Springer: Boston, MA, USA, 2002; pp. 135–144. [Google Scholar] [Green Version]
- He, J.; Balzano, L.; Szlam, A. Incremental gradient on the Grassmannian for online foreground and background separation in subsampled video. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition(CVPR2012), Providence, RI, USA, 16–21 June 2012; pp. 1568–1575. [Google Scholar]
- Zhou, X.; Yang, C.; Yu, W. Moving Object Detection by Detecting Contiguous Outliers in the Low-Rank Representation. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 597–610. [Google Scholar] [CrossRef] [Green Version]
- Sobral, A. BGSLibrary: An opencv c++ background subtraction library. In Proceedings of the IX Workshop De Visão Computacional, Botafogo, Rio de Janeiro, Brazil, 3–5 June 2013; pp. 1–6. [Google Scholar]




| Notations | Descriptions |
|---|---|
| s | the number of Gaussian distribution |
| the weight of the Gaussian distribution | |
| the mean of the Gaussian distribution | |
| the variance of the Gaussian distribution | |
| a vector stacked by an image with n pixels | |
| a compressive sensing measurement vector with m dimensions | |
| a sparse basis matrix composed by q n-dim basis vectors | |
| a measurement matrix composed by m n-dim Gaussian distribution | |
| the weighting coefficients vector of in the domain | |
| a constant for Gaussian distribution identification | |
| the learning rate of weight of the Gaussian distribution | |
| the learning rate of mean and variance of the Gaussian distribution | |
| the value of the Gaussian distribution matched or not | |
| the value of the linear measurement matched or not | |
| a threshold for identifying image patch maintain target or not | |
| a matrix composed by r rows and c columns block matrices | |
| G | a matrix composed by a group of vectorized consecutive patches |
| L | the low-rank matrix decomposed from matrix G via RPCA |
| S | the sparse matrix decomposed from matrix G via RPCA |
| R | the rank of the low-rank matrix L |
| K | the sparse degree of the sparse matrix S |
| a weight parameter for tradeoff the matrices L and S | |
| the column vector of matrix U after SVD | |
| the column vector of matrix V after SVD | |
| a subset of the entire set of singular vectors | |
| a subset of the entire set of position support terms |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Wang, T.; Wang, E.; Sun, E.; Luo, Z. Flying Small Target Detection for Anti-UAV Based on a Gaussian Mixture Model in a Compressive Sensing Domain. Sensors 2019, 19, 2168. https://doi.org/10.3390/s19092168
Wang C, Wang T, Wang E, Sun E, Luo Z. Flying Small Target Detection for Anti-UAV Based on a Gaussian Mixture Model in a Compressive Sensing Domain. Sensors. 2019; 19(9):2168. https://doi.org/10.3390/s19092168
Chicago/Turabian StyleWang, Chuanyun, Tian Wang, Ershen Wang, Enyan Sun, and Zhen Luo. 2019. "Flying Small Target Detection for Anti-UAV Based on a Gaussian Mixture Model in a Compressive Sensing Domain" Sensors 19, no. 9: 2168. https://doi.org/10.3390/s19092168
APA StyleWang, C., Wang, T., Wang, E., Sun, E., & Luo, Z. (2019). Flying Small Target Detection for Anti-UAV Based on a Gaussian Mixture Model in a Compressive Sensing Domain. Sensors, 19(9), 2168. https://doi.org/10.3390/s19092168





