A Hydrodynamic Model for Measuring Fluid Density and Viscosity by Using Quartz Tuning Forks
Abstract
:1. Introduction
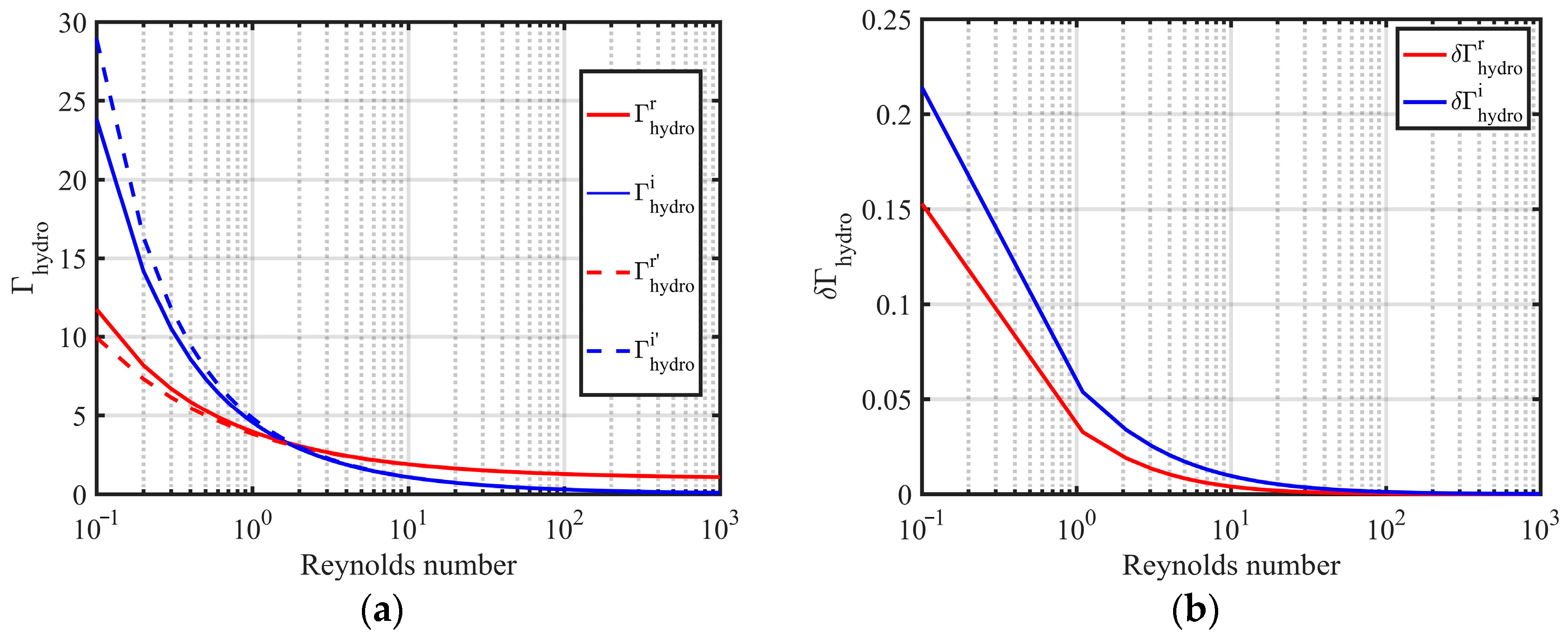
2. Hydrodynamic Model
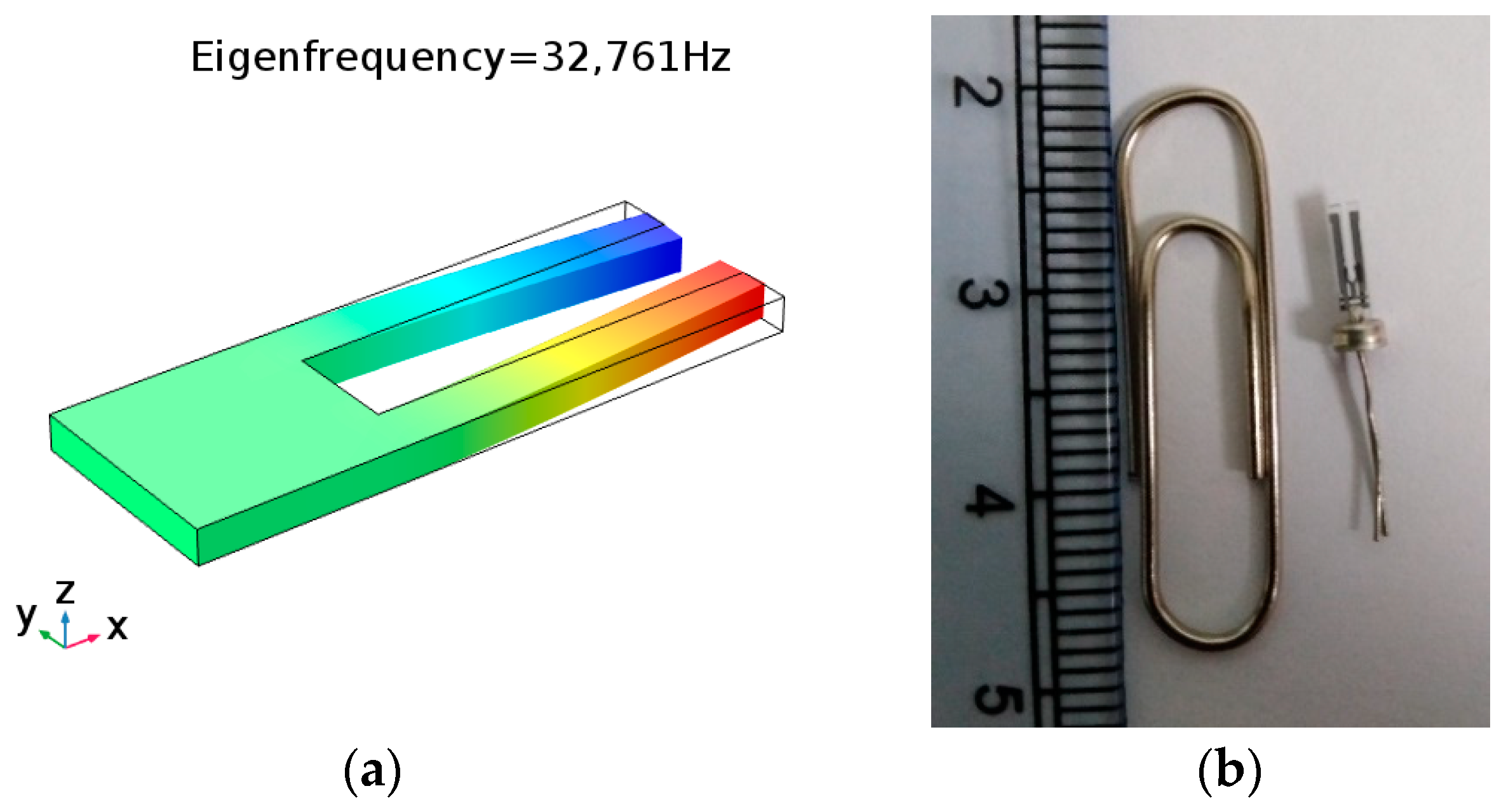
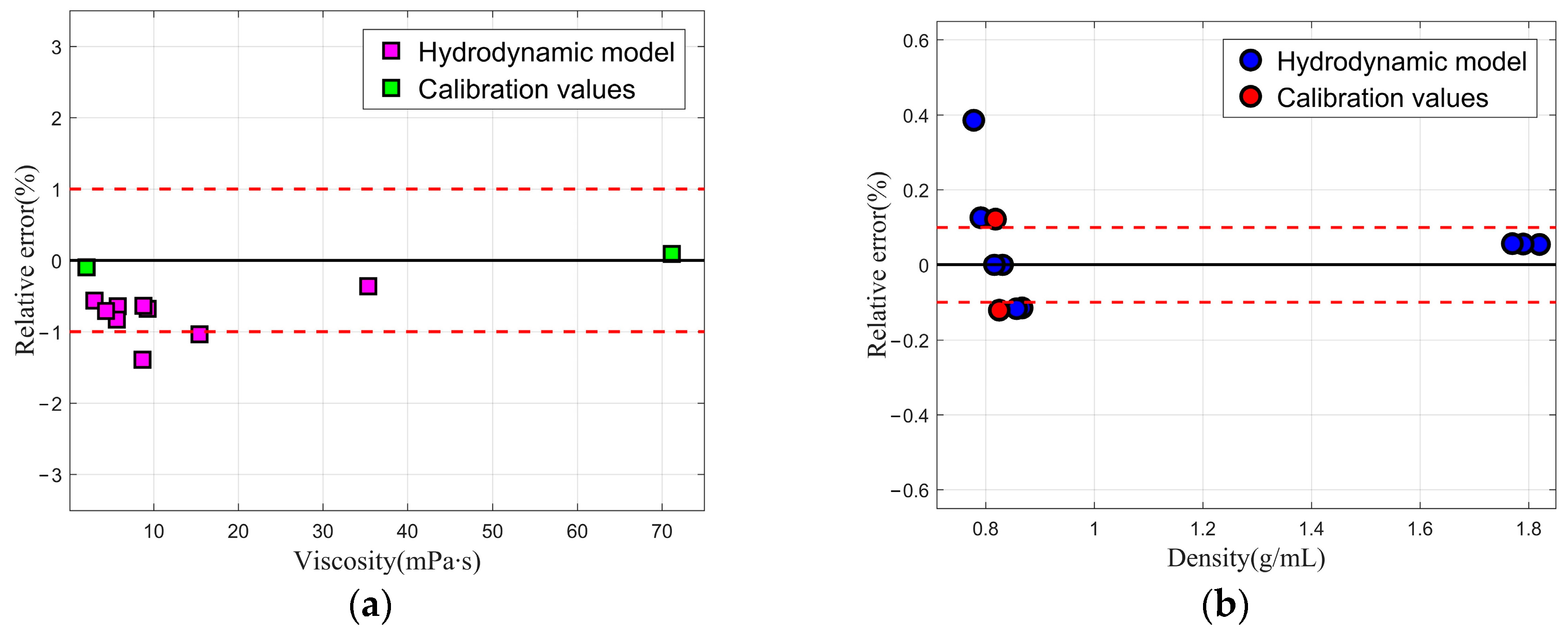
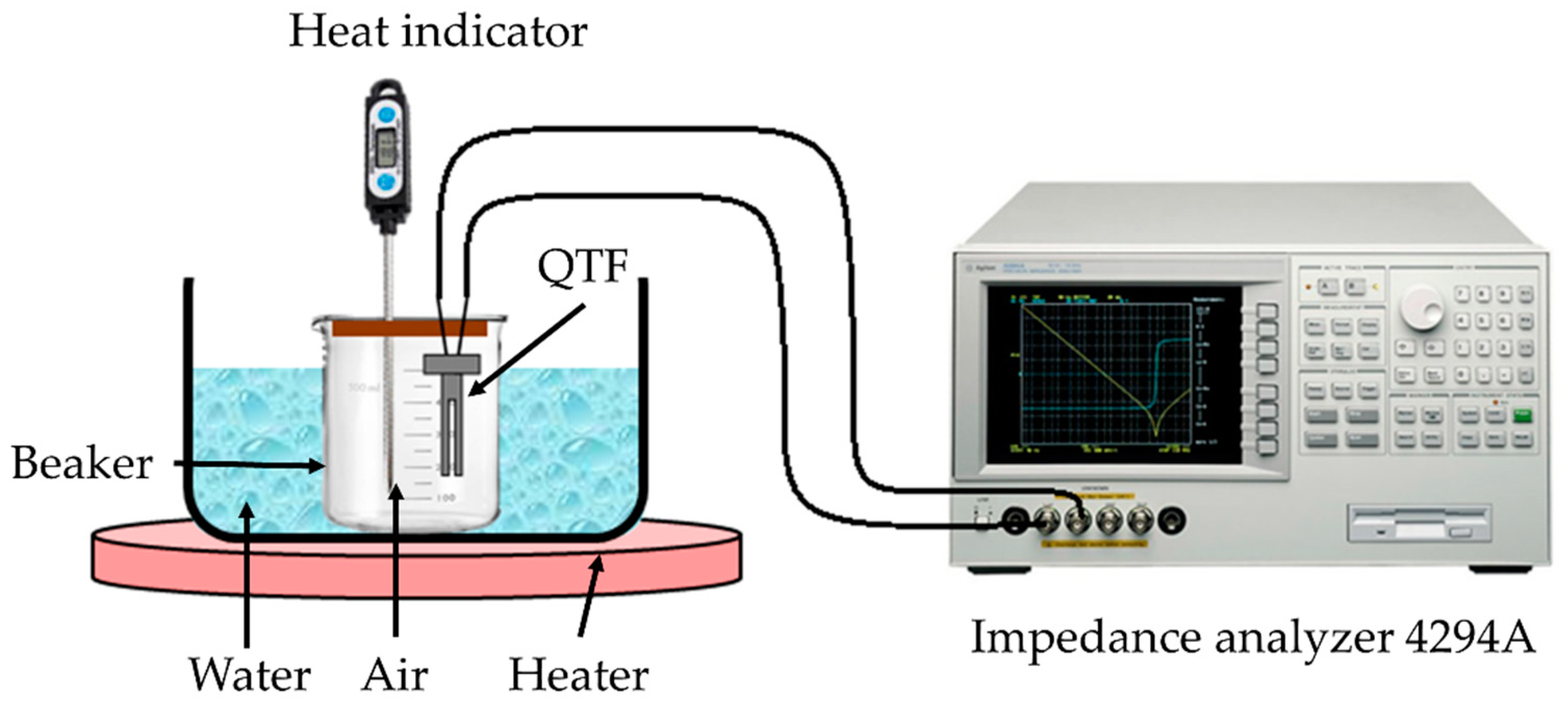
3. Model Validation
3.1. Example 1
3.2. Example 2
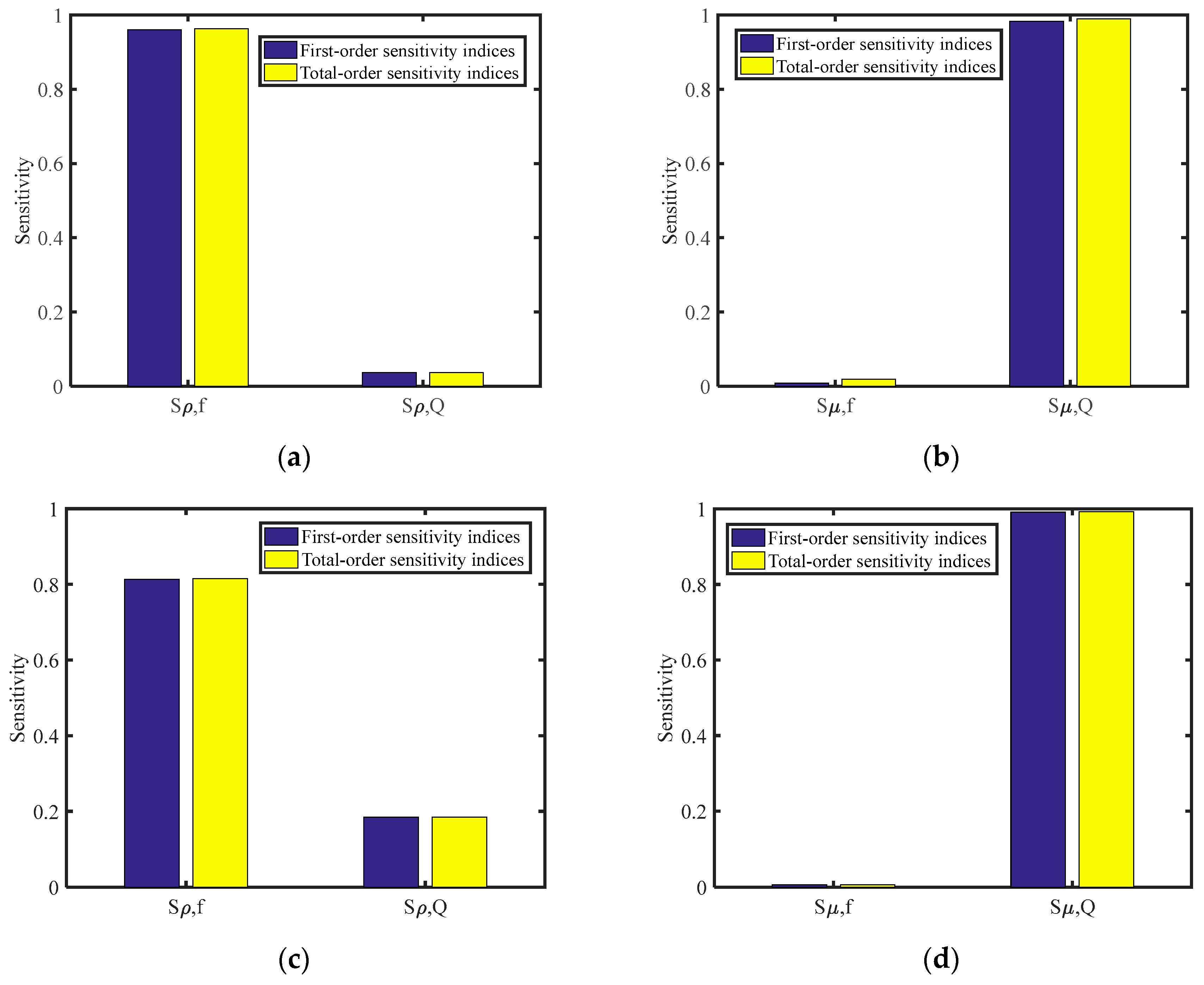
4. Sensitivity Analysis
5. Sensitivity to Temperature
6. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Toledo, J.; Manzaneque, T.; Ruiz-Díez, V.; Jiménez-Márquez, F.; Kucera, M.; Pfusterschmied, G.; Wistrela, E.; Schmid, U.; Sánchez-Rojas, J.L. Comparison of in-plane and out-of-plane piezoelectric microresonators for real- time monitoring of engine oil contamination with diesel. Microsyst. Technol. 2016, 22, 1781–1790. [Google Scholar] [CrossRef]
- Toledo, J.; Jiménez-Márquez, F.; Úbeda, J.; Ruiz-Díez, V.; Pfusterschmied, G.; Schmid, U.; Sánchez-Rojas, J.L. Piezoelectric MEMS resonators for monitoring grape must fermentation. In Proceedings of the Micromechanics Europe 2016: 27th Micromechanics and Microsystems Europe Workshop, Cork, Ireland, 28–30 August 2016. [Google Scholar]
- Toledo, J.; Ruiz-Díez, V.; Pfusterschmied, G.; Schmid, U.; Sánchez-Rojas, J.L. Flow-through sensor based on piezoelectric MEMS resonator for the in-line monitoring of wine fermentation. Sens. Actuators B Chem. 2018, 254, 291–298. [Google Scholar] [CrossRef]
- González, M.; Ham, G. Downhole viscosity measurement platform using tuning fork oscillators. In Proceedings of the IEEE SENSORS 2015, Busan, Korea, 13–15 November 2015; pp. 1–4. [Google Scholar]
- González, M.; Seren, H.; Buzi, E.; Deffenbaugh, M. Fast downhole fluid viscosity and density measurements using a self-oscillating tuning fork device. In Proceedings of the 2017 IEEE Sensors Applications Symposium, Glassboro, NJ, USA, 13–15 March 2017. [Google Scholar]
- Matsiev, L.F.; Bennett, J.; Kolosov, O. High precision tuning fork sensor for liquid property measurements. In Proceedings of the 2005 IEEE Ultrasonics Symposium, Rotterdam, The Netherlands, 18–21 September 2005; pp. 1492–1495. [Google Scholar]
- Burdett, I.; Lynn, T.; Kolosov, O.; Zilker, D.P.; Matsiev, L. Monitoring Bed of Polymer Particles in a Fluidized Bed Polymerization Reactor System Involves Contacting a Mechanical Resonator Sensor with Polymer Particles in the Reactor System; and Monitoring a Response of the Resonator. U.S. Patent 2007/0003450 A1, 4 January 2007. [Google Scholar]
- Matsiev, L.F. Application of Flexural Mechanical Resonators to High Throughput Liquid Characterization. In Proceedings of the 2000 IEEE Ultrasonics Symposium, San Juan, PR, USA, 22–25 October 2000; pp. 427–434. [Google Scholar]
- Rocco, D.; Difoggio, R.; Walkow, A.; Bergren, P.; Reittinger, P.W. Downhole Tool for Drilling or Wire Line Operations, Has Flexural Mechanical Resonator Which is Actuated in Response to Sonde Output to Determine Fluid Parameters. EP Patent 1397661 B1, 10 September 2008. [Google Scholar]
- Yi, X.; Jingbo, Z.; Deyang, C.; Chenguan, Z.; Wentong, F. The research of tight gas reservoir fluid identification in Kuche. Chin. J. Eng. Geophys. 2014, 11, 137–141. [Google Scholar]
- Hongxin, Z.; Lusheng, Z.; Cong, Y.; Hongme, W.; Ningde, J. Capacitive phase shift detection for measuring water holdup in horizontal oil–water two-phase flow. Sensors 2018, 18, 2234. [Google Scholar]
- Waszczuk, K.; Piasecki, T.; Nitsch, K.; Gotszalk, T. Application of piezoelectric tuning forks in liquid viscosity and density measurements. Sens. Actuators B Chem. 2011, 160, 517–523. [Google Scholar] [CrossRef]
- Matsiev, L. Measurements of liquid density and viscosity with flexural resonators using noise as an excitation source. In Proceedings of the 2006 IEEE Ultrasonics Symposium, Vancouver, BC, Canada, 3–6 October 2006; pp. 880–883. [Google Scholar]
- Sell, J.K.; Niedermayer, A.O.; Babik, S.; Jakoby, B. Gas density sensor for real-time monitoring in a high pressure reactor. Procedia Chem. 2009, 1, 108–111. [Google Scholar] [CrossRef] [Green Version]
- Friedt, J.M.; Carry, É. Introduction to the quartz tuning fork. Am. J. Phys. 2007, 75, 415–422. [Google Scholar] [CrossRef] [Green Version]
- Sell, J.K.; Niedermayer, A.O.; Jakoby, B. Reactance-locked loop for driving resonant sensors. In Proceedings of the 2012 IEEE International Instrumentation and Measurement Technology Conference, Graz, Austria, 13–16 May 2012. [Google Scholar]
- Matsiev, L.F.; Bennett, J.W.; McFarland, E.W. Application of flexural mechanical resonators to simultaneous measurements of liquid density and viscosity. In Proceedings of the 1999 IEEE Ultrasonics Symposium, Nevada, NV, USA, 17–20 October 1999; pp. 457–460. [Google Scholar]
- Toledo, J.; Manzaneque, T.; Hernando-Garcia, J.; Vazquez, J.; Ababneh, A.; Seidel, H.; Lapuerta, M.; Sanchez-Rojas, J.L. Application of quartz tuning forks and extensional microresonators for viscosity and density measurements in oil/fuel mixtures. Microsyst. Technol. 2014, 20, 945–953. [Google Scholar] [CrossRef]
- Liu, Y.; Rocco, D.; Kerry, S.; Louis, P.; Jinsong, Z. Measurement of density and viscosity of dodecane and decane with a piezoelectric tuning fork over 298–448K and 0.1–137.9MPa. Sens. Actuators A Phys. 2011, 167, 347–353. [Google Scholar] [CrossRef]
- Pfusterschmied, G.; Kucera, M.; Wistrela, E.; Manzaneque, T.; Ruiz-Díez, V.; Sánchez-Rojas, J. Temperature dependent performance of piezoelectric MEMS resonators for viscosity and density determination of liquids. J. Micromech. Microeng. 2015, 25, 5–14. [Google Scholar] [CrossRef]
- Ruiz-Díez, V.; Toledo, J.; Hernando-García, J.; Ababneh, A.; Seidel, H.; Sánchez-Rojas, J. A geometrical study on the roof tile-shaped modes in AlN-based piezoelectric microcantilevers as viscosity–density sensors. Sensors 2019, 19, 658. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Voglhuber-Brunnmaier, T.; Niedermayer, A.O.; Heinisch, M.; Abdallah, A.; Reichel, E.K.; Jakoby, B.; Putz, V.; Beigelbeck, R. Modeling-free evaluation of resonant liquid sensors for measuring viscosity and density. In Proceedings of the 2015 9th International Conference on Sensing Technology (ICST), Auckland, New Zealand, 8–10 December 2015; pp. 300–305. [Google Scholar]
- Zhang, J.; Dai, C.; Su, X.; O’Shea, S.J. Determination of liquid density with a low frequency mechanical sensor based on quartz tuning fork. Sens. Actuators B Chem. 2002, 84, 123–128. [Google Scholar] [CrossRef]
- Cox, R.; Josse, F.; Heinrich, S.M.; Brand, O.; Dufour, I. Characteristics of laterally vibrating resonant microcantilevers in viscous liquid media. J. Appl. Phys. 2012, 111, 014907. [Google Scholar] [CrossRef] [Green Version]
- Heinisch, M.; Voglhuber-Brunnmaier, T.; Reichel, E.K.; Dufour, I.; Jakoby, B. Electromagnetically driven torsional resonators for viscosity and mass density sensing application. Sens. Actuators A Phys. 2015, 229, 182–191. [Google Scholar] [CrossRef] [Green Version]
- He, Y.; Ma, Y.; Tong, Y.; Yu, X.; Tittel, F.K. Ultra-high sensitive light-induced thermoelastic spectroscopy sensor with a high Q-factor quartz tuning fork and a multipass cell. Opt. Lett. 2019, 44, 1904–1907. [Google Scholar] [CrossRef]
- He, Y.; Ma, Y.; Tong, Y.; Yu, X.; Peng, Z.; Gao, J.; Tittel, F.K. Long distance, distributed gas sensing based on micro-nano fiber evanescent wave quartz-enhanced photoacoustic spectroscopy. Appl. Phys. Lett. 2017, 111, 241102. [Google Scholar] [CrossRef]
- Ma, Y.; He, Y.; Tong, Y.; Yu, X.; Tittel, F.K. Quartz-tuning-fork enhanced photothermal spectroscopy for ultra-high sensitive trace gas detection. Opt. Express 2018, 26, 32103–32110. [Google Scholar] [CrossRef] [Green Version]
- Sangmin, A.; Kunyoung, L.; Bongsu, K.; Haneol, N.; Jongwoo, K.; Soyoung, K.; Manhee, L.; Mun-Heon, H.; Wonho, J. Nanopipette combined with quartz tuning fork-atomic force microscope for force spectroscopy/microscopy and liquid delivery-based nanofabrication. Rev. Sci. Instrum. 2014, 85, 033702. [Google Scholar] [CrossRef]
- Ooe, H.; Sakuishi, T.; Nogami, M.; Tomitori, M.; Arai, T. Resonance frequency-retuned quartz tuning fork as a force sensor for noncontact atomic force microscopy. Appl. Phys. Lett. 2014, 105, 043107. [Google Scholar] [CrossRef]
- Jahng, J.; Lee, M.; Noh, H.; Seo, Y.; Jhe, W. Active Q control in tuning-fork-based atomic force microscopy. Appl. Phys. Lett. 2007, 91, 023103. [Google Scholar] [CrossRef] [Green Version]
- Seo, Y.; Jhe, W. High-speed near-field scanning optical microscopy with a quartz crystal resonator. Rev. Sci. Instrum. 2002, 73, 2057–2059. [Google Scholar] [CrossRef]
- Karrai, K.; Grober, R.D. Piezoelectric tip-sample distance control for near field optical microscopes. Appl. Phys. Lett. 1995, 66, 1842–1844. [Google Scholar] [CrossRef]
- Serebryakov, D.V.; Cherkun, A.P.; Loginov, B.A.; Letokhov, V.S. Tuning-fork-based fast highly sensitive surface-contact sensor for atomic force microscopy/near-field scanning optical microscopy. Rev. Sci. Instrum. 2002, 73, 1795–1802. [Google Scholar] [CrossRef]
- Sader, J.E. Frequency response of cantilever beams immersed in viscous fluids with applications to the atomic force microscope. J. Appl. Phys. 1998, 84, 64–76. [Google Scholar] [CrossRef] [Green Version]
- Sader, J.E.; Pacifico, J.; Green, C.P.; Mulvaney, P. General scaling law for stiffness measurement of small bodies with applications to the atomic force microscope. J. Appl. Phys. 2005, 97, 124903. [Google Scholar] [CrossRef] [Green Version]
- Sader, J.E.; Jungchul, L.; Scott, R.M. Energy dissipation in microfluidic beam resonators: Dependence on mode number. J. Appl. Phys. 2010, 108, 114507. [Google Scholar] [CrossRef] [Green Version]
- Heinisch, M.; Reichel, E.K.; Dufour, I.; Jakoby, B. A U-shaped wire for viscosity and mass density sensing. Sens. Actuators A Phys. 2014, 214, 245–251. [Google Scholar] [CrossRef]
- Heinisch, M.; Voglhuber-Brunnmaier, T.; Reichel, E.K.; Dufour, I.; Jakoby, B. Reduced order models for resonant viscosity and mass density sensors. Sens. Actuators A Phys. 2014, 220, 76–84. [Google Scholar] [CrossRef] [Green Version]
- Van Eysden, C.A.; Sader, J.E. Frequency response of cantilever beams immersed in viscous fluids with applications to the atomic force microscope: Arbitrary mode order. J. Appl. Phys. 2007, 101, 044908. [Google Scholar] [CrossRef]
- Lighthill, M.; Rosenhead, L. Laminar Boundary Layers; Clarendon Press: Oxford, UK, 1963. [Google Scholar]
- Voglhuber-Brunnmaier, T.; Niedermayer, A.O.; Feichtinger, F.; Jakoby, B. Fluid sensing using quartz tuning forks—Measurement technology and applications. Sensors 2019, 19, 2336. [Google Scholar] [CrossRef] [Green Version]
- Saltelli, A. Global Sensitivity Analysis: The Primer; John Wiley & Sons Ltd.: Chichester, UK, 2008. [Google Scholar]


| Fluid | Tuning Fork | Evaluated Values | Relative Deviations | |||
|---|---|---|---|---|---|---|
| Q | f1 (Hz) | μ (mPa∙s) | ρ (g/mL) | δμ (%) | δρ (%) | |
| Heptane | 163.76 | 29,804.5 | 0.37 | 0.699 | −2.63 | 2.95 |
| Methanol | 133.87 | 29,400.0 | 0.50 | 0.809 | −7.41 | 2.15 |
| Ethanol | 86.18 | 29,299.5 | 1.21 | 0.820 | 16.35 | 4.46 |
| 2-Propanol | 70.45 | 29,298.0 | 1.86 | 0.808 | −5.10 | 3.46 |
| D5 | 46.92 | 29,033.9 | 4.17 | 0.853 | −12.03 | 2.16 |
| N10 | 26.68 | 28,756.4 | 14.01 | 0.857 | −3.38 | 1.06 |
| S20 | 17.87 | 28,460.0 | 35.37 | 0.846 | −4.20 | −1.05 |
| N35 | 14.75 | 28,253.0 | 57.05 | 0.837 | 2.76 | −1.99 |
| Sample | Tuning Fork | Evaluated Values | Relative Deviations | |||
|---|---|---|---|---|---|---|
| Q | f1 (Hz) | μ (mPa∙s) | ρ (g/mL) | δμ (%) | δρ (%) | |
| 1 | 25.8858 | 28,599 | 15.270 | 0.866 | −1.037 | −0.115 |
| 2 | 34.8459 | 28,769 | 8.575 | 0.856 | −1.391 | −0.117 |
| 3 | 60.0072 | 29,025 | 2.986 | 0.831 | −0.566 | 0 |
| 4 | 72.6525 | 29,108 | 2.064 | 0.819 | −0.097 | 0.122 |
| 5 | 11.8873 | 28,157 | 71.213 | 0.824 | 0.090 | −0.121 |
| 6 | 17.1759 | 28,514 | 35.222 | 0.816 | −0.362 | 0 |
| 7 | 34.4446 | 28,990 | 9.218 | 0.792 | −0.679 | 0.126 |
| 8 | 44.1299 | 29,119 | 5.713 | 0.781 | −0.643 | 0.386 |
| 9 | 28.1085 | 25,808 | 8.747 | 1.821 | −0.636 | 0.055 |
| 10 | 35.2417 | 25,977 | 5.606 | 1.791 | −0.831 | 0.056 |
| 11 | 40.1609 | 26,073 | 4.339 | 1.771 | −0.709 | 0.057 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Chen, D.; He, X.; Wang, X. A Hydrodynamic Model for Measuring Fluid Density and Viscosity by Using Quartz Tuning Forks. Sensors 2020, 20, 198. https://doi.org/10.3390/s20010198
Zhang M, Chen D, He X, Wang X. A Hydrodynamic Model for Measuring Fluid Density and Viscosity by Using Quartz Tuning Forks. Sensors. 2020; 20(1):198. https://doi.org/10.3390/s20010198
Chicago/Turabian StyleZhang, Mi, Dehua Chen, Xiao He, and Xiuming Wang. 2020. "A Hydrodynamic Model for Measuring Fluid Density and Viscosity by Using Quartz Tuning Forks" Sensors 20, no. 1: 198. https://doi.org/10.3390/s20010198
APA StyleZhang, M., Chen, D., He, X., & Wang, X. (2020). A Hydrodynamic Model for Measuring Fluid Density and Viscosity by Using Quartz Tuning Forks. Sensors, 20(1), 198. https://doi.org/10.3390/s20010198




