Modeling of an Optically Heated MEMS-Based Micromechanical Bimaterial Sensor for Heat Capacitance Measurements of Single Biological Cells
Abstract
:1. Introduction
2. BMC Structure and Theory
3. Generation of Numerical Data
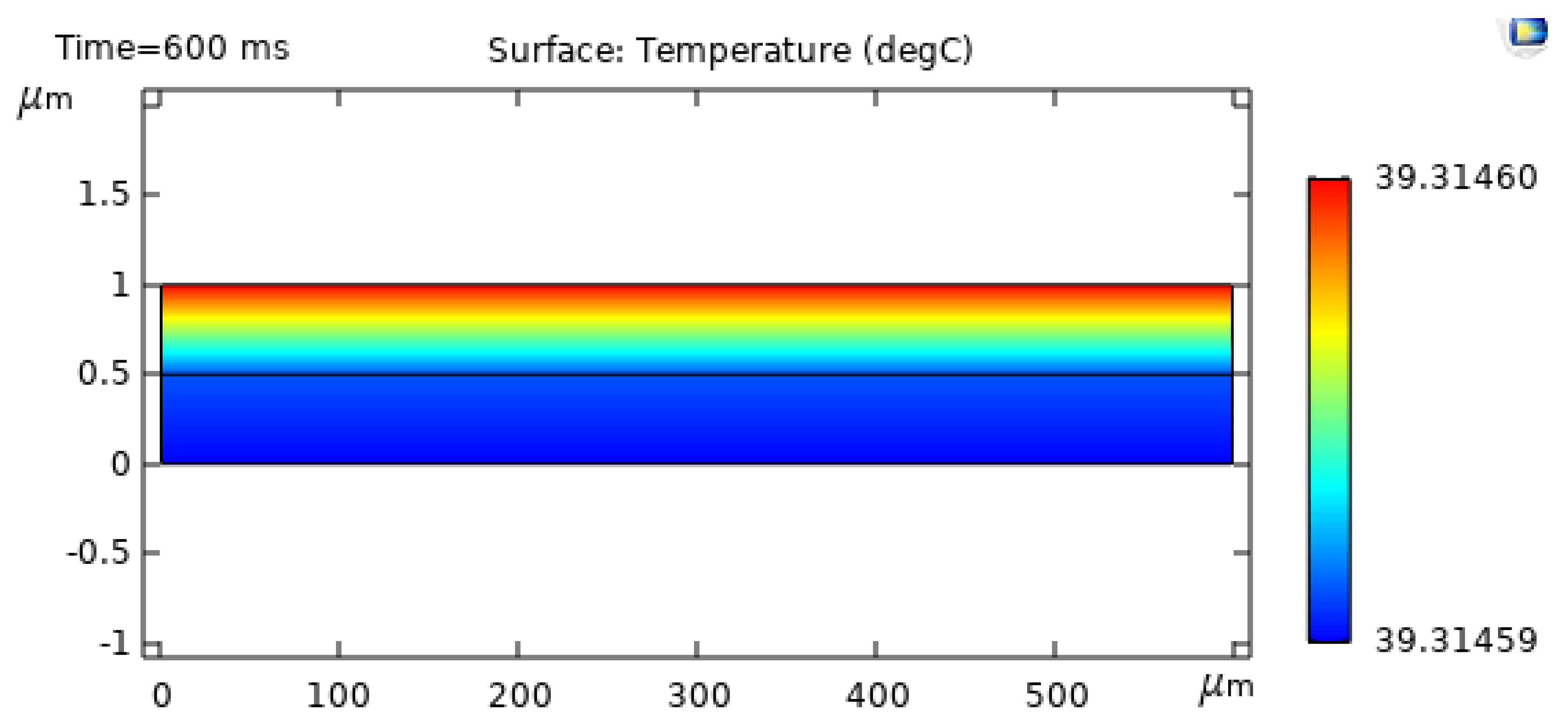
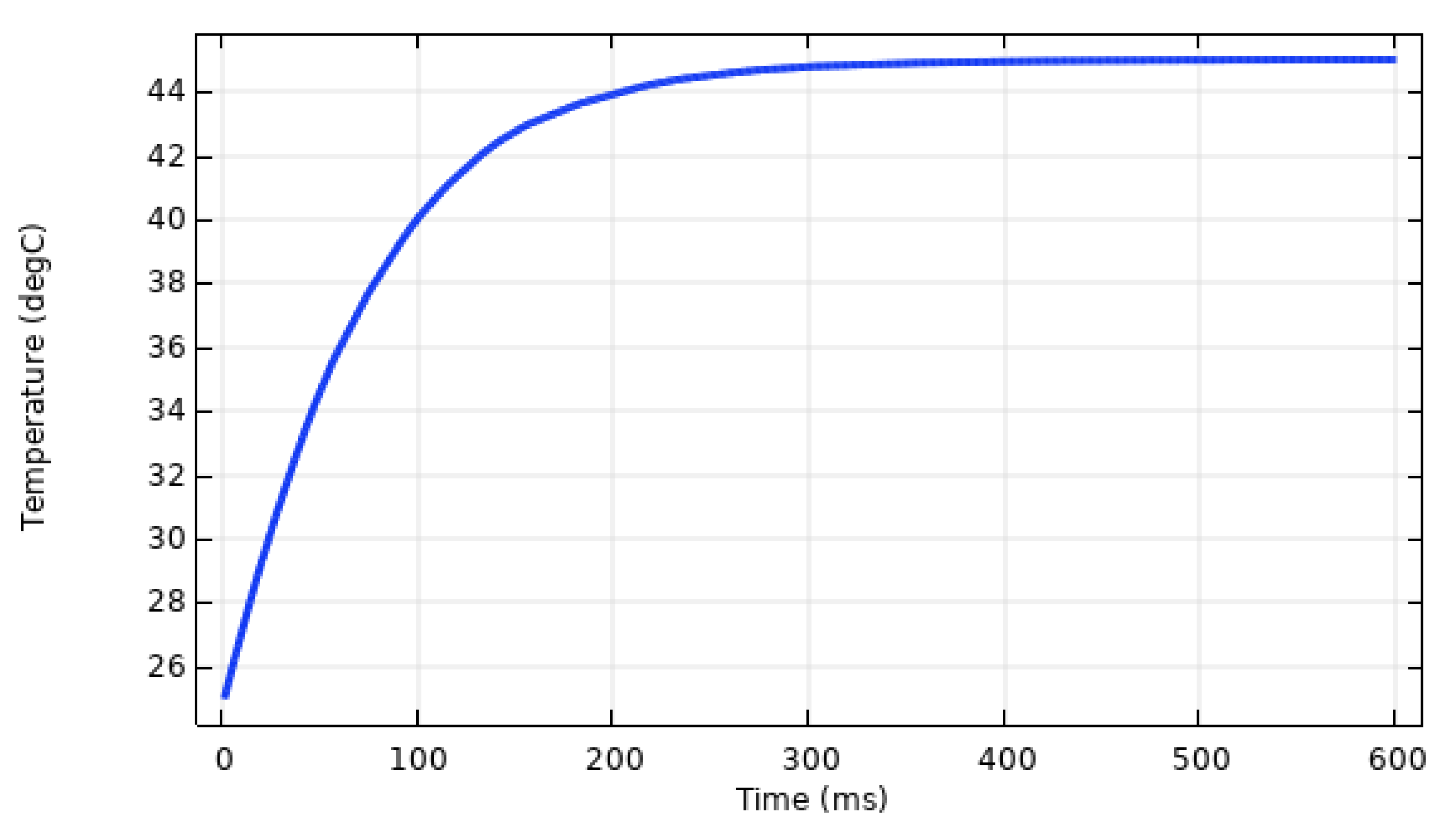
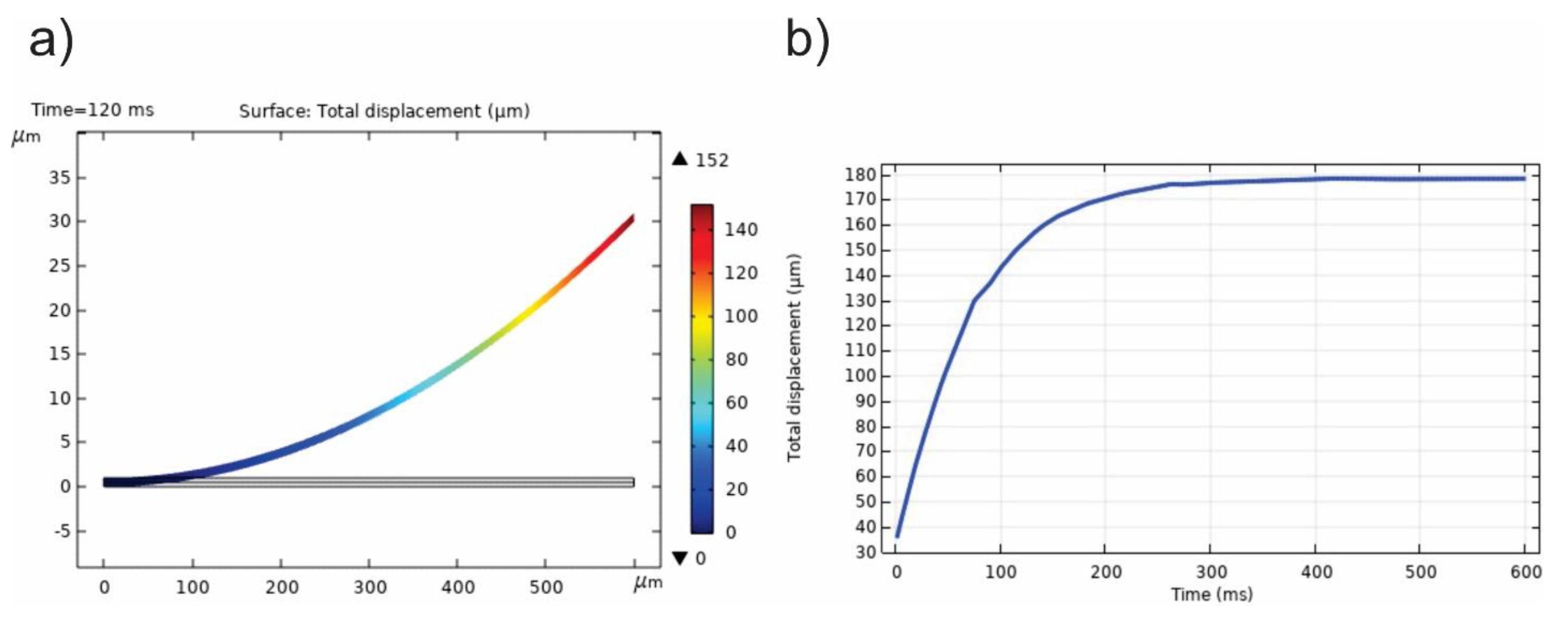
4. Results and Discussion
5. Conclusions
Funding
Conflicts of Interest
References
- Raiteri, R.; Grattarola, M.; Butt, H.-J.; Skládal, P. Micromechanical cantilever-based biosensors. Sens. Actuators B Chem. 2001, 79, 115–126. [Google Scholar] [CrossRef]
- Chen, A.; Chatterjee, S. Nanomaterials based electrochemical sensors for biomedical applications. Chem. Soc. Rev. 2013, 42, 5425. [Google Scholar] [CrossRef]
- Lee, C.-S.; Kim, S.K.; Kim, M. Ion-Sensitive Field-Effect Transistor for Biological Sensing. Sensors 2009, 9, 7111–7131. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Xu, L.; Koh, D.; Nyayapathi, N.; Oh, K.W. Various On-Chip Sensors with Microfluidics for Biological Applications. Sensors 2014, 14, 17008–17036. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Koren, K.; Kühl, M. A simple laminated paper-based sensor for temperature sensing and imaging. Sens. Actuators B Chem. 2015, 210, 124–128. [Google Scholar] [CrossRef]
- Ricciardi, A.; Crescitelli, A.; Vaiano, P.; Quero, G.; Consales, M.; Pisco, M.; Esposito, E.; Cusano, A. Lab-on-fiber technology: A new vision for chemical and biological sensing. Analyst 2015, 140, 8068–8079. [Google Scholar] [CrossRef]
- Lee, J.; Kim, J.; Kim, S.; Min, D.-H. Biosensors based on graphene oxide and its biomedical application. Adv. Drug Deliv. Rev. 2016, 105, 275–287. [Google Scholar] [CrossRef]
- Maduraiveeran, G.; Sasidharan, M.; Ganesan, V. Electrochemical sensor and biosensor platforms based on advanced nanomaterials for biological and biomedical applications. Biosens. Bioelectron. 2018, 103, 113–129. [Google Scholar] [CrossRef]
- Materón, E.M.; Lima, R.S.; Joshi, N.; Shimizu, F.M.; Oliveira, O.N. Graphene-Containing Microfluidic and Chip-Based Sensor Devices for Biomolecules. Graphene-Based Electrochem. Sens. Biomol. 2019, 321–336. [Google Scholar] [CrossRef]
- Guo, Z.; Niu, Q.; Yang, Q.; Li, T.; Chi, H. A highly selective and sensitive dual-mode sensor for colorimetric and turn-on fluorescent detection of cyanide in water, agro-products and living cells. Anal. Chim. Acta 2019, 1065, 113–123. [Google Scholar] [CrossRef]
- Inomata, N.; Toda, M.; Ono, T. Highly sensitive thermometer using a vacuum-packed Si resonator in a microfluidic chip for the thermal measurement of single cells. Lab Chip 2016, 16, 3597–3603. [Google Scholar] [CrossRef] [PubMed]
- Okabe, K.; Sakaguchi, R.; Shi, B.; Kiyonaka, S. Intracellular thermometry with fluorescent sensors for thermal biology. Pflüg. Arch. 2018, 470, 717–731. [Google Scholar] [CrossRef] [PubMed]
- Yamada, T.; Inomata, N.; Ono, T. Sensitive thermal microsensor with pn junction for heat measurement of a single cell. Jpn. J. Appl. Phys. 2016, 55, 27001. [Google Scholar] [CrossRef]
- Takei, Y.; Arai, S.; Murata, A.; Takabayashi, M.; Oyama, K.; Ishiwata, S.; Takeoka, S.; Suzuki, M. A Nanoparticle-Based Ratiometric and Self-Calibrated Fluorescent Thermometer for Single Living Cells. ACS Nano 2013, 8, 198–206. [Google Scholar] [CrossRef]
- Sato, M.K.; Toda, M.; Inomata, N.; Maruyama, H.; Okamatsu-Ogura, Y.; Arai, F.; Ono, T.; Ishijima, A.; Inoue, Y. Temperature Changes in Brown Adipocytes Detected with a Bimaterial Microcantilever. Biophys. J. 2014, 106, 2458–2464. [Google Scholar] [CrossRef] [Green Version]
- Lowell, B.B.; Spiegelman, B.M. Towards a molecular understanding of adaptive thermogenesis. Nature 2000, 404, 652–660. [Google Scholar] [CrossRef]
- Wang, C.; Xu, R.; Tian, W.; Jiang, X.; Cui, Z.; Wang, M.; Sun, H.; Fang, K.; Gu, N. Determining intracellular temperature at single-cell level by a novel thermocouple method. Cell Res. 2011, 21, 1517–1519. [Google Scholar] [CrossRef] [Green Version]
- Nedergaard, J.; Cannon, B.; Lindberg, O. Microcalorimetry of isolated mammalian cells. Nature 1977, 267, 518–520. [Google Scholar] [CrossRef]
- Clark, D.G.; Brinkman, M.; Neville, S.D.; Falcou, R.; Bouillaud, F.; Mory, G.; Apfelbaum, M.; Ricquier, D.; Raasmaja, A.; York, D.A.; et al. Microcalorimetric measurements of heat production in brown adipocytes from control and cafeteria-fed rats. Biochem. J. 1986, 235, 337–342. [Google Scholar] [CrossRef] [Green Version]
- Park, B.K.; Yi, N.; Park, J.; Kim, D. Thermal conductivity of single biological cells and relation with cell viability. Appl. Phys. Lett. 2013, 102, 203702. [Google Scholar] [CrossRef] [Green Version]
- Kucsko, G.; Maurer, P.C.; Yao, N.Y.; Kubo, M.; Noh, H.J.; Lo, P.K.; Park, H.; Lukin, M.D. Nanometre-scale thermometry in a living cell. Nature 2013, 500, 54–58. [Google Scholar] [CrossRef] [PubMed]
- Gota, C.; Okabe, K.; Funatsu, T.; Harada, Y.; Uchiyama, S. Hydrophilic Fluorescent Nanogel Thermometer for Intracellular Thermometry. J. Am. Chem. Soc. 2009, 131, 2766–2767. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.-M.; Yang, H.; Lin, L. Quantum Dot Nano Thermometers Reveal Heterogeneous Local Thermogenesis in Living Cells. ACS Nano 2011, 5, 5067–5071. [Google Scholar] [CrossRef] [PubMed]
- Vyalikh, A.; Wolter, A.U.; Hampel, S.; Haase, D.; Ritschel, M.; Leonhardt, A.; Grafe, H.-J.; Taylor, A.; Kramer, K.; Büchner, B.; et al. A carbon-wrapped nanoscaled thermometer for temperature control in biological environments. Nanomedicine 2008, 3, 321–327. [Google Scholar] [CrossRef]
- Zohar, O.; Ikeda, M.; Shinagawa, H.; Inoue, H.; Nakamura, H.; Elbaum, D.; Alkon, D.L.; Yoshioka, T. Thermal imaging of receptor-activated heat production in single cells. Biophys. J. 1998, 74, 82–89. [Google Scholar] [CrossRef] [Green Version]
- Verhaegen, K.; Baert, K.; Simaels, J.; Van Driessche, W. A high-throughput silicon microphysiometer. Sens. Actuators A Phys. 2000, 82, 186–190. [Google Scholar] [CrossRef]
- Johannessen, E.A.; Weaver, J.M.R.; Cobbold, P.H.; Cooper, J. Heat conduction nanocalorimeter for pl-scale single cell measurements. Appl. Phys. Lett. 2002, 80, 2029–2031. [Google Scholar] [CrossRef]
- Inomata, N.; Ishijima, A.; Toda, M.; Sato, M.; Ono, T. Pico calorimeter for detection of heat produced in an individual brown fat cell. Appl. Phys. Lett. 2012, 100, 154104. [Google Scholar] [CrossRef]
- Barnes, J.R.; Stephenson, R.J.; Woodburn, C.N.; O’Shea, S.J.; Welland, M.E.; Rayment, T.; Gimzewski, J.K.; Gerber, C. A femtojoule calorimeter using micromechanical sensors. Rev. Sci. Instrum. 1994, 65, 3793–3798. [Google Scholar] [CrossRef]
- Toda, M.; Ono, T.; Liu, F.; Voiculescu, I. Evaluation of bimaterial cantilever beam for heat sensing at atmospheric pressure. Rev. Sci. Instrum. 2010, 81, 55104. [Google Scholar] [CrossRef]
- Privorotskaya, N.; Liu, Y.-S.; Lee, J.; Zeng, H.; Carlisle, J.A.; Radadia, A.; Millet, L.; Bashir, R.; King, W.P. Rapid thermal lysis of cells using silicon–diamond microcantilever heaters. Lab Chip 2010, 10, 1135–1141. [Google Scholar] [CrossRef] [PubMed]
- Singamaneni, S.; Lemieux, M.C.; Lang, H.P.; Gerber, C.; Lam, Y.; Zauscher, S.; Datskos, P.G.; Lavrik, N.V.; Jiang, H.; Naik, R.R.; et al. Bimaterial Microcantilevers as a Hybrid Sensing Platform. Adv. Mater. 2008, 20, 653–680. [Google Scholar] [CrossRef]
- Canetta, C.; Narayanaswamy, A. Sub-picowatt resolution calorimetry with a bi-material microcantilever sensor. Appl. Phys. Lett. 2013, 102, 103112. [Google Scholar] [CrossRef] [Green Version]
- Toda, M.; Inomata, N.; Ono, T.; Voiculescu, I. Cantilever beam temperature sensors for biological applications. IEEJ Trans. Electr. Electron. Eng. 2017, 12, 153–160. [Google Scholar] [CrossRef] [Green Version]
- Etayash, H.; Khan, M.F.; Kaur, K.; Thundat, T. Microfluidic cantilever detects bacteria and measures their susceptibility to antibiotics in small confined volumes. Nat. Commun. 2016, 7, 12947. [Google Scholar] [CrossRef] [PubMed]
- Rahimi, M.; Chae, I.; Hawk, J.E.; Mitra, S.K.; Thundat, T. Methane sensing at room temperature using photothermal cantilever deflection spectroscopy. Sens. Actuators B Chem. 2015, 221, 564–569. [Google Scholar] [CrossRef]
- Khan, M.F.; Miriyala, N.; Lee, J.; Hassanpourfard, M.; Kumar, A.; Thundat, T. Heat capacity measurements of sub-nanoliter volumes of liquids using bimaterial microchannel cantilevers. Appl. Phys. Lett. 2016, 108, 211906. [Google Scholar] [CrossRef]
- Varesi, J.; Lai, J.; Perazzo, T.; Shi, Z.; Majumdar, A. Photothermal measurements at picowatt resolution using uncooled micro-optomechanical sensors. Appl. Phys. Lett. 1997, 71, 306–308. [Google Scholar] [CrossRef]
- Frederick, K.K.; Marlow, M.S.; Valentine, K.G.; Wand, A.J. Conformational entropy in molecular recognition by proteins. Nature 2007, 448, 325–329. [Google Scholar] [CrossRef]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; DeWitt, D.P. Fundamentals of Heat and Mass Transfer; Wiley: New York, NY, USA, 1996; Volume 4. [Google Scholar]
- ASHRAE Handbook Refrigeration, SI ed.; American Society of Heating, Refrigerating and Air-Conditioning Engineers Inc.: Atlanta, GA, USA, 2010.
- Kim, S.; Thundat, T. Photothermal Cantilever Deflection Spectroscopy. Electrochem. Soc. Interface 2019, 28, 55–57. [Google Scholar] [CrossRef]
- Prashanthi, K.; Phani, A.; Thundat, T. Photothermal Electrical Resonance Spectroscopy of Physisorbed Molecules on a Nanowire Resonator. Nano Lett. 2015, 15, 5658–5663. [Google Scholar] [CrossRef] [PubMed]
- Alodhayb, A.; Khan, F.; Etayash, H.; Thundat, T. Nanomechanical Calorimetric Infrared Spectroscopy using Bi-Material Microfluidic Cantilevers. J. Electrochem. Soc. 2020, 167, 037504. [Google Scholar] [CrossRef]
- Ceccacci, A.C.; Cagliani, A.; Marizza, P.; Schmid, S.; Boisen, A. Thin Film Analysis by Nanomechanical Infrared Spectroscopy. ACS Omega 2019, 4, 7628–7635. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alves, G.M.A.; Goswami, S.B.; Mansano, R.D.; Boisen, A. Temperature Modulated Nanomechanical Thermal Analysis. IEEE Sens. J. 2018, 18, 4001–4007. [Google Scholar] [CrossRef] [Green Version]
- Carron, C.; Getz, P.; Heinrich, S.M.; Josse, F.; Brand, O. Cantilever-based resonant microsensors with integrated temperature modulation for transient chemical analysis. In Proceedings of the 2015 Transducers—2015 18th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Anchorage, AK, USA, 21–25 June 2015; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2015; pp. 1511–1514. [Google Scholar]


© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alodhayb, A. Modeling of an Optically Heated MEMS-Based Micromechanical Bimaterial Sensor for Heat Capacitance Measurements of Single Biological Cells. Sensors 2020, 20, 215. https://doi.org/10.3390/s20010215
Alodhayb A. Modeling of an Optically Heated MEMS-Based Micromechanical Bimaterial Sensor for Heat Capacitance Measurements of Single Biological Cells. Sensors. 2020; 20(1):215. https://doi.org/10.3390/s20010215
Chicago/Turabian StyleAlodhayb, Abdullah. 2020. "Modeling of an Optically Heated MEMS-Based Micromechanical Bimaterial Sensor for Heat Capacitance Measurements of Single Biological Cells" Sensors 20, no. 1: 215. https://doi.org/10.3390/s20010215
APA StyleAlodhayb, A. (2020). Modeling of an Optically Heated MEMS-Based Micromechanical Bimaterial Sensor for Heat Capacitance Measurements of Single Biological Cells. Sensors, 20(1), 215. https://doi.org/10.3390/s20010215




