Hourly PWV Dataset Derived from GNSS Observations in China
Abstract
:1. Introduction
2. Data and Method
2.1. Data Description
2.2. Interpolation Method
2.3. Retrieval of PWV
3. Evaluation of ERA5-Derived P and T over China
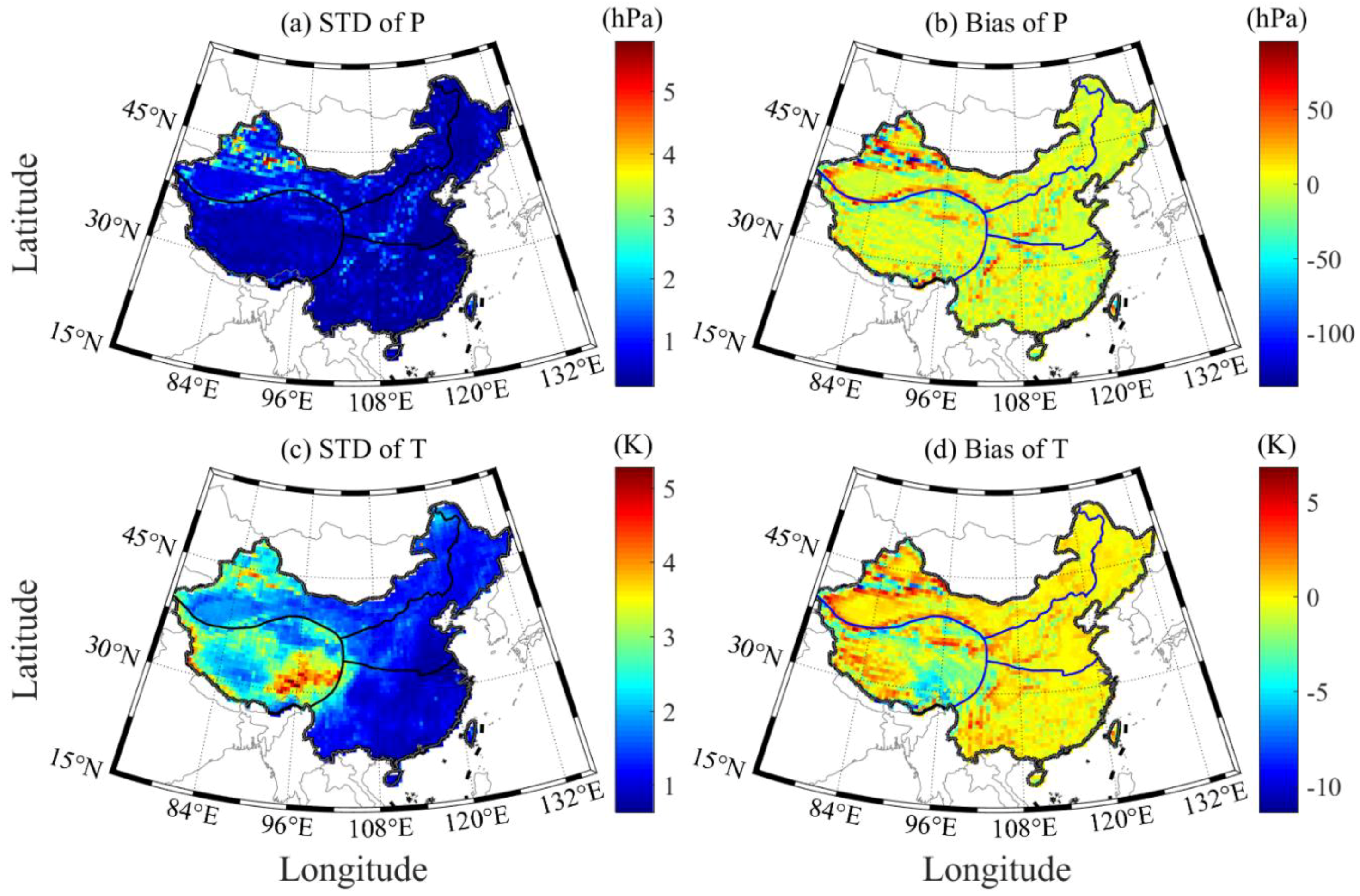
3.1. Comparison between ERA5 and ERA-Interim Products
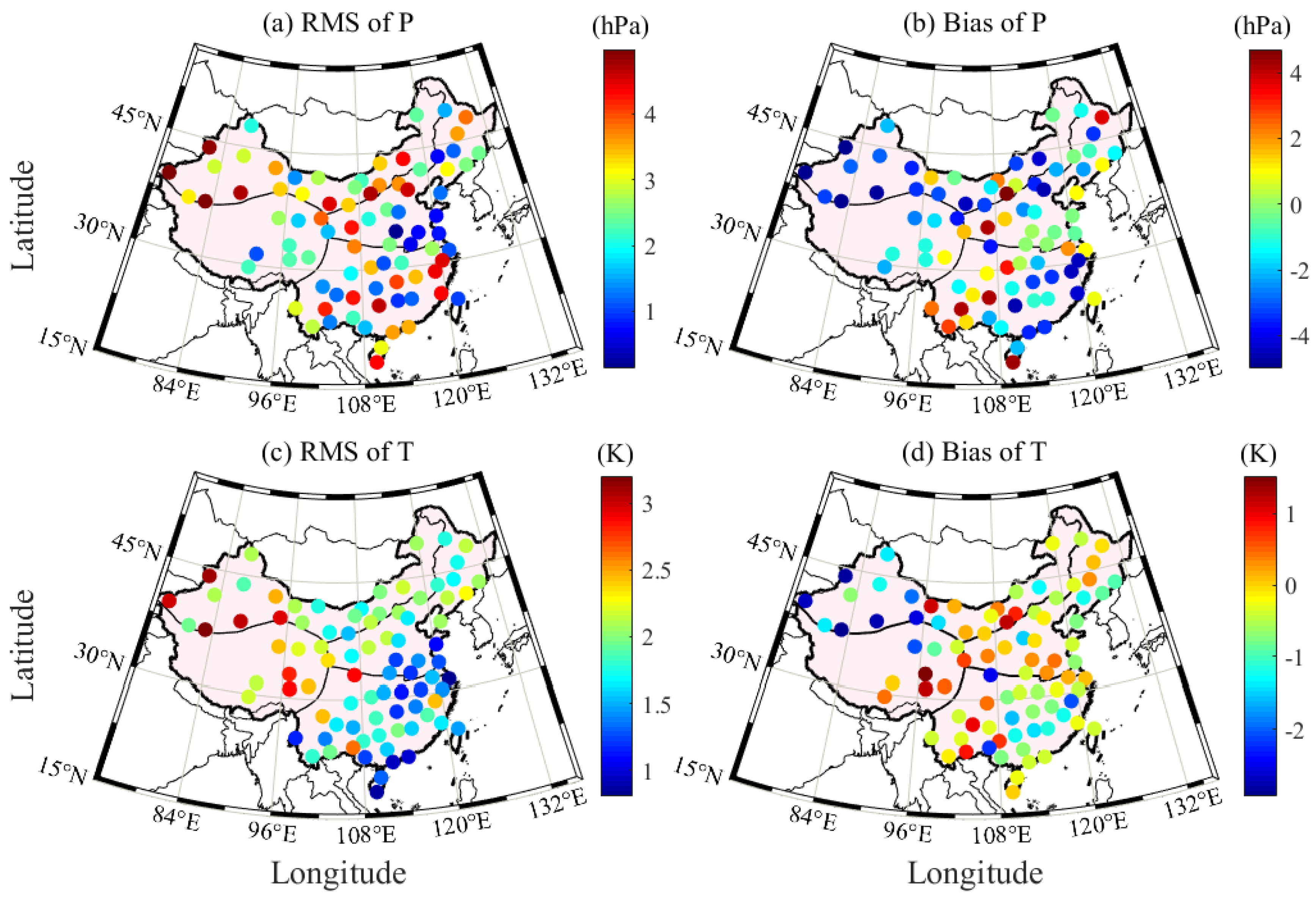
3.2. Comparison of ERA5 Products with Radiosonde Data
4. Hourly PWV Derived from CMONOC and ERA5
4.1. Analysis of GNSS-Derived ZTD from CMONOC
4.2. Theoretical Error of PWV Calculated Using the Hourly P and T from ERA5
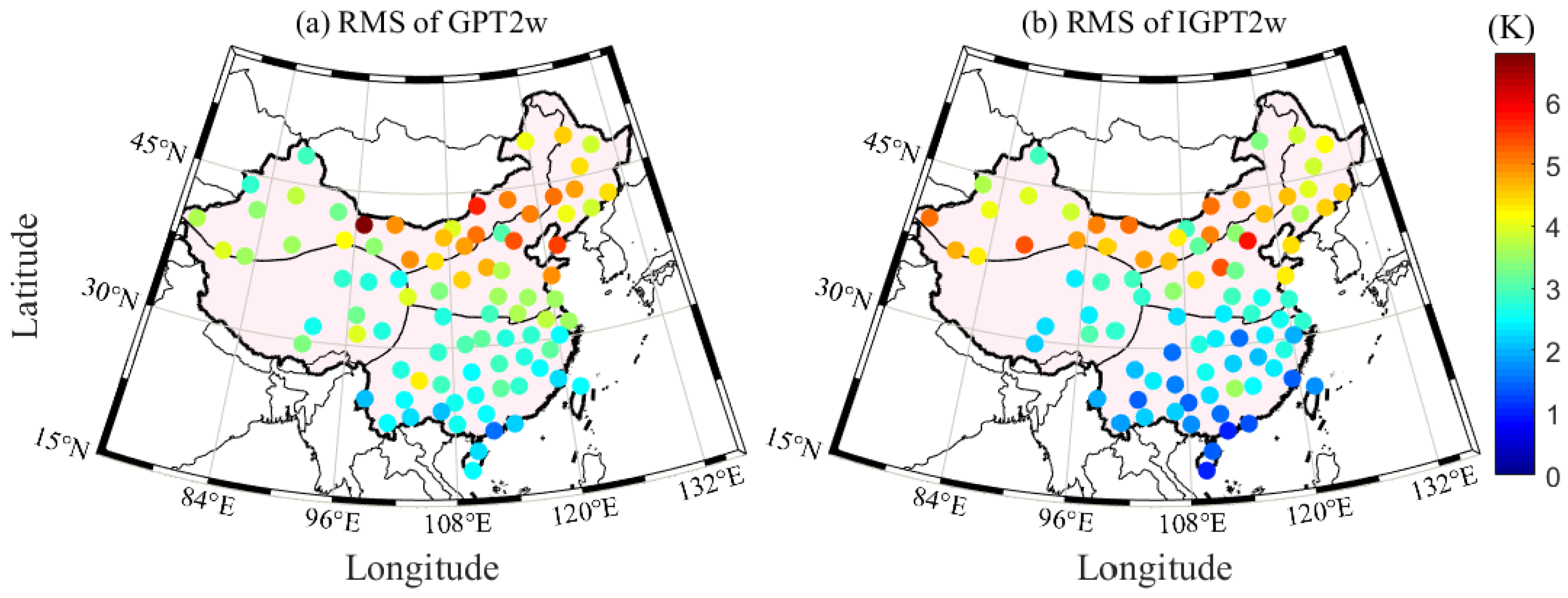
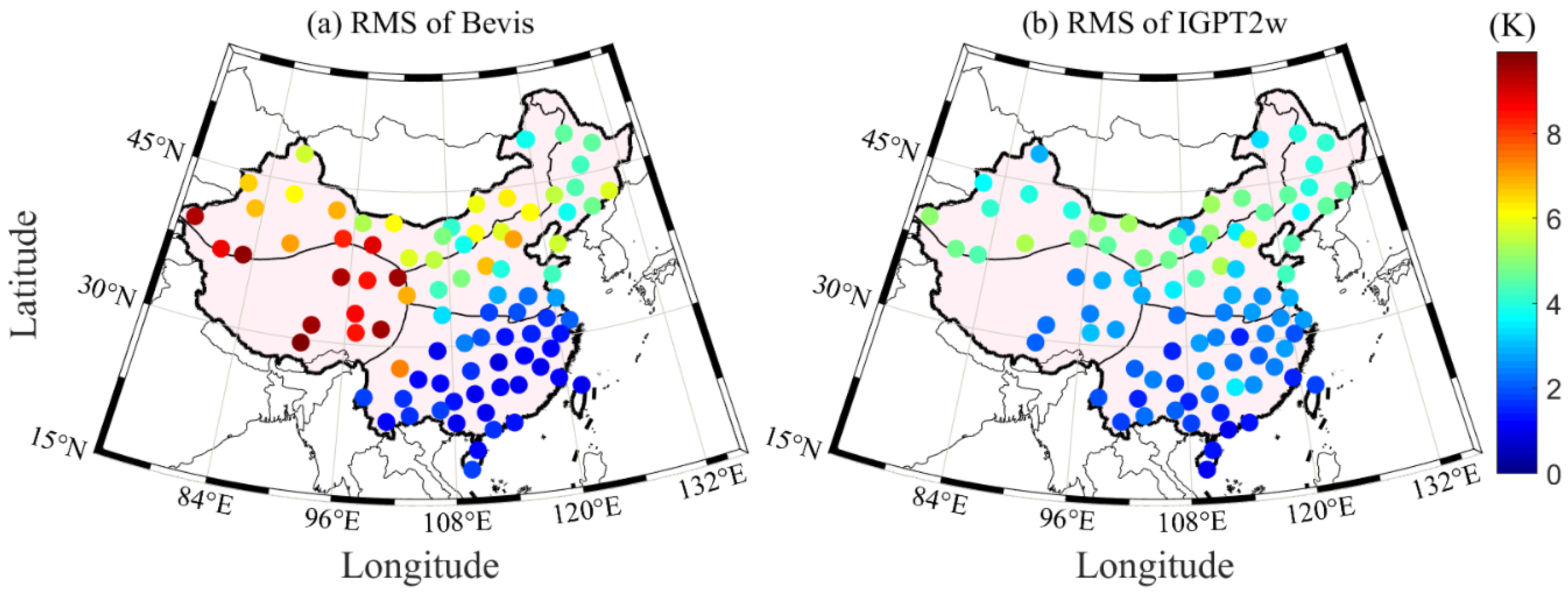
4.3. Tm Calculation Using Improved GPT2w (IGPT2w) Model
5. Validation and Analysis of Hourly PWV Dataset
5.1. Comparison of Hourly PWV Dataset with AERONET Data
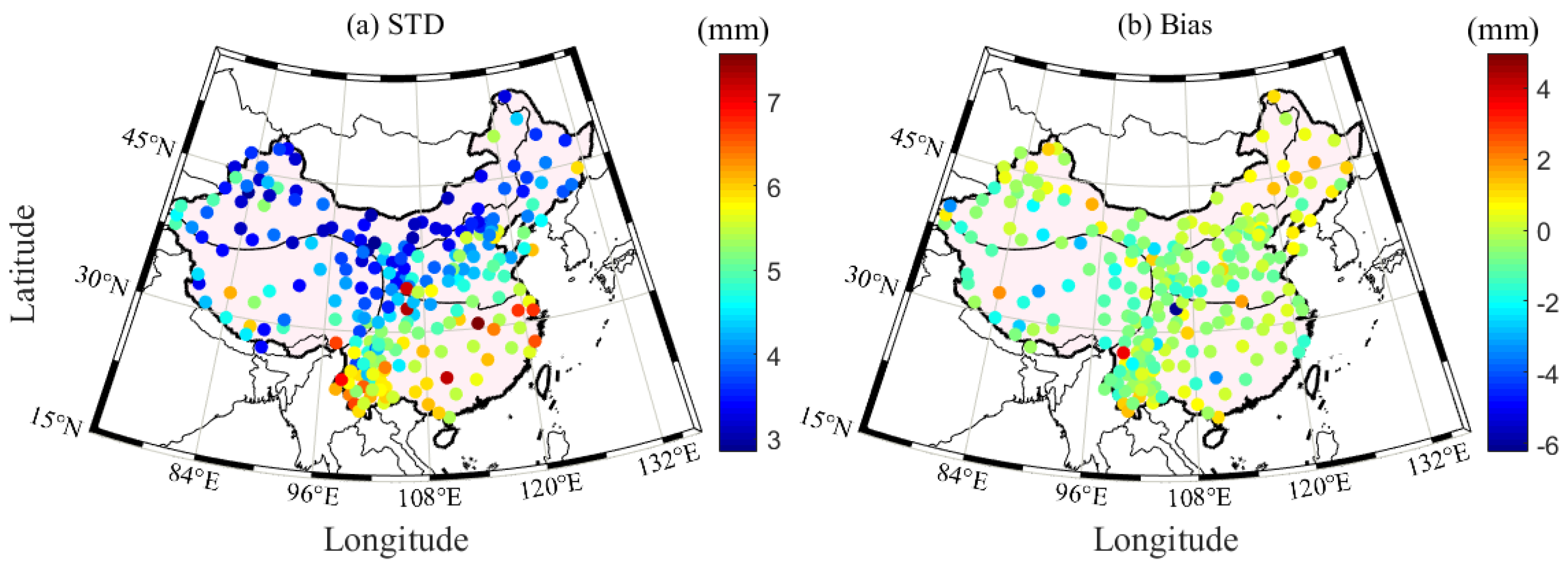
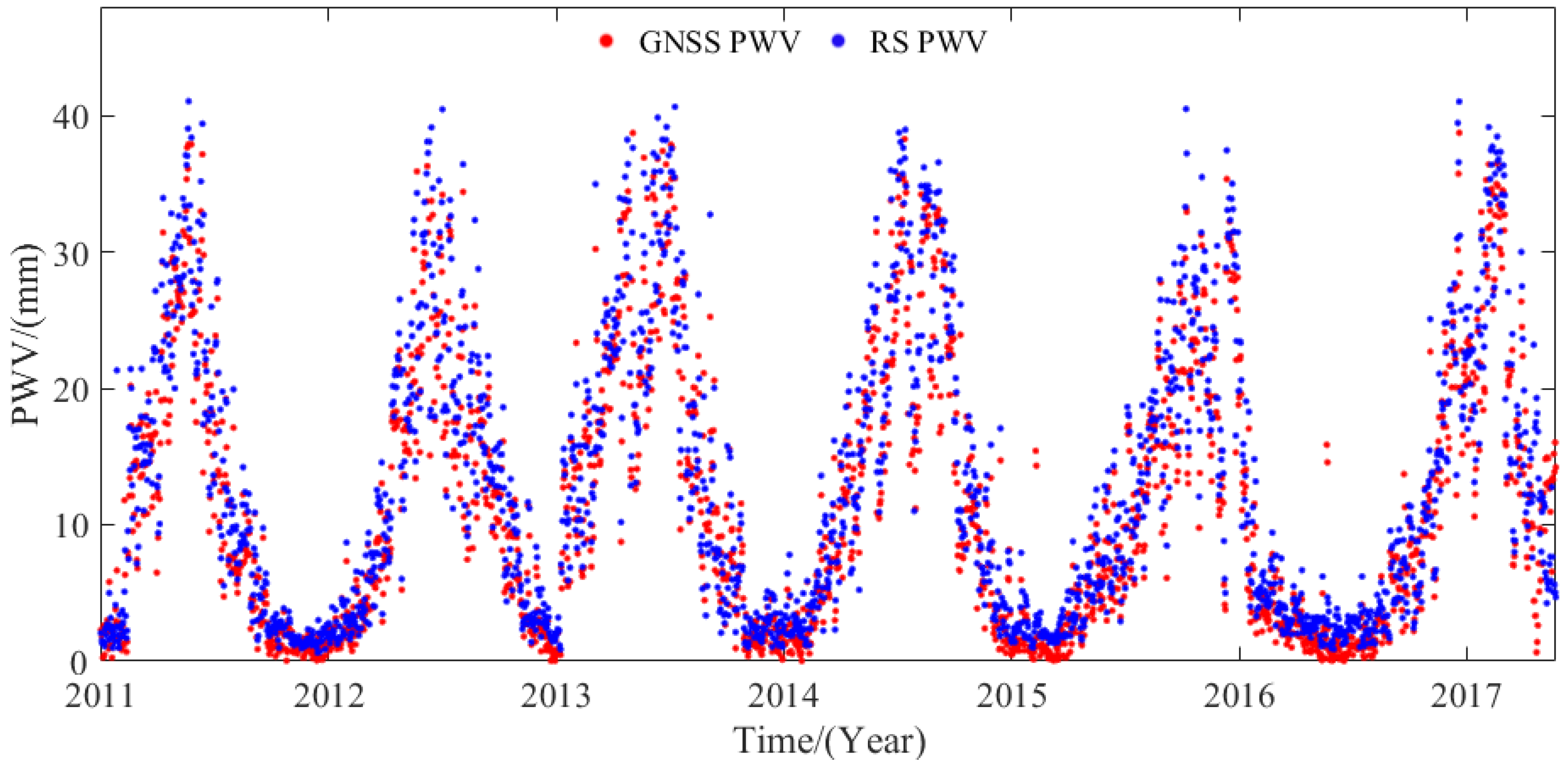
5.2. Comparison of Hourly PWV Dataset with RS Data
5.3. Comparison of PWV Image with ERA5
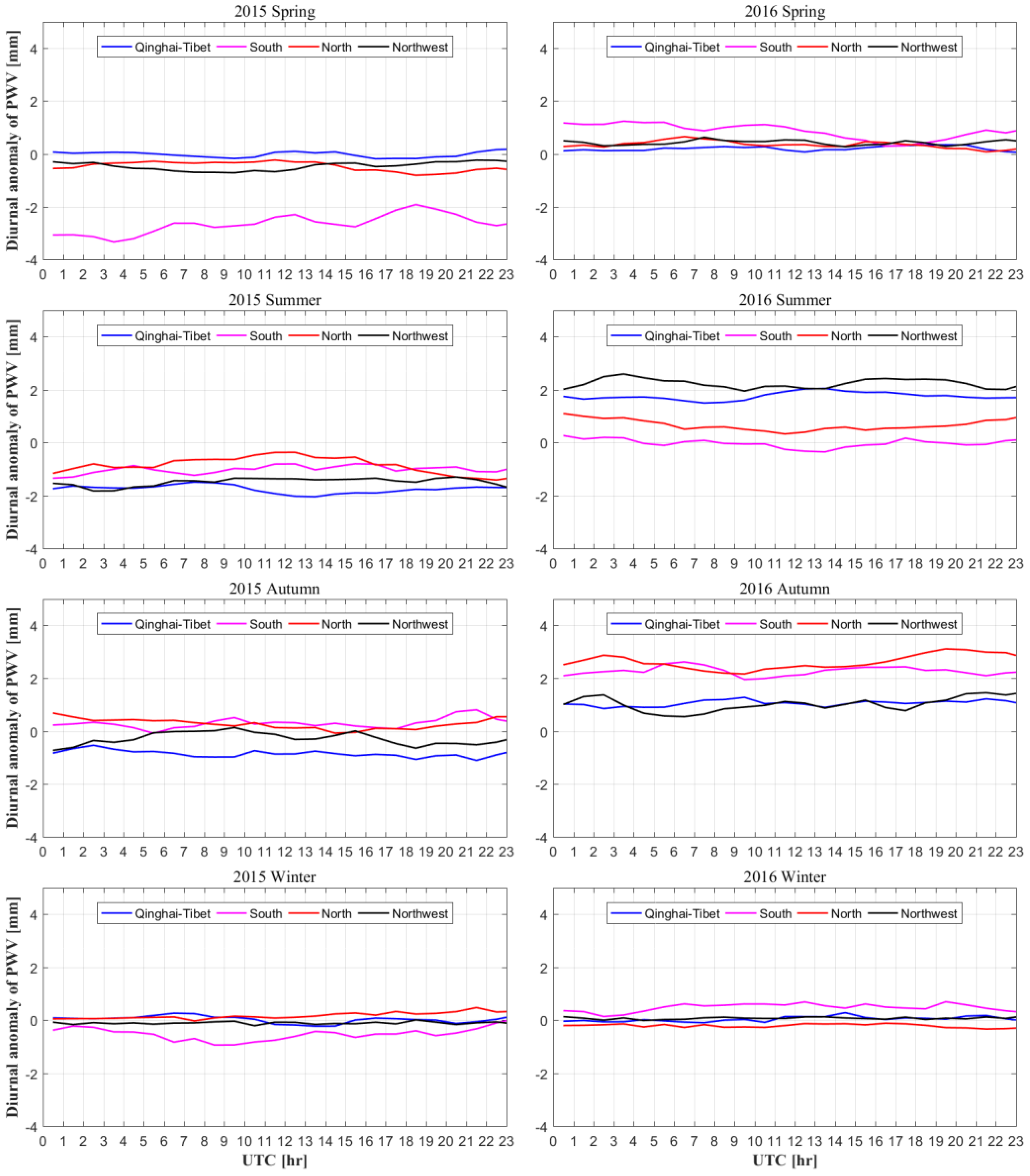
5.4. Analysis of Diurnal PWV Variations in China
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jin, S.; Li, Z.; Cho, J. Integrated water vapor field and multiscale variations over China from GPS measurements. J. Appl. Meteorol. Climatol. 2008, 47, 3008–3015. [Google Scholar] [CrossRef]
- Wong, M.S.; Jin, X.; Liu, Z.; Nichol, J.; Chan, P.W. Multi-sensors study of precipitable water vapour over mainland China. Int. J. Climatol. 2015, 35, 3146–3159. [Google Scholar] [CrossRef]
- Niell, A.E.; Coster, A.J.; Solheim, F.S.; Mendes, V.B.; Toor, P.C.; Langley, R.B.; Upham, C.A. Comparison of measurements of atmospheric wet delay by radiosonde, water vapor radiometer, GPS, and VLBI. J. Atmos. Ocean. Technol. 2001, 18, 830–850. [Google Scholar] [CrossRef] [Green Version]
- Li, Z. Comparison of precipitable water vapor derived from radiosonde, GPS, and Moderate-Resolution Imaging Spectroradiometer measurements. J. Geophys. Res. 2003, 108, 4651. [Google Scholar] [CrossRef]
- Han, Y.; Westwater, E.R. Remote Sensing of Tropospheric Water Vapor and Cloud Liquid Water by Integrated Ground-Based Sensors. J. Atmos. Ocean. Technol. 1995, 12, 1050–1059. [Google Scholar] [CrossRef] [Green Version]
- Madhulatha, A.; Rajeevan, M.; Venkat Ratnam, M.; Bhate, J.; Naidu, C.V. Nowcasting severe convective activity over southeast India using ground-based microwave radiometer observations. J. Geophys. Res. Atmos. 2013, 118, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS meteorology: Remote sensing of atmospheric water vapor using the Global Positioning System. J. Geophys. Res. Atmos. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Shi, H.; Zhang, R.; Nie, Z.; Li, Y.; Chen, Z.; Wang, T. Research on variety characteristics of mainland China troposphere based on CMONOC. Geod. Geodyn. 2018, 9, 411–417. [Google Scholar] [CrossRef]
- Saastamoinen, J. Atmospheric correction for the troposphere and stratosphere in radio ranging satellites. Use Artif. Satell. Geod. 1972, 15, 247–251. [Google Scholar]
- Bevis, M.; Businger, S.; Chiswell, S.; Herring, T.A.; Anthes, R.A.; Rocken, C.; Ware, R.H. GPS meteorology: Mapping zenith wet delays onto precipitable water. J. Appl. Meteorol. 1994, 33, 379–386. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Dai, A.; Van Hove, T.; Van Baelen, J. A near-global, 2-hourly data set of atmospheric precipitable water from ground-based GPS measurements. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef] [Green Version]
- Jin, S.; Luo, O.F. Variability and climatology of PWV from global 13-year GPS observations. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1918–1924. [Google Scholar]
- Zhao, Q.; Yao, Y.; Yao, W.Q.; Li, Z. Near-global GPS-derived PWV and its analysis in the El Niño event of 2014–2016. J. Atmos. Sol.-Terr. Phys. 2018, 179, 69–80. [Google Scholar] [CrossRef]
- Huang, L.; Jiang, W.; Liu, L.; Chen, H.; Ye, S. A new global grid model for the determination of atmospheric weighted mean temperature in GPS precipitable water vapor. J. Geod. 2019, 93, 159–176. [Google Scholar] [CrossRef]
- Zhang, W.; Lou, Y.; Haase, J.S.; Zhang, R.; Zheng, G.; Huang, J.; Shi, C.; Liu, J. The use of ground-based GPS precipitable water measurements over China to assess radiosonde and ERA-Interim moisture trends and errors from 1999 to 2015. J. Clim. 2017, 30, 7643–7667. [Google Scholar] [CrossRef]
- Zhao, Q.; Yao, Y.; Yao, W.; Zhang, S. GNSS-derived PWV and comparison with radiosonde and ECMWF ERA-Interim data over mainland China. J. Atmos. Sol.-Terr. Phys. 2019, 182, 85–92. [Google Scholar] [CrossRef]
- Isioye, O.A.; Combrinck, L.; Botai, J. Modelling weighted mean temperature in the West African region: Implications for GNSS meteorology. Meteorol. Appl. 2016, 23, 614–632. [Google Scholar] [CrossRef]
- Huang, L.; Liu, L.; Chen, H.; Jiang, W. An improved atmospheric weighted mean temperature model and its impact on GNSS precipitable water vapor estimates for China. GPS Solut. 2019, 23, 51. [Google Scholar] [CrossRef]
- Herring, T.A.; King, R.W.; McClusky, S.C. Documentation of the GAMIT GPS Analysis Software Release 10.4; Department of Earth and Planetary Sciences, Massachusetts Institute of Technology: Cambridge, MA, USA, 2010; pp. 1–171. [Google Scholar]
- Altamimi, Z.; Collilieux, X.; Métivier, L. ITRF2008: An improved solution of the international terrestrial reference frame. J. Geod. 2011, 85, 457–473. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Lou, Y.; Huang, J.; Zheng, F.; Cao, Y.; Liang, H.; Shi, C.; Liu, J. Multiscale Variations of Precipitable Water over China Based on 1999–2015 Ground-Based GPS Observations and Evaluations of Reanalysis Products. J. Clim. 2018, 31, 945–962. [Google Scholar] [CrossRef]
- Che, H.; Gui, K.; Chen, Q.; Zheng, Y.; Yu, J.; Sun, T.; Zhang, X.; Shi, G. Calibration of the 936 nm water-vapor channel for the China aerosol remote sensing NETwork (CARSNET) and the effect of the retrieval water-vapor on aerosol optical property over Beijing, China. Atmos. Pollut. Res. 2016, 7, 743–753. [Google Scholar] [CrossRef] [Green Version]
- Gui, K.; Che, H.; Chen, Q.; Zeng, Z.; Liu, H.; Wang, Y.; Zheng, Y.; Sun, T.; Liao, T.; Wang, H.; et al. Evaluation of radiosonde, MODIS-NIR-Clear, and AERONET precipitable water vapor using IGS ground-based GPS measurements over China. Atmos. Res. 2017, 197, 461–473. [Google Scholar] [CrossRef]
- Bokoye, A.I.; Royer, A.; O’Neill, N.T.; Cliche, P.; McArthur, L.J.B.; Teillet, P.M.; Fedosejevs, G.; Thériault, J.M. Multisensor analysis of integrated atmospheric water vapor over Canada and Alaska. J. Geophys. Res. Atmos. 2003, 108, D15. [Google Scholar] [CrossRef]
- Smirnov, A.; Holben, B.N.; Slutsker, I.; Welton, E.J.; Formenti, P. Optical properties of Saharan dust during ACE 2. J. Geophys. Res. Atmos. 1998, 103, 28079–28092. [Google Scholar] [CrossRef] [Green Version]
- Böehm, J.; Heinkelmann, R.; Schuh, H. Short note: A global model of pressure and temperature for geodetic applications. J. Geod. 2007, 81, 679–683. [Google Scholar] [CrossRef]
- Zhao, Q.; Yao, Y.; Yao, W. Troposphere Water Vapour Tomography: A Horizontal Parameterised Approach. Remote Sens. 2018, 10, 1241. [Google Scholar] [CrossRef] [Green Version]
- Tregoning, P.; Herring, T.A. Impact of a priori zenith hydrostatic delay errors on GPS estimates of station heights and zenith total delays. Geophys. Res. Lett. 2006, 33, 23. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Q.; Yao, Y.; Yao, W. GPS-based PWV for precipitation forecasting and its application to a typhoon event. J. Atmos. Sol.-Terr. Phys. 2018, 167, 124–133. [Google Scholar] [CrossRef]
- Shi, C.; Zhao, Q.; Geng, J.; Lou, Y.; Ge, M.; Liu, J. Recent development of PANDA software in GNSS data processing. In International Conference on Earth Observation Data Processing and Analysis (ICEODPA); International Society for Optics and Photonics: Bellingham, WA, USA, 2008; p. 7285. [Google Scholar]
- Zhang, H.; Yuan, Y.; Li, W.; Ou, J.; Li, Y.; Zhang, B. GPS PPP-derived precipitable water vapor retrieval based on Tm/Ps from multiple sources of meteorological data sets in China. J. Geophys. Res. Atmos. 2017, 122, 4165–4183. [Google Scholar] [CrossRef]
- Jing-nan, L.; Mao-Rong, G.E. PANDA software and its preliminary result of positioning and orbit determination. Wuhan Univ. J. Nat. Sci. 2003, 8, 603. [Google Scholar] [CrossRef]
- Ning, T.; Wang, J.; Elgered, G.; Dick, G.; Wickert, J.; Bradke, M.; Sommer, M.; Querel, R.; Smale, D. The uncertainty of the atmospheric integrated water vapour estimated from GNSS observations. Atmos. Meas. Tech. 2016, 9, 79–92. [Google Scholar] [CrossRef] [Green Version]
- Böhm, J.; Möller, G.; Schindelegger, M.; Pain, G.; Weber, R. Development of an improved empirical model for slant delays in the troposphere (GPT2w). GPS Solut. 2015, 19, 433–441. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Y.; Zhang, K.; Rohm, W.; Choy, S.; Norman, R.; Wang, C.S. Real-time retrieval of precipitable water vapor from GPS precise point positioning. J. Geophys. Res. Atmos. 2014, 119, 10044–10057. [Google Scholar] [CrossRef]



| Data | Spatial and Temporal Resolution | Temporal Coverage/Year | Sources | |
|---|---|---|---|---|
| ECMWF-Derived P and T | 0.5° × 0.5° | hourly | 2005–5017 | https://www.ecmwf.int |
| CMONOC-Derived ZTD | station | hourly | 2011–2017 | ftp://ftp.cgps.ac.cn/ |
| RS-Derived P, T and PWV | station | 12 h | 1957–2016 | ftp://ftp.ncdc.noaa.gov |
| AERONET-Derived PWV | station | hourly | 2001–2017 | http://aeronet.gsfc.nasa.gov |
| Area | P/hPa | T/K | ||
|---|---|---|---|---|
| Bias | STD | Bias | STD | |
| South | −0.53 | 0.52 | −0.15 | 1.13 |
| Qinghai-Tibet | −2.54 | 0.59 | −1.24 | 2.71 |
| northwest | 1.95 | 1.05 | 0.09 | 1.87 |
| north | −0.47 | 0.58 | −0.09 | 1.25 |
| china | −0.36 | 0.71 | −0.33 | 1.77 |
| Area | Total Station | P/hPa | T/K | ||||
|---|---|---|---|---|---|---|---|
| Station Utilization (%) | RMS | Bias | Station Utilization (%) | RMS | Bias | ||
| North | 20 | 100 | 2.16 | −0.54 | 100 | 1.74 | −0.30 |
| South | 34 | 88 | 2.45 | −0.70 | 100 | 1.66 | −0.59 |
| Northwest | 24 | 100 | 2.66 | −2.12 | 100 | 2.20 | −0.87 |
| Qinghai-Tibet | 9 | 100 | 2.90 | −1.24 | 100 | 2.40 | 0.10 |
| China | 87 | 95 | 2.71 | −1.11 | 100 | 1.88 | −0.51 |
| Area | Total Station | Station Utilization (%) | STD (mm) | Bias (mm) |
|---|---|---|---|---|
| North | 69 | 100 | 4.37 | −0.24 |
| Qinghai-Tibet | 38 | 97 | 4.50 | −0.80 |
| South | 85 | 96 | 5.50 | −0.42 |
| Northwest | 52 | 100 | 3.69 | −0.32 |
| China | 244 | 98 | 4.60 | −0.40 |
| Area | Theoretical Error of PWV (mm) |
|---|---|
| North | 1.29 |
| South | 1.35 |
| Northwest | 1.54 |
| Qinghai-Tibet | 1.97 |
| China | 1.85 |
| Area | Total Station | Station Utilization (%) | RMS (mm) | Bias (mm) |
|---|---|---|---|---|
| North | 13 | 100 | 1.53 | 0.61 |
| Qinghai-Tibet | 7 | 71 | 3.09 | 3.44 |
| South | 18 | 94 | 2.35 | 2.43 |
| Northwest | 14 | 100 | 2.52 | 0.73 |
| China | 52 | 94 | 2.25 | 1.57 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Q.; Yang, P.; Yao, W.; Yao, Y. Hourly PWV Dataset Derived from GNSS Observations in China. Sensors 2020, 20, 231. https://doi.org/10.3390/s20010231
Zhao Q, Yang P, Yao W, Yao Y. Hourly PWV Dataset Derived from GNSS Observations in China. Sensors. 2020; 20(1):231. https://doi.org/10.3390/s20010231
Chicago/Turabian StyleZhao, Qingzhi, Pengfei Yang, Wanqiang Yao, and Yibin Yao. 2020. "Hourly PWV Dataset Derived from GNSS Observations in China" Sensors 20, no. 1: 231. https://doi.org/10.3390/s20010231
APA StyleZhao, Q., Yang, P., Yao, W., & Yao, Y. (2020). Hourly PWV Dataset Derived from GNSS Observations in China. Sensors, 20(1), 231. https://doi.org/10.3390/s20010231





