Research on Mechanical Fault Prediction Method Based on Multifeature Fusion of Vibration Sensing Data
Abstract
:1. Introduction
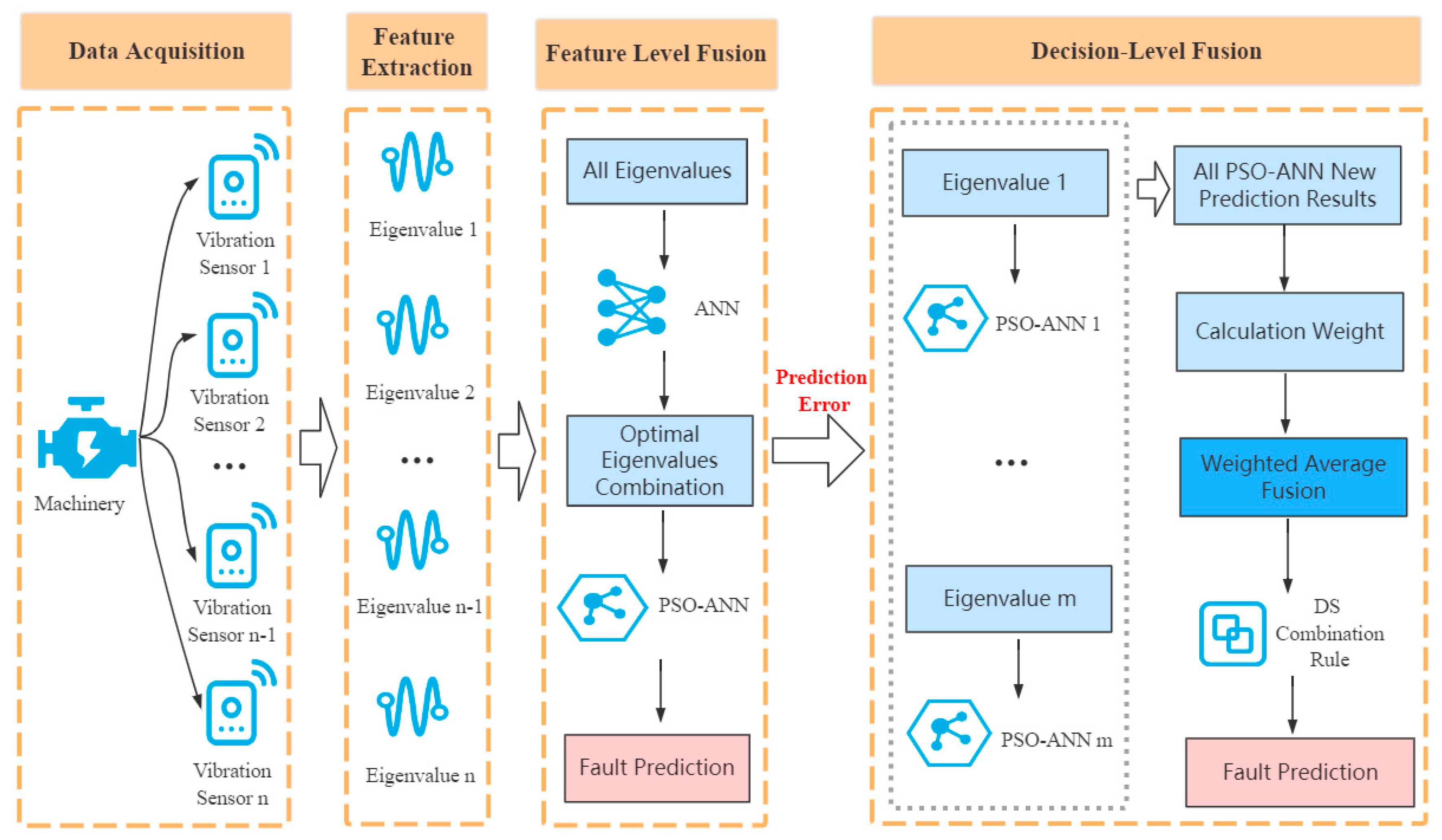
2. Multifeature Fusion Model Based on Vibration Sensing Data
3. Feature Extraction Method Based on Vibration Sensing Data
4. Feature-Level Fusion Based on the Use of a PSO-ANN
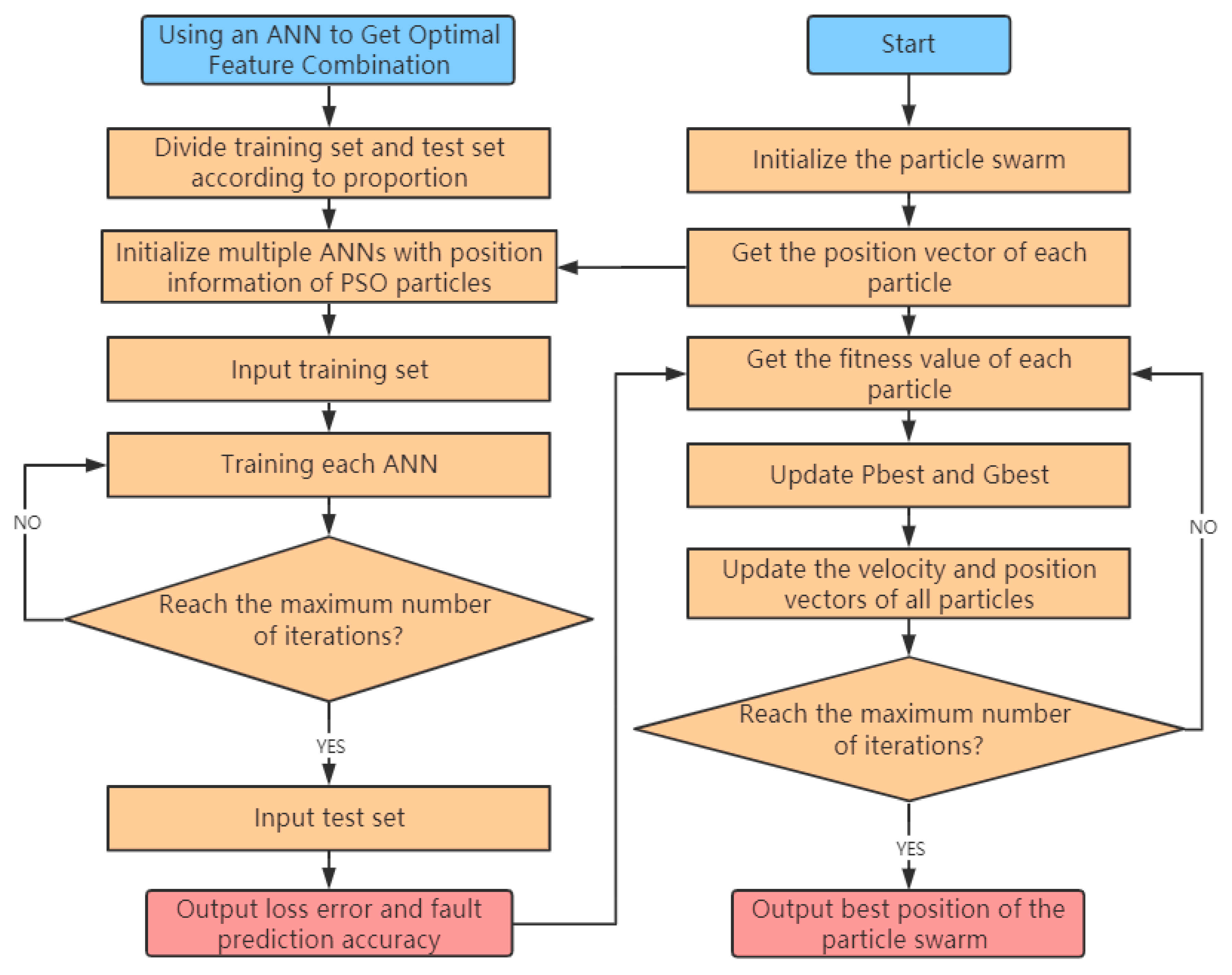
4.1. Artificial Neural Network and the Strategy to Obtain the Optimal Eigenvalues Combination
4.2. Optimization Principle Using the Particle Swarm Optimization Algorithm
4.3. Algorithm Principle of Feature-Level Fusion Using a PSO-ANN
| Algorithm 1: PSO-ANN algorithm. |
| Input: All the eigenvalues of the optimal feature combination. |
| Output: The best position of the particle swarm Gbest, and the best prediction accuracy. |
| 01: Set the parameters {n,, , , , } 02: for i = 1 to n do /* n is the number of particles */ 03: Initialize = (), = (), 04: end for 05: Acquire training set , and test set , 06: Set the particle with best to be 07: for k = 1 do 08: Update with Equation (3) 09: Update , with Equation (4) 10: for i = 1 to n do 11: ann_model(learning_rate = , hidden_layer_ neurons = , 12: momentum_parameter = , rmsprop_parameter = ) 13: .fit(, ) /* Training ANN model */ 14: = .loss_value 15: = .score(, ) 16: if ( > fitness().loss_value and 17: < fitness().prediction_accuracy) then 18: 19: end if 20: if ( > fitness().loss_value and 21: < fitness().prediction_accuracy) then 22: 23: end if 24: for j = 1 to 4 do 25: 26: 27: end for 28: end for 29: end for |
5. Decision-Level Fusion Based on Multiple PSO-ANN Models and Dempster-Shafer Evidence Theory
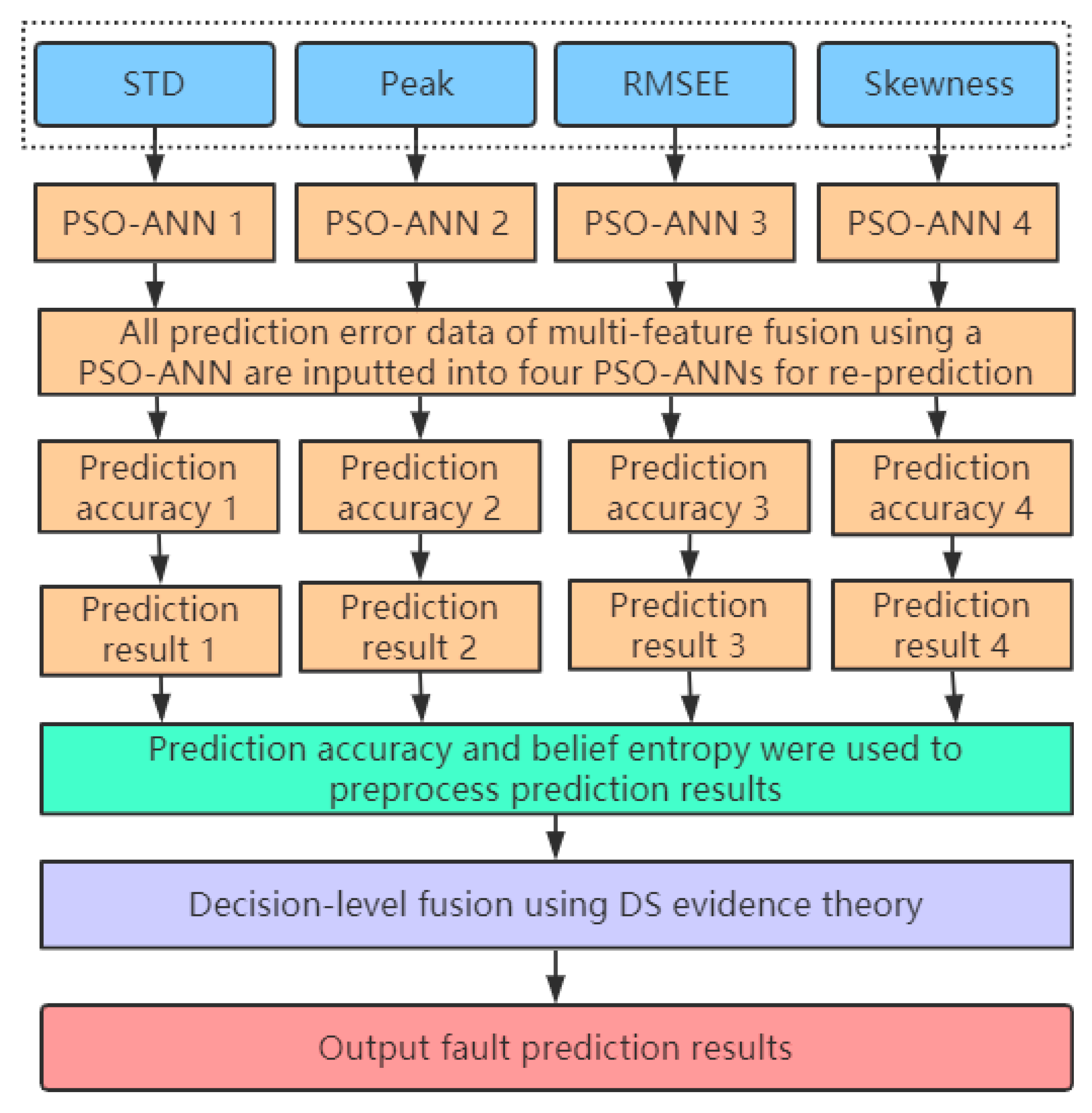
5.1. Running Process of a PSO-ANN-DS
5.2. Algorithm Principle of Decision-Level Fusion Using a PSO-ANN-DS
| Algorithm 2: PSO-ANN-DS algorithm. |
| Input: Four single eigenvalues, and fault data with high levels of uncertainty. |
| Output: Decision-level fusion result Fus(m). |
| 01: /* Step 1 */ 02: Train_data = {STD, Peak, RMSEE, Skewness} /* Four single eigenvalues */ 03: for i = 1 to 4 do 04: = PSO-ANN_algorithm(Input = Train_data [i]) 05: PRE[i] = (test_data = fault data with high 06: uncertainty). prediction_accuracy 07: end for 08: /* Step 2 */ 09: for i = 1 to 4 do 10: CRD[i] = PRE[i] / sum(PRE) 11: end for 12: /* Step 3 */ 13: for i = 1 to 4 do 14: MUN[i] = Calculate the value with Equation (8) and (9) 15: end for 16: /* Step 4 */ 17: for i = 1 to 4 do 18: MCRD[i] = CRD[i] * MUN[i] 19: end for 20: /* Step 5 */ 21: for i = 1 to 4 do 22: NMCRD[i] = MCRD[i] / sum(MCRD) 23: end for 24: /* Step 6 */ 25: for j = 1 to J do /* J is the number of fault types */ 26: WAE[j] = 0 27: for i = 1 to 4 do 28: WAE[j] = WAE[j] + NMCRD[i] * .prediction_result(fault_type = j) 29: end for 30: end for 31: /* Step 7 */ 32: Fus(m) = WAE 33: for i = 1 to 3 do /* There are 4 single features, which need to be merged 3 times. */ 34: Fus(m) = Fus(m) WAE /* refers to the DS fusion rule */ 35: end for |
6. Bearing Fault Prediction Experiment Based on Vibration Sensing Data
6.1. Introduction to Data Set and Experimental Environment
6.2. Using an ANN to Get Optimal Feature Combination
6.3. Feature-Level Fusion Fault Prediction Experiment Based on a PSO-ANN
6.4. Decision-Level Fusion Fault Prediction Experiment Based on PSO-ANN-DS
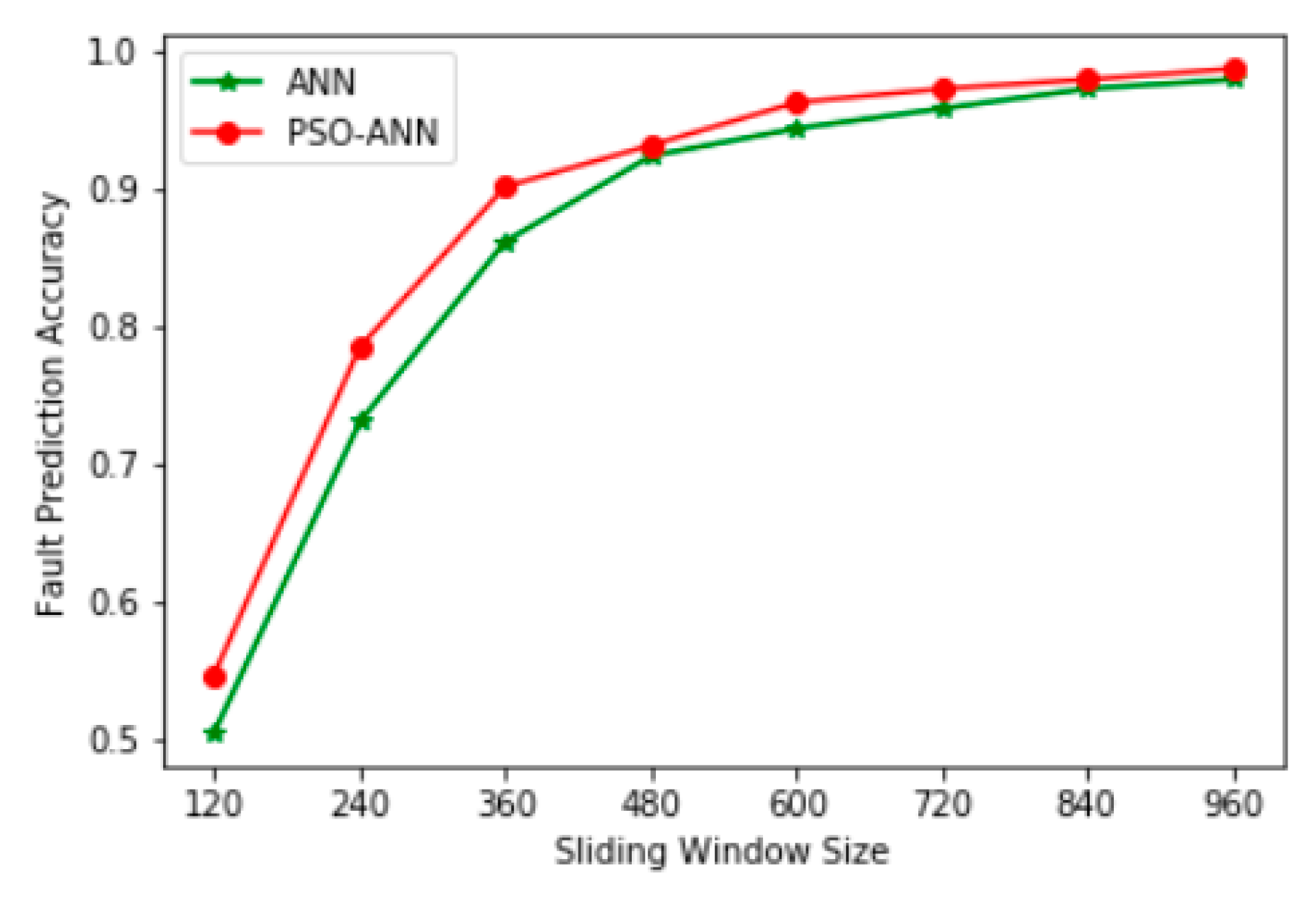
6.5. Comparison and Analysis of Fault Prediction Accuracy of Various Models
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Glowacz, A.; Glowacz, W. Vibration-Based Fault Diagnosis of Commutator Motor. Shock Vib. 2018, 2018, 1–10. [Google Scholar] [CrossRef]
- Wang, H.; Li, S.; Song, L.; Cui, L. A novel convolutional neural network based fault recognition method via image fusion of multi-vibration-signals. Comput. Ind. 2019, 105, 182–190. [Google Scholar] [CrossRef]
- Huang, M.; Liu, Z.; Tao, Y. Mechanical fault diagnosis and prediction in IoT based on multi-source sensing data fusion. Simul. Model. Pract. Theory. [CrossRef]
- Yu, Y.; Li, W.; Sheng, D.; Chen, J. A novel sensor fault diagnosis method based on Modified Ensemble Empirical Mode Decomposition and Probabilistic Neural Network. Measurement 2015, 68, 328–336. [Google Scholar] [CrossRef]
- Wu, L.; Yao, B.; Peng, Z.; Guan, Y. Fault Diagnosis of Roller Bearings Based on a Wavelet Neural Network and Manifold Learning. Appl. Sci. 2017, 7, 158. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Z.; Xu, Q.; Jia, M. Improved shuffled frog leaping algorithm-based BP neural network and its application in bearing early fault diagnosis. Neural Comput. Appl. 2016, 27, 375–385. [Google Scholar] [CrossRef]
- Liu, Z.; Guo, W.; Tang, Z.; Chen, Y. Multi-Sensor Data Fusion Using a Relevance Vector Machine Based on an Ant Colony for Gearbox Fault Detection. Sensors 2015, 15, 21857–21875. [Google Scholar] [CrossRef] [Green Version]
- Qi, G.; Zhu, Z.; Erqinhu, K.; Chen, Y.; Chai, Y.; Sun, J. Fault-diagnosis for reciprocating compressors using big data and machine learning. Simul. Model. Pract. Theory 2018, 80, 104–127. [Google Scholar] [CrossRef]
- Guo, S.; Yang, T.; Gao, W.; Zhang, C.; Zhang, Y. An Intelligent Fault Diagnosis Method for Bearings with Variable Rotating Speed Based on Pythagorean Spatial Pyramid Pooling CNN. Sensors 2018, 18, 3857. [Google Scholar] [CrossRef] [Green Version]
- Xie, J.; Du, G.; Shen, C.; Chen, N.; Chen, L.; Zhu, Z. An End-to-End Model Based on Improved Adaptive Deep Belief Network and Its Application to Bearing Fault Diagnosis. IEEE Access 2018, 6, 63584–63596. [Google Scholar] [CrossRef]
- Lei, J.; Liu, C.; Jiang, D. Fault diagnosis of wind turbine based on Long Short-term memory networks. Renew. Energy 2019, 133, 422–432. [Google Scholar] [CrossRef]
- Ben Ali, J.; Fnaiech, N.; Saidi, L.; Chebel-Morello, B.; Fnaiech, F. Application of empirical mode decomposition and artificial neural network for automatic bearing fault diagnosis based on vibration signals. Appl. Acoust. 2015, 89, 16–27. [Google Scholar] [CrossRef]
- Jiang, L.; Yin, H.; Li, X.; Tang, S. Fault Diagnosis of Rotating Machinery Based on Multisensor Information Fusion Using SVM and Time-Domain Features. Shock Vib. 2014, 2014, 1–8. [Google Scholar] [CrossRef]
- Su, L.; Ma, L.; Qin, N.; Huang, D.; Kemp, A.H. Fault Diagnosis of High-Speed Train Bogie by Residual-Squeeze Net. IEEE Trans. Ind. Inform. 2019, 15, 3856–3863. [Google Scholar] [CrossRef]
- Yang, J.; Guo, Y.; Zhao, W. Long short-term memory neural network based fault detection and isolation for electro-mechanical actuators. Neurocomputing 2019, 360, 85–96. [Google Scholar] [CrossRef]
- Dai, J.; Song, H.; Sheng, G.; Jiang, X. Dissolved gas analysis of insulating oil for power transformer fault diagnosis with deep belief network. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 2828–2835. [Google Scholar] [CrossRef]
- Jiang, G.; He, H.; Xie, P.; Tang, Y. Stacked Multilevel-Denoising Autoencoders: A New Representation Learning Approach for Wind Turbine Gearbox Fault Diagnosis. IEEE Trans. Instrum. Meas. 2017, 66, 2391–2402. [Google Scholar] [CrossRef]
- Illias, H.A.; Chai, X.R.; Abu Bakar, A.H. Hybrid modified evolutionary particle swarm optimisation-time varying acceleration coefficient-artificial neural network for power transformer fault diagnosis. Measurement 2016, 90, 94–102. [Google Scholar] [CrossRef]
- Alnaqi, A.A.; Moayedi, H.; Shahsavar, A.; Nguyen, T.K. Prediction of energetic performance of a building integrated photovoltaic/thermal system thorough artificial neural network and hybrid particle swarm optimization models. Energy Convers. Manag. 2019, 183, 137–148. [Google Scholar] [CrossRef]
- Liao, Y.; Zhang, L.; Li, W. Regrouping particle swarm optimization based variable neural network for gearbox fault diagnosis. J. Intell. Fuzzy Syst. 2018, 34, 3671–3680. [Google Scholar] [CrossRef]
- Chatterjee, S.; Sarkar, S.; Hore, S.; Dey, N.; Ashour, A.S.; Balas, V.E. Particle swarm optimization trained neural network for structural failure prediction of multistoried RC buildings. Neural Comput. Appl. 2017, 28, 2005–2016. [Google Scholar] [CrossRef]
- Yang, L.; Chen, H. Fault diagnosis of gearbox based on RBF-PF and particle swarm optimization wavelet neural network. Neural Comput. Appl. 2019, 31, 4463–4478. [Google Scholar] [CrossRef]
- Li, S.; Liu, G.; Tang, X.; Lu, J.; Hu, J. An Ensemble Deep Convolutional Neural Network Model with Improved D-S Evidence Fusion for Bearing Fault Diagnosis. Sensors 2017, 17, 1729. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hui, K.H.; Ooi, C.S.; Lim, M.H.; Leong, M.S. A hybrid artificial neural network with Dempster-Shafer theory for automated bearing fault diagnosis. J. VibroEng. 2016, 18, 4409–4418. [Google Scholar] [CrossRef]
- Deng, Y. Deng entropy. Chaos Solitons Fractals 2016, 91, 549–553. [Google Scholar] [CrossRef]
- Jiroušek, R.; Shenoy, P.P. A new definition of entropy of belief functions in the Dempster–Shafer theory. Int. J. Approx. Reason. 2018, 92, 49–65. [Google Scholar] [CrossRef] [Green Version]
- Pan, L.; Deng, Y. A new belief entropy to measure uncertainty of basic probability assignments based on belief function and plausibility function. Entropy 2018, 20, 842. [Google Scholar] [CrossRef] [Green Version]
- Cui, H.; Liu, Q.; Zhang, J.; Kang, B. An improved deng entropy and its application in pattern recognition. IEEE Access 2019, 7, 18284–18292. [Google Scholar] [CrossRef]
- Jiang, W.; Wei, B.; Xie, C.; Zhou, D. An evidential sensor fusion method in fault diagnosis. Adv. Mech. Eng. 2016, 8, 1687814016641820. [Google Scholar] [CrossRef] [Green Version]
- Tang, Y.; Zhou, D.; Xu, S.; He, Z. A weighted belief entropy-based uncertainty measure for multi-sensor data fusion. Sensors 2017, 17, 928. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Xiao, F. An improved multisensor data fusion method and its application in fault diagnosis. IEEE Access 2019, 7, 3928–3937. [Google Scholar] [CrossRef]
- Xiao, F.; Qin, B. A weighted combination method for conflicting evidence in multi-sensor data fusion. Sensors 2018, 18, 1487. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pan, S.; Han, T.; Tan, A.C.C.; Lin, T.R. Fault Diagnosis System of Induction Motors Based on Multiscale Entropy and Support Vector Machine with Mutual Information Algorithm. Shock Vib. 2016, 2016, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Ai, Y.-T.; Guan, J.-Y.; Fei, C.-W.; Tian, J.; Zhang, F.-L. Fusion information entropy method of rolling bearing fault diagnosis based on n-dimensional characteristic parameter distance. Mech. Syst. Signal Process. 2017, 88, 123–136. [Google Scholar] [CrossRef]
- Zhu, K.; Song, X.; Xue, D. A roller bearing fault diagnosis method based on hierarchical entropy and support vector machine with particle swarm optimization algorithm. Measurement 2014, 47, 669–675. [Google Scholar] [CrossRef]
- Boudiaf, A.; Moussaoui, A.; Dahane, A.; Atoui, I. A Comparative Study of Various Methods of Bearing Faults Diagnosis Using the Case Western Reserve University Data. J. Fail. Anal. Prev. 2016, 16, 271–284. [Google Scholar] [CrossRef]
- Feng, Z.; Qin, S.; Liang, M. Time–frequency analysis based on Vold-Kalman filter and higher order energy separation for fault diagnosis of wind turbine planetary gearbox under nonstationary conditions. Renew. Energy 2016, 85, 45–56. [Google Scholar] [CrossRef]
- Gai, J.; Hu, Y.; Shen, J. A Bearing Performance Degradation Modeling Method Based on EMD-SVD and Fuzzy Neural Network. Shock Vib. 2019, 2019, 1–10. [Google Scholar] [CrossRef]
- Bin, G.F.; Gao, J.J.; Li, X.J.; Dhillon, B.S. Early fault diagnosis of rotating machinery based on wavelet packets—Empirical mode decomposition feature extraction and neural network. Mech. Syst. Signal Process. 2012, 27, 696–711. [Google Scholar] [CrossRef]
- Lv, Y.; Yuan, R.; Song, G. Multivariate empirical mode decomposition and its application to fault diagnosis of rolling bearing. Mech. Syst. Signal Process. 2016, 81, 219–234. [Google Scholar] [CrossRef]
- Zhang, Q.; Gao, J.; Dong, H.; Mao, Y. WPD and DE/BBO-RBFNN for solution of rolling bearing fault diagnosis. Neurocomputing 2018, 312, 27–33. [Google Scholar] [CrossRef]
- Zhao, L.-Y.; Wang, L.; Yan, R.-Q. Rolling bearing fault diagnosis based on wavelet packet decomposition and multi-scale permutation entropy. Entropy 2015, 17, 6447–6461. [Google Scholar] [CrossRef] [Green Version]
- Mahamad, A.K.; Saon, S.; Hiyama, T. Predicting remaining useful life of rotating machinery based artificial neural network. Comput. Math. Appl. 2010, 60, 1078–1087. [Google Scholar] [CrossRef] [Green Version]
- Ben Ali, J.; Chebel-Morello, B.; Saidi, L.; Malinowski, S.; Fnaiech, F. Accurate bearing remaining useful life prediction based on Weibull distribution and artificial neural network. Mech. Syst. Signal Process. 2015, 56, 150–172. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, S.; Li, W. Bearing performance degradation assessment using long short-term memory recurrent network. Comput. Ind. 2019, 106, 14–29. [Google Scholar] [CrossRef]
- Bottou, L. Stochastic Gradient Descent Tricks. In Neural Networks: Tricks of the Trade, 2nd ed.; Montavon, G., Orr, G.B., Müller, K.-R., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; pp. 421–436. ISBN 978-3-642-35289-8. [Google Scholar]
- Rehman, M.Z.; Nawi, N.M. The Effect of Adaptive Momentum in Improving the Accuracy of Gradient Descent Back Propagation Algorithm on Classification Problems. In Proceedings of the Software Engineering and Computer Systems; Springer: Berlin/Heidelberg, Germany, 2011; pp. 380–390. [Google Scholar]
- Dozat, T. Incorporating Nesterov Momentum into Adam. In Proceedings of the International Conference on Learning Representations, San Juan, Philippines, 2–4 May 2016; pp. 1–6. [Google Scholar]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science (MHS’95), Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Huang, H.; Qin, H.; Hao, Z.; Lim, A. Example-based learning particle swarm optimization for continuous optimization. Inf. Sci. 2012, 182, 125–138. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A Modified Particle Swarm Optimizer; IEEE: Anchorage, AK, USA, 1998; pp. 69–73. [Google Scholar]
- Deng, W.; Yao, R.; Zhao, H.; Yang, X.; Li, G. A novel intelligent diagnosis method using optimal LS-SVM with improved PSO algorithm. Soft Comput. 2019, 23, 2445–2462. [Google Scholar] [CrossRef]
- Janocha, K.; Czarnecki, W.M. On loss functions for deep neural networks in classification. arXiv 2017, arXiv:1702.05659. [Google Scholar] [CrossRef]
- Dempster, A.P. Upper and Lower Probabilities Induced by a Multivalued Mapping. In Classic Works of the Dempster-Shafer Theory of Belief Functions; Yager, R.R., Liu, L., Eds.; Studies in Fuzziness and Soft Computing; Springer: Berlin/Heidelberg, Germany, 2008; pp. 57–72. ISBN 978-3-540-44792-4. [Google Scholar]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976; ISBN 978-0-691-10042-5. [Google Scholar]
- Murphy, C.K. Combining belief functions when evidence conflicts. Decis. Support Syst. 2000, 29, 1–9. [Google Scholar] [CrossRef]
- Case Western Reserve University Bearing Data Center Website. Available online: https://csegroups.case.edu/bearingdatacenter/pages/welcome-case-western-reserve-university-bearing-data-center-website (accessed on 30 July 2019).





| Serial Number | Feature Name | Formula |
|---|---|---|
| 1 | Root mean square (RMS) | |
| 2 | Standard deviation (STD) | |
| 3 | Peak | |
| 4 | Root mean square entropy estimator (RMSEE) | |
| 5 | Waveform entropy (WFE) | |
| 6 | Kurtosis | |
| 7 | Skewness | |
| 8 | Crest factor (CRF) | |
| 9 | Impulse factor (IMF) |
| Noise Location | Reason | Explanation |
|---|---|---|
| Mechanical equipment | Eddy noise | Increased external air velocity causes eddies around machinery. |
| Rotating noise | The vibration force of rotating machinery deviates easily from the normal value when encountering strong air flow. | |
| Energy shortage | Energy issues (for example, oil level below average) cause large levels of noise pollution. | |
| Impact noise | Large levels of noise pollution caused by impacts. | |
| Other reasons | Suddenly increasing the operating power of mechanical equipment, manual operation of mechanical equipment. | |
| Vibration sensor | Temperature factor | In general, the higher the temperature, the greater the measurement error. |
| Resonant frequency | The closer the vibration frequency of the machine is to the value of the resonance frequency, the greater the measurement error. | |
| Placement deviation | Vibration sensors generally get acceleration sensing data in three directions. The larger the deviation in the placement direction, the greater the measurement error. | |
| Original error | Different types of vibration sensors have different original errors. | |
| Other environmental factors | Under the condition of a strong electrostatic field, alternating magnetic field, or nuclear radiation, the measurement error may become larger. |
| Fault Type | File Name |
|---|---|
| Normal Baseline Data | 98.mat |
| 48K Drive End Bearing Fault Data (Inner Race) | 110.mat |
| 48K Drive End Bearing Fault Data (Ball) | 123.mat |
| 48K Drive End Bearing Fault Data (Outer Race Orthogonal@3:00) | 149.mat |
| 48K Drive End Bearing Fault Data (Outer Race Centered@6:00) | 136.mat |
| 48K Drive End Bearing Fault Data (Outer Race Opposite@12:00) | 162.mat |
| Eigenvalue | Sliding Window Size | |||||||
|---|---|---|---|---|---|---|---|---|
| 120 | 240 | 360 | 480 | 600 | 720 | 840 | 960 | |
| RMS | 31.67% | 52.11% | 77.22% | 86.11% | 88.67% | 88.11% | 91.33% | 91.89% |
| STD | 30.11% | 52.11% | 76.78% | 85.89% | 88.44% | 88.00% | 91.22% | 91.78% |
| Peak | 30.67% | 41.89% | 63.67% | 73.22% | 76.89% | 79.00% | 81.56% | 80.44% |
| RMSEE | 23.89% | 41.78% | 46.22% | 52.33% | 53.78% | 55.44% | 56.78% | 52.78% |
| WFE | 1.11% | 7.22% | 7.22% | 20.22% | 24.11% | 27.22% | 39.78% | 46.44% |
| Kurtosis | 2.67% | 9.67% | 20.78% | 23.44% | 12.33% | 12.11% | 29.56% | 31.00% |
| Skewness | 1.78% | 6.56% | 15.11% | 20.11% | 23.11% | 22.89% | 22.11% | 23.78% |
| CRF | 0.44% | 2.89% | 1.56% | 3.56% | 10.22% | 10.67% | 10.56% | 14.22% |
| IMF | 1.89% | 6.89% | 8.89% | 21.33% | 12.78% | 12.22% | 10.33% | 12.22% |
| All | 48.33% | 73.00% | 86.11% | 92.33% | 94.33% | 95.78% | 97.22% | 97.89% |
| Eigenvalue | RMS | STD | Peak | RMSEE | WFE | Kurtosis | Skewness | CRF | IMF |
|---|---|---|---|---|---|---|---|---|---|
| RMS | 79.67% | 79.00% | 80.33% | 82.78% | 83.89% | 85.11% | 86.33% | 86.11% | |
| STD | 79.67% | 79.00% | 80.33% | 82.78% | 83.89% | 84.67% | 86.33% | 86.00% | |
| Peak | 79.22% | 79.44% | 80.00% | 82.89% | 83.89% | 84.56% | 85.67% | 85.11% | |
| RMSEE | 79.67% | 81.33% | 79.78% | 82.89% | 83.78% | 85.33% | 86.00% | 86.22% | |
| WFE | 81.78% | 82.33% | 83.11% | 83.22% | 84.00% | 84.33% | 85.44% | 86.00% | |
| Kurtosis | 82.44% | 84.11% | 82.89% | 83.00% | 84.00% | 83.89% | 85.00% | 85.56% | |
| Skewness | 82.22% | 82.56% | 83.22% | 83.44% | 84.44% | 84.44% | 85.44% | 85.00% | |
| CRF | 81.33% | 80.44% | 81.11% | 81.44% | 82.33% | 84.89% | 85.33% | 85.00% | |
| IMF | 82.33% | 83.67% | 82.11% | 82.44% | 83.00% | 83.89% | 84.78% | 86.22% |
| Sliding Window Size | Optimal Feature Combination | Accuracy | |
|---|---|---|---|
| All | Optimal Combination | ||
| 120 | {Kurtosis,RMS,STD,Peak,RMSEE,WFE,Skewness,CRF} | 48.33% | 50.44% |
| 240 | {RMS,STD,Peak,RMSEE,WFE,Kurtosis,Skewness,CRF,IMF} | 73.00% | 73.00% |
| 360 | {RMS,STD,Peak,RMSEE,WFE,Kurtosis,Skewness,CRF} | 86.11% | 86.33% |
| 480 | {WFE,RMS,STD,Peak,RMSEE,Kurtosis,Skewness,CRF,IMF} | 92.33% | 93.00% |
| 600 | {RMS, STD,Peak,RMSEE,WFE,Kurtosis,Skewness,CRF,IMF} | 94.33% | 94.33% |
| 720 | {IMF,RMS,STD,Peak,RMSEE,WFE,Kurtosis,Skewness} | 95.78% | 96.44% |
| 840 | {Skewness,RMS,STD,Peak,RMSEE,WFE,Kurtosis,CRF,IMF} | 97.22% | 97.67% |
| 960 | {RMS,STD,Peak,RMSEE,WFE,Kurtosis,Skewness,CRF,IMF} | 97.89% | 97.89% |
| Parameter | Range Interval/Value |
|---|---|
| Number of hidden layers | 1 |
| Number of hidden layer units | [10, 100] |
| Learning rate | [0.0001, 0.1] |
| Momentum parameter | [0.001, 0.999] |
| RMSprop parameter | [0.001, 0.999] |
| Number of Particles | Learning Rate | Momentum Parameter | RMSprop Parameter | Number of Hidden Layer Neurons | Loss Value | Accuracy |
|---|---|---|---|---|---|---|
| 10 | 0.021404 | 0.999 | 0.999 | 100 | 0.372830 | 89.22% |
| 20 | 0.007614 | 0.609325 | 0.658986 | 58 | 0.479214 | 89.44% |
| 30 | 0.006649 | 0.573852 | 0.966601 | 81 | 0.464076 | 89.89% |
| 40 | 0.008156 | 0.467269 | 0.989776 | 77 | 0.467528 | 89.22% |
| 50 | 0.014367 | 0.998993 | 0.999 | 90 | 0.347928 | 90.11% |
| 60 | 0.010740 | 0.999 | 0.999 | 81 | 0.349434 | 89.67% |
| Eigenvalue | Sliding Window Size | |||||||
|---|---|---|---|---|---|---|---|---|
| 120 | 240 | 360 | 480 | 600 | 720 | 840 | 960 | |
| RMS | 40.00% | 58.89% | 78.33% | 87.11% | 89.22% | 88.78% | 91.56% | 92.00% |
| STD | 41.22% | 64.22% | 78.00% | 86.44% | 89.22% | 88.56% | 91.78% | 92.11% |
| Peak | 42.67% | 58.11% | 68.00% | 76.33% | 77.44% | 81.11% | 82.22% | 81.78% |
| RMSEE | 33.00% | 47.67% | 59.44% | 62.44% | 70.89% | 70.89% | 72.44% | 75.33% |
| WFE | 7.33% | 10.67% | 20.56% | 30.33% | 32.33% | 42.56% | 47.44% | 49.89% |
| Kurtosis | 5.89% | 11.44% | 24.33% | 25.67% | 21.00% | 23.11% | 41.44% | 47.00% |
| Skewness | 3.22% | 11.44% | 19.78% | 20.44% | 23.56% | 24.11% | 23.56% | 30.22% |
| CRF | 1.11% | 4.89% | 7.89% | 20.11% | 21.78% | 11.44% | 12.56% | 15.67% |
| IMF | 4.11% | 10.33% | 20.00% | 23.89% | 14.78% | 14.22% | 34.78% | 32.56% |
| All | 54.67% | 78.44% | 90.11% | 93.11% | 96.22% | 97.22% | 97.89% | 98.67% |
| PSO-ANN Model | Fault Type | |||||
|---|---|---|---|---|---|---|
| Normal State | Inner Race Fault | Rolling Element Fault | Outer Race Orthogonal@3:00 Fault | Outer Race Centered@6:00 Fault | Outer Race Opposite@12:00 Fault | |
| STD | 0 | 0.2979 | 0.0053 | 0.1500 | 0.2961 | 0.2507 |
| Peak | 0 | 0.267 | 0.0608 | 0.1630 | 0.2214 | 0.2878 |
| RMSEE | 0 | 0.2763 | 0.0846 | 0.1170 | 0.2759 | 0.2462 |
| Skewness | 0.0926 | 0.0674 | 0.1257 | 0.2928 | 0.227 | 0.1945 |
| Parameter Name | PSO-ANN Trained by a Single Feature | |||
|---|---|---|---|---|
| STD | Peak | RMSEE | Skewness | |
| PRE | 0.2941 | 0.2623 | 0.2672 | 0.1789 |
| CRD | 0.2934 | 0.2616 | 0.2665 | 0.1785 |
| MUN | 7.3255 | 8.8422 | 8.9058 | 11.2462 |
| MCRD | 2.1493 | 2.3132 | 2.3734 | 2.0073 |
| NMCRD | 0.243 | 0.2616 | 0.2684 | 0.227 |
| Fusion Times of DS | Fault Type | |||||
|---|---|---|---|---|---|---|
| Normal State | Inner Race Fault | Rolling Element Fault | Outer Race Orthogonal@3:00 Fault | Outer Race Centered@6:00 Fault | Outer Race Opposite@12:00 Fault | |
| 0 | 0.021 | 0.2317 | 0.0684 | 0.1769 | 0.2555 | 0.2465 |
| 1 | 0.002 | 0.2484 | 0.0217 | 0.1448 | 0.302 | 0.2811 |
| 2 | 0.0001 | 0.249 | 0.0065 | 0.1109 | 0.3338 | 0.2997 |
| 3 | 0 | 0.2435 | 0.0019 | 0.0828 | 0.36 | 0.3118 |
| Method | Sliding Window Size | |||||||
|---|---|---|---|---|---|---|---|---|
| 120 | 240 | 360 | 480 | 600 | 720 | 840 | 960 | |
| Basic DS | 67.89% | 82.00% | 92.44% | 95.89% | 97.44% | 97.89% | 98.89% | 98.89% |
| Literature [30] | 67.56% | 82.56% | 92.44% | 96.22% | 97.44% | 97.89% | 98.89% | 98.78% |
| Literature [31] | 68.44% | 81.78% | 92.33% | 96.22% | 97.44% | 98.00% | 98.78% | 98.89% |
| Literature [32] | 68.22% | 81.67% | 92.33% | 96.22% | 97.33% | 98.00% | 98.78% | 98.89% |
| We Proposed | 68.33% | 82.67% | 92.44% | 96.44% | 97.44% | 98.22% | 99.00% | 99.00% |
| Model | Sliding Window Size | |||||||
|---|---|---|---|---|---|---|---|---|
| 120 | 240 | 360 | 480 | 600 | 720 | 840 | 960 | |
| KNN | 57.78% | 74.45% | 84.33% | 90.11% | 93.11% | 94.67% | 95.44% | 96.44% |
| Decision tree | 57.22% | 75.44% | 86.89% | 91.44% | 94.00% | 95.67% | 97.11% | 98.22% |
| Random forest | 61.89% | 78.00% | 89.33% | 94.00% | 96.44% | 97.33% | 97.78% | 98.44% |
| Naive Bayes | 62.11% | 76.33% | 83.67% | 90.56% | 93.78% | 95.00% | 97.44% | 98.11% |
| ANN | 50.44% | 73.00% | 86.33% | 93.00% | 94.33% | 96.44% | 97.67% | 97.89% |
| SVM | 63.67% | 78.89% | 88.00% | 92.67% | 95.11% | 96.78% | 97.78% | 98.00% |
| LSTM | 57.89% | 72.89% | 80.11% | 84.22% | 88.33% | 91.56% | 93.00% | 96.11% |
| PSO-ANN | 54.67% | 78.44% | 90.11% | 93.11% | 96.22% | 97.22% | 97.89% | 98.67% |
| PSO-ANN-DS | 68.33% | 82.67% | 92.44% | 96.44% | 97.44% | 98.22% | 99.00% | 99.00% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, M.; Liu, Z. Research on Mechanical Fault Prediction Method Based on Multifeature Fusion of Vibration Sensing Data. Sensors 2020, 20, 6. https://doi.org/10.3390/s20010006
Huang M, Liu Z. Research on Mechanical Fault Prediction Method Based on Multifeature Fusion of Vibration Sensing Data. Sensors. 2020; 20(1):6. https://doi.org/10.3390/s20010006
Chicago/Turabian StyleHuang, Min, and Zhen Liu. 2020. "Research on Mechanical Fault Prediction Method Based on Multifeature Fusion of Vibration Sensing Data" Sensors 20, no. 1: 6. https://doi.org/10.3390/s20010006
APA StyleHuang, M., & Liu, Z. (2020). Research on Mechanical Fault Prediction Method Based on Multifeature Fusion of Vibration Sensing Data. Sensors, 20(1), 6. https://doi.org/10.3390/s20010006





