A Novel LSTM for Multivariate Time Series with Massive Missingness
Abstract
:1. Introduction
- exploring a new LSTM-based architecture, integrating jointly two decay mechanisms with the missing rate of each variable, to learn the missing pattern informatively;
- concluding that not all missing patterns provide informative data in the meteorological settings.
2. Related Works
3. Methods
3.1. LSTM
3.2. FB-LSTM
3.3. FBVS-LSTM
4. Experiments
4.1. Dataset Description and Preprocessing
4.2. Metric
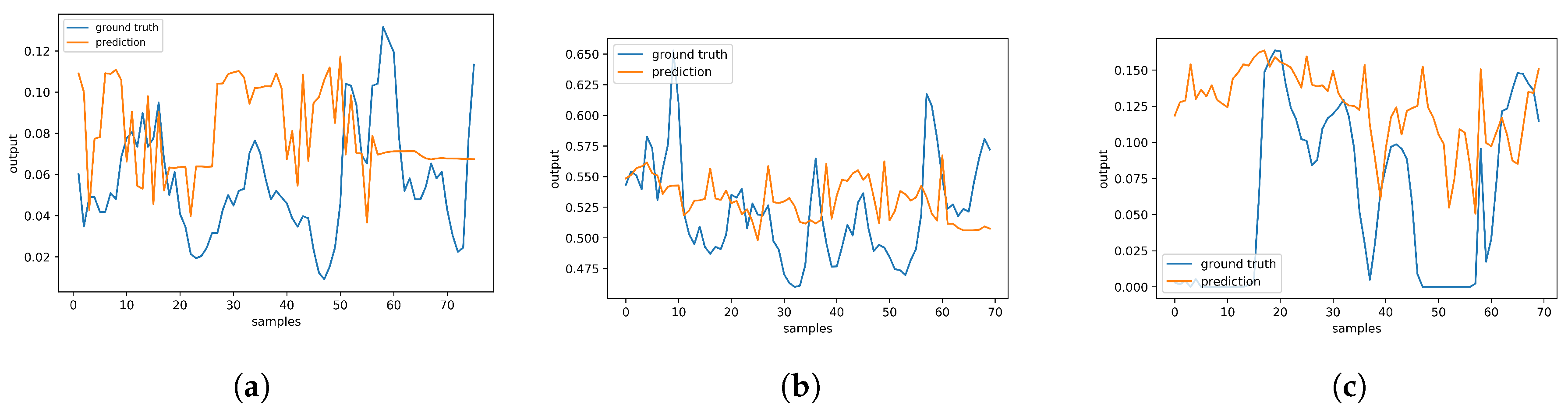
4.3. Evaluation and Results
4.4. Statistical Analysis
- H0: The proposed method performed similarly w.r.t. other assessment models.
- H1: The proposed method performed differently w.r.t. other assessment models.
5. Conclusions and Future Works
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lewis, R.; Reinsel, G.C. Prediction of multivariate time series by autoregressive model fitting. J. Multivar. Anal. 1985, 16, 393–411. [Google Scholar] [CrossRef] [Green Version]
- Han, M.; Fan, M.; Xi, J. Study of Nonlinear Multivariate Time Series Prediction Based on Neural Networks. In Advances in Neural Networks; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3497, pp. 618–623. [Google Scholar]
- Cai, Y.; Wang, H.; Ye, X.; An, L. Multivariate Time Series Prediction Based on Multi-Output Support Vector Regression. In Knowledge Engineering and Management; Springer: Berlin/Heidelberg, Germany, 2014; pp. 385–395. [Google Scholar]
- Jin, X.; Yu, X.; Wang, X.; Bai, Y.; Su, T.; Kong, J. Prediction for Time Series with CNN and LSTM. In Proceedings of the 11th International Conference on Modelling, Identification and Control (ICMIC2019), Tianjin, China, 13–15 July 2019; Springer: Singapore, 2019; pp. 631–641. [Google Scholar]
- Du, S.; Li, T.; Yang, Y.; Horng, S.J. Multivariate time series forecasting via attention-based encoder–decoder framework. Neurocomputing 2020, 388, 269–279. [Google Scholar] [CrossRef]
- Pratama, I.; Permanasari, A.E.; Ardiyanto, I.; Indrayani, R. A review of missing values handling methods on time-series data. In Proceedings of the IEEE International Conference on Information Technology Systems and Innovation (ICITSI), Bandung-Bali, Indonesia, 24–27 October 2016; pp. 1–6. [Google Scholar]
- Kotsiantis, S.; Kostoulas, A.; Lykoudis, S.; Argiriou, A.; Menagias, K. Filling missing temperature values in weather data banks. In Proceedings of the 2nd IET International Conference on Intelligent Environments, IE 06, IET, Athens, Greece, 5–6 July 2006; Volume 1, pp. 327–334. [Google Scholar]
- Howell, D.C. The treatment of missing data. In The SAGE Handbook of Social Science Methodology; Outhwaite, W., Turner, S.P., Eds.; SAGE Publications Ltd.: Thousand Oaks, CA, USA, 2007; pp. 212–226. Available online: https://study.sagepub.com/sites/default/files/Howell.pdf (accessed on 15 May 2020).
- Ghorbani, A.; Zou, J.Y. Embedding for informative missingness: Deep learning with incomplete data. In Proceedings of the 56th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 2–5 October 2018; pp. 437–445. [Google Scholar]
- Gómez, V.; Maravall, A.; Peña, D. Missing observations in ARIMA models: Skipping approach versus additive outlier approach. J. Econ. 1999, 88, 341–363. [Google Scholar] [CrossRef]
- Damsleth, E. Interpolating missing values in a time series. Scand. Stat. Theory Appl. 1980, 7, 33–39. [Google Scholar]
- García-Laencina, P.J.; Sancho-Gómez, J.L.; Figueiras-Vidal, A.R. Pattern classification with missing data: A review. Neural Comput. Appl. 2010, 19, 263–282. [Google Scholar] [CrossRef]
- Gnauck, A. Interpolation and approximation of water quality time series and process identification. Anal. Bioanal. Chem. 2004, 380, 484–492. [Google Scholar] [CrossRef]
- Yu, H.F.; Rao, N.; Dhillon, I.S. Temporal regularized matrix factorization for high-dimensional time series prediction. In Proceedings of the 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 847–855. [Google Scholar]
- Schneider, T. Analysis of incomplete climate data: Estimation of mean values and covariance matrices and imputation of missing values. J. Clim. 2001, 14, 853–871. [Google Scholar] [CrossRef]
- Rivero, C.R.; Pucheta, J.; Laboret, S.; Patiño, D.; Sauchelli, V. Forecasting short time series with missing data by means of energy associated to series. Appl. Math. 2015, 6, 1611–1619. [Google Scholar] [CrossRef] [Green Version]
- Oehmcke, S.; Zielinski, O.; Kramer, O. KNN ensembles with penalized DTW for multivariate time series imputation. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 2774–2781. [Google Scholar]
- Amato, A.; Calabrese, M.; Di Lecce, V. Decision trees in time series reconstruction problems. In Proceedings of the 25th IEEE Instrumentation and Measurement Technology Conference, Victoria, BC, Canada, 12–15 May 2008; pp. 895–899. [Google Scholar]
- Che, Z.; Purushotham, S.; Cho, K.; Sontag, D.; Liu, Y. Recurrent neural networks for multivariate time series with missing values. Sci. Rep. 2018, 8, 6085. [Google Scholar] [CrossRef] [Green Version]
- Strauman, A.S.; Bianchi, F.M.; Mikalsen, K.Ø.; Kampffmeyer, M.; Soguero-Ruíz, C.; Jenssen, R. Classification of postoperative surgical site infections from blood measurements with missing data using recurrent neural networks. In Proceedings of the IEEE International Conference on Biomedical & Health Informatics (BHI), Las Vegas, NV, USA, 4–7 March 2018; pp. 307–310. [Google Scholar]
- Li, Q.; Xu, Y. VS-GRU: A variable sensitive gated recurrent neural network for multivariate time series with massive missing values. Appl. Sci. 2019, 9, 3041. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.J.; Chi, M. Temporal belief memory: Imputing missing data during RNN training. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence IJCAI-18, Stockholm, Sweden, 13–19 July 2018; pp. 2326–2332. [Google Scholar]
- LEE, M.; AN, J.; LEE, Y. Missing-value imputation of continuous missing based on deep imputation network using correlations among multiple IoT data streams in a smart space. IEICE Trans. Inf. Syst. 2019, E102.D, 289–298. [Google Scholar] [CrossRef] [Green Version]
- Singh, B.P.; Deznabi, I.; Narasimhan, B.; Kucharski, B.; Uppaal, R.; Josyula, A.; Fiterau, M. Multi-resolution networks for flexible irregular time series modeling (Multi-FIT). arXiv 2019, arXiv:1905.00125. [Google Scholar]
- Liang, X.; Zou, T.; Guo, B.; Li, S.; Zhang, H.; Zhang, S.; Huang, H.; Chen, S.X. Assessing Beijing’s PM2.5 pollution: Severity, weather impact, APEC and winter heating. Proc. R. Soc. A 2015, 471, 20150257. [Google Scholar] [CrossRef] [Green Version]
- Vito, S.D.; Massera, E.; Piga, M.; Martinotto, L.; Francia, G.D. On field calibration of an electronic nose for benzene estimation in an urban pollution monitoring scenario. Sens. Actuators B Chem. 2008, 129, 750–757. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, B.; Dong, A.; He, J.; Xu, Z.; Chen, S.X. Cautionary tales on air-quality improvement in Beijing. Proc. R. Soc. A 2017, 473, 20170457. [Google Scholar] [CrossRef] [Green Version]
- Cai, X.; Zhang, N.; Venayagamoorthy, G.K.; Wunsch, D.C. Time series prediction with recurrent neural networks trained by a hybrid PSO–EA algorithm. Neurocomputing 2007, 70, 2342–2353. [Google Scholar] [CrossRef]
- Bashir, F.; Wei, H.L. Handling missing data in multivariate time series using a vector autoregressive model-imputation (VAR-IM) algorithm. Neurocomputing 2018, 276, 23–30. [Google Scholar] [CrossRef]
- Liu, J.; Kumar, S.; Palomar, D.P. Parameter Estimation of Heavy-Tailed AR Model with Missing Data Via Stochastic EM. IEEE Trans. Signal. Process. 2019, 67, 2159–2172. [Google Scholar] [CrossRef] [Green Version]
- Guo, Z.; Wan, Y.; Ye, H. A data imputation method for multivariate time series based on generative adversarial network. Neurocomputing 2019, 360, 185–197. [Google Scholar] [CrossRef]
- Holden, K.; Broomhead, A. An examination of vector autoregressive forecasts for the U.K. economy. Int. J. Forecast. 1990, 6, 11–23. [Google Scholar] [CrossRef]
- Zhang, Y.; Thorburn, P.J.; Xiang, W.; Fitch, P. SSIM—A Deep Learning Approach for Recovering Missing Time Series Sensor Data. IEEE Internet Things J. 2019, 6, 6618–6628. [Google Scholar] [CrossRef]
- Feng, T.; Narayanan, S.S. Imputing Missing Data In Large-Scale Multivariate Biomedical Wearable Recordings Using Bidirectional Recurrent Neural Networks with Temporal Activation Regularization. In Proceedings of the 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 2529–2534. [Google Scholar]
- Liu, T.; Wei, H.; Zhang, K. Wind power prediction with missing data using Gaussian process regression and multiple imputation. Appl. Soft. Comput. 2018, 71, 905–916. [Google Scholar] [CrossRef]
- Lipton, Z.C.; Kale, D.; Wetzel, R. Directly modeling missing data in sequences with RNNs: Improved classification of clinical time series. In Proceedings of the 1st Machine Learning for Healthcare Conference, Los Angeles, CA, USA, 19–20 August 2016; pp. 253–270. [Google Scholar]
- Yoon, J.; Zame, W.R.; van der Schaar, M. Estimating missing data in temporal data streams using multi-directional recurrent neural networks. IEEE Trans. Biomed. Eng. 2017, 66, 1477–1490. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fortuin, V.; Baranchuk, D.; Rätsch, G.; Mandt, S. GP-VAE: Deep Probabilistic Time Series Imputation. arXiv 2020, arXiv:1907.04155. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Santos, M.S.; Pereira, R.C.; Costa, A.F.; Soares, J.P.; Santos, J.; Abreu, P.H. Generating synthetic missing data: A review by missing mechanism. IEEE Access 2019, 7, 11651–11667. [Google Scholar] [CrossRef]








| Dataset | Features | Missing Rate |
|---|---|---|
| Beijing PM2.5 | PM2.5 | 75% |
| dew | 52% | |
| temperature | 66% | |
| pressure | 49% | |
| wind direction | 89% | |
| wind speed | 67% | |
| snow | 1% | |
| rain | 5% | |
| Italy Air Quality | PT08.S1(CO) | 34% |
| PT08.S2(NMHC) | 38% | |
| PT08.S3(NOx) | 88% | |
| PT08.S4(NO2) | 32% | |
| PT08.S5(O3) | 45% | |
| Beijing Multi-Site Air-Quality | PM2.5 | 34% |
| PM10 | 28% | |
| SO2 | 81% | |
| NO2 | 22% | |
| CO | 36% | |
| O3 | 38% |
| Datasets | Parameters | ||||
|---|---|---|---|---|---|
| Epoch Number | Learning Rate | Hidden Layers | Features (Input Size) | Output Size | |
| Beijing PM2.5 | 30 | 0.01 | 24 | 8 | 1 |
| Italy Air Quality | 30 | 0.01 | 24 | 5 | 1 |
| Beijing Multi-Site Air-Quality | 30 | 0.01 | 24 | 6 | 1 |
| Dataset | Model | MSE ± STD | |
|---|---|---|---|
| Train Error | Test Error | ||
| Beijin PM2.5 | LSTM-0 | 0.021 ± 0.020 | 0.016 ± 0.009 |
| LSTM-mean | 0.021 ± 0.016 | 0.015 ± 0.011 | |
| B-LSTM | 0.016 ± 0.008 | 0.010 ± 0.004 | |
| F-LSTM | 0.180 ± 0.324 | 0.172 ± 0.323 | |
| BVS-LSTM | 0.013 ± 0.006 | 0.010 ± 0.004 | |
| FBVS-LSTM | 0.012 ± 0.004 | 0.011 ± 0.005 | |
| Italy Air Quality | LSTM-0 | 0.122 ± 0.123 | 0.130 ± 0.142 |
| LSTM-mean | 0.063 ± 0.078 | 0.066 ± 0.082 | |
| B-LSTM | 0.027 ± 0.003 | 0.027 ± 0.009 | |
| F-LSTM | 0.030 ± 0.007 | 0.029 ± 0.015 | |
| BVS-LSTM | 0.031 ± 0.011 | 0.031 ± 0.013 | |
| FBVS-LSTM | 0.023 ± 0.002 | 0.024 ± 0.006 | |
| Beijing Multi-Site Air-Quality | LSTM-0 | 0.049 ± 0.029 | 0.06± 0.032 |
| LSTM-mean | 0.038 ± 0.015 | 0.03 ± 0.023 | |
| B-LSTM | 0.031 ± 0.011 | 0.03 ± 0.016 | |
| F-LSTM | 0.179 ± 0.3 | 0.148 ± 0.25 | |
| BVS-LSTM | 0.034 ± 0.008 | 0.040 ± 0.024 | |
| FBVS-LSTM | 0.026 ± 0.019 | 0.031 ± 0.002 | |
| Dataset | Model | FBVS-LSTM | |
|---|---|---|---|
| t-Value | p-Value | ||
| Beijin PM2.5 | LSTM-0 | −1.62 | 0.11 |
| LSTM-mean | −0.87 | 0.39 | |
| B-LSTM | −0.5 | 0.61 | |
| F-LSTM | −78.23 | 0.0001 | |
| BVS-LSTM | −0.02 | 0.98 | |
| Italy Air Quality | LSTM-0 | −135.68 | 0.0002 |
| LSTM-mean | −24.17 | 0.0005 | |
| B-LSTM | −1.58 | 0.12 | |
| F-LSTM | −1.87 | 0.06 | |
| BVS-LSTM | −1.51 | 0.13 | |
| Beijing Multi-Site Air-Quality | LSTM-0 | −15.07 | 0.0001 |
| LSTM-mean | −868.89 | 0.0004 | |
| B-LSTM | −0.37 | 0.71 | |
| F-LSTM | −52.92 | 0.0008 | |
| BVS-LSTM | −6.00 | 0.0001 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fouladgar, N.; Främling, K. A Novel LSTM for Multivariate Time Series with Massive Missingness. Sensors 2020, 20, 2832. https://doi.org/10.3390/s20102832
Fouladgar N, Främling K. A Novel LSTM for Multivariate Time Series with Massive Missingness. Sensors. 2020; 20(10):2832. https://doi.org/10.3390/s20102832
Chicago/Turabian StyleFouladgar, Nazanin, and Kary Främling. 2020. "A Novel LSTM for Multivariate Time Series with Massive Missingness" Sensors 20, no. 10: 2832. https://doi.org/10.3390/s20102832
APA StyleFouladgar, N., & Främling, K. (2020). A Novel LSTM for Multivariate Time Series with Massive Missingness. Sensors, 20(10), 2832. https://doi.org/10.3390/s20102832






