1. Introduction
In the last few decades, applications of terahertz systems in sensing [
1,
2], imaging [
3,
4], and communications [
5,
6] have drawn great attention. The reasons are that terahertz waves can penetrate many dielectric materials that are opaque for optical waves, allow better spatial resolution, and promise an extremely high data rate compared to the microwaves due to their shorter wavelengths (higher carrier frequencies). The applications mentioned above often require beam control techniques to manipulate the shape of the terahertz beam (beamforming) and direction of the terahertz beam (beam steering). Furthermore, beamforming and beam steering based on phased arrays consisting of two or more sources increase the total radiation power by free-space power combining. It overcomes the low power issue caused by the limited radiation power of a single terahertz source and high atmospheric absorption of terahertz radiation. Terahertz beam steering based on various means, such as phased arrays and electromagnetic metasurfaces, has been comprehensively summarized in [
7,
8]. Generally, there are two kinds of terahertz phased arrays. The first kind is modulating the phase within the microwave or optical bands that are then up or down-converted to the terahertz range [
9,
10,
11,
12,
13]. In the second kind, the phase of the terahertz wave is directly shifted or modulated, for example, by using liquid crystals [
14,
15], or graphene-based terahertz phase shifters [
16], metasurfaces [
17], leaky wave antennas [
18], or micro-electro-mechanical system (MEMS)-based diffraction gratings [
19,
20]. MEMS-based diffraction gratings are more promising and feasible for terahertz beam steering compared to other means for realizing the terahertz phased arrays mentioned above. It is structurally uncomplicated because it does not require coherent feed networks and phase shifters together with their control units. In addition to that, MEMS allows terahertz beam steering with wide steering ranges at different frequencies by reconfiguring the grating structure. Monnai et al. [
20] have successfully demonstrated beam steering at frequencies from 0.15 THz to 0.9 THz using a MEMS-based diffraction grating. However, the diffraction grating efficiency is relatively low due to the limited vertical displacement of the cantilevers [
20].
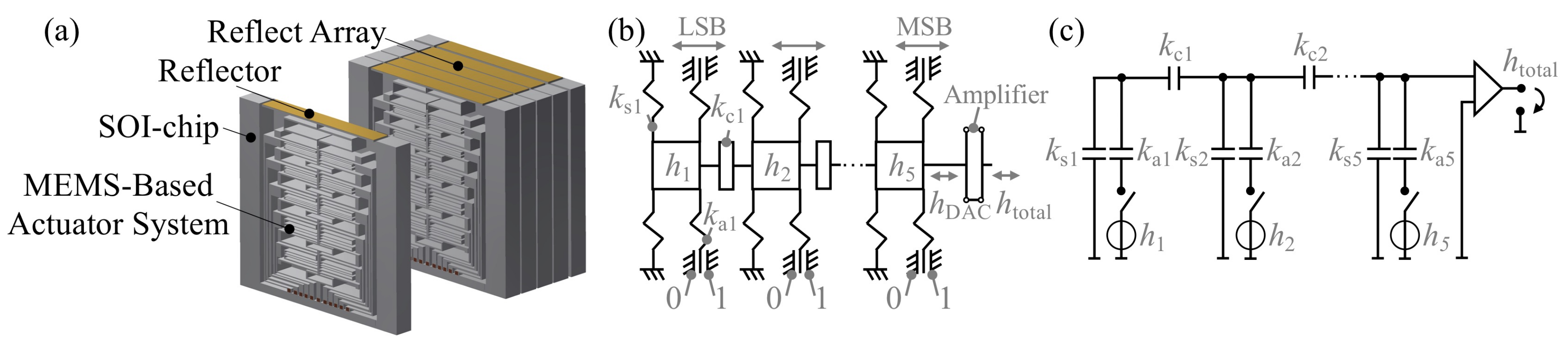
The diffraction grating efficiency can be improved and maximized in a desired diffraction order by a blazed grating. In this paper, we introduce a structure that approximates a reflective sawtooth-like blazed grating. The surface is realized with multiple translating subwavelength MEMS reflectors. Every single MEMS reflector has its own 5-bit actuation system with a total throw of 600 m, which allows them to move up and down stepwise and independently from each other. By changing the number of reflectors per grating period and the vertical displacement of each reflector, discrete steering angles with high directivity at different frequencies can be achieved. We propose a mathematical model to calculate the far-field radiation pattern of the terahertz wave reflected by the designed grating and compare the calculated radiation patterns with results from electromagnetic (EM) simulations.
The paper is structured as follows. In
Section 2, we present the device design of the MEMS reflector array. In
Section 3, we provide a mathematical model for a general reflection grating and show far-field radiation patterns of the terahertz wave interacting with various configurations of the MEMS reflection grating structure at different frequencies. At last, in
Section 4 we verify the proposed mathematical model by EM simulations of the same reflection grating and comparing the radiation patterns.
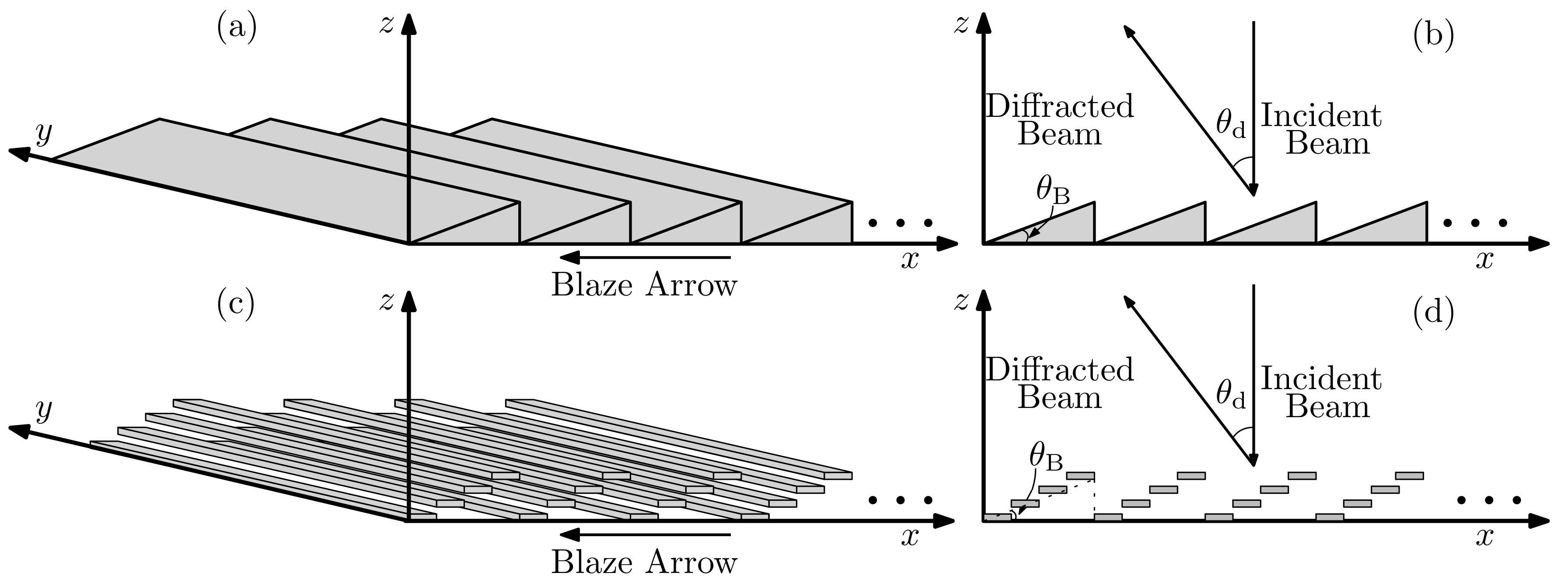
3. Mathematical Model
The simplified structure of a MEMS reflector array-based sawtooth-like reflection grating is shown in
Figure 5. The gray area represents the reflective surface of the reflectors. We assume a plane wave that is normally incident on the grating. The phase
of the wave reflected by the reflectors is spatially modulated. It is determined by the
x and
z-coordinates of the reflectors.
We place the reflection grating symmetrically to the
z-axis, so its reflective surface spans the range
along the
x-axis, where
w is the width of a single reflector and
is the total number of reflectors constructing the reflection grating. The
z-coordinate of the reflective surface of one grating element
is the summation of multiple rectangular functions with linearly increasing heights.
where
N is the number of reflectors per grating period
and
h is the displacement step between adjacent reflectors. The
z-coordinate of the reflective surface of the complete grating
repeats the values of
with the grating period
.
The phase shift of the plane wave along the
x-axis on the reflective surface of the reflectors can then be expressed as the multiplication of the
z-coordinate of the reflective surface with the wavenumber in free space
where
is the wavelength of the plane wave in free-space. Now, we assume that the electric field of the plane wave only has a component in
x direction and no amplitude variation in the
x and
z directions. The reflected component of the electric field
of the plane wave just above the reflective surface of the reflectors can be expressed as
where
is a constant amplitude of the electric field of the plane wave and
is the unit vector in
x direction. The plane wave on the reflective surface can be modeled as the combination of the electric field from many small isotropic radiators according to the Huygens–Fresnel principle, so that in the far-field region, the electric field
of the reflected plane wave at distance
r in a spherical coordinate system can be calculated from the superposition of the contributions from all isotropic radiators:
where
is the unit vector in
z direction. To maximize the grating efficiency in the first diffraction order, the height difference
h must be chosen so that the geometry of the designed grating is as close as possible to the geometry of a blazed grating. Therefore,
h is determined by
where
is the minimum bitwise displacement of the reflector. With Equations (
3), (11), and (
12), we can then calculate the radiation pattern with the following specifications according to
Section 2:
According to Equation (2), the maximum steering angle at one single frequency is limited by the smallest possible grating period
or in our case the smallest possible number of reflectors per grating period
N. To obtain the smallest possible value of
N, for which the beam is not only successfully steered in the desired angle but also its directivity is significantly higher compared to the undesired diffraction angles, we calculate the radiation patterns of the beam reflected from the grating with increasing
N starting with
. With
, the grating period
m is smaller than the wavelength at frequencies from 0.3 THz to 1 THz; therefore, no diffraction occurs. With
, the grating period
m is greater than the wavelength
m at 0.6 THz, so the grating equation (Equation (2)) has solutions. However, its radiation pattern shown in
Figure 6a shows a dominant specular reflection. Inserting
into Equation (
12), we get
Inserting Equation (
3) into Equation (
13), and using the theorems
and
for positive
x, we get
The displacement step
results in a phase shift
. The beam experiences twice the phase shift induced by the displacement step
h: once when the beam is incident on the two reflectors and again when the beam is reflected from the two reflectors. Therefore, the total phase shift induced by the displacement step
h is
. For single-frequency operation, the phase shift can be wrapped to 2
. Thus, the wrapped phase shift is a lot smaller than the desired phase shift for a blazed grating
. Consequently, the structure designed with two reflectors per grating period
has poor grating efficiency. With
, the first-order diffraction angles on both sides of the grating normal show strong radiation at 0.6 THz, as shown in
Figure 6b. The reason is that the ambiguity of 2
results in the ambiguity of the phase shift distribution induced by the displacement step
h among the three reflectors. The phase shift distribution
induced when the beam interacts with the three reflectors can also be interpreted as
. While the power is efficiently steered to the diffraction angle on the left side of the grating normal with the first phase distribution, the power is efficiently steered to the diffraction angle on the right side of the grating normal with the second phase distribution. With
N equal to or greater than four, we are able to steer the beam to the desired grating angle with its directivity at least 10 dB higher than the sidelobes, as shown in
Figure 6c,d. Hence in our design we choose the smallest number of mirrors per grating period
for frequencies from 0.3 THz to 1 THz so that the grating equation (Equation (2)) has solutions and the 2
ambiguity problem is avoided.
The minimum steering angle is limited by the minimum bitwise displacement . When the steering angle gets smaller, the required displacement step h decreases. The minimum steering angle occurs once the required displacement step h falls below the minimum bitwise displacement .
Figure 7 shows the radiation patterns that are calculated at the frequencies 0.3 THz, 0.6 THz, and 0.9 THz. The calculated steering angles match the ones determined from Equation (2), and the directivity of the steered beam is at least 10 dB higher than the specular reflection at
.
Figure 8 shows the calculated steering range of the reflection grating at frequencies from 0.3 THz to 1 THz. With increasing frequency, the steering range decreases. By changing the direction of the blaze arrow, the same steering range for the other side of the grating normal can be achieved as well. Besides the main lobe in the desired direction and the specular reflection at 0
, the radiation patterns of the reflection gratings show distinct grating lobes. For each achievable steering angle, we determine the corresponding directivity of the main lobe at frequencies different from those of the calculated radiation pattern. The results are depicted in
Figure 9. The directivity of the MEMS-based reflection grating increases with increasing frequency as the structure becomes electrically larger. It is nearly constant across the steering range and can be perfectly predicted by the theoretical directivity of an equivalent uniform antenna array. The distinct dips in the directivity occur wherever the level of the grating lobes is particularly high. This effect is quantified by the diffraction grating efficiency shown in
Figure 10. Low diffraction grating efficiencies are caused by deviations between the geometry of the designed MEMS-based gratings and the geometry of an ideal blazed grating due to the limited vertical displacement resolution of the MEMS actuators.
4. Simulation Results
To verify the mathematical model proposed in
Section 3, we conducted EM simulations for different configurations of the MEMS reflection grating structure using the finite-difference time-domain (FDTD) solver Empire XPU.
Figure 11 shows the simulation setup. The reflectors (in blue color) with the width
m, length
m, and thickness
m were modeled as perfect electric conductors. The reflection grating consisting of 80 MEMS reflectors lay in an excitation box (in red color) where a plane wave whose polarization was parallel to
x-axis was normally incident on the grating. Inside of the excitation box, both the incident field and the field reflected by the grating existed, whereas outside the box only the field reflected from the grating was present. Therefore, we specified a region (in yellow color) right above the excitation box to record the near-field of the reflected wave. The far-field radiation pattern was then calculated using the near-to-far-field transformation. The far-field radiation pattern we observed and obtained was the radiation pattern in the upper part of the
-plane. In the simulation the perfectly matched layer (PML) absorbing boundary condition was used. We left a space of two wavelengths between the PML boundary and the edges of the excitation box as well as the recording region. We created a mesh for the structure based on the following rules: at least 15 cells per wavelength and at least four cells per object and gap. There are 100 temporal sampling points per period at the highest simulation frequency.
In
Section 3, we calculated the radiation patterns of nine different configurations of the MEMS reflection grating structure for the maximum steering angle, the center of the steering range, and the minimum steering angle at the frequencies of 0.3 THz, 0.6 THz, and 0.9 THz, respectively. For an intuitive comparison, we simulated the same nine configurations of the MEMS reflection grating structure and obtained the far-field radiation patterns shown in
Figure 12. The calculated and simulated radiation patterns show an agreement not only in the main lobe at the desired steering angle, but also in the side lobes. Furthermore, the simulated side lobe levels for all nine different configurations of the MEMS reflection grating structure are almost identical to the calculated ones.
The recorded near-field during the simulation and the calculated electric field of the plane wave on the reflective surfaces of the reflectors are inherently multiplied by a rectangular function due to the finite size of the reflection grating structure. This corresponds to a far-field pattern that has the shape of a sinc-function. Therefore, there are excessive side lobes around the main lobe which can be seen both in the calculated and simulated radiation patterns. This effect is known from the theory of antenna arrays and aperture antennas [
23]. The first side lobes of the sinc-function are approximately 13.46 dB lower than the main lobe. The calculated radiation patterns are in excellent agreement with this number. The side lobe level could be improved at the cost of a reduction in directivity by choosing a suitable non-uniform amplitude distribution for the incident electric field. The grating lobes and side lobes can have different undesired effects. In any application, the grating lobes steal power from the main lobe, thereby reducing the radiated power in the desired direction. This is expressed by the grating efficiency discussed above. In certain sensing applications, such as radar, grating lobes and side lobes are particularly deleterious, as they may reduce the angular selectivity of the sensor system.
The calculated and simulated radiation patterns show an agreement in main lobe and side lobes levels. This verifies our mathematical model as an effective tool for estimation of the far-field radiation pattern of the beam reflected from the MEMS grating.