Efficient Resource Allocation for Backhaul-Aware Unmanned Air Vehicles-to-Everything (U2X)
Abstract
:1. Introduction
Our Contributions
- A backhaul-aware U2X scenario with the support of multi-layer UAVs is presented along with a resource allocation problem with the constraints on the number of transfers.
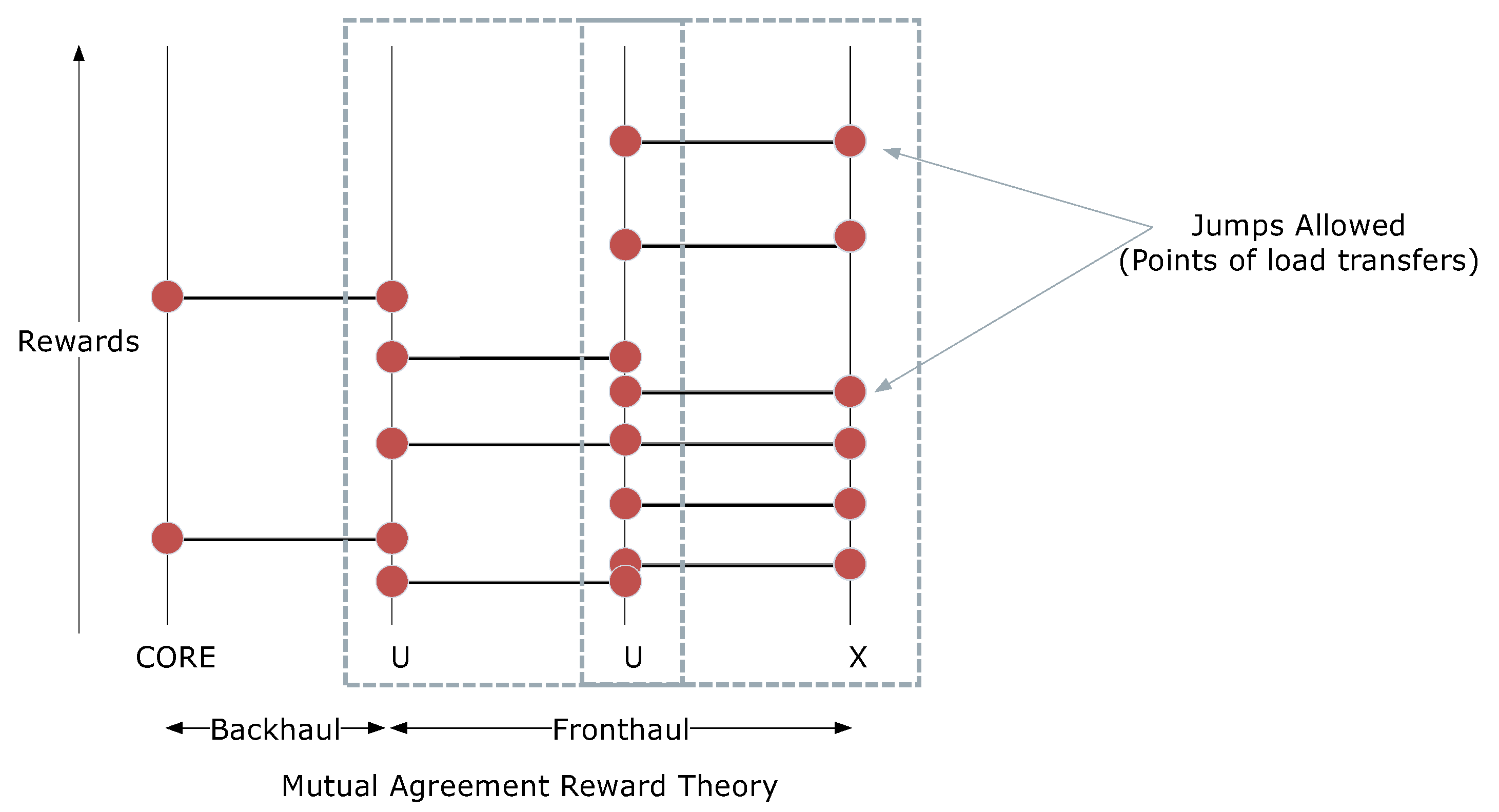
- Mutual agreement reward theory is applied to understand the problem of resource allocation in U2X.
- The entire problem is resolved using coordinated resource allocation, which is accounted for using a reward-jump mechanism.
- Hazard tracking and ownership procedures are used to decide the control over the network and reshuffling amongst layers.
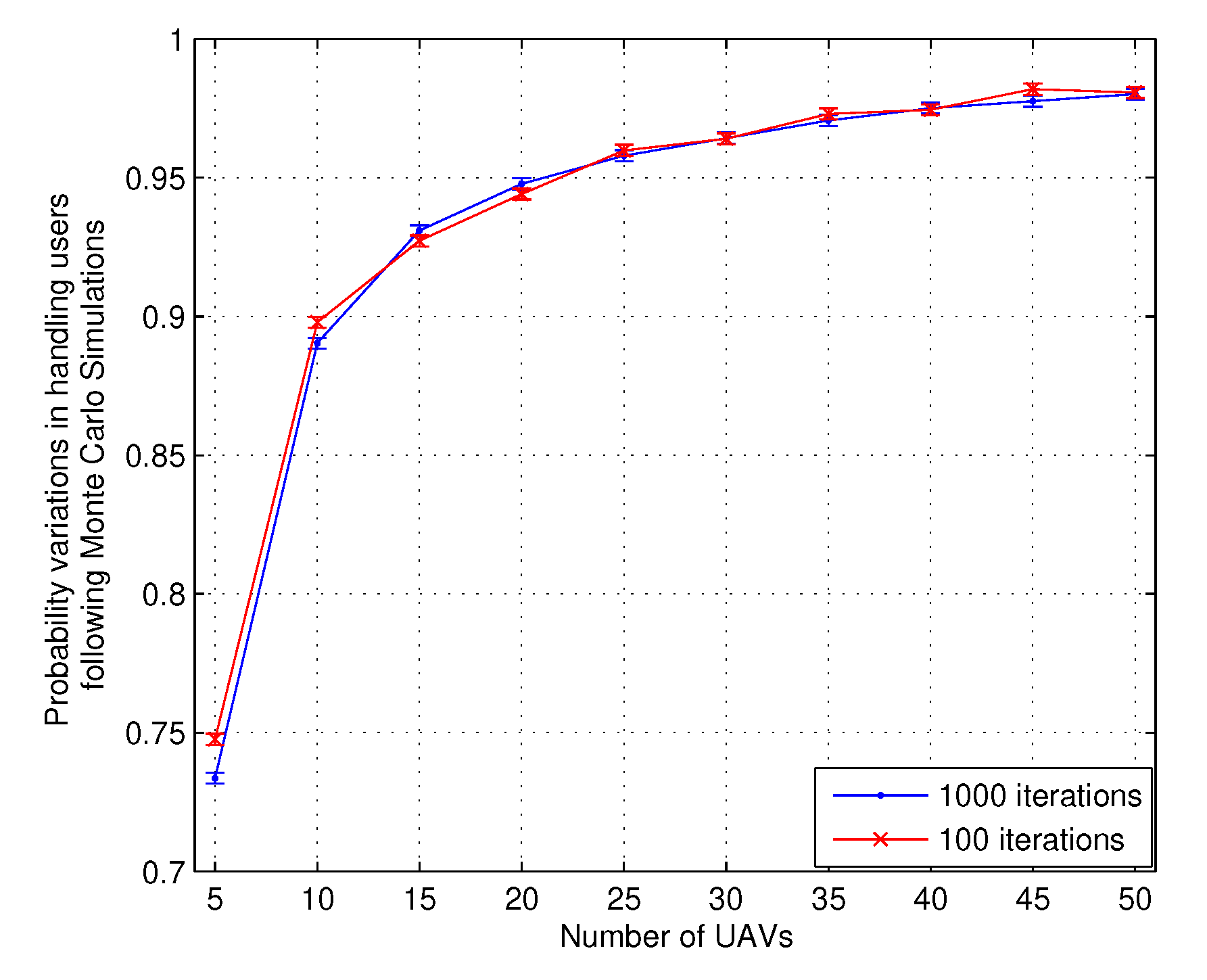
- Monte-Carlo simulations are used to evaluate the proposed approach by generating scenarios with various numbers of failures for different numbers of UAVs.
2. Related Works
3. Proposed Approach
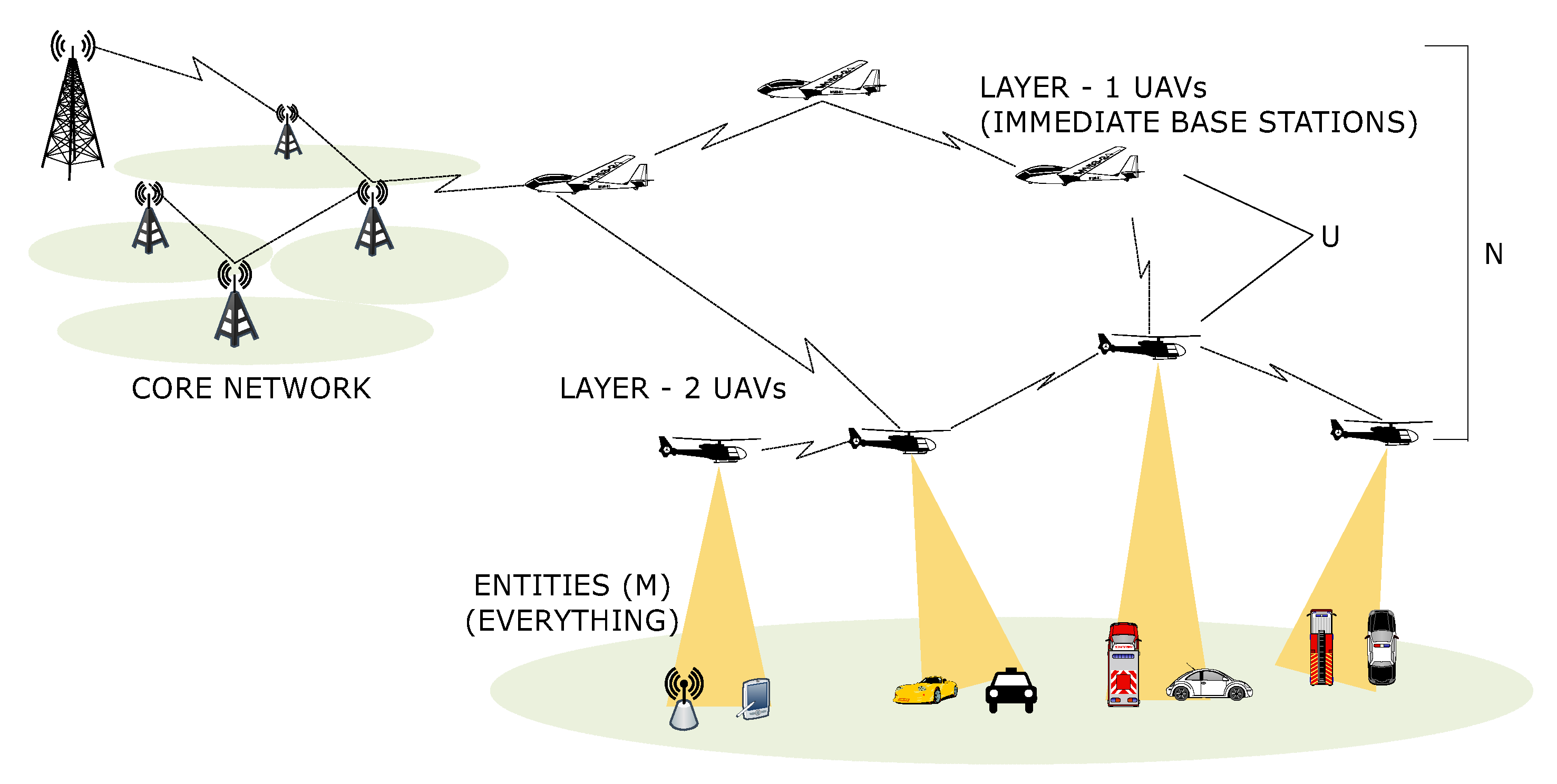
3.1. System Model and Problem Formulation
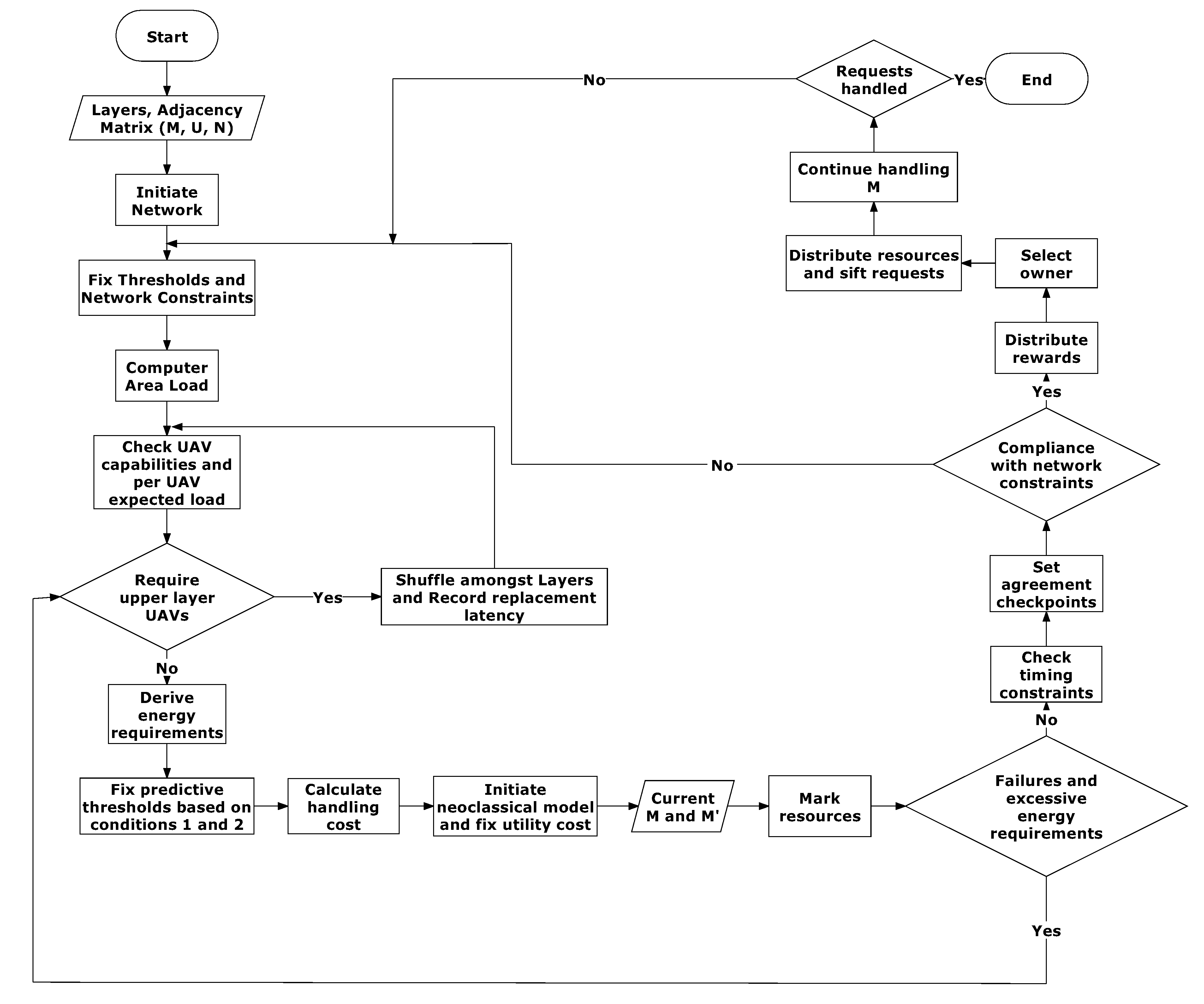
3.2. Coordinated Resource Allocation
- The proposed approach aims at maximizing the resources handled by UAVs while decreasing the exchange or limiting the shifting users across the UAVs, except for the scenarios wherein UAVs fail in batches. Irrespective of such failures, the proposed approach controls the network and offloads the traffic with limiting iterations.
- For multiple tiers scenarios, the UAVs which support the backhaul links are the ones which make a decision on the load sharing capabilities of fronthaul UAVs by considering , , and , whereas for scenarios with single tier UAVs, the decision on load sharing is only taken based on the mutual agreement reward theory only between and . It is to be considered that the former offers better evaluation in case of failures, while the latter is effective in low-overheads with less resistance to failures.
- Let be an incremental reward function with an initial value at 0, which increases as the number of times the network obeys the set constraints. This increment is the actual value assigned to , and it may vary for different scenarios. In certain cases, it may follow an increment or decrement value depending on the failure rate of the network. Additionally, the reward function may vary for the types of entities and their connectivity as shown in Figure 2.
- Once is defined, a threshold is set for each of the categories and the network is evaluated against it to allow a decision on load balancing/resource allocation/offloading.
- The value of is also used to take a critical decision of the entity, which will be dominating the decision on resource allocation.
3.3. Backhaul Coordination
3.4. U2X Coordination
3.5. Hazard Tracking and Ownership
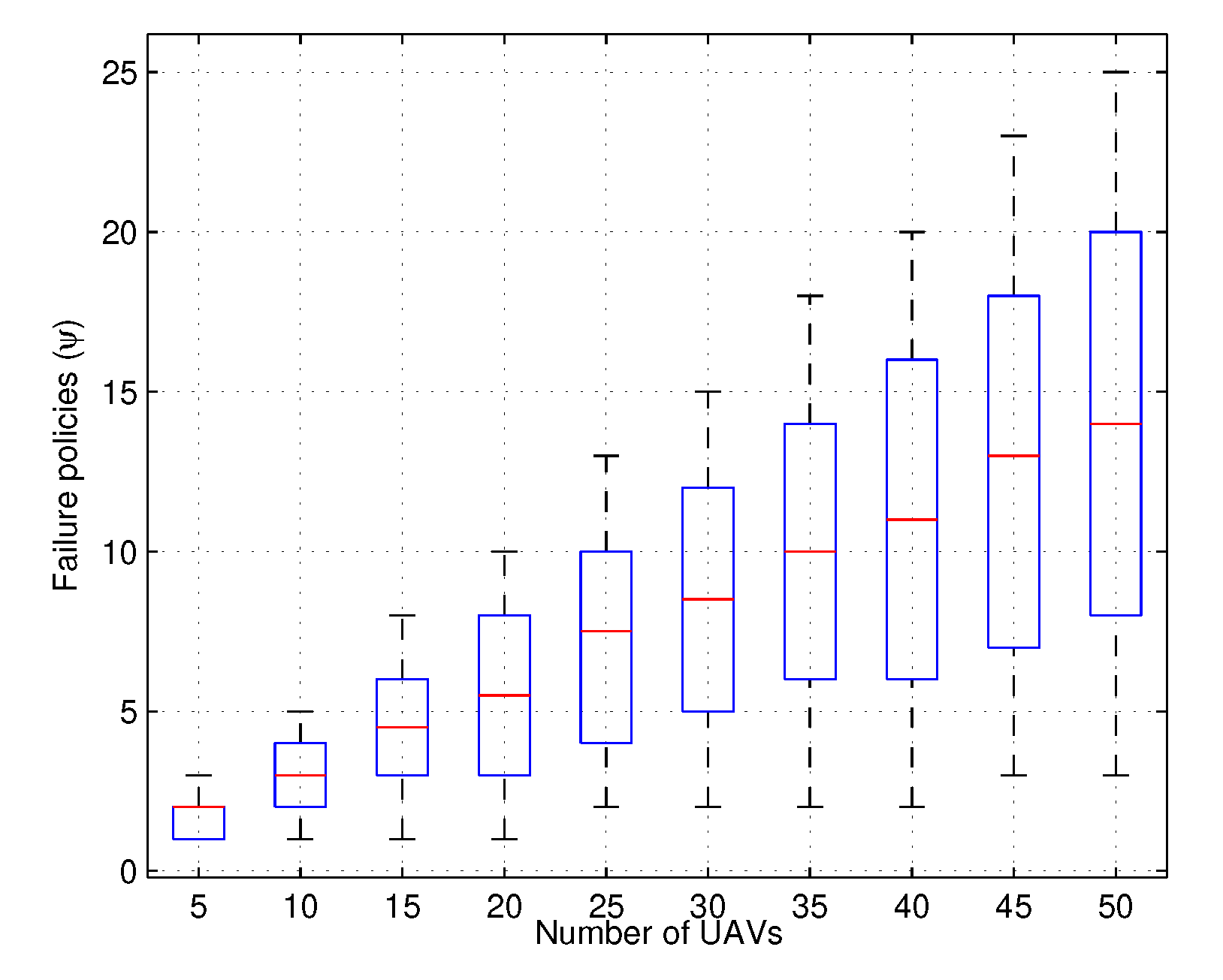
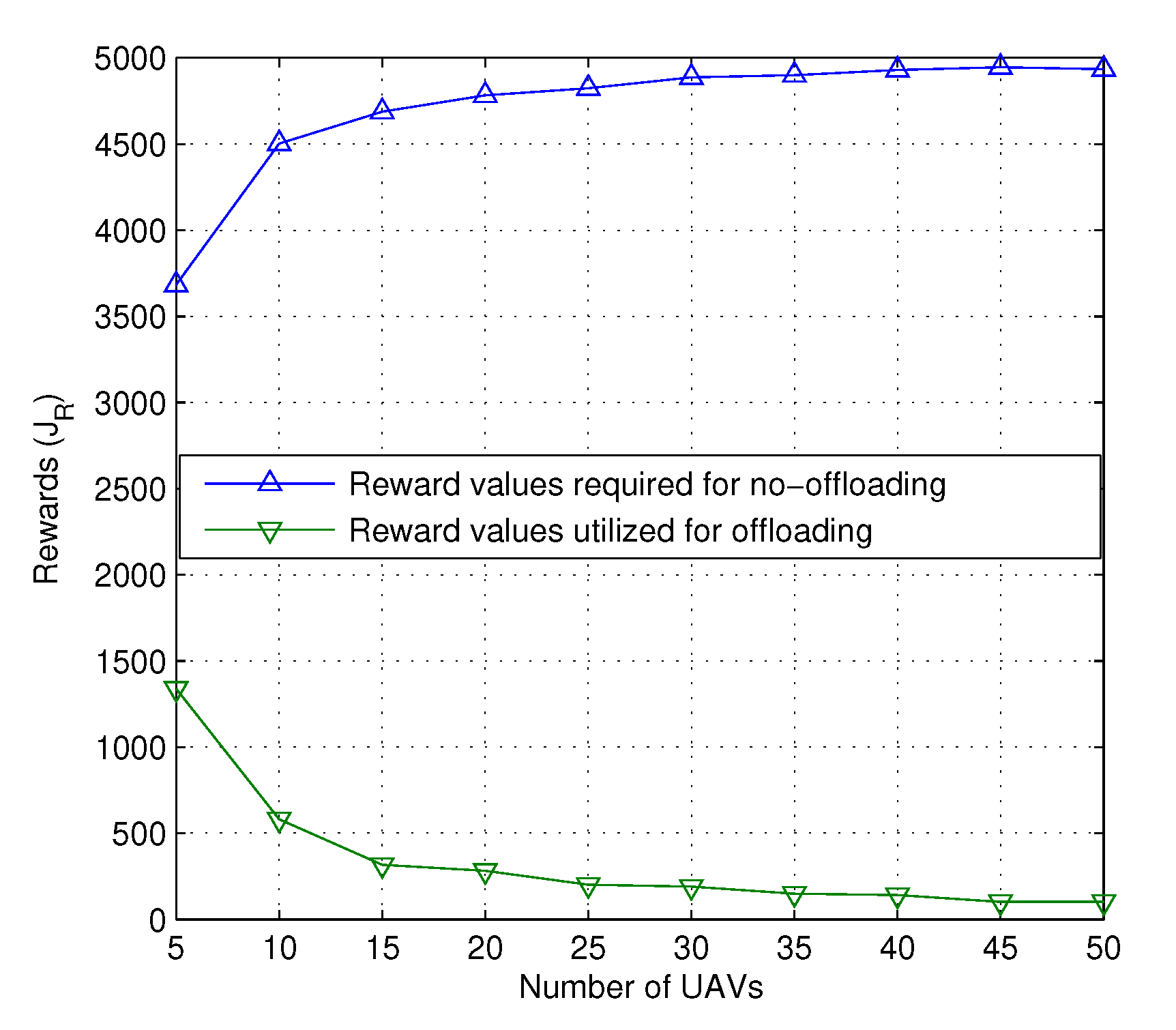
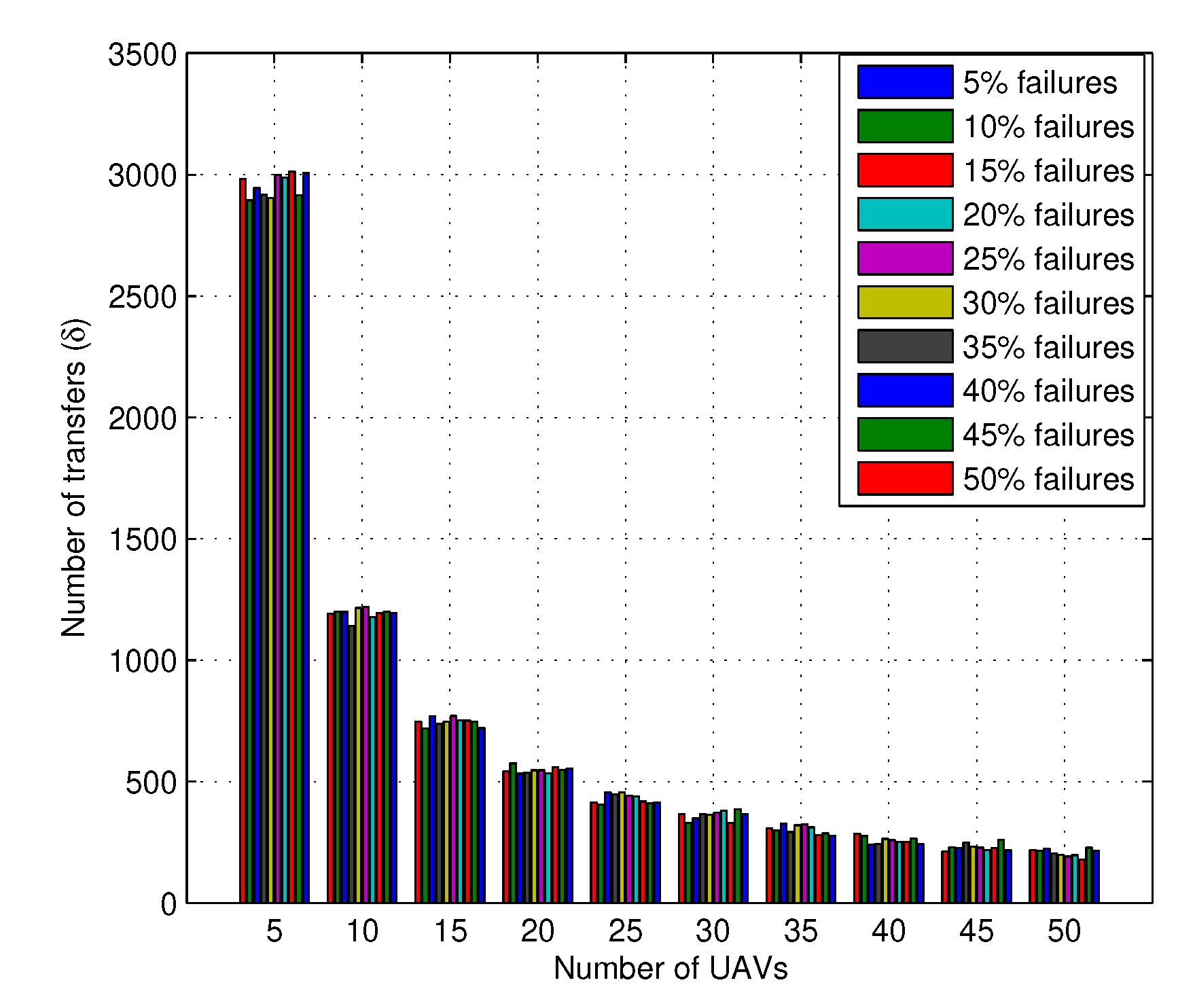
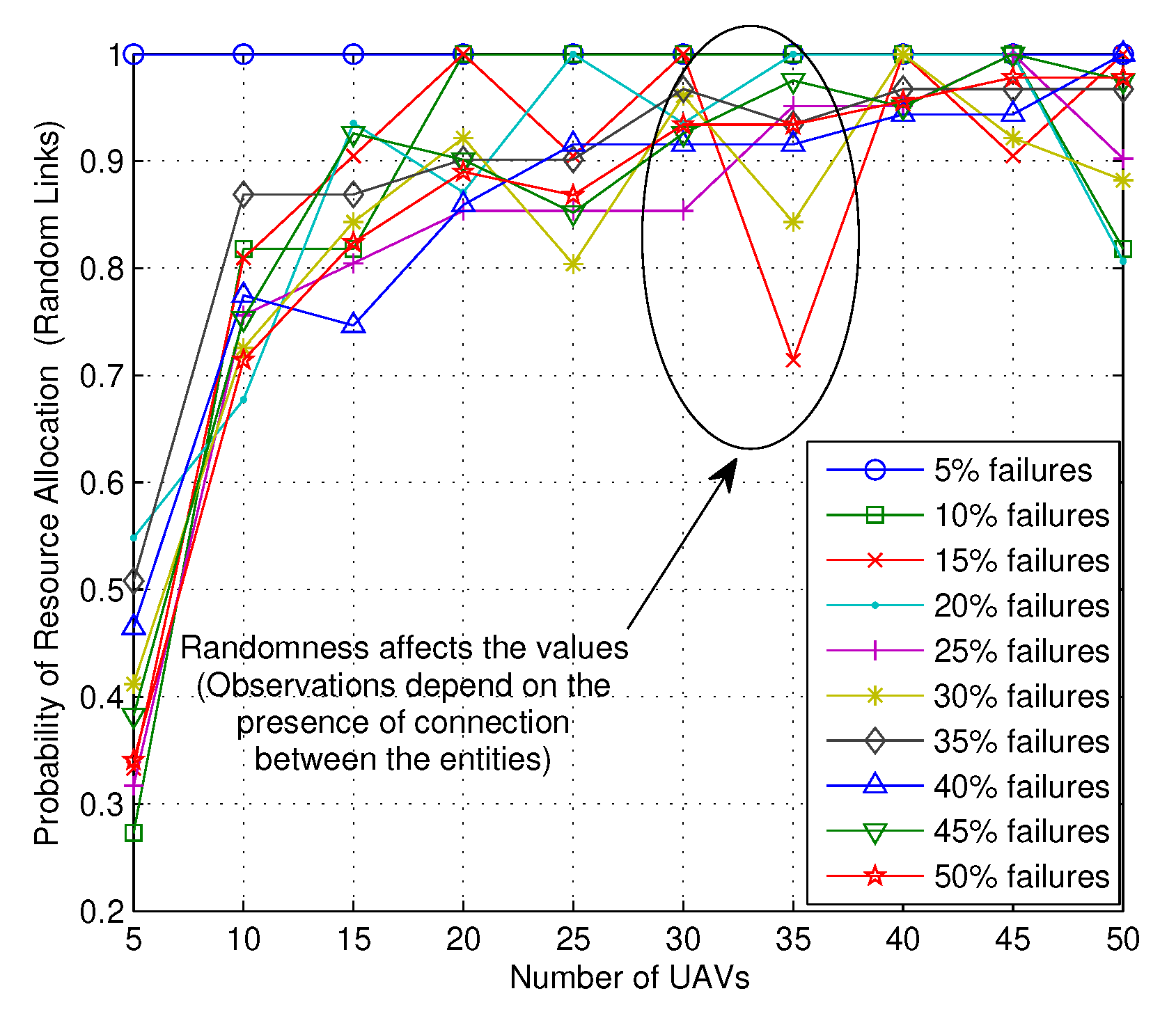
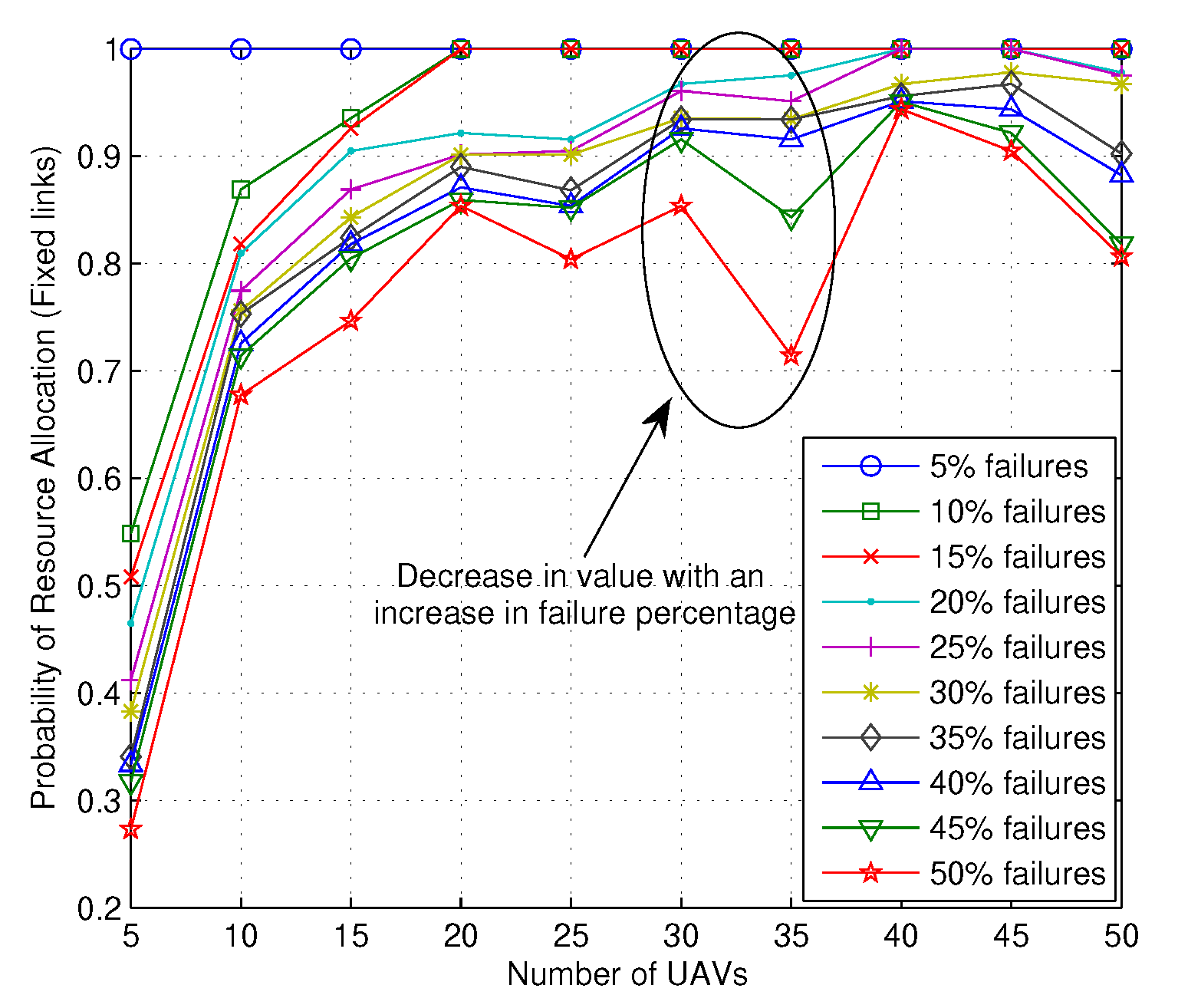
4. Performance Evaluation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xue, Z.; Wang, J.; Ding, G.; Wu, Q.; Lin, Y.; Tsiftsis, T.A. Device-to-Device Communications Underlying UAV-Supported Social Networking. IEEE Access 2018, 6, 34488–34502. [Google Scholar] [CrossRef]
- Sharma, N.; Magarini, M.; Jayakody, D.N.K.; Sharma, V.; Li, J. On-demand ultra-dense cloud drone networks: Opportunities, challenges and benefits. IEEE Commun. Mag. 2018, 56, 85–91. [Google Scholar] [CrossRef]
- Yuan, Z.; Jin, J.; Sun, L.; Chin, K.W.; Muntean, G.M. Ultra-Reliable IoT Communications with UAVs: A Swarm Use Case. IEEE Commun. Mag. 2018, 56, 90–96. [Google Scholar] [CrossRef]
- Zhao, N.; Lu, W.; Sheng, M.; Chen, Y.; Tang, J.; Yu, F.R.; Wong, K.K. UAV-Assisted Emergency Networks in Disasters. IEEE Wirel. Commun. 2019, 26, 45–51. [Google Scholar] [CrossRef] [Green Version]
- Sharma, V.; Song, F.; You, I.; Chao, H. Efficient management and fast handovers in software defined wireless networks using UAVs. IEEE Network 2017, 31, 78–85. [Google Scholar] [CrossRef]
- Sharma, V.; You, I.; Kumar, R. Energy efficient data dissemination in multi-UAV coordinated wireless sensor networks. Mob. Inf. Syst. 2016, 2016, 8475820:1–8475820:13. [Google Scholar] [CrossRef] [Green Version]
- Sharma, V.; Chen, H.C.; Kumar, R. Driver behaviour detection and vehicle rating using multi-UAV coordinated vehicular networks. J. Comput. Syst. Sci. 2017, 86, 3–32. [Google Scholar] [CrossRef]
- Al-Turjman, F.; Alturjman, S. 5G/IoT-enabled UAVs for multimedia delivery in industry-oriented applications. Multimed. Tools Appl. 2020, 79, 8627–8648. [Google Scholar] [CrossRef]
- Wang, L.; Yang, H.; Long, J.; Wu, K.; Chen, J. Enabling ultra-dense uav-aided network with overlapped spectrum sharing: Potential and approaches. IEEE Netw. 2018, 32, 85–91. [Google Scholar] [CrossRef]
- Sharma, V.; Choudhary, G.; Ko, Y.; You, I. Behavior and Vulnerability Assessment of Drones-Enabled Industrial Internet of Things (IIoT). IEEE Access 2018, 6, 43368–43383. [Google Scholar] [CrossRef]
- Sharma, V.; You, I.; Seo, J.T.; Guizani, M. Secure and Reliable Resource Allocation and Caching in Aerial-Terrestrial Cloud Networks (ATCNs). IEEE Access 2019, 7, 13867–13881. [Google Scholar] [CrossRef]
- Choudhary, G.; Sharma, V.; You, I. Sustainable and secure trajectories for the military Internet of Drones (IoD) through an efficient Medium Access Control (MAC) protocol. Comput. Electr. Eng. 2019, 74, 59–73. [Google Scholar] [CrossRef]
- Guvenc, I. Interference and mObility Management in UAV-Assisted Wireless Networks. U.S. Patent 9,986,440, 29 May 2018. [Google Scholar]
- Khosravi, Z.; Gerasimenko, M.; Andreev, S.; Koucheryavy, Y. Performance Evaluation of UAV-Assisted mmWave Operation in Mobility-Enabled Urban Deployments. In Proceedings of the 2018 IEEE 41st International Conference on Telecommunications and Signal Processing (TSP), Athens, Greece, 4–6 July 2018; pp. 1–5. [Google Scholar]
- Taqieddin, E.; Awad, F.; Ahmad, H. Location-Aware and Mobility-Based Performance Optimization for Wireless Sensor Networks. J. Wirel. Mob. Netw. Ubiquitous Comput. Dependable Appl. 2017, 8(4), 37–59. [Google Scholar]
- Yang, Z.; Pan, C.; Shikh-Bahaei, M.; Xu, W.; Chen, M.; Elkashlan, M.; Nallanathan, A. Joint altitude, beamwidth, location, and bandwidth optimization for UAV-enabled communications. IEEE Commun. Lett. 2018, 22, 1716–1719. [Google Scholar] [CrossRef] [Green Version]
- You, I.; Sharma, V.; Atiquzzaman, M.; Choo, K.-K.R. GDTN: Genome-based delay tolerant network formation in heterogeneous 5G using inter-UA collaboration. PLoS ONE 2016, 11, e0167913. [Google Scholar] [CrossRef]
- Chen, M.; Yang, Z.; Saad, W.; Yin, C.; Poor, H.V.; Cui, S. A joint learning and communications framework for federated learning over wireless networks. arXiv 2019, arXiv:1909.07972. [Google Scholar]
- Li, L.; Wen, X.; Lu, Z.; Pan, Q.; Jing, W.; Hu, Z. Energy-Efficient UAV-Enabled MEC System: Bits Allocation Optimization and Trajectory Design. Sensors 2019, 19, 4521. [Google Scholar] [CrossRef] [Green Version]
- Mitsis, G.; Tsiropoulou, E.E.; Papavassiliou, S. Data Offloading in UAV-Assisted Multi-Access Edge Computing Systems: A Resource-Based Pricing and User Risk-Awareness Approach. Sensors 2020, 20, 2434. [Google Scholar] [CrossRef]
- Sekander, S.; Tabassum, H.; Hossain, E. Multi-tier drone architecture for 5G/B5G cellular networks: Challenges, trends, and prospects. IEEE Commun. Mag. 2018, 56, 96–103. [Google Scholar] [CrossRef] [Green Version]
- Sharma, V.; Sharma, N.; Rehmani, M.H.; Pervaiz, H. Control over Skies: Survivability, Coverage and Mobility Laws for Hierarchical Aerial Base Stations. arXiv 2019, arXiv:1903.03725. [Google Scholar]
- Almeida, E.N.; Campos, R.; Ricardo, M. Traffic-aware multi-tier flying network: Network planning for throughput improvement. In Proceedings of the 2018 IEEE Wireless Communications and Networking Conference (WCNC), Barcelona, Spain, 15–18 April 2018; pp. 1–6. [Google Scholar]
- Li, J.; Han, Y. Optimal resource allocation for packet delay minimization in multi-layer UAV networks. IEEE Commun. Lett. 2017, 21, 580–583. [Google Scholar] [CrossRef]
- Sharma, V.; Sabatini, R.; Ramasamy, S. UAVs assisted delay optimization in heterogeneous wireless networks. IEEE Commun. Lett. 2016, 20, 2526–2529. [Google Scholar] [CrossRef]
- Yang, Z.; Pan, C.; Wang, K.; Shikh-Bahaei, M. Energy Efficient Resource Allocation in UAV-Enabled Mobile Edge Computing Networks. arXiv 2019, arXiv:1902.03158. [Google Scholar] [CrossRef]
- Lemaire, T.; Alami, R.; Lacroix, S. A distributed tasks allocation scheme in multi-UAV context. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA’04), New Orleans, LA, USA, 26 April–1 May 2004; Volume 4, pp. 3622–3627. [Google Scholar]
- Fan, R.; Cui, J.; Jin, S.; Yang, K.; An, J. Optimal node placement and resource allocation for UAV relaying network. IEEE Commun. Lett. 2018, 22, 808–811. [Google Scholar] [CrossRef]
- Nguyen, M.N.; Nguyen, L.D.; Duong, T.Q.; Tuan, H.D. Real-time optimal resource allocation for embedded UAV communication systems. IEEE Wirel. Commun. Lett. 2019, 8, 225–228. [Google Scholar] [CrossRef] [Green Version]
- Kawamoto, Y.; Nishiyama, H.; Kato, N.; Ono, F.; Miura, R. Toward Future Unmanned Aerial Vehicle Networks: Architecture, Resource Allocation and Field Experiments. IEEE Wirel. Commun. 2018, 26, 94–99. [Google Scholar] [CrossRef]
- Hua, M.; Wang, Y.; Li, C.; Huang, Y.; Yang, L. Energy-Efficient Optimization for UAV-aided Cellular Offloading. IEEE Wirel. Commun. Lett. 2019, 8, 769–772. [Google Scholar] [CrossRef]
- Du, Y.; Wang, K.; Yang, K.; Zhang, G. Energy-Efficient Resource Allocation in UAV Based MEC System for IoT Devices. In Proceedings of the 2018 IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, UAE, 9–13 December 2018; pp. 1–6. [Google Scholar]
- Galkin, B.; Kibiłda, J.; DaSilva, L.A. A stochastic geometry model of backhaul and user coverage in urban UAV networks. arXiv 2017, arXiv:1710.03701. [Google Scholar]
- Fouda, A.; Ibrahim, A.S.; Guvenc, I.; Ghosh, M. UAV-Based in-band Integrated Access and Backhaul for 5G Communications. arXiv 2018, arXiv:1807.07230. [Google Scholar]
- Sharma, V.; Ko, Y.; Kim, J.; You, I. Security management for backhaul-aware 5G-V2X. arXiv 2018, arXiv:1811.08273. [Google Scholar]
- Galkin, B.; Kibilda, J.; DaSilva, L.A. Backhaul for low-altitude UAVs in urban environments. In Proceedings of the 2018 IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar]
- Gapeyenko, M.; Petrov, V.; Moltchanov, D.; Andreev, S.; Himayat, N.; Koucheryavy, Y. Flexible and Reliable UAV-Assisted Backhaul Operation in 5G mmWave Cellular Networks. IEEE J. Sel. Areas Commun. 2018, 36, 2486–2496. [Google Scholar] [CrossRef]
- Choudhary, G.; Kim, J.; Sharma, V. Security of 5G-Mobile Backhaul Networks: A Survey. J. Wirel. Mob. Netw. Ubiquitous Comput. Dependable Appl. 2018, 9, 41–70. [Google Scholar]
- Zhang, S.; Zhang, H.; Di, B.; Song, L. Cellular UAV-to-X communications: Design and optimization for multi-UAV networks. IEEE Trans. Wirel. Commun. 2019, 18, 1346–1359. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Zhang, H.; Di, B.; Song, L. Resource allocation and trajectory design for cellular UAV-to-X communication networks in 5G. In Proceedings of the 2018 IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, UAE, 9–13 December 2018; pp. 1–6. [Google Scholar]
- Lee, K.; Kim, J.; Park, Y.; Wang, H.; Hong, D. Latency of cellular-based V2X: Perspectives on TTI-proportional latency and TTI-independent latency. IEEE Access 2017, 5, 15800–15809. [Google Scholar] [CrossRef]
- Hart, O.; Demsetz, H. Firms, Contracts, and Financial Structure: Clarendon Lectures in Economics. J. Polit. Econ. 1998, 106, 446–451. [Google Scholar]
- Balakrishnan, N. Handbook of the Logistic Distribution; CRC Press: Oxon, UK, 1991. [Google Scholar]
- Meeker, W.Q.; Escobar, L.A. Statistical Methods for Reliability Data; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Cantrell, C.D. Modern Mathematical Methods for Physicists and Engineers; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Merigó, J.M.; Gil-Lafuente, A.M. Using the OWA operator in the Minkowski distance. Int. J. Comput. Sci. 2008, 3, 149–157. [Google Scholar]
- Tseng, C.M.; Chau, C.K.; Elbassioni, K.; Khonji, M. Flight tour planning with recharging optimization for battery-operated autonomous drones. arXiv 2017, arXiv:1703.10049. [Google Scholar]
- Yang, G.; Lin, X.; Li, Y.; Cui, H.; Xu, M.; Wu, D.; Rydén, H.; Redhwan, S.B. A Telecom Perspective on the Internet of Drones: From LTE-Advanced to 5G. arXiv 2018, arXiv:1803.11048. [Google Scholar]



| Articles | Key Contribution | R1 | R2 | U2X |
|---|---|---|---|---|
| [26] | Energy-efficient resource allocation scheme | Yes | No | No |
| [27] | Distributed tasks allocation scheme | Yes | No | No |
| [24] | Resources allocation mechanism for minimize packet transmission delay | Yes | No | No |
| [28] | Node placement and communication resource allocation scheme | Yes | No | No |
| [29] | Real-time optimal resource allocation | Yes | No | No |
| [30] | Resource allocation for a three-UAV network | Yes | No | No |
| [31] | Energy-efficient optimization scheme | Yes | No | No |
| [11] | Secure resource allocation scheme in ATCNs | Yes | No | No |
| [32] | Energy efficient resource allocation | Yes | No | No |
| [33] | Stochastic geometry model of backhaul | No | Yes | No |
| [34] | In-band integrated access and backhaul management | Yes | Yes | No |
| [35] | Security management scheme for backhaul-aware C-V2X | No | Yes | No |
| [36] | Model for wireless backhaul to UAVs | No | Yes | No |
| [37] | UAV-assisted backhaul scheme for 5G mmWave Cellular Networks | No | Yes | No |
| [39] | Optimized cellular UAV-to-X communications | Yes | No | Yes |
| [40] | Resource allocation and trajectory design | Yes | No | Yes |
| Parameter | Values | Description |
|---|---|---|
| N | 2 | Number of tiers |
| M | 100–1000 | Number of devices/entities |
| U | 10–50 | Number of UAVs |
| 1.08× J | Maneuvering energy of UAVs [47] | |
| 0.32 J + 0.25 J | Link establishment | |
| 0.32 J | Transmission energy | |
| 1 J | Scheduling energy | |
| 1000 s | Total operational time | |
| 20–40 ms | Transmission latency [48] | |
| 0.5 s | Decision latency | |
| 0.5 s | Replacement latency | |
| 5–50% of U | Hazardous constant | |
| A | 2500 sq.m | Area under evaluation |
| W | 100 MHz | Bandwidth |
| 200 Mbps | Offered rate | |
| 100 | SINR | |
| 200 kbps–200 Mbps | per UAV handling capacity | |
| 10 | Step interval |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gupta, T.; Arena, F.; You, I. Efficient Resource Allocation for Backhaul-Aware Unmanned Air Vehicles-to-Everything (U2X). Sensors 2020, 20, 2994. https://doi.org/10.3390/s20102994
Gupta T, Arena F, You I. Efficient Resource Allocation for Backhaul-Aware Unmanned Air Vehicles-to-Everything (U2X). Sensors. 2020; 20(10):2994. https://doi.org/10.3390/s20102994
Chicago/Turabian StyleGupta, Takshi, Fabio Arena, and Ilsun You. 2020. "Efficient Resource Allocation for Backhaul-Aware Unmanned Air Vehicles-to-Everything (U2X)" Sensors 20, no. 10: 2994. https://doi.org/10.3390/s20102994
APA StyleGupta, T., Arena, F., & You, I. (2020). Efficient Resource Allocation for Backhaul-Aware Unmanned Air Vehicles-to-Everything (U2X). Sensors, 20(10), 2994. https://doi.org/10.3390/s20102994







