Flight and Interaction Control of an Innovative Ducted Fan Aerial Manipulator
Abstract
1. Introduction
2. Modeling of the Aerial Manipulator
2.1. System Introduction
2.2. Aerial Vehicle
2.2.1. Kinematic Model
2.2.2. Dynamic Model
2.3. Manipulator
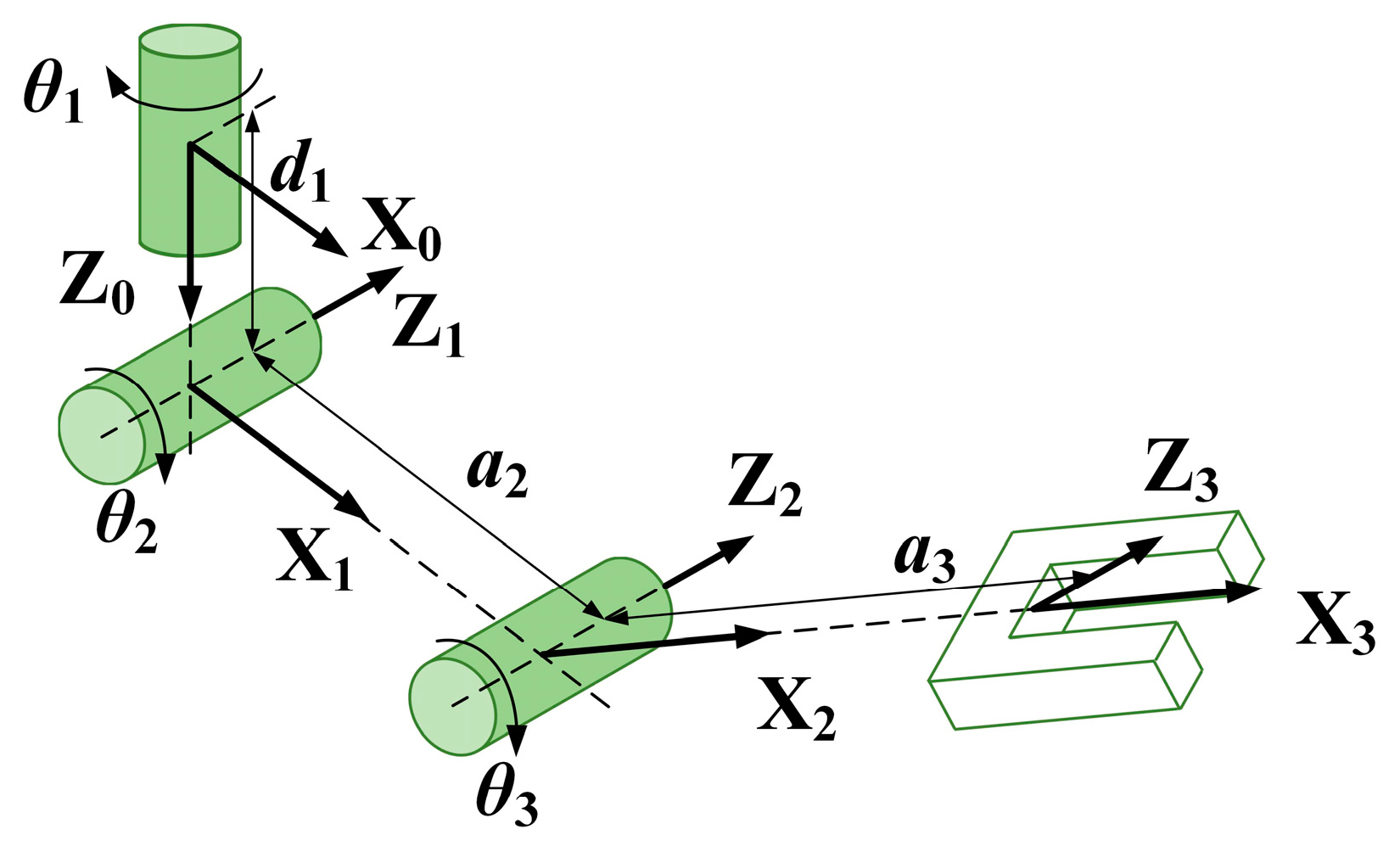
2.3.1. Kinematic Model
2.3.2. Dynamic Model
2.4. Environment
3. Composite Controller Design of the Aerial Manipulator
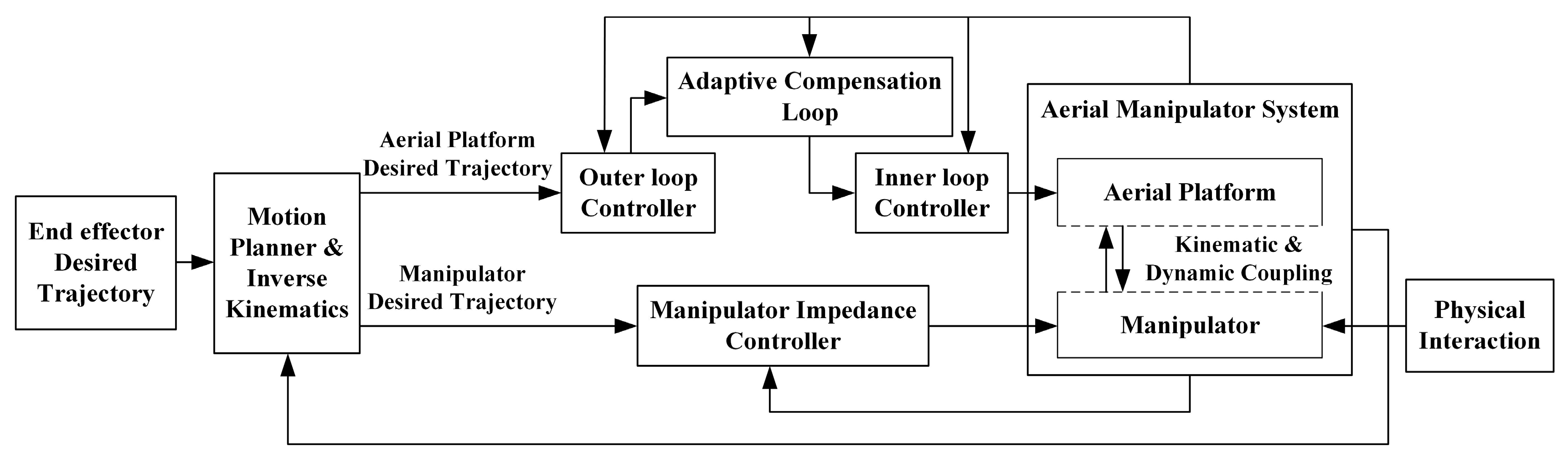
3.1. Control System Overview
3.2. Aerial Vehicle Controller Design
3.3. Manipulator Controller Design
3.4. Simulation Analyses
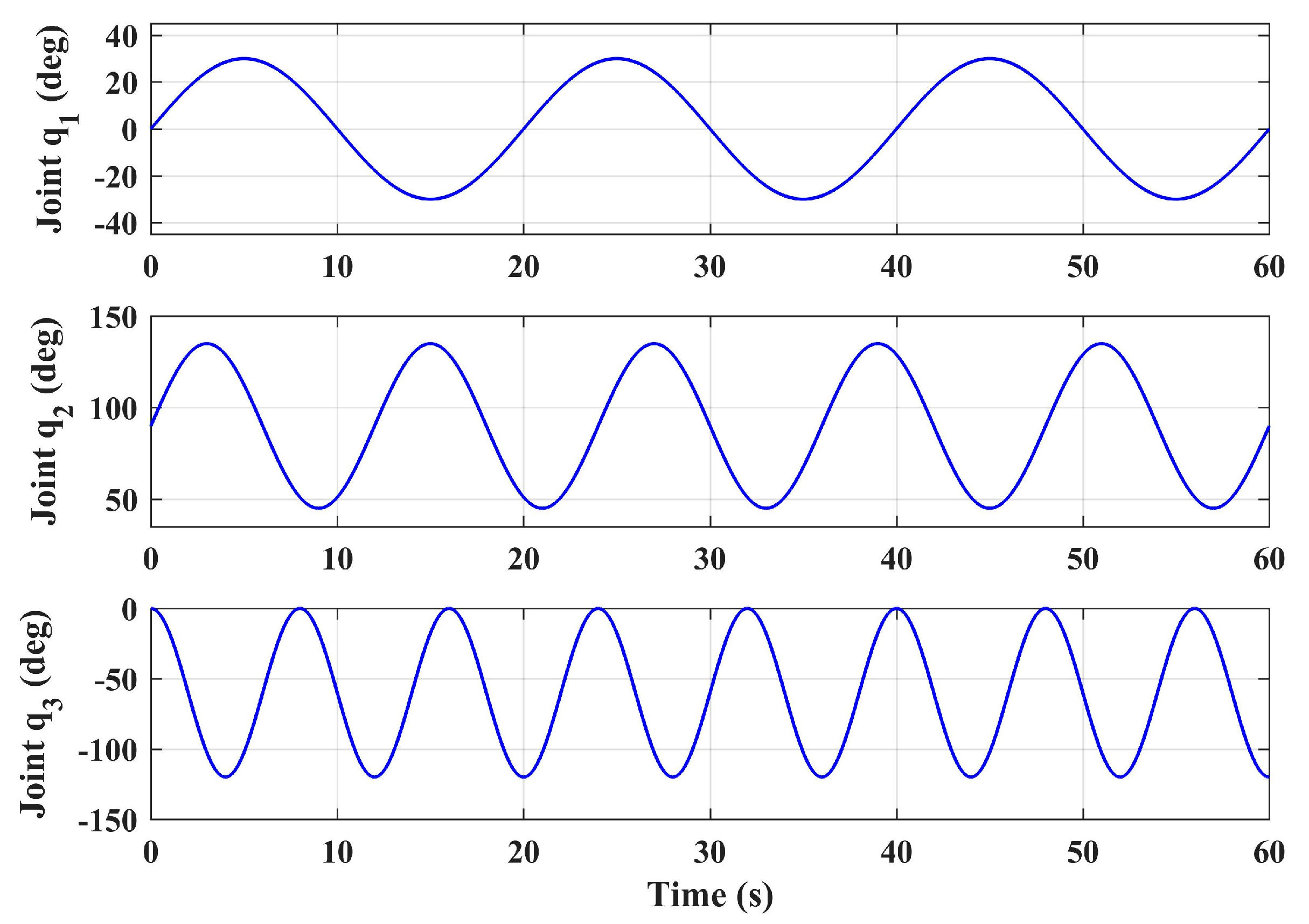
3.4.1. Flight Test Simulation
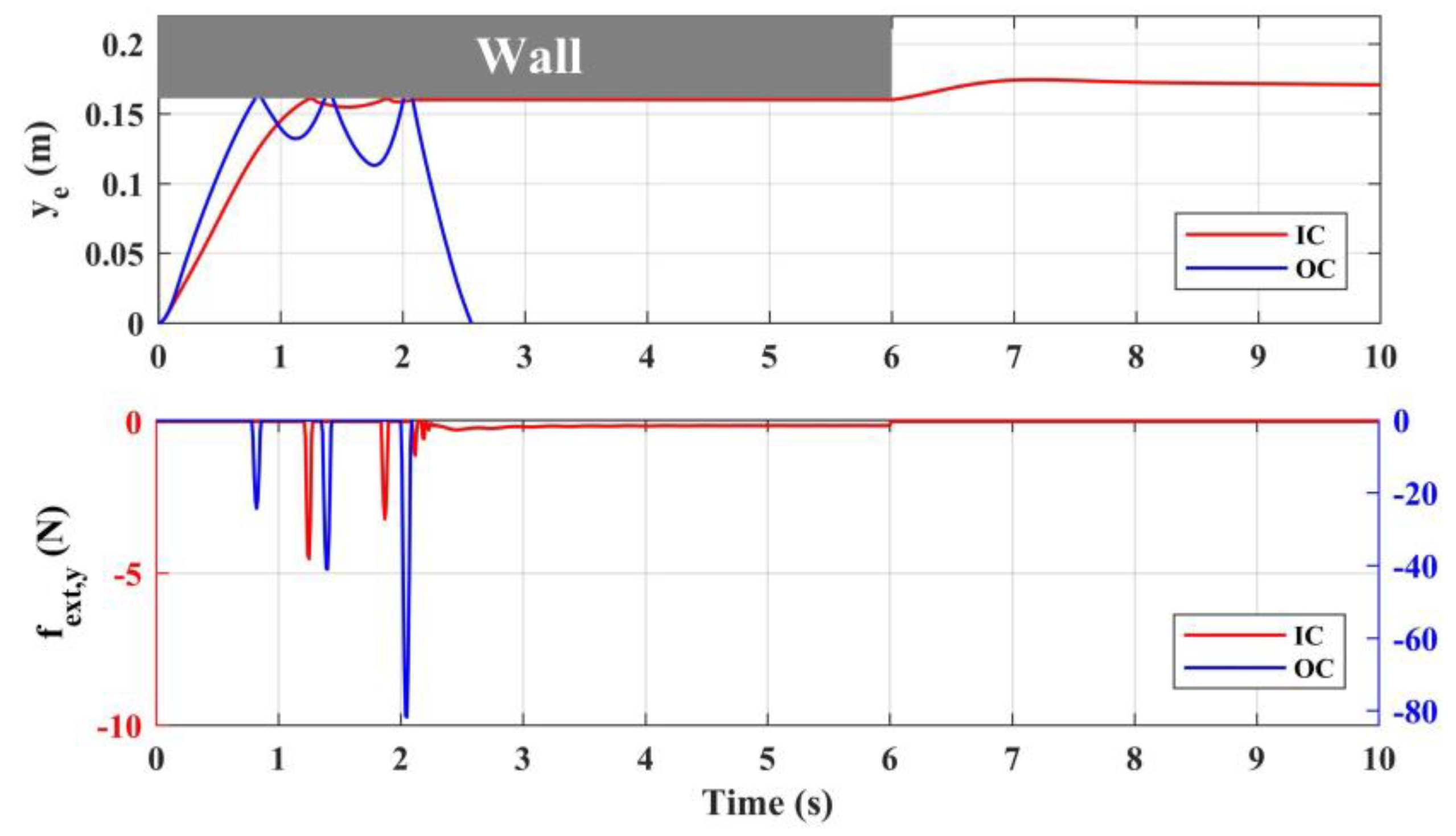
3.4.2. Contact Test Simulation
4. Experimental Tests and Verification
4.1. Experiment Description
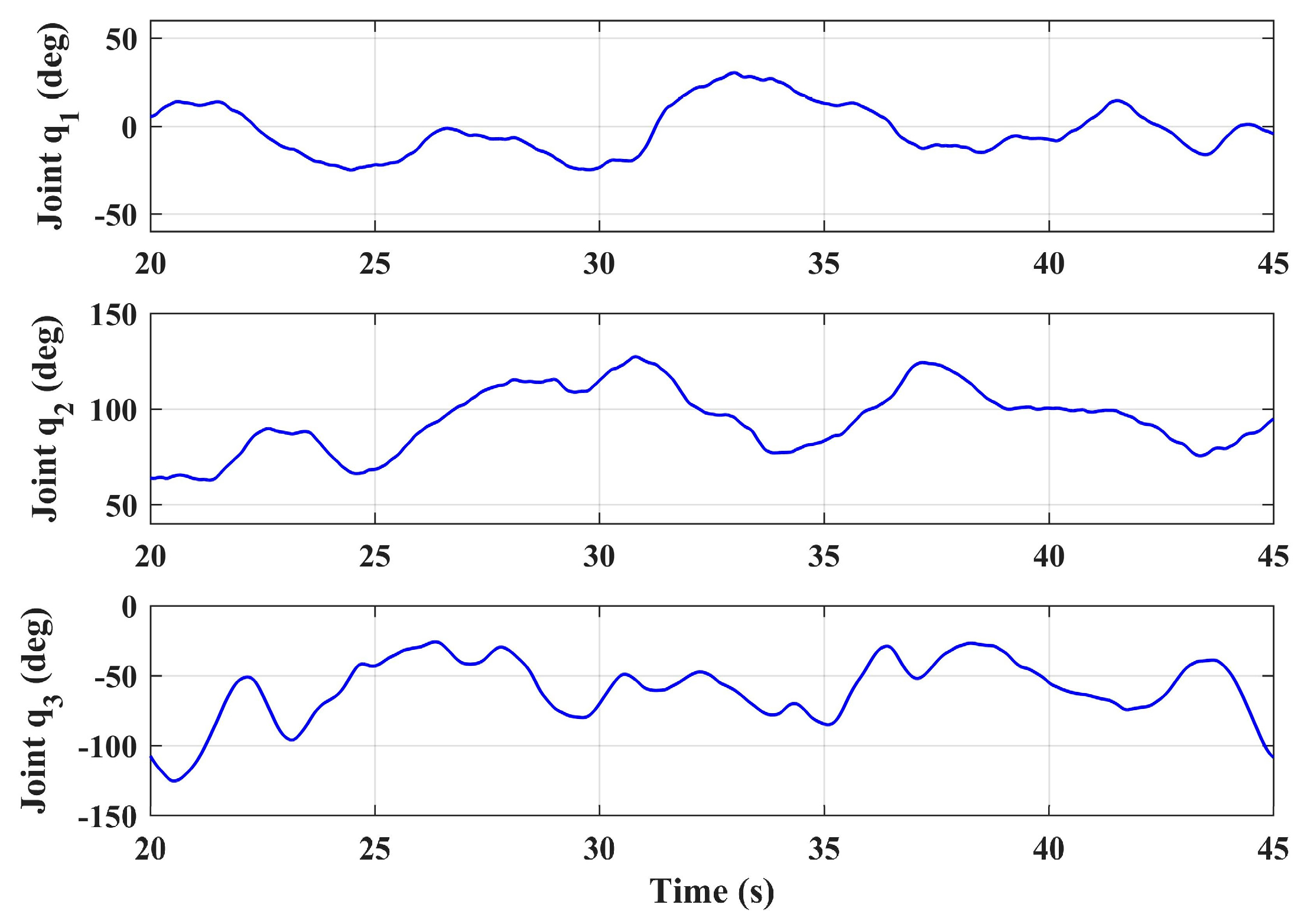
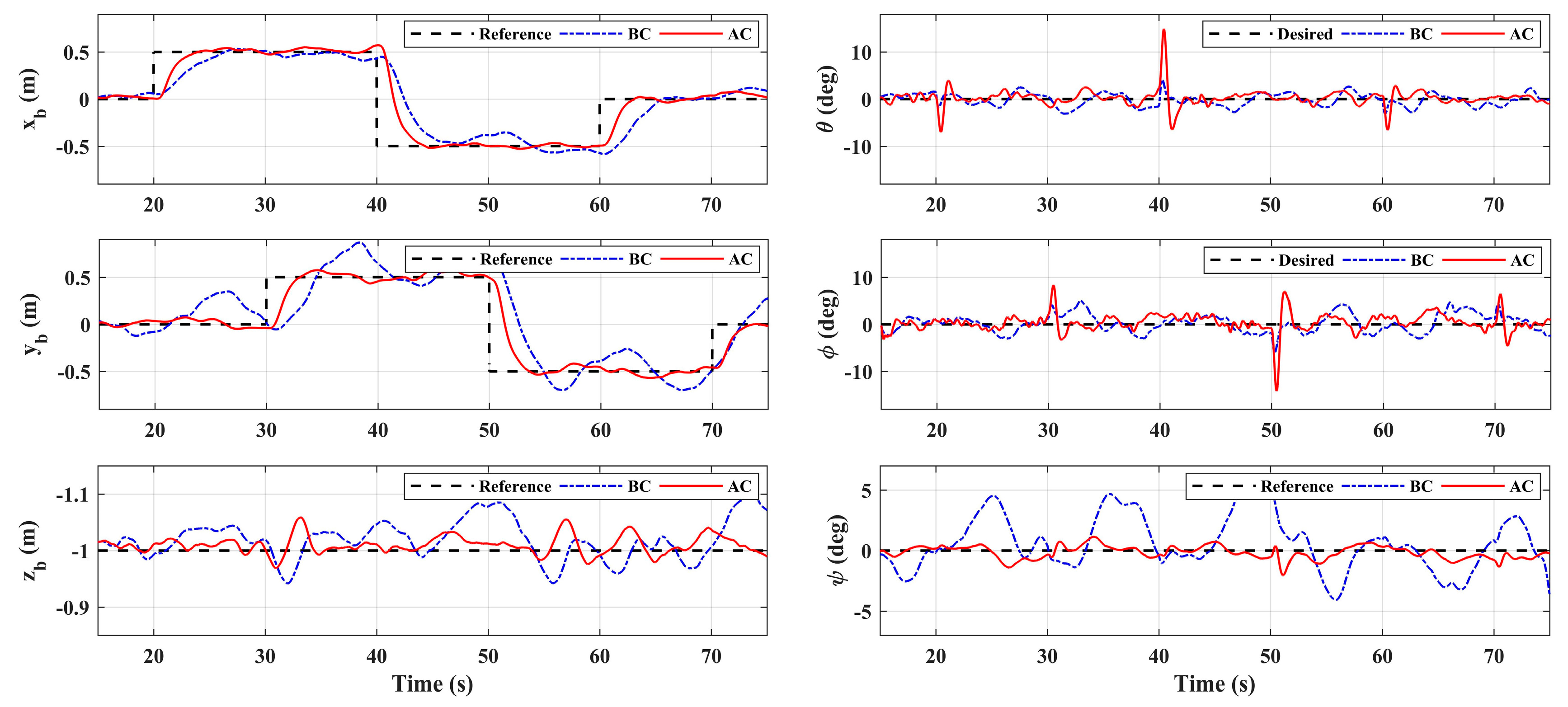
4.2. Flight Test Results and Analyses
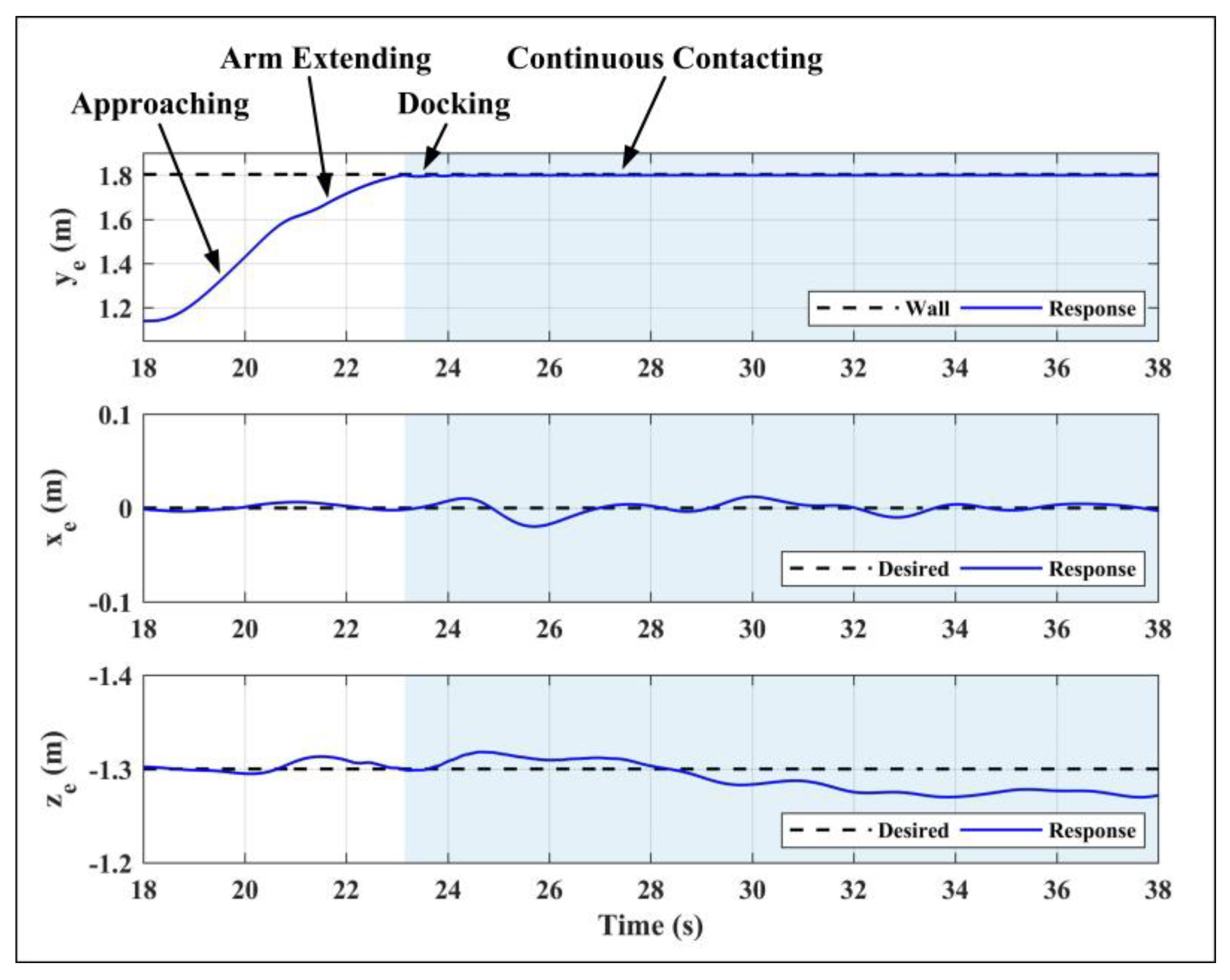
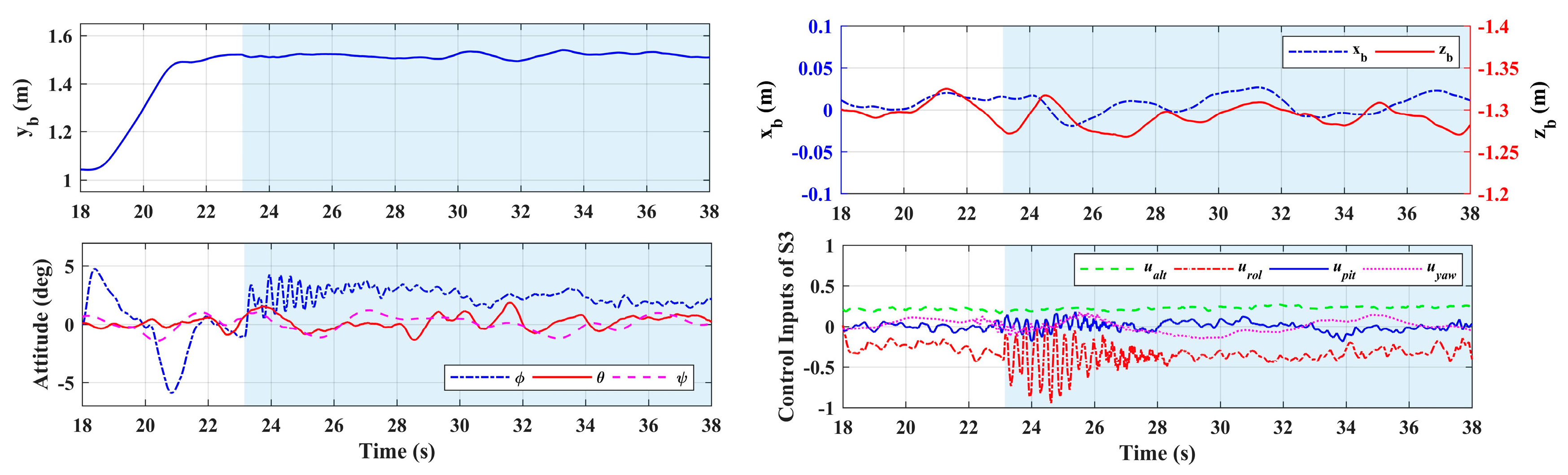
4.3. Contact Test Results and Analyses
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mastelic, T.; Lorincz, J.; Ivandic, I.; Boban, M. Aerial Imagery Based on Commercial Flights as Remote Sensing Platform. Sensors 2020, 20, 1658. [Google Scholar] [CrossRef]
- Yungaicela-Naula, N.; Garza-Castañon, L.E.; Zhang, Y.; Minchala-Avila, L.I. UAV-Based Air Pollutant Source Localization Using Combined Metaheuristic and Probabilistic Methods. Appl. Sci. 2019, 9, 3712. [Google Scholar] [CrossRef]
- Rubio, J.D.J. Robust feedback linearization for nonlinear processes control. Isa Trans. 2018, 74, 155–164. [Google Scholar] [CrossRef]
- Naldi, R.; Gentili, L.; Marconi, L. Modeling and control of the interaction between flying robots and the environment. IFAC Proc. Vol. 2010, 43, 975–980. [Google Scholar] [CrossRef]
- Alexis, K.; Darivianakis, G.; Burri, M.; Siegwart, R. Aerial robotic contact-based inspection: Planning and control. Auton. Robot. 2016, 40, 631–655. [Google Scholar] [CrossRef]
- Heredia, G.; Jimenez-Cano, A.E.; Sanchez, I.; Llorente, D.; Vega, V.; Braga, J.; Acosta, J.A.; Ollero, A. Control of a multirotor outdoor aerial manipulator. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 3417–3422. [Google Scholar]
- Lin, S.; Wang, J.; Peng, R.; Yang, W. Development of an Autonomous Unmanned Aerial Manipulator Based on a Real-Time Oriented-Object Detection Method. Sensors 2019, 19, 2396. [Google Scholar] [CrossRef] [PubMed]
- Trujillo, M.; Martínez-de Dios, J.; Martín, C.; Viguria, A.; Ollero, A. Novel Aerial Manipulator for Accurate and Robust Industrial NDT Contact Inspection: A New Tool for the Oil and Gas Inspection Industry. Sensors 2019, 19, 1305. [Google Scholar] [CrossRef] [PubMed]
- Qin, H.; Cui, J.Q.; Li, J.; Bi, Y.; Lan, M.; Shan, M.; Liu, W.; Wang, K.; Lin, F.; Zhang, Y.F.; et al. Design and implementation of an unmanned aerial vehicle for autonomous firefighting missions. In Proceedings of the 2016 12th IEEE International Conference on Control and Automation (ICCA), Kathmandu, Nepal, 1–3 June 2016; pp. 62–67. [Google Scholar]
- Yi, K.; Liang, X.; He, Y.; Yang, L.; Han, J. Active-Model-Based Control for the Quadrotor Carrying a Changed Slung Load. Electronics 2019, 8, 461. [Google Scholar] [CrossRef]
- Pounds, P.E.I.; Dollar, A.M. Stability of Helicopters in Compliant Contact under PD-PID Control. IEEE Trans. Robot. 2014, 30, 1472–1486. [Google Scholar] [CrossRef]
- Korpela, C.; Brahmbhatt, P.; Orsag, M.; Oh, P. Towards the realization of mobile manipulating unmanned aerial vehicles (MM-UAV): Peg-in-hole insertion tasks. In Proceedings of the 2013 IEEE Conference on Technologies for Practical Robot Applications (TePRA), Woburn, MA, USA, 22–23 April 2013; pp. 1–6. [Google Scholar]
- Jimenez-Cano, A.E.; Braga, J.; Heredia, G.; Ollero, A. Aerial manipulator for structure inspection by contact from the underside. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 1879–1884. [Google Scholar]
- Suarez, A.; Jimenez-Cano, A.E.; Vega, V.M.; Heredia, G.; Rodriguez-Casta, A.; Ollero, A. Lightweight and human-size dual arm aerial manipulator. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; pp. 1778–1784. [Google Scholar]
- Garimella, G.; Kobilarov, M. Towards model-predictive control for aerial pick-and-place. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 4692–4697. [Google Scholar]
- Kutia, J.R.; Stol, K.A.; Xu, W. Aerial Manipulator Interactions With Trees for Canopy Sampling. IEEE/ASME Trans. Mechatron. 2018, 23, 1740–1749. [Google Scholar] [CrossRef]
- Pflimlin, J.M.; Soueres, P.; Hamel, T. Position control of a ducted fan VTOL UAV in crosswind. Int. J. Control 2007, 80, 666–683. [Google Scholar] [CrossRef]
- Naldi, R.; Marconi, L. A Prototype of Ducted-Fan Aerial Robot with Redundant Control Surfaces. J. Intell. Robot. Syst. 2014, 76, 137–150. [Google Scholar] [CrossRef]
- Meng, X.; He, Y.; Han, J. Survey on Aerial Manipulator: System, Modeling, and Control. Robotica 2019, 1–30. [Google Scholar] [CrossRef]
- Zhang, G.; He, Y.; Dai, B.; Gu, F.; Yang, L.; Han, J.; Liu, G. Aerial Grasping of an Object in the Strong Wind: Robust Control of an Aerial Manipulator. Appl. Sci. 2019, 9, 2230. [Google Scholar] [CrossRef]
- Ghadiok, V.; Goldin, J.; Wei, R. Autonomous indoor aerial gripping using a quadrotor. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 4645–4651. [Google Scholar]
- Chen, H.; Quan, F.; Fang, L.; Zhang, S. Aerial Grasping with a Lightweight Manipulator Based on Multi-Objective Optimization and Visual Compensation. Sensors 2019, 19, 4253. [Google Scholar] [CrossRef] [PubMed]
- Quan, F.; Chen, H.; Li, Y.; Lou, Y.; Chen, J.; Liu, Y. Singularity-Robust Hybrid Visual Servoing Control for Aerial Manipulator. In Proceedings of the 2018 IEEE International Conference on Robotics and Biomimetics (ROBIO), Kuala Lumpur, Malaysia, 12–15 December 2018; pp. 562–568. [Google Scholar]
- Augugliaro, F.; D’Andrea, R. Admittance control for physical human-quadrocopter interaction. In Proceedings of the 2013 European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 1805–1810. [Google Scholar]
- Alexis, K.; Huerzeler, C.; Siegwart, R. Hybrid predictive control of a coaxial aerial robot for physical interaction through contact. Control Eng. Pract. 2014, 32, 96–112. [Google Scholar] [CrossRef]
- Nguyen, H.; Lee, D. Hybrid force/motion control and internal dynamics of quadrotors for tool operation. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 3458–3464. [Google Scholar]
- Craig, J.J. Introduction to Robotics: Mechanics and Control; Pearson Prentice Hall: London, UK, 2005. [Google Scholar]
- Pflimlin, J.M.; Binetti, P.; Souères, P.; Hamel, T.; Trouchet, D. Modeling and attitude control analysis of a ducted-fan micro aerial vehicle. Control Eng. Pract. 2010, 18, 209–218. [Google Scholar] [CrossRef]
- Han, H.; Xiang, C.; Xu, B.; Yu, Y. Experimental and computational analysis of microscale shrouded coaxial rotor in hover. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; pp. 1092–1100. [Google Scholar]
- Zhang, Y.; Xiang, C.; Xu, B. Modeling and Comprehensive Analysis of an Innovative Coaxial Ducted Fan Aircraft. In Proceedings of the 2018 International Conference on Advanced Mechatronic Systems (ICAMechS), Zhengzhou, China, 30 August–2 September 2018; pp. 78–85. [Google Scholar]
- Wang, X.; Xiang, C.; Xu, B.; Fan, W. System identification and robust stabilization using structured controller for a novel ducted fan flying robot. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2017, 233, 197–214. [Google Scholar] [CrossRef]
- Forte, F.; Naldi, R.; Macchelli, A.; Marconi, L. Impedance control of an aerial manipulator. In Proceedings of the 2012 American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 3839–3844. [Google Scholar]
- Gahinet, P.; Apkarian, P. Frequency-domain tuning of fixed-structure control systems. In Proceedings of the 2012 UKACC International Conference on Control, Cardiff, UK, 3–5 September 2012; pp. 178–183. [Google Scholar]
- Pomet, J.B.; Praly, L. Adaptive nonlinear regulation: Estimation from the Lyapunov equation. IEEE Trans. Autom. Control 1992, 37, 729–740. [Google Scholar] [CrossRef]
- Hovakimyan, N.; Cao, C. L1 Adaptive Control Theory: Guaranteed Robustness with Fast Adaptation; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2010; Volume 21. [Google Scholar]
- Lippiello, V.; Siciliano, B.; Villani, L. Interaction Control of Robot Manipulators Using Force and Vision. Int. J. Optomechatroni 2008, 2, 257–274. [Google Scholar] [CrossRef]
- Ott, C.; Albu-Schaffer, A.; Kugi, A.; Hirzinger, G. On the Passivity-Based Impedance Control of Flexible Joint Robots. IEEE Trans. Robot. 2008, 24, 416–429. [Google Scholar] [CrossRef]
- Tummers, R.T.L.M.; Fumagalli, M.; Carloni, R. Aerial Grasping: Modeling and Control of a Flying Hand. arXiv 2017, arXiv:1706.00036. [Google Scholar]










| Parameter | Physical Description | Value |
|---|---|---|
| mtotal | Total mass of the aerial manipulator | 5.5 kg |
| mb | Mass of the vehicle platform | 4.6 kg |
| Ixx | Inertia tensor of the vehicle around x-axis | 0.092 kg·m2 |
| Iyy | Inertia tensor of the vehicle around y-axis | 0.283 kg·m2 |
| Izz | Inertia tensor of the vehicle around z-axis | 0.245 kg·m2 |
| pcd | Distance between duct center and C.G. of vehicle | 0.32 m |
| R | Duct radius | 0.165 m |
| n | Blade number of each disc | 4 |
| c | Blade chord length | 0.027 m |
| θ0 | Attack angle at the root of blade | 35 deg |
| Link | a (m) | α (deg) | d (m) | θ Range (deg) |
|---|---|---|---|---|
| 1 | 0 | 90 | 0.08 | 180 [−90, 90] |
| 2 | 0.15 | 0 | 0 | 150 [0, 150] |
| 3 | 0.16 | 0 | 0 | 150 [−150, 0] |
| State Variables | xb (m) | yb (m) | zb (m) | φ (deg) | θ (deg) | ψ (deg) |
|---|---|---|---|---|---|---|
| Basic Controller | 0.0320 | 0.1305 | 0.0272 | 1.6484 | 0.7839 | 2.8236 |
| Adaptive Controller | 0.0176 | 0.0252 | 0.0126 | 1.0476 | 0.6448 | 0.6304 |
| State Variables | xb (m) | yb (m) | zb (m) | φ (deg) | θ (deg) | ψ (deg) |
|---|---|---|---|---|---|---|
| Basic Controller | 0.2324 | 0.2944 | 0.0399 | 1.9523 | 1.3520 | 2.8339 |
| Adaptive Controller | 0.1837 | 0.1735 | 0.0187 | 1.9606 | 1.7468 | 0.5584 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Xu, B.; Xiang, C.; Fan, W.; Ai, T. Flight and Interaction Control of an Innovative Ducted Fan Aerial Manipulator. Sensors 2020, 20, 3019. https://doi.org/10.3390/s20113019
Zhang Y, Xu B, Xiang C, Fan W, Ai T. Flight and Interaction Control of an Innovative Ducted Fan Aerial Manipulator. Sensors. 2020; 20(11):3019. https://doi.org/10.3390/s20113019
Chicago/Turabian StyleZhang, Yibo, Bin Xu, Changle Xiang, Wei Fan, and Tianfu Ai. 2020. "Flight and Interaction Control of an Innovative Ducted Fan Aerial Manipulator" Sensors 20, no. 11: 3019. https://doi.org/10.3390/s20113019
APA StyleZhang, Y., Xu, B., Xiang, C., Fan, W., & Ai, T. (2020). Flight and Interaction Control of an Innovative Ducted Fan Aerial Manipulator. Sensors, 20(11), 3019. https://doi.org/10.3390/s20113019




