Deep Trench Isolation and Inverted Pyramid Array Structures Used to Enhance Optical Efficiency of Photodiode in CMOS Image Sensor via Simulations
Abstract
:1. Introduction
2. Simulation Methodology
2.1. FDTD Application
2.2. Photodiode Analysis Developed for Optical Efficiency Evaluations
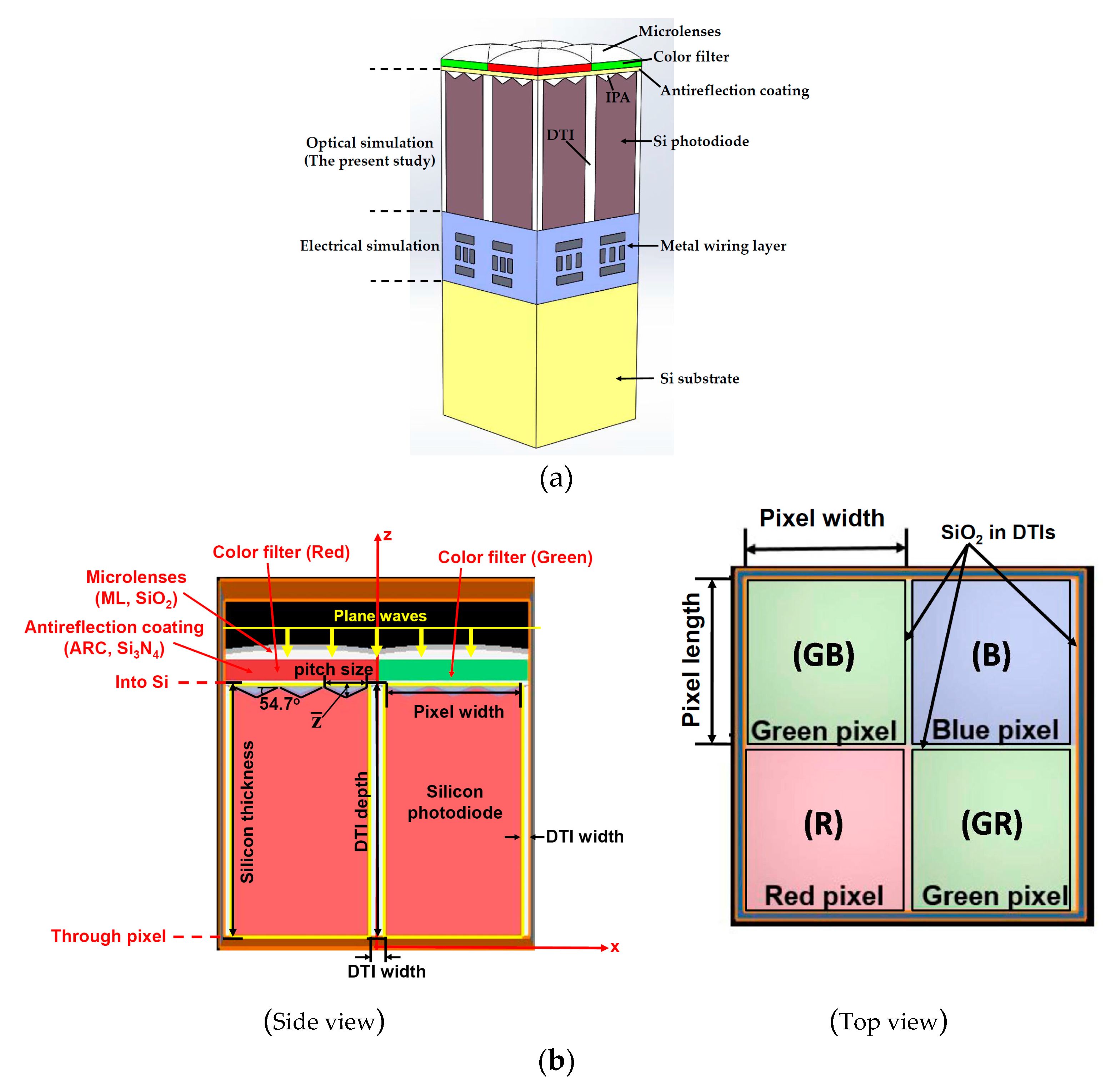
2.2.1. Photodiode in RGB Pixel Array
2.2.2. Material Settings
2.2.3. Incident Light Source Settings
2.2.4. Boundary Condition Settings
2.2.5. Quantum Efficiency for CMOS Sensors
3. Results and Discussion
4. Conclusions
- (1)
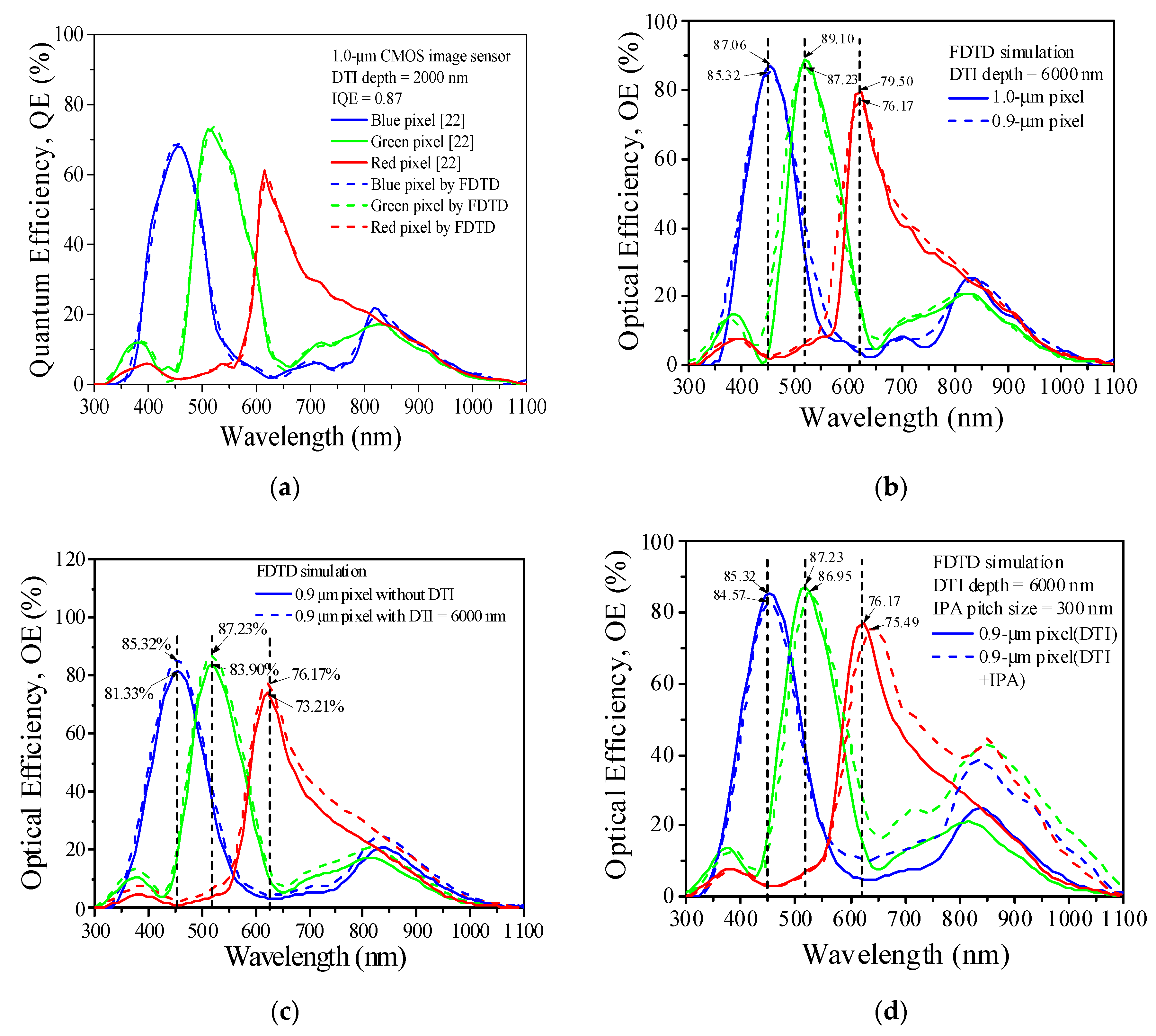
- With the geometries and materials reported in a literature and the optical properties of refraction index (n) and extinction coefficient (k) for a wide range of wavelengths, the simulational QE results predicted by the present model are very close to the experimental ones for the RGB pixels in the entire wavelength range. This model can be extended to evaluate the effects of various DTI and d combinations on the OEmax. values arising in the visible light (~300–700 nm) and NIR (~701–1100 nm) wavelength regions precisely.
- (2)
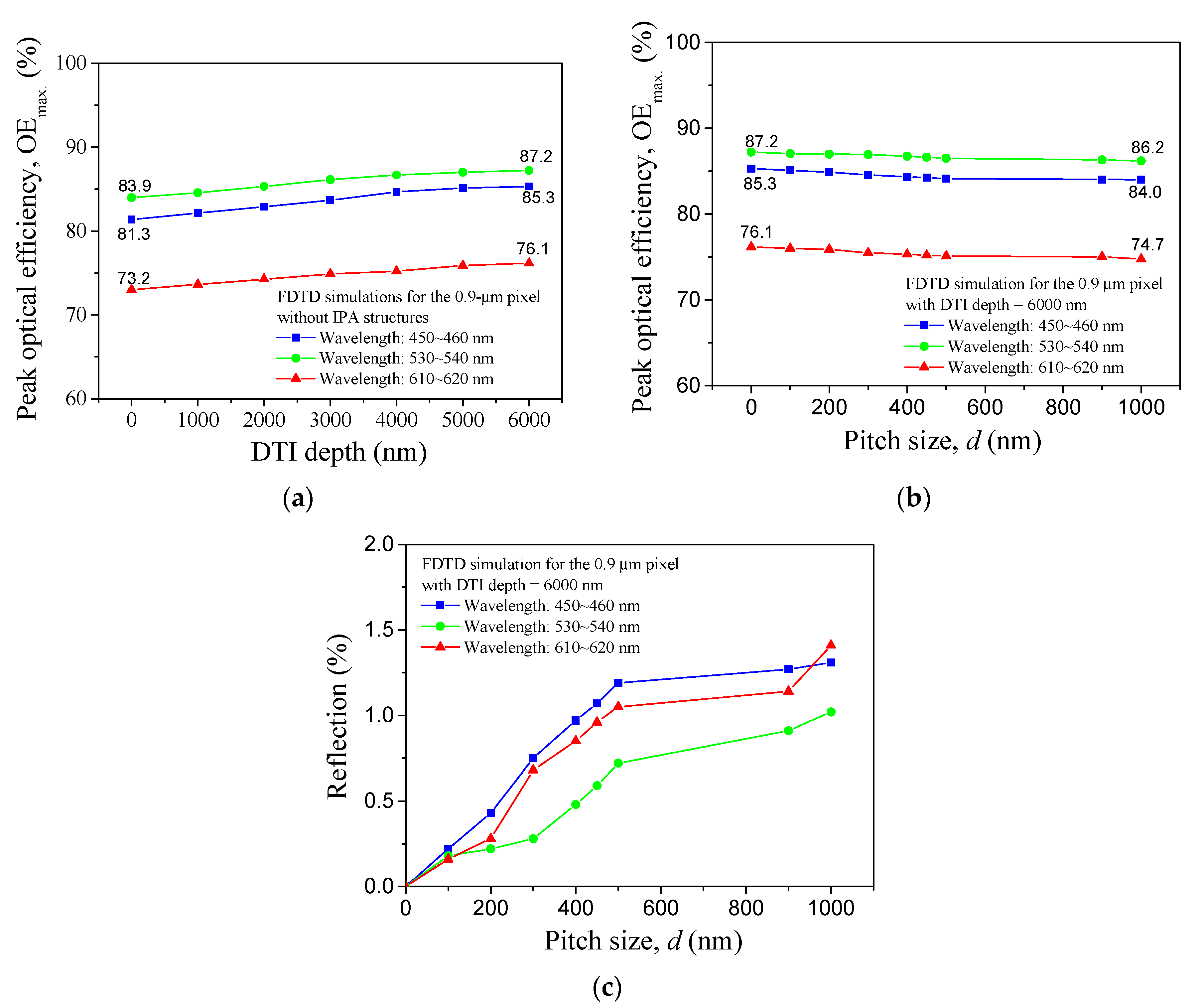
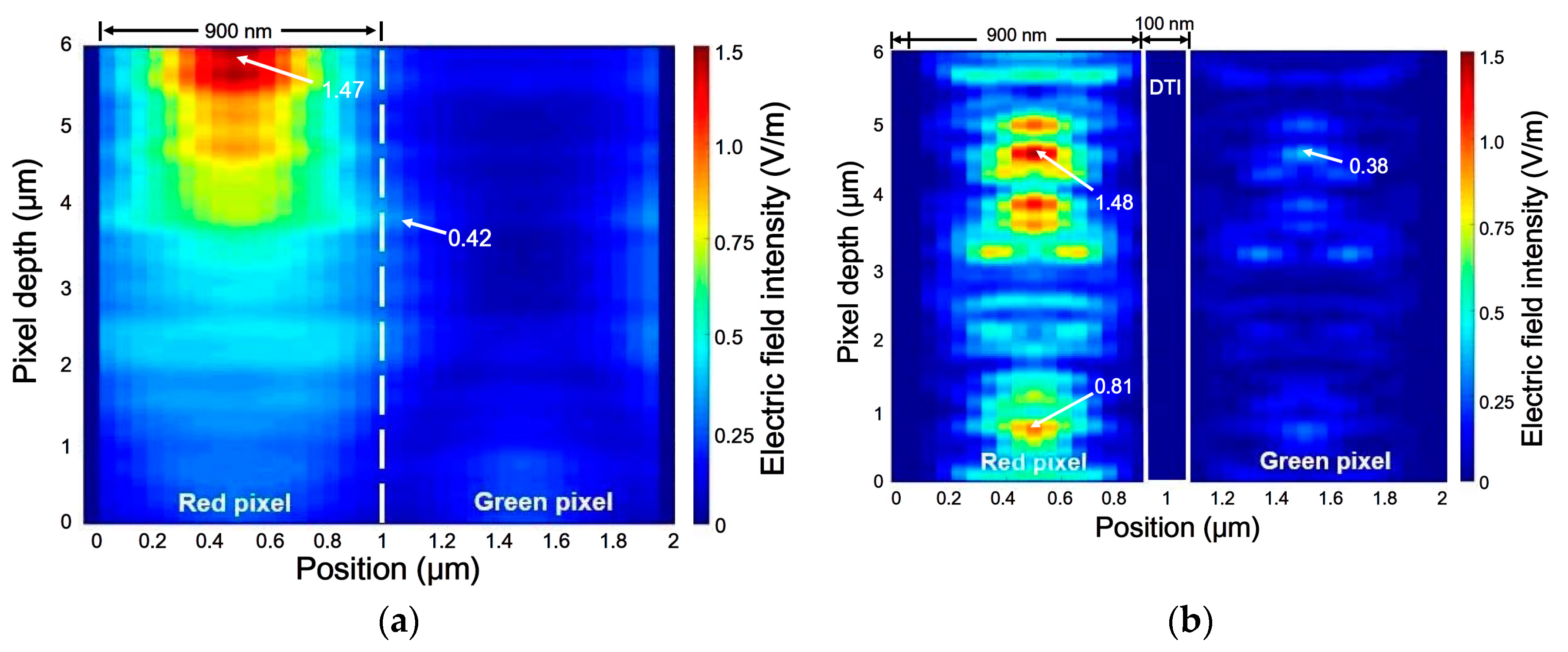
- Increasing the DTI can lead to monotonous OEmax. rises in the entire wavelength region, irrespective of the d value. A flat plane without the IPA structure (d = 0 nm) incorporating with DTI depth = 6000 nm is needed to produce the Max. OEmax. of every CF pixel in the visible light wavelength region. For a fixed DTI depth, the highest OEmax value occurs at a fixed d value strongly dependent on the DTI depth and the wavelength region we specify. A flat plane is needed for the Max. OEmax formed in the visible light wavelength regions, and a nonzero d is required for the Max. OEmax. formed in the NIR wavelength region.
- (3)
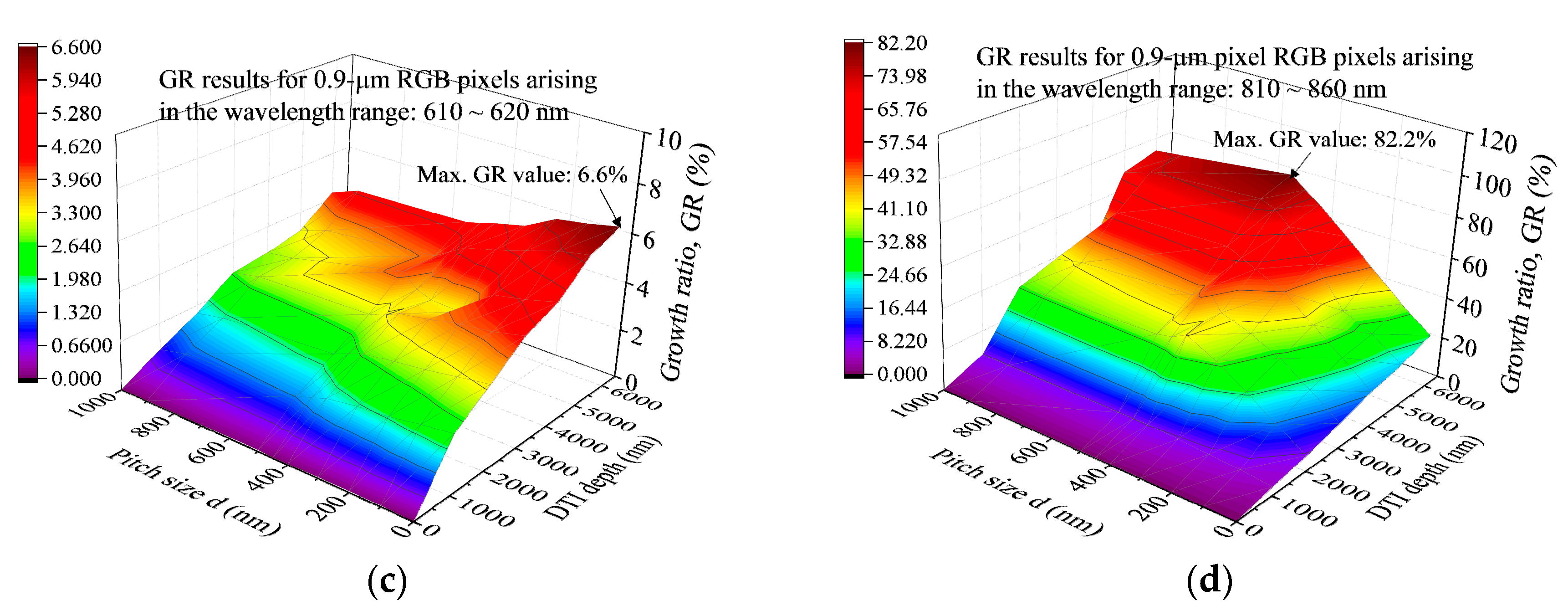
- The GR of OE defined on the bases of the pixel arrays without and with the DTI + IPA structure is useful to evaluate the OE promotions in the three visible light and one NIR wavelength regions due to the uses of various DTI and d combinations. The max. GR for the peaks in the NIR range of 810–860 nm has its value (82.2%) much higher than those (4.9% for blue, 4.2% for green and 6.6% for red) arising in the RGB pixels operating in the visible light wavelength regions with their OEmax. The combinations of various nonzero DTI and d values can bring in a definitely positive GR value for the NIR wavelength region.
Author Contributions
Funding
Conflicts of Interest
References
- Gamal, A.E.; Eltoukhy, H. CMOS image sensors—An introduction to the technology, design, and performance limits, presenting recent developments and future directions. IEEE Circ. Dev. Mag. 2005, 21, 23. [Google Scholar]
- Kozlowsk, L.J.; Liao, J.; Kleinhans, W.E.; Liu, T. Comparison of passive and active pixel schemes for CMOS visible imagers. In Proceedings of the SPIE 3360, Infrared Readout Electronics IV, Orlando, FL, USA, 14 September 1998. [Google Scholar]
- Ahn, J.; Moon, C.R.; Kim, B.; Lee, K.; Kim, Y.; Lim, M.; Lee, W.; Park, H.; Moon, K.; Yoo, J.; et al. Advanced image sensor technology for pixel scaling down toward 1.0 μm. In Proceedings of the 2008 IEEE International Electron Devices Meeting, San Francisco, CA, USA, 15–17 December 2008. [Google Scholar]
- Park, B.J.; Jung, J.W.; Moon, C.R.; Hwang, S.H.; Lee, Y.W.; Kim, D.W.; Paik, K.H.; Yoo, J.R.; Lee, D.H.; Kim, K. Deep trench isolation for crosstalk suppression in active pixel sensor with 1.7 μm pixel pitch. Jap. J. Appl. Phys. 2007, 46, 2454–2457. [Google Scholar] [CrossRef]
- Tournier, A.; Leverd, F.; Favennec, L.; Perrot, C.; Pinzelli, L.; Gntefait, M.; Cherault, N.; Jeanijean, D.; Carrere, J.P.; Hirigoyan, F.; et al. Pixel-to-pixel isolation by deep trench technology: Application to CMOS image sensor. In Proceedings of the 2011 International Image Sensor Workshop, Hokkaido, Japan, 8–11 June 2011. [Google Scholar]
- Kitamura, Y.; Aikawa, H.; Kakehi, K.; Yousyou, T.; Eda, K.; Minami, T.; Uya, S.; Takegawa, Y.; Yamashita, H.; Kohyama, Y. Suppression of crosstalk by using backside deep trench isolation for 1.12 μm backside illuminated CMOS image sensor. In Proceedings of the 2012 International Electron Devices Meeting, San Francisco, CA, USA, 10–13 December 2012. IEDM12-537-540. [Google Scholar]
- Bayer, E.B. Inventor; Eastman Kodak Company, assignee. Color imaging array. U.S. Patent No. 3,971,065, 20 July 1976. [Google Scholar]
- Hu, L.; Chen, G. Analysis of optical absorption in silicon nanowire arrays for photovoltaic applications. Nano Lett. 2007, 7, 3249–3252. [Google Scholar] [CrossRef] [PubMed]
- Han, S.E.; Chen, G. Optical absorption enhancement in silicon nanohole arrays for solar photovoltaics. Nano Lett. 2010, 10, 1012–1015. [Google Scholar] [CrossRef] [PubMed]
- Han, S.E.; Chen, G. Toward the Lambertian limit of light trapping in thin nanostructured silicon solar cells. Nano Lett. 2010, 10, 4692–4696. [Google Scholar] [CrossRef] [PubMed]
- Mavrokefalos, A.; Han, S.E.; Yerci, S.; Branham, M.S.; Chen, G. Efficient light trapping in inverted nanopyramid thin crystalline silicon membranes for solar cell applications. Nano Lett. 2012, 12, 2792–2796. [Google Scholar] [CrossRef]
- Yokogawa, S.; Oshiyama, I.; Ikeda, H.; Ebiko, Y.; Hirano, T.; Saito, S.; Oinoue, T.; Hagimoto, Y.; Iwamoto, H. IR sensitivity enhancement of CMOS image sensor with diffractive light trapping pixels. Sci. Rep. 2017, 7, 3832. [Google Scholar] [CrossRef]
- Vaillant, J.; Crocherie, A.; Hirigoyen, F.; Cadien, A.; Pond, J. Uniform illumination and rigorous electromagnetic simulations applied to CMOS image sensor. Opt. Expr. 2007, 15, 5494–5503. [Google Scholar] [CrossRef]
- Crocherie, A.; Vaillant, J.; Hirigoyen, F. Three-dimensional broadband FDTD optical simulations of CMOS image sensor. In Proceedings of the SPIE 7100, Optical Design and Engineering III, Scotland, UK, 2–5 September 2008. [Google Scholar]
- Yee, K.S. Numerical solution of initial boundary value problems involving Mawwell’s equations in isotropic media. IEEE Trans. Anten. Prop. 1996, 14, 302–307. [Google Scholar]
- Taflove, A.; Hagness, S.C. Computational Electrodynamics: The Finite-Difference Time-Domain Method, 2nd ed.; Schrank, H.E., Ed.; Series Editor Artech House: Boston, MA, USA, 2000. [Google Scholar]
- Lumerical Solutions 8.19, Lumerical Solutions, Inc. 2019. Available online: https://www.lumerical.com/tcad-products/fdtd/ (accessed on 6 December 2017).
- Hirigoyen, F.; Crocherie, A.; Vaillant, J.; Cazaux, Y. FDTD-based optical simulations methodology for CMOS image sensor pixels architecture and process optimization. In Proceedings of the SPIE 6816, Sensors, Cameras, and Systems for Industrial/Scientific Applications IX, San Jose, CA, USA, 27–31 January 2008. [Google Scholar]
- Taflove, A.; Brodwin, M.E. Numerical solution of steady-state electromagnetic scattering problems using the time-dependent Maxwell’s equations. IEEE Trans. Microw. Theory Tech. 1975, 23, 623–630. [Google Scholar] [CrossRef]
- Sun, C.H.; Jiang, P.; Jiang, B. Broadband moth-eye antireflection coatings on silicon. Appl. Phys. Lett. 2008, 92, 061112. [Google Scholar] [CrossRef] [Green Version]
- Venezia, V.C.; Hsiung, C.W.; Yang, W.Z.; Zhang, Y.Y.; Zhao, C.; Lin, Z.; Grant, L.A. Second Generation Small Pixel Technology Using Hybrid Bond Stacking. Sensors 2018, 18, 667. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- HOYA. Available online: http://www.hoyacandeo.co.jp/english/products/eo/color/index.html (accessed on 1 April 2014).
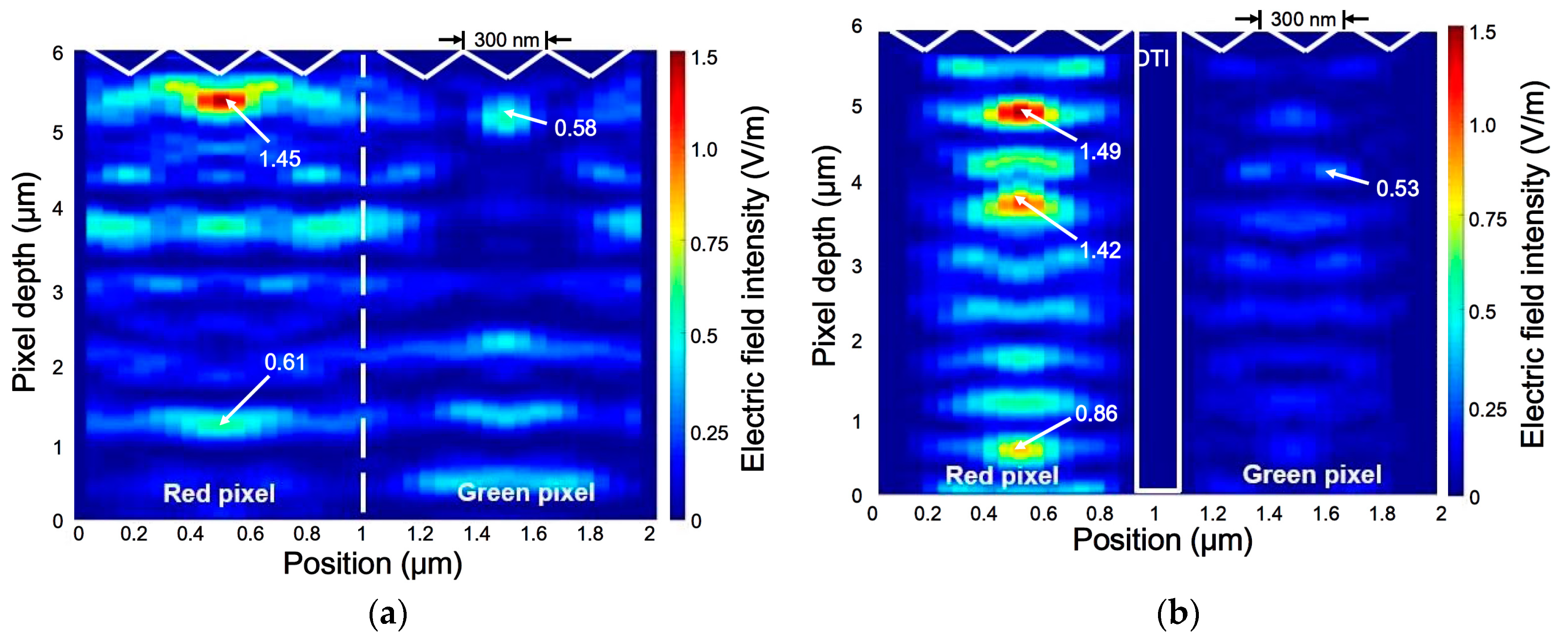
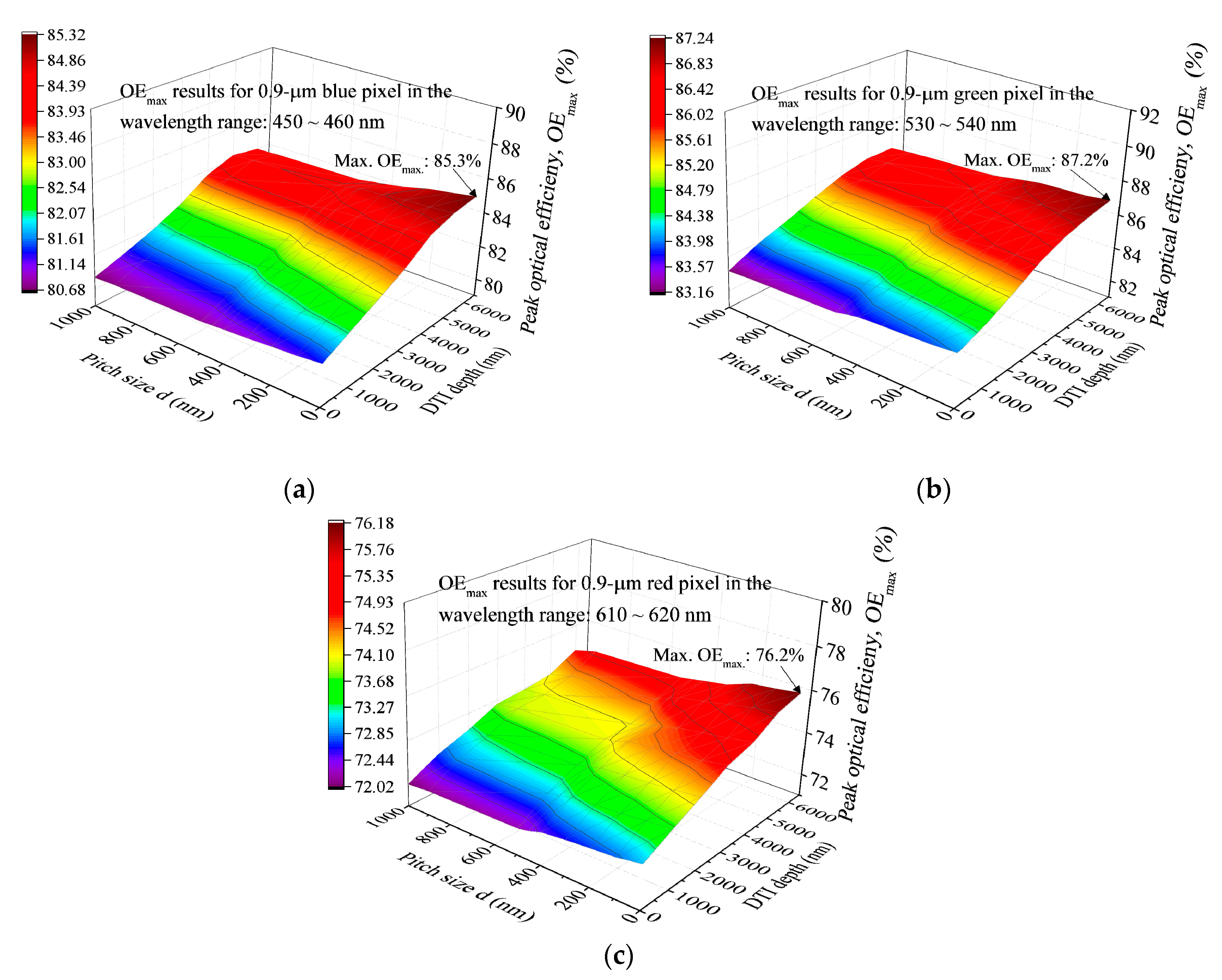
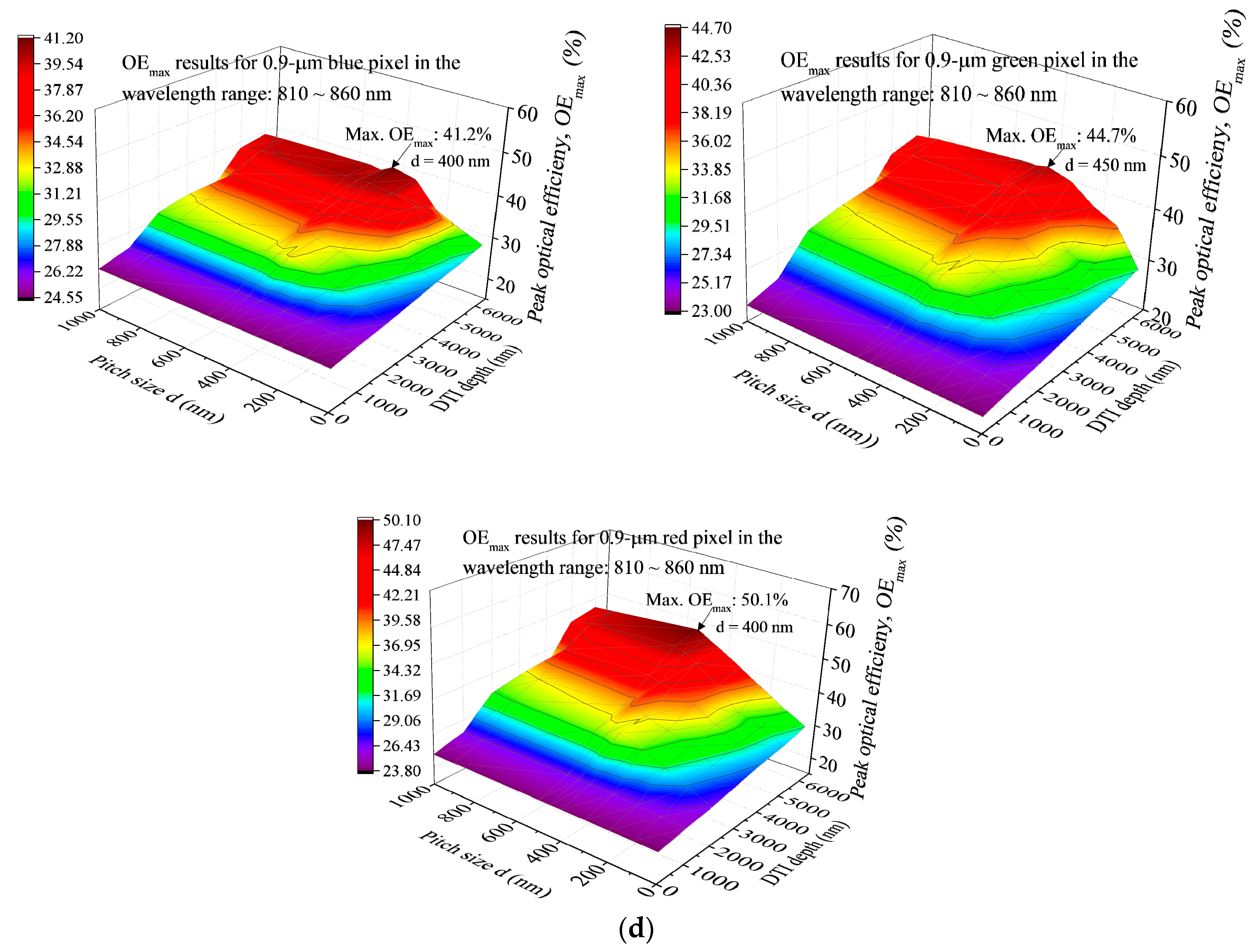
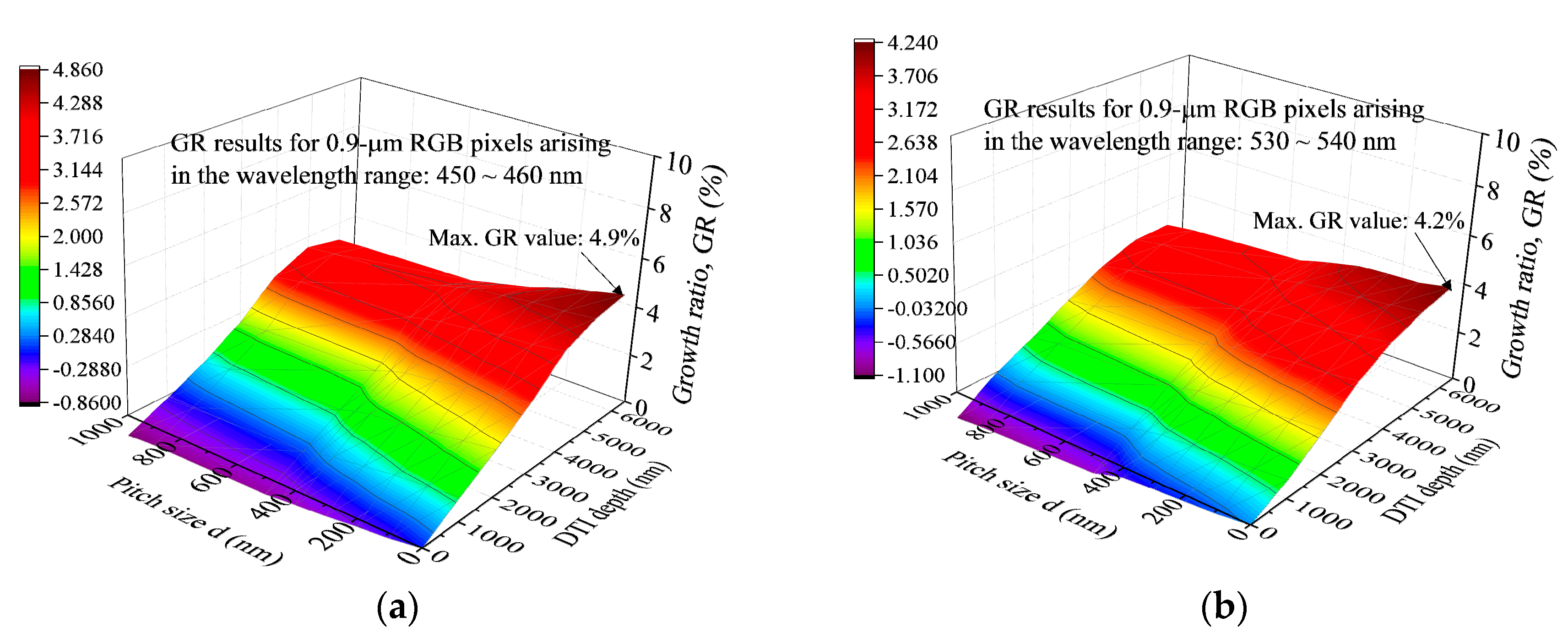
| Wavelength (nm) | Silicon Photodiode (Si) [17] | SiO2 Microlenses [17] | Si3N4 Antireflection Coating [17] | Blue Filter [21,22] | Green Filter [21,22] | Red Filter [21,22] | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | k | n | k | n | k | n | k | n | k | n | k | |
| 300 | 4.52 | 0.03 | 1.47 | 0 | 2.10 | 0 | 1.552 | 1.1 × 10−5 | 1.623 | 0.8× 10-3 | 1.538 | 8.3 × 10-5 |
| 400 | 5.57 | 0.39 | 1.47 | 0 | 2.08 | 0 | 1.549 | 1.4 × 10−5 | 1.601 | 1.0× 10-3 | 1.536 | 6.5 × 10-5 |
| 500 | 4.28 | 0.07 | 1.46 | 0 | 2.03 | 0 | 1.539 | 4.3 × 10−5 | 1.585 | 8.1× 10−5 | 1.532 | 3.1 × 10−5 |
| 600 | 3.90 | 0.03 | 1.45 | 0 | 2.01 | 0 | 1.534 | 1.6 × 10−4 | 1.576 | 1.0 × 10−4 | 1.529 | 9.7 × 10−6 |
| 700 | 3.78 | 0.01 | 1.45 | 0 | 2.00 | 0 | 1.531 | 9.0 × 10−5 | 1.572 | 2.2 × 10−4 | 1.528 | 6.6 × 10−6 |
| 800 | 3.69 | 0.07 | 1.45 | 0 | 1.99 | 0 | 1.529 | 9.1 × 10−5 | 1.569 | 2.1 × 10−4 | 1.527 | 7.5 × 10−6 |
| 900 | 3.61 | 4 × 10−3 | 1.45 | 0 | 1.99 | 0 | 1.528 | 9.3 × 10−5 | 1.567 | 2.2 × 10−4 | 1.526 | 3.7× 10−6 |
| 1000 | 3.58 | 5 × 10−4 | 1.45 | 0 | 1.98 | 0 | 1.527 | 7.9 × 10−5 | 1.565 | 1.8 × 10−4 | 1.526 | 2.3 × 10−6 |
| 1100 | 3.55 | 1 × 10−4 | 1.45 | 0 | 1.98 | 0 | 1.527 | 6.2 × 10−5 | 1.565 | 1.1 × 10−4 | 1.525 | 2.2 × 10−6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, C.-F.; Chiou, J.-M.; Lin, J.-F. Deep Trench Isolation and Inverted Pyramid Array Structures Used to Enhance Optical Efficiency of Photodiode in CMOS Image Sensor via Simulations. Sensors 2020, 20, 3062. https://doi.org/10.3390/s20113062
Han C-F, Chiou J-M, Lin J-F. Deep Trench Isolation and Inverted Pyramid Array Structures Used to Enhance Optical Efficiency of Photodiode in CMOS Image Sensor via Simulations. Sensors. 2020; 20(11):3062. https://doi.org/10.3390/s20113062
Chicago/Turabian StyleHan, Chang-Fu, Jiun-Ming Chiou, and Jen-Fin Lin. 2020. "Deep Trench Isolation and Inverted Pyramid Array Structures Used to Enhance Optical Efficiency of Photodiode in CMOS Image Sensor via Simulations" Sensors 20, no. 11: 3062. https://doi.org/10.3390/s20113062
APA StyleHan, C.-F., Chiou, J.-M., & Lin, J.-F. (2020). Deep Trench Isolation and Inverted Pyramid Array Structures Used to Enhance Optical Efficiency of Photodiode in CMOS Image Sensor via Simulations. Sensors, 20(11), 3062. https://doi.org/10.3390/s20113062





