Effect of Substrate Etching on Terahertz Metamaterial Resonances and Its Liquid Sensing Applications
Abstract
:1. Introduction
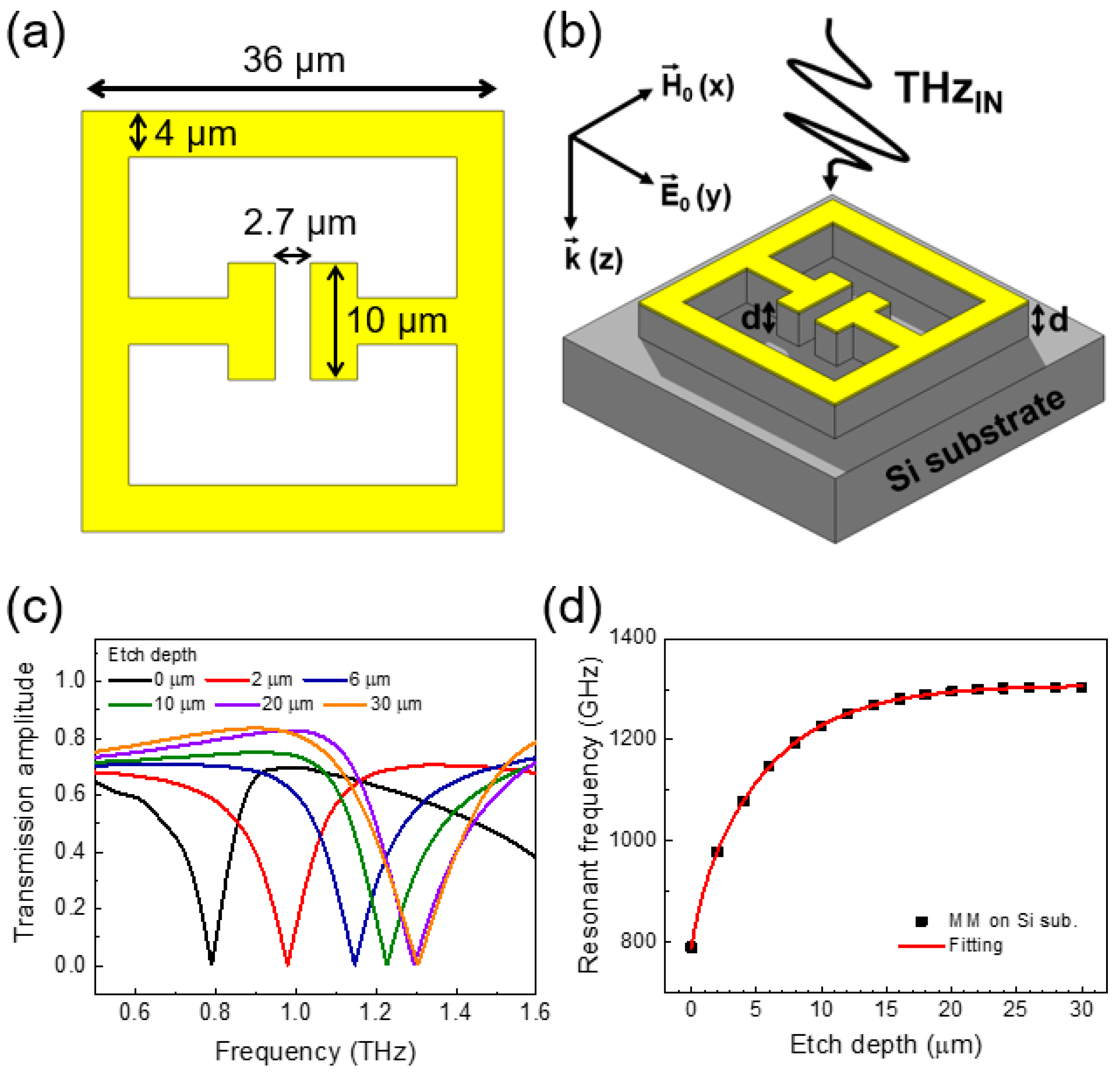
2. Simulation Methods
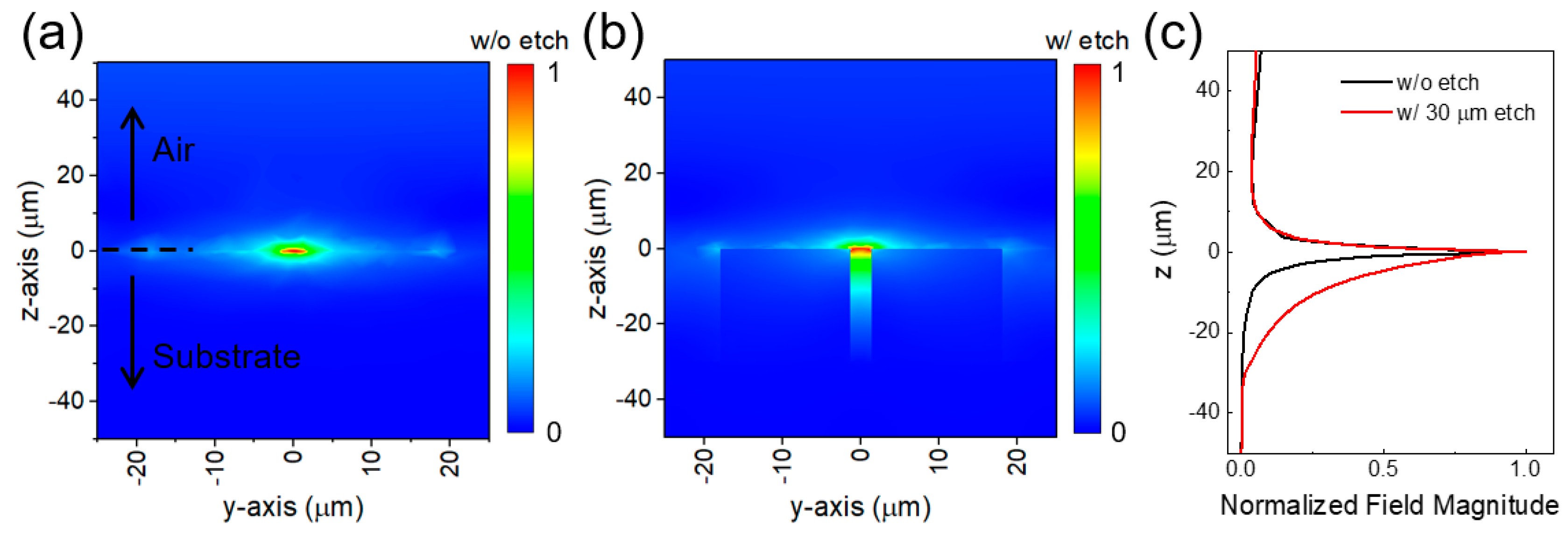
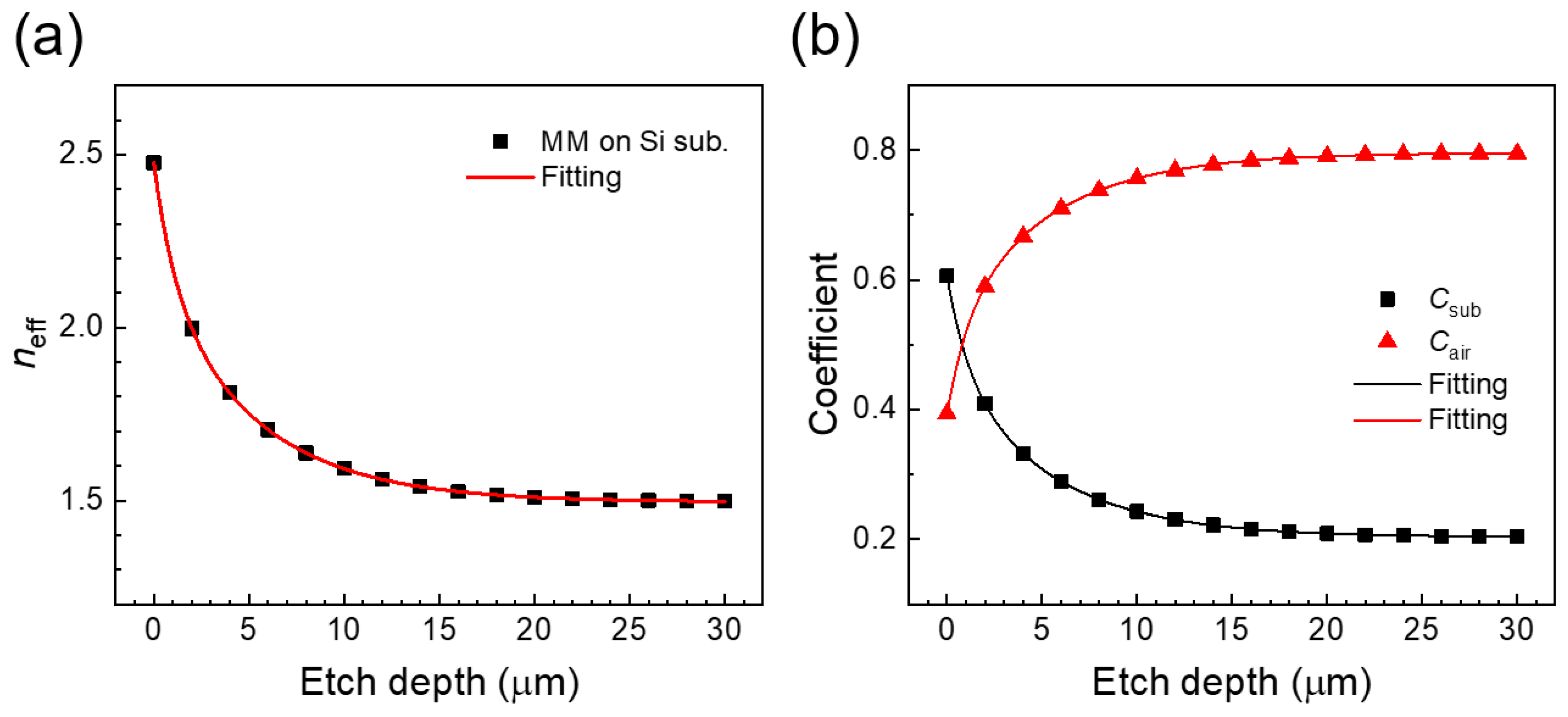
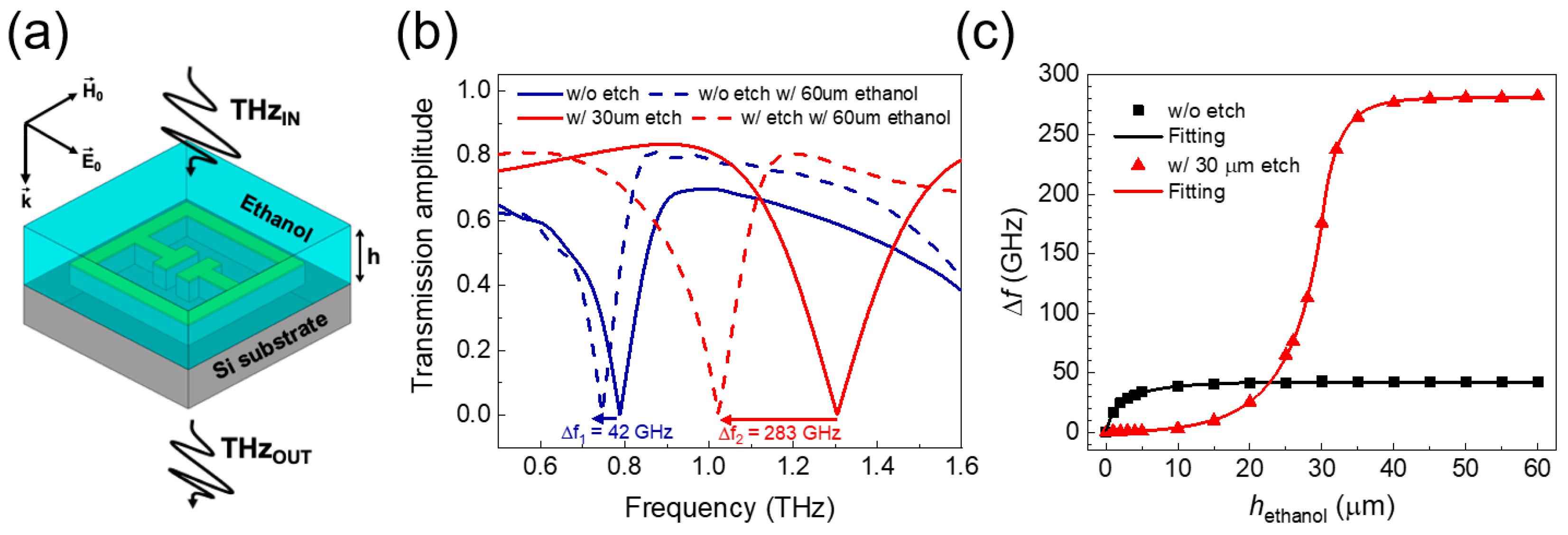
3. Simulation Results and Discussions
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, H.T.; Padilla, W.J.; Zide, J.M.O.; Gossard, A.C.; Taylor, A.J.; Averitt, R.D. Active terahertz metamaterial devices. Nature 2006, 444, 597–600. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Padilla, W.J.; Taylor, A.J.; Highstrete, C.; Lee, M.; Averitt, R.D. Dynamical electric and magnetic metamaterial response at terahertz frequencies. Phys. Rev. Lett. 2006, 96, 107401. [Google Scholar] [CrossRef] [PubMed]
- Padilla, W.J.; Aronsson, M.T.; Highstrete, C.; Lee, M.; Taylor, A.J.; Averitt, R.D. Electrically resonant terahertz metamaterials: Theoretical and experimental investigations. Phys. Rev. B 2007, 75, 041102. [Google Scholar] [CrossRef] [Green Version]
- Tao, H.; Bingham, C.M.; Strikwerda, A.C.; Pilon, D.; Shrekenhamer, D.; Landy, N.I.; Fan, K.; Zhang, X.; Padilla, W.J.; Averitt, R.D. Highly flexible wide angle of incidence terahertz metamaterial absorber: Design, fabrication, and characterization. Phys. Rev. B 2008, 78, 241103. [Google Scholar] [CrossRef]
- Tao, H.; Strikwerda, A.C.; Fan, K.; Bingham, C.M.; Padilla, W.J.; Zhang, X.; Averitt, R.D. Terahertz metamaterials on free-standing highly-flexible polyimide substrates. J. Phys. D 2008, 41, 232004. [Google Scholar] [CrossRef] [Green Version]
- Park, S.J.; Hong, J.T.; Choi, S.J.; Kim, H.S.; Park, W.K.; Han, S.T.; Park, J.Y.; Lee, S.; Kim, D.S.; Ahn, Y.H. Detection of microorganisms using terahertz metamaterials. Sci. Rep. 2014, 4, 4988. [Google Scholar] [CrossRef]
- Chen, H.T.; O’Hara, J.F.; Azad, A.K.; Taylor, A.J.; Averitt, R.D.; Shrekenhamer, D.B.; Padilla, W.J. Experimental demonstration of frequency-agile terahertz metamaterials. Nat. Photonics 2008, 2, 295–298. [Google Scholar] [CrossRef]
- Liu, M.; Hwang, H.Y.; Tao, H.; Strikwerda, A.C.; Fan, K.; Keiser, G.R.; Sternbach, A.J.; West, K.G.; Kittiwatanakul, S.; Lu, J.; et al. Terahertz-field-induced insulator-to-metal transition in vanadium dioxide metamaterial. Nature 2012, 487, 345–348. [Google Scholar] [CrossRef]
- Park, D.J.; Park, S.J.; Park, I.; Ahn, Y.H. Dielectric substrate effect on the metamaterial resonances in terahertz frequency range. Curr. Appl. Phys. 2014, 14, 570–574. [Google Scholar] [CrossRef]
- Park, S.J.; Ahn, Y.H. Substrate effects on terahertz metamaterial resonances for various metal thicknesses. J. Korean Phys. Soc. 2014, 65, 1843–1847. [Google Scholar] [CrossRef]
- Park, S.J.; Son, B.H.; Choi, S.J.; Kim, H.S.; Ahn, Y.H. Sensitive detection of yeast using terahertz slot antennas. Opt. Express 2014, 22, 30467–30472. [Google Scholar] [CrossRef] [PubMed]
- Tao, H.; Strikwerda, A.C.; Liu, M.; Mondia, J.P.; Ekmekci, E.; Fan, K.; Kaplan, D.L.; Padilla, W.J.; Zhang, X.; Averitt, R.D.; et al. Performance enhancement of terahertz metamaterials on ultrathin substrates for sensing applications. Appl. Phys. Lett. 2010, 97, 261909. [Google Scholar] [CrossRef]
- Gupta, M.; Srivastava, Y.K.; Manjappa, M.; Singh, R. Sensing with toroidal metamaterial. Appl. Phys. Lett. 2017, 110, 121108. [Google Scholar] [CrossRef]
- Ahmadivand, A.; Gerislioglu, B.; Ahuja, R.; Kumar Mishra, Y. Terahertz plasmonics: The rise of toroidal metadevices towards immunobiosensings. Mater. Today 2020, 32, 108–130. [Google Scholar] [CrossRef]
- Ahmadivand, A.; Gerislioglu, B.; Manickam, P.; Kaushik, A.; Bhansali, S.; Nair, M.; Pala, N. Rapid detection of infectious envelope proteins by magnetoplasmonic toroidal metasensors. ACS Sens. 2017, 2, 1359–1368. [Google Scholar] [CrossRef]
- Park, S.J.; Cha, S.H.; Shin, G.A.; Ahn, Y.H. Sensing viruses using terahertz nano-gap metamaterials. Biomed. Opt. Express 2017, 8, 3551–3558. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, Y.K.; Cong, L.; Singh, R. Dual-surface flexible THz Fano metasensor. Appl. Phys. Lett. 2017, 111, 201101. [Google Scholar] [CrossRef]
- Lapadatu, D.; Pyka, A.; Dziuban, J.; Puers, R. Corrugated silicon nitride membranes as suspensions in micromachined silicon accelerometers. J. Micromech. Microeng. 1996, 6, 73–76. [Google Scholar] [CrossRef]
- Meng, K.; Park, S.J.; Burnett, A.D.; Gill, T.; Wood, C.D.; Rosamond, M.; Li, L.H.; Chen, L.; Bacon, D.R.; Freeman, J.R.; et al. Increasing the sensitivity of terahertz split ring resonator metamaterials for dielectric sensing by localized substrate etching. Opt. Express 2019, 27, 23164–23172. [Google Scholar] [CrossRef]
- Park, S.J.; Yoon, S.A.N.; Ahn, Y.H. Effective sensing volume of terahertz metamaterial with various gap widths. J. Opt. Soc. Korea 2016, 20, 628–632. [Google Scholar] [CrossRef] [Green Version]
- Sultana, J.; Islam, M.S.; Ahmed, K.; Dinovitser, A.; Ng, B.W.H.; Abbott, D. Terahertz detection of alcohol using a photonic crystal fiber sensor. Appl. Opt. 2018, 57, 2426–2433. [Google Scholar] [CrossRef] [PubMed]
- Park, S.J.; Yoon, S.A.N.; Ahn, Y.H. Dielectric constant measurements of thin films and liquids using terahertz metamaterials. RSC Adv. 2016, 6, 69381–69386. [Google Scholar] [CrossRef]
- Park, S.J.; Ahn, Y.H. Accurate measurement of THz dielectric constant using metamaterials on a quartz substrate. Curr. Opt. Photonics 2017, 1, 637–641. [Google Scholar]
- Srivastava, Y.K.; Ako, R.T.; Gupta, M.; Bhaskaran, M.; Sriram, S.; Singh, R. Terahertz sensing of 7 nm dielectric film with bound states in the continuum metasurfaces. Appl. Phys. Lett. 2019, 115, 151105. [Google Scholar] [CrossRef] [Green Version]
- Chiam, S.Y.; Singh, R.; Zhang, W.; Bettiol, A.A. Controlling metamaterial resonances via dielectric and aspect ratio effects. Appl. Phys. Lett. 2010, 97, 191906. [Google Scholar] [CrossRef] [Green Version]
| Structure Type | Substrate Type | RIU Sensitivity | References |
|---|---|---|---|
| Asymmetric SRR | 25 µm thick cyclic olefin copolymer | 1 GHz/nm | [24] |
| Double SRR | 1 µm thick silicon | 0.07 GHz/nm | [25] |
| SRR with localized substrate etching | 500 µm thick silicon | 0.25 GHz/nm | [19] |
| Toroidal SRR | 25 µm thick mylar | 186 GHz | [13] |
| SRR with substrate etching | 500 µm thick silicon | 515 GHz | This work |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.J.; Cunningham, J. Effect of Substrate Etching on Terahertz Metamaterial Resonances and Its Liquid Sensing Applications. Sensors 2020, 20, 3133. https://doi.org/10.3390/s20113133
Park SJ, Cunningham J. Effect of Substrate Etching on Terahertz Metamaterial Resonances and Its Liquid Sensing Applications. Sensors. 2020; 20(11):3133. https://doi.org/10.3390/s20113133
Chicago/Turabian StylePark, Sae June, and John Cunningham. 2020. "Effect of Substrate Etching on Terahertz Metamaterial Resonances and Its Liquid Sensing Applications" Sensors 20, no. 11: 3133. https://doi.org/10.3390/s20113133
APA StylePark, S. J., & Cunningham, J. (2020). Effect of Substrate Etching on Terahertz Metamaterial Resonances and Its Liquid Sensing Applications. Sensors, 20(11), 3133. https://doi.org/10.3390/s20113133





