Towards Robust and Accurate Detection of Abnormalities in Musculoskeletal Radiographs with a Multi-Network Model
Abstract
1. Introduction
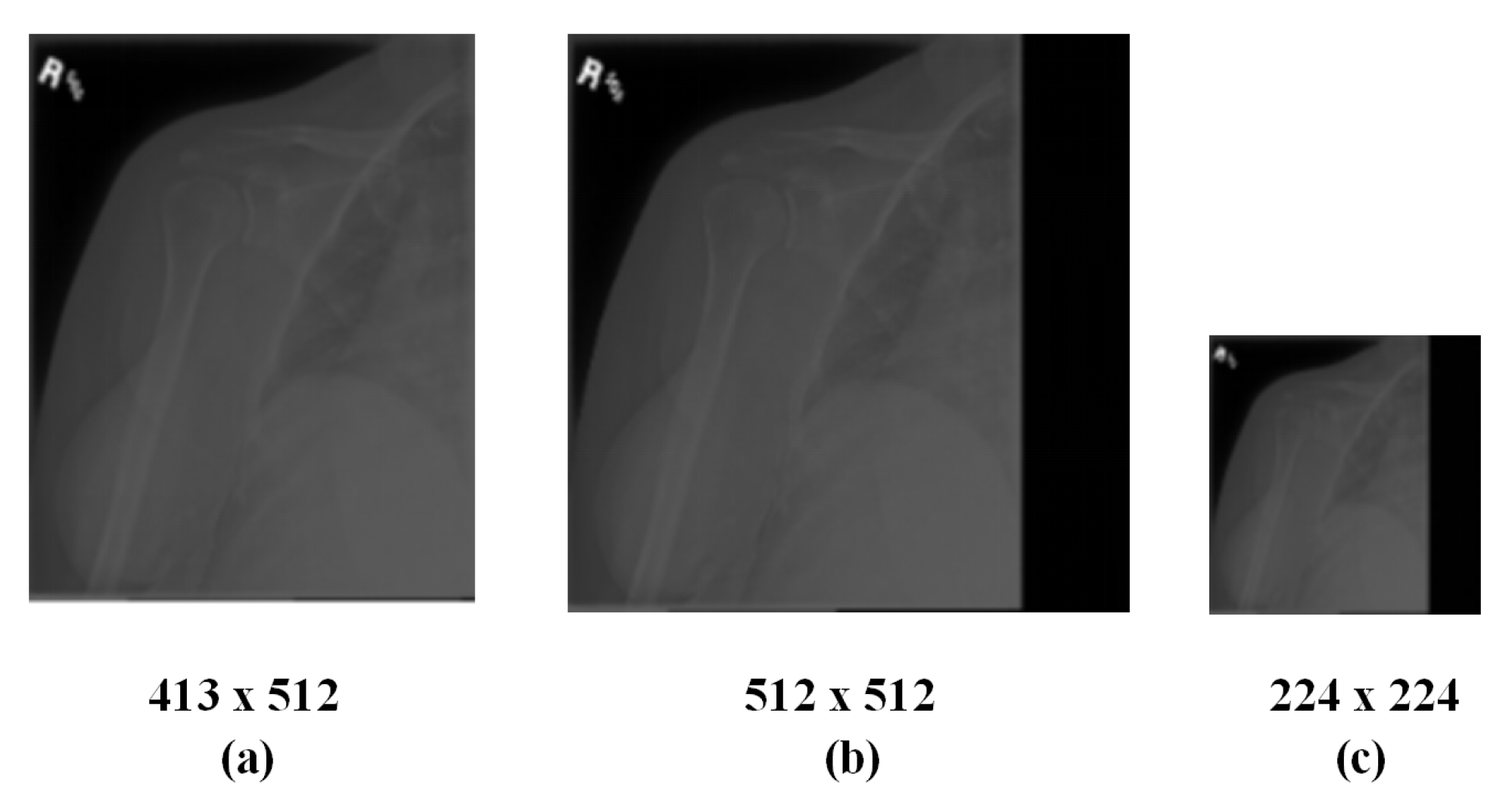
- A preprocessing scheme of radiographs is proposed to create an identity map from the original image to the expected input image, utilizing an image padding method [29] to pad the original image with square proportions and then zooming it to the appropriate size;
- The network structure of the CNN is deeply analyzed and a multi-scale network structure with powerful discriminating ability and characteristics of high-resolution feature map is proposed. Three different resolution subnetwork sequences are adopted and each sequence is connected to all other sequences through upsampling or downsampling to perform salient feature fusion;
- A graph convolutional neural network is employed, with the aim to extract global structure information and context information of radiographs, while utilizing the embedding method [28] to abstract the image into graph data. Graph convolution is then conducted on the data to extract structure features and the context relationship, which is hidden in the graph data;
- The high accuracy and strong robustness of the proposed framework are demonstrated. This structure combines the two network streams via concatenation on the flat layer to perform structure feature and salient feature fusion. It can maintain high-resolution representations, while obtaining effective representations of the structural features.
2. Related Works
2.1. High Resolution Neural Network (HRNet)
2.2. Graph Convolutional Network (GCN)
3. Proposed Method
3.1. Method of Radiographs Preprocessing
- Calculate the maximum value between the width and height as L.
- Create a new square image with L as the edge and 0 as each pixel value.
- Align the original image with the top left corner of the newly created image and merge both.
- Shrink the merged image expected size.
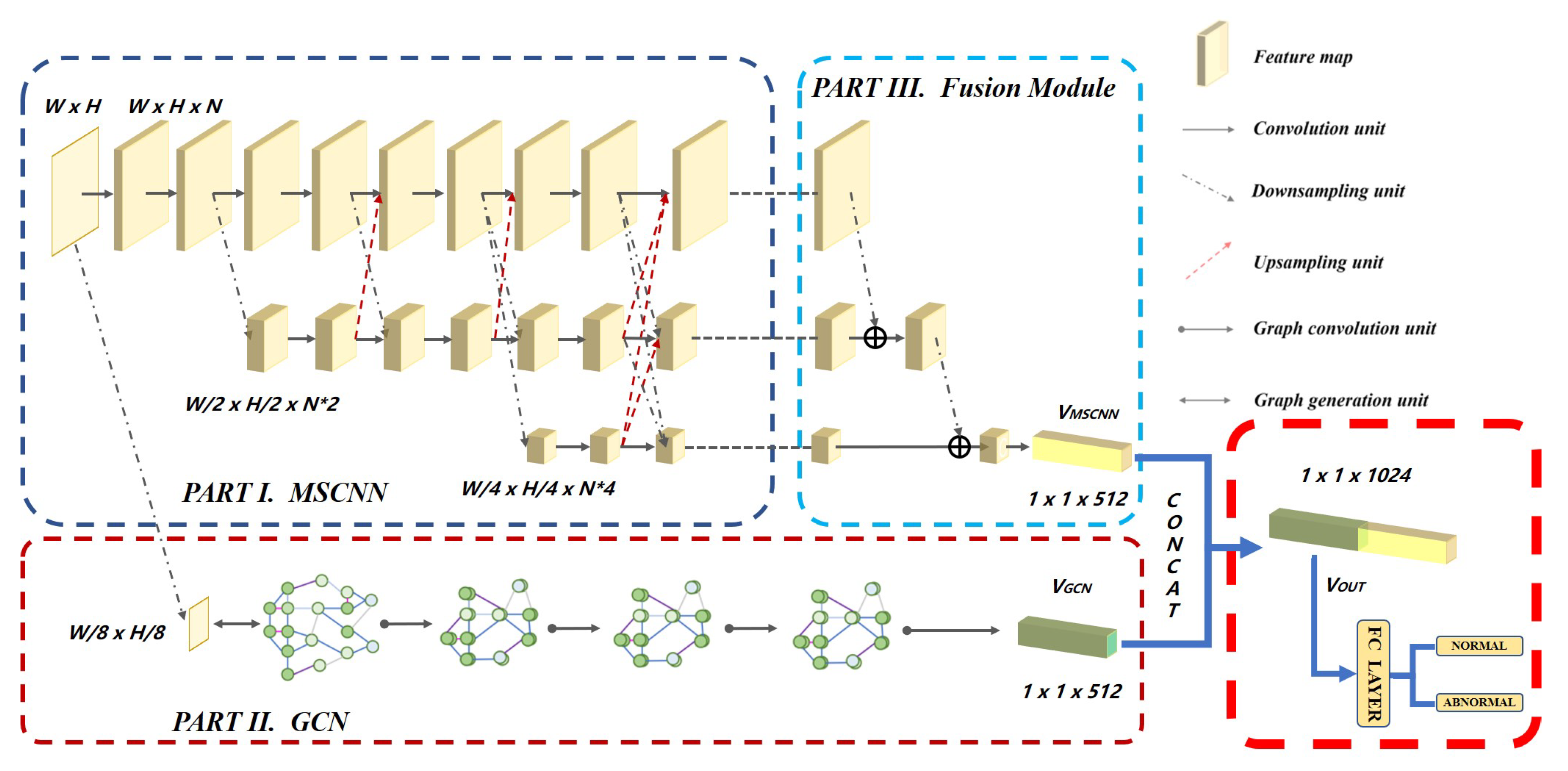
3.2. Proposed Multi-Scale Convolution Neural Network (MSCNN)
3.3. Proposed Graph Convolution Network (GCN)
3.4. Proposed Fusion Module
3.5. Proposed Framework
4. Experiments and Discussion
4.1. MURA Dataset
4.2. Evaluation Metrics
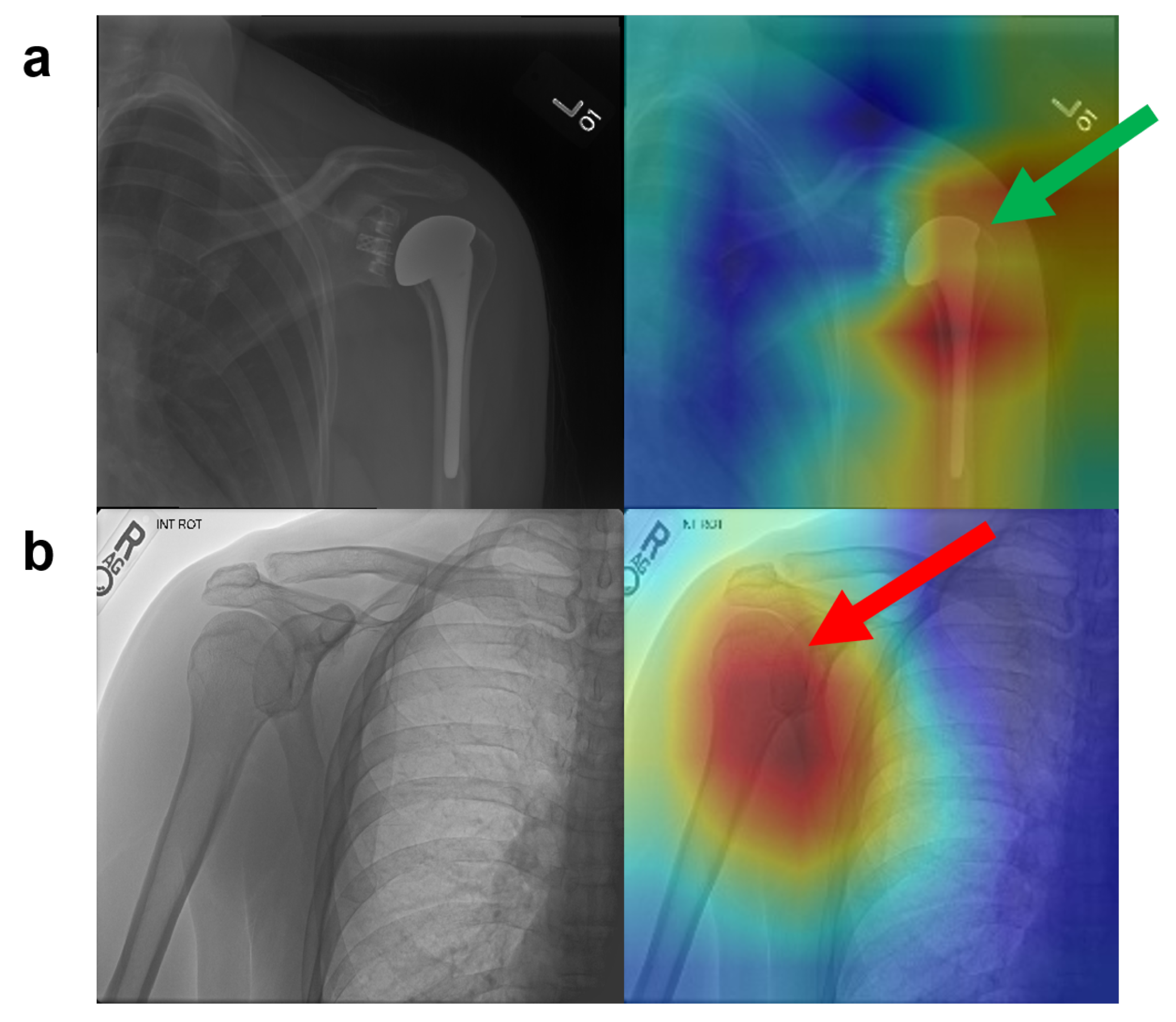
4.3. Results and Discussion
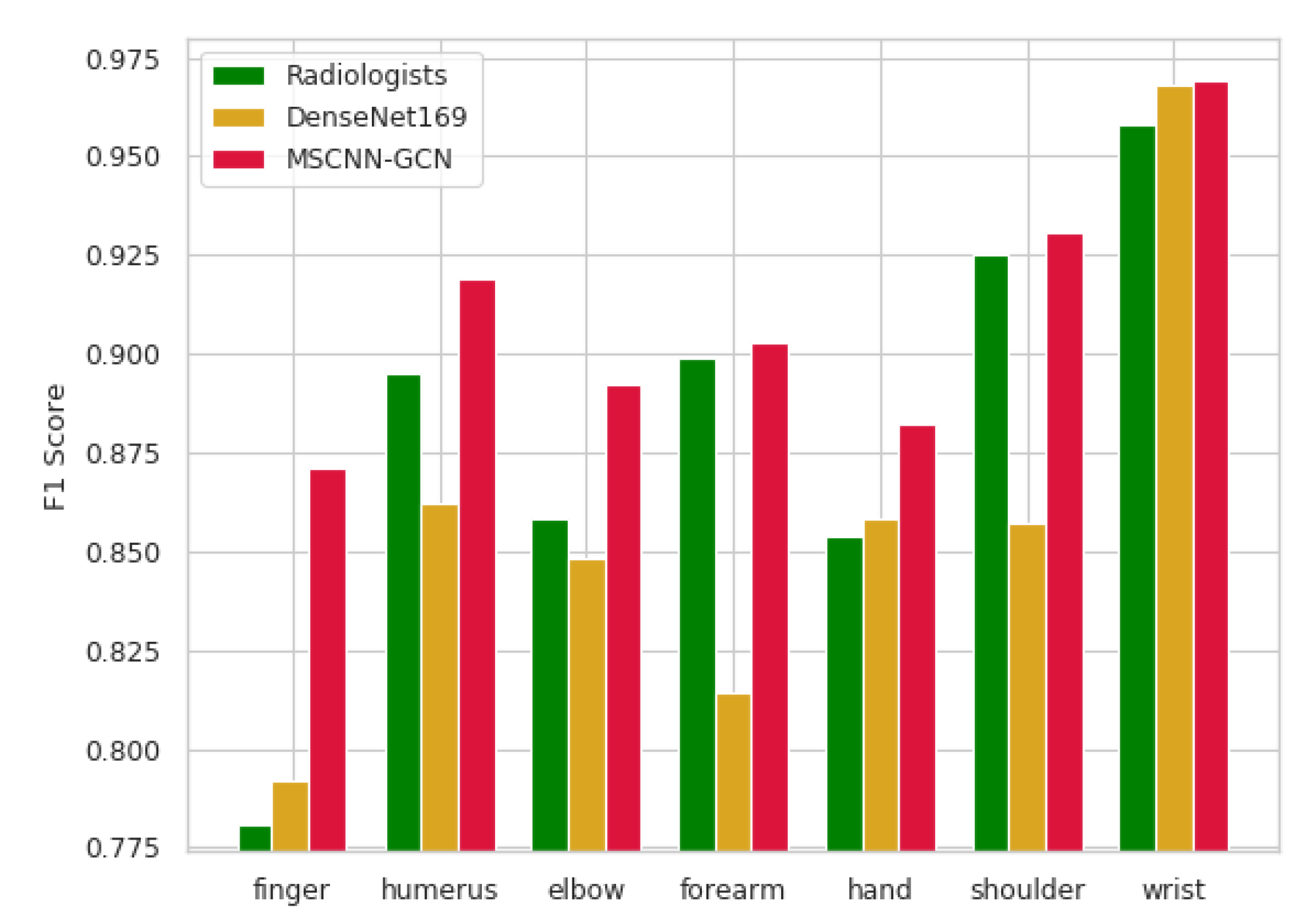
4.3.1. Experiment A: F1 score (MSCNN-GCN, DenseNet169, Radiologists)
4.3.2. Experiment B-Kappa Score (MSCNN-GCN, CapsNet and DenseNet169)
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CNN | Convolution Neural Network |
| MSCNN | Multi-Scale Convolution Neural Network |
| GCN | Graph Convolution Network |
| CT | Computed Tomography |
| MRI | Magnetic Resonance Imaging |
| DenseNet | Densely Connected Neural Network |
| ResNet | Residual Neural Network |
| HRNet | High Resolution Neural Network |
| MAP | Mean Average Precision |
References
- Woolf, A.D.; Pfleger, B. Burden of major musculoskeletal conditions. Bull. World Health Organ. 2003, 81, 646–656. [Google Scholar]
- Vahedi, G.; Kanno, Y.; Furumoto, Y.; Jiang, K.; Parker, S.C.; Erdos, M.R.; Davis, S.R.; Roychoudhuri, R.; Restifo, N.P.; Gadina, M.; et al. Super-enhancers delineate disease-associated regulatory nodes in T cells. Nature 2015, 520, 558–562. [Google Scholar] [CrossRef]
- Manaster, B.J.; May, D.A.; Disler, D.G. Musculoskeletal Imaging: The Requisites E-Book; Elsevier Health Sciences: Philadelphia, PA, USA, 2013. [Google Scholar]
- Al-antari, M.A.; Al-masni, M.A.; Choi, M.T.; Han, S.M.; Kim, T.S. A fully integrated computer-aided diagnosis system for digital X-ray mammograms via deep learning detection, segmentation, and classification. Int. J. Med. Inf. 2018, 117, 44–54. [Google Scholar] [CrossRef]
- Hind, K.; Slater, G.; Oldroyd, B.; Lees, M.; Thurlow, S.; Barlow, M.; Shepherd, J. Interpretation of dual-energy X-ray Absorptiometry-Derived body composition change in athletes: A review and recommendations for best practice. J. Clin. Densitom. 2018, 21, 429–443. [Google Scholar] [CrossRef]
- Mallinson, P.I.; Coupal, T.M.; McLaughlin, P.D.; Nicolaou, S.; Munk, P.L.; Ouellette, H.A. Dual-energy CT for the musculoskeletal system. Radiology 2016, 281, 690–707. [Google Scholar] [CrossRef] [PubMed]
- Kogan, F.; Broski, S.M.; Yoon, D.; Gold, G.E. Applications of PET-MRI in musculoskeletal disease. J. Magn. Reson. Imaging 2018, 48, 27–47. [Google Scholar] [CrossRef] [PubMed]
- Beaulieu, J.; Dutilleul, P. Applications of computed tomography (CT) scanning technology in forest research: A timely update and review. Can. J. For. Res. 2019, 49, 1173–1188. [Google Scholar] [CrossRef]
- Wolf, M.; Wolf, C.; Weber, M. Neurogenic myopathies and imaging of muscle denervation. Radiologe 2017, 57, 1038–1051. [Google Scholar] [CrossRef] [PubMed]
- Wei, H.; Fang, Y.; Mulligan, P.; Chuirazzi, W.; Fang, H.H.; Wang, C.; Ecker, B.R.; Gao, Y.; Loi, M.A.; Cao, L.; et al. Sensitive X-ray detectors made of methylammonium lead tribromide perovskite single crystals. Nat. Photonics 2016, 10, 333. [Google Scholar] [CrossRef]
- Babar, P.; Lokhande, A.; Pawar, B.; Gang, M.; Jo, E.; Go, C.; Suryawanshi, M.; Pawar, S.; Kim, J.H. Electrocatalytic performance evaluation of cobalt hydroxide and cobalt oxide thin films for oxygen evolution reaction. Appl. Surf. Sci. 2018, 427, 253–259. [Google Scholar] [CrossRef]
- Kumar, A.; Kim, J.; Lyndon, D.; Fulham, M.; Feng, D. An ensemble of fine-tuned convolutional neural networks for medical image classification. IEEE J. Biomed. Health. Inf. 2016, 21, 31–40. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neu. Inf. Pro. Sys. 2012, 1, 1097–1105. [Google Scholar] [CrossRef]
- Shin, H.C.; Roth, H.R.; Gao, M.; Lu, L.; Xu, Z.; Nogues, I.; Yao, J.; Mollura, D.; Summers, R.M. Deep convolutional neural networks for computer-aided detection: CNN architectures, dataset characteristics and transfer learning. IEEE Trans. Med. Imaging 2016, 35, 1285–1298. [Google Scholar] [CrossRef]
- Litjens, G.; Kooi, T.; Bejnordi, B.E.; Setio, A.A.A.; Ciompi, F.; Ghafoorian, M.; Van Der Laak, J.A.; Van Ginneken, B.; Sánchez, C.I. A survey on deep learning in medical image analysis. Med. Image Anal. 2017, 42, 60–88. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Wu, Z.; Shen, C.; Van Den Hengel, A. Wider or deeper: Revisiting the resnet model for visual recognition. Pattern Recognit. 2019, 90, 119–133. [Google Scholar] [CrossRef]
- Leibig, C.; Allken, V.; Ayhan, M.S.; Berens, P.; Wahl, S. Leveraging uncertainty information from deep neural networks for disease detection. Sci. Rep. 2017, 7, 1–14. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Rajpurkar, P.; Irvin, J.; Bagul, A.; Ding, D.; Duan, T.; Mehta, H.; Yang, B.; Zhu, K.; Laird, D.; Ball, R.; et al. Mura dataset: Towards radiologist-level abnormality detection in musculoskeletal radiographs. arXiv 2017, arXiv:1712.06957. [Google Scholar]
- Murphree, D.H.; Ngufor, C. Transfer learning for melanoma detection: Participation in ISIC 2017 skin lesion classification challenge. arXiv 2017, arXiv:1703.05235. [Google Scholar]
- Sun, K.; Xiao, B.; Liu, D.; Wang, J. Deep high-resolution representation learning for human pose estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 5693–5703. [Google Scholar]
- Voulodimos, A.; Doulamis, N.; Doulamis, A.; Protopapadakis, E. Deep learning for computer vision: A brief review. Comput. Intell. Neurosci. 2018, 2018. [Google Scholar] [CrossRef]
- Zhang, Z.; Cui, P.; Zhu, W. Deep learning on graphs: A survey. arXiv 2018, arXiv:1812.04202. [Google Scholar] [CrossRef]
- Chen, Z.M.; Wei, X.S.; Wang, P.; Guo, Y. Multi-label image recognition with graph convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 5177–5186. [Google Scholar]
- Bruna, J.; Zaremba, W.; Szlam, A.; Lecun, Y. Spectral networks and locally connected networks on graphs. In Proceedings of the International Conference on Learning Representations (ICLR2014), CBLS, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. Adv. Neu. Inf. Pro. Sys. 2016, 25, 3844–3852. [Google Scholar]
- Tang, H.; Ortis, A.; Battiato, S. The Impact of Padding on Image Classification by Using Pre-trained Convolutional Neural Networks. In Proceedings of the International Conference on Image Analysis and Processing, Trento, Italy, 9–13 September 2019; pp. 337–344. [Google Scholar]
- Stanfordmlgroup. MURA Dataset: Towards Radiologist-Level Abnormality Detection in Musculoskeletal Radiographs. Available online: http://stanfordmlgroup.github.io/competitions/mura/ (accessed on 12 March 2020).
- McHugh, M.L. Interrater reliability: The kappa statistic. Biochem. Med. (Zagreb) 2012, 22, 276–282. [Google Scholar] [CrossRef] [PubMed]
- Saif, A.; Shahnaz, C.; Zhu, W.P.; Ahmad, M.O. Abnormality Detection in Musculoskeletal Radiographs Using Capsule Network. IEEE Access 2019, 7, 81494–81503. [Google Scholar] [CrossRef]


| Study | Train | Validation | Total | ||
|---|---|---|---|---|---|
| Normal | Abnormal | Normal | Abnormal | ||
| Elbow | 1094 | 660 | 92 | 66 | 1912 |
| Finger | 1280 | 655 | 92 | 83 | 2110 |
| Hand | 1497 | 521 | 101 | 66 | 2185 |
| Humerus | 321 | 271 | 68 | 67 | 727 |
| Forearm | 590 | 287 | 69 | 64 | 1010 |
| Shoulder | 1364 | 1457 | 99 | 95 | 3015 |
| Wrist | 2134 | 1326 | 140 | 97 | 3697 |
| Total | 8280 | 5177 | 661 | 538 | 14656 |
| Image | Train-Validation Accuracy | Validation Accuracy | Validation Balanced Accuracy |
|---|---|---|---|
| Finger | 93.90% | 87.08% | 87.53% |
| Humerus | 93.51% | 92.19% | 92.06% |
| Elbow | 93.19% | 89.25% | 89.70% |
| Forearm | 94.19% | 89.82% | 90.24% |
| Hand | 93.72% | 91.88% | 92.47% |
| Shoulder | 94.89% | 93.12% | 93.36% |
| Wrist | 96.94% | 95.20% | 95.27% |
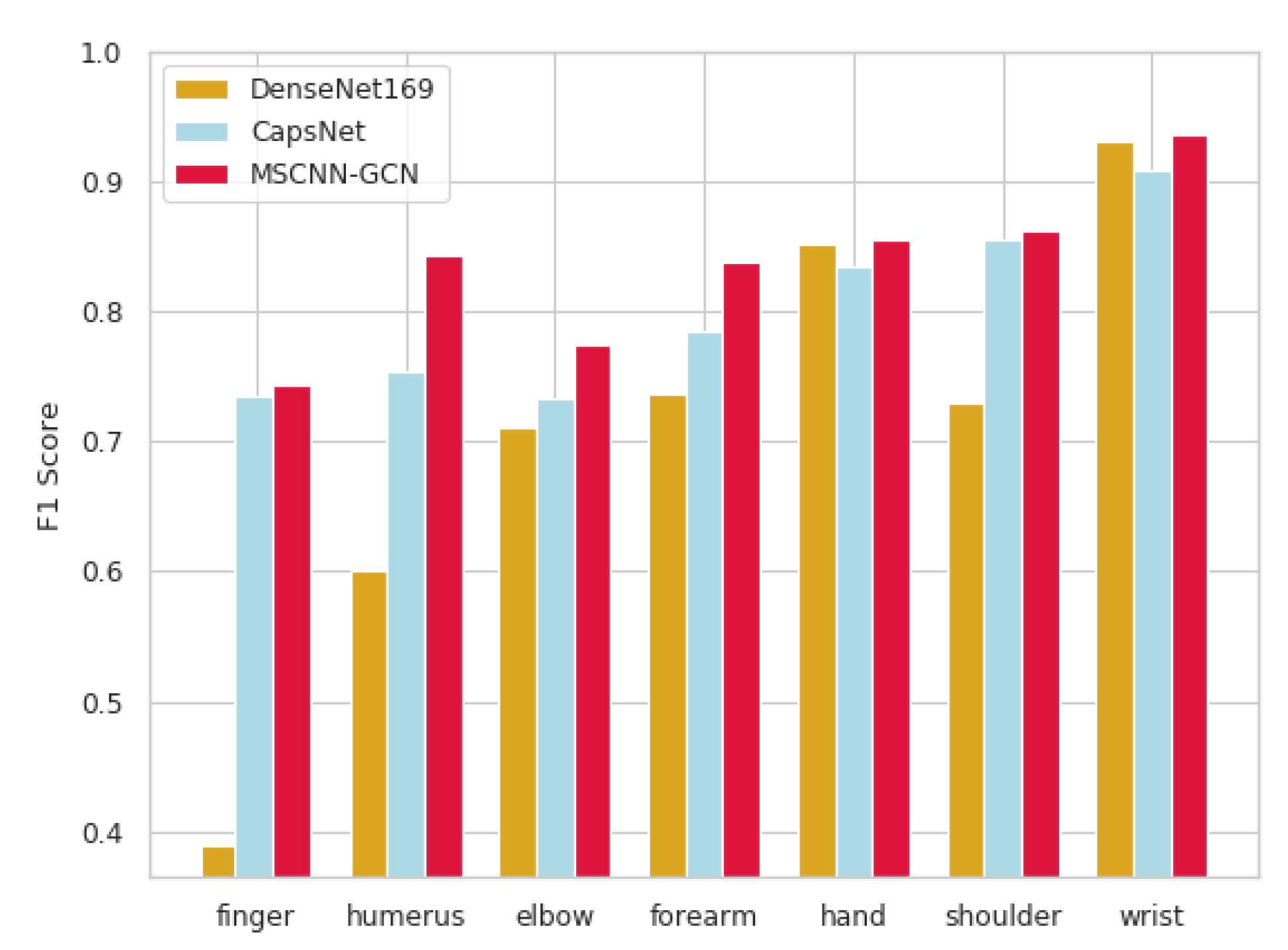
| Image | DenseNet169 (95% CI) | CapsNet (95% CI) | MSCNN-GCN (95% CI) |
|---|---|---|---|
| Finger | 0.389 (0.446, 0.332) | 0.735 (0.959, 0.512) | 0.744 (0.806, 0.682) |
| Humerus | 0.600 (0.642, 0.558) | 0.754 (0.896, 0.612) | 0.843 (0.936, 0.749) |
| Elbow | 0.710 (0.745, 0.674) | 0.733 (0.754, 0.713) | 0.774 (0.831, 0.717) |
| Forearm | 0.737 (0.766, 0.707) | 0.785 (0.795, 0.775) | 0.837 (0.912, 0.762) |
| Hand | 0.851 (0.871, 0.830) | 0.835 (0.856, 0.881) | 0.855 (0.897, 0.814) |
| Shoulder | 0.729 (0.760, 0.697) | 0.856 (0.876, 0.836) | 0.862 (1.000, 0.678) |
| Wrist | 0.931 (0.940, 0.922) | 0.908 (0.917, 0.898) | 0.936 (0.948, 0.924) |
| Average | 0.705 (0.700, 0.710) | 0.801 (0.865, 0.738) | 0.836 (0.911, 0.761) |
| Image | Radiologists(95% CI) | DenseNet169(95% CI) | MSCNN-GCN(95% CI) |
|---|---|---|---|
| Finger | 0.781 (0.638, 0.871) | 0.792 (0.588, 0.933) | 0.871 (0.842, 0.900) |
| Humerus | 0.895 (0.774, 0.976) | 0.862 (0.709, 0.968) | 0.919 (0.875, 0.968) |
| Elbow | 0.858 (0.707, 0.959) | 0.848 (0.691, 0.955) | 0.892 (0.865, 0.920) |
| Forearm | 0.899 (0.804, 0.960) | 0.814 (0.633, 0.942) | 0.903 (0.777, 0.989) |
| Hand | 0.854 (0.676, 0.958) | 0.858 (0.658, 0.978) | 0.882 (0.833, 0.952) |
| Shoulder | 0.925 (0.811, 0.989) | 0.857 (0.667, 0.974) | 0.931 (0.838, 1.000) |
| Wrist | 0.958 (0.908, 0.988) | 0.968 (0.889, 1.000) | 0.969 (0.912, 0.991) |
| Average | 0.884 (0.843, 0.918) | 0.859 (0.804, 0.905) | 0.909 (0.849, 0.960) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, S.; Gu, Y. Towards Robust and Accurate Detection of Abnormalities in Musculoskeletal Radiographs with a Multi-Network Model. Sensors 2020, 20, 3153. https://doi.org/10.3390/s20113153
Liang S, Gu Y. Towards Robust and Accurate Detection of Abnormalities in Musculoskeletal Radiographs with a Multi-Network Model. Sensors. 2020; 20(11):3153. https://doi.org/10.3390/s20113153
Chicago/Turabian StyleLiang, Shuang, and Yu Gu. 2020. "Towards Robust and Accurate Detection of Abnormalities in Musculoskeletal Radiographs with a Multi-Network Model" Sensors 20, no. 11: 3153. https://doi.org/10.3390/s20113153
APA StyleLiang, S., & Gu, Y. (2020). Towards Robust and Accurate Detection of Abnormalities in Musculoskeletal Radiographs with a Multi-Network Model. Sensors, 20(11), 3153. https://doi.org/10.3390/s20113153






