Quality Assessment of the Neural Algorithms on the Example of EIT-UST Hybrid Tomography
Abstract
:1. Introduction
1.1. Literature Review
1.2. Goal and Novelties
2. Materials and Methods
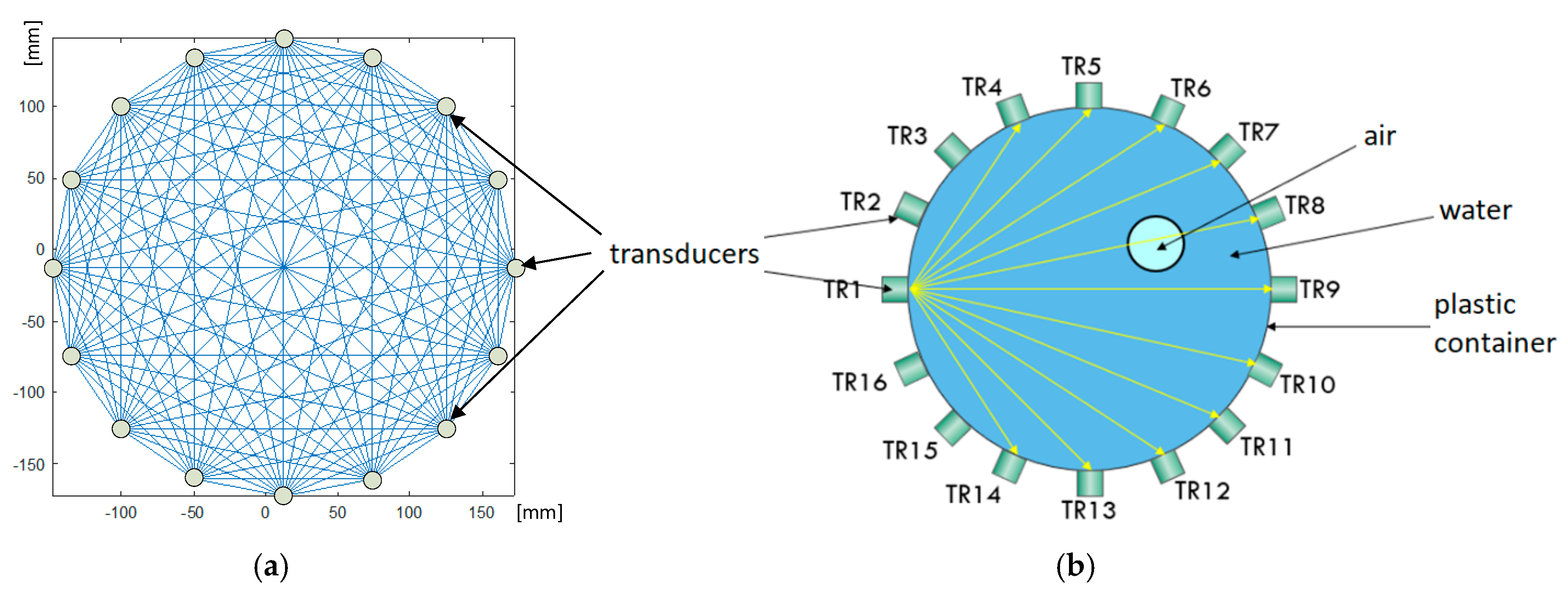
2.1. Hardware
2.2. Electrical Impedance Tomography (EIT)
2.3. Ultrasonic Tomography (UST)
2.4. EIT-UST Hybrid Algorithm Principle
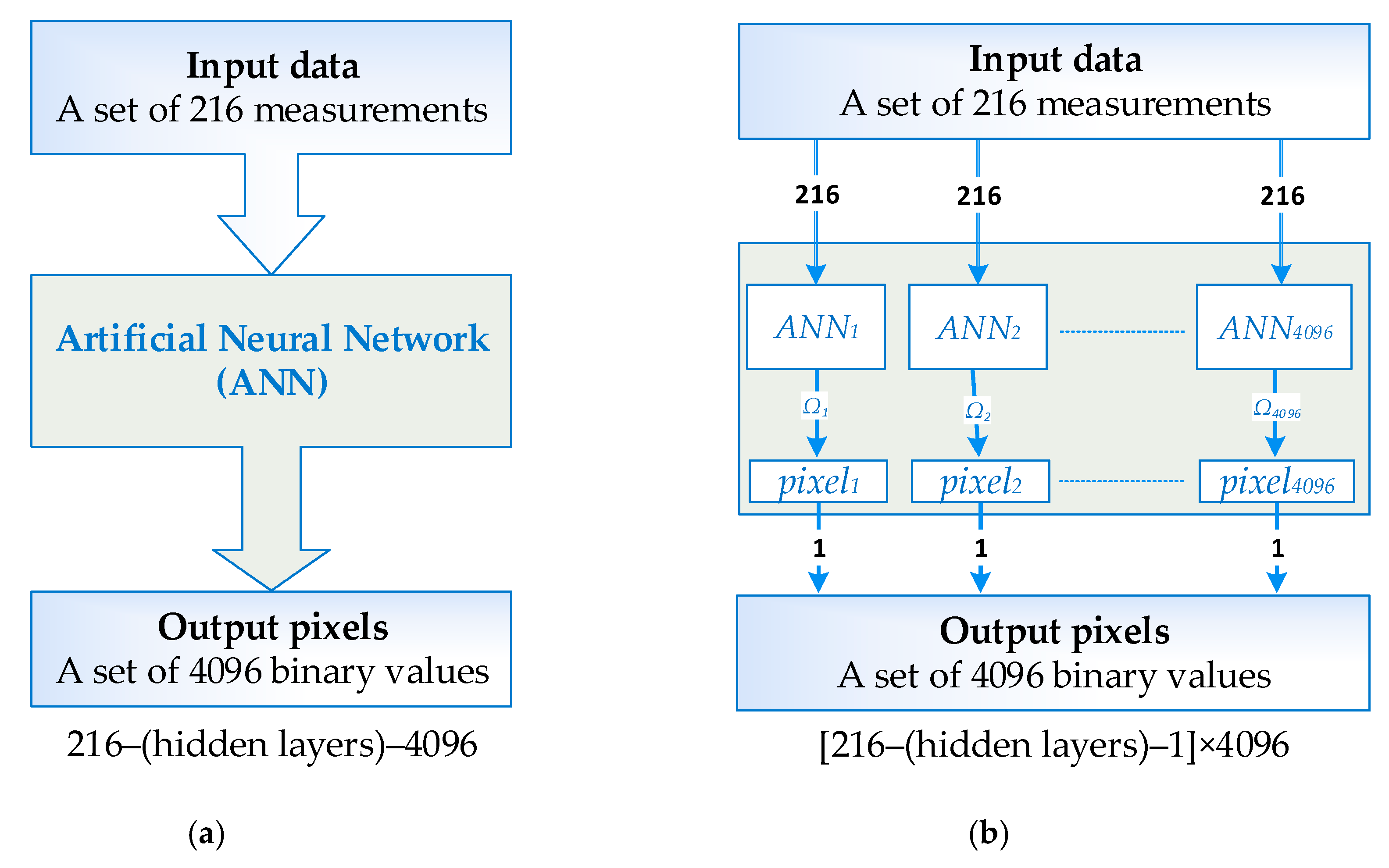
2.5. Neural Networks Training
2.5.1. Data Preparation
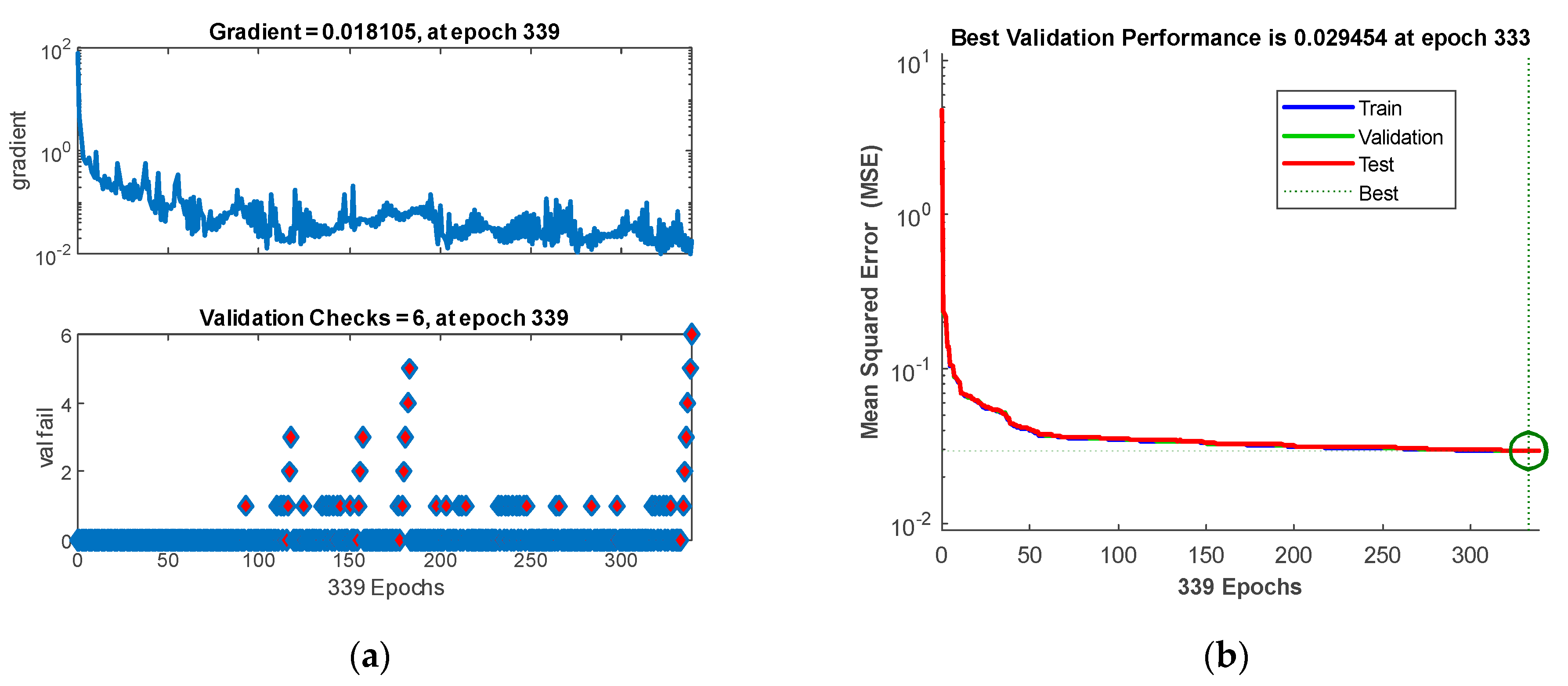
2.5.2. MANN Parameters and Training
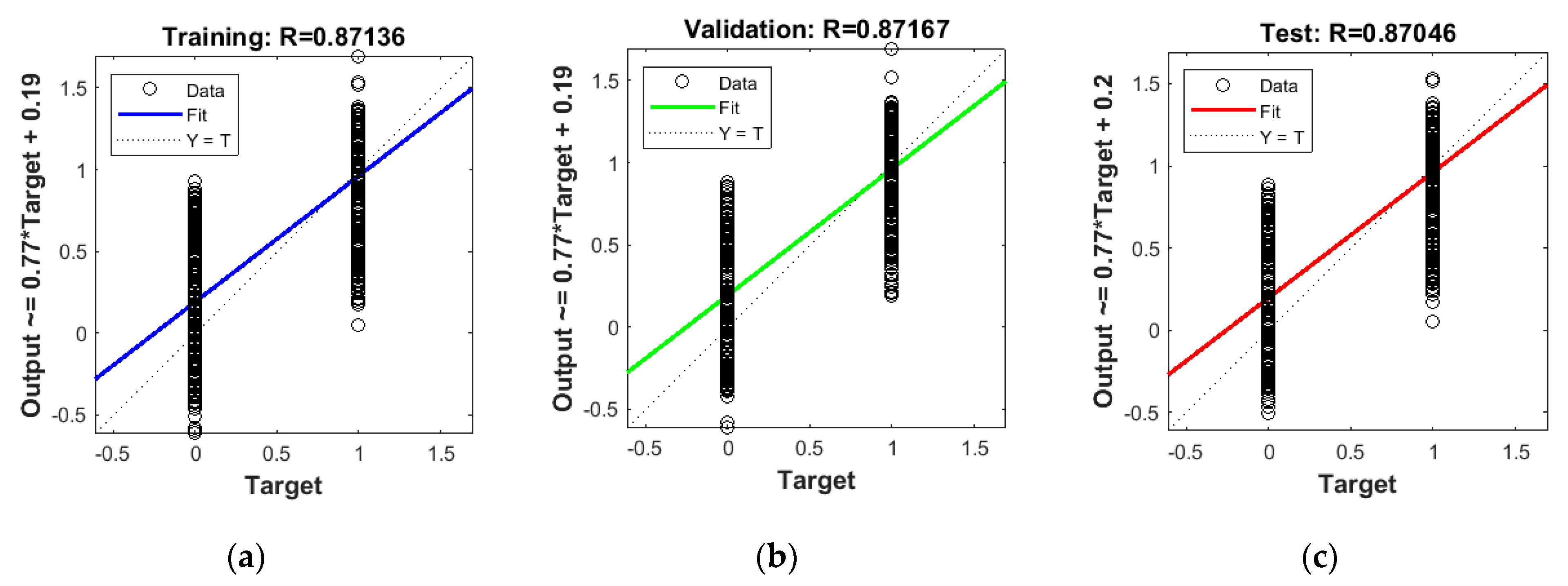
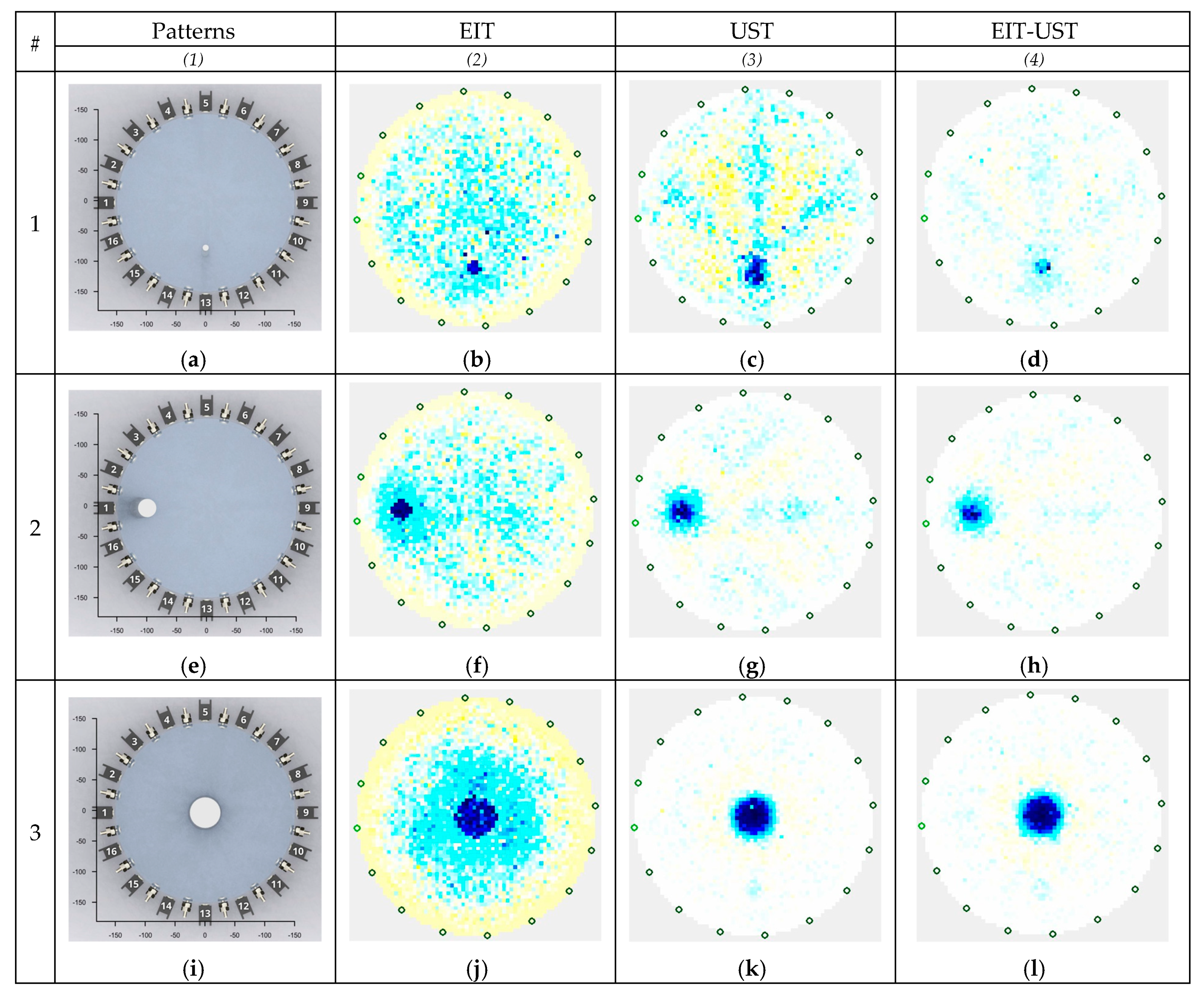
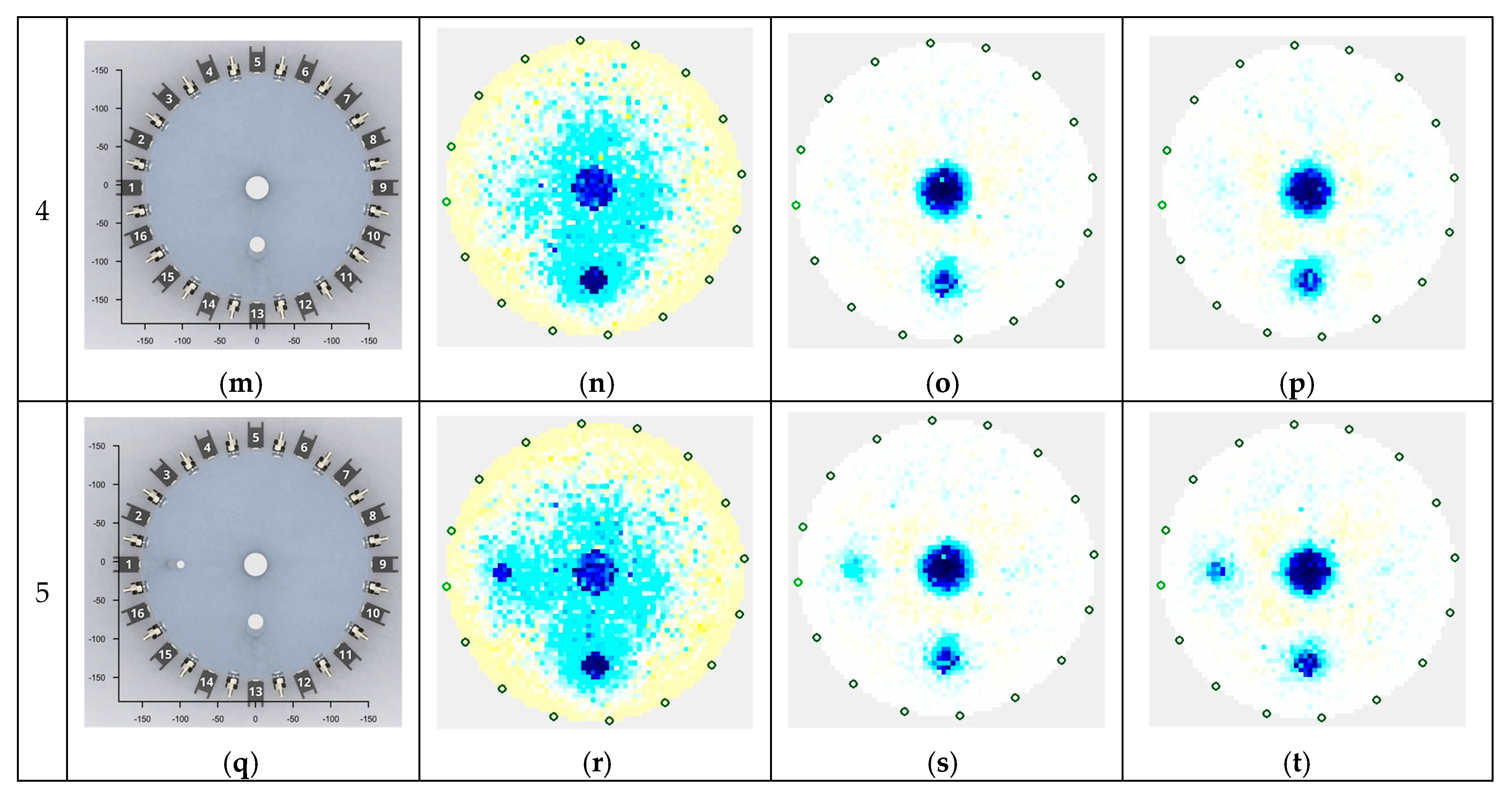
3. Results
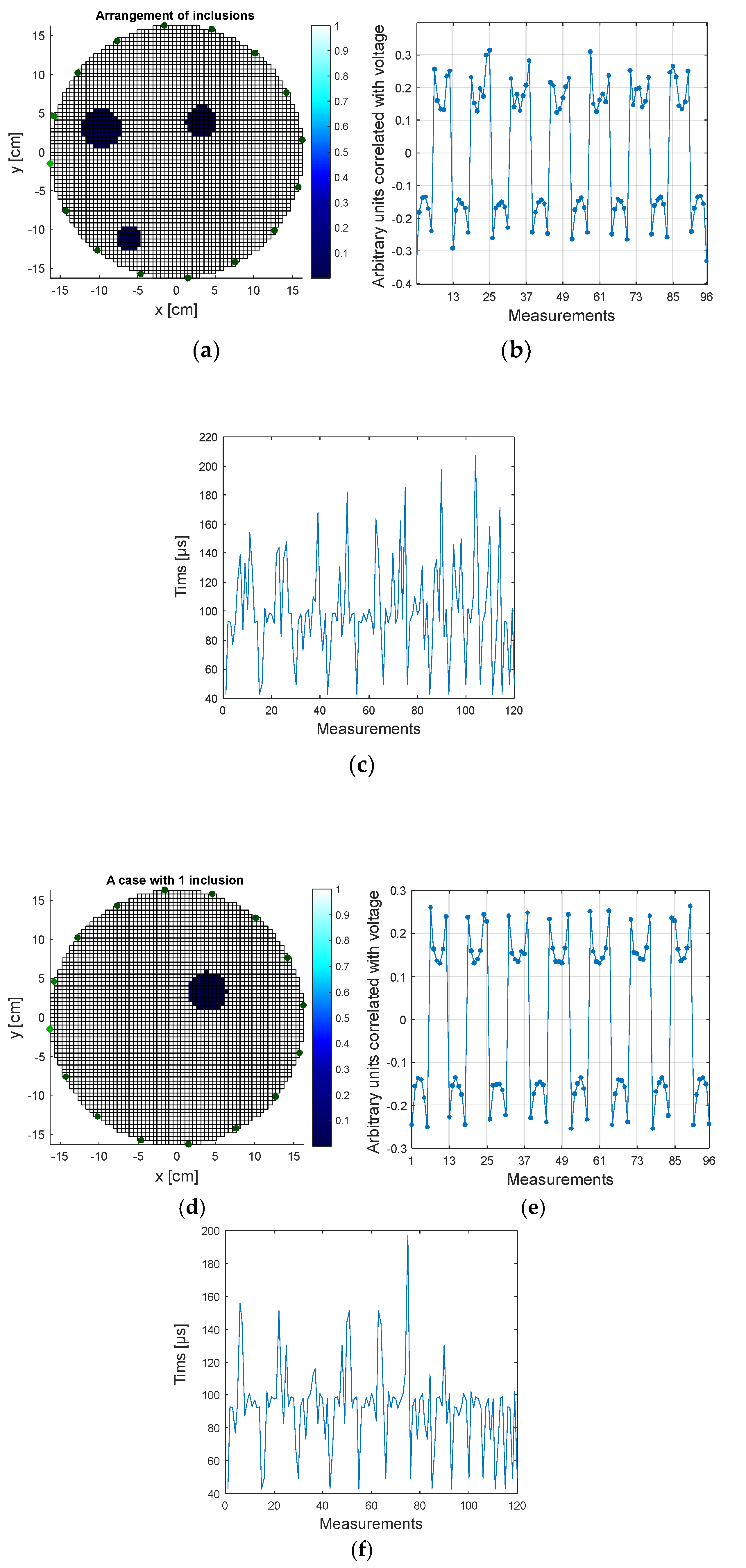
3.1. Tomographic Reconstructions
3.2. Comparative Assessment of Methods and Algorithms
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rymarczyk, T.; Kłosowski, G. Innovative methods of neural reconstruction for tomographic images in maintenance of tank industrial reactors. Eksploat. i Niezawodn. Maint. Reliab. 2019, 21, 261–267. [Google Scholar] [CrossRef]
- Abdullah, B.; Adesina, A.A. Evaluation of gas-liquid mass transfer in gas-induced stirred tank reactor using electrical resistance tomography. J. Chem. Technol. Biotechnol. 2017, 92, 2123–2133. [Google Scholar] [CrossRef]
- Antosz, K.; Pasko, L.; Gola, A. The Use of Intelligent Systems to Support the Decision-Making Process in Lean Maintenance Management. IFAC-PapersOnLine 2019, 52, 148–153. [Google Scholar] [CrossRef]
- Kluz, R.; Antosz, K.; Trzepieciński, T.; Gola, A. Predicting the error of a Robot’s positioning repeatability with artificial neural networks. In Proceedings of the International Symposium on Distributed Computing and Artificial Intelligence, Ávila, Spain, 26–28 June 2019; pp. 41–48. [Google Scholar]
- Babout, L.; Grudzień, K.; Wiącek, J.; Niedostatkiewicz, M.; Karpiński, B.; Szkodo, M. Selection of material for X-ray tomography analysis and DEM simulations: Comparison between granular materials of biological and non-biological origins. Granul. Matter 2018, 20, 38. [Google Scholar] [CrossRef] [Green Version]
- Romanowski, A. Contextual Processing of Electrical Capacitance Tomography Measurement Data for Temporal Modeling of Pneumatic Conveying Process. In Proceedings of the 2018 Federated Conference on Computer Science and Information Systems (FedCSIS), Poznan, Poland, 9–12 September 2018; pp. 283–286. [Google Scholar]
- Grudzien, K.; Chaniecki, Z.; Romanowski, A.; Sankowski, D.; Nowakowski, J.; Niedostatkiewicz, M. Application of twin-plane ECT sensor for identification of the internal imperfections inside concrete beams. In Proceedings of the 2016 IEEE International Instrumentation and Measurement Technology Conference Proceedings, Taipei, Taiwan, 23–26 May 2016; pp. 1–6. [Google Scholar]
- Kryszyn, J.; Smolik, W.T.; Radzik, B.; Olszewski, T.; Szabatin, R. Switchless charge-discharge circuit for electrical capacitance tomography. Meas. Sci. Technol. 2014, 25, 115009. [Google Scholar] [CrossRef]
- Kryszyn, J.; Smolik, W. Toolbox for 3D modelling and image reconstruction in electrical capacitance tomography. Inform. Control Meas. Econ. Environ. Prot. 2017, 7, 137–145. [Google Scholar] [CrossRef]
- Majchrowicz, M.; Kapusta, P.; Jackowska-Strumiłło, L.; Sankowski, D. Acceleration of image reconstruction process in the electrical capacitance tomography 3D in heterogeneous, multi-GPU system. Inform. Control Meas. Econ. Environ. Prot. 2017, 7, 37–41. [Google Scholar] [CrossRef]
- Romanowski, A. Big Data-Driven Contextual Processing Methods for Electrical Capacitance Tomography. IEEE Trans. Ind. Inform. 2019, 15, 1609–1618. [Google Scholar] [CrossRef]
- Mei, I.L.S.; Ismail, I.; Shafquet, A.; Abdullah, B. Real-time monitoring and measurement of wax deposition in pipelines via non-invasive electrical capacitance tomography. Meas. Sci. Technol. 2016, 27, 025403. [Google Scholar] [CrossRef]
- Dusek, J.; Hladky, D.; Mikulka, J. Electrical impedance tomography methods and algorithms processed with a GPU. In Proceedings of the 2017 Progress In Electromagnetics Research Symposium - Spring (PIERS), St. Petersburg, Russia, 22–25 May 2017; pp. 1710–1714. [Google Scholar]
- Kłosowski, G.; Rymarczyk, T. Using neural networks and deep learning algorithms in electrical impedance tomography. Inform. Autom. Pomiary Gospod. Ochr. Śr. 2017, 7, 99–102. [Google Scholar] [CrossRef]
- Ziolkowski, M.; Gratkowski, S.; Zywica, A.R. Analytical and numerical models of the magnetoacoustic tomography with magnetic induction. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2018, 37, 538–548. [Google Scholar] [CrossRef]
- Kłosowski, G.; Rymarczyk, T.; Kania, K.; Świć, A.; Cieplak, T. Maintenance of industrial reactors supported by deep learning driven ultrasound tomography. Eksploat. Niezawodn. Maint. Reliab. 2020, 22, 138–147. [Google Scholar] [CrossRef]
- Rymarczyk, T.; Adamkiewicz, P.; Polakowski, K.; Sikora, J. Effective ultrasound and radio tomography imaging algorithm for two-dimensional problems. Przegląd Elektrotechniczny 2018, 94, 62–69. [Google Scholar]
- Ma, J.; Wu, F.; Zhu, J.; Xu, D.; Kong, D. A pre-trained convolutional neural network based method for thyroid nodule diagnosis. Ultrasonics 2017, 73, 221–230. [Google Scholar] [CrossRef] [PubMed]
- Rymarczyk, T.; Kłosowski, G.; Kozłowski, E. A Non-Destructive System Based on Electrical Tomography and Machine Learning to Analyze the Moisture of Buildings. Sensors 2018, 18, 2285. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Poudel, J.; Lou, Y.; Anastasio, M.A. A survey of computational frameworks for solving the acoustic inverse problem in three-dimensional photoacoustic computed tomography. Phys. Med. Biol. 2019, 64, 14TR01. [Google Scholar] [CrossRef] [PubMed]
- Rymarczyk, T.; Kozłowski, E.; Kłosowski, G.; Rymarczyk, P.; Adamkiewicz, P.; Sikora, J. Elastic net method in the image reconstruction infiltration of water in the embankment. In Proceedings of the 2018 Applications of Electromagnetics in Modern Techniques and Medicine (PTZE), Racławice, Poland, 9–12 September 2018; pp. 212–215. [Google Scholar]
- Rymarczyk, T.; Kłosowski, G.; Kozłowski, E.; Tchórzewski, P. Comparison of Selected Machine Learning Algorithms for Industrial Electrical Tomography. Sensors 2019, 19, 1521. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sánchez Lasheras, J.E.; González Donquiles, C.; García Nieto, P.J.; Jiménez Moleon, J.J.; Salas, D.; Suárez Gómez, S.L.; de la Torre, A.J.M.; González-Nuevo, J.; Bonavera, L.; Carballido Landeira, J.; et al. A methodology for detecting relevant single nucleotide polymorphism in prostate cancer with multivariate adaptive regression splines and backpropagation artificial neural networks. Neural Comput. Appl. 2020, 32, 1231–1238. [Google Scholar] [CrossRef]
- Vališ, D.; Mazurkiewicz, D. Application of selected Levy processes for degradation modelling of long range mine belt using real-time data. Arch. Civ. Mech. Eng. 2018, 18, 1430–1440. [Google Scholar] [CrossRef]
- Kłosowski, G.; Kozłowski, E.; Gola, A. Integer Linear Programming in Optimization of Waste After Cutting in the Furniture Manufacturing. In Proceedings of the International Conference on Intelligent Systems in Production Engineering and Maintenance, Wroclaw, Poland, 28–29 September 2017; pp. 260–270. [Google Scholar]
- Kozłowski, E.; Mazurkiewicz, D.; Kowalska, B.; Kowalski, D. Binary Linear Programming as a Decision-Making Aid for Water Intake Operators. In Proceedings of the International Conference on Intelligent Systems in Production Engineering and Maintenance, Wroclaw, Poland, 28–29 September 2017; pp. 199–208. [Google Scholar]
- Lopato, P.; Chady, T.; Sikora, R.; Gratkowski, S.; Ziolkowski, M. Full wave numerical modelling of terahertz systems for nondestructive evaluation of dielectric structures. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2013, 32, 736–749. [Google Scholar] [CrossRef]
- Gola, A.; Kłosowski, G. Application of Fuzzy Logic and Genetic Algorithms in Automated Works Transport Organization. In Proceedings of the International Symposium on Distributed Computing and Artificial Intelligence, Porto, Portugal, 21–23 June 2017; pp. 29–36. [Google Scholar]
- Kosinski, T.; Obaid, M.; Wozniak, P.W.; Fjeld, M.; Kucharski, J. A fuzzy data-based model for Human-Robot Proxemics. In Proceedings of the 2016 25th IEEE International Symposium on Robot and Human Interactive Communication (RO-MAN), New York, NY, USA, 26–31 August 2016; pp. 335–340. [Google Scholar]
- Fraczyk, A.; Kucharski, J. Surface temperature control of a rotating cylinder heated by moving inductors. Appl. Therm. Eng. 2017, 125, 767–779. [Google Scholar] [CrossRef]
- Pawłowski, S.; Plewako, J.; Korzeniewska, E. Analysis of flow field distribution in a thin conductive layer with an elliptical defect. Prz. Elektrotechniczny 2020, 96, 234–237. [Google Scholar]
- Szczesny, A.; Korzeniewska, E. Selection of the method for the earthing resistance measurement. Przegląd Elektrotechniczny 2018, 94, 178–181. [Google Scholar]
- Farha, M. Endarko Combined algorithm of total variation and gauss-Newton for image reconstruction in two-dimensional Electrical Impedance Tomography (EIT). In Proceedings of the 2017 International Seminar on Sensors, Instrumentation, Measurement and Metrology (ISSIMM), Surabaya, Indonesia, 25–26 August 2017; pp. 37–41. [Google Scholar]
- Yang, Y.; Jia, J.; Polydorides, N.; McCann, H. Effect of structured packing on EIT image reconstruction. In Proceedings of the 2014 IEEE International Conference on Imaging Systems and Techniques (IST) Proceedings, Santorini, Greece, 14–17 October 2014; pp. 53–58. [Google Scholar]
- Wang, H.; Wang, C.; Yin, W. A pre-iteration method for the inverse problem in electrical impedance tomography. IEEE Trans. Instrum. Meas. 2004, 53, 1093–1096. [Google Scholar] [CrossRef]
- Li, T.; Kao, T.J.; Isaacson, D.; Newell, J.C.; Saulnier, G.J. Adaptive Kaczmarz method for image reconstruction in electrical impedance tomography. Physiol. Meas. 2013, 34, 595. [Google Scholar] [CrossRef] [Green Version]
- González, G.; Kolehmainen, V.; Seppänen, A. Isotropic and anisotropic total variation regularization in electrical impedance tomography. Comput. Math. Appl. 2017, 74, 564–576. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, X. A real-time EIT imaging system based on the split augmented Lagrangian shrinkage algorithm. Meas. J. Int. Meas. Confed. 2017, 110, 27–42. [Google Scholar] [CrossRef]
- Liu, X.; Yao, J.; Zhao, T.; Obara, H.; Cui, Y.; Takei, M. Image Reconstruction under Contact Impedance Effect in Micro Electrical Impedance Tomography Sensors. IEEE Trans. Biomed. Circuits Syst. 2018, 12, 623–631. [Google Scholar] [CrossRef]
- Rymarczyk, T.; Klosowski, G.; Cieplak, T.; Kozlowski, E.; Kania, K. Application of a regressive neural network with autoencoder for monochromatic images in ultrasound tomography. In Proceedings of the 2019 Applications of Electromagnetics in Modern Engineering and Medicine (PTZE), Janow Podlaski, Poland, 9–12 June 2019; pp. 156–160. [Google Scholar]
- Zeng, X.; Leung, M.R.; Zeev-Ben-Mordehai, T.; Xu, M. A convolutional autoencoder approach for mining features in cellular electron cryo-tomograms and weakly supervised coarse segmentation. J. Struct. Biol. 2018, 202, 150–160. [Google Scholar] [CrossRef]
- Rymarczyk, T.; Kłosowski, G. The use of elastic net and neural networks in industrial process tomography. Prz. Elektrotechniczny 2019, 95, 59–62. [Google Scholar] [CrossRef]
- Arevalo, J.; González, F.A.; Ramos-Pollán, R.; Oliveira, J.L.; Guevara Lopez, M.A. Representation learning for mammography mass lesion classification with convolutional neural networks. Comput. Methods Programs Biomed. 2016, 127, 248–257. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Song, J.; Xia, H.; Li, Y.; Liu, G. Three-dimensional model of conductivity imaging for magneto-acousto-electrical tomography. J. Appl. Phys. 2020, 127, 104701. [Google Scholar] [CrossRef]
- Rymarczyk, T.; Kozłowski, E.; Kłosowski, G. Electrical impedance tomography in 3D flood embankments testing – elastic net approach. Trans. Inst. Meas. Control 2019, 42, 680–690. [Google Scholar] [CrossRef]
- Szumowski, J.; Oleszek, M.; Rymarczyk, T.; Adamkiewicz, P.; Sikora, J. Hybrid tomographic device for acquisition of electrical tomography data. In Proceedings of the 2018 International Interdisciplinary PhD Workshop (IIPhDW 2018), Swinoujscie, Poland, 9–12 May 2018; pp. 162–164. [Google Scholar]
- Leshno, M.; Lin, V.Y.; Pinkus, A.; Schocken, S. Multilayer feedforward networks with a nonpolynomial activation function can approximate any function. Neural Netw. 1993, 6, 861–867. [Google Scholar] [CrossRef] [Green Version]
- Raskutti, G.; Wainwright, M.J.; Yu, B. Early stopping and non-parametric regression: An optimal data-dependent stopping rule. J. Mach. Learn. Res. 2014, 15, 335–366. [Google Scholar]
- Nombo, J.; Mwambela, A.; Kisangiri, M. A Grey Level Fitting Mechanism based on Gompertz Function for Two Phase Flow Imaging using Electrical Capacitance Tomography Measurement Systems. Int. J. Comput. Appl. 2014, 101, 7–12. [Google Scholar] [CrossRef]







| # | ANN Structure | Number of Training Cases Used | ||
|---|---|---|---|---|
| 1. | 216–100–1 | 21,600 | 152,653 | 24,500 |
| 2. | 96–45–1 | 4224 | 27,809 | 24,500 |
| 3. | 120–55–1 | 6480 | 43,561 | 24,500 |
| 4. | 120–4096–4096 | 884,736 | 174,040,058 | not applied |
| All Cases | Training Set | Validation Set | Testing Set |
|---|---|---|---|
| 100% | 70% | 15% | 15% |
| 35,000 | 24,500 | 5250 | 5250 |
| Set Type | EIT | UST | EIT-UST | |||
|---|---|---|---|---|---|---|
| Evaluation metrics | MSE | R | MSE | R | MSE | R |
| Training set | 0.0652 | 0.73093 | 0.0366 | 0.85855 | 0.0292 | 0.88855 |
| Validation set | 0.0644 | 0.72995 | 0.0370 | 0.85540 | 0.0295 | 0.88726 |
| Testing set | 0.0652 | 0.71986 | 0.0371 | 0.85404 | 0.0297 | 0.88653 |
| Evaluation Metrics | Methods | Tested Cases | Mean | ||||
|---|---|---|---|---|---|---|---|
| #1 | #2 | #3 | #4 | #5 | |||
| DE | EIT | 68.94 | 81.69 | 160.45 | 155.46 | 167.25 | 126.76 |
| UST | 64.22 | 69.73 | 74.14 | 83.67 | 100.34 | 78.42 | |
| EIT-UST | 52.97 | 65.27 | 73.65 | 81.84 | 79.16 | 70.58 | |
| ICC | EIT | 0.9922 | 0.9886 | 0.9551 | 0.9578 | 0.9513 | 0.9690 |
| UST | 0.9924 | 0.9911 | 0.9905 | 0.9879 | 0.9826 | 0.9889 | |
| EIT-UST | 0.9949 | 0.9922 | 0.9906 | 0.9884 | 0.9893 | 0.9911 | |
| RIE | EIT | 0.0483 | 0.0574 | 0.1139 | 0.1103 | 0.1189 | 0.0898 |
| UST | 0.0450 | 0.0490 | 0.0526 | 0.0594 | 0.0713 | 0.0555 | |
| EIT-UST | 0.0371 | 0.0459 | 0.0523 | 0.0581 | 0.0563 | 0.0499 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kłosowski, G.; Rymarczyk, T.; Cieplak, T.; Niderla, K.; Skowron, Ł. Quality Assessment of the Neural Algorithms on the Example of EIT-UST Hybrid Tomography. Sensors 2020, 20, 3324. https://doi.org/10.3390/s20113324
Kłosowski G, Rymarczyk T, Cieplak T, Niderla K, Skowron Ł. Quality Assessment of the Neural Algorithms on the Example of EIT-UST Hybrid Tomography. Sensors. 2020; 20(11):3324. https://doi.org/10.3390/s20113324
Chicago/Turabian StyleKłosowski, Grzegorz, Tomasz Rymarczyk, Tomasz Cieplak, Konrad Niderla, and Łukasz Skowron. 2020. "Quality Assessment of the Neural Algorithms on the Example of EIT-UST Hybrid Tomography" Sensors 20, no. 11: 3324. https://doi.org/10.3390/s20113324
APA StyleKłosowski, G., Rymarczyk, T., Cieplak, T., Niderla, K., & Skowron, Ł. (2020). Quality Assessment of the Neural Algorithms on the Example of EIT-UST Hybrid Tomography. Sensors, 20(11), 3324. https://doi.org/10.3390/s20113324






