Measurement of Shear Strain Field in a Soft Material Using a Sensor System Consisting of Distributed Piezoelectric Polymer Film
Abstract
1. Introduction
2. Soft Material Shear Strain Sensing Methodology
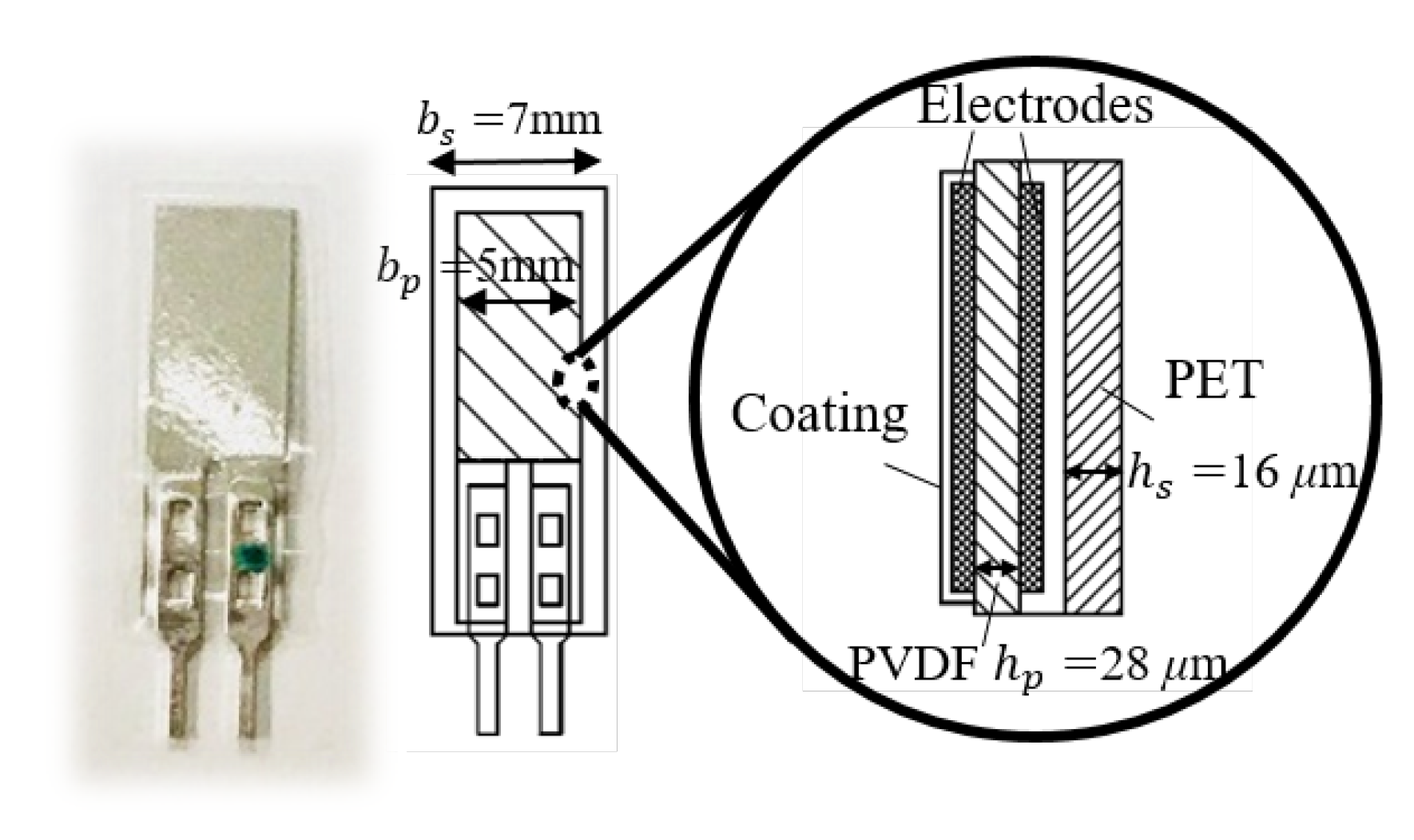
2.1. Sensor System Hardware
2.2. Soft Material Shear Strain Sensing Model
2.3. Signal Conditioning: Charge Amplifier Circuit
3. Numerical Simulation of Shear Strain Field
4. Shear Strain Distribution Measurement
4.1. Experimental Design and Setup
4.2. Calibration
4.3. Measurement Result
5. Discussion
6. Conclusions
7. Patents
Author Contributions
Funding
Conflicts of Interest
References
- Hassan, P.; Verma, G.; Ganguly, R. Soft materials-properties and applications. In Functional Materials: Preparation, Processing and Applications; Elsevier: London, UK, 2011; p. 1. [Google Scholar]
- Mao, X.; Yamada, Y.; Akiyama, Y.; Okamoto, S. Characteristics of Dummy Skin Contact Mechanics During Developing Process of Skin Abrasion Trauma. Tribol. Lett. 2017, 65, 133. [Google Scholar] [CrossRef]
- Bashir, S.J.; Chew, A.L. Mechanical injury to the skin. In Rook’s Textbook of Dermatology, 9th ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2016; pp. 1–37. [Google Scholar]
- Sanders, J.E.; Goldstein, B.S.; Leotta, D.F. Skin response to mechanical stress: Adaptation rather than breakdown-a review of the literature. J. Rehabil. Res. Dev. 1995, 32, 214. [Google Scholar]
- Ito, M.; Pramudita, J.A.; Watanabe, R.; Shimizu, Y.; Tanabe, Y. Investigation of skin laceration threshold under a specific condition: Blade penetration test on porcine skin. J. Mech. Med. Biol. 2017, 17, 1750114. [Google Scholar] [CrossRef]
- Akiyama, Y.; Okamoto, S.; Yamada, Y.; Ishiguro, K. Measurement of contact behavior including slippage of cuff when using wearable physical assistant robot. IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 24, 784–793. [Google Scholar] [CrossRef] [PubMed]
- Mao, X.; Yamada, Y.; Akiyama, Y.; Okamoto, S.; Yoshida, K. Safety verification method for preventing friction blisters during utilization of physical assistant robots. Adv. Robot. 2017, 31, 680–694. [Google Scholar] [CrossRef]
- Naylor, P. Experimental friction blisters. Br. J. Dermatol. 1955, 67, 327–342. [Google Scholar] [CrossRef] [PubMed]
- Naylor, P. The skin surface and friction. Br. J. Dermatol. 1955, 67, 239–248. [Google Scholar] [CrossRef] [PubMed]
- Jacobs, T.; Virk, G.S. ISO 13482-The new safety standard for personal care robots. In Proceedings of the ISR/Robotik 2014 41st International Symposium on Robotics, Munich, Germany, 2–3 June 2014; pp. 1–6. [Google Scholar]
- Grey, J.E.; Harding, K.G.; Enoch, S. Pressure ulcers. BMJ 2006, 332, 472–475. [Google Scholar] [CrossRef]
- Akiyama, Y.; Yamada, Y.; Okamoto, S. Interaction forces beneath cuffs of physical assistant robots and their motion-based estimation. Adv. Robot. 2015, 29, 1315–1329. [Google Scholar] [CrossRef]
- Ozioko, O.; Karipoth, P.; Hersh, M.; Dahiya, R. Wearable Assistive Tactile Communication Interface based on Integrated Touch Sensors and Actuators. IEEE Trans. Neural Syst. Rehabil. Eng. 2020. [Google Scholar] [CrossRef]
- Dahiya, R.S.; Metta, G.; Valle, M.; Sandini, G. Tactile sensing—from humans to humanoids. IEEE Trans. Robot. 2009, 26, 1–20. [Google Scholar] [CrossRef]
- Yao, K.; Kaboli, M.; Cheng, G. Tactile-based object center of mass exploration and discrimination. In Proceedings of the 2017 IEEE-RAS 17th International Conference on Humanoid Robotics (Humanoids), Birmingham, UK, 15–17 November 2017; pp. 876–881. [Google Scholar]
- Kaboli, M.; Feng, D.; Cheng, G. Active tactile transfer learning for object discrimination in an unstructured environment using multimodal robotic skin. Int. J. Humanoid Robot. 2018, 15, 1850001. [Google Scholar] [CrossRef]
- Feng, D.; Kaboli, M.; Cheng, G. Active prior tactile knowledge transfer for learning tactual properties of new objects. Sensors 2018, 18, 634. [Google Scholar] [CrossRef] [PubMed]
- Lenzi, T.; Vitiello, N.; De Rossi, S.M.M.; Persichetti, A.; Giovacchini, F.; Roccella, S.; Vecchi, F.; Carrozza, M.C. Measuring human–robot interaction on wearable robots: A distributed approach. Mechatronics 2011, 21, 1123–1131. [Google Scholar] [CrossRef]
- Noda, K.; Hoshino, K.; Matsumoto, K.; Shimoyama, I. A shear stress sensor for tactile sensing with the piezoresistive cantilever standing in elastic material. Sens. Actuators A Phys. 2006, 127, 295–301. [Google Scholar] [CrossRef]
- Shih, B.; Shah, D.; Li, J.; Thuruthel, T.G.; Park, Y.L.; Iida, F.; Bao, Z.; Kramer-Bottiglio, R.; Tolley, M.T. Electronic skins and machine learning for intelligent soft robots. Sci. Robot. 2020, 5. [Google Scholar] [CrossRef]
- Yogeswaran, N.; Dang, W.; Navaraj, W.T.; Shakthivel, D.; Khan, S.; Polat, E.O.; Gupta, S.; Heidari, H.; Kaboli, M.; Lorenzelli, L.; et al. New materials and advances in making electronic skin for interactive robots. Adv. Robot. 2015, 29, 1359–1373. [Google Scholar] [CrossRef]
- Luo, M.; Liu, D.; Luo, H. Real-time deflection monitoring for milling of a thin-walled workpiece by using PVDF thin-film sensors with a cantilevered beam as a case study. Sensors 2016, 16, 1470. [Google Scholar] [CrossRef]
- Ma, C.C.; Chuang, K.C.; Pan, S.Y. Polyvinylidene fluoride film sensors in collocated feedback structural control: Application for suppressing impact-induced disturbances. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 2539–2554. [Google Scholar] [CrossRef]
- Shirinov, A.V.; Schomburg, W.K. Pressure sensor from a PVDF film. Sens. Actuators A Phys. 2008, 142, 48–55. [Google Scholar] [CrossRef]
- Yi, J.; Liang, H. A PVDF-based deformation and motion sensor: Modeling and experiments. IEEE Sens. J. 2008, 8, 384–391. [Google Scholar]
- Yi, J. A piezo-sensor-based “smart tire” system for mobile robots and vehicles. IEEE/ASME Trans. Mechatron. 2008, 13, 95–103. [Google Scholar] [CrossRef]
- Li, F.; Akiyama, Y.; Wan, X.; Yamada, Y.; Okamoto, S. Shear Stress Sensor for Soft Material with Built-In Piezoelectric Polymer Films. In Proceedings of the 2019 IEEE 8th Global Conference on Consumer Electronics (GCCE), Osaka, Japan, 15–18 October 2019; pp. 656–658. [Google Scholar]
- Specialties, M. Piezo Film Sensors Technical Manual. Available online: https://www.sparkfun.com/datasheets/Sensors/Flex/MSI-techman.pdf (accessed on 19 June 2020).
- Sirohi, J.; Chopra, I. Fundamental understanding of piezoelectric strain sensors. J. Intell. Mater. Syst. Struct. 2000, 11, 246–257. [Google Scholar] [CrossRef]
- Beer, F.P.; Johnston, R.; Dewolf, J.; Mazurek, D. Mechanics of Materials; McGraw-Hill: New York, NY, USA, 1981; pp. 150–233. [Google Scholar]
- Timošenko, S.P.; Goodier, J.N. Theory of Elasticity; McGraw-Hill: New York, NY, USA, 1951. [Google Scholar]
- Johnson, K.L.; Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar] [CrossRef]
- Kengo, Y.; Yoji, Y. Development of Specialized Dummy Coating for Viscoelasticity of Skin for Dummy for Safety Tests. Graduation Thesis, Nagoya University, Nagoya, Japan, 2014. [Google Scholar]
- Akiyama, Y.; Yamada, Y.; Ito, K.; Oda, S.; Okamoto, S.; Hara, S. Test method for contact safety assessment of a wearable robot-analysis of load caused by a misalignment of the knee joint. In Proceedings of the 2012 IEEE RO-MAN: The 21st IEEE International Symposium on Robot and Human Interactive Communication, Paris, France, 9–13 September 2012; pp. 539–544. [Google Scholar]











© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Akiyama, Y.; Wan, X.; Okamoto, S.; Yamada, Y. Measurement of Shear Strain Field in a Soft Material Using a Sensor System Consisting of Distributed Piezoelectric Polymer Film. Sensors 2020, 20, 3484. https://doi.org/10.3390/s20123484
Li F, Akiyama Y, Wan X, Okamoto S, Yamada Y. Measurement of Shear Strain Field in a Soft Material Using a Sensor System Consisting of Distributed Piezoelectric Polymer Film. Sensors. 2020; 20(12):3484. https://doi.org/10.3390/s20123484
Chicago/Turabian StyleLi, Fengyu, Yasuhiro Akiyama, Xianglong Wan, Shogo Okamoto, and Yoji Yamada. 2020. "Measurement of Shear Strain Field in a Soft Material Using a Sensor System Consisting of Distributed Piezoelectric Polymer Film" Sensors 20, no. 12: 3484. https://doi.org/10.3390/s20123484
APA StyleLi, F., Akiyama, Y., Wan, X., Okamoto, S., & Yamada, Y. (2020). Measurement of Shear Strain Field in a Soft Material Using a Sensor System Consisting of Distributed Piezoelectric Polymer Film. Sensors, 20(12), 3484. https://doi.org/10.3390/s20123484





