On Exploiting Millimeter-Wave Spectrum Trading in Countrywide Mobile Network Operators for High Spectral and Energy Efficiencies in 5G/6G Era
Abstract
:1. Introduction
1.1. Background
1.2. Related Work
1.3. Contribution
1.4. Organization
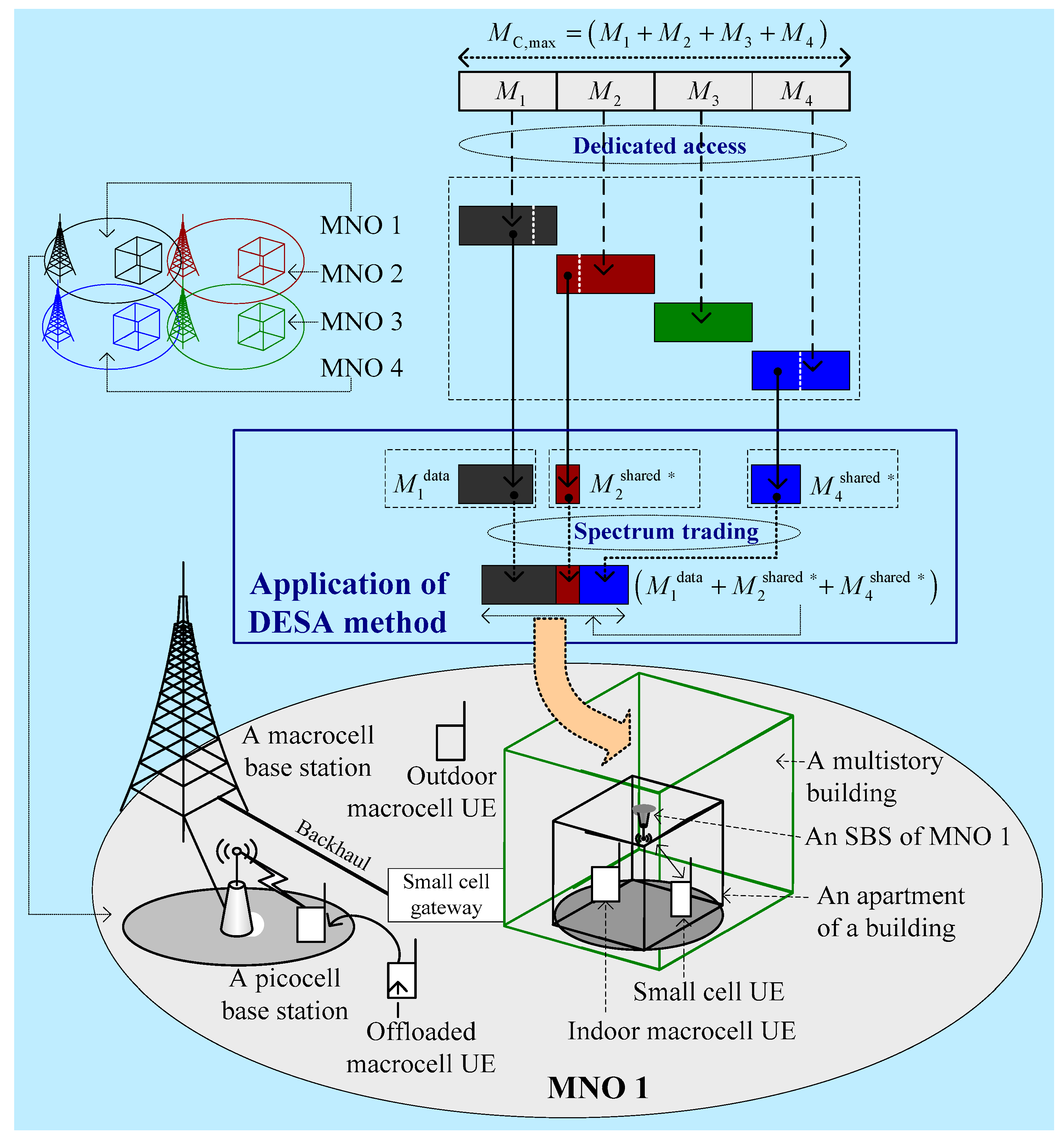
2. System Architecture and Proposed Method
2.1. System Architecture
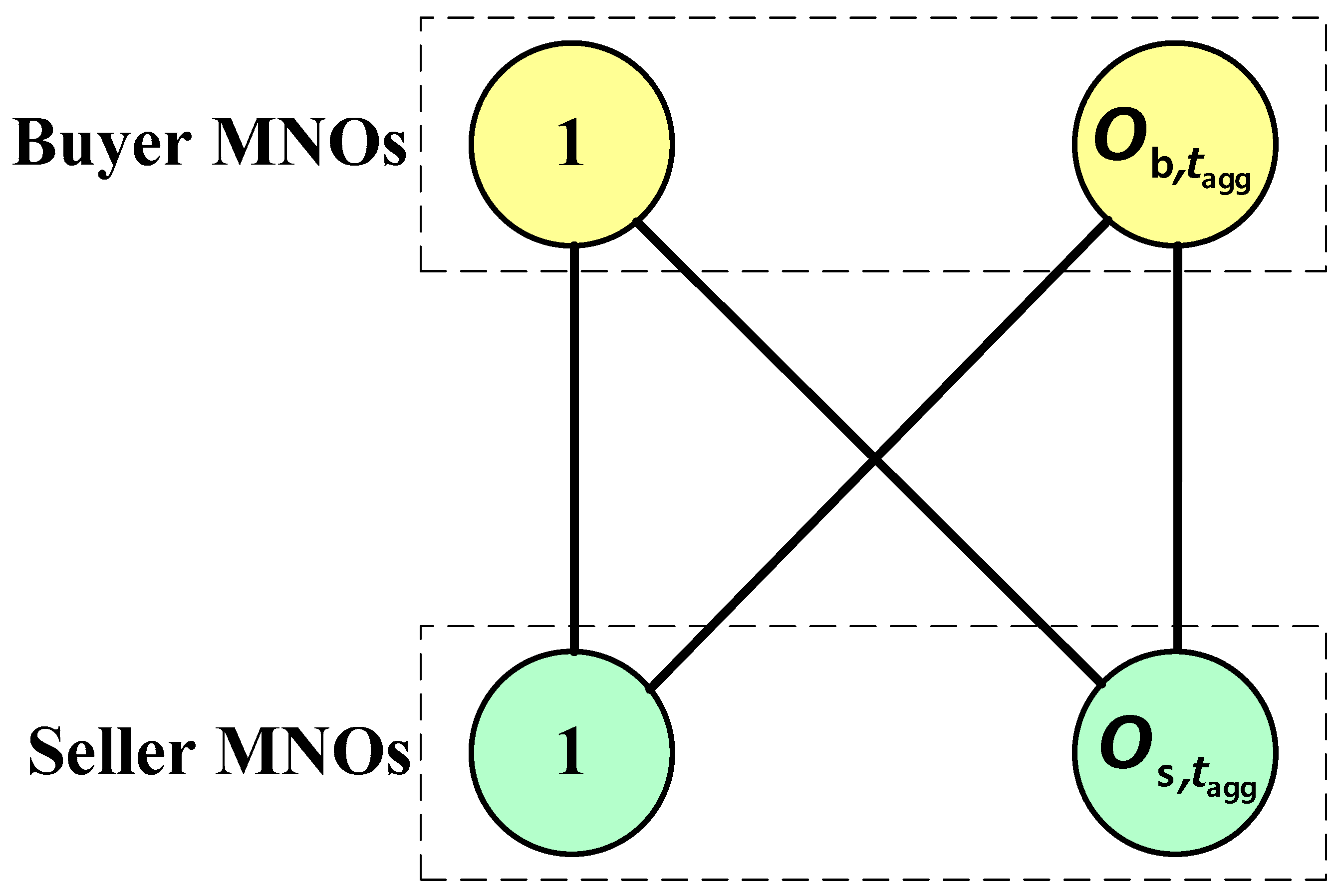
2.2. Proposed Method
2.2.1. Principle
2.2.2. Problem Formulation
2.2.3. Iterative Algorithm
3. Mathematical Analysis
3.1. Preliminaries
3.2. System-Level Performance
3.2.1. Case 1: Single MNO
3.2.2. Case 2: All MNOs Countrywide
3.3. Small Cell Network Performance
3.3.1. Average Capacity
3.3.2. Spectral Efficiency
3.3.3. Energy Efficiency
3.3.4. Cost Efficiency
4. Performance Evaluation
4.1. Default Parameter and Assumption
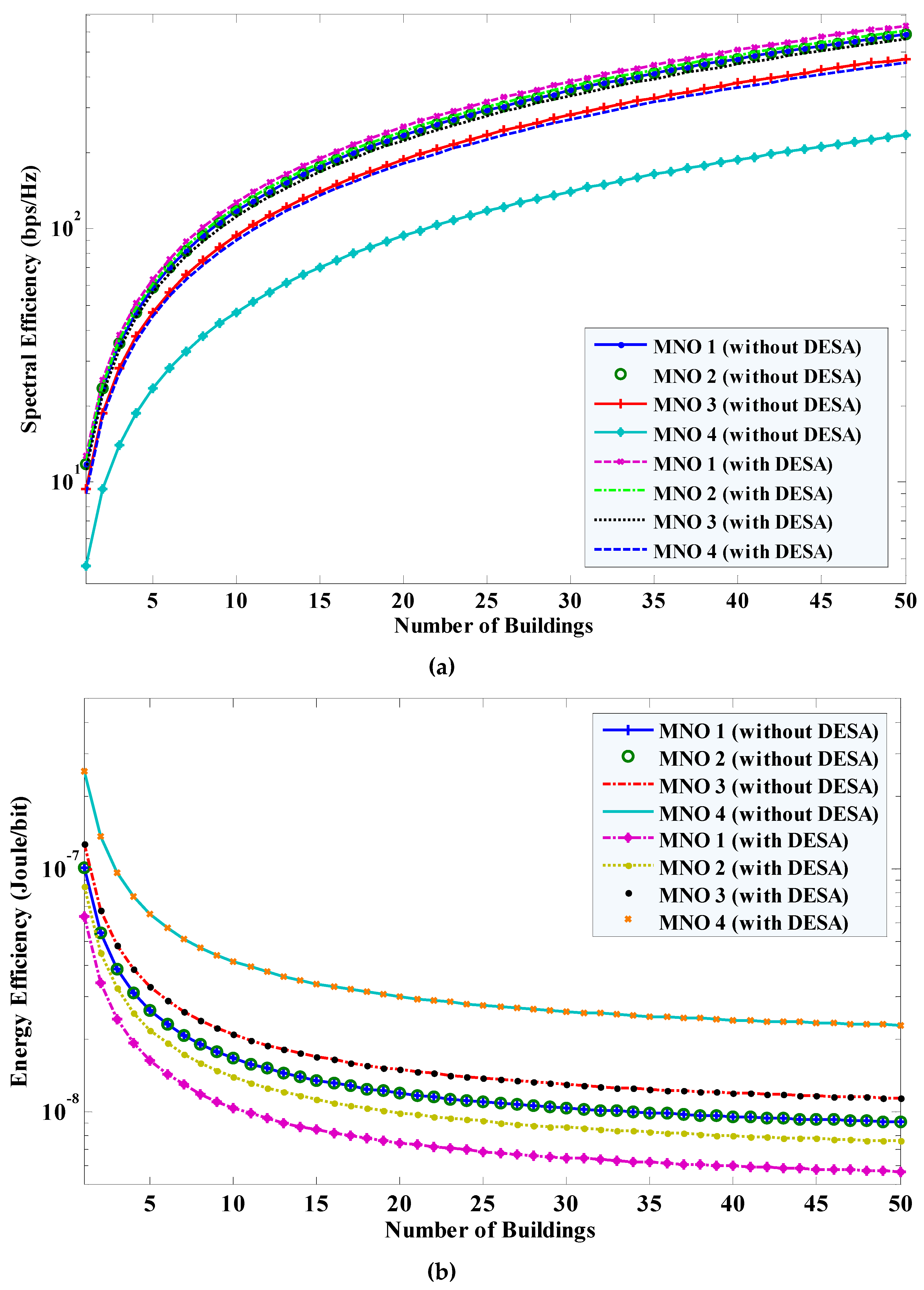
4.2. Performance Result
4.2.1. Shared Spectrum per MNO
4.2.2. Performance Metrics of all MNOs
5. Performance Comparison and Case Study
5.1. Performance Comparison
5.2. Case Study-Applying DESA in the Perspective of Four MNOs in a Country for 5G
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Notation | Description |
|---|---|
| The total amount of mmWave spectrum in RBs allocated to a country | |
| O | Maximum number of MNOs of a country |
| An agreement term | |
| i, t, o, | Index of an RB, a transmission time interval (TTI), and an MNO, respectively, |
| L | Number of buildings of small cells per macrocell |
| Total number of subscribers for an MNO o at | |
| Maximum number of subscribers of all MNOs of a country at | |
| Required data traffic spectrum in RBs for an MNO o at | |
| Reserved spectrum in RBs of an MNO o at | |
| Shared or leased spectrum in RBs for each MNO o at | |
| M | An equal amount of licensed mmWave spectrum per MNO in RBs |
| Operating spectrum of a macrocell for an MNO o in RBs | |
| Q | Maximum simulation run time in TTI |
| Received signal-to-interference-plus-noise ratio for a UE at RB = i in TTI = t for an MNO o at | |
| A link throughput for a UE at RB = i in TTI = t for an MNO o at | |
| , , | System-level average capacity, spectral efficiency, and energy efficiency, respectively, of an MNO o at |
| , , | Average capacity, spectral efficiency, and energy efficiency, respectively, of the only mmWave enabled small cells of an MNO o at |
| , , | Average capacity, spectral efficiency, and energy efficiency, respectively, for an MNO o at with applying DESA for mmWave enabled small cells only |
| , , | Average capacity, spectral efficiency, and energy efficiency, respectively, for an MNO o at without applying DESA for mmWave enabled small cells only |
| , , | Improvement factor in average capacity, spectral efficiency, and energy efficiency, respectively, due to applying DESA for an MNO o at |
| Cost of the total amount of mmWave spectrum allocated to a country expressed in per Hertz of the licensed spectrum | |
| Cost of the mmWave spectrum paid by an MNO o expressed in per Hertz of the licensed spectrum | |
| , | Cost efficiency of small cell networks at for an MNO o with applying and without applying DESA, respectively, |
| Improvement factor in cost efficiency due to applying DESA for an MNO o at |
References
- Saha, R.K. Countrywide Mobile Spectrum Sharing with Small Indoor Cells for Massive Spectral and Energy Efficiencies in 5G and Beyond Mobile Networks. Energies 2019, 12, 3825. [Google Scholar] [CrossRef] [Green Version]
- Hassan, R.; Karmakar, G.C.; Kamruzzaman, J.; Srinivasan, B. Exclusive Use Spectrum Access Trading Models in Cognitive Radio Networks: A Survey. IEEE Commun. Surv. Tutor. 2017, 19, 2192–2231. [Google Scholar] [CrossRef]
- Krishna, T.V.; Das, A. A survey on MAC protocols in OSA networks. Comput. Netw. 2009, 53, 1377–1394. [Google Scholar] [CrossRef]
- Akyildiz, I.F.; Lee, W.-Y.; Vuran, M.C.; Mohanty, S. NeXt generation/dynamic spectrum access/cognitive radio wireless networks: A survey. Comput. Netw. 2006, 50, 2127–2159. [Google Scholar] [CrossRef]
- Kolodzy, P.; Avoidance, I. Spectrum Policy Task Force; Federal Communications Commission: Washington, DC, USA, 2002; pp. 147–158. Available online: https://www.fcc.gov/document/spectrum-policy-task-force (accessed on 4 June 2020).
- Federal Communications Commission. Notice of Proposed Rule Marking in the Matter of Unlicensed Operation in the TV Broadcast Bands; Federal Communications Commission: Washington, DC, USA, 2004; pp. 4–186. [Google Scholar]
- Saha, R.K. Realization of Licensed/Unlicensed Spectrum Sharing Using eICIC in Indoor Small Cells for High Spectral and Energy Efficiencies of 5G Networks. Energies 2019, 12, 2828. [Google Scholar] [CrossRef] [Green Version]
- Tehrani, R.H.; Vahid, S.; Triantafyllopoulou, D.; Lee, H.; Moessner, K. Licensed Spectrum Sharing Schemes for Mobile Operators: A Survey and Outlook. IEEE Commun. Surv. Tutor. 2016, 18, 2591–2623. [Google Scholar] [CrossRef] [Green Version]
- Attiah, M.L.; Isa, A.A.M.; Zakaria, Z.; AbdulHameed, M.K.; Mohsen, M.K.; Ali, I. A survey of mmWave user association mechanisms and spectrum sharing approaches: An overview, open issues and challenges, future research trends. Wirel. Netw. 2019, 26, 2487–2514. [Google Scholar] [CrossRef]
- Hamdaoui, B.; Khalfi, B.; Zorba, N. Dynamic Spectrum Sharing in the Age of Millimeter Wave Spectrum Access. IEEE Netw. 2020, 1–7. [Google Scholar] [CrossRef]
- Park, J.; Andrews, J.G.; Heath, R.W. Inter-Operator Base Station Coordination in Spectrum-Shared Millimeter Wave Cellular Networks. IEEE Trans. Cogn. Commun. Netw. 2018, 4, 513–528. [Google Scholar] [CrossRef]
- Rebato, M.; Boccardi, F.; Mezzavilla, M.; Rangan, S.; Zorzi, M. Hybrid Spectrum Sharing in mmWave Cellular Networks. IEEE Trans. Cogn. Commun. Netw. 2017, 3, 155–168. [Google Scholar] [CrossRef]
- Hossain, E.; Niyato, D.; Han, Z. Dynamic Spectrum Access and Management in Cognitive Radio Networks; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Li, F.; Lam, K.-Y.; Li, X.; Liu, X.; Wang, L.; Leung, V.C.M. Dynamic Spectrum Access Networks With Heterogeneous Users: How to Price the Spectrum? IEEE Trans. Veh. Technol. 2018, 67, 5203–5216. [Google Scholar] [CrossRef]
- Garg, P.K.; Dua, T.R.; Chandra, A. Spectrum Challenges for Modern Mobile Services. J. ICT Stand. 2013, 1, 137–158. [Google Scholar] [CrossRef] [Green Version]
- Prasad, R. 5G: 2020 and Beyond; River Publishers: Gistrup, Denmark, 2014; pp. 1–125. [Google Scholar]
- Song, Q.; You, M.; Lv, T. Incentives to spectrum trading. In Proceedings of the 2009 IEEE International Conference on Network Infrastructure and Digital Content, Newark, NJ, USA, 6 November 2009; pp. 948–952. [Google Scholar]
- Hu, F.; Chen, B.; Wang, J.; Li, M.; Li, P.; Pan, M. MastDP: Matching Based Double Auction Mechanism for Spectrum Trading with Differential Privacy. In Proceedings of the 2019 IEEE Global Communications Conference, Waikoloa Village, HI, USA, 9 December 2019; pp. 1–6. [Google Scholar]
- Qiu, J.; Grace, D.; Ding, G.; Yao, J.; Wu, Q. Blockchain-Based Secure Spectrum Trading for Unmanned-Aerial-Vehicle-Assisted Cellular Networks: An Operator’s Perspective. IEEE Internet Things J. 2020, 7, 451–466. [Google Scholar] [CrossRef]
- Hu, Z.; Zheng, Z.; Song, L.; Wang, T.; Li, X. UAV Offloading: Spectrum Trading Contract Design for UAV Assisted Cellular Networks. IEEE Trans. Wirel. Commun. 2018, 17, 1. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, W.; Yang, L.; Yeo, C.K.; Chen, S. Two-Tier Spectrum Trading Strategy for Heterogeneous Cognitive Radio Networks. In Proceedings of the 2019 29th International Telecommunication Networks and Applications Conference, Auckland, New Zealand, 27 November 2019; pp. 1–6. [Google Scholar]
- Farshbafan, M.K.; Bahonar, M.H.; Khaiehraveni, F. Spectrum Trading for Device-to-Device Communication in Cellular Networks using Incomplete Information Bandwidth-Auction Game. In Proceedings of the 2019 27th Iranian Conference on Electrical Engineering, Yazd, Iran, 30 April 2019; pp. 1441–1447. [Google Scholar]
- Li, X.; Ding, H.; Pan, M.; Lorenzo, B.; Wang, J.; Fang, Y. Service-Oriented Hybrid-Database-Assisted Spectrum Trading: A Blueprint for Future Licensed Spectrum Sharing. IEEE Wirel. Commun. 2019, 26, 156–163. [Google Scholar] [CrossRef]
- MacKenzie, A.B.; DaSilva, L.A. Game Theory for Wireless Engineers. Synth. Lect. Commun. 2006, 1, 1–86. [Google Scholar] [CrossRef]
- Niyato, D.; Hossain, E. Competitive spectrum sharing in cognitive radio networks: A dynamic game approach. IEEE Trans. Wirel. Commun. 2008, 7, 2651–2660. [Google Scholar] [CrossRef]
- Duan, L.; Huang, J.; Shou, B. Duopoly Competition in Dynamic Spectrum Leasing and Pricing. IEEE Trans. Mob. Comput. 2011, 11, 1706–1719. [Google Scholar] [CrossRef]
- Xing, Y.; Chandramouli, R.; Cordeiro, C. Price dynamics in competitive agile spectrum access markets. IEEE J. Sel. Areas Commun. 2007, 25, 613–621. [Google Scholar] [CrossRef]
- Niyato, D.; Hossain, E.; Han, Z. Dynamics of Multiple-Seller and Multiple-Buyer Spectrum Trading in Cognitive Radio Networks: A Game-Theoretic Modeling Approach. IEEE Trans. Mob. Comput. 2008, 8, 1009–1022. [Google Scholar] [CrossRef]
- Zhu, K.; Niyato, D.; Wang, P.; Han, Z. Dynamic Spectrum Leasing and Service Selection in Spectrum Secondary Market of Cognitive Radio Networks. IEEE Trans. Wirel. Commun. 2012, 11, 1136–1145. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, G.; Chen, Y.; Guo, L. A spectrum trading algorithm using an agent in cognitive radio networks. In Proceedings of the 2014 6th International Congress on Ultra Modern Telecommunications and Control Systems and Workshops, St. Petersburg, Russia, 6–8 October 2014; pp. 386–389. [Google Scholar]
- Yi, C.; Cai, J. Two-Stage Spectrum Sharing With Combinatorial Auction and Stackelberg Game in Recall-Based Cognitive Radio Networks. IEEE Trans. Commun. 2014, 62, 3740–3752. [Google Scholar] [CrossRef]
- Ellenbeck, J.; Schmidt, J.; Korger, U.; Hartmann, C. A Concept for Efficient System-Level Simulations of OFDMA Systems with Proportional Fair Fast Scheduling. In Proceedings of the 2009 IEEE Globecom Workshops, Honolulu, HI, USA, 1–4 December 2009; pp. 1–6. [Google Scholar]
- Saha, R.K.; Aswakul, C. A tractable analytical model for interference characterization and minimum distance enforcement to reuse resources in three-dimensional in-building dense small cell networks. Int. J. Commun. Syst. 2017, 30, e3240. [Google Scholar] [CrossRef]
- Chen, S.; Liang, Y.-C.; Sun, S.; Kang, S.; Cheng, W.; Peng, M. Vision, Requirements, and Technology Trend of 6G: How to Tackle the Challenges of System Coverage, Capacity, User Data-Rate and Movement Speed. IEEE Wirel. Commun. 2020, 27, 218–228. [Google Scholar] [CrossRef] [Green Version]
- Japan Assigns 5G Spectrum to Four Operators-5G Observatory. Available online: https://5gobservatory.eu/japan-assigns-5g-spectrum-to-four-operators/ (accessed on 22 April 2020).
- TSI 3rd Generation Partnership Project. Evolved Universal Terrestrial Radio Access (E-UTRA); Radio Frequency (RF) System Scenarios. In 3GPP TR 36.942 Version 8.2.0 Release 8; ETSI: Sophia Antipolis Cedex, France, 2007; Available online: https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=2592 (accessed on 15 February 2020).
- TSI 3rd Generation Partnership Project. Simulation Assumptions and Parameters for FDD HeNB RF Requirements; ETSI: Sophia Antipolis Cedex, France, 2010; Available online: https://www.3gpp.org/ftp/tsg_ran/WG4_Radio/TSGR4_51/Documents/ (accessed on 13 February 2020).
- Geng, S.; Kivinen, J.; Zhao, X.; Vainikainen, P. Millimeter-Wave Propagation Channel Characterization for Short-Range Wireless Communications. IEEE Trans. Veh. Technol. 2008, 58, 3–13. [Google Scholar] [CrossRef]
- Saha, R.K.; Aswakul, C.; Saengudomlert, P. Evolution Toward 5G Mobile Networks—A Survey on Enabling Technologies. Eng. J. 2016, 20, 87–119. [Google Scholar] [CrossRef]
- MacCartney, G.R.; Rappaport, T.S.; Sun, S.; Deng, S. Indoor Office Wideband Millimeter-Wave Propagation Measurements and Channel Models at 28 and 73 GHz for Ultra-Dense 5G Wireless Networks. IEEE Access 2015, 3, 2388–2424. [Google Scholar] [CrossRef]
- International Telecommunication Union. Guidelines for Evaluation of Radio Interface Technologies for IMT-2020; Report ITU-R M.2412-0 (10/2017); International Telecommunication Union: Geneva, Switzerland, 2017; Available online: https://www.itu.int/dms_pub/itu-r/opb/rep/R-REP-M.2412-2017-PDF-E.pdf (accessed on 13 February 2020).
- Zhang, Z.; Xiao, Y.; Ma, Z.; Xiao, M.; Ding, Z.-G.; Lei, X.; Karagiannidis, G.K.; Fan, P. 6G Wireless Networks: Vision, Requirements, Architecture, and Key Technologies. IEEE Veh. Technol. Mag. 2019, 14, 28–41. [Google Scholar] [CrossRef]
- Wang, C.-X.; Haider, F.; Gao, X.; XiaoHu, Y.; Yang, Y.; Yuan, D.; Aggoune, H.; Haas, H.; Fletcher, S.; Hepsaydir, E. Cellular architecture and key technologies for 5G wireless communication networks. IEEE Commun. Mag. 2014, 52, 122–130. [Google Scholar] [CrossRef] [Green Version]
- Auer, G.; Giannini, V.; Desset, C.; Gódor, I.; Skillermark, P.; Olsson, M.; Imran, M.A.; Sabella, D.; Gonzalez, M.; Blume, O.; et al. How much energy is needed to run a wireless network? IEEE Wirel. Commun. 2011, 18, 40–49. [Google Scholar] [CrossRef]
- Saha, R.K. A dynamic exclusive-use spectrum access method for millimeter-wave mobile systems toward 6G. In Proceedings of the IEEE 92nd Vehicular Technology Conference, Victoria, BC, Canada, 4–7 October 2020; pp. 1–6. [Google Scholar]





| Parameters and Assumptions | Value | ||
|---|---|---|---|
| For all MNOs countrywide | |||
| Countrywide total of 28 GHz spectrum bandwidth | 200 MHz | ||
| Countrywide total number of MNOs and subscribers | 4 and | ||
| Number of subscribers for MNOs 1, 2, 3, and 4, respectively | 40%, 30%, 20%, and 10% of | ||
| Total 28 GHz mmWave spectrum bandwidth and reserved spectrum for each MNO | 50 MHz and 10 MHz (for 28 GHz) | ||
| For each MNO | |||
| E-UTRA simulation case 1 | 3GPP Case 3 | ||
| Cellular layout 2, Inter-site distance (ISD) 1,2, transmit direction | Hexagonal grid, dense urban, 3 sectors per macrocell site, 1732 m, and downlink | ||
| Carrier frequency 2,3 | Licensed 2 GHz non-LOS (NLOS) microwave spectrum band for macrocells and picocells, licensed 28 GHz LOS mmWave spectrum band for small cells | ||
| Number of cells | 1 macrocell, 2 picocells, 48 small cells per building | ||
| Total BS transmit power 1 (dBm) | 46 for macrocell 1,4, 37 for picocells 1, 19 for 28 GHz for small cells 1,3,4,6 | ||
| Co-channel small-scale fading model 1,5,6 | Frequency selective Rayleigh for 2 GHz NLOS spectrum for macrocells and picocells, no small-scale fading for 28 GHz LOS spectrum for small cells | ||
| External wall penetration loss 1 (Low) | 20 dB for 2 GHz spectrum | ||
| Path loss | MBS and a UE 1 | Outdoor macrocell UE | PL(dB) = 15.3 + 37.6log10R, R is in m |
| Indoor macrocell UE | PL(dB) = 15.3 + 37.6log10R + Low, R is in m | ||
| PBS and a UE 1 | PL(dB) = 140.7 + 36.7log10R, R is in km | ||
| SBS and a UE 1,2,3,5 | PL(dB) = 61.38 + 17.97log10R, R is m | ||
| Lognormal shadowing standard deviation (dB) | 8 for MBS 2, 10 for PBS 1, and 9.9 for 28 GHz LOS spectrum for SBS 2,3,5 | ||
| Antenna configuration | Single-input single-output for all BSs and UEs | ||
| Antenna pattern (horizontal) | Directional (120°) for MBS 1, omnidirectional for PBS 1 and SBS 1 | ||
| Antenna gain plus connector loss (dBi) | 14 for MBS 2, 5 for PBS 1, 5 for SBS 1,3,6 | ||
| UE antenna gain 2,3,6 | 0 dBi (for 2 GHz), 5 dBi (for 28 GHz, Biconical horn) | ||
| UE noise figure2,6 and UE speed 1 | 9 dB (for 2 GHz) and 10 dB (for 28 GHz), 3 km/hr | ||
| Total number of macrocell UEs | 30 | ||
| Picocell coverage and macrocell UEs offloaded to all picocells 1 | 40 m (radius), 2/15 | ||
| Indoor macrocell UEs 1 | 35% | ||
| 3D multistory building and SBS models (for regular square-grid structure) | Number of buildings | L | |
| Number of floors per building | 6 | ||
| Number of apartments per floor | 8 | ||
| Number of SBSs per apartment | 1 | ||
| Total number of SBSs per building | 48 | ||
| Area of an apartment | 10 × 10 m2 | ||
| Location of an SBS in an apartment | Center of the ceiling | ||
| Scheduler and traffic model 2 | Proportional Fair (PF) and full buffer | ||
| Type of SBSs | Closed Subscriber Group (CSG) femtocell base stations | ||
| Channel State Information (CSI) | Ideal | ||
| TTI1, scheduler time constant (tc), tagg | 1 ms, 100 ms, 6 months | ||
| Total simulation run time | 8 ms | ||
| MNO | L (To Satisfy both Average SE and EE Requirements for 6G Mobile Systems) | ||||||
|---|---|---|---|---|---|---|---|
| Without DESA | With DESA | Without DESA | With DESA | Without DESA | With DESA | With DESA/Without DESA | |
| 1 | 32 | 30 | 1 | 1 | 32 | 30 | 0.937 |
| 2 | 32 | 31 | 1 | 1 | 32 | 31 | 0.968 |
| 3 | 40 | 34 | 1 | 1 | 40 | 34 | 0.85 |
| 4 | 80 | 42 | 1 | 1 | 80 | 42 | 0.525 |
| All | 40 | 32 | 1 | 1 | 40 | 32 | 0.80 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saha, R.K. On Exploiting Millimeter-Wave Spectrum Trading in Countrywide Mobile Network Operators for High Spectral and Energy Efficiencies in 5G/6G Era. Sensors 2020, 20, 3495. https://doi.org/10.3390/s20123495
Saha RK. On Exploiting Millimeter-Wave Spectrum Trading in Countrywide Mobile Network Operators for High Spectral and Energy Efficiencies in 5G/6G Era. Sensors. 2020; 20(12):3495. https://doi.org/10.3390/s20123495
Chicago/Turabian StyleSaha, Rony Kumer. 2020. "On Exploiting Millimeter-Wave Spectrum Trading in Countrywide Mobile Network Operators for High Spectral and Energy Efficiencies in 5G/6G Era" Sensors 20, no. 12: 3495. https://doi.org/10.3390/s20123495






