The Energy Compensation of the HRG Based on the Double-Frequency Parametric Excitation of the Discrete Electrode
Abstract
:1. Introduction
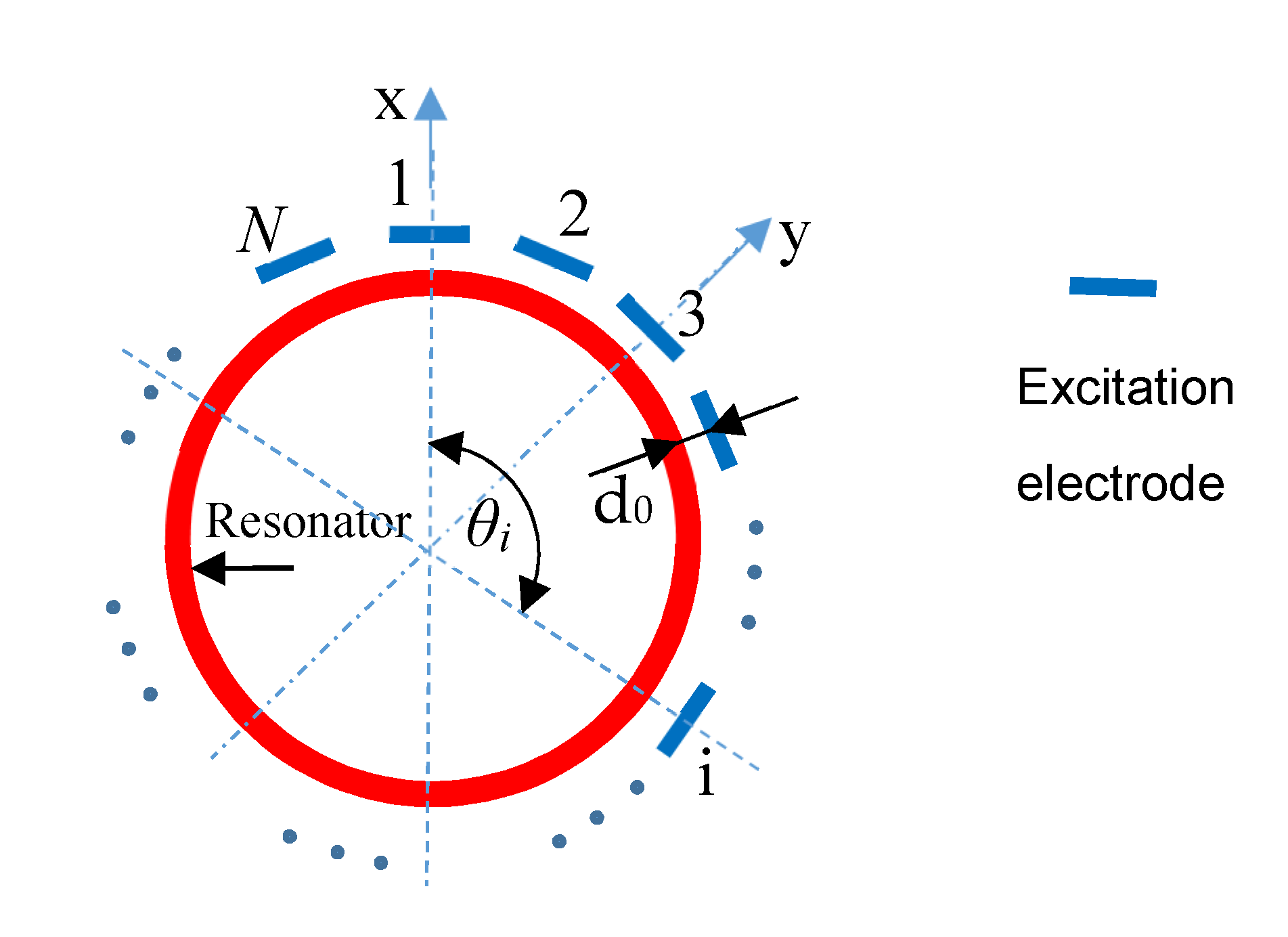
2. The Theory of Parametric Excitation of the Discrete Electrode
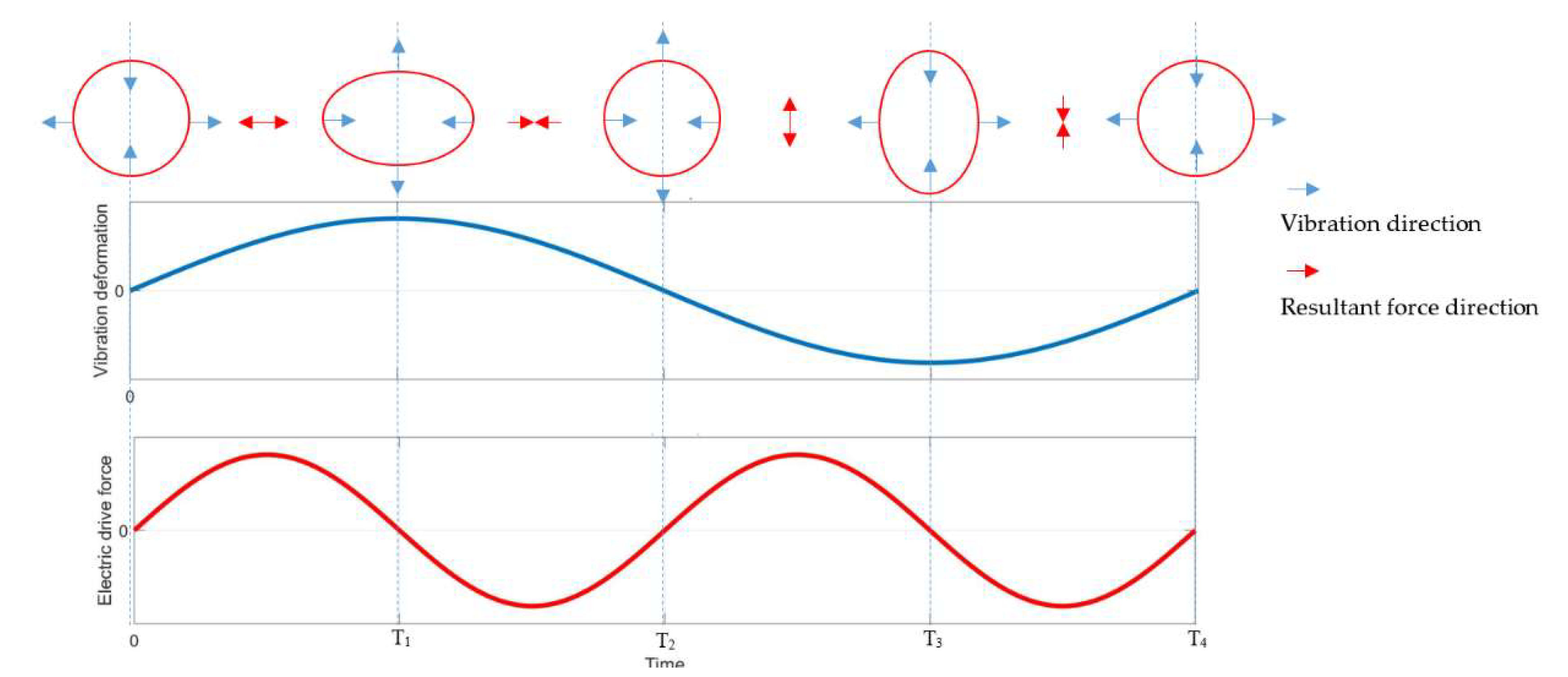
2.1. The Parametric Excitation Method
2.2. The Dynamic Equations of Resonators Excited by the Discrete Electrode
2.3. The Stability Boundary of the Double-Frequency Parametric Excitation
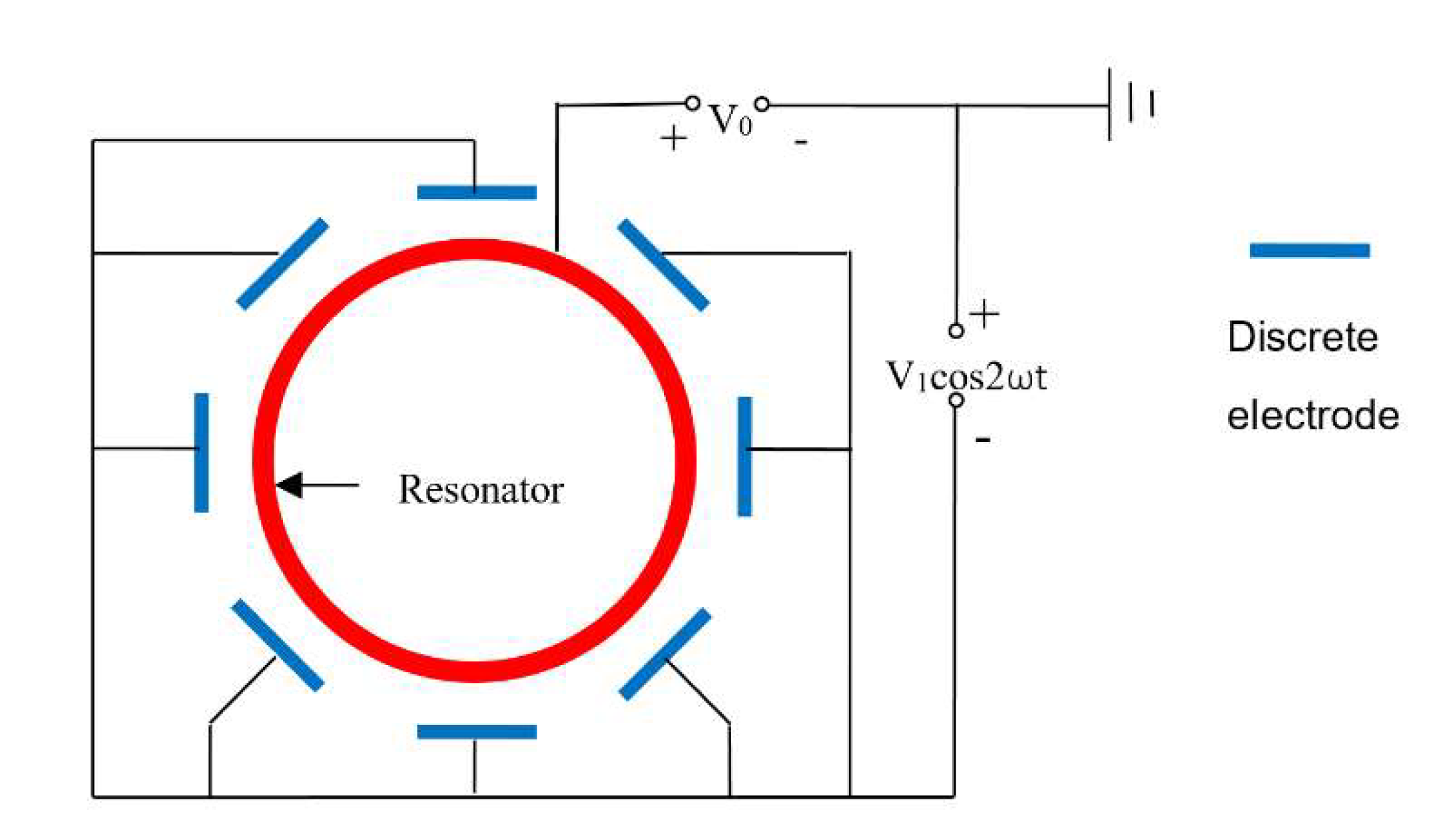
3. The Energy Control Scheme of the Double-Frequency Parametric Excitation
4. Simulation of the Energy Compensation of Double-Frequency Parametric Excitation by the Discrete Electrode
4.1. The Simulation Parameter
4.2. The Evolutionary Simulation of the Resonator with Different Excitation Parameters
- (1)
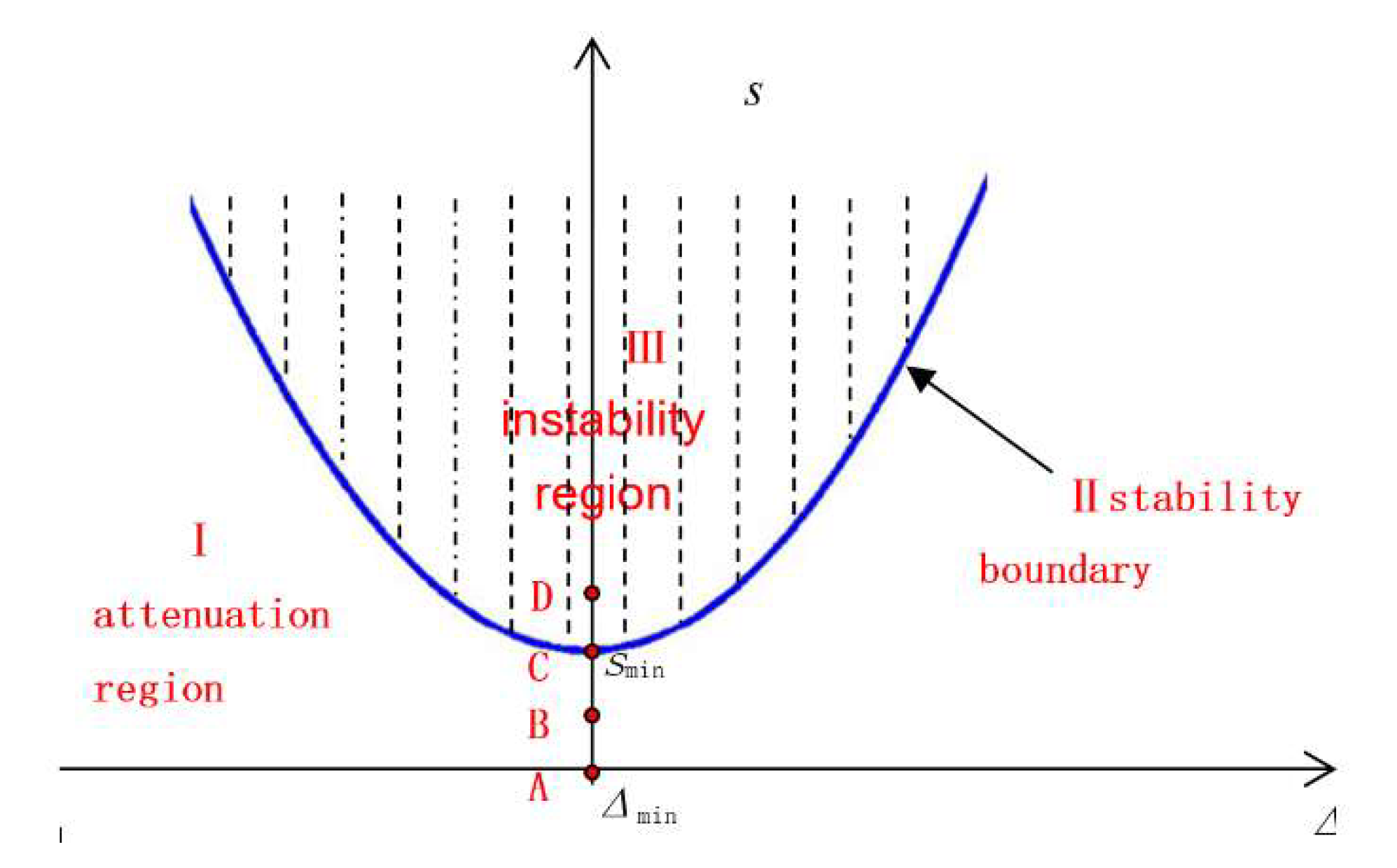
- In the state of S = 0 (i.e., V1 is 0 voltage), the resonator will be freely damping; even if the resonator is vibrating, it will eventually decay to 0.
- (2)
- In region I, the vibration of the resonator will gradually decline to 0; that is, the supplementary energy of the resonator is not enough to maintain the vibration of the resonator.
- (3)
- In region II, the vibration of the resonator remains constant and the energy of the resonator is equal to the energy consumed.
- (4)
- In region III, the vibration of the resonator will increase gradually; the supplementary energy is higher than that necessary to maintain the vibration of the resonator.
4.3. Total Energy Stability Simulation of the Resonator with the Parametric Excitation
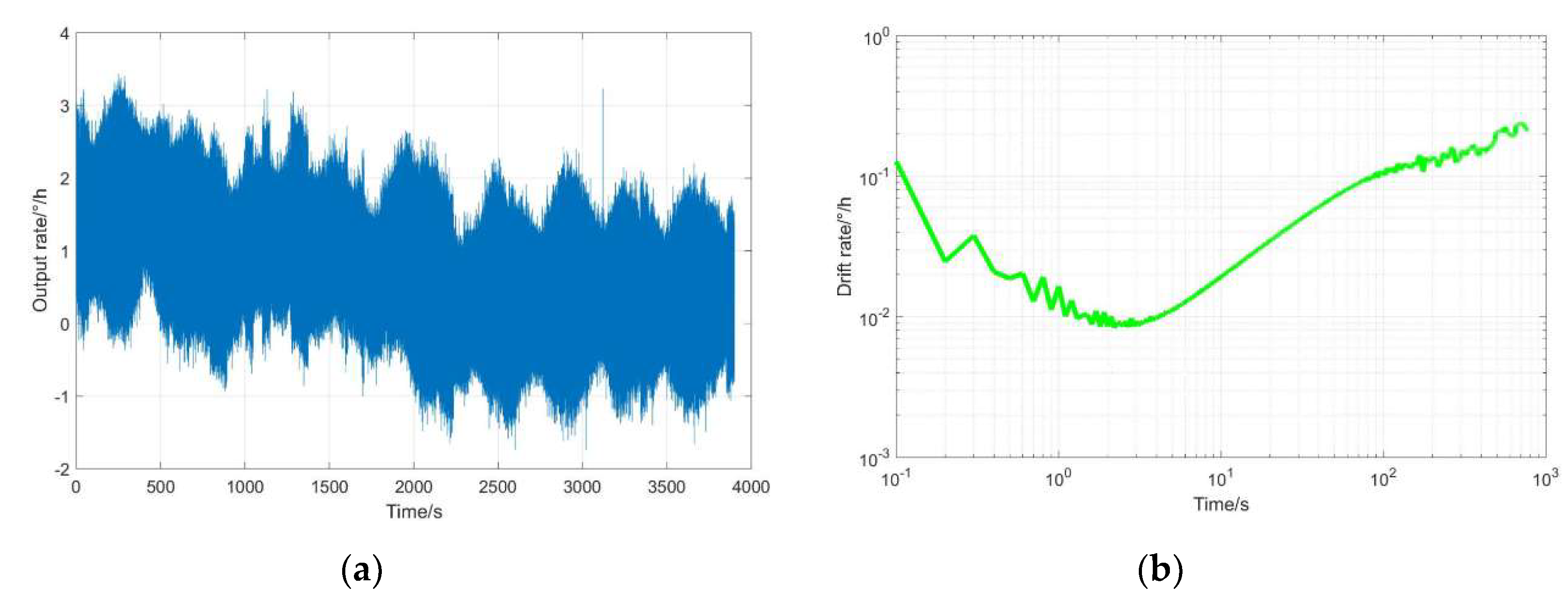
5. The Experiments and Analysis
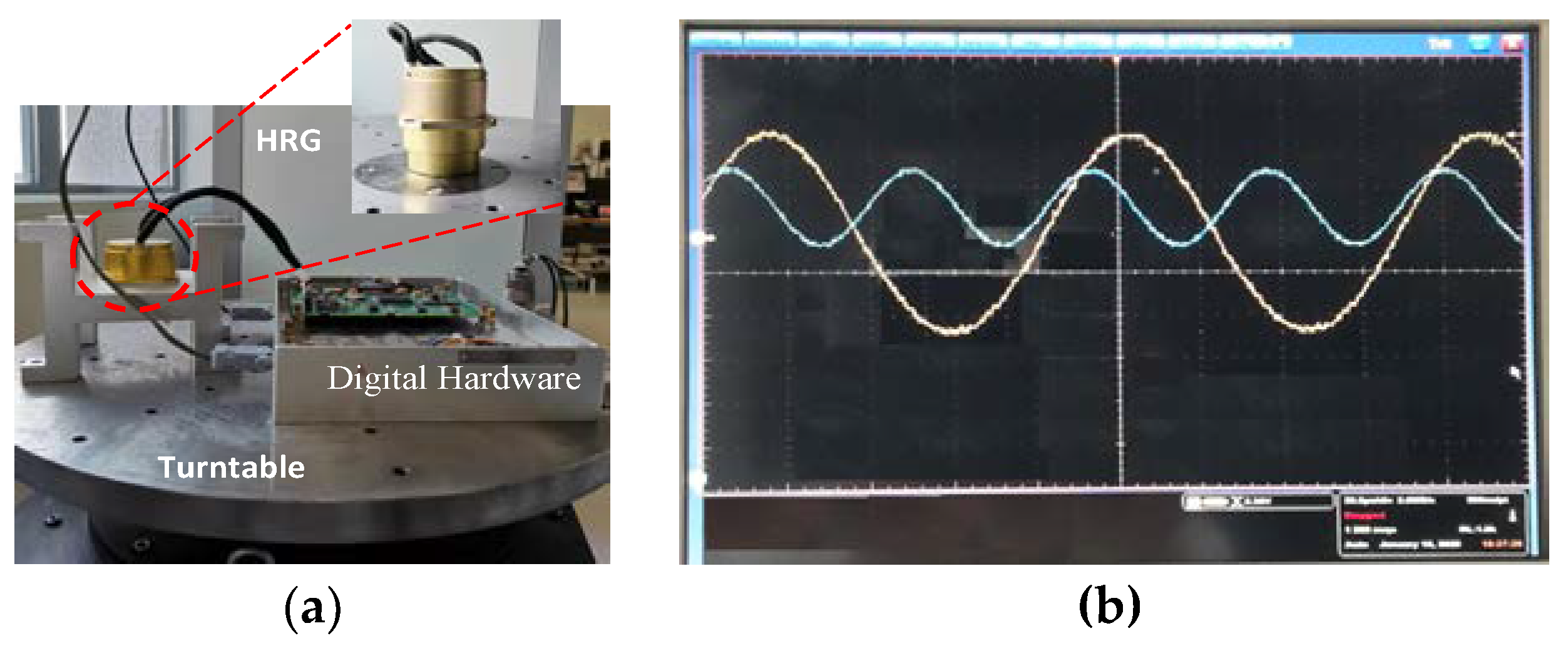
5.1. The Experimental Device
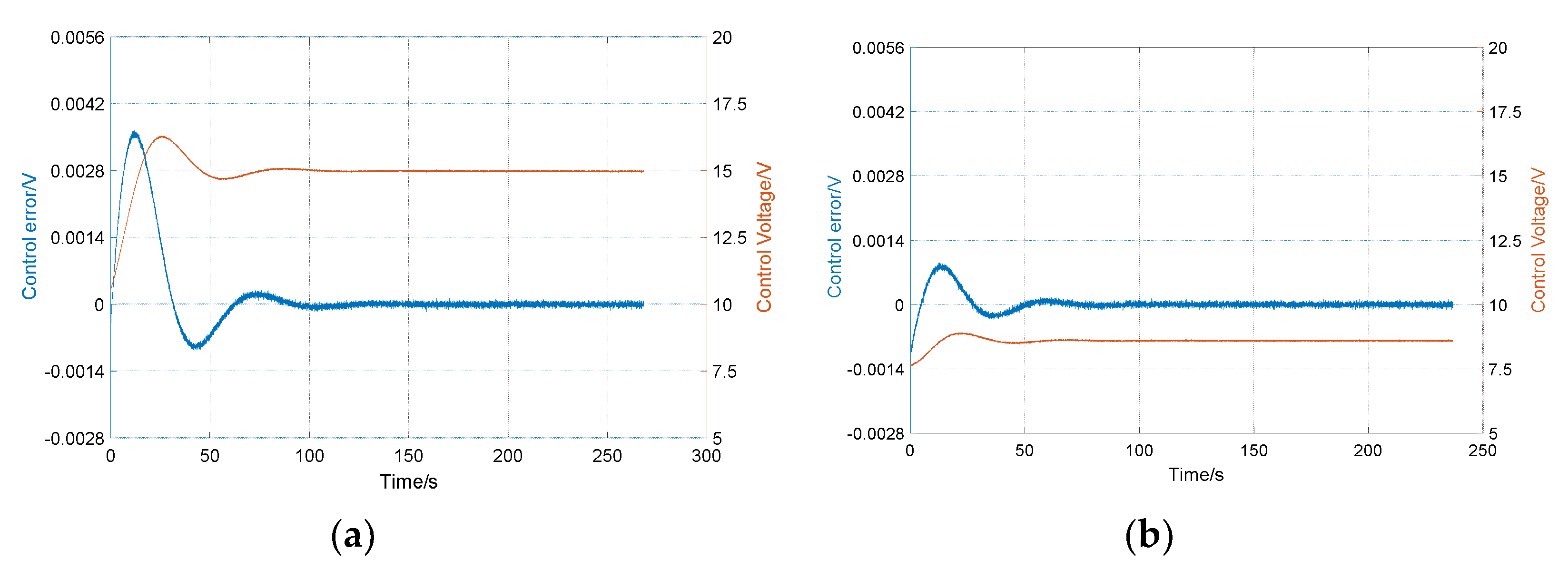
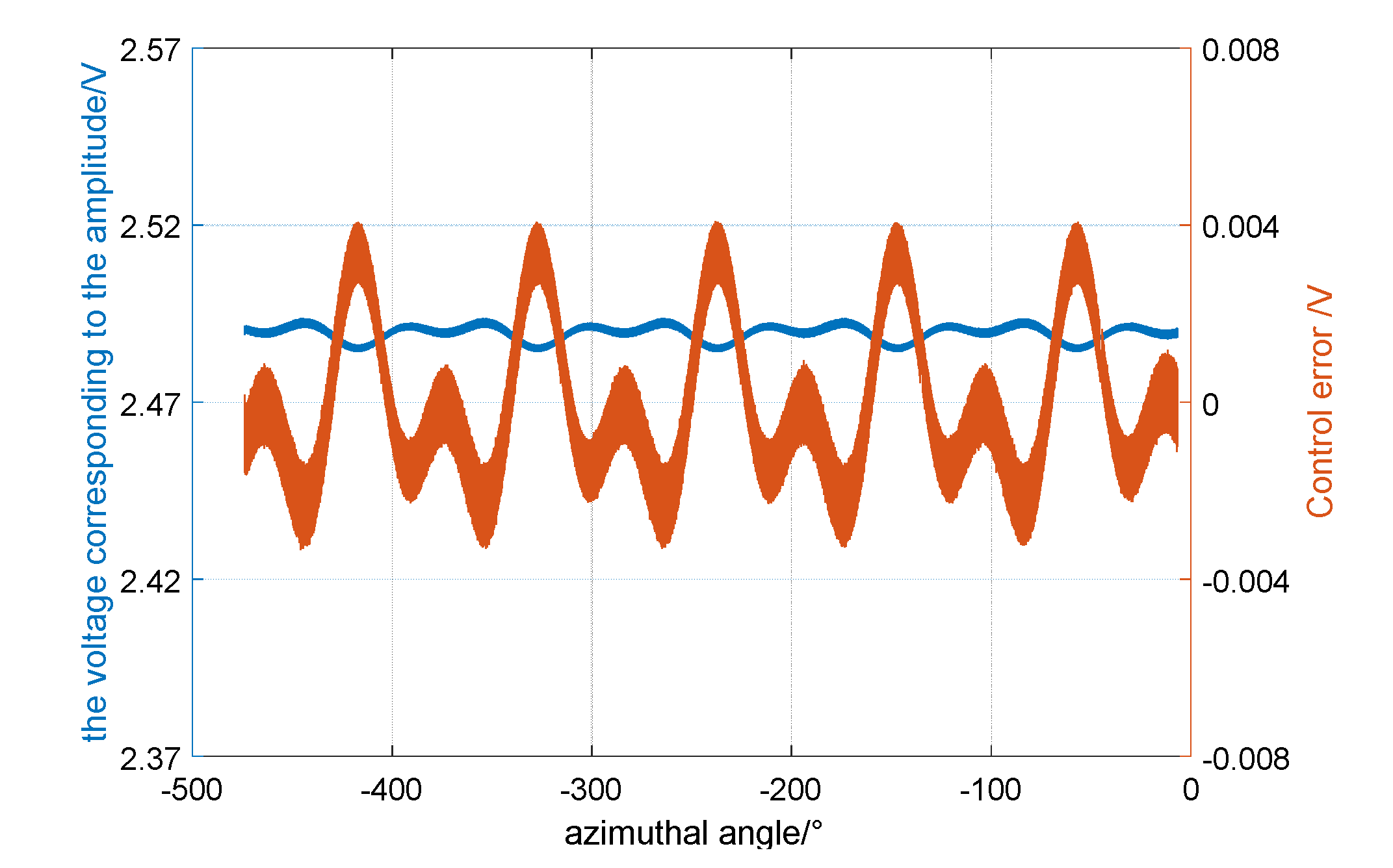
5.2. The Experimental Results and Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Sciences, A.; Rozelle, D.; Grumman, N.; Rozelle, D. The Hemispherical Resonator Gyro: From Wineglass to the Planets. In Proceedings of the 19th AAS/AIAA Space Flight Mechanics Meeting, Savannah, GA, USA, 8–12 February 2009. [Google Scholar]
- Anthony, M. The Operation and Mechanization of the Hemispherical Resonator Gyroscope. In Proceedings of the IEEE/ION PLANS, Monterey, CA, USA, 7–14 April 2018. [Google Scholar]
- Jeanroy, A.; Grosset, G.; Goudon, J.C.; Delhaye, F. HRG by Sagem from laboratory to mass production. In Proceedings of the IEEE International Symposium on Inertial Sensors and Systems, Laguna Beach, CA, USA, 22–25 February 2016; pp. 1–4. [Google Scholar]
- Jeanroy, A.; Bouvet, A.; Remillieux, G. HRG and marine applications. Gyroscopy Navig. 2014, 5, 67–74. [Google Scholar] [CrossRef]
- Ragot, V.; Remillieux, G. A New Control Mode Greatly Improving Performance of Axisymmetrical Vibrating Gyroscopes. Gyroscopy Navig. 2011, 2, 229–238. [Google Scholar] [CrossRef]
- Delhaye, F. HRG by SAFRAN: The game-changing technology. In Proceedings of the 2018 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Moltrasio, Italy, 26–29 March 2018; pp. 1–4. [Google Scholar]
- Xia, Y.; Qi, Y.N.; Cai, X. Method to reduce angular increment error of hemispherical resonators unit by time management. Fligth Control. Detect. 2018, 1, 41–46. [Google Scholar]
- Wang, X.; Wu, W.; Fang, Z.; Luo, B.; Li, Y.; Jiang, Q. Temperature Drift Compensation for Hemispherical Resonator Gyro Based on Natural Frequency. Sensors 2012, 12, 6434–6446. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, H.B.; Ren, S.Q.; Teng, H.J. Establishment of steady state model of amplitude-control for hemispherical resonator gyro under force-rebalance mod. J. Chin. Inert. Technol. 2013, 21, 106–111. [Google Scholar]
- Gregory, J.A.; Cho, J.; Najafi, K. Novel mismatch compensation methods for rate-integrating gyroscopes. In Proceedings of the 2012 IEEE/ION Position, Location and Navigation Symposium, Myrtle Beach, SC, USA, 23–26 April 2012; pp. 252–258. [Google Scholar]
- Loper, E., Jr.; Lynch, D.D. Sonic Vibrating Bell Gyro. U.S. Patent 4157041, 5 January 1979. [Google Scholar]
- Loper, E., Jr.; Lynch, D.D. Vibratory Rotation Sensor. U.S. Patent 4951508, 28 August 1990. [Google Scholar]
- Matveyev, V.; Lunin, B.; Basarab, M. Solid-State Wave Gyro; National Defense Industry Press: Beijing, China, 2009; pp. 156–157. [Google Scholar]
- Zhuravlev, V. Drift of An Imperfect Hemispherical resonator gyro. Mech. Solids 2004, 39, 15–18. [Google Scholar]
- Wei, Z.; Yi, G.; Huo, Y.; Qi, Z.; Xu, Z. The Synthesis Model of Flat-Electrode Hemispherical Resonator Gyro. Sensors 2019, 19, 1690. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nayfeh, A.H.; Mook, A.D. Nonlinear Oscillations; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Zhang, L.X.; Zhao, W.L.; Li, S.L.; Chen, Y.S.; Wang, W. Signal Processing and Control Method of Whole Angle Mode Hemispherical Resonator Gyros. Navig. Position. Timing 2019, 6, 98–104. [Google Scholar]
- Lynch, D.D. Coriolis Vibratory Gyros. Symposium Gyro Technology. In Proceedings of the Symposium Gyro Technology, Stuttgart, Germany, 21 September 1998. [Google Scholar]
- Lynch, D.D. Vibratory gyro analysis by the method of averaging. In Proceedings of the 2nd International Conference on Gyroscopic Technology and Navigation, St. Petersburg, Russia, 24 May 1995; pp. 26–34. [Google Scholar]
- Lynch, D.D. MRIG frequency mismatch and quadrature control. In Proceedings of the 2014 International Symposium on Inertial Sensors and Systems (ISISS), Laguna Beach, CA, USA, 23 February 2014; pp. 1–4. [Google Scholar]
- Wang, Y.; Pan, Y.; Qu, T.; Jia, Y.; Yang, K.; Luo, H. Decreasing Frequency Splits of Hemispherical Resonators by Chemical Etching. Sensors 2018, 18, 3772. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, S.L.; Yang, H.; Xia, Y. Measurement Method of Hemispherical Resonator Frequency Splitting and Normal-mode Axis Azimuth Based on Amplitude Frequency Response Characteristics. Fligth Control. Detect. 2020, 3, 69–74. [Google Scholar]
- Pan, Y.; Qu, T.; Wang, D.; Wu, S.; Liu, J.; Tan, Z.; Yang, K.; Luo, H. Observation and analysis of the quality factor variation behavior in a monolithic fused silica cylindrical resonator. Sens. Actuators A Phys. 2017, 260, 81–89. [Google Scholar] [CrossRef] [Green Version]
- Zhbanov, Y.K. Self-tuning control loop for suppression of quadrature in a hemispherical resonator gyro. In Proceedings of the Saint Petersburg International Conference on Integrated Navigation Systems, Saint Petersburg, Russia, 29–31 May 2006. [Google Scholar]
- Zhbanov, Y.K. Amplitude control contour in a hemispherical resonator gyro with automatic compensation for difference in Q-factors. Mech. Solids 2008, 43, 328–332. [Google Scholar] [CrossRef]
- Shatalov, M.; Coetzee, C. Dynamics of Rotating and Vibrating Thin Hemispherical Shell with Mass and Damping Imperfections and Parametrically Driven by Discrete Electrodes. Gyroscopy Navig. 2011, 2, 27–33. [Google Scholar] [CrossRef]




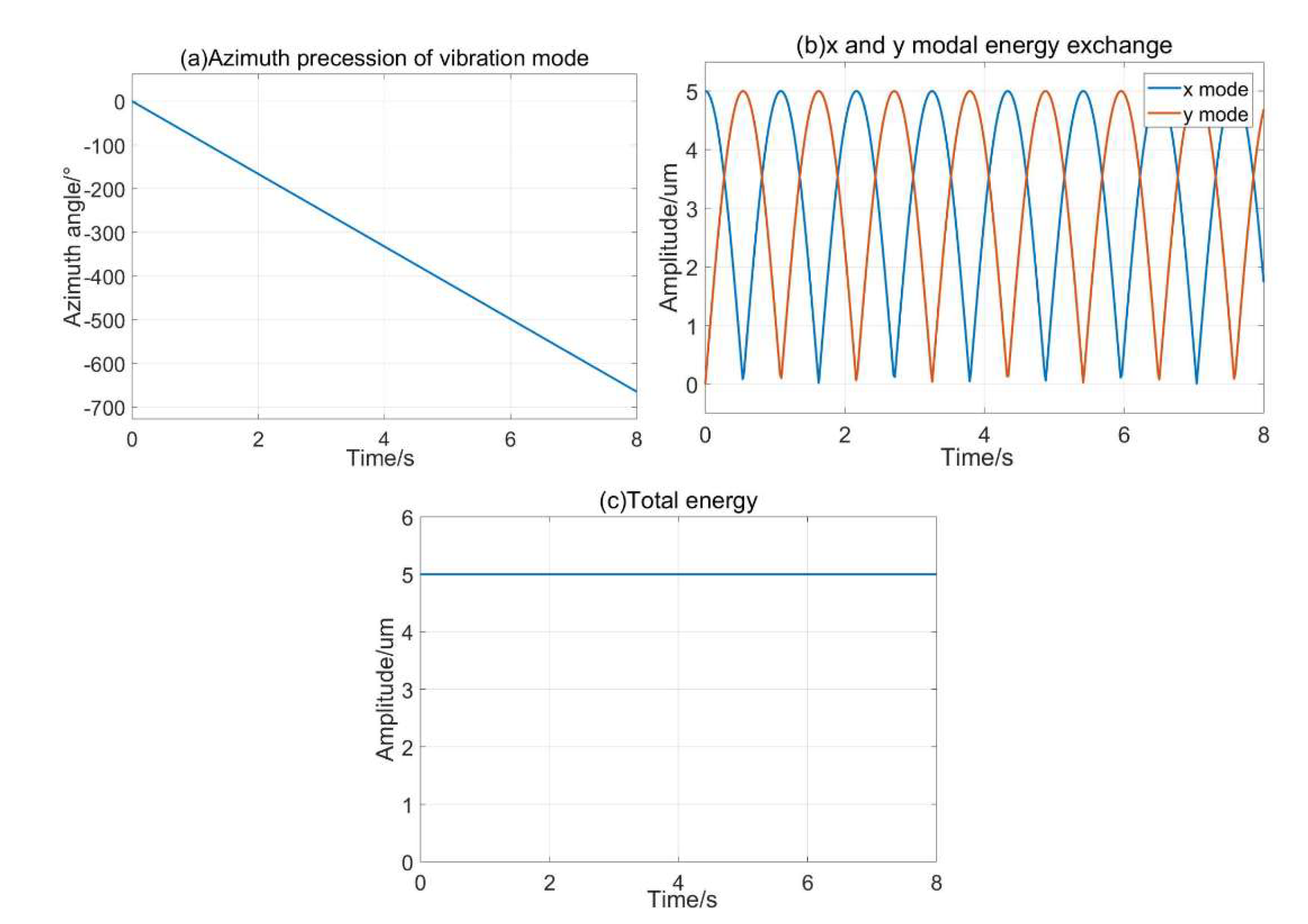

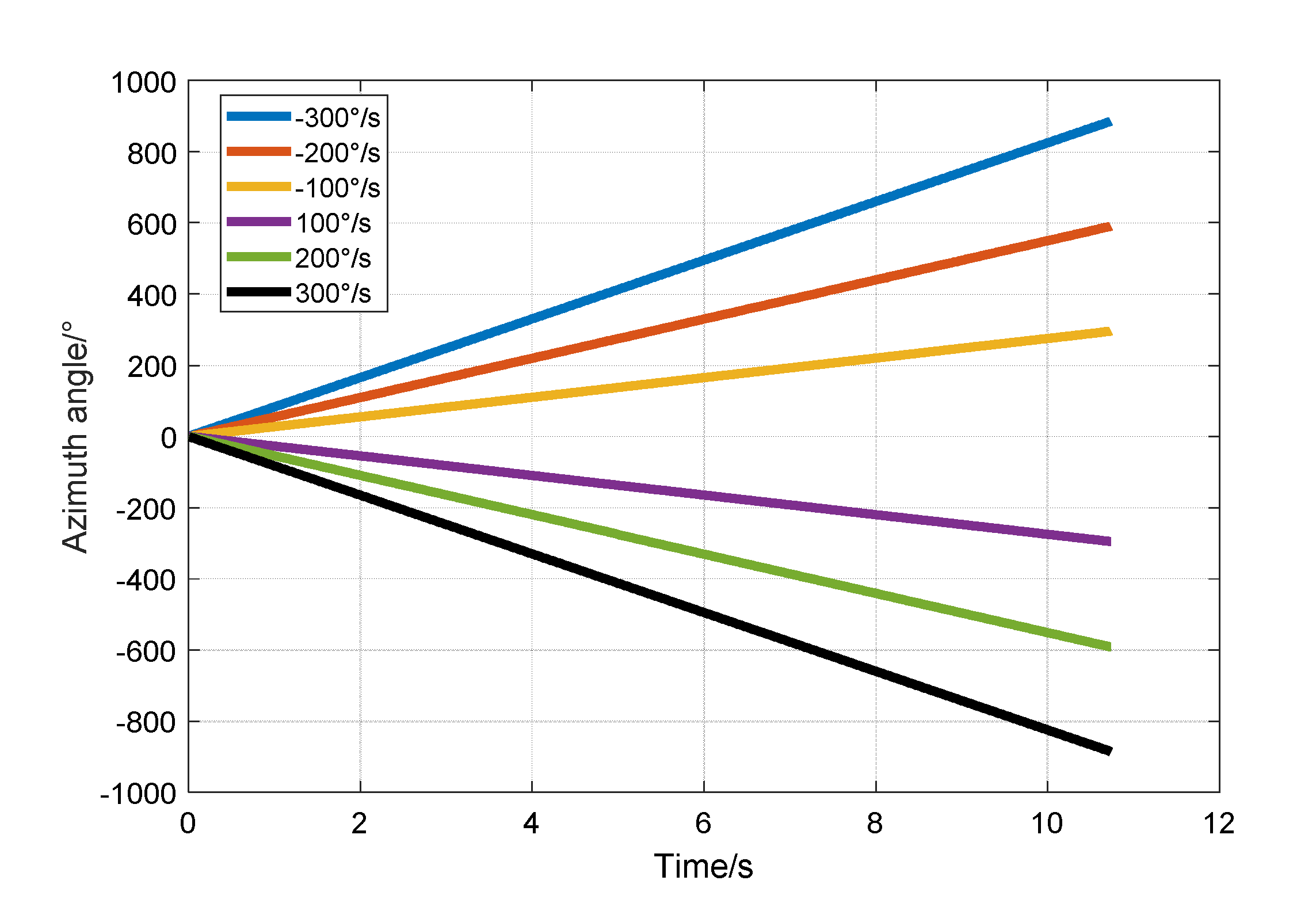
| 3 | 4500 × 2π | 100 | 100 |
| Modal x initial amplitude (um) | Modal y initial amplitude (um) | ||
| 2.2 | 7,200,000 | 5 | 1 |
| External Input Angular Velocity | Standing Wave Precession Angular Velocity | Precession Scale Factor |
|---|---|---|
| −300°/s | 82.76°/s | −0.2758 |
| −200°/s | 55.10°/s | −0.2755 |
| −100°/s | 27.57°/s | −0.2757 |
| 100°/s | −27.56°/s | −0.2756 |
| 200°/s | −55.28°/s | −0.2764 |
| 300°/s | −82.84°/s | −0.2761 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, W.; Yang, H.; Liu, F.; Su, Y.; Song, L. The Energy Compensation of the HRG Based on the Double-Frequency Parametric Excitation of the Discrete Electrode. Sensors 2020, 20, 3549. https://doi.org/10.3390/s20123549
Zhao W, Yang H, Liu F, Su Y, Song L. The Energy Compensation of the HRG Based on the Double-Frequency Parametric Excitation of the Discrete Electrode. Sensors. 2020; 20(12):3549. https://doi.org/10.3390/s20123549
Chicago/Turabian StyleZhao, Wanliang, Hao Yang, Fucheng Liu, Yan Su, and Lijun Song. 2020. "The Energy Compensation of the HRG Based on the Double-Frequency Parametric Excitation of the Discrete Electrode" Sensors 20, no. 12: 3549. https://doi.org/10.3390/s20123549
APA StyleZhao, W., Yang, H., Liu, F., Su, Y., & Song, L. (2020). The Energy Compensation of the HRG Based on the Double-Frequency Parametric Excitation of the Discrete Electrode. Sensors, 20(12), 3549. https://doi.org/10.3390/s20123549




