Road Profile Estimation Using a 3D Sensor and Intelligent Vehicle
Abstract
:1. Introduction
2. System Structure
3. Method
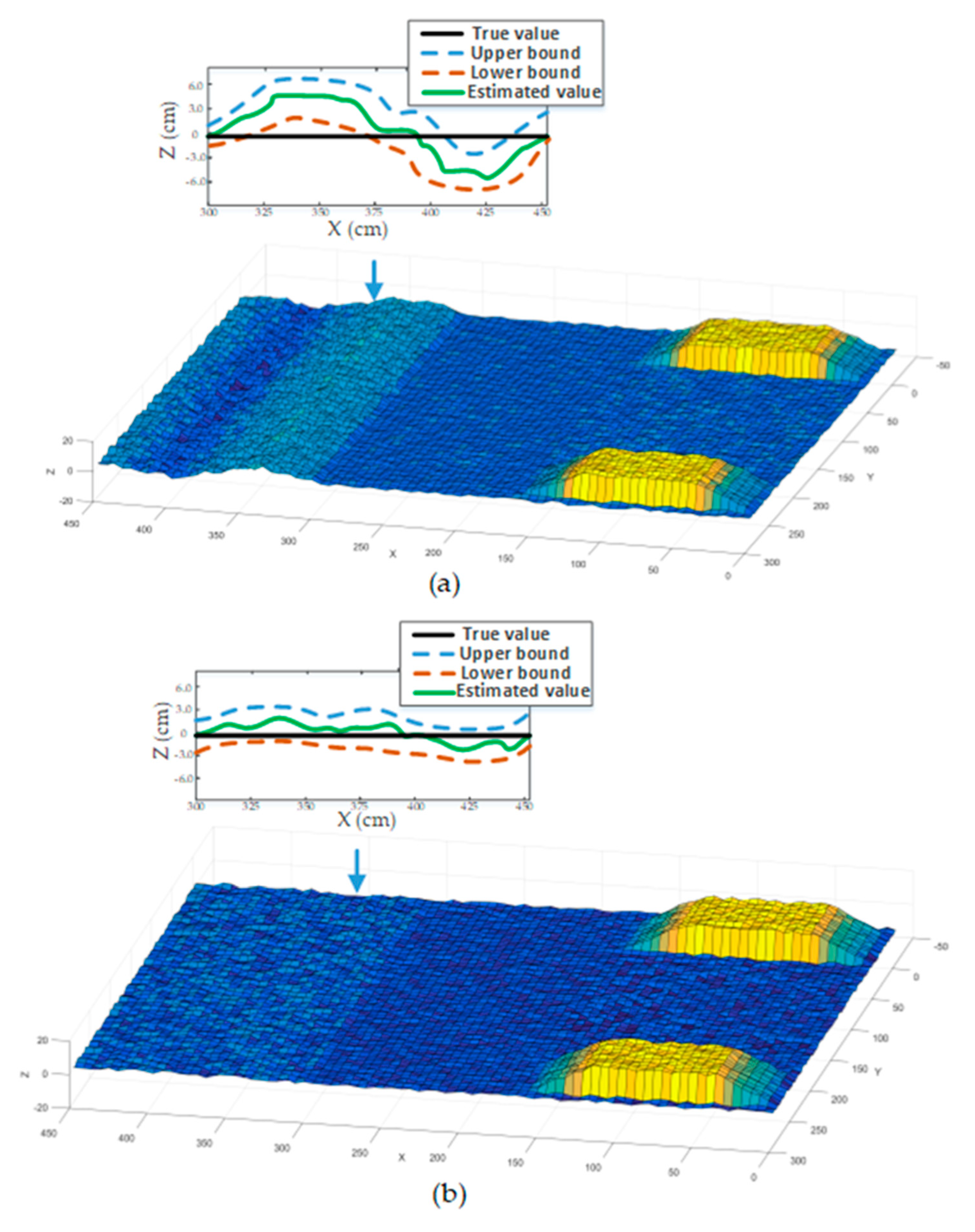
3.1. Elevation Map Estimation
3.1.1. Coordinate System Definition
3.1.2. Uncertain Estimation of Location System
3.1.3. Uncertain Estimation of LiDAR System
3.1.4. Elevation Map Update Method
3.2. Model Predictive Control with Preview
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hemann, G.; Singh, S.; Kaess, M. Long-range GPS-denied aerial inertial navigation with LIDAR localization. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 1659–1666. [Google Scholar]
- Levinson, J.; Thrun, S. Robust vehicle localization in urban environments using probabilistic maps. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation(ICRA), Anchorage, AK, USA, 3–7 May 2010; pp. 4372–4378. [Google Scholar]
- Chong, Z.; Qin, B.; Bandyopadhyay, T.; Rus, D. Synthetic 2D LiDAR for precise vehicle localization in 3D urban environment. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, Germany, 6–10 May 2013; pp. 1554–1559. [Google Scholar]
- Yoneda, K.; Tehrani, H.; Ogawa, T.; Hukuyama, N. LiDAR scan feature for localization with highly precise 3D map. In Proceedings of the 2014 IEEE Intelligent Vehicles Symposium, Dearborn, MI, USA, 8–11 June 2014; pp. 1659–1666. [Google Scholar]
- Soloviev, A. Tight coupling of GPS, laser scanner, and inertial measurements for navigation in urban environments. In Proceedings of the 2008 IEEE/ION Position, Location and Navigation Symposium, Monterey, CA, USA, 5–8 May 2008. [Google Scholar]
- Gao, Y.; Liu, S.; Atia, M.M.; Noureldin, A. INS/GPS/LiDAR integrated navigation system for urban and indoor environments using hybrid scan matching algorithm. Sensors 2015, 15, 23286–23302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wan, G.W.; Yang, X.L.; Cai, R.L.; Li, H.; Zhou, Y.; Wang, H.; Song, S.X. Robust and Precise Vehicle Localization based on Multi-sensor Fusion in Diverse City Scenes. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 4670–4677. [Google Scholar]
- Wolcott, R.W.; Eustice, R.M. Robust LIDAR localization using multiresolution gaussian mixture maps for autonomous driving. Int. J. Robot. Res. 2017, 35, 292–319. [Google Scholar] [CrossRef]
- Tang, J.; Chen, Y.; Niu, X.; Wang, L.; Chen, L.; Liu, J.; Shi, C.; Hyyppä, J. LiDAR Scan Matching Aided Inertial Navigation System in GNSS-Denied Environments. Sensors 2015, 15, 16710–16728. [Google Scholar] [CrossRef] [PubMed]
- Chang, L.; Niu, X.; Liu, T.; Tang, J.; Qian, C. GNSS/INS/LiDAR-SLAM Integrated Navigation System Based on Graph Optimization. Remote Sens. 2019, 11, 1009. [Google Scholar] [CrossRef] [Green Version]
- Qin, T.; Li, P.; Shen, S. VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef] [Green Version]
- Qian, C.; Liu, H.; Tang, J.; Chen, Y.; Kaartinen, H.; Kukko, A.; Zhu, L.; Liang, X.; Chen, L.; Hyyppä, J. An integrated GNSS/INS/LiDAR-SLAM positioning method for highly accurate forest stem mapping. Remote Sens. 2016, 9, 3. [Google Scholar] [CrossRef] [Green Version]
- Pierzchała, M.; Giguère, P.; Astrup, R. Mapping forests using an unmanned ground vehicle with 3D LiDAR and graph-SLAM. Comput. Electron. Agric. 2018, 145, 217–225. [Google Scholar] [CrossRef]
- Cole, D.M.; Newman, P.M. Using laser range data for 3D SLAM in outdoor environments. In Proceedings of the IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006; pp. 1556–1563. [Google Scholar]
- Droeschel, D.; Schwarz, M.; Behnke, S. Continuous mapping and localization for autonomous navigation in rough terrain using a 3D laser scanner. Robot. Auton. Syst. 2017, 88, 104–115. [Google Scholar] [CrossRef]
- Dingxuan, Z.; Lili, W.; Yilei, L.; Miaomiao, D. Extraction of preview elevation of road based on 3D sensor. Measurement 2018, 127, 104–114. [Google Scholar]
- Peter, F.; Michael, B.; Marco, H. Probabilistic Terrain Mapping for Mobile Robots with Uncertain Localization. IEEE Robot. Autom. Lett. 2018, 3, 3019–3026. [Google Scholar]
- Wang, L.L.; Zhao, D.X.; Ni, T.; Liu, S. Extraction of preview elevation information based on terrain mapping and trajectory prediction in real-time. IEEE Access 2020, 8, 76618–76631. [Google Scholar] [CrossRef]
- Ryu, S.; Park, Y.; Suh, M. Ride quality analysis of a tracked vehicle suspension with a preview control. J. Terramechanics 2011, 48, 409–417. [Google Scholar] [CrossRef]
- Youn, I.; Khan, M.A.; Uddin, N. Road disturbance estimation for the optimal preview control of an active suspension systems based on tracked vehicle model. Int. J. Automot. Technol. 2017, 18, 307–316. [Google Scholar] [CrossRef]
- Göhrle, C.; Schindler, A.; Wagner, A. Model Predictive Control of semi-active and active suspension systems with available road preview. In Proceedings of the 2013 European Control Conference (ECC), Zürich, Switzerland, 17–19 July 2013; pp. 1499–1504. [Google Scholar]
- Mehra, R.; Amin, J.; Hedrick, K.; Osorio, C.; Gopalasamy, S. Active suspension using preview information and model predictive control. In Proceedings of the 1997 IEEE International Conference on Control Applications, Hartford, FL, USA, 5–7 October 1997; pp. 860–865. [Google Scholar]
- Huang, Y.; Na, J.; Wu, X.; Liu, X.; Guo, Y. Adaptive control of nonlinear uncertain active suspension systems with prescribed performance. ISA Trans. 2015, 54, 145–155. [Google Scholar] [CrossRef] [PubMed]
- Marzbanrad, J.; Ahmadi, G.; Zohoor, H.; Hojjat, Y. Stochastic optimal preview control of a vehicle suspension. J. Sound Vib. 2004, 275, 973–990. [Google Scholar] [CrossRef]
- Pan, H.; Sun, W.; Jing, X.; Gao, H.; Yao, J. Adaptive tracking control for active suspension systems with non-ideal actuators. J. Sound Vib. 2017, 399, 2–20. [Google Scholar] [CrossRef]
- Youn, I.; Tchamna, R.; Lee, S.H.; Uddin, N.; Lyu, S.K.; Tomizuka, M. Preview suspension control for a full tracked vehicle. Int. J. Automot. Technol. 2014, 15, 399–410. [Google Scholar] [CrossRef]
- Göhrle, C.; Schindler, A. Road profile estimation and preview control for low band width active suspension systems. IEEE/ASME Trans. Mechatron. 2015, 20, 2299–2310. [Google Scholar] [CrossRef]
- Theunissen, J.; Sorniotti, A.; Gruber, P. Regionless Explicit Model Predictive Control of Active Suspension Systems with Preview. IEEE Trans. Ind. Electron. 2020, 67, 4877–4888. [Google Scholar] [CrossRef]
- Du, M.; Zhao, D.; Yang, M. Nonlinear extended state observer-based output feedback stabilization control for uncertain nonlinear half-car active suspension systems. Nonlinear Dyn. 2020, 100, 2483–2503. [Google Scholar] [CrossRef]
- Sun, W.; Zhao, Y.; Li, J. Active Suspension Control with Frequency Band Constraints and Actuator Input Delay. IEEE Trans. Ind. Electron. 2012, 59, 530–537. [Google Scholar]
- Pan, H.; Sun, W. Nonlinear Output Feedback Finite-Time Control for Vehicle Active Suspension Systems. IEEE Trans. Ind. Inform. 2019, 15, 2073–2082. [Google Scholar] [CrossRef]











| Velocity | Type | Passive | OFC | MPC |
|---|---|---|---|---|
| 35 km/h | Heave (cm) | 4.13 | 2.61 (−37%) | 1.22 (−71%) |
| Pitch (deg) | 1.26 | 0.74 (−41%) | 0.39 (−70%) | |
| Roll (deg) | 1.01 | 0.53 (−46%) | 0.37 (−63%) | |
| 45 km/h | Heave (cm) | 5.05 | 3.68 (−27%) | 1.66 (−67%) |
| Pitch (deg) | 1.72 | 0.62 (−30%) | 0.61 (−64%) | |
| Roll (deg) | 1.61 | 0.61 (−31%) | 0.64 (−60%) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ni, T.; Li, W.; Zhao, D.; Kong, Z. Road Profile Estimation Using a 3D Sensor and Intelligent Vehicle. Sensors 2020, 20, 3676. https://doi.org/10.3390/s20133676
Ni T, Li W, Zhao D, Kong Z. Road Profile Estimation Using a 3D Sensor and Intelligent Vehicle. Sensors. 2020; 20(13):3676. https://doi.org/10.3390/s20133676
Chicago/Turabian StyleNi, Tao, Wenhang Li, Dingxuan Zhao, and Zhifei Kong. 2020. "Road Profile Estimation Using a 3D Sensor and Intelligent Vehicle" Sensors 20, no. 13: 3676. https://doi.org/10.3390/s20133676
APA StyleNi, T., Li, W., Zhao, D., & Kong, Z. (2020). Road Profile Estimation Using a 3D Sensor and Intelligent Vehicle. Sensors, 20(13), 3676. https://doi.org/10.3390/s20133676





