A Method for the Assessment of Textile Pilling Tendency Using Optical Coherence Tomography
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fabric Material and Laser Processing
2.2. Abrasion Tests
2.3. Textile Image Acquisition and Pre-Processing
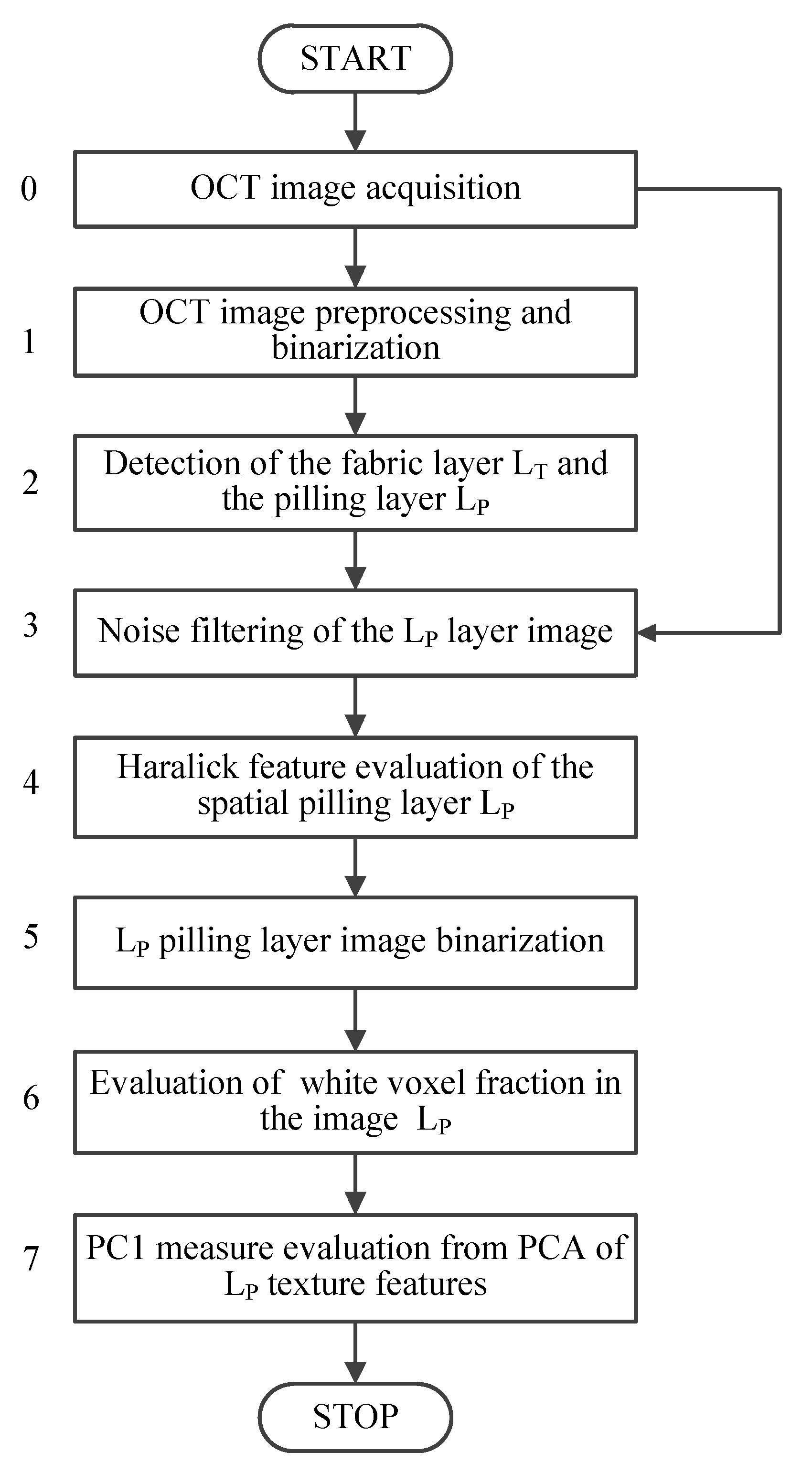
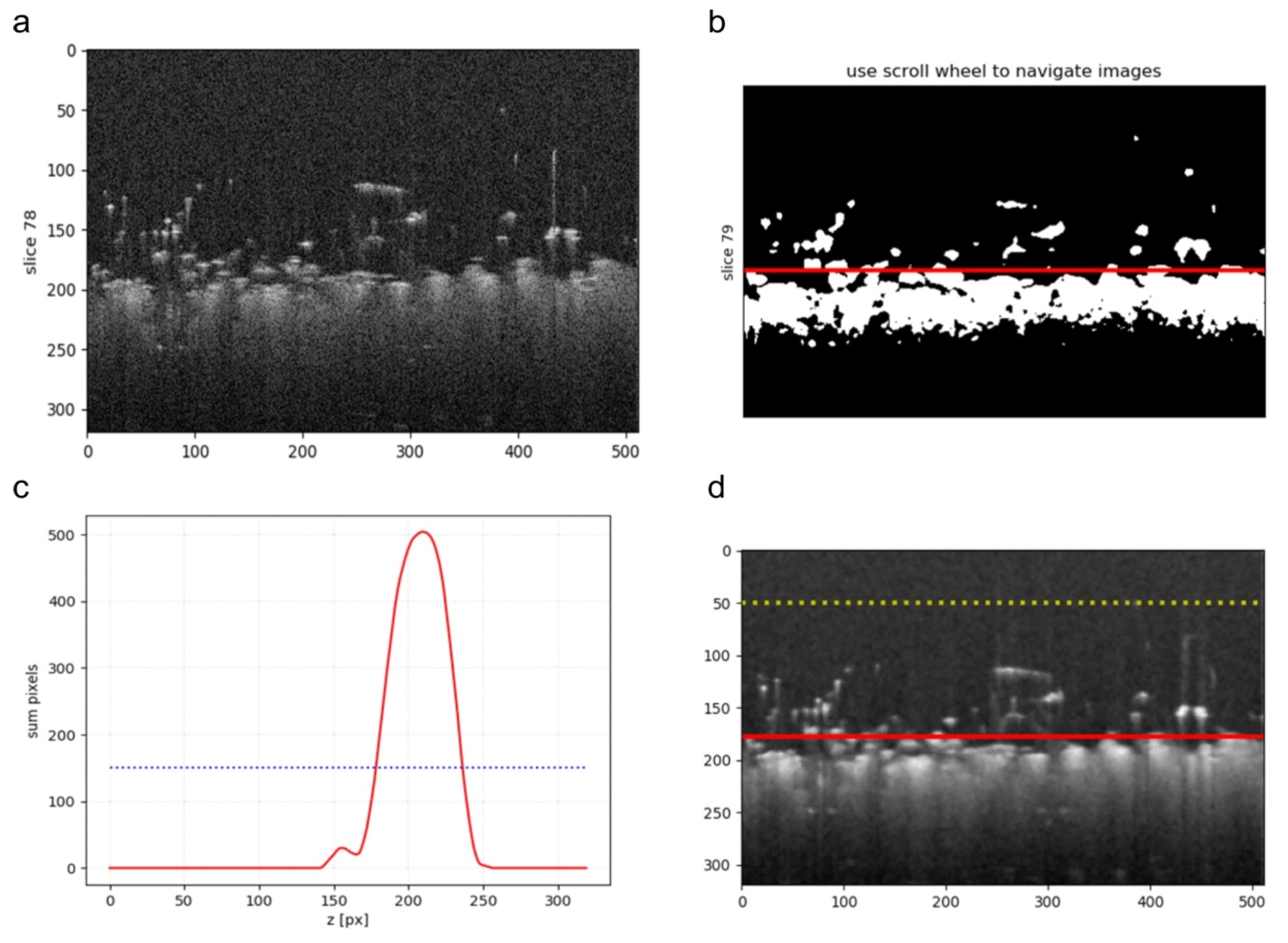
2.4. Fabric and Pilling Layer Detection
2.5. Assessment of Pilling Layer Textural Features
3. Results
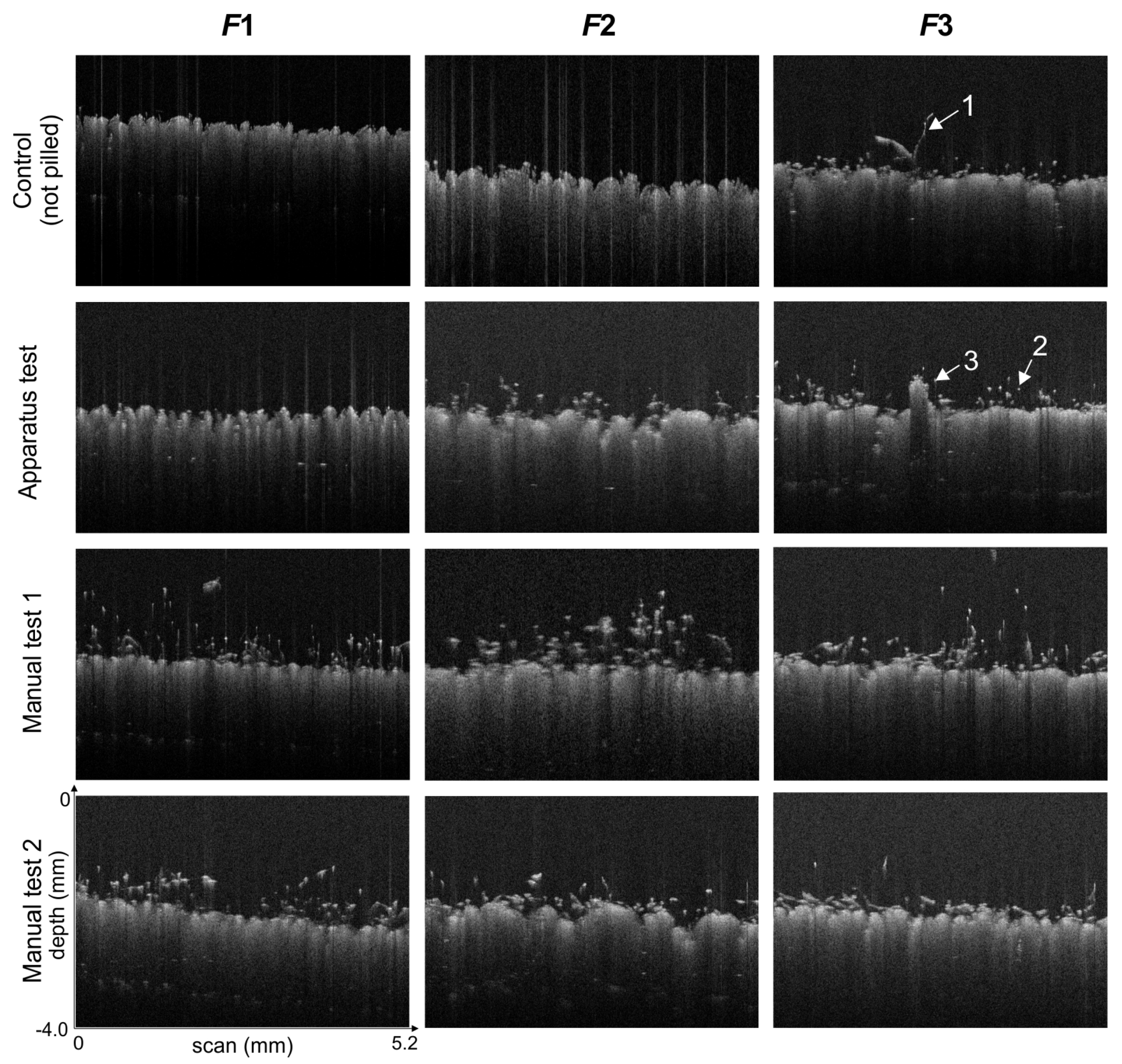
3.1. Pilling Visual Assessment
3.2. Pilling Feature Analysis in OCT Images
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| OCT | optical coherence tomography |
| SS-OCT | swept-source OCT |
| MEMS | Micro-Electro-Mechanical Systems |
| SD-OCT | spectral domain OCT |
| GLCM | Gray-Level Co-occurrence Matrix |
| PN-EN | Polish Norm introducing the European Norm |
| PN-EN ISO | Polish Norm introducing the International Norm |
| ISO | International Organization for Standardization |
| SPI | Southampton Photonics Inc. |
| ASTM | American Society for Testing and Materials |
| PC | personal computer |
| PCA | principal component analysis |
| principal component | |
| first principal component | |
| second principal component | |
| NP | not pilled |
| AT | apparatus test |
| T1 | Test 1 |
| T2 | Test 2 |
References
- Gintis, D.; Mead, E. The mechanism of pilling. Text. Res. J. 1959, 15, 578–585. [Google Scholar] [CrossRef]
- Cooke, W.D. The Influence of Fibre Fatigue on the Pilling Cycle, Part 1, Fuzz formation. J. Text. Inst. 1982, 1, 13–19. [Google Scholar] [CrossRef]
- Bilisik, K.; Yolakan, G. Abrasion Properties of Upholstery Flocked Fabrics. Text. Res. J. 2009, 79, 1625–1632. [Google Scholar] [CrossRef]
- Techniková, L.; Tunak, M. Comparison of Two Different Principles of 3D Fabric Surface Reconstruction. Fibres Text. East. Eur. 2016, 24, 38–43. [Google Scholar] [CrossRef]
- Kang, T.J.; Kim, S.C.; Sul, I.H.; Youn, J.R.; Chung, K. Fabric surface roughness evaluation using wavelet-fractal method. Part I: Wrinkle, smoothness and seam pucker. Text. Res. J. 2005, 75, 751–760. [Google Scholar] [CrossRef]
- Saharkhiz, S.; Abdorazaghi, M. The Performance of Different Clustering Methods in the Objective Assessment of Fabric Pilling. J. Eng. Fibers Fabr. 2012, 7, 35–41. [Google Scholar] [CrossRef] [Green Version]
- Gao, W.D.; Wang, S.Y.; Pan, R.R.; Liu, J.H. Automatic Location of Pills in Woven Fabric Based on Gabor Filter. Key Eng. Mater. 2011, 464, 745–748. [Google Scholar] [CrossRef]
- Jing, J.; Kang, X. Fabric Pilling Image Segmentation Based on Mean Shift. Commun. Comput. Inf. Sci. 2011, 143, 80–84. [Google Scholar]
- Deng, Z.; Wang, L.; Wang, X. An integrated method of feature extraction and objective evaluation of fabric pilling. J. Text. Inst. 2011, 102, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Wang, X.; Palmer, S. The Robustness of Objective Fabric Pilling Evaluation Method. Fibers Polym. 2012, 10, 108–115. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.C.; Kang, T. Fabric surface roughness evaluation using wavelet-fractal method. Part II: Fabric pilling evaluation. Text. Res. J. 2005, 75, 761–770. [Google Scholar] [CrossRef]
- Furferi, R.; Governi, L.; Volpe, Y. Machine Vision-Based Pilling Assessment: A Review. J. Eng. Fibers Fabr. 2015, 10, 79–93. [Google Scholar] [CrossRef]
- Huang, D.; Swanson, E.A.; Lin, C.P.; Schuman, J.S.; Stinson, W.G.; Chang, W.; Hee, M.R.; Flotte, T.; Gregory, K.; Puliafito, C.A. Optical coherence tomography. Science 1991, 254, 1178–1181. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xiong, Q.; Tong, X.; Deng, C.; Zhang, C.; Wang, P.; Zheng, Z.; Liu, F. A Novel Mach-Zehnder Interferometer Using Eccentric-Core Fiber Design for Optical Coherence Tomography. Sensors 2018, 18, 1540. [Google Scholar] [CrossRef] [Green Version]
- Drexler, W.; Liu, M.; Kumar, A.; Kamali, T.; Unterhuber, A.; Leitgeb, R.A. Optical coherence tomography today: Speed, contrast, and multimodality. J. Biomed. Opt. 2014, 19, 071412. [Google Scholar] [CrossRef]
- Wollweber, M.; Roth, B. Raman sensing and its multimodal combination with optoacoustics and OCT for applications in the life sciences. Sensors 2019, 19, 2387. [Google Scholar] [CrossRef] [Green Version]
- Yi, L.; Sun, L.; Zou, M.; Hou, B. Dual-channel spectral domain optical coherence tomography based on a single spectrometer using compressive sensing. Sensors 2019, 19, 4006. [Google Scholar] [CrossRef] [Green Version]
- Choi, W.J.; Jayaraman, V.; Cable, A.E.; Hornegger, J.; Duker, J.S.; Fujimoto, J.G. Handheld ultrahigh speed swept source optical coherence tomography instrument using a MEMS scanning mirror. Biomed. Opt. Express 2014, 5, 293–311. [Google Scholar] [CrossRef] [Green Version]
- Cogliati, A.; Canavesi, C.; Hayes, A.; Tankam, P.; Duma, V.F.; Santhanam, A.; Thompson, K.P.; Rolland, J.P. MEMS-based handheld scanning probe with pre-shaped input signals for distortion-free images in Gabor-domain optical coherence microscopy. Opt. Express 2016, 24, 13365–13374. [Google Scholar] [CrossRef]
- Laopornpichayanuwat, W.; Visessamit, J.; Tianprateep, M. 3-D Surface roughness profile of 316-stainless steel using vertical scanning interferometry with a superluminescent diode. Meas. J. Int. Meas. Confed. 2012, 45, 2400–2406. [Google Scholar] [CrossRef]
- Hutiu, G.; Duma, V.F.; Demian, D.; Bradu, A.; Podoleanu, A. Assessment of Ductile, Brittle, and Fatigue Fractures of Metals Using Optical Coherence Tomography. Metals 2018, 8, 117. [Google Scholar] [CrossRef] [Green Version]
- Korzeniewska, E.; Sekulska-Nalewajko, J.; Gocławski, J.; Rosik, R.; Szczęsny, A.; Starowicz, Z. Surface Morphology Analysis of Metallic Structures Formed on Flexible Textile Composite Substrates. Sensors 2020, 20, 2128. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, Y.; Choi, E.S.; Kwak, W.; Shin, Y.; Jung, W.; Ahn, Y.C.; Chen, Z. Three-dimensional non-destructive optical evaluation of laser-processing performance using optical coherence tomography. Opt. Laser Technol. 2008, 40, 625–631. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stifter, D.; Wiesauer, K.; Wurm, M.; Schlotthauer, E.; Kastner, J.; Pircher, M.; Götzinger, E.; Hitzenberger, C.K. Investigation of polymer and polymer/fibre composite materials with optical coherence tomography. Meas. Sci. Technol. 2008, 19, 1–8. [Google Scholar] [CrossRef]
- Gliścińska, E.; Sankowski, S.; Krucińska, I.; Gocławski, J.; Michalak, M.; Rowińska, Z.; Sekulska-Nalewajko, J. Optical coherence tomography image analysis of polymer surface layers in sound-absorbing fibrous composite materials. Polym. Test. 2017, 63, 194–203. [Google Scholar] [CrossRef]
- Sabuncu, M.; Özdemir, H.; Akdogan, M.U. Automatic Identification of Weave Patterns of Checked and Colored Fabrics Using Optical Coherence Tomography. IEEE Photonics J. 2017, 9, 1–8. [Google Scholar] [CrossRef]
- Sabuncu, M.; Özdemir, H. Recognition of Weave Patterns of Striped Fabrics Using Optical Coherence Tomography. Fibres Text. East. Eur. 2018, 26, 98–103. [Google Scholar] [CrossRef] [Green Version]
- Bodnarova, A.; Bennamoun, M.; Kubik, K.K. Suitability analysis of techniques for flaw detection in textiles using texture analysis. Pattern Anal. Appl. 2000, 3, 254–266. [Google Scholar] [CrossRef]
- Hu, Y.; Long, Z.; Sundaresan, A.; Alfarraj, M.; AlRegib, G.; Park, S.; Jayaraman, S. Fabric surface characterization: Assessment of deep learning-based texture representations using a challenging dataset. J. Text. Inst. 2020, 29, 1–3. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, 3, 610–621. [Google Scholar] [CrossRef] [Green Version]
- Haralick, R.M.; Shapiro, L.G. Computer and Robot Vision; Addison-Wesley Longman Publishing Co.: Boston, MA, USA, 1992; p. 459. [Google Scholar]
- Korzeniewska, E.; Sekulska-Nalewajko, J.; Gocławski, J.; Maria, W. Assessment of pilling effect on the laser modified textile substrates. In Proceedings of the 2018 Applications of Electromagnetic in Modern Techniques and Medicine (PTZE), Racławice, Poland, 9–12 September 2018; pp. 129–132. [Google Scholar] [CrossRef]
- Testex Sales Team. Martindale Abrasion & Pilling Tester. Available online: https://www.testextextile.com/product/martindale-abrasion-pilling-tester-tf210/ (accessed on 15 June 2020).
- Wasatch Photonics. WP OCT 1300 nm: Ultra Deep Imaging|Wasatch Photonics. Available online: https://wasatchphotonics.com/product-category/optical-coherence-tomography/wp-oct-1300/ (accessed on 17 February 2019).
- Dey, S. Hands-On Image Processing with Python: Expert Techniques for Advanced Image Analysis and Effective Interpretation of Image Data; Packt: Birmingham, UK, 2018; p. 492. [Google Scholar]
- Gouillart, E. Scikit-Image: Image Processing. 2018. Available online: http://scipy-lectures.org/preface.html (accessed on 17 February 2019).
- Gonzalez, R.C.; Woods, R.E.R.E. Digital Image Processing, 4th ed.; Pearson: London, UK, 2017; p. 1168. [Google Scholar]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef] [Green Version]
- Duda, R.O.; Hart, P.E. Use of the Hough transformation to detect lines and curves in pictures. Commun. ACM 1972, 15, 11–15. [Google Scholar] [CrossRef]
- Lim, J.S. Two-Dimensional Signal and Image Processing; Prentice Hall: Englewood Cliffs, NJ, USA, 1990; p. 694. [Google Scholar]
- Aksoy, S.; Haralick, R.M. Feature normalization and likelihood-based similarity measures for image retrieval. Pattern Recognit. Lett. 2001, 22, 563–582. [Google Scholar] [CrossRef] [Green Version]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]








| Name | Composition | Weight | Pilling Grade | Laser Power [W] | Pilling Grade after Ablation |
|---|---|---|---|---|---|
| 100% polyester | 240 | 5 | 14 | 5 | |
| 65% polyester | 240 | 2 | 18 | 3 | |
| 35% polyacrylonitrile | |||||
| 68.1% cotton | 240 | 2–3 | 16 | 3 | |
| 31.9% poliamid |
| Textile | Not Pilled (Control) | SD | Manual Test 1 | SD | Manual Test 2 | SD | Apparatus Test | SD |
|---|---|---|---|---|---|---|---|---|
| 0.43 | 0.22 | 2.56 | 0.38 | 2.93 | 0.46 | 0.24 | 0.02 | |
| 0.90 | 0.06 | 2.54 | 0.30 | 1.88 | 0.34 | 2.67 | 0.14 | |
| 0.89 | 0.08 | 2.89 | 0.07 | 1.64 | 0.19 | 2.16 | 0.14 |
| Feature | Textile | Not Pilled (Control) | SD | Manual Test 1 | SD | Manual Test 2 | SD | Apparatus Test | SD |
|---|---|---|---|---|---|---|---|---|---|
| Energy | 0.0045 | 0.0006 | 0.0021 | 0.0002 | 0.0024 | 0.0002 | 0.0036 | 0.0006 | |
| 0.0034 | 0.0003 | 0.0021 | 0.0004 | 0.0032 | 0.0004 | 0.0030 | 0.0004 | ||
| 0.0035 | 0.0005 | 0.0027 | 0.0006 | 0.0030 | 0.0007 | 0.0025 | 0.0003 | ||
| Contrast | 17.08 | 0.46 | 64.39 | 7.56 | 69.24 | 7.05 | 24.60 | 1.19 | |
| 33.08 | 3.26 | 75.53 | 16.37 | 47.79 | 4.97 | 68.24 | 3.78 | ||
| 41.83 | 1.24 | 87.57 | 1.97 | 62.24 | 8.24 | 68.77 | 2.89 | ||
| Variance | 33.43 | 4.28 | 177.85 | 13.77 | 181.26 | 20.83 | 55.89 | 14.90 | |
| 84.43 | 11.99 | 196.26 | 35.95 | 121.02 | 17.00 | 175.34 | 12.64 | ||
| 94.49 | 8.26 | 205.17 | 5.96 | 151.98 | 28.13 | 174.91 | 17.20 | ||
| Homogeneity | 0.299 | 0.006 | 0.241 | 0.005 | 0.249 | 0.001 | 0.283 | 0.002 | |
| 0.276 | 0.005 | 0.244 | 0.008 | 0.270 | 0.007 | 0.257 | 0.005 | ||
| 0.280 | 0.002 | 0.259 | 0.006 | 0.266 | 0.007 | 0.258 | 0.003 | ||
| Sum average | 122.05 | 7.01 | 115.82 | 11.46 | 109.41 | 15.92 | 65.58 | 4.67 | |
| 123.38 | 6.34 | 118.30 | 10.90 | 125.57 | 6.52 | 100.63 | 8.37 | ||
| 84.50 | 1.29 | 65.98 | 4.99 | 90.78 | 5.11 | 72.59 | 3.18 | ||
| Entropy | 8.35 | 0.18 | 9.86 | 0.10 | 9.71 | 0.15 | 8.76 | 0.25 | |
| 8.96 | 0.16 | 9.89 | 0.30 | 9.15 | 0.18 | 9.37 | 0.18 | ||
| 8.93 | 0.18 | 9.51 | 0.23 | 9.31 | 0.33 | 9.54 | 0.15 |
| Textile | Not Pilled | Manual Test 1 | Manual Test 2 | Apparatus Test |
|---|---|---|---|---|
| 99.43 | 95.85 | 98.17 | 96.36 | |
| 95.37 | 99.23 | 25.52 | 89.70 | |
| 98.44 | 91.11 | 85.43 | 99.03 | |
| 99.49 | 99.15 | 71.26 | 99.90 | |
| 97.89 | 14.18 | 99.48 | 94.56 | |
| 95.93 | 96.41 | 94.70 | 99.36 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sekulska-Nalewajko, J.; Gocławski, J.; Korzeniewska, E. A Method for the Assessment of Textile Pilling Tendency Using Optical Coherence Tomography. Sensors 2020, 20, 3687. https://doi.org/10.3390/s20133687
Sekulska-Nalewajko J, Gocławski J, Korzeniewska E. A Method for the Assessment of Textile Pilling Tendency Using Optical Coherence Tomography. Sensors. 2020; 20(13):3687. https://doi.org/10.3390/s20133687
Chicago/Turabian StyleSekulska-Nalewajko, Joanna, Jarosław Gocławski, and Ewa Korzeniewska. 2020. "A Method for the Assessment of Textile Pilling Tendency Using Optical Coherence Tomography" Sensors 20, no. 13: 3687. https://doi.org/10.3390/s20133687
APA StyleSekulska-Nalewajko, J., Gocławski, J., & Korzeniewska, E. (2020). A Method for the Assessment of Textile Pilling Tendency Using Optical Coherence Tomography. Sensors, 20(13), 3687. https://doi.org/10.3390/s20133687






