Degradation Monitoring of Insulation Systems Used in Low-Voltage Electromagnetic Coils under Thermal Loading Conditions from a Creep Point of View
Abstract
:1. Introduction
- ➢
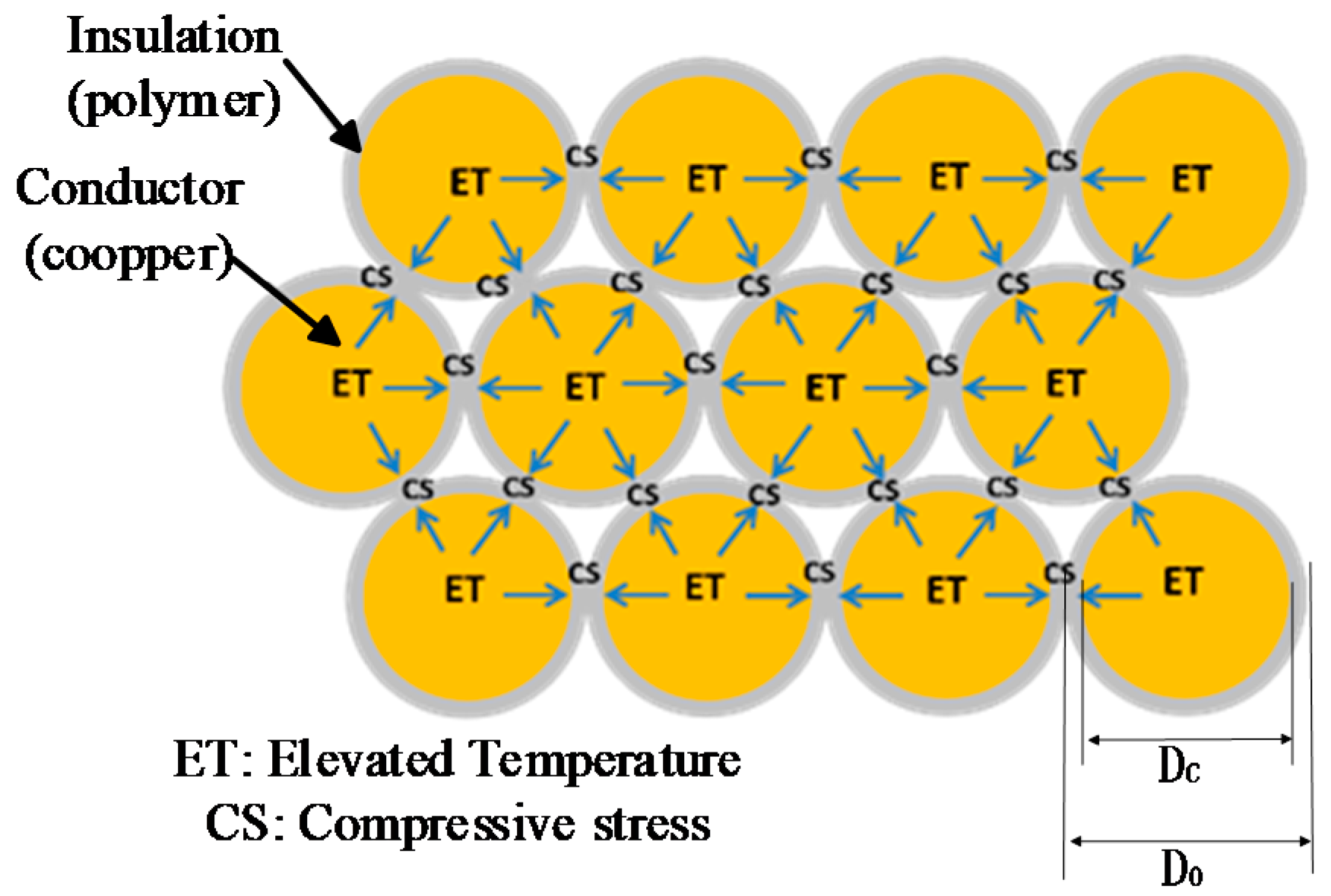
- Incipient degradation phase: As a current is passed through the wire, Joule heating causes an increase in the wire temperature, which results in expansion of the conductor (usually copper) and thus compressive stress on turn-to-turn insulation (usually a polymer). Under the long-term effects of compressive and thermal stresses on the turn-to-turn insulation, the insulation materials degrade and lead to a turn-to-turn short.
- ➢
- Late degradation phase: After the turn-to-turn short occurs, the direct-current (DC) resistance of the coil decreases, and thus current increases, which makes the coil temperature increase. A hot spot can form at the location of the short. Turn-to-turn short faults will spread quickly around the hot spot, which causes the coil to burn out, finally resulting in failure of the complete coil.
- (1)
- There are contradictory claims for the evolving trends of high-frequency electrical parameters in the literature. For example, Perisse et al. [32] and Savin et al. [34] claimed that the capacitance increased over the aging period while Younsi et al. [40] and Zhang et al. [41] found that the capacitance decreased during the aging time.
- (2)
- Perisse et al. [33] set a failure threshold of 95% of the healthy coil resonant frequency and mentioned that once the failure threshold is crossed, the coil should be maintained under monitoring. However, the experimental results in Jameson et al. [42] showed that the resonant frequency changed by only 2.5% before a short formed.
2. Coil Creep Degradation Mechanism Analysis
2.1. Creep Degradation of Inter-Turn Insulation Systems under Thermal Loading Conditions
2.2. Coil Electrical Behavior Analysis from a Creep Point of View
3. A Mapping Method from Coil Electrical Parameters to Inter-Turn Insulation Creep Deformation
4. Experimental Setup and Results
4.1. Outer Radius Measurement of the Magnet Wires
4.2. Coil Electrical Parameter Measurement
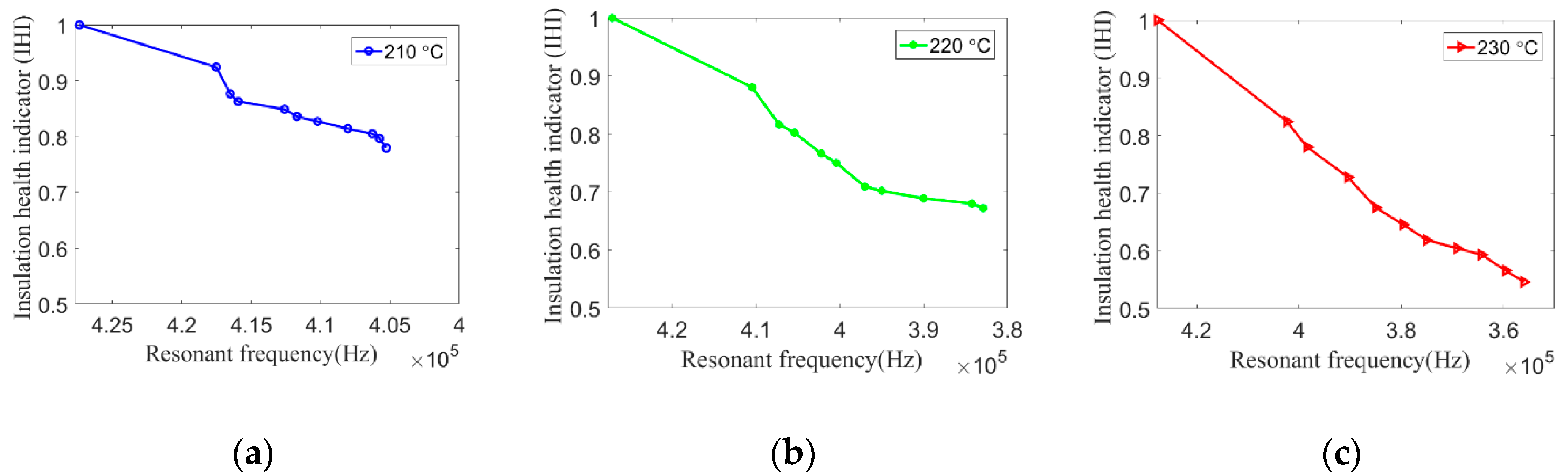
4.3. Experimental Result Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jameson, N.J.; Azarian, M.H.; Pecht, M. Impedance-based Condition Monitoring for Insulation Systems used in Low-voltage Electromagnetic Coils. IEEE Trans. Ind. Electron. 2017, 64, 3748–3757. [Google Scholar] [CrossRef]
- 2. Motor Reliability Working Group. Report of Large Motor Reliability Survey of Industrial and Commercial Installations, Part I. IEEE Trans. Ind. Appl. 1985, IA-21, 853–864. [CrossRef]
- 3. Motor Reliability Working Group. Report of Large Motor Reliability Survey of Industrial and Commercial Installations, Part II. IEEE Trans. Ind. Appl. 1985, IA-21, 865–872. [CrossRef]
- Thorsen, O.V.; Dalva, M. A Survey of Faults on Induction Motors in Offshore Oil Industry, Petrochemical Industry, Gas Terminals, and Oil Refineries. IEEE Trans. Ind. Appl. 1995, 31, 1186–1196. [Google Scholar] [CrossRef]
- Albrecht, P.F.; Appiarius, J.C.; McCoy, R.M.; Owen, E.L.; Sharma, D.K. Assessment of the reliability of motors in utility applications—Updated. IEEE Trans. Energy Convers. 1986, EC-1, 39–46. [Google Scholar] [CrossRef]
- Bacanskas, V.; Roberts, G.; Toman, G. Aging and Service Wear of Solenoid-Operated Valves Used in Safety Systems of Nuclear Power Plants: Volume 1, Operating Experience and Failure Identification; Technical Report; Franklin Research Center: Philadelphia, PA, USA; Oak Ridge National Lab.: Oak Ridge, TN, USA; Nuclear Regulatory Commission: Washington, DC, USA, 1987. [Google Scholar]
- Sant’Ana, W.C.; Salomon, C.P.; Lambert-Torres, G.; da Silva, L.E.B.; Bonaldi, E.L.; de Oliveira, L.E.L.; da Silva, J.G.B. Early Detection of Insulation Failures on Electric Generators through Online Frequency Response Analysis. Electr. Power Syst. Res. 2016, 140, 337–343. [Google Scholar] [CrossRef]
- Survey of Hydrogenerator Failures. Available online: https://e-cigre.org/publication/392-survey-of-hydrogenerator-failures (accessed on 26 June 2020).
- Arabian-Hoseynabadi, H.; Oraee, H.; Tavner, P.J. Failure Modes and Effects Analysis (FMEA) for Wind Turbines. Int. J. Electr. Power Energy Syst. 2010, 32, 817–824. [Google Scholar] [CrossRef] [Green Version]
- Salameh, F.; Picot, A.; Chabert, M.; Maussion, P. Regression Methods for Improved Lifespan Modeling of Low Voltage Machine Insulation. Math. Comput. Simul. 2017, 113, 200–216. [Google Scholar] [CrossRef] [Green Version]
- Tavner, P.J. Review of Condition Monitoring of Rotating Electrical Machines. IET Elect. Power Appl. 2008, 2, 215–247. [Google Scholar] [CrossRef]
- Grubic, S.; Aller, J.M.; Lu, B.; Habetler, T.G. A Survey on Testing and Monitoring Methods for Stator Insulation Systems of Low-Voltage Induction Machines Focusing on Turn Insulation Problems. IEEE Trans. Ind. Electron. Dec. 2008, 55, 4127–4136. [Google Scholar] [CrossRef] [Green Version]
- Nussbaumer, P.; Vogelsberger, M.A.; Wolbank, T.M. Induction Machine Insulation Health State Monitoring Based on Online Switching Transient Exploitation. IEEE Trans. Ind. Electron. 2015, 62, 1835–1845. [Google Scholar] [CrossRef]
- Stone, G.C. Condition Monitoring and Diagnostics of Motor and Stator Windings—A Review. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 2073–2080. [Google Scholar] [CrossRef]
- Stone, G.C. Recent important changes in IEEE Motor and Generator Winding Insulation Diagnostic Testing Standards. IEEE Trans. Ind. Appl. 2005, 41, 91–100. [Google Scholar] [CrossRef]
- Gyftakis, K.N.; Cardoso, A.J. Reliable Detection of Stator Inter-Turn Faults of Very Low Severity Level in Induction Motors. IEEE Trans. Ind. Electron. 2020. [Google Scholar] [CrossRef]
- Wang, K.; Guo, H.; Xu, A.; Jameson, N.J.; Pecht, M.; Yan, B. Creating Self-Aware Low-Voltage Electromagnetic Coils for Incipient Insulation Degradation Monitoring for Smart Manufacturing. IEEE Access 2018, 6, 69860–69868. [Google Scholar] [CrossRef]
- Radecki, A.; Dębowski, A.; Wójcik, M.; Lipnicki, P. Evaluation of a Diagnostic Information on Common Electrical Faults Contained in Signals of an Inverter-fed AC IM Drive with Current-oriented Control. In Proceedings of the 2016 10th International Conference on Compatibility, Power Electronics and Power Engineering, Bydgoszcz, Poland, 29 June–1 July 2016; pp. 286–291. [Google Scholar]
- Faiz, J.; Nejadi-Koti, H.; Valipour, Z. Comprehensive Review on Inter-turn Fault Indexes in Permanent Magnet Motors. IET Electr. Power Appl. 2017, 11, 142–156. [Google Scholar] [CrossRef]
- Malekpour, M.; Phung, B.T.; Ambikairajah, E. Online Technique for Insulation Assessment of Induction Motor Stator Windings under Different Load Conditions. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 349–358. [Google Scholar] [CrossRef]
- Devi, N.R.; Sarma, D.S.; Rao, P.R. Diagnosis and Classification of Stator Winding Insulation Faults on a Three-phase Induction Motor Using Wavelet and MNN. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 2543–2555. [Google Scholar] [CrossRef]
- Lee, S.B.; Tallam, R.M.; Habetler, T.G. A Robust, On-line Turn-fault Detection Technique for Induction Machines Based on Monitoring the Sequence Component Impedance Matrix. IEEE Trans. Power Electron. 2003, 18, 865–872. [Google Scholar]
- Cruz, S.M.A.; Cardoso, A.J.M. Stator Winding Fault Diagnosis in Three-phase Synchronous and Asynchronous Motors, by the Extended Park’s Vector Approach. IEEE Trans. Ind. Appl. 2001, 37, 1227–1233. [Google Scholar] [CrossRef]
- Bazan, G.H.; Scalassara, P.R.; Endo, W.; Goedtel, A.; Godoy, W.F.; Palácios, R.H. Stator Fault Analysis of Three-phase Induction Motors Using Information Measures and Artificial Neural Networks. Electr. Power Syst. Res. 2017, 143, 347–356. [Google Scholar] [CrossRef]
- Yagami, Y.; Araki, C.; Mizuno, Y.; Nakamura, H. Turn-to-Turn Insulation Failure Diagnosis of Stator Winding of Low Voltage Induction Motor with the Aid of Support Vector Machine. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 3099–3106. [Google Scholar] [CrossRef]
- Sun, Y.; Yu, X.; Wei, K.; Huang, Z.; Wang, X. A New Type of Search Coil for Detecting Inter-turn Faults in Synchronous Machines. Proc. Chin. Soc. Electr. Eng. 2014, 34, 917–924. [Google Scholar]
- Surya, G.N.; Khan, Z.J.; Ballal, M.S.; Suryawanshi, H.M. A Simplified Frequency-domain Detection of Stator Turn Fault in Squirrel-cage Induction Motors Using an Observer Coil Technique. IEEE Trans. Ind. Electron. 2017, 64, 1495–1506. [Google Scholar] [CrossRef]
- Ghanbari, T.; Farjah, A. A Magnetic Leakage Flux-based Approach for Fault Diagnosis in Electrical Machines. IEEE Sens. J. 2014, 14, 2981–2988. [Google Scholar] [CrossRef]
- Henao, H.; Demian, C.; Capolino, G.-A. A Frequency-domain Detection of Stator Winding Faults in Induction Machines Using an External Flux Sensor. IEEE Trans. Ind. Appl. 2003, 39, 1272–1279. [Google Scholar] [CrossRef]
- Gerada, C.; Bradley, K.; Sumner, M.; Wheeler, P.; Pickering, S.; Clare, J.; Whitley, C.; Towers, G. The Results Do Mesh. IEEE Ind. Appl. Mag. 2007, 13, 62–72. [Google Scholar] [CrossRef]
- Werynski, P.; Roger, D.; Corton, R.; Brudny, J.F. Proposition of a New Method for in Service Monitoring of the Aging of Stator Winding Insulation in AC Motors. IEEE Trans. Energy Convers. 2006, 21, 673–681. [Google Scholar] [CrossRef]
- Perisse, F.; Werynski, P.; Roger, D. A New Method for AC Machine Turn Insulation Diagnostic Based on High Frequency Resonances. IEEE Trans. Dielectr. Electr. Insul. 2007, 14, 1308–1315. [Google Scholar] [CrossRef]
- Perisse, F.; Mercier, D.; Lefevre, E.; Roger, D. Robust Diagnostics of Stator Insulation Based on High Frequency Resonances Measurements. IEEE Trans. Dielectr. Electr. Insul. 2009, 16, 1496–1502. [Google Scholar] [CrossRef]
- Savin, S.; Ait-Amar, S.; Roger, D. Turn-to-turn Capacitance Variations Correlated to PDIV for AC Motors Monitoring. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 34–41. [Google Scholar] [CrossRef]
- Savin, S.; Ait-Amar, S.; Roger, D.; Velu, G. Aging Effects on the AC Motor Windings: A Correlation between the Variation of Turn-to-turn Capacitance and the PDIV. In Proceedings of the Annual Report Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Cancun, Mexico, 16–19 October 2011; pp. 64–67. [Google Scholar]
- Zoeller, C.; Vogelsberger, M.A.; Fasching, R.; Grubelnik, W.; Wolbank, T.M. Evaluation and Current-Response Based Identification of Insulation Degradation for High Utilized Electrical Machines in Railway Application. IEEE Trans. Ind. Appl. 2017, 53, 2679–2689. [Google Scholar] [CrossRef]
- Zoeller, C.; Vogelsberger, M.; Bazant, M.; Ertl, H.; Wolbank, T.M. Diagnostic Technique for Traction Motor Insulation Condition Monitoring by Transient Signal Assessment. In Proceedings of the PCIM Europe 2018, Nuremberg, Germany, 5–7 June 2018; pp. 1170–1177. [Google Scholar]
- Zoeller, C.; Wolbank, T.M.; Vogelsberger, M.A. Influence of Voltage Excitation and Current Sensors on Monitoring of Stator Winding Insulation Based on Transient Current Step Response. In Proceedings of the Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 2854–2861. [Google Scholar]
- Jameson, N.J.; Azarian, M.H.; Pecht, M. Correlation Analysis for Impedance-based Health Monitoring of Electromagnetic Coils. In Proceedings of the IEEE International Conference on Prognostics and Health Management, Ottawa, ON, Canada, 20–22 June 2016; pp. 1–6. [Google Scholar]
- Younsi, K.; Neti, P.; Shah, M.; Zhou, J.Y.; Krahn, J.; Weeber, K.; Whitefield, C.D. On-line Capacitance and Dissipation Factor Monitoring of AC Stator Insulation. IEEE Trans. Dielectr. Electr. Insul. 2010, 17, 1441–1452. [Google Scholar] [CrossRef]
- Zhang, P.; Neti, P.; Younsi, K. Online Monitoring of Capacitance and Dissipation Factor of Motor Stator Winding Insulation during Accelerated Life Testing. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 3267–3271. [Google Scholar]
- Jameson, N.J.; Azarian, M.H.; Pecht, M. Improved Electromagnetic Coil Insulation Health Monitoring Using Equivalent Circuit Model Analysis. Int. J. Electr. Power Energy Syst. 2020, 119, 1–8. [Google Scholar] [CrossRef]
- Gandhi, A.; Corrigan, T.; Parsa, L. Recent Advances in Modeling and Online Detection of Stator Interturn Faults in Electrical Motors. IEEE Trans. Ind. Electron. 2011, 58, 1564–1575. [Google Scholar] [CrossRef]
- McPherson, J.W. Reliability physics and Engineering: Time-To-Failure Modeling; Springer: Berlin/Heidelberg, Germany, 2010; ISBN 978-7-03-038824-7. [Google Scholar]
- Li, J.; Dasgupta, A. Failure-Mechanism Models for Creep and Creep Rupture. IEEE Trans. Reliab. 1993, 42, 339–353. [Google Scholar] [CrossRef]
- Massarini, A.; Kazimierczuk, M.K. Self-Capacitance of Inductors. IEEE Trans. Power Electron. 1997, 12, 671–676. [Google Scholar] [CrossRef] [Green Version]
- Li, B.; Yang, W.; Zhou, X.; Zhai, G. Research on Method Used for Extracting Multilayer Coil’s Stray Capacitance of Electromagnetic Relay. Low Volt. App. 2011, 12, 8–12. [Google Scholar]





















| Parameter Properties | Numerical Value |
|---|---|
| (Ω) | 5.41 |
| Magnet wire insulation class | Class B |
| Insulation composition | Polyester |
| (m) | 2.65 × 10−1 |
| 3.5 | |
| 8.8541878 × 10−12 | |
| (m) | 0.576 × 10−3 |
| (H) | 0.001075 |
| (m) | 0.482 × 10−3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Guo, H.; Xu, A.; Pecht, M. Degradation Monitoring of Insulation Systems Used in Low-Voltage Electromagnetic Coils under Thermal Loading Conditions from a Creep Point of View. Sensors 2020, 20, 3696. https://doi.org/10.3390/s20133696
Wang K, Guo H, Xu A, Pecht M. Degradation Monitoring of Insulation Systems Used in Low-Voltage Electromagnetic Coils under Thermal Loading Conditions from a Creep Point of View. Sensors. 2020; 20(13):3696. https://doi.org/10.3390/s20133696
Chicago/Turabian StyleWang, Kai, Haifeng Guo, Aidong Xu, and Michael Pecht. 2020. "Degradation Monitoring of Insulation Systems Used in Low-Voltage Electromagnetic Coils under Thermal Loading Conditions from a Creep Point of View" Sensors 20, no. 13: 3696. https://doi.org/10.3390/s20133696
APA StyleWang, K., Guo, H., Xu, A., & Pecht, M. (2020). Degradation Monitoring of Insulation Systems Used in Low-Voltage Electromagnetic Coils under Thermal Loading Conditions from a Creep Point of View. Sensors, 20(13), 3696. https://doi.org/10.3390/s20133696






