Sensor Modeling and Calibration Method Based on Extinction Ratio Error for Camera-Based Polarization Navigation Sensor
Abstract
:1. Introduction
- (1)
- The influence of the inconsistency of the extinction ratio between orthogonal polarizers on sensor was quantitative analyzed. Accordingly, a new camera-based polarization sensor model based on the extinction ratio coefficient was established. As such, the light intensity of the two orthogonal channels could be unified with the aid of extinction ratio coefficient. Unlike the existing polarization sensor model [26,28,29], a model with extinction ratio parameter was considered as a fine structure model. Moreover, the effect of extinction ratio error on the sensor was carefully analyzed.
- (2)
- A new calibration method integrated both the AOP and DOP error is proposed. With the addition of DOP error, the estimation accuracy of sensor calibration model parameters was further improved. Meanwhile the stability and robustness of AOP and DOP could be improved simultaneously.
2. Bionic Camera-Based Polarization Sensor
2.1. Polarization Sensor Structure
- (1)
- The lens layer is used to sense the polarization pattern with a wide field of view. The FE185C057HA-1 wide-angle lens is adopted. Its focal length is 1.8 mm, and the field of view is about 185° × 185°.
- (2)
- The polarization optical information acquisition layer is used to detect the optical characteristics of polarized skylight. A pixel-level polarization complementary metal oxide semiconductor (CMOS) camera (Sony IMX250MZR) is employed as shown in Figure 1a. The polarization camera includes a CMOS where 2 × 2 matrices of polarizers are used in front of every 2 × 2 photosensors. The array polarizer contains 2048 × 2448-pixel channels to measure the polarized skylight, and the size of each pixel channel is 3.45 × 3.45 μm2. As shown in Figure 1b, four adjacent pixel channels constitute a polarization unit, and the polarizer installation directions of corresponding channels are 0°, 45°, 90° and 135°, respectively. In addition, the CMOS camera is used to acquire the polarized skylight intensity information.
- (3)
- The control and processing circuit layer ensures real-time acquisition and processing of polarized images obtained by the CMOS camera. It consists of a control module, a communication module and a memory module. In the control module, a Linux system is used to process the polarized skylight intensity images to finally obtain polarization information. Finally, the sun vector information is obtained according to the vertical relationship between the sun vector and the polarization vector, which is stored in the memory module.
2.2. Polarization Calculation
3. Camera-Based Polarization Sensor Calibration
3.1. Sensor Model of Camera-Based Polarization Sensor
3.1.1. Array Polarizer Model with Extinction Ratio
3.1.2. CMOS Camera Photosensitivity Model
3.2. Calibration Method
3.2.1. The CMOS Camera Photosensitivity Model Calibration
3.2.2. The Array Polarizer Model Calibration
4. Experiment Results and Analysis
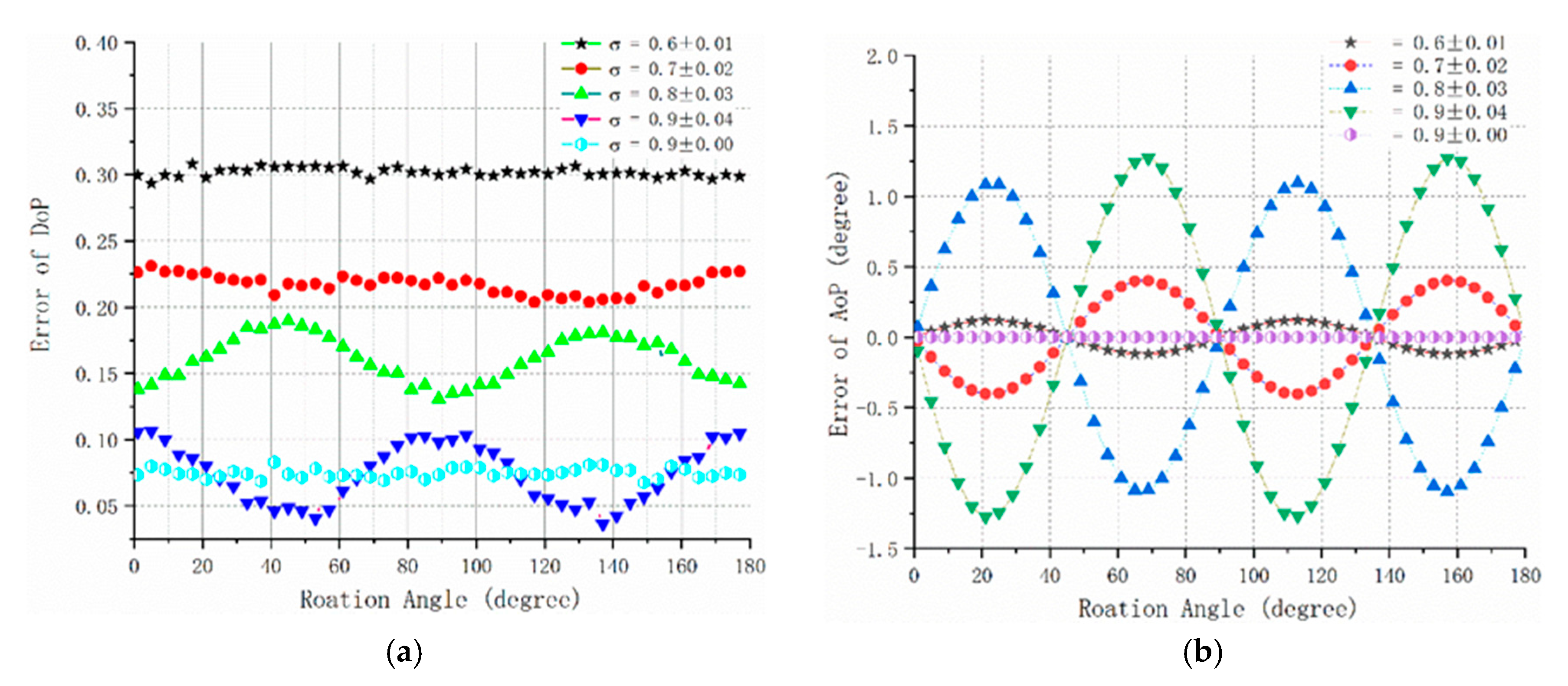
4.1. Simulation Experiment for Extinction Ratio Analysis
4.2. Indoor Calibration Experiment
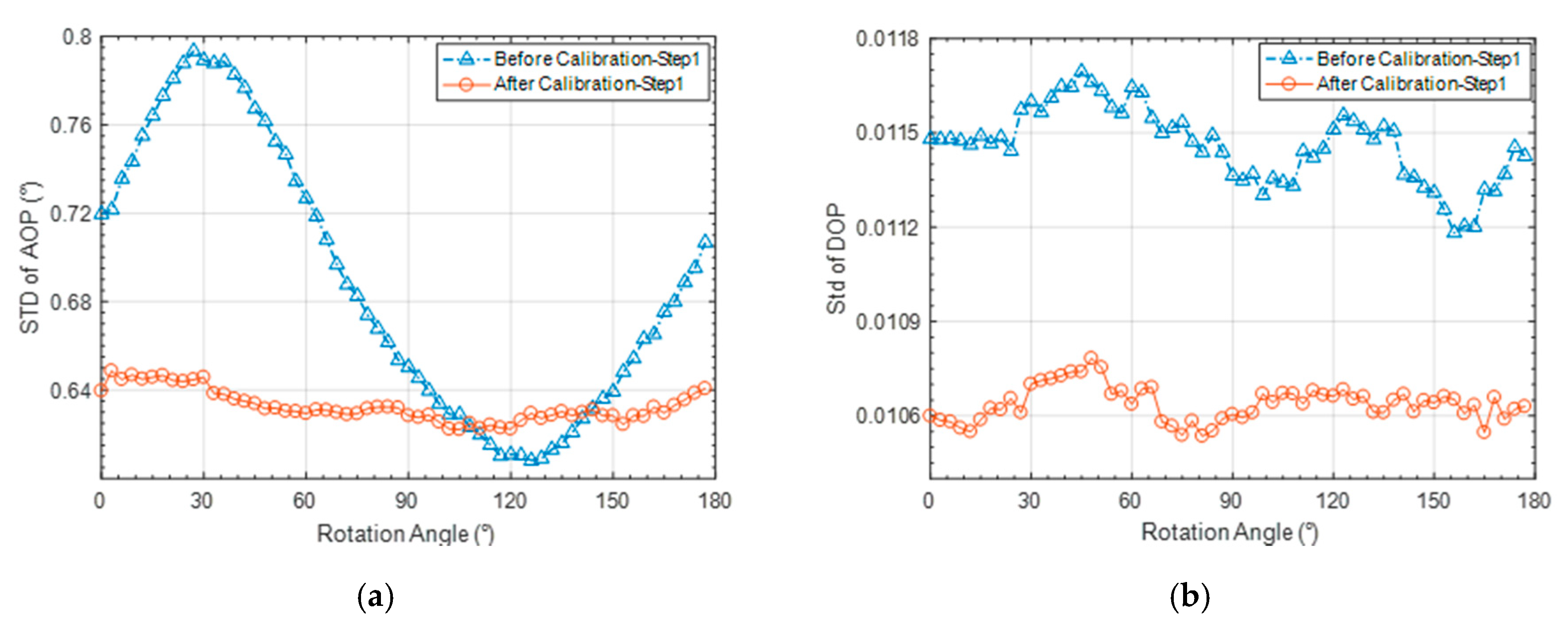
4.2.1. Calibration Results
4.2.2. Performance Analysis of Calibration Model and Method
4.3. Outdoor Calibration Experiment
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Heinze, S. Unraveling the neural basis of insect navigation. Curr. Opin. Insect. Sci. 2017, 24, 58–67. [Google Scholar] [CrossRef]
- Uwe, H.; Stanley, H.; Keram, P.; Michiyo, K.; Basil, J. Central neural coding of sky polarization in insects. Philos. Trans. Biol. Sci. 2011, 366, 680–687. [Google Scholar]
- Labhart, T. Specialized photoreceptors at the dorsal rim of the honeybee’s compound eye: Polarizational and angular sensitivity. J. Comp. Physiol. 1980, 141, 19–30. [Google Scholar] [CrossRef]
- Rossel, S.; Wehner, R. Polarization vision in bees. Nature 1986, 323, 128–131. [Google Scholar] [CrossRef]
- Collett, M.; Collett, T.; Bisch, S.; Wehner, R. Local and global vectors in desert ant navigation. Nature 1998, 394, 269–272. [Google Scholar] [CrossRef]
- Zhao, K.; Chu, J.; Wang, T.; Zhang, Q. A novel angle algorithm of polarization sensor for navigation. IEEE Trans. Instrum. Meas. 2009, 58, 2791–2796. [Google Scholar] [CrossRef]
- Dupeyroux, J.; Serres, J.; Viollet, S. AntBot: A six-legged walking robot able to home like desert ants in outdoor environments. Sci. Robot. 2019, 4, eaau0307. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Du, T.; Niu, B.; Li, C.; Qian, J.; Guo, L. A bionic polarization navigation sensor based on polarizing beam splitter. IEEE Access 2018, 6, 11472–11481. [Google Scholar] [CrossRef]
- Salmah, K.; Diah, S.; Ille, G. Bio-inspired polarized skylight-based navigation sensors: A review. Sensors 2012, 12, 14232–14261. [Google Scholar]
- Lambrinos, D.; Kobayashi, H.; Pfeifer, R.; Maris, M.; Labhart, T.; Wehner, R. An autonomous agent navigating with a polarized light compass. Adapt. Behav. 1997, 6, 131–161. [Google Scholar] [CrossRef]
- Zhao, H.; Xu, W. A Bionic Polarization navigation sensor and its calibration method. Sensors 2016, 16, 1223. [Google Scholar] [CrossRef] [Green Version]
- Zhi, W.; Chu, J.; Li, J.; Wang, Y. A novel attitude determination system aided by polarization sensor. Sensors 2018, 18, 158. [Google Scholar] [CrossRef] [Green Version]
- Dupeyroux, J.; Viollet, S.; Serres, J. An ant-inspired celestial compass applied to autonomous outdoor robot navigation. Robot. Auton. Syst. 2019, 117, 40–56. [Google Scholar] [CrossRef]
- Barta, A.; Horváth, G. Why is it advantageous for animals to detect celestial polarization in the ultraviolet? Skylight polarization under clouds and canopies is strongest in the UV. J. Theor. Biol. 2004, 226, 429–437. [Google Scholar] [CrossRef]
- Dupeyroux, J.; Diperi, J.; Boyron, M.; Viollet, S.; Serres, J. A bio-inspired celestial compass applied to an ant-inspired robot for autonomous navigation. In Proceedings of the 2017 European Conference on Mobile Robots (ECMR), Paris, France, September 2017; pp. 1–6. [Google Scholar]
- Pomozi, I.; Horváth, G.; Wehner, R. How the clear-sky angle of polarization pattern continues underneath clouds: Full-sky measurements and implications for animal orientation. J. Exp. Biol. 2001, 204, 2933. [Google Scholar]
- Ahsan, M.; Cai, Y.; Zhang, W. Information extraction of bionic camera-based polarization navigation patterns under noisy weather conditions. J. Shanghai Jiaotong Univ. (Sci.) 2020, 25, 18–26. [Google Scholar] [CrossRef]
- Zhang, W.; Cao, Y.; Zhang, X.; Liu, Z. Sky light polarization detection with linear polarizer triplet in light field camera inspired by insect vision. Appl. Opt. 2015, 54, 8962. [Google Scholar] [CrossRef]
- Mukul, S.; David, S.; Chris, H.; Albert, T. Biologically inspired autonomous agent navigation using an integrated polarization analyzing CMOS image sensor. Procedia Eng. 2010, 5, 673–676. [Google Scholar]
- Powell, S.; Gruev, V. Calibration methods for division-of-focal-plane polarimeters. Opt. Express 2013, 21, 21039. [Google Scholar] [CrossRef]
- Powell, S.; Gruev, V. Evaluation of calibration methods for visible-spectrum division-of-focal-plane polarimeters. SPIE Opt. Eng. Appl. 2013, 8873, 887306. [Google Scholar]
- Wolfgang, S.; Carey, N. A fisheye camera system for polarization detection on UAVs. Computer Vision–ECCV 2012, 7584, 431–440. [Google Scholar]
- Wolfgang, S. A lightweight single-camera polarization compass with covariance estimation. IEEE ICCV 2017, 1, 5363–5371. [Google Scholar]
- Zhang, S.; Liang, H.; Zhu, H.; Wang, D.; Yu, B. A camera-based real-time polarization sensor and its application to mobile robot navigation. IEEE ROBIO 2014, 271–276. [Google Scholar]
- Wang, D.; Liang, H.; Zhu, H.; Zhang, S. A bionic camera-based polarization navigation sensor. Sensors 2014, 14, 13006–13023. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, S.; Gao, J.; Wang, D.; Yang, T.; Wang, X. Improved models of imaging of skylight polarization through a fisheye lens. Sensors 2019, 19, 4844. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lu, H.; Zhao, K.; You, Z.; Huang, K. Real-time polarization imaging algorithm for camera-based polarization navigation sensors. Appl. Opt. 2017, 56, 3199. [Google Scholar] [CrossRef] [PubMed]
- Fan, C.; Hu, X.; Lian, J.; Zhang, L.; He, X. Design and calibration of a novel camera-based bio-inspired polarization navigation sensor. IEEE Sens. J. 2016, 16, 3640–3648. [Google Scholar] [CrossRef]
- Han, G.; Hu, X.; Lian, J.; He, X.; Zhang, L.; Wang, Y.; Dong, F. Design and calibration of a novel bio-inspired pixelated polarized light compass. Sensors 2017, 17, 2623. [Google Scholar] [CrossRef] [Green Version]
- Aycock, T.; Lompado, A.; Wheeler, B. Using atmospheric polarization patterns for azimuth sensing. SPIE Def. Secur. 2014, 9085, 90850B. [Google Scholar]
- Todd, A.; Art, L.; Troy, W.; David, C. Passive optical sensing of atmospheric polarization for GPS denied operations. Proc. SPIE 2016, 9838, 98380Y. [Google Scholar]
- Xian, Z.; Hu, X.; Lian, J.; Zhang, L.; Cao, J.; Wang, Y.; Ma, T. A novel angle computation and calibration algorithm of bio-inspired sky-light polarization navigation sensor. Sensors 2014, 14, 17068–17088. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Chu, J.; Zhang, R.; Li, J.; Guo, X.; Lin, M. A bio-inspired polarization sensor with high outdoor accuracy and central-symmetry calibration method with integrating sphere. Sensors 2019, 19, 3448. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rogers, A. Polarization optics. Essent. Optoelectron. 1997. [Google Scholar] [CrossRef]
- Gruev, V.; Perkins, R.; York, T. CCD polarization imaging sensor with aluminum nanowire optical filters. Opt. Express 2010, 18, 19087–19094. [Google Scholar] [CrossRef]
- Kiyotaka, S.; Sanshiro, S.; Keisuke, A.; Hitoshi, M.; Toshihiko, N.; Takashi, T.; Kiyomi, K.; Jun, O. Image sensor pixel with on-chip high extinction ratio polarizer based on 65-nm standard CMOS technology. Opt. Express 2013, 21, 11132–11140. [Google Scholar]
- Hagen, N.; Shu, S.; Otani, Y. Calibration and performance assessment of microgrid polarization cameras. Opt. Eng. 2019, 58, 082408. [Google Scholar]
- Zhang, H.; Zhang, J.; Yang, B.; Yan, C. Calibration for polarization remote sensing system with focal plane divided by multi-linear array. Acta. Optica. Sinica. 2016, 36, 1128003. [Google Scholar] [CrossRef]
- York, T.; Gruev, V. Optical characterization of a polarization imager. In Proceedings of the International Symposium on Circuits and Systems (ISCAS 2011), Rio de Janeiro, Brazil, 15–19 May 2011; pp. 1576–1579. [Google Scholar]
- Zavrsnik, M.; Donlagic, D. Fiber optic polarimetric thermometer using low extinction ratio polarizer and low coherence source. In Proceedings of the 16th IEEE Instrumentation and Measurement Technology Conference, Venice, Italy, 24–26 May 1999; Volume 3, pp. 1520–1525. [Google Scholar]
- Liao, Y. Polarization Optics; Beijing Science Press: Beijing, China, 2003; Volume 55, pp. 49–51. [Google Scholar]
- Golub, G. Numerical methods for solving linear least squares problems. Numer. Math. 1965, 7, 206–216. [Google Scholar] [CrossRef]
- Yang, J.; Niu, B.; Du, T.; Liu, X.; Wang, S.; Guo, L. Disturbance analysis and performance test of the polarization sensor based on polarizing beam splitter. Sen. Rev. 2019, 39, 341–351. [Google Scholar] [CrossRef]













| Intensity Level (lux) | 140 | 300 | 500 | 700 |
|---|---|---|---|---|
| SD (°) | 0.14 | 0.10 | 0.11 | 0.07 |
| MAXE (°) | 0.38 | 0.24 | 0.26 | 0.21 |
| Calibration | Original | Step 1 | Step 2 |
|---|---|---|---|
| SD (°) | 2.62 | 0.22 | 0.04 |
| MAXE (°) | 7.39 | 0.47 | 0.10 |
| MAE (°) | 3.51 | 0.20 | 0.03 |
| Types | Model | Method |
|---|---|---|
| Case1 | without ER | based solely on error of AOP |
| Case2 | with ER | based solely on error of AOP |
| Case3 | with ER | based on error of both AOP and DOP |
| Types | Case1 | Case2 | Case3 |
|---|---|---|---|
| SD (×10−3) | 4.02 | 2.15 | 1.04 |
| MAXE (×10−3) | 7.70 | 3.93 | 2.98 |
| MAE (×10−3) | 3.71 | 1.84 | 0.82 |
| Types | Case1 | Case2 | Case3 |
|---|---|---|---|
| SD (×10−2 °) | 4.08 | 4.00 | 4.06 |
| MAXE (×10−2 °) | 11.3 | 10.5 | 10.3 |
| MAE (×10−2 °) | 3.20 | 3.19 | 3.22 |
| Calibration | Original | Step 1 | Step 2 |
|---|---|---|---|
| SD (°) | 2.13 | 1.16 | 0.71 |
| MAE (°) | 2.73 | 1.32 | 0.68 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, H.; Yang, J.; Liu, X.; Huang, P.; Guo, L. Sensor Modeling and Calibration Method Based on Extinction Ratio Error for Camera-Based Polarization Navigation Sensor. Sensors 2020, 20, 3779. https://doi.org/10.3390/s20133779
Ren H, Yang J, Liu X, Huang P, Guo L. Sensor Modeling and Calibration Method Based on Extinction Ratio Error for Camera-Based Polarization Navigation Sensor. Sensors. 2020; 20(13):3779. https://doi.org/10.3390/s20133779
Chicago/Turabian StyleRen, Haonan, Jian Yang, Xin Liu, Panpan Huang, and Lei Guo. 2020. "Sensor Modeling and Calibration Method Based on Extinction Ratio Error for Camera-Based Polarization Navigation Sensor" Sensors 20, no. 13: 3779. https://doi.org/10.3390/s20133779
APA StyleRen, H., Yang, J., Liu, X., Huang, P., & Guo, L. (2020). Sensor Modeling and Calibration Method Based on Extinction Ratio Error for Camera-Based Polarization Navigation Sensor. Sensors, 20(13), 3779. https://doi.org/10.3390/s20133779




