Single-Bit, Self-Powered Digital Counter Using a Wiegand Sensor for Rotary Applications
Abstract
1. Introduction
2. Energy Harvesting from a Wiegand Sensor
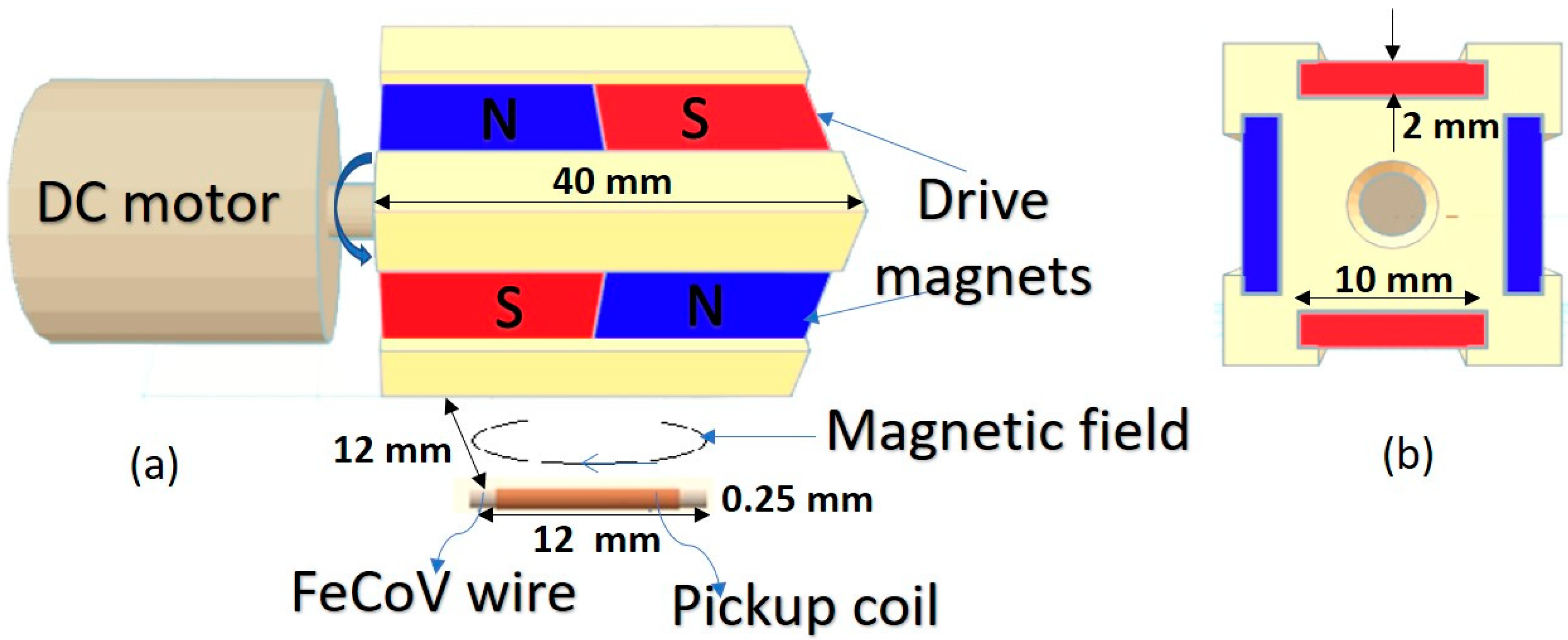
2.1. Experimental Setup
2.2. Relationship between Rotational Frequency and Rotational Speed
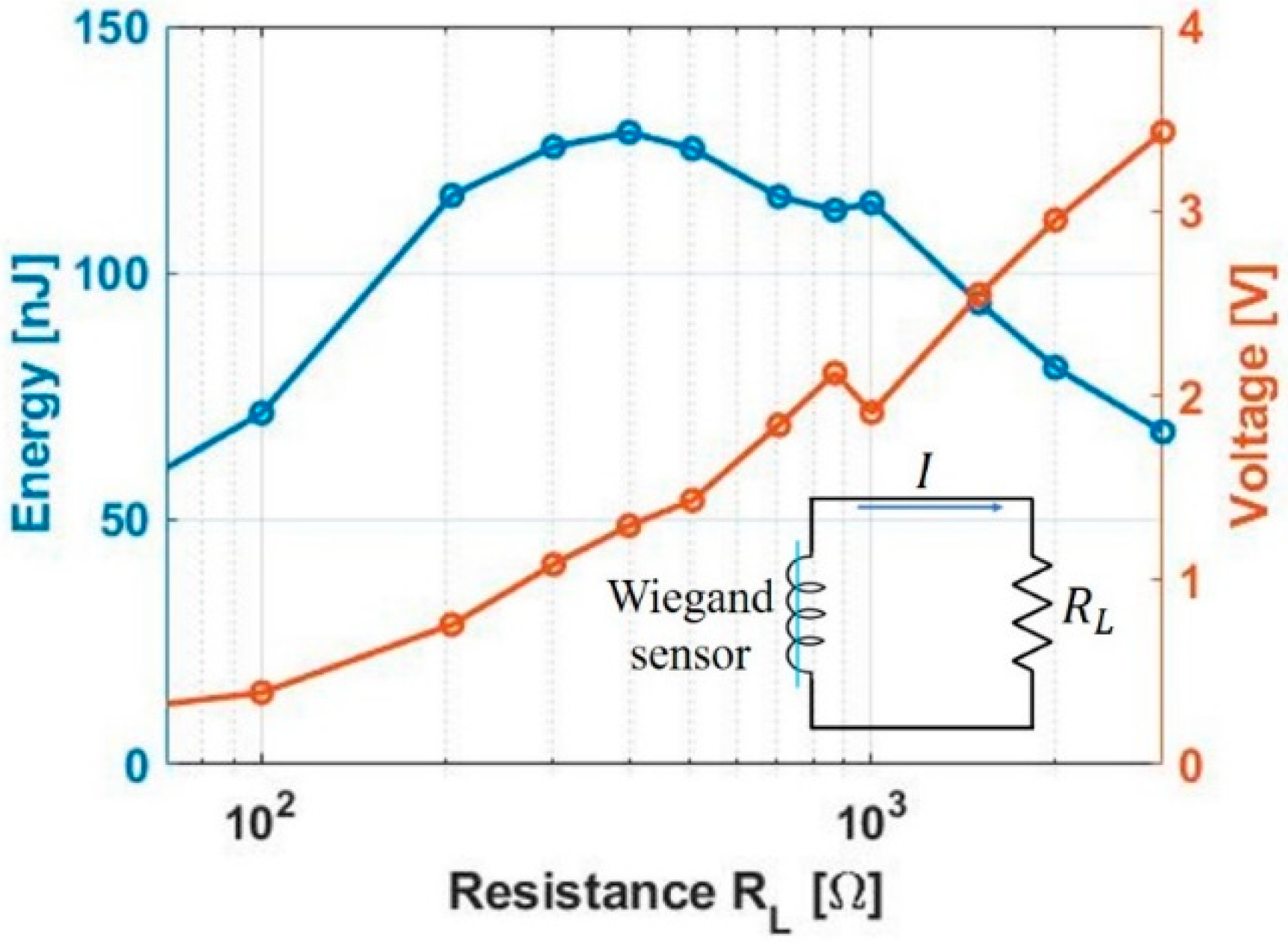
2.3. Maximum Energy per Pulse
3. Single-Bit, Self-Powered Digital Counter Design
4. Results and Discussion
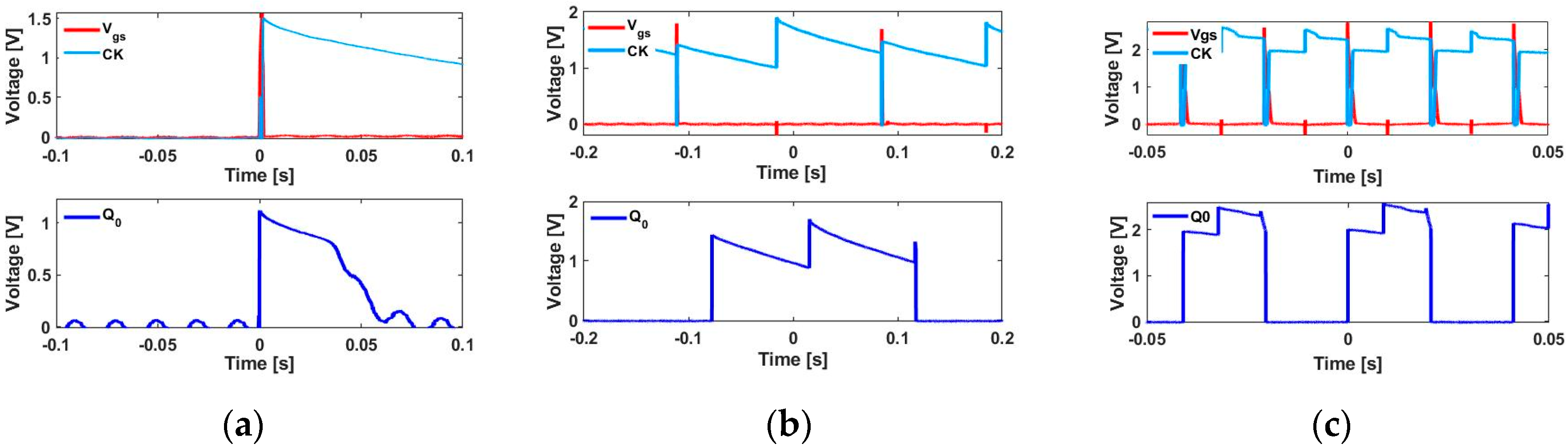
4.1. Selection of the Optimal Capacitor Value
4.2. Comparing the Performance of an Active Rectifier and a Diode Bridge Rectifier
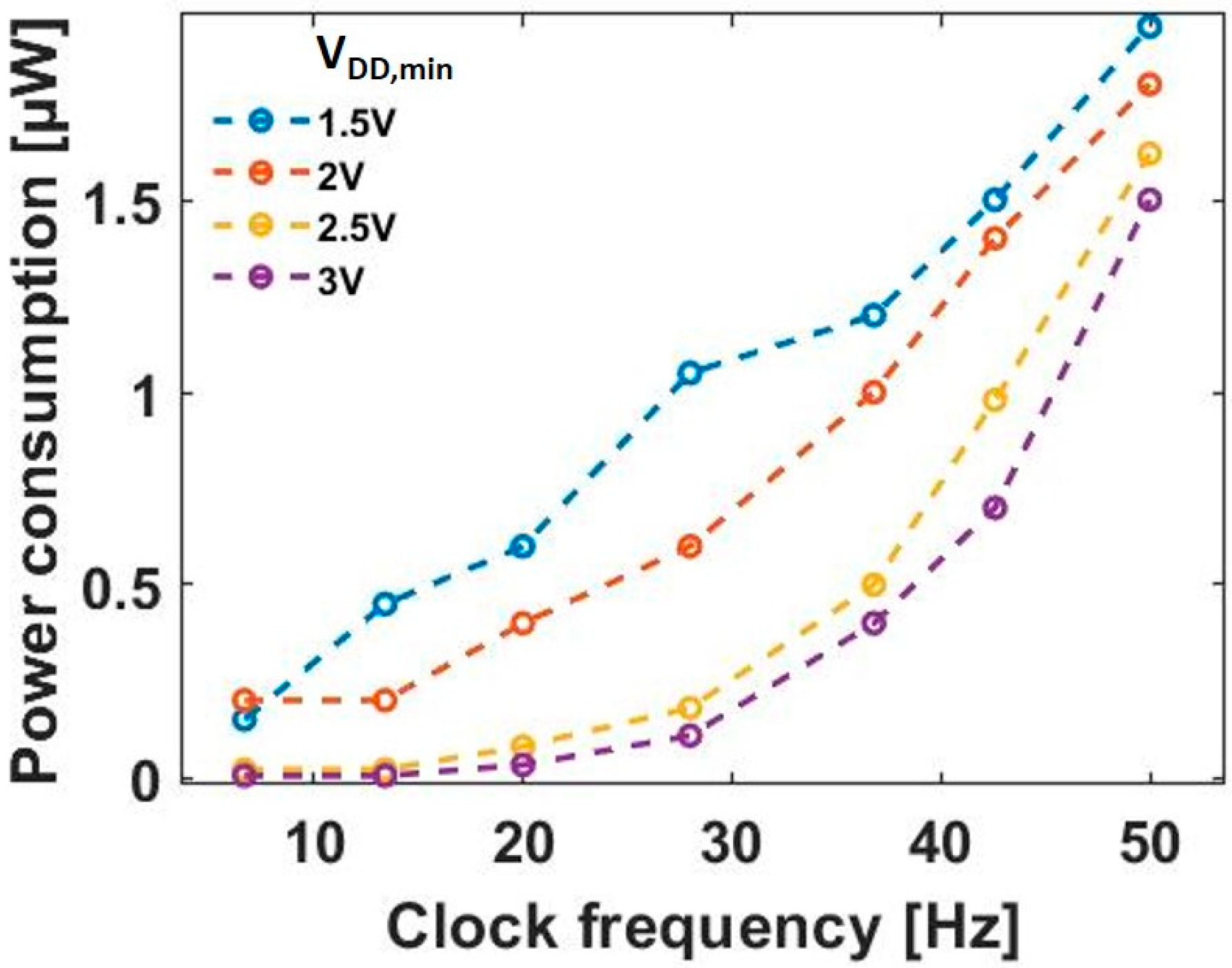
4.3. Relationship between Output of the D Flip-Flop and Rotational Speed
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Vullers, R.; Schaijk, R.; Visser, H.; Penders, J.; Hoof, C. Energy Harvesting for Autonomous Wireless Sensor Networks. IEEE Solid State Circuits Mag. 2010, 2, 29–38. [Google Scholar] [CrossRef]
- Munirathinam, S. Industry 4.0: Industrial Internet of Things (IIOT). In Advances in Computers; Elsevier: Manassas, VA, USA, 2020; Volume 117, pp. 129–164. ISBN 978-0-12-818756-2. [Google Scholar]
- Hou, L.; Tan, S.; Zhang, Z.; Bergmann, N.W. Thermal Energy Harvesting WSNs Node for Temperature Monitoring in IIoT. IEEE Access 2018, 6, 35243–35249. [Google Scholar] [CrossRef]
- Alegret, R.N.; Aragones, R.; Oliver, J.; Ferrer, C. Exploring IIoT and Energy Harvesting Boundaries. In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; pp. 6732–6736. [Google Scholar]
- Cho, J.Y.; Kim, J.; Kim, K.-B.; Ryu, C.H.; Hwang, W.; Lee, T.H.; Sung, T.H. Significant power enhancement method of magneto-piezoelectric energy harvester through directional optimization of magnetization for autonomous IIoT platform. Appl. Energy 2019, 254, 113710. [Google Scholar] [CrossRef]
- Guan, M.; Liao, W.-H. Design and analysis of a piezoelectric energy harvester for rotational motion system. Energy Convers. Manag. 2016, 111, 239–244. [Google Scholar] [CrossRef]
- Zou, H.-X.; Zhang, W.; Li, W.-B.; Wei, K.-X.; Gao, Q.-H.; Peng, Z.-K.; Meng, G. Design and experimental investigation of a magnetically coupled vibration energy harvester using two inverted piezoelectric cantilever beams for rotational motion. Energy Convers. Manag. 2017, 148, 1391–1398. [Google Scholar] [CrossRef]
- Febbo, M.; Machado, S.P.; Gatti, C.D.; Ramirez, J.M. An out-of-plane rotational energy harvesting system for low frequency environments. Energy Convers. Manag. 2017, 152, 166–175. [Google Scholar] [CrossRef]
- Siddique, A.R.M.; Mahmud, S.; Heyst, B.V. A comprehensive review on vibration based micro power generators using electromagnetic and piezoelectric transducer mechanisms. Energy Convers. Manag. 2015, 106, 728–747. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, J.; Zhu, H.; Lei, Y. Design, modeling and experimental verification of circular Halbach electromagnetic energy harvesting from bearing motion. Energy Convers. Manag. 2019, 180, 811–821. [Google Scholar] [CrossRef]
- Xu, Y.; Bader, S.; Oelmann, B. Design, modeling and optimization of an m-shaped variable reluctance energy harvester for rotating applications. Energy Convers. Manag. 2019, 195, 1280–1294. [Google Scholar] [CrossRef]
- Wiegand, J.R. Bistable Magnetic Device. US Patent US3820090A, 25 June 1974. [Google Scholar]
- Wiegand, J.R. Switchable Magnetic Device. US4247601A, 27 January 1981. [Google Scholar]
- Fujinaga, N.; Takebuchi, A.; Yamada, T.; Takemura, Y. Battery-less Hall sensor operated by energy harvesting from a single Wiegand pulse. In Proceedings of the 2017 IEEE International Magnetics Conference (INTERMAG), Dublin, Ireland, 24–28 April 2017; p. 1. [Google Scholar]
- Saggini, S.; Ongaro, F.; Corradini, L.; Affanni, A. Low-Power Energy Harvesting Solutions for Wiegand Transducers. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 766–779. [Google Scholar] [CrossRef]
- iC Haus. Energy-Harvesting Multiturn Counter/Encoder. Available online: https://www.ichaus.de/product/iC-PM (accessed on 3 May 2020).
- Takahashi, K.; Takebuchi, A.; Yamada, T.; Takemura, Y. Power Supply for Medical Implants by Wiegand Pulse Generated from Magnetic Wire. J. Magn. Soc. Jpn. 2018, 42, 49–54. [Google Scholar] [CrossRef]
- Sun, X.; Yamada, T.; Takemura, Y. Output Characteristics and Circuit Modeling of Wiegand Sensor. Sensors 2019, 19, 2991. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, K.; Yamada, T.; Takemura, Y. Circuit Parameters of a Receiver Coil Using a Wiegand Sensor for Wireless Power Transmission. Sensors 2019, 19, 2710. [Google Scholar] [CrossRef] [PubMed]
- Popovich, M.; Mezhiba, A.V.; Friedman, E.G. Power Distribution Networks with On-Chip Decoupling Capacitors; Springer: New York, NY, USA, 2007; ISBN 978-0-387-71601-5. [Google Scholar]
- Texas Instruments. CMOS Dual D Type Flip-Flop. Available online: http://www.ti.com/lit/ds/symlink/cd4013b.pdf (accessed on 3 May 2020).
- Peters, C.; Kessling, O.; Henrici, F.; Ortmanns, M.; Manoli, Y. CMOS Integrated Highly Efficient Full Wave Rectifier. In Proceedings of the 2007 IEEE International Symposium on Circuits and Systems, New Orleans, LA, USA, 27–30 May 2007; pp. 2415–2418. [Google Scholar]
- ON Semiconductor. N-Channel MOSFET. Available online: https://www.onsemi.cn/PowerSolutions/document/2N7000-D.PDF (accessed on 3 May 2020).
- Diodes. ZVP4424C P-Channel Enhancement Mode Vertical DMOS FET. Available online: https://www.diodes.com/assets/Datasheets/products_inactive_data/ZVP4424C.pdf (accessed on 3 May 2020).
- Vishay Intertechnology. Schottky Barrier Diode. Available online: https://www.vishay.com/docs/85513/bat85s.pdf (accessed on 3 May 2020).
- Fujitsu. Non Volatile Random Access memory FRAM. Available online: https://www.fujitsu.com/uk/Images/MB85RS256TY-Industrial.pdf (accessed on 3 May 2020).





| Component | Value |
|---|---|
| D flip-flop | CD4013B |
| N-channel MOSFET | 2N7000 |
| P-Channel MOSFET | ZVP442 |
| Schottky diode | BAT85 |
| Capacitance C | 0.1 µF |
| Resistance R | 200 kΩ |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chotai, J.; Thakker, M.; Takemura, Y. Single-Bit, Self-Powered Digital Counter Using a Wiegand Sensor for Rotary Applications. Sensors 2020, 20, 3840. https://doi.org/10.3390/s20143840
Chotai J, Thakker M, Takemura Y. Single-Bit, Self-Powered Digital Counter Using a Wiegand Sensor for Rotary Applications. Sensors. 2020; 20(14):3840. https://doi.org/10.3390/s20143840
Chicago/Turabian StyleChotai, Janki, Manish Thakker, and Yasushi Takemura. 2020. "Single-Bit, Self-Powered Digital Counter Using a Wiegand Sensor for Rotary Applications" Sensors 20, no. 14: 3840. https://doi.org/10.3390/s20143840
APA StyleChotai, J., Thakker, M., & Takemura, Y. (2020). Single-Bit, Self-Powered Digital Counter Using a Wiegand Sensor for Rotary Applications. Sensors, 20(14), 3840. https://doi.org/10.3390/s20143840





