On the Use of a Single Beam Acoustic Current Profiler for Multi-Point Velocity Measurement in a Wave and Current Basin
Abstract
1. Introduction
Single Beam Acoustic Doppler Profiler for 1-D Multi-Point Measurements
2. Materials and Methods
2.1. Test Set-Up
2.2. Instrumentation
2.3. Tank Conditions
2.4. Data Processing
2.5. Analysis
3. Results
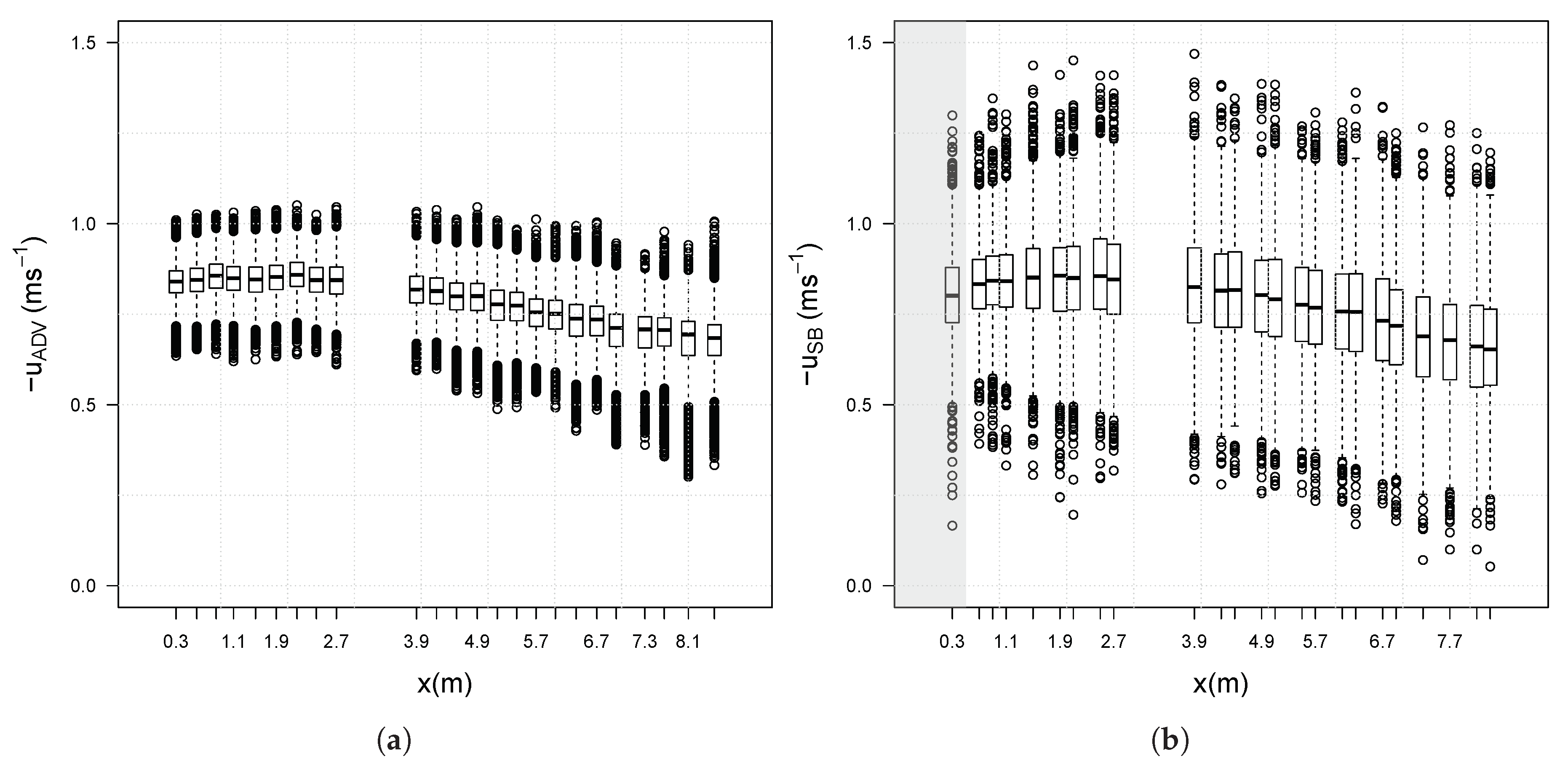
3.1. Inter-Instrument Comparison Along Measurement Profile at 0.8 m/s
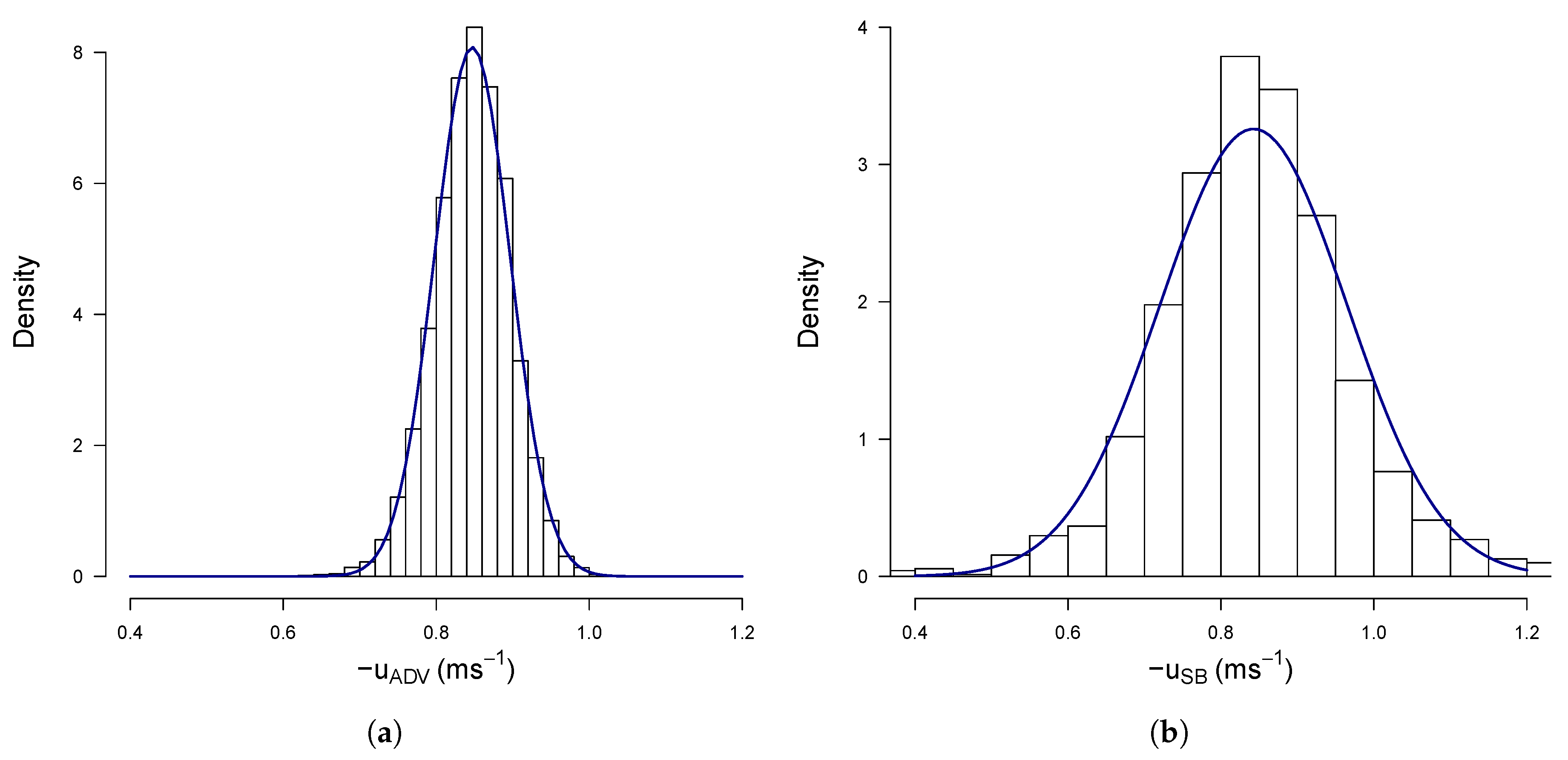
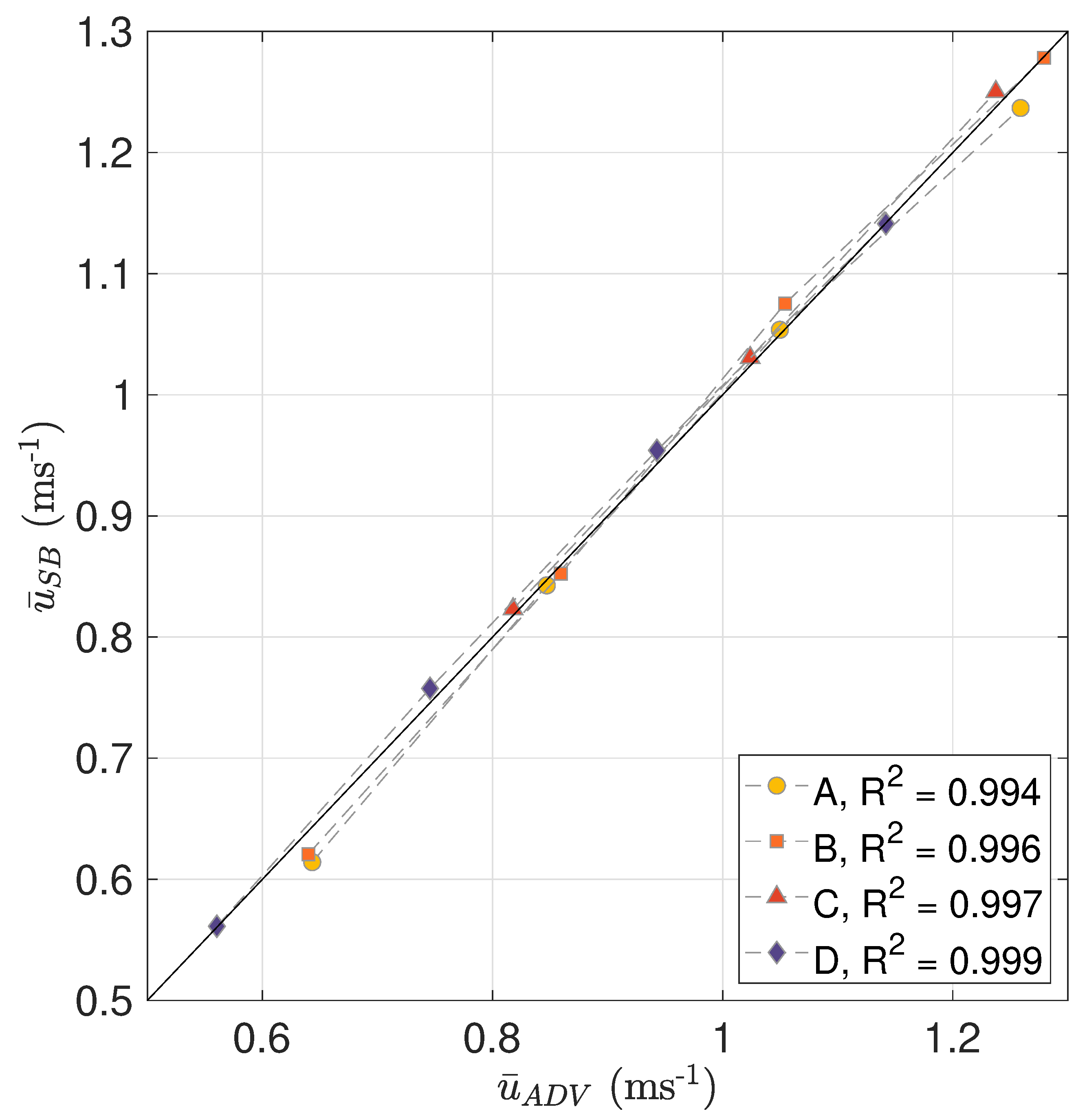
3.2. Inter-Instrument Comparison Across Velocity Range
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ADV | acoustic Doppler velocimeter |
| ADP | acoustic Doppler profiler |
| SB-ADP | single beam acoustic Doppler profiler |
| ORE | offshore renewable energy |
| TI | turbulent intensity |
| LDV | laser Doppler velocimeter |
| SNR | signal to noise ratio |
| NaN | Not a Number |
| ANOVA | analysis of variance |
| HSD | honestly significant difference |
References
- Draycott, S.; Sellar, B.; Davey, T.; Noble, D.; Venugopal, V.; Ingram, D. Capture and simulation of the ocean environment for offshore renewable energy. Renew. Sustain. Energy Rev. 2019, 104, 15–29. [Google Scholar] [CrossRef]
- EquiMar Project. Equitable Testing and Evaluation of Marine Energy Extraction Devices in Terms of Performance, Cost and Environmental Imapct. Deliverable D2.2—Wave and Tidal Resource Characterisation. Technical Report; 2011. Available online: https://tethys.pnnl.gov/sites/default/files/publications/EquiMar_D3.3.pdf (accessed on 4 February 2020).
- Maganga, F.; Germain, G.; King, J.; Pinon, G.; Rivoalen, E. Experimental characterisation of flow effects on marine current turbine behaviour and on its wake properties. IET Renew. Power Gener. 2010, 4, 498–509. [Google Scholar] [CrossRef]
- Mycek, P.; Gaurier, B.; Germain, G.; Pinon, G.; Rivoalen, E. Numerical and experimental study of the interaction between two marine current turbines. Int. J. Mar. Energy 2013, 1, 70–83. [Google Scholar] [CrossRef]
- Mycek, P.; Gaurier, B.; Germain, G.; Pinon, G.; Rivoalen, E. Experimental study of the turbulence intensity effects on marine current turbines behaviour. Part I: One single turbine. Renew. Energy 2014, 66, 729–746. [Google Scholar] [CrossRef]
- Mycek, P.; Gaurier, B.; Germain, G.; Pinon, G.; Rivoalen, E. Experimental study of the turbulence intensity effects on marine current turbines behaviour. Part II: Two interacting turbines. Renew. Energy 2014, 68, 876–892. [Google Scholar] [CrossRef]
- Gaurier, B.; Carlier, C.; Germain, G.; Pinon, G.; Rivoalen, E. Three tidal turbines in interaction: An experimental study of turbulence intensity effects on wakes and turbine performance. Renew. Energy 2020, 148, 1150–1164. [Google Scholar] [CrossRef]
- Noble, D.R.; Draycott, S.; Nambiar, A.; Sellar, B.G.; Steynor, J.; Kiprakis, A. Experimental Assessment of Flow, Performance, and Loads for Tidal Turbines in a Closely-Spaced Array. Energies 2020, 13, 1977. [Google Scholar] [CrossRef]
- Draycott, S.; Noble, D.; Ordonez, S.; Porter, K.; Johnstone, C.; FInch, S.; Judge, F.; Desmond, C.; Varela, B.; Lopez Mendia, J.; et al. D 2.1 Test Recommendations and Gap Analysis Report, MaRINET2. 2018, Volume 32. Available online: https://www.researchgate.net/publication/325781217_Test_recommendations_and_gap_analysis_report_MaRINET2_Deliverable_21 (accessed on 14 January 2020).
- Noble, D.R.; Davey, T.A.D.; Smith, H.C.M.; Kaklis, P.; Robinson, A.; Bruce, T. Spatial variation in currents generated in the FloWave Ocean Energy Research Facility. In Proceedings of the 11th European Wave and Tidal Energy Conference (EWTEC2015), Nantes, France, 6–11 September 2015; pp. 1–8. [Google Scholar]
- Nezu, I.; Rodi, W. Open-channel Flow Measurements with a Laser Doppler Anemometer. J. Hydraul. Eng. 1986, 112, 335–355. [Google Scholar] [CrossRef]
- George, W.K.; Lumley, J.L. The laser-Doppler velocimeter and its application to the measurement of turbulence. J. Fluid Mech. 1973, 60, 321–362. [Google Scholar] [CrossRef]
- Kraus, N.C.; Lohrmann, A.; Cabrera, R. New Acoustic Meter for Measuring 3D Laboratory Flows. J. Hydraul. Eng. 1994, 120, 406–412. [Google Scholar] [CrossRef]
- Voulgaris, G.; Trowbridge, J.H. Evaluation of the Acoustic Doppler Velocimeter (ADV) for Turbulence Measurements. J. Atmos. Ocean. Technol. 1997, 15, 272–289. [Google Scholar] [CrossRef]
- Lohrmann, A.; Cabrera, R.; Gelfenbaum, G.; Haines, J. Direct Measurement of Reynolds Stress with an Acoustic Doppler Velocimeter. In Proceedings of the IEEE Fifth Working Conference on Current Measurement, St. Petersburg, FL, USA, 7–9 February 1995. [Google Scholar]
- Sutherland, D.R.; Noble, D.R.; Steynor, J.; Davey, T.; Bruce, T. Characterisation of current and turbulence in the FloWave Ocean Energy Research Facility. Ocean. Eng. 2017, 139, 103–115. [Google Scholar] [CrossRef]
- Sutherland, D.; Ordonez-Sanchez, S.; Belmont, M.R.; Moon, I.; Steynor, J.; Davey, T.; Bruce, T. Experimental optimisation of power for large arrays of cross-flow tidal turbines. Renew. Energy 2018, 116, 685–696. [Google Scholar] [CrossRef]
- Walters, P. Acoustic Doppler Current Profiler Principles of Operation A Practical Primer. Technical Report. Rd Instruments: Poway, CA, USA, January 2011; pp. 1–56. Available online: https://www.comm-tec.com/Docs/Manuali/RDI/BBPRIME.pdf (accessed on 7 January 2020).
- Nortek AS. Signature Principles of Operation. Technical Report. Nortek AS: Rud, Norway; pp. 1–39. Available online: https://www.nortekgroup.com/assets/software/N3015-011-SignaturePrinciples.pdf (accessed on 15 January 2020).
- RD Instruments Sentinel V ADCP. Available online: http://www.teledynemarine.com/sentinel-v-adcp (accessed on 28 April 2020).
- ROWE Technologies SeaWatch DF. Available online: https://www.rowetechinc.com/dualfrequency/ (accessed on 28 April 2020).
- SonTek Argonaut-XR for Near Shore Deployments. Available online: https://www.sontek.com/argonaut-xr{#} (accessed on 28 April 2020).
- Nystrom, E.A.; Rehmann, C.R.; Asce, M.; Oberg, K.A. Evaluation of Mean Velocity and Turbulence Measurements with ADCPs. J. Hydraul. Eng. 2007, 133, 1310–1318. [Google Scholar] [CrossRef]
- Harrold, M.; Bromley, P.; Broudic, M.; Clelland, D.; Kiprakis, A.; Abusara, M. Assessment of an ADCP’s capabilities in laboratory conditions. In Proceedings of the 2015 IEEE/OES 11th Current, Waves and Turbulence Measurement, CWTM 2015, St. Petersburg, FL, USA, 2–6 March 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Sellar, B.; Wakelam, G. Characterisation of Tidal Flows at the European Marine Energy Centre in the Absence of Ocean Waves. Energy 2018, 11, 176. [Google Scholar] [CrossRef]
- Theriault, K.B. Incoherent multibeam doppler current profiler performance: Part II - Spatial response. IEEE J. Ocean. Eng. 1986, OE-11, 7–15. [Google Scholar] [CrossRef]
- Brumley, B.H.; Cabrera, R.G.; Deines, K.L.; Terray, E.A. Performance of a Broad-Band Acoustic Doppler Current Profiler. IEEE J. Ocean. Eng. 1991, 16, 402–407. [Google Scholar] [CrossRef]
- Ingram, D.; Wallace, R.; Robinson, A.; Bryden, I. The design and commissioning of the first, circular, combined current and wave test basin. In Proceedings of the OCEANS 2014 MTS/IEEE 2014, Taipei, Taiwan, 7–10 April 2014. [Google Scholar]
- Noble, D.R.; Draycott, S.; Nambiar, A.; Sellar, B.; Steynor, J.; Lennon, M.; Davey, T.; Kiprakis, A. Flow data around three SuperGen UKCMER Tidal Turbines in a closely spaced staggered array at FloWave. In Edinb. DataShare; The University of Edinburgh, School of Engineering, Institute for Energy Systems: Edinburgh, UK, 2020; Available online: https://datashare.is.ed.ac.uk/handle/10283/3564 (accessed on 16 April 2020).
- Robinson, A.; Ingram, D.; Bryden, I.; Bruce, T. The generation of 3D flows in a combined current and wave tank. Ocean. Eng. 2015, 93, 1–10. [Google Scholar] [CrossRef]
- Nortek AS. Nortek Signature 1000/500 Datasheet. Available online: https://www.nortekgroup.com/products/signature-1000/pdf (accessed on 11 February 2020).
- Nortek AS. The Comprehensive Manual for Velocimeters. Technical Report. 2018. Available online: https://support.nortekgroup.com/hc/en-us/articles/360029839351-The-Comprehensive-Manual-Velocimeters (accessed on 7 January 2020).
- Nortek AS. Vectrino Profiler Datasheet. Technical Report. Available online: http://www.nortek-es.com/lib/data-sheets/datasheet-vectrino-profiler/view (accessed on 24 February 2020).
- Jourdain de Thieulloy, M.; Dorward, M.; Sellar, B.; Old, C.; Davey, T.; Gabl, R.; Ingram, D. Experimental Flow Data from Co-Located Single Beam Acoustic Doppler Profiler and Acoustic Doppler Velocimeter in the FloWave Ocean Energy Research Facility. 2020. Available online: https://datashare.is.ed.ac.uk/handle/10283/3654 (accessed on 8 June 2020).
- Jourdain De Thieulloy, M.; Dorward, M.; Old, C.; Gabl, R.; Davey, T.; Ingram, D.M.; Sellar, B.G. Single-beam Acoustic Doppler Profiler and Co-Located Acoustic Doppler Velocimeter Flow Velocity Data. Data 2020. Available online: https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&ved=2ahUKEwiK07nRx8TqAhUOCawKHXazAyYQFjAAegQIARAB&url=https%3A%2F%2Fdatashare.is.ed.ac.uk%2Fbitstream%2Fhandle%2F10283%2F3654%2FDataDescription.pdf%3Fsequence%3D2%26isAllowed%3Dy&usg=AOvVaw34HaxqHe29IZwDlWNUHn34 (accessed on 11 July 2020).
- Mori, N.; Suzuki, T.; Kakuno, S. Noise of Acoustic Doppler Velocimeter Data in Bubbly Flows. J. Eng. Mech. 2007, 133, 122–125. [Google Scholar] [CrossRef]
- Mori, N. Despiking MATLAB Central File Exchange. 2014. Available online: https://uk.mathworks.com/matlabcentral/fileexchange/15361-despiking (accessed on 25 October 2019).
- Goring, D.G.; Nikora, V.I. Despiking Acoustic Doppler Velocimeter Data. J. Hydraul. Eng. 2002, 128, 117–126. [Google Scholar] [CrossRef]

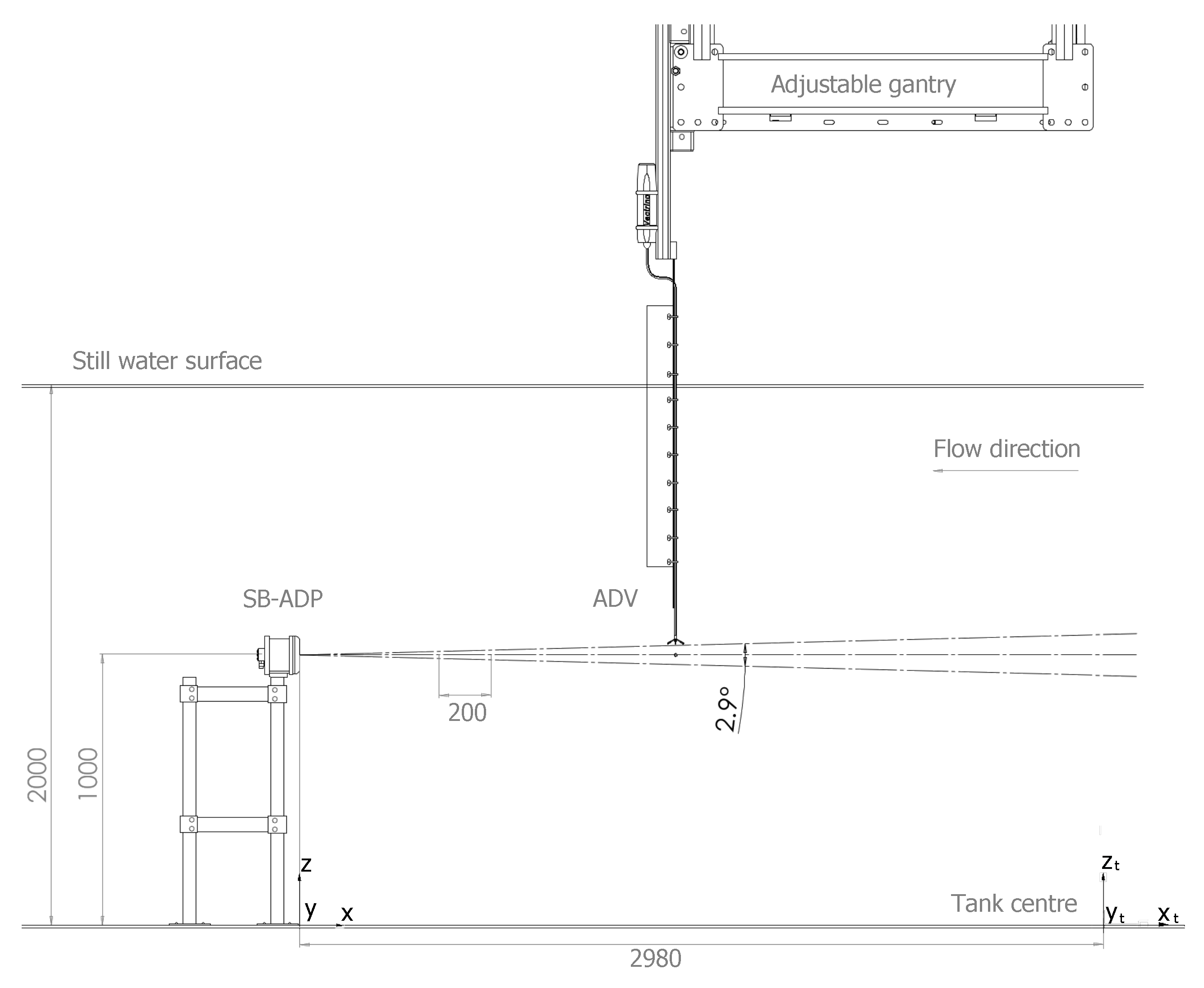
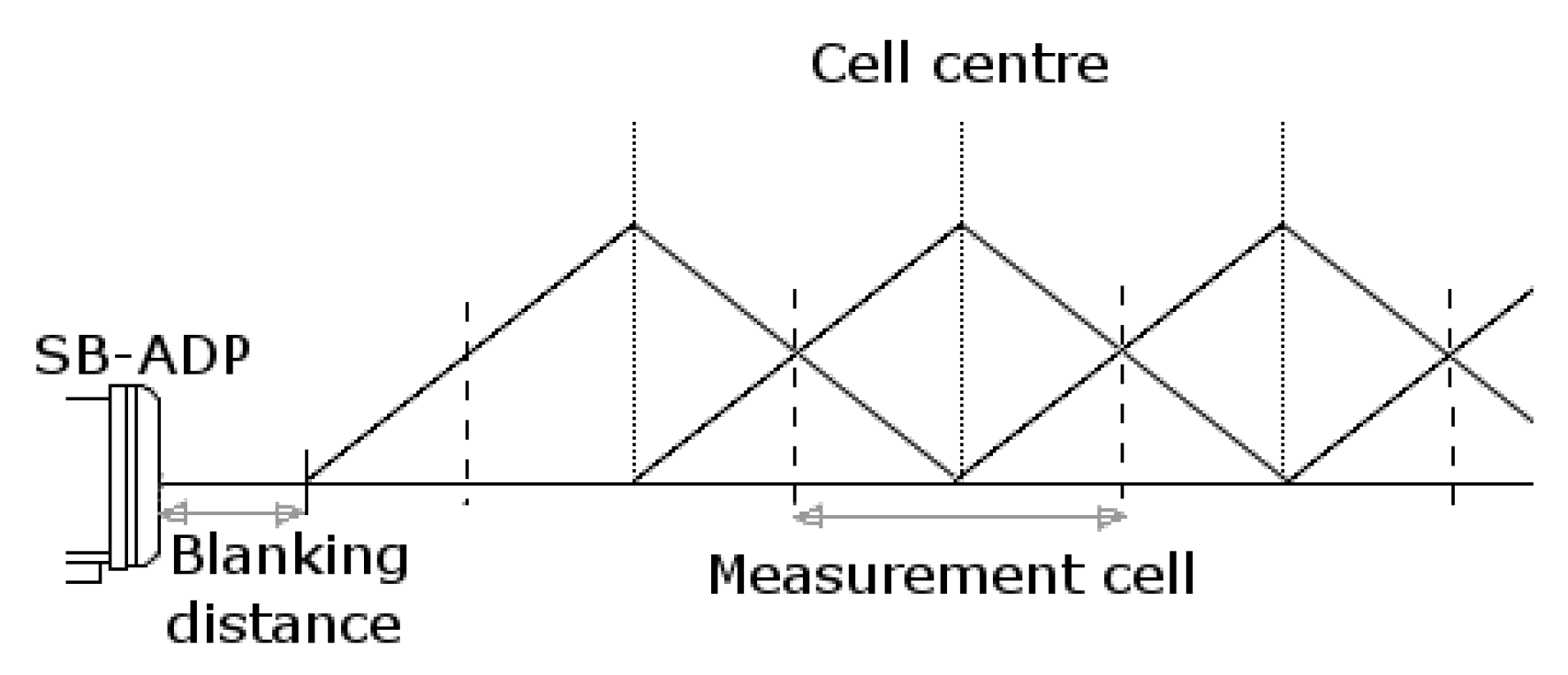



| Instrument | Coordinates (m) | ||
|---|---|---|---|
| SB-ADP | −2.98 | −0.55 | 1.00 |
| ADV | variable | −0.55 | 1.00 |
| Instrument Type | Model | Abbreviation | Operating Frequency (MHz) | Sample Rate (Hz) | Cell size (cm) |
|---|---|---|---|---|---|
| Acoustic Doppler Profiler | Nortek Single-beam | SB-ADP | 1 | 16 | 20 |
| Velocimeter | Nortek Vectrino Profiler | ADV | 10 | 100 | 0.4 |
| ADV Measurement Location | Corresponding SB-ADP Cell | x Error (m) | ||
|---|---|---|---|---|
| (m) | x (m) | Number | Centroid Location x (m) | |
| −2.647 | 0.333 | 1 | 0.30 | 0.03 |
| −2.336 | 0.644 | 3 | 0.70 | 0.06 |
| −2.05 | 0.93 | 4 | 0.90 | 0.03 |
| −1.785 | 1.195 | 5 | 1.10 | 0.09 |
| −1.459 | 1.521 | 7 | 1.50 | 0.02 |
| −1.145 | 1.835 | 9 | 1.90 | 0.06 |
| −0.843 | 2.137 | 10 | 2.10 | 0.04 |
| −0.545 | 2.435 | 12 | 2.50 | 0.06 |
| −0.255 | 2.725 | 13 | 2.70 | 0.02 |
| 0.045 | 3.025 | 15 | 3.10 | 0.07 |
| 0.349 | 3.329 | 16 | 3.30 | 0.03 |
| 0.660 | 3.640 | 18 | 3.70 | 0.06 |
| 0.952 | 3.932 | 19 | 3.90 | 0.03 |
| 1.252 | 4.232 | 21 | 4.30 | 0.07 |
| 1.553 | 4.533 | 22 | 4.50 | 0.03 |
| 1.855 | 4.835 | 24 | 4.90 | 0.06 |
| 2.156 | 5.136 | 25 | 5.10 | 0.04 |
| 2.453 | 5.433 | 27 | 5.50 | 0.07 |
| 2.744 | 5.724 | 28 | 5.70 | 0.02 |
| 3.027 | 6.007 | 30 | 6.10 | 0.09 |
| 3.339 | 6.319 | 31 | 6.30 | 0.02 |
| 3.646 | 6.626 | 33 | 6.70 | 0.07 |
| 3.942 | 6.922 | 34 | 6.90 | 0.02 |
| 4.366 | 7.346 | 36 | 7.30 | 0.05 |
| 4.663 | 7.643 | 38 | 7.70 | 0.06 |
| 5.025 | 8.005 | 40 | 8.10 | 0.09 |
| 5.406 | 8.386 | 41 | 8.30 | 0.08 |
| ADV Measurement Location | Corresponding SB-ADP Cell | |||||
|---|---|---|---|---|---|---|
| (m) | x (m) | Centre x (m) | Centre x (m) | |||
| A | −2.181 | 0.799 | 3 | 0.70 | 4 | 0.90 |
| B | −0.774 | 2.206 | 10 | 2.10 | 11 | 2.30 |
| C | 1.019 | 3.999 | 19 | 3.90 | 20 | 4.10 |
| D | 3.013 | 5.993 | 29 | 5.90 | 30 | 6.10 |
| Instrument | Nominal Tank Velocity (ms−1) | Data Remaining after Process (%) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Despiking Algorithm | Correlation Threshold | |||||||||||
| ADV | 0.6 | 1.0 | 1.2 | 99.4 | 99.2 | 99.3 | 99.4 | 99.2 | 99.1 | |||
| SB-ADP | 0.6 | 0.8 | 1.0 | 1.2 | 98.6 | 98.6 | 99.5 | 99.7 | 86.5 | 90.7 | 96.3 | 97.2 |
| Cell Number | 1 | 3 | 4 | 5 | 7 | 9 | 10 | 12 | 13 | 19 | 21 | 22 |
| Cell Centre x (m) | 0.3 | 0.7 | 0.9 | 1.1 | 1.5 | 1.9 | 2.1 | 2.5 | 2.7 | 3.9 | 4.3 | 4.5 |
| (ms−1) | 83.9 | 84.4 | 85.4 | 84.7 | 84.5 | 85.1 | 85.9 | 84.4 | 84.3 | 81.8 | 81.4 | 79.9 |
| Bias in(ms−1) | −3.8 | −1.0 | −1.4 | −0.4 | 0.5 | −0.3 | −0.9 | 1.6 | 0.7 | 1.0 | 0.3 | 1.8 |
| Relative bias (%) | 4.5 | 1.2 | 1.6 | 0.5 | 0.6 | 0.4 | 1.1 | 1.9 | 0.8 | 1.2 | 0.3 | 2.2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cell Number | 24 | 25 | 27 | 28 | 30 | 31 | 33 | 34 | 36 | 38 | 40 | 41 |
| Cell Centre x (m) | 4.9 | 5.1 | 5.5 | 5.7 | 6.1 | 6.3 | 6.7 | 6.9 | 7.3 | 7.7 | 8.1 | 8.3 |
| (ms−1) | 79.7 | 77.3 | 77.0 | 75.4 | 74.6 | 73.2 | 73.0 | 70.3 | 69.7 | 69.4 | 67.4 | 67.6 |
| Bias in (ms−1) | 0.7 | 2.1 | 1.1 | 1.8 | 1.2 | 2.2 | 0.4 | 1.4 | −1.1 | −1.8 | −0.9 | −1.7 |
| Relative bias (%) | 0.8 | 2.8 | 1.4 | 2.4 | 1.6 | 3.0 | 0.5 | 2.0 | 1.5 | 2.6 | 1.4 | 2.5 |
| Degree of Freedom | Sums of Squares | Mean Squares | F Value | p Value | |
|---|---|---|---|---|---|
| Sample location | 46 | 1287 | 27.99 | 4571.77 | |
| Instrument | 1 | 0.2 | 0.245 | 39.95 | |
| Residual | 328973 | 2014.7 | 0.006 |
| Nominal Tank Velocity (ms−1) | |||||||
|---|---|---|---|---|---|---|---|
| 0.6 1.0 1.2 | |||||||
| cell | (×10−2 ms−1) | (%) | (×10−2 ms−1) | (%) | (×10−2 ms−1) | (%) | |
| A | −3.2 | 5.0 | - | - | −2.9 | 2.3 | |
| −2.6 | 4.0 | 0.4 | 0.4 | −1.5 | 1.2 | ||
| −2.9 | 4.5 | 0.4 | 0.4 | −2.2 | 1.8 | ||
| B | −2.2 | 3.5 | 2.2 | 2.1 | −0.2 | 0.2 | |
| −1.6 | 2.5 | 2.0 | 2.0 | 0.0 | 0.0 | ||
| −1.9 | 3.0 | 2.1 | 2.0 | −0.1 | 0.1 | ||
| C | - | - | 1.1 | 1.0 | 1.6 | 1.3 | |
| - | - | 0.3 | 0.3 | 1.0 | 0.8 | ||
| - | - | 0.7 | 0.6 | 1.3 | 1.0 | ||
| D | 0.1 | 0.2 | 1.7 | 1.8 | 0.6 | 0.5 | |
| 0.1 | 0.1 | 0.6 | 0.6 | −0.7 | 0.6 | ||
| 0.1 | 0.1 | 1.1 | 1.2 | −0.1 | 0.1 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jourdain de Thieulloy, M.; Dorward, M.; Old, C.; Gabl, R.; Davey, T.; Ingram, D.M.; Sellar, B.G. On the Use of a Single Beam Acoustic Current Profiler for Multi-Point Velocity Measurement in a Wave and Current Basin. Sensors 2020, 20, 3881. https://doi.org/10.3390/s20143881
Jourdain de Thieulloy M, Dorward M, Old C, Gabl R, Davey T, Ingram DM, Sellar BG. On the Use of a Single Beam Acoustic Current Profiler for Multi-Point Velocity Measurement in a Wave and Current Basin. Sensors. 2020; 20(14):3881. https://doi.org/10.3390/s20143881
Chicago/Turabian StyleJourdain de Thieulloy, Marilou, Mairi Dorward, Chris Old, Roman Gabl, Thomas Davey, David M. Ingram, and Brian G. Sellar. 2020. "On the Use of a Single Beam Acoustic Current Profiler for Multi-Point Velocity Measurement in a Wave and Current Basin" Sensors 20, no. 14: 3881. https://doi.org/10.3390/s20143881
APA StyleJourdain de Thieulloy, M., Dorward, M., Old, C., Gabl, R., Davey, T., Ingram, D. M., & Sellar, B. G. (2020). On the Use of a Single Beam Acoustic Current Profiler for Multi-Point Velocity Measurement in a Wave and Current Basin. Sensors, 20(14), 3881. https://doi.org/10.3390/s20143881








