Low Cost and Compact FMCW 24 GHz Radar Applications for Snowpack and Ice Thickness Measurements
Abstract
:1. Introduction
2. Fundamentals
2.1. Ice Thickness Derivation
2.2. Snow Water Equivalent (SWE) Derivation
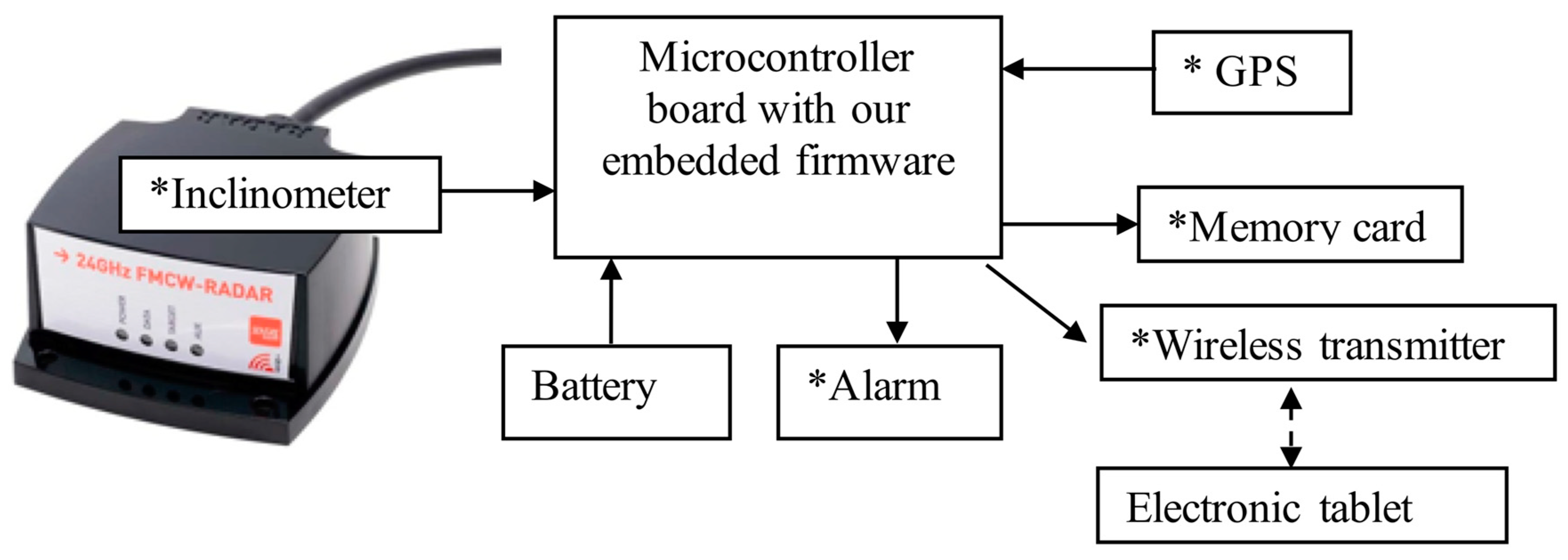
3. Sensor Description and Operating Modes
3.1. Sensor Description
3.2. Distance Resolution of the Radar System and Offset
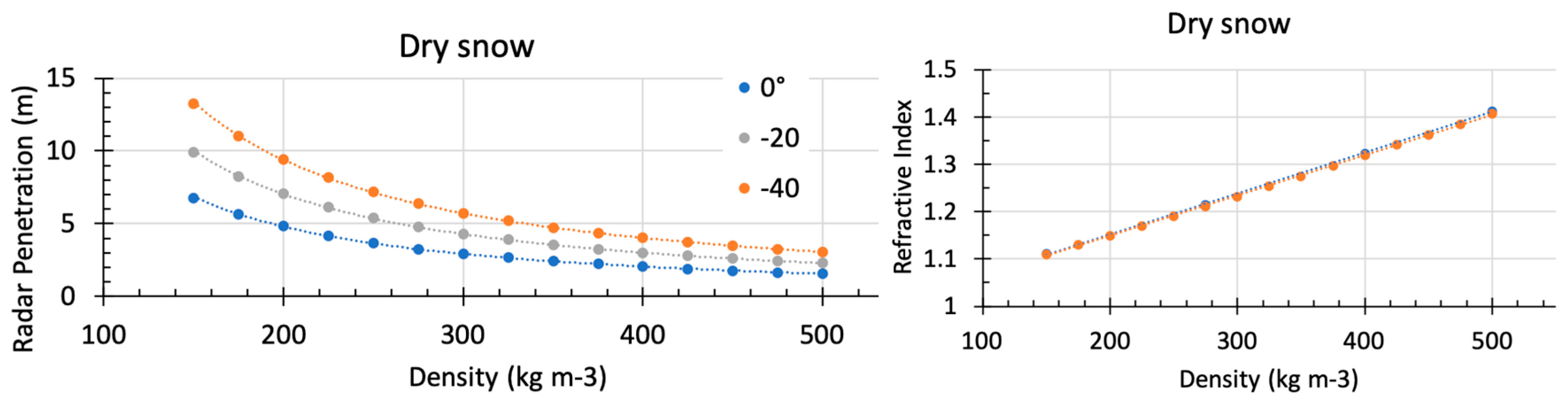
3.3. Penetration Depth
3.4. Operating Modes
4. Results: Radar Performance Tests
- In situ ice thickness: Manual in situ lake ice thickness measurements recorded by walking on the lake or from a stationary snowmobile. The system was not been tested on a moving snowmobile, although this is possible in a continuous recording mode.
- Ice thickness measurements from a remotely piloted aircraft (RPA) system: A preliminary test was conducted to evaluate the potential of measuring ice thickness with the radar mounted on a RPA.
- In situ SWE: The manual in situ snow water equivalent (SWE) measurement was based on known snow depth value, measured using an avalanche-type snow depth probe.
- In situ snow density: We tested the system in particular conditions in Antarctica to assess temporal snow surface density fluctuations.
- Monitoring SWE: Continuous automatic measurements of SWE evolution during the winter at a weather station. In this case, the radar measurements were combined with a synchronized and collocated automatic snow depth sensor (ultrasonic or LiDAR sensor).
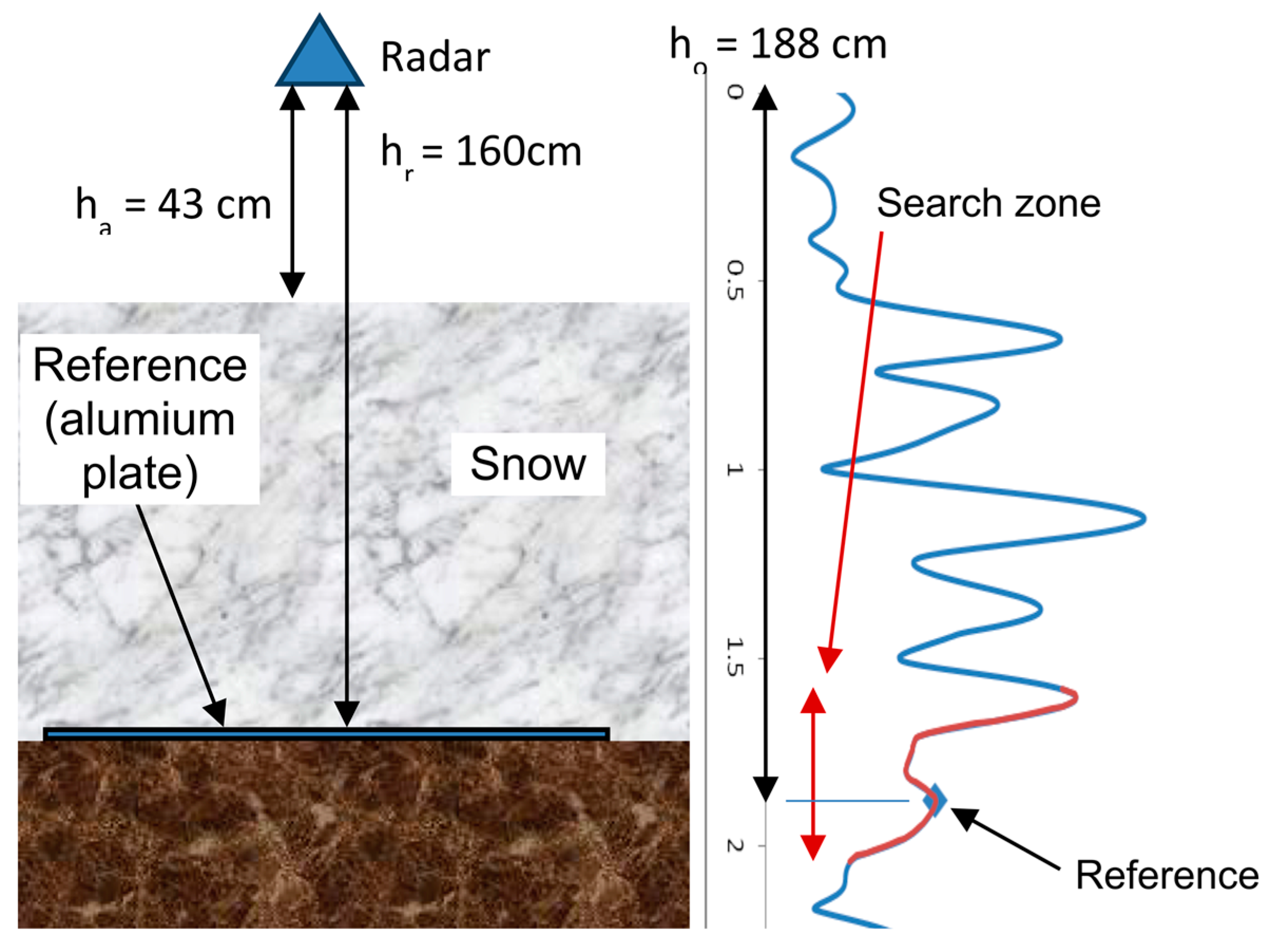
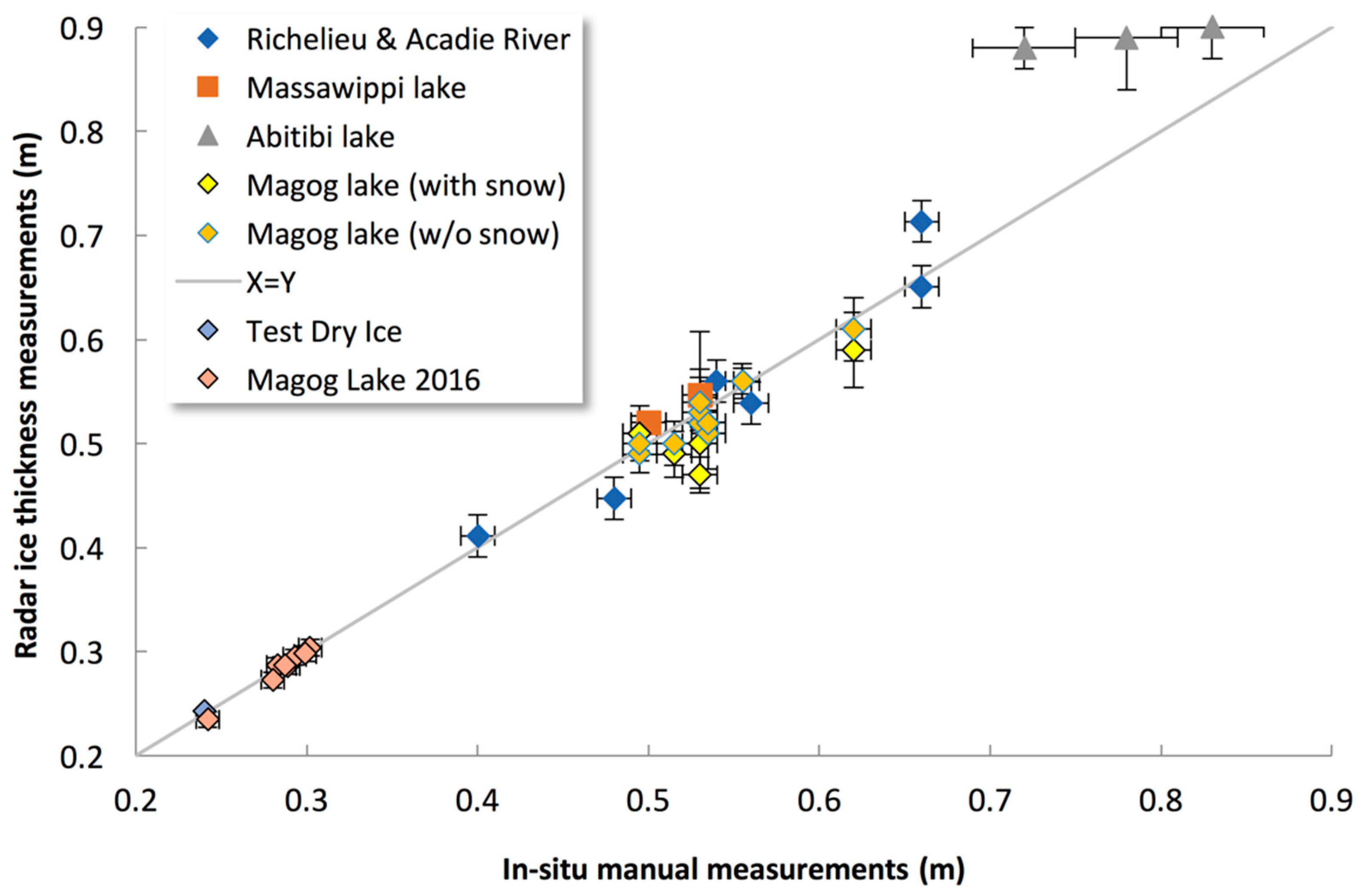
4.1. In Situ Ice Thickness
4.1.1. Shallow Ice Experiment from A Bridge
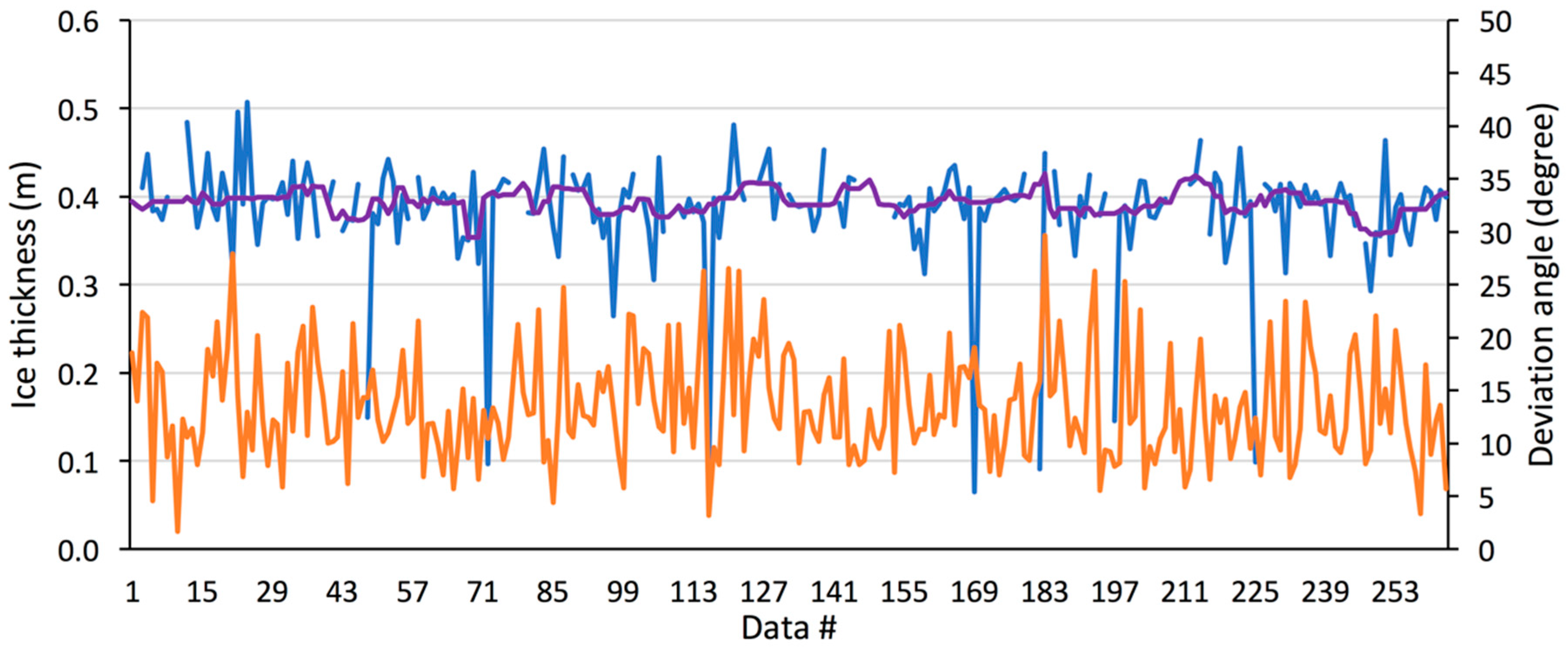
4.1.2. In Situ Ice Thickness Measurements
4.1.3. Limitations of Ice Thickness Detection
4.2. Ice Thickness Retrieval from Remotely Piloted Aircraft (RPA)
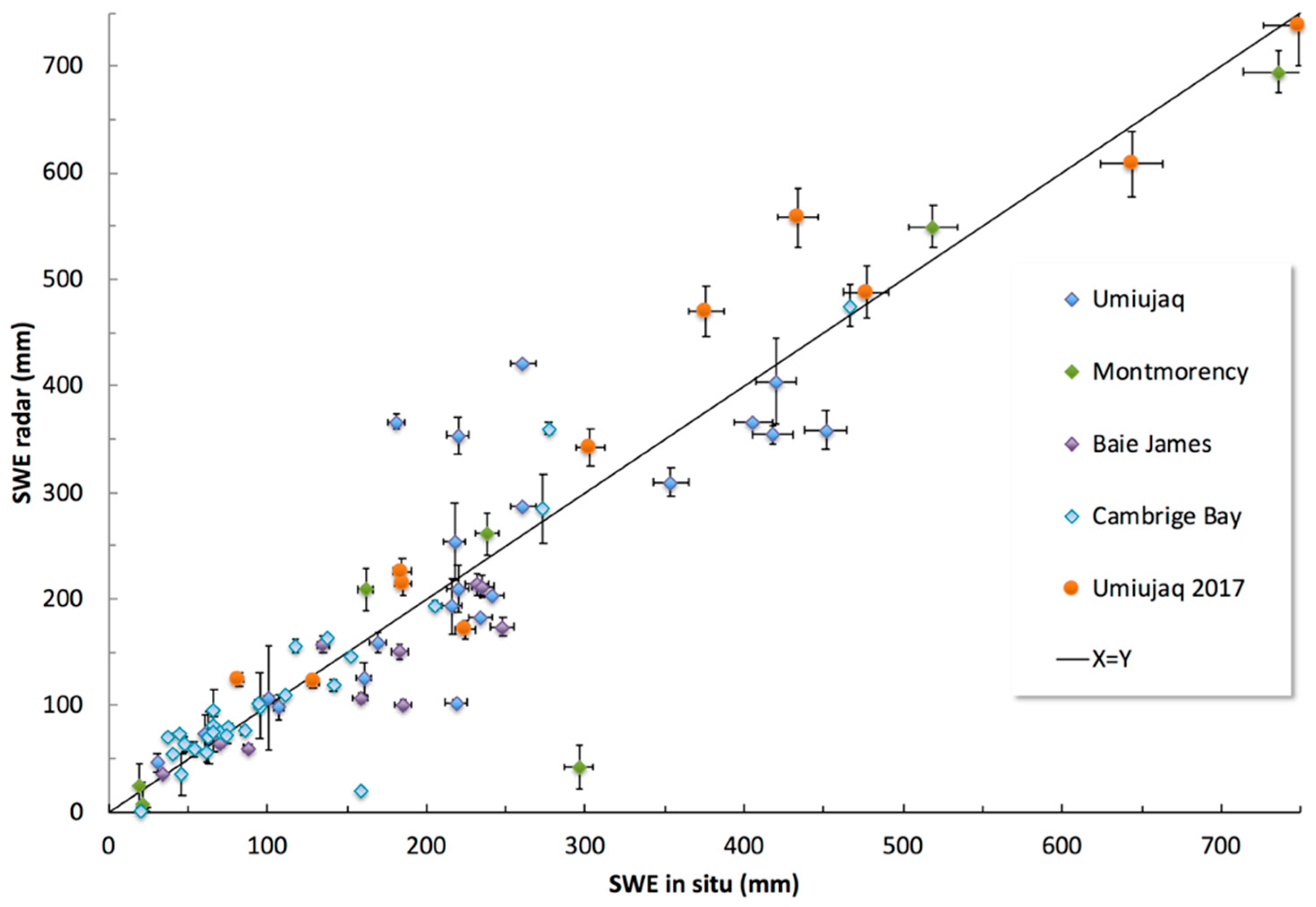
4.3. In Situ Snow Water Equivalent (SWE)
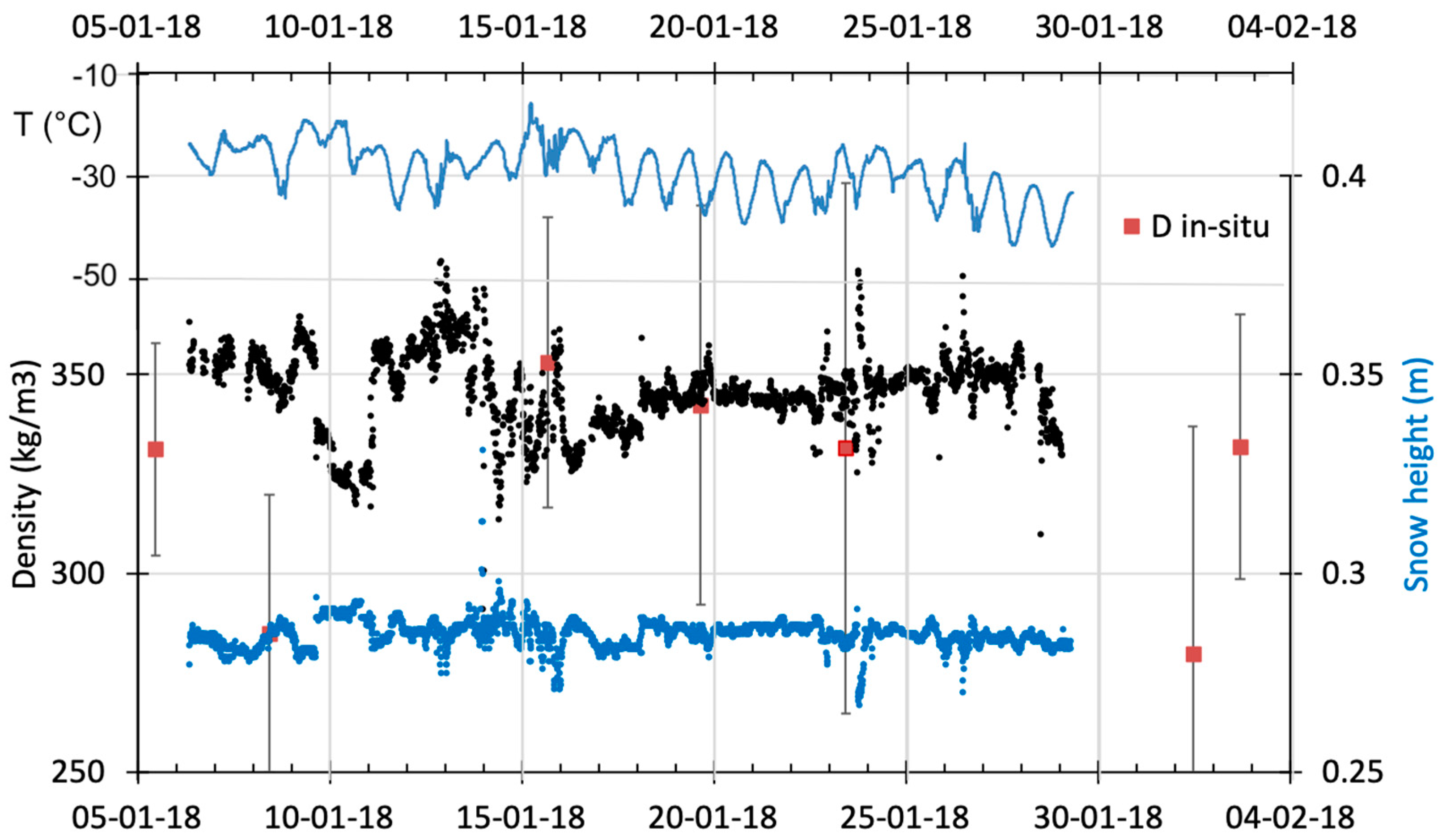
4.4. In Situ Density Monitoring in Antarctica
4.5. Continuous and Autonomous SWE Measurements
5. Discussion
6. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Ice and Snow Refractive Index and Penetration Depth Values
| Refractive Index (n) | Radar Penetration Depth (m) | Remarks | |||
|---|---|---|---|---|---|
| Ice | = 2.5555E-04 T + 1.7158 | = −1.9298E-02 T + 6.0610 | T in K | ||
| Water | T = 0 °C | = 4.82626971 | 0 | [68] | |
| T = −5 °C | = 4.46116371 | ||||
| Dry snow | = 8.6148E-04 + 9.7949E-01 for T = 0 °C | T = 0 °C | = 3.1975E+03 −1.2269 | in kg m−3 Very slight dependence in T for | |
| T = −20 °C | = 4.6162E+03 −1.2244 | ||||
| T = −40°C | = 6.0949E+03 −1.2224 | ||||
| Wet snow | = 150 kg m−3 | = 0.3861 + 1.1101 | See Figure A3 left | are for LWC 0.25 and T = 0 °C | |
| = 275 kg m−3 | = 0.7892 + 1.2111 | ||||
| = 400 kg m−3 | = 1.2268 + 1.3188 | ||||


Appendix B. FMCW Radar Simplified Link Budget
References
- Canada Red Cross. Available online: https://www.redcross.ca (accessed on 12 July 2006).
- IPCC Special Report on the Ocean and Cryosphere in a Changing Climate. Available online: https://www.ipcc.ch/srocc/chapter/chapter-3-2/ (accessed on 12 July 2019).
- López-Moreno, J.I.; Fassnacht, S.; Heath, J.; Musselman, K.; Re- vuelto, J.; Latron, J.; Moran-Tejeda, E.; Jonas, T. Small scale spatial variability of snow density and depth over complex alpine terrain: Implications for estimating snow water equivalent. Adv. Water Resour. 2013, 55, 40–52. [Google Scholar]
- Turcotte, R.; Fortier Filion, T.-C.; Lacombe, P.; Fortin, V.; Roy, A.; Royer, A. Simulation hydrologique des derniers jours de la crue de printemps: Le problème de la neige manquante. Hydrol. Sci. J. 2010, 55, 872–882. [Google Scholar] [CrossRef] [Green Version]
- WMO-GCW. Global Cryosphere Watch (GCW) Implementation Plan, Version 1.6; World Meteorological Organization Report; WMO: Geneva, Switzerland, 2015. [Google Scholar]
- AMAP and the Arctic Council. Available online: https://www.amap.no (accessed on 12 July 2017).
- Observations: Cryosphere, in Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Available online: https://www.ipcc.ch/site/assets/uploads/2018/02/WG1AR5_Chapter04_FINAL.pdf (accessed on 12 July 2013).
- Serreze, M.C.; Barry, R.G. Processes and impacts of Arctic amplification. A research synthesis. Glob. Planet. Chang. 2011, 77, 85–96. [Google Scholar] [CrossRef]
- Brown, R.D. Analysis of snow cover variability and change in Quebec. Hydrol. Processes 2010, 24, 1929–1954. [Google Scholar] [CrossRef]
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 2005, 438, 303–309. [Google Scholar] [CrossRef]
- Rasmussen, R.; Baker, B.; Kochendorfer, J.; Meyers, T.; Landolt, S.; Fischer, A.P.; Black, J.; Thériault, J.M.; Kucera, P.; Gochis, D.; et al. How well are we measuring snow: The NOAA/FAA/NCAR winter precipitation test bed. Am. Meteorol. Soc. 2012, 93, 811–829. [Google Scholar] [CrossRef] [Green Version]
- Mortimer, C.; Mudryk, L.; Derksen, C.; Luojus, K.; Brown, R.; Kelly, R.; Tedesco, M. Evaluation of long-term Northern Hemisphere snow water equivalent products. Cryosphere 2020, 14, 1579–1594. [Google Scholar] [CrossRef]
- Natural Resources Conservation Service (NRCS). Available online: https://www.nrcs.usda.gov (accessed on 1 June 2020).
- British Columbia Network. Snow Survey Data and Automated Snow Weather Station Data in British Columbia, Ca. Available online: https://www2.gov.bc.ca. (accessed on 1 June 2020).
- Brown, R.D.; Fang, B.; Mudryk, L. Update of Canadian historical snow survey data and analysis of snow water equivalent trends, 1967–2016. Atmos. Ocean 2019, 57, 1–8. [Google Scholar] [CrossRef]
- Choquette, Y.; Ducharme, P.; Rogoza, J. CS725, an accurate sensor for the snow water equivalent and soil moisture measurements. In Proceedings of the International Snow Science Workshop, Grenoble, France, 7–11 October 2013. [Google Scholar]
- Bulygina, O.; Groisman, P.; Ya Razuvaev, V.; Korshunova, N. Changes in snow cover characteristics over Northern Eurasia since 1966. Environ. Res. Lett. 2011, 6, 045204. [Google Scholar] [CrossRef]
- Takala, M.; Ikonen, J.; Luojus, K.; Lemmetyinen, J.; Metsämäki, S.; Cohen, J.; Arslan, A.N.; Pulliainen, J. New snow water equivalent processing system with improved resolution over Europe and its applications in hydrology. IEEE J-STARS 2017, 10, 428–436. [Google Scholar] [CrossRef]
- Gottardi, F.; Carrier, P.; Paquet, E.; Laval, M.-T.; Gailhard, J.; Garçon, R. Le NRC: Une décennie de mesures de l’équivalent en eau du manteau neigeux dans les massifs montagneux français. In Proceedings of the International Snow Science Workshop Grenoble, 7–11 October 2013; pp. 926–930. [Google Scholar]
- Holmes, R.M.; Shiklomanov, A.I.; Suslova, A.; Tretiakov, M.; McClelland, J.W.; Spencer, R.G.M.; Tank, S.E. Arctic River Discharge. Arctic Report 2018 Cards. Available online: https://arctic.noaa.gov/Report-Card (accessed on 1 June 2020).
- Morgan, M.A. Ultra-Wideband Impulse Scattering Measurements. IEEE Trans. Antennas Propag. 1994, 42, 840–846. [Google Scholar] [CrossRef]
- Schmid, L.; Heilig, A.; Mitterer, C.; Schweizer, J.; Maurer, H.; Okorn, R.; Eisen, O. Continuous snowpack monitoring using upward-looking ground-penetrating radar technology. J. Glaciol. 2014, 60, 509–525. [Google Scholar] [CrossRef] [Green Version]
- Nobes, D.C. Ground Penetrating Radar Measurements Over Glaciers. In Encyclopedia of Snow, Ice and Glaciers; Springer: Dordrecht, The Netherlands, 2011; pp. 490–503. [Google Scholar]
- Riek, L.; Crane, R.K.; O’Neill, K. Signal-processing algorithm for the extraction of thin freshwater-ice thickness from short pulse radar data. IEEE Trans. Geosci. Remote Sens. 1990, 28, 137–145. [Google Scholar] [CrossRef]
- MALAÅ Geoscience. (n.d.). Case Studies for GPR in Geophysical Surveys. From MALAÅ Geoscience. Available online: http://www.malags.com/getattachment/465a6999-c36c-46bc-80bc-2183c3b7ebb0/Case-Studies-1 (accessed on 1 June 2020).
- Peng, Z.; Li, C. Portable Microwave Radar Systems for Short-Range Localization and Life Tracking: A Review. Sensors 2019, 19, 1136. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schneider, M. Automotive radar—Status and trends. In Proceedings of the German Microwave Conference, Ulm, Germany, 5–7 April 2005; pp. 144–147. [Google Scholar]
- Ellerbruch, D.; Boyne, H. Snow Stratigraphy and Water Equivalence Measured with an Active Microwave System. J. Glaciol. 1980, 26, 225–233. [Google Scholar] [CrossRef]
- Marshall, H.-P.; Koh, G. FMCW radars for snow research. Cold Reg. Sci. Technol. 2008, 52, 118–131. [Google Scholar] [CrossRef]
- Yankielun, N.; Rosenthal, W.; Robert, D. Alpine snow depth measurements from aerial FMCW radar. Cold Reg. Sci. Technol. 2004, 40, 123–134. [Google Scholar] [CrossRef]
- Fujino, K.; Wakahama, G.; Suzuki, M.; Matsumoto, T.; Kuroiwa, D. Snow stratigraphy measured by an active microwave sensor. Ann. Glaciol. 1985, 6, 207–210. [Google Scholar] [CrossRef] [Green Version]
- Marshall, H.; Koh, G.; Forster, R. Estimating alpine snowpack properties using FMCW radar. Ann. Glaciol. 2005, 40, 157–162. [Google Scholar] [CrossRef] [Green Version]
- Koh, G.; Yankielun, N.E.; Baptista, A.I. Snow cover characterization using multiband FMCW radars. Hydrol. Process. 1996, 10, 1609–1617. [Google Scholar] [CrossRef]
- Yan, J.B.; Alvestegui, D.G.-G.; McDaniel, J.W.; Li, Y.; Gogineni, S.; Rodriguez-Morales, F.; Brozena, J.; Leuschen, C.J. Ultrawideband FMCW Radar for Airborne Measurements of Snow Over Sea Ice and Land. IEEE Trans. Geosci. Remote Sens. 2017, 55, 834–843. [Google Scholar] [CrossRef]
- Ghosh, G.; Chakravarty, D. Circularly Polarized Proximity Feed Patch Antenna for FMCW Radar. In Proceedings of the 2019 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting, Atlanta, GA, USA, 7–12 July 2019; pp. 1783–1784. [Google Scholar]
- Li, J.; Vélez González, J.A.; Leuschen, C.; Harish, A.; Gogineni, P.; Montagnat, M.; Weikusat, I.; Rodriguez-Morales, F.; Paden, J. Multi-channel and multi-polarization radar measurements around the NEEM site. Cryosphere 2018, 12, 2689–2705. [Google Scholar] [CrossRef] [Green Version]
- Gubler, H.; Hiller, M. The use of microwave FMCW radar in snow and avalanche research. Cold Reg. Sci. Technol. 1984, 9, 109–119. [Google Scholar] [CrossRef]
- Griffiths, H.D. New ideas in FM radar. Electron. Commun. Eng. J. 1990, 2, 185–194. [Google Scholar] [CrossRef]
- Stove, A.G. Linear FMCW radar techniques. IEEE Proc. F. 1992, 139, 342–350. [Google Scholar] [CrossRef]
- Rodriguez-Morales, F.; Gogineni, S.; Leuschen, C.J.; Paden, J.D.; Li, J.; Lewis, C.C.; Panzer, B.; Alvestegui, D.G.-G.; Patel, A.; Byers, K.; et al. Advanced multifrequency radar instrumentation for polar research. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2824–2842. [Google Scholar] [CrossRef]
- Hu, X.; Ma, C.; Hu, R.; Yeo, T.S. Imaging for Small UAV-Borne FMCW SAR. Sensors 2019, 19, 87. [Google Scholar] [CrossRef] [Green Version]
- Meta, A.; Hoogeboom, P.; Ligthart, L. Signal processing for FMCW SAR. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3519–3532. [Google Scholar] [CrossRef]
- Ayhan, S.; Pauli, M.; Scherr, S.; Göttel, B.; Bhutani, A. Millimeter-Wave Radar Sensor for Snow Height Measurements. IEEE Trans. Geosci. Remote Sens. 2017, 55, 854–861. [Google Scholar] [CrossRef]
- Okorn, R.; Brunnhofer, G.; Platzer, T.; Heilig, A.; Schmid, L.; Mitterer, C.; Schweizer, J.; Eisen, O. Upward-looking L-band FMCW radar for snow cover monitoring. Cold Reg. Sci. Technol. 2014, 103, 31–40. [Google Scholar] [CrossRef] [Green Version]
- Vriend, N.M.; McElwaine, J.N.; Sovilla, B.; Keylock, C.J.; Ash, M.; Brennan, P.V. High-resolution radar measurements of snow avalanches. Geophys. Res. Lett. 2013, 40, 727–731. [Google Scholar] [CrossRef] [Green Version]
- Marshall, H.-P.; Schneebeli, M.; Koh, G. Snow stratigraphy measurements with high-frequency FMCW radar: Comparison with snow micro-penetrometer. Cold Reg. Sci. Technol. 2007, 47, 108–117. [Google Scholar] [CrossRef]
- Xu, X.; Baldi, C.; Bleser, J.-W.; Lei, Y.; Yueh, S.; Esteban-Fernandez, D. Multi-Frequency Tomography Radar Observations of Snow Stratigraphy at Fraser During SnowEx. In Proceedings of the IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018. [Google Scholar]
- Gunn, G.E.; Duguay, C.R.; Brown, L.C.; King, J.; Atwood, D.; Kasurak, A. Freshwater Lake Ice Thickness Derived Using Surface-based X- and Ku-band FMCW Scatterometers. Cold Reg. Sci. Technol. 2015, 120, 115–126. [Google Scholar] [CrossRef]
- Yankielun, N.E.; Ferrick, M.G.; Weyrick, P.B. Development of an airborne millimeter-wave FM-CW radar for mapping river ice. Can. J. Civ. Eng. 1993, 20, 1057–1064. [Google Scholar] [CrossRef]
- Rodriguez, S.; Marshall, H.P.; Rodriguez, P. Applications of low cost and low power FMCW radar in the characterization of dry snow. In Proceedings of the International Snow Science Workshop, Banff, UK, 28 September–3 October 2014; pp. 857–861. [Google Scholar]
- IMST sentireTM Radar Module 24 GHz sR-1200 Series User Manual. Available online: http://www.radar-sensor.com/ (accessed on 1 June 2020).
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. 1981, 1982, 1986: Microwave Remote Sensing, Active and Passive; Artech House, Inc.: Norwood, MA, USA, 1986; Volume 3. [Google Scholar]
- Mätzler, C.; Wegmuller, U. Dielectric Properties of freshwater ice at microwave frequencies. J. Phys. D Appl. Phys. 1987, 20, 1623–1630. [Google Scholar] [CrossRef]
- Li, Z.; Jia, Q.; Zhang, B.; Leppäranta, M.; Peng, L.; Huang, W. Influences of gas bubble and ice density on ice thickness measurement by GPR. Appl. Geophys. 2010, 7, 105–113. [Google Scholar] [CrossRef]
- Mätzler, C. Microwave permittivity of dry snow. IEEE Trans. Geosci. Remote Sens. 1986, 48, 50–58. [Google Scholar] [CrossRef]
- Hallikainen, H.; Ulaby, F.T.; Abdelrazik, M. Dielectric properties of snow in the 3- to 37-GHz range. IEEE Trans. Antennas Propagat. 1986, 34, 1329–1340. [Google Scholar] [CrossRef]
- Tiuri, M.; Sihvola, A.; Nyfors, E.; Hallikainen, M. The complex dielectric constant of snow at microwave frequencies. IEEE J. Ocean. Eng. 1984, 9, 377–382. [Google Scholar] [CrossRef]
- Sadiku, M.N. Refractive index of snow at microwave frequencies. Appl. Optics 1985, 24, 572–575. [Google Scholar] [CrossRef]
- Huining, W.; Pulliainen, J.; Hallikainen, M. Effective Permittivity of Dry Snow in the 18 to 90 GHz Range. Prog. Electromagn. Res. 1999, 24, 119–138. [Google Scholar] [CrossRef] [Green Version]
- Rees, W.G. Physical Principles of Remote Sensing; Cambridge University Press: Cambridge, UK, 2013; p. 441. [Google Scholar]
- Proksch, M.; Rutter, N.; Fierz, C.; Schneebeli, M. Intercomparison of snow density measurements: Bias, precision, and vertical resolution. Cryosphere 2016, 10, 371–384. [Google Scholar] [CrossRef]
- Picard, G.; Arnaud, L.; Panel, J.-M.; Morin, S. Design of a scanning laser meter for monitoring the spatio-temporal evolution of snow depth and its application in the Alps and in Antarctica. Cryosphere 2016, 10, 1495–1511. [Google Scholar] [CrossRef] [Green Version]
- Picard, G.; Royer, A.; Arnaud, L.; Fily, M. Influence of meter-scale wind-formed features on the variability of the microwave brightness temperature around Dome C in Antarctica. Cryosphere 2014, 8, 1105–1119. [Google Scholar] [CrossRef] [Green Version]
- Champollion, N.; Picard, G.; Arnaud, L.; Lefebvre, É.; Macelloni, G.; Rémy, F.; Fily, M. Marked decrease of the near surface snow density retrieved by AMSR-E satellite at Dome C, Antarctica, between 2002 and 2011. Cryosphere 2019, 13, 1215–1232. [Google Scholar] [CrossRef] [Green Version]
- Campbell Scientific Canada. CS725 Snow Water Equivalent Sensor. Available online: https://www.campbellsci.ca/cs725 (accessed on 1 June 2020).
- Langley, K.; Hamran, S.-E.; Hogda, K.; Storvold, R.; Brandt, O.; Kohler, J.; Hagen, J. From glacier facies to SAR backscatter zones via GPR. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2506–2516. [Google Scholar] [CrossRef] [Green Version]
- Picard, G.; Sandells, M.; Löwe, H. SMRT: An active/passive microwave radiative transfer model for snow with multiple microstructure and scattering formulations (v1.0). Geosci. Model Dev. 2018, 11, 2763–2788. [Google Scholar] [CrossRef] [Green Version]
- Meissner, T.; Wentz, F.J. The Complex Dielectric Constant of Pure and Sea Water from Microwave Satellite Observations. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1836–1849. [Google Scholar] [CrossRef] [Green Version]
- Pouliguen, P.; Hemon, R.; Bourlier, C.; Damiens, J.; Saillard, J. Analytical formulae for radar cross section of flat plates in near field and normal incidence. Prog. Electromagn. Res. 2008, 9, 263–279. [Google Scholar] [CrossRef] [Green Version]











| Parameters | Specifications |
|---|---|
| General | |
| Modulation | CW or FMCW mode |
| Operating Frequency | 24.25 GHz, band width B = 2.5 GHz |
| Discrete time-domain signal | 1024 data samples |
| Number of Channels | 1 Transmit-Channel, 2 Receive-Channels with I/Q demodulator for each channel |
| Data Interface | SPI *, CAN **, Ethernet (with PoE ***) |
| Antenna | |
| Antenna Type | Integrated Patch Antenna |
| Number of antennas | 1 transmitter antenna and 2 receiver antennas |
| Antenna Characteristics | ±32.5° azimuth and ±12° elevation (± 2–3°) |
| Antenna Polarization | linear |
| Measurement | |
| Measurement Range | 0.6–307 m |
| Operation Parameters | |
| Frequency Ramp Duration (Tr) | 1–100 ms |
| Update Rate | typically 10–200 Hz |
| EIRP **** Output Power | typ. 10–19 dBm (tunable) |
| Operating Temperature | minimum −40 °C, maximum 60 °C |
| Power Supply | |
| Operation Voltage | 10.5–13 V, 44–54 V PoE |
| Standby Power | 3.0 W |
| Operating Power | 4.5 W |
| Parameter | Specification |
|---|---|
| Dimension (L × W × H) | 98.0 mm × 87.0 mm × 42.5 mm (Housing) 114.0 mm × 87.0 mm × 42.5 mm (with Bushing) |
| Weight | 280 g |
| Mounting | 4 Mounting Holes (Ø 5 mm) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pomerleau, P.; Royer, A.; Langlois, A.; Cliche, P.; Courtemanche, B.; Madore, J.-B.; Picard, G.; Lefebvre, É. Low Cost and Compact FMCW 24 GHz Radar Applications for Snowpack and Ice Thickness Measurements. Sensors 2020, 20, 3909. https://doi.org/10.3390/s20143909
Pomerleau P, Royer A, Langlois A, Cliche P, Courtemanche B, Madore J-B, Picard G, Lefebvre É. Low Cost and Compact FMCW 24 GHz Radar Applications for Snowpack and Ice Thickness Measurements. Sensors. 2020; 20(14):3909. https://doi.org/10.3390/s20143909
Chicago/Turabian StylePomerleau, Patrick, Alain Royer, Alexandre Langlois, Patrick Cliche, Bruno Courtemanche, Jean-Benoît Madore, Ghislain Picard, and Éric Lefebvre. 2020. "Low Cost and Compact FMCW 24 GHz Radar Applications for Snowpack and Ice Thickness Measurements" Sensors 20, no. 14: 3909. https://doi.org/10.3390/s20143909





