Damage Detection of Bridges under Environmental Temperature Changes Using a Hybrid Method
Abstract
:1. Introduction
2. Hybrid Method for Damage Detection of Bridges under Environmental Temperature Changes
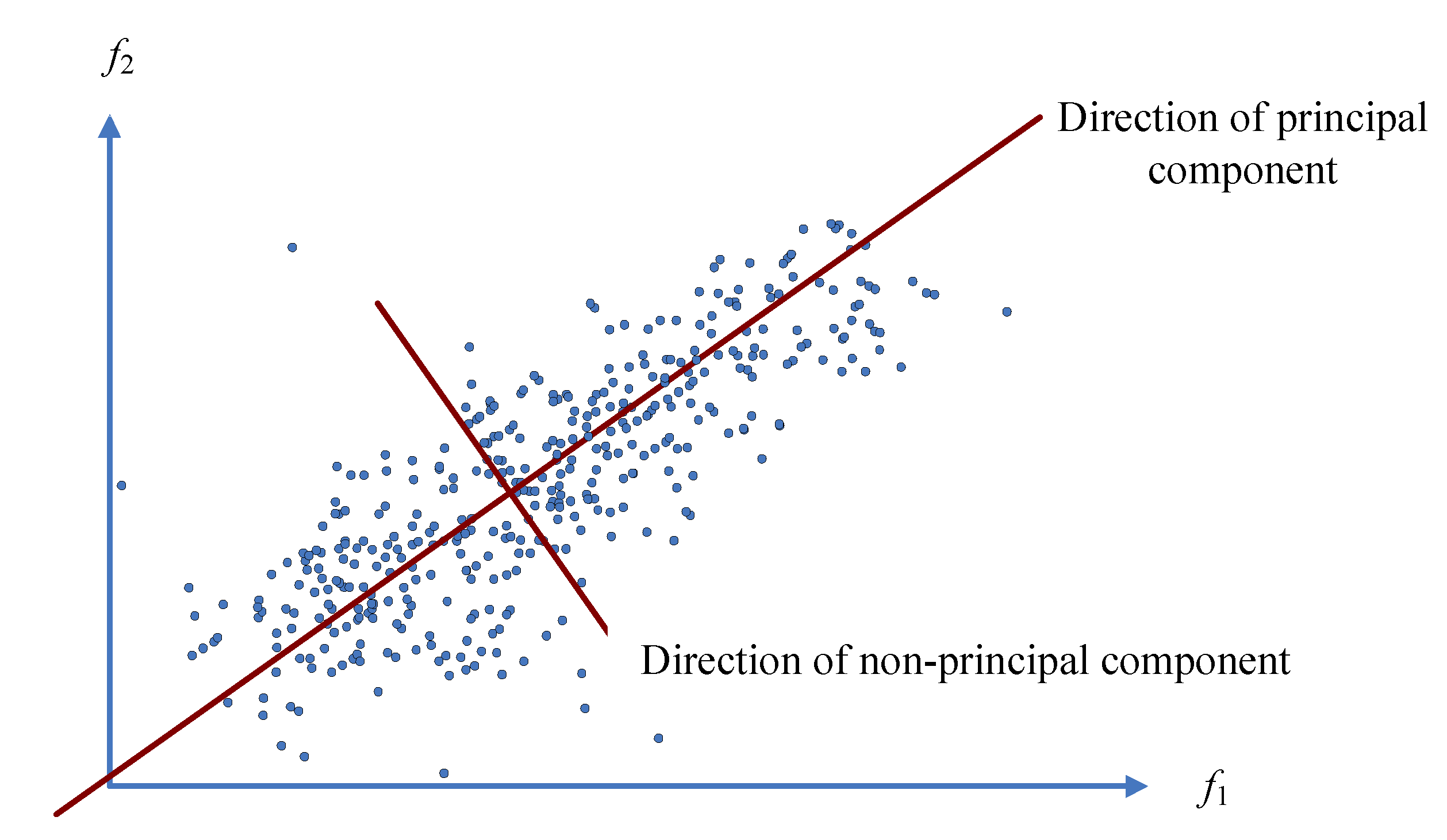
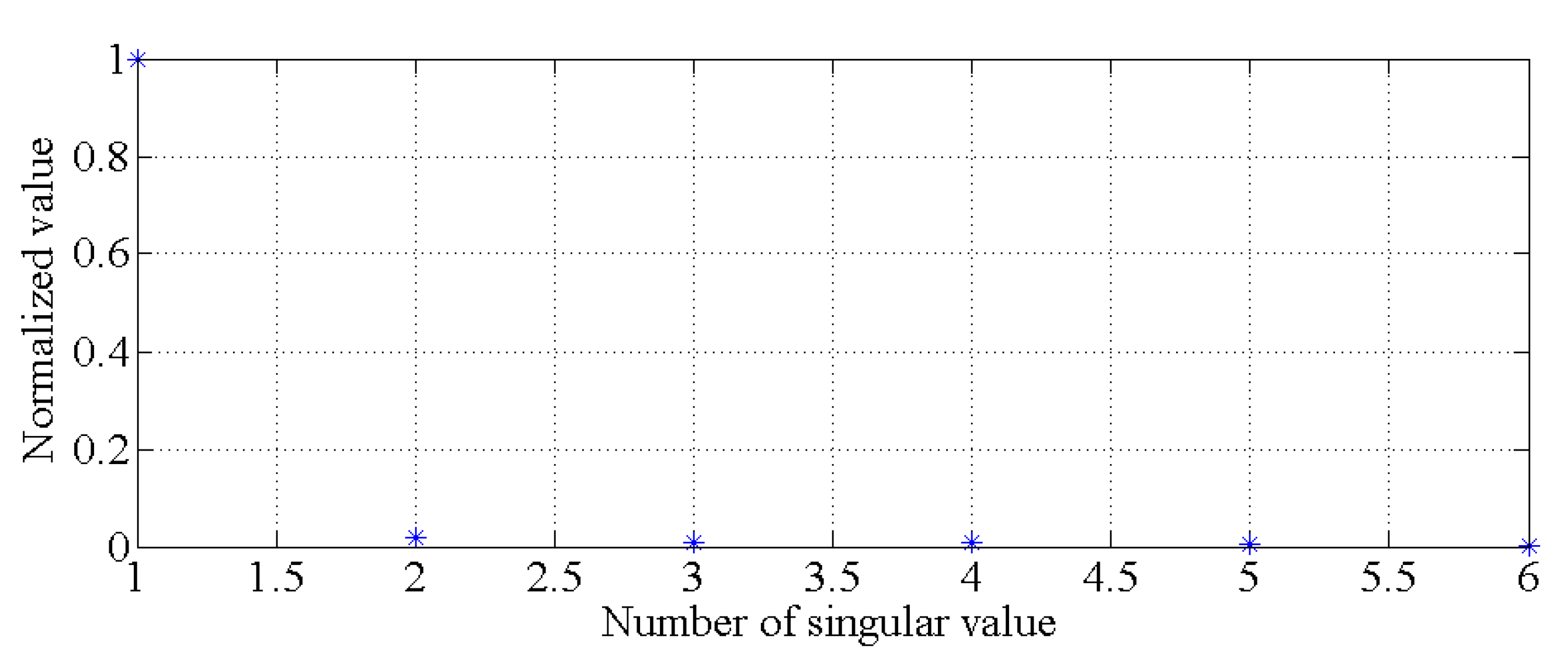
2.1. Discussion of the Effectiveness of the PCA-Based Method for Damage Detection of Bridges
2.2. Classification of the Damage Features Projected in the Direction of Principal Components Using GMM
2.3. Procedure of the Proposed Hybrid Method
3. Numerical Example
3.1. Description of the Numerical Bridge-Like Model
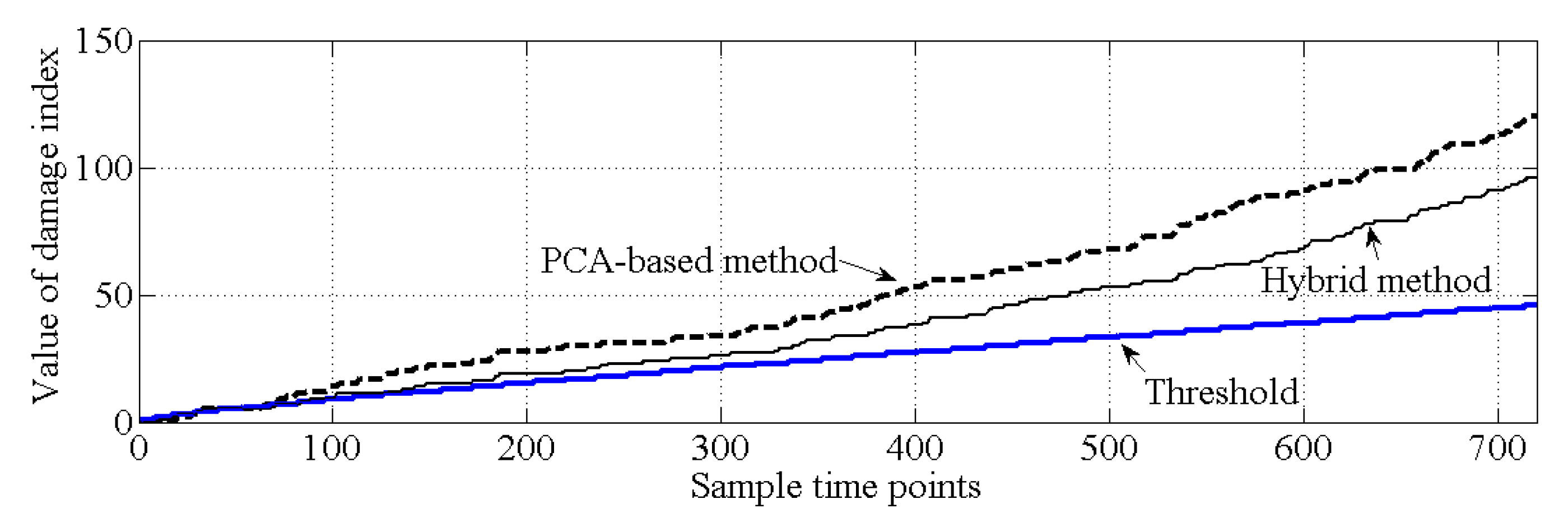
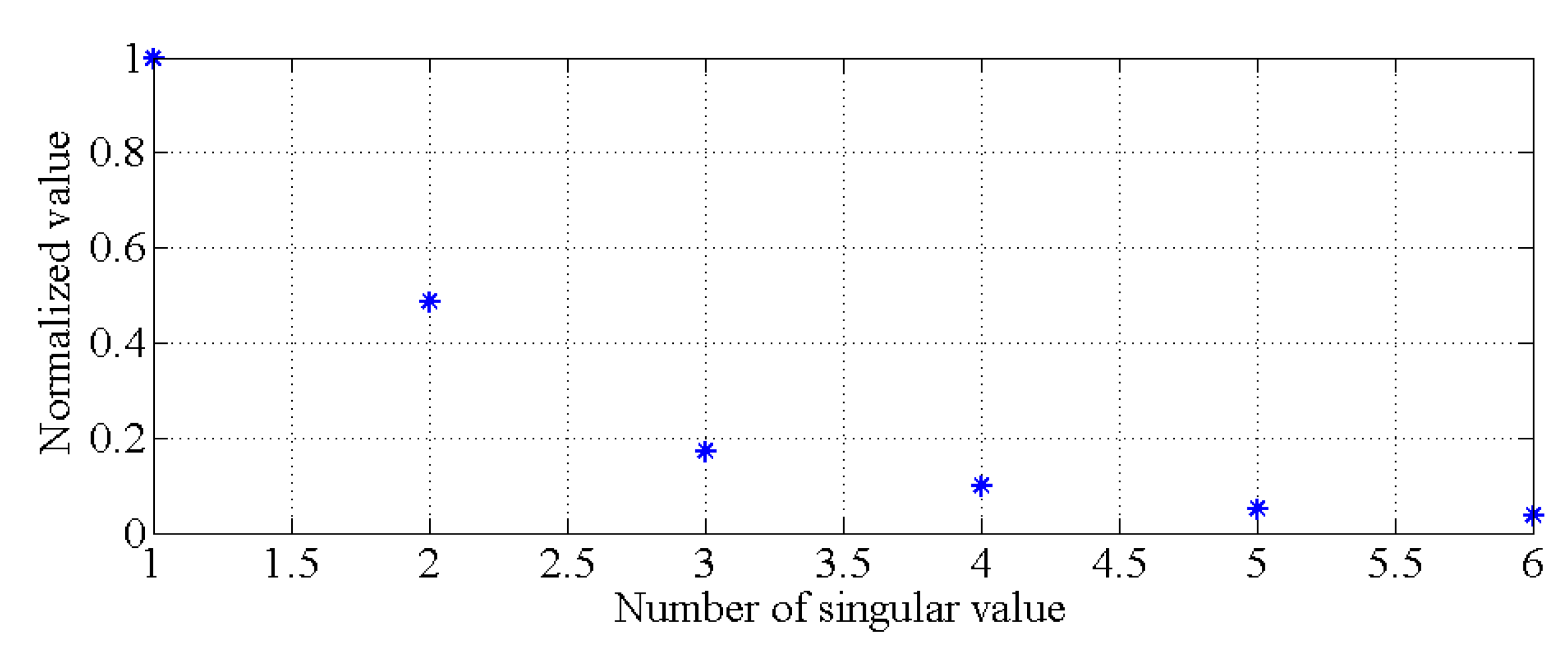
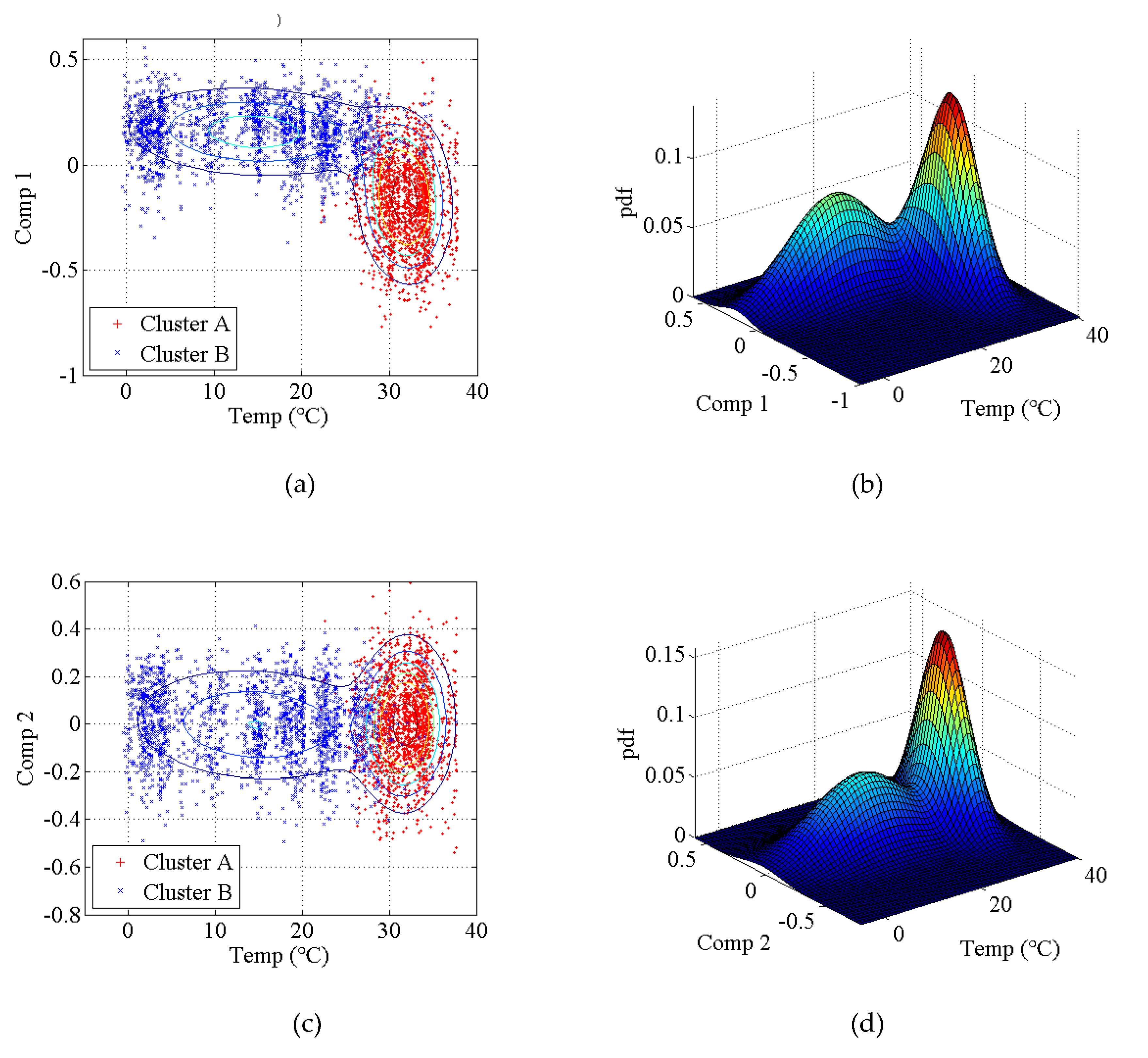
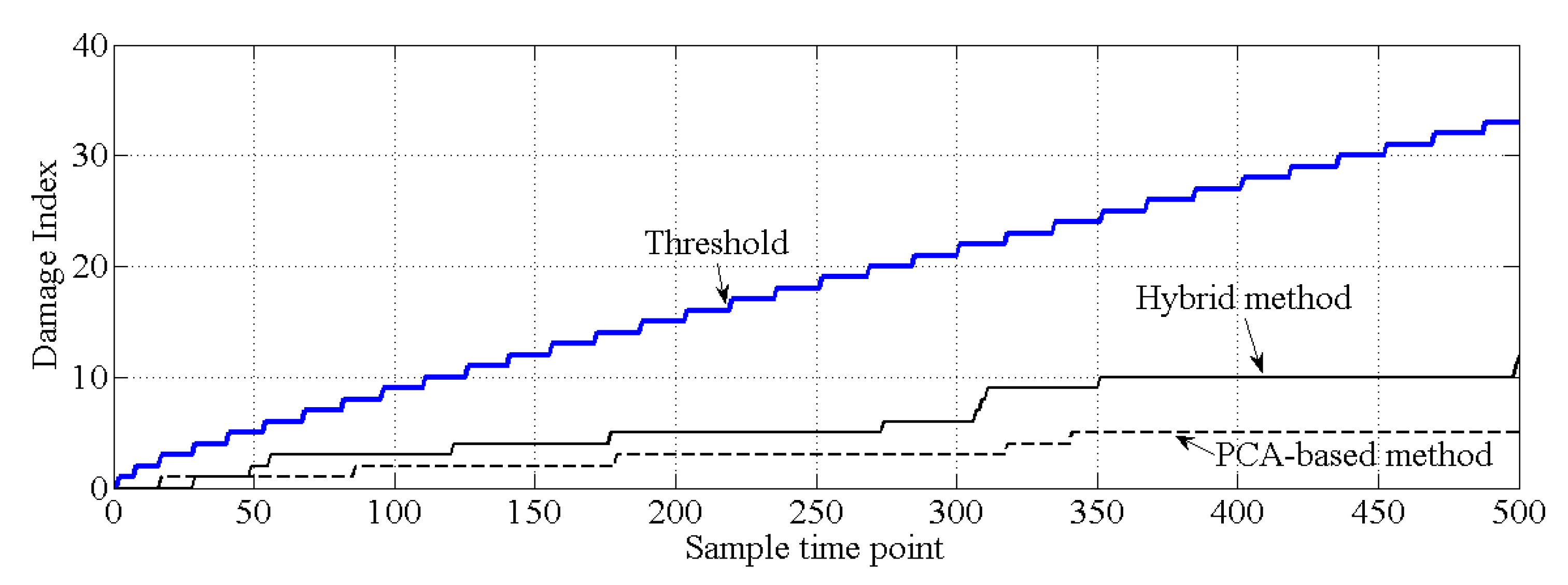
3.2. Comparison of the Performance Levels of the PCA-Based Method and the Proposed Hybrid Method
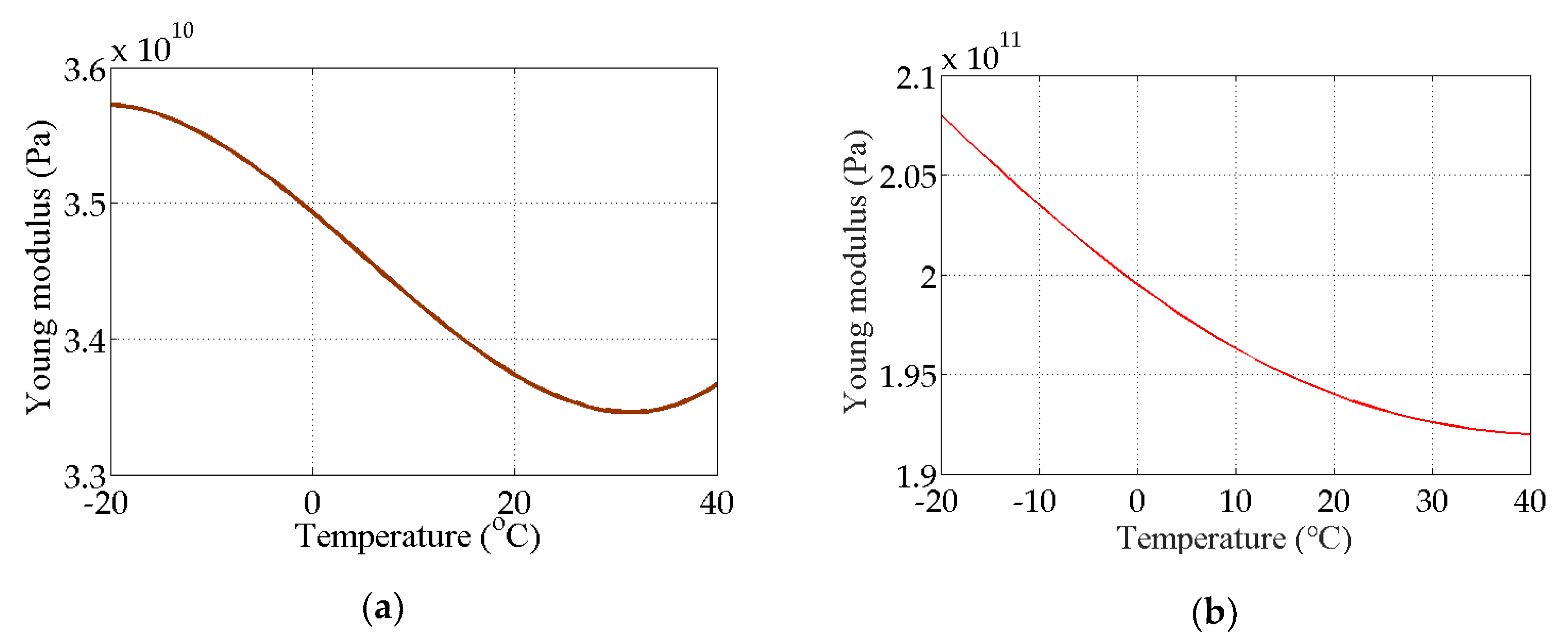
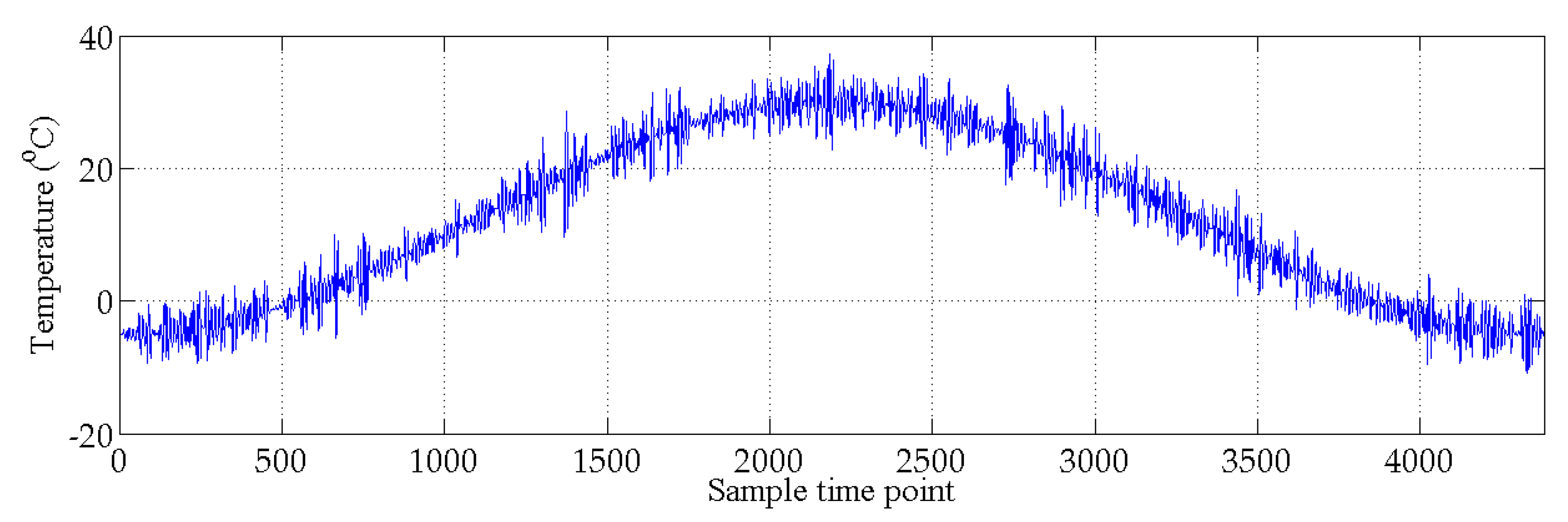
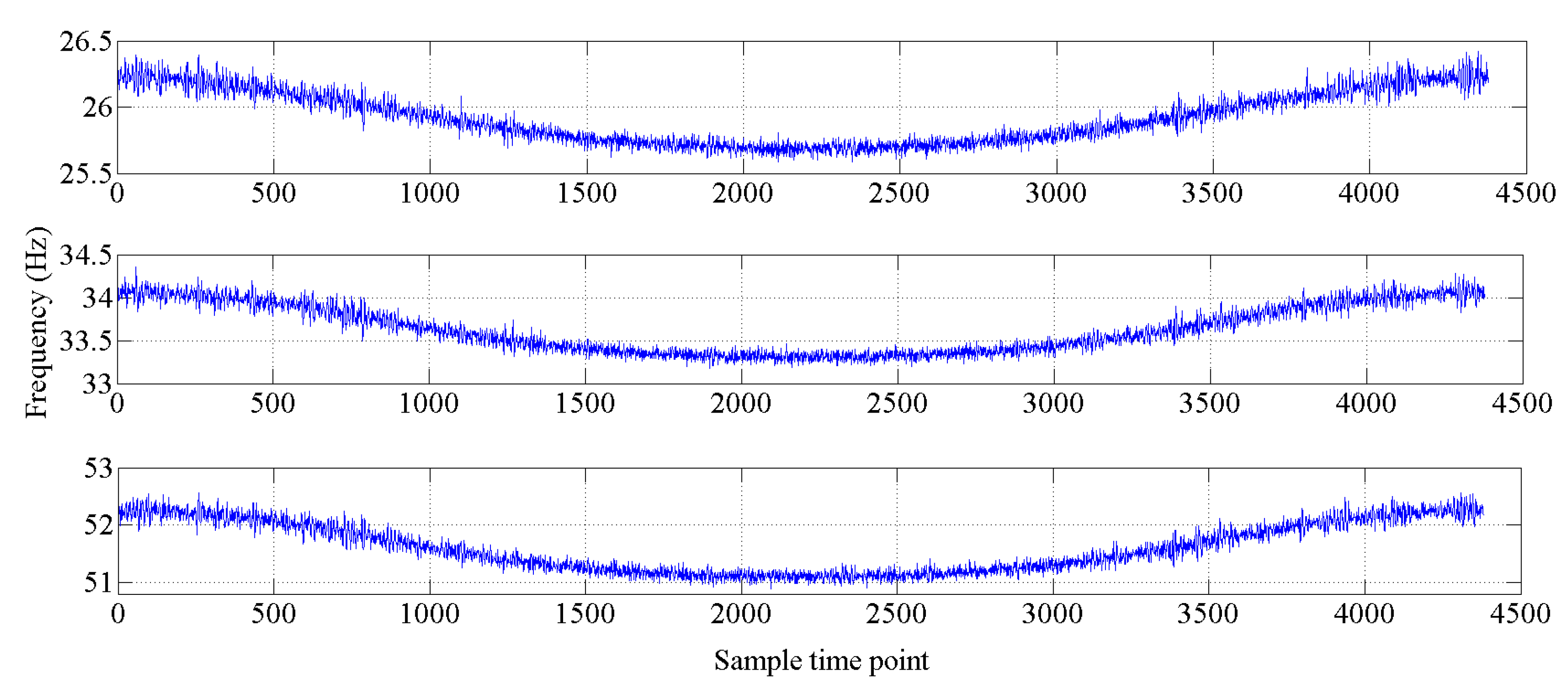
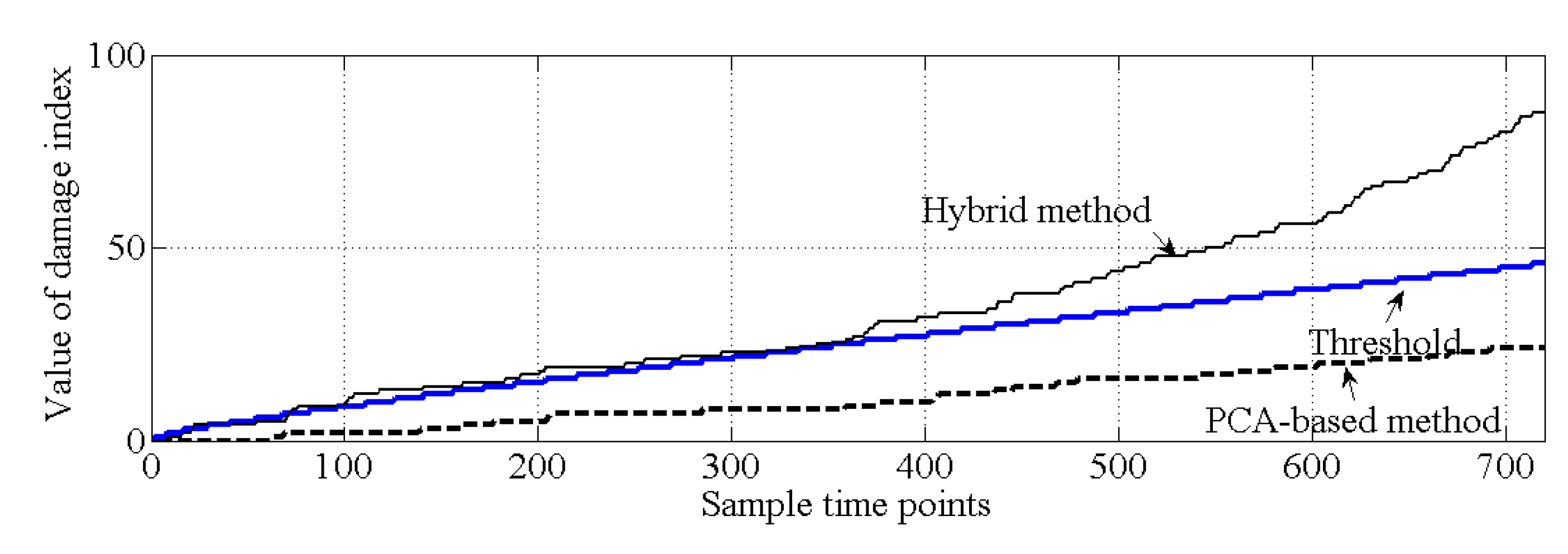
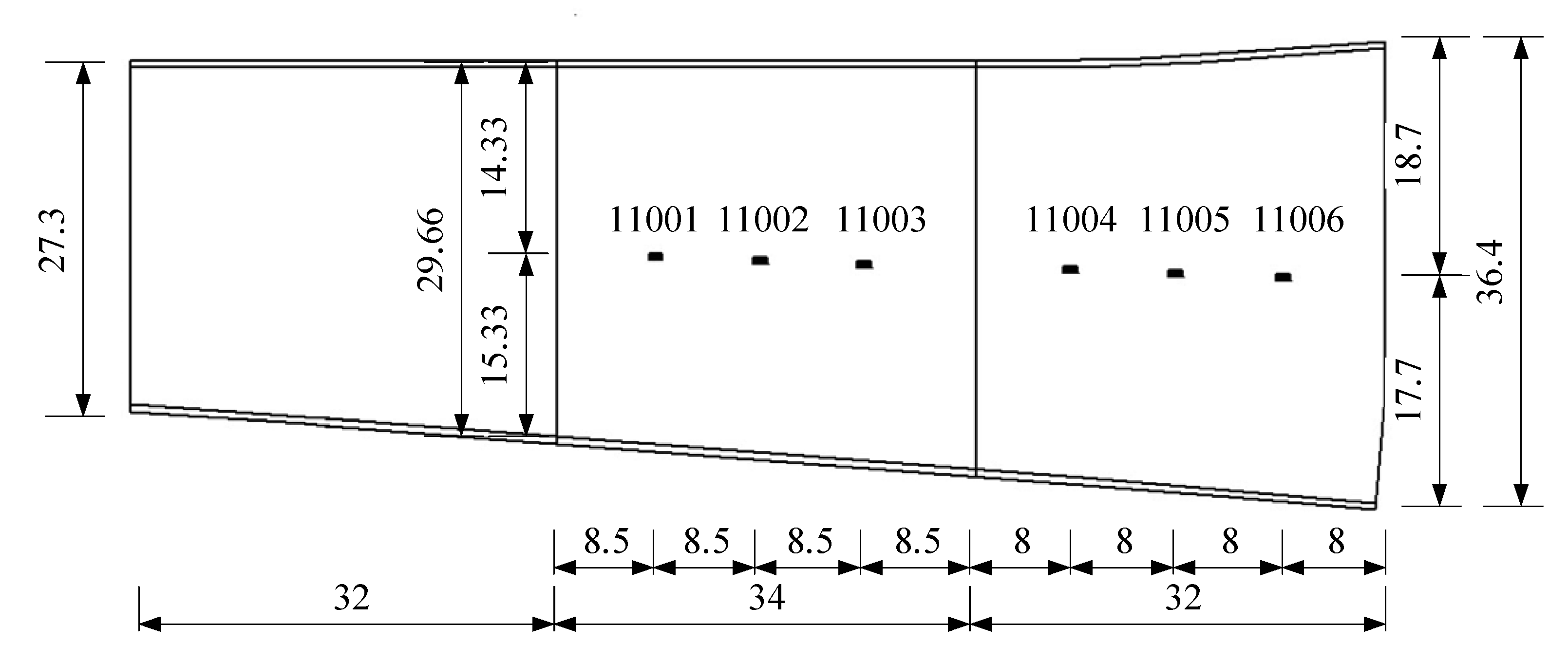
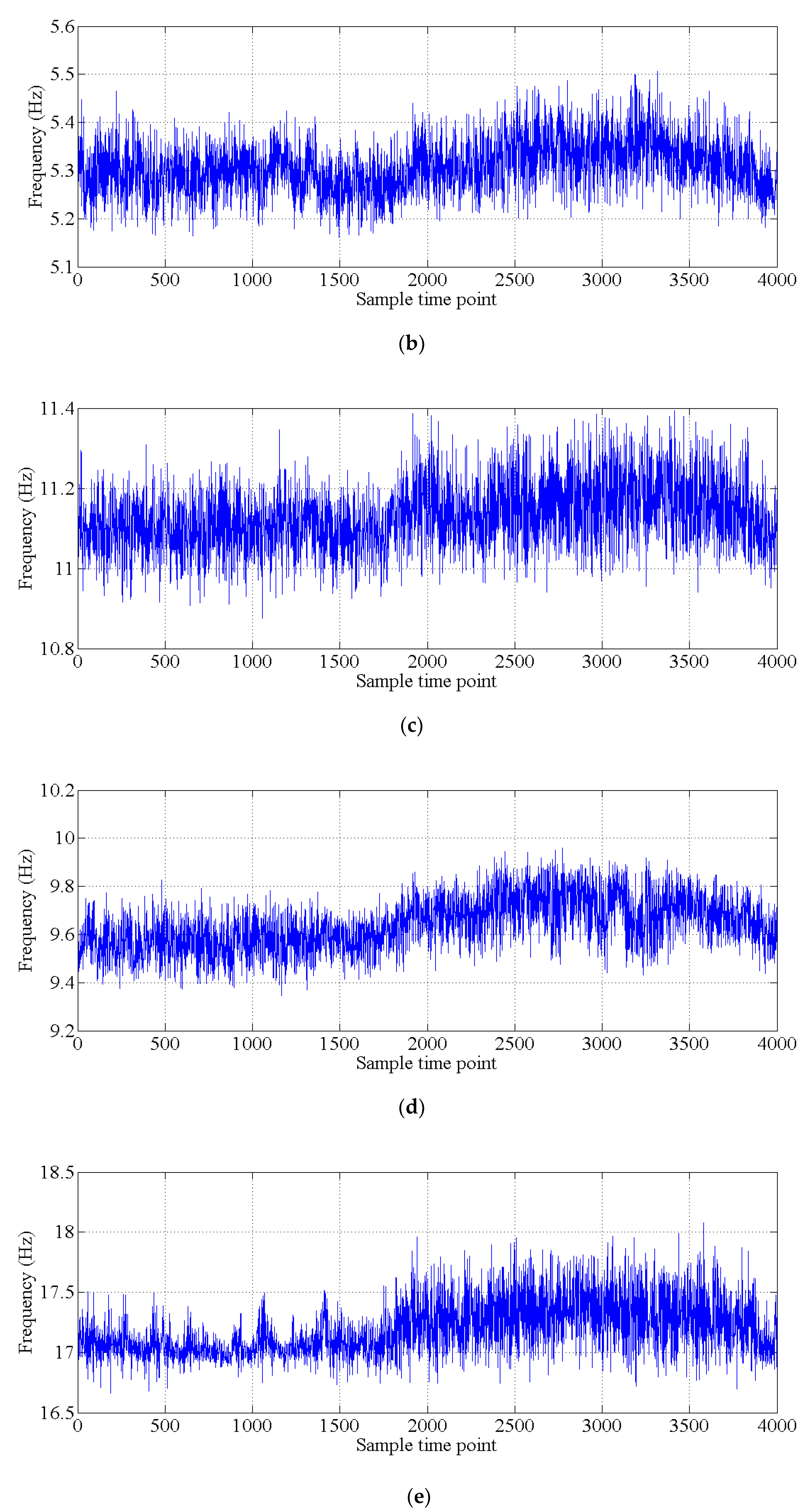
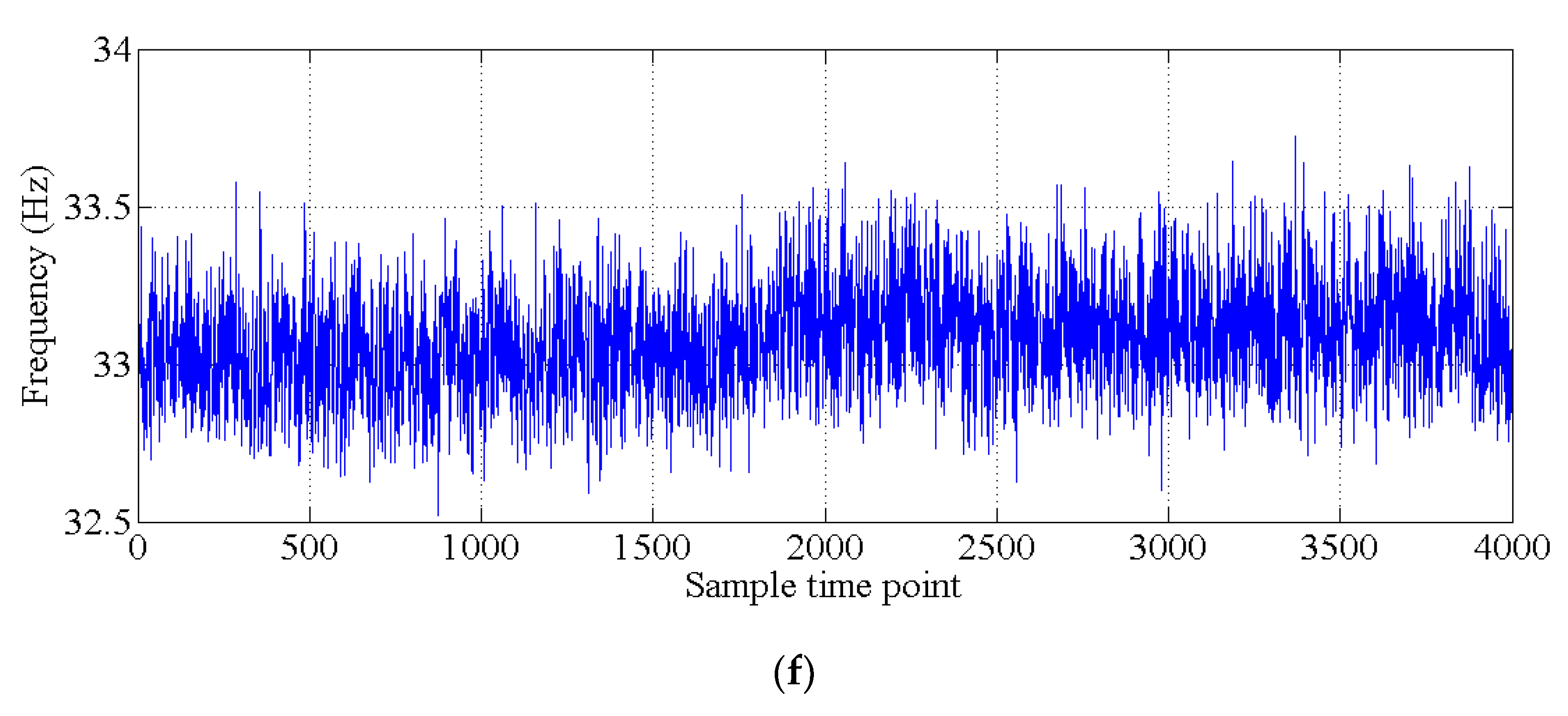
4. Example of an Actual Bridge
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Seventekidis, P.; Giagopoulos, D.; Arailopoulos, A.; Markogiannaki, O. Structural Health Monitoring using deep learning with optimal finite element model generated data. Mech. Syst. Sig. Process. 2020, 145, 106972. [Google Scholar] [CrossRef]
- Annamdas, V.G.M.; Bhalla, S.; Soh, C.K. IWSHM 2015: Applications of structural health monitoring technology in Asia. Struct. Heal. Monit. 2016, 16, 324–346. [Google Scholar] [CrossRef]
- Vagnoli, M.; Remenyte-Prescott, R.; Andrews, J. Railway bridge structural health monitoring and fault detection: State-of-the-art methods and future challenges. Struct. Heal. Monit. 2017, 17, 971–1007. [Google Scholar] [CrossRef]
- Ngeljaratan, L.; Moustafa, M.A. Structural health monitoring and seismic response assessment of bridge structures using target-tracking digital image correlation. Eng. Struct. 2020, 213, 110551. [Google Scholar] [CrossRef]
- Zhang, Q.; Hou, J.; Jankowski, Ł. Bridge Damage Identification Using Vehicle Bump Based on Additional Virtual Masses. Sensors 2020, 20, 394. [Google Scholar] [CrossRef] [Green Version]
- Doebling, S.W.; Farrar, C.R.; Prime, M.B. A Summary Review of Vibration-Based Damage Identification Methods. Shock. Vib. Dig. 1998, 30, 91–105. [Google Scholar] [CrossRef] [Green Version]
- Alvandi, A.; Crémona, C. Assessment of vibration-based damage identification techniques. J. Sound Vib. 2006, 292, 179–202. [Google Scholar] [CrossRef]
- Kim, B.; Min, C.; Kim, H.; Cho, S.-G.; Oh, J.; Ha, S.-H.; Yi, J.-H. Structural Health Monitoring with Sensor Data and Cosine Similarity for Multi-Damages. Sensors 2019, 19, 3047. [Google Scholar] [CrossRef] [Green Version]
- Sohn, H.; Dzwonczyk, M.; Straser, E.G.; Kiremidjian, A.S.; Law, K.H.; Meng, T. An experimental study of temperature effect on modal parameters of the Alamosa Canyon Bridge. Earthquake Eng. Struct. Dyn. 1999, 28, 879–897. [Google Scholar] [CrossRef]
- Farrar, C.R.; Doebling, S.W.; Cornwell, P.J.; Straser, E.G. Variability of modal parameters measured on the Alamosa Canyon bridge. In Proceedings of the 15th International Modal Analysis Conference, Orlando, FL, USA, 3–6 February 1997. [Google Scholar]
- Peeters, B.; De Roeck, G. One-year monitoring of the Z24-Bridge: Environmental effects versus damage events. Earthq. Eng. Struct. Dyn. 2001, 30, 149–171. [Google Scholar] [CrossRef]
- Maeck, J.; Peeters, B.; De Roeck, G. Damage identification on the Z24 bridge using vibration monitoring. Smart Mater. Struct. 2001, 10, 512–517. [Google Scholar] [CrossRef]
- Peeters, B.; Maeck, J.; De Roeck, G. Vibration-based damage detection in civil engineering: Excitation sources and temperature effects. Smart Mater. Struct. 2001, 10, 518–527. [Google Scholar] [CrossRef]
- Ko, J.M.; Chak, K.K.; Wang, J.Y.; Ni, Y.; Chan, T. Formulation of an uncertainty model relating modal parameters and environmental factors by using long-term monitoring data. Proc. SPIE Smart Struct. Mater. Smart Syst. Nondestruct. Eval. Civ. Infrastruct. 2003, 5057, 298–307. [Google Scholar] [CrossRef] [Green Version]
- Ni, Y.; Fan, K.Q.; Zheng, G.; Chan, T.; Ko, J.M. Automatic modal identification of cable-supported bridges instrumented with a long-term monitoring system. Smart Mater. Struct. 2003, 5057, 329–340. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.-T.; Park, J.-H.; Lee, B.-J. Vibration-based damage monitoring in model plate-girder bridges under uncertain temperature conditions. Eng. Struct. 2007, 29, 1354–1365. [Google Scholar] [CrossRef]
- Zhang, H.; Gül, M.; Kostić, B. Eliminating Temperature Effects in Damage Detection for Civil Infrastructure Using Time Series Analysis and Autoassociative Neural Networks. J. Aerosp. Eng. 2019, 32, 04019001. [Google Scholar] [CrossRef]
- Yan, W.-J.; Papadimitriou, C.; Katafygiotis, L.S.; Chronopoulos, D. An analytical perspective on Bayesian uncertainty quantification and propagation in mode shape assembly. Mech. Syst. Signal Process. 2020, 135, 106376. [Google Scholar] [CrossRef]
- Dai, H.; Zhang, H.; Wang, W. A Multiwavelet Neural Network-Based Response Surface Method for Structural Reliability Analysis. Comput. Civ. Infrastruct. Eng. 2014, 30, 151–162. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y.; Wang, D.; Zhang, S. Model Updating of Complex Structures Using the Combination of Component Mode Synthesis and Kriging Predictor. Sci. World J. 2014, 2014, 1–13. [Google Scholar] [CrossRef]
- Dai, H.; Xue, G.; Wang, W. An Adaptive Wavelet Frame Neural Network Method for Efficient Reliability Analysis. Comput. Civ. Infrastruct. Eng. 2014, 29, 801–814. [Google Scholar] [CrossRef]
- Dai, H.; Cao, Z. A Wavelet Support Vector Machine-Based Neural Network Metamodel for Structural Reliability Assessment. Comput. Civ. Infrastruct. Eng. 2017, 32, 344–357. [Google Scholar] [CrossRef]
- Kullaa, J. Elimination of environmental influences from damage-sensitive features in a structural health monitoring system. In Structural Health Monitoring—the Demands and Challenges; CRC Press: Boca Raton, FL, USA, 2001; pp. 742–749. [Google Scholar]
- Deraemaeker, A.; Reynders, E.; De Roeck, G.; Kullaa, J. Vibration-based structural health monitoring using output-only measurements under changing environment. Mech. Syst. Signal Process. 2008, 22, 34–56. [Google Scholar] [CrossRef] [Green Version]
- Hsu, T.Y.; Loh, C.H. Damage detection accommodating nonlinear environmental effects by nonlinear principal component analysis. Struct. Control Health Monit. 2009, 17, 338–354. [Google Scholar] [CrossRef]
- Candès, E.; Li, X.; Ma, Y.; Wright, J. Robust principal component analysis? J. ACM 2011, 58, 1–37. [Google Scholar] [CrossRef]
- Mujica, L.E.; Ruiz, M.; Pozo, F.; Rodellar, J.; Güemes, A. A structural damage detection indicator based on principal component analysis and statistical hypothesis testing. Smart Mater. Struct. 2013, 23, 25014. [Google Scholar] [CrossRef]
- Mujica, L.E.; Rodellar, J.; Fernandez, A.; Guemes, A. Q-statistic and T2-statistic PCA-based measures for damage assessment in structures. Struct. Health Monit. 2011, 10, 539–553. [Google Scholar] [CrossRef]
- Mojtahedi, A.; Lotfollahi-Yaghin, M.; Ettefagh, M.M.; Hassanzadeh, Y.; Fujikubo, M. Detection of nonlinearity effects in structural integrity monitoring methods for offshore jacket-type structures based on principal component analysis. Mar. Struct. 2013, 33, 100–119. [Google Scholar] [CrossRef]
- Huang, B.; Koh, B.-H.; Kim, H.S. PCA-based damage classification of delaminated smart composite structures using improved layerwise theory. Comput. Struct. 2014, 141, 26–35. [Google Scholar] [CrossRef]
- Jabid, Q.; Luis, M.; Rodolfo, V.; Magda, R.; Johanatan, C. PCA based stress monitoring of cylindrical specimens using pzts and guided waves. Sensors 2017, 17, 2788. [Google Scholar]
- Koo, K.Y.; Park, S.; Lee, J.J.; Yun, C.B. Temperature effects-free impedance-based structural health monitoring using principal component analysis. In Proceedings of the IMAC-XXVI: Conference & Exposition on Structural Dynamics, Orlando, FL, USA, 4–7 February 2008; pp. 1–6. [Google Scholar]
- Bellino, A.; Fasana, A.; Garibaldi, L.; Marchesiello, S. PCA-based detection of damage in time-varying systems. Mech. Syst. Signal Process. 2010, 24, 2250–2260. [Google Scholar] [CrossRef] [Green Version]
- Giraldo, D.F.; Dyke, S.J.; Caicedo, J.M. Damage Detection Accommodating Varying Environmental Conditions. Struct. Heal. Monit. 2006, 5, 155–172. [Google Scholar] [CrossRef]
- Reynders, E.; Wursten, G.; De Roeck, G. Output-only structural health monitoring in changing environmental conditions by means of nonlinear system identification. Struct. Health Monit. 2013, 13, 82–93. [Google Scholar] [CrossRef]
- Zhu, Y.; Ni, Y.; Jin, H.; Inaudi, D.; Laory, I. A temperature-driven MPCA method for structural anomaly detection. Eng. Struct. 2019, 190, 447–458. [Google Scholar] [CrossRef]
- Yan, A.-M.; Kerschen, G.; De Boe, P.; Golinval, J.-C. Structural damage diagnosis under varying environmental conditions—Part I: A linear analysis. Mech. Syst. Signal Process. 2005, 19, 847–864. [Google Scholar] [CrossRef]
- Yan, A.-M.; Kerschen, G.; De Boe, P.; Golinval, J.-C. Structural damage diagnosis under varying environmental conditions—part II: Local PCA for non-linear cases. Mech. Syst. Signal Process. 2005, 19, 865–880. [Google Scholar] [CrossRef]
- Worden, K.; Sohn, H.; Farrar, C. Novelty detection in a changing environment: regression and interpolation approaches. J. Sound Vib. 2002, 258, 741–761. [Google Scholar] [CrossRef]
- Sohn, H.; Worden, K.; Farrar, C.R. Novelty detection under changing environmental conditions. In Proceedings of the Spie’s 8th Annual International Symposium on Smart Structures and Materials, Newport Beach, CA, USA, 4–8 March 2001; 4330, pp. 108–119. [Google Scholar] [CrossRef] [Green Version]
- Cross, E.; Manson, G.; Worden, K.; Pierce, S.G. Features for damage detection with insensitivity to environmental and operational variations. Proc. R. Soc. A: Math. Phys. Eng. Sci. 2012, 468, 4098–4122. [Google Scholar] [CrossRef]
- Kokkinakis, K.; Nandi, A.K. Exponent parameter estimation for generalized Gaussian probability density functions with application to speech modeling. Signal Process. 2005, 85, 1852–1858. [Google Scholar] [CrossRef]
- Zhang, R.; Li, L.; Dai, H. A copula-based Gaussian mixture closure method for stochastic response of nonlinear dynamic systems. Probabilistic Eng. Mech. 2020, 59, 103015. [Google Scholar] [CrossRef]
- Ki, Y.L. Local fuzzy PCA based GMM with dimension reduction on speaker identification. Pattern Recognit. Lett. 2004, 25, 1811–1817. [Google Scholar]
- Seo, C.; Lee, K.Y.; Lee, J. GMM based on local PCA for speaker identification. Electron. Lett. 2001, 37, 1486. [Google Scholar] [CrossRef]
- Noureldaim, E.; Jedra, M.; Zahid, N. Multiple Tracking of Moving Objects with Kalman Filtering and PCA-GMM Method. Intell. Inf. Manag. 2013, 5, 42–47. [Google Scholar] [CrossRef] [Green Version]
- Choi, S.W.; Park, J.H.; Lee, I.-B. Process monitoring using a Gaussian mixture model via principal component analysis and discriminant analysis. Comput. Chem. Eng. 2004, 28, 1377–1387. [Google Scholar] [CrossRef]
- Atasever, U.H.; Gunen, M.A.; Besdok, E. A new unsupervised change detection approach based on PCA based blocking and GMM clustering for detecting flood damage. Fresenius Environ. Bull. 2018, 27, 1688–1694. [Google Scholar]
- Jiang, Q.; Huang, B.; Yan, X. GMM and optimal principal components-based Bayesian method for multimode fault diagnosis. Comput. Chem. Eng. 2016, 84, 338–349. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, Y. Damage detection of bridges monitored within one cluster based on the residual between the cumulative distribution functions of strain monitoring data. Struct. Heal. Monit. 2020, 1475921719895955. [Google Scholar] [CrossRef]
- Juang, J.-N.; Pappa, R.S. An eigensystem realization algorithm for modal parameter identification and model reduction. J. Guid. Control. Dyn. 1985, 8, 620–627. [Google Scholar] [CrossRef]









| Case Number | Description of Case |
|---|---|
| Case 1 | Healthy structure |
| Case 2 | Damaged structure with 20% reduction in stiffness at element 17 |
| Case 3 | Damaged structure with 20% reduction in stiffness at element 7 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Gao, Q.; Liu, Y. Damage Detection of Bridges under Environmental Temperature Changes Using a Hybrid Method. Sensors 2020, 20, 3999. https://doi.org/10.3390/s20143999
Wang X, Gao Q, Liu Y. Damage Detection of Bridges under Environmental Temperature Changes Using a Hybrid Method. Sensors. 2020; 20(14):3999. https://doi.org/10.3390/s20143999
Chicago/Turabian StyleWang, Xiang, Qingfei Gao, and Yang Liu. 2020. "Damage Detection of Bridges under Environmental Temperature Changes Using a Hybrid Method" Sensors 20, no. 14: 3999. https://doi.org/10.3390/s20143999







