Performance, Accuracy and Generalization Capability of RFID Tags’ Constellation for Indoor Localization
Abstract
:1. Introduction
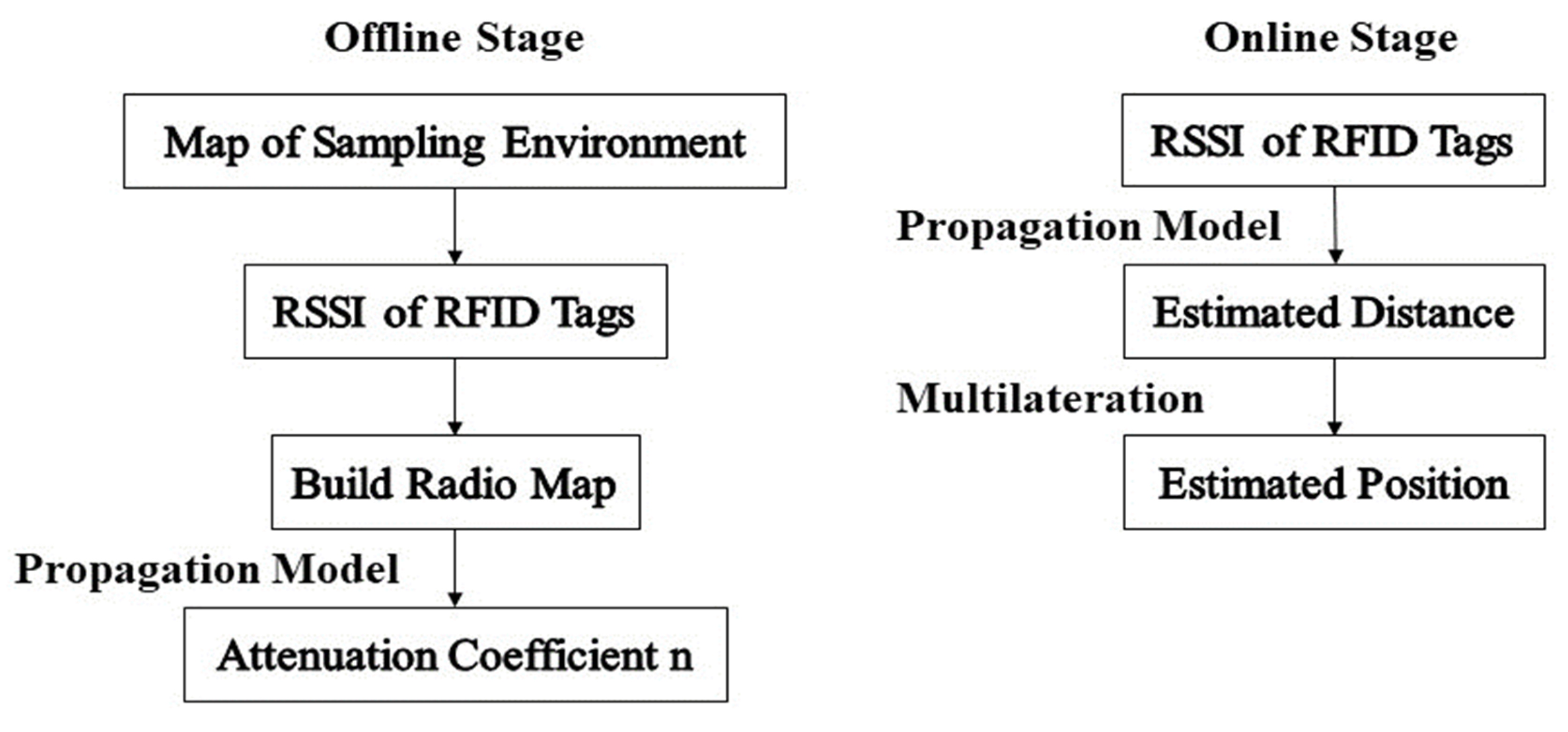
2. RFID-Based Localization System
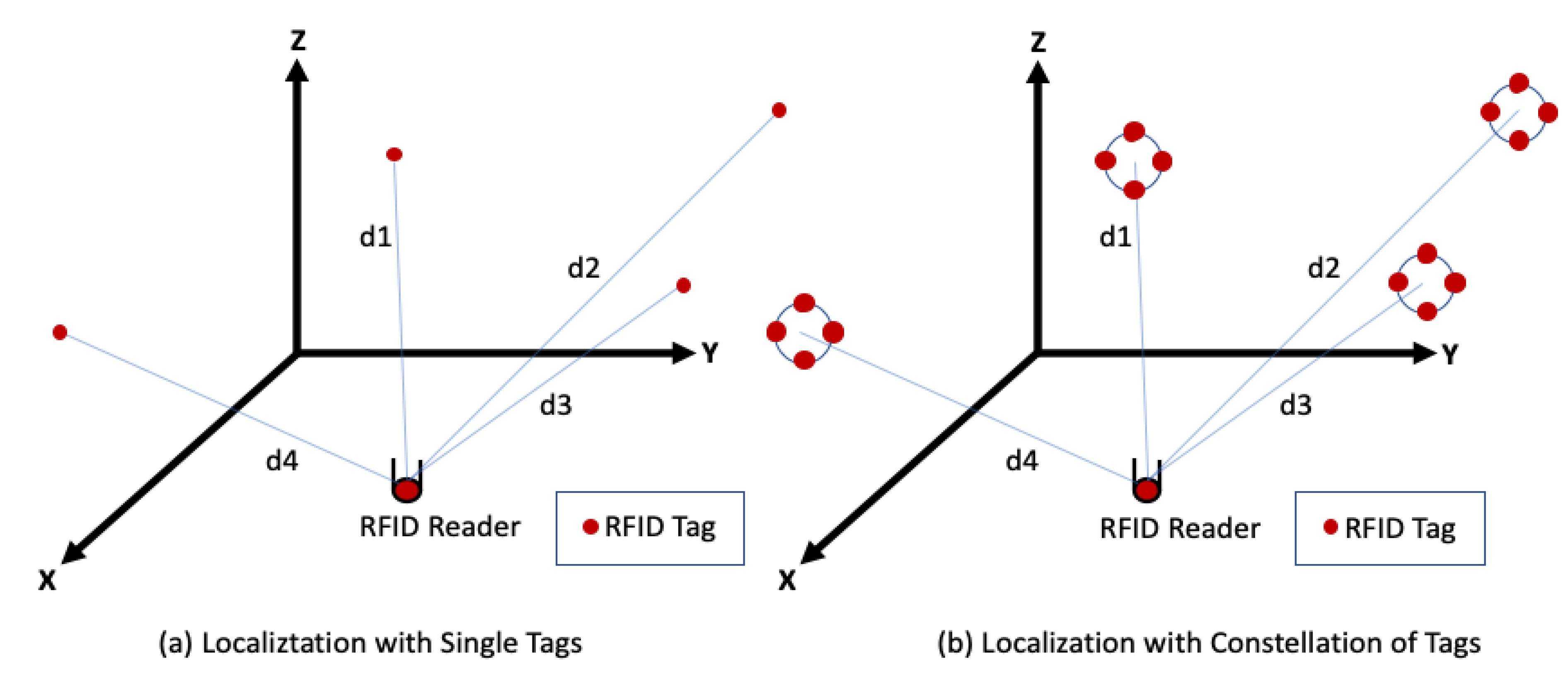
2.1. Localization System Principle
2.2. Propagation Models
2.3. (Tag-Reader) Distance Estimation
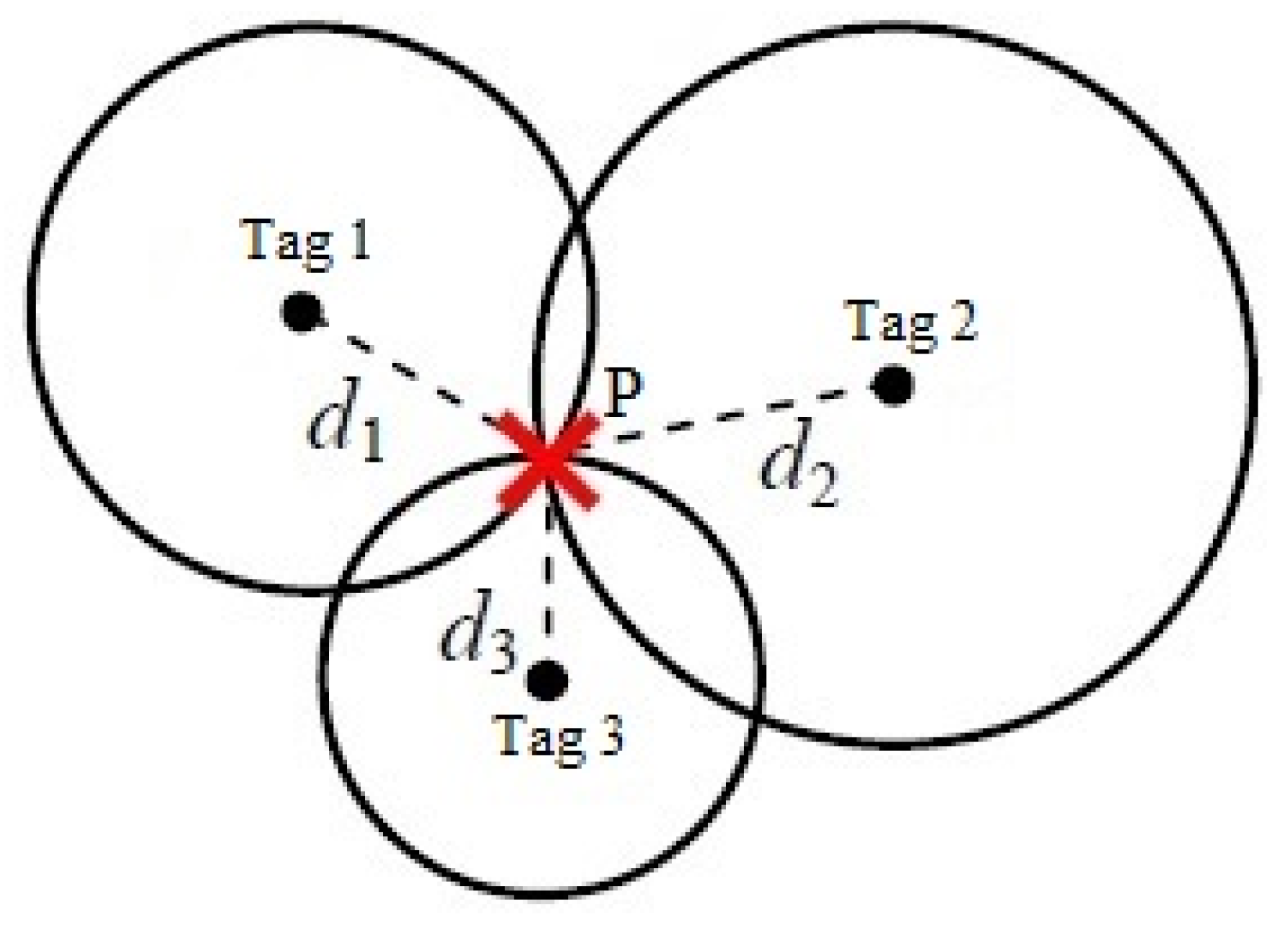
2.4. The Multilateration Technique
3. The Constellation Approach
3.1. MISO-Based Indoor Localization System
3.2. Constellation of UHF-RFID Tags for Reader Localization
3.3. Optimal Constellation’s Radius
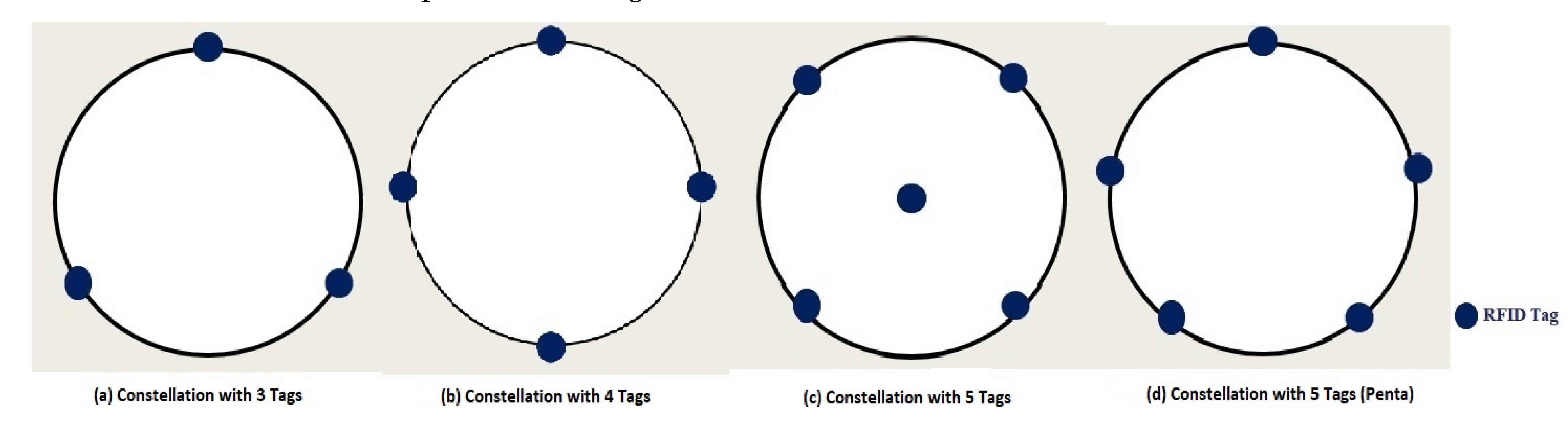
3.4. Optimal Shape and Number of Tags
4. Constellation vs. Single Tag
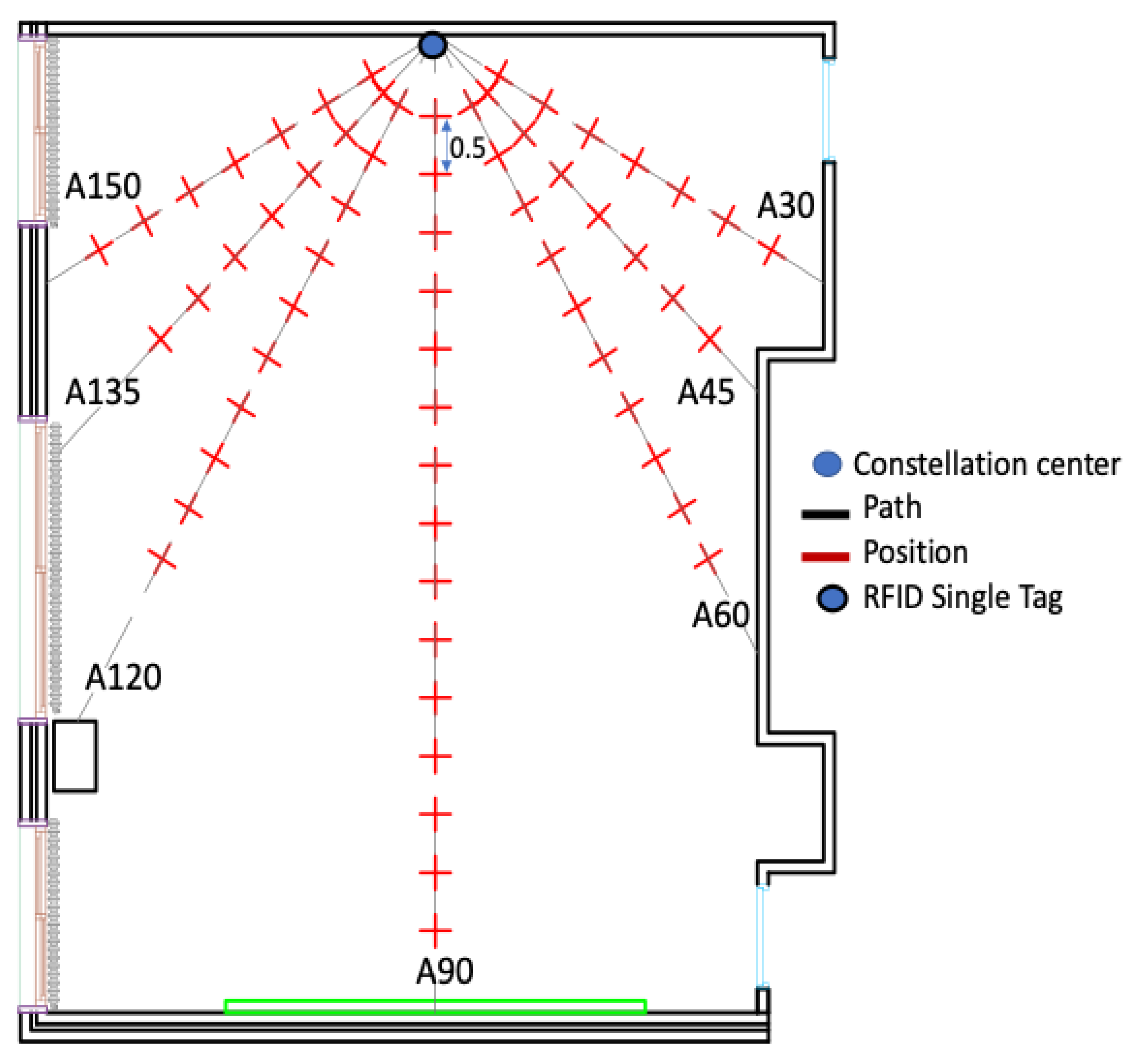
4.1. RFID Equipment
4.2. Experiment Environment
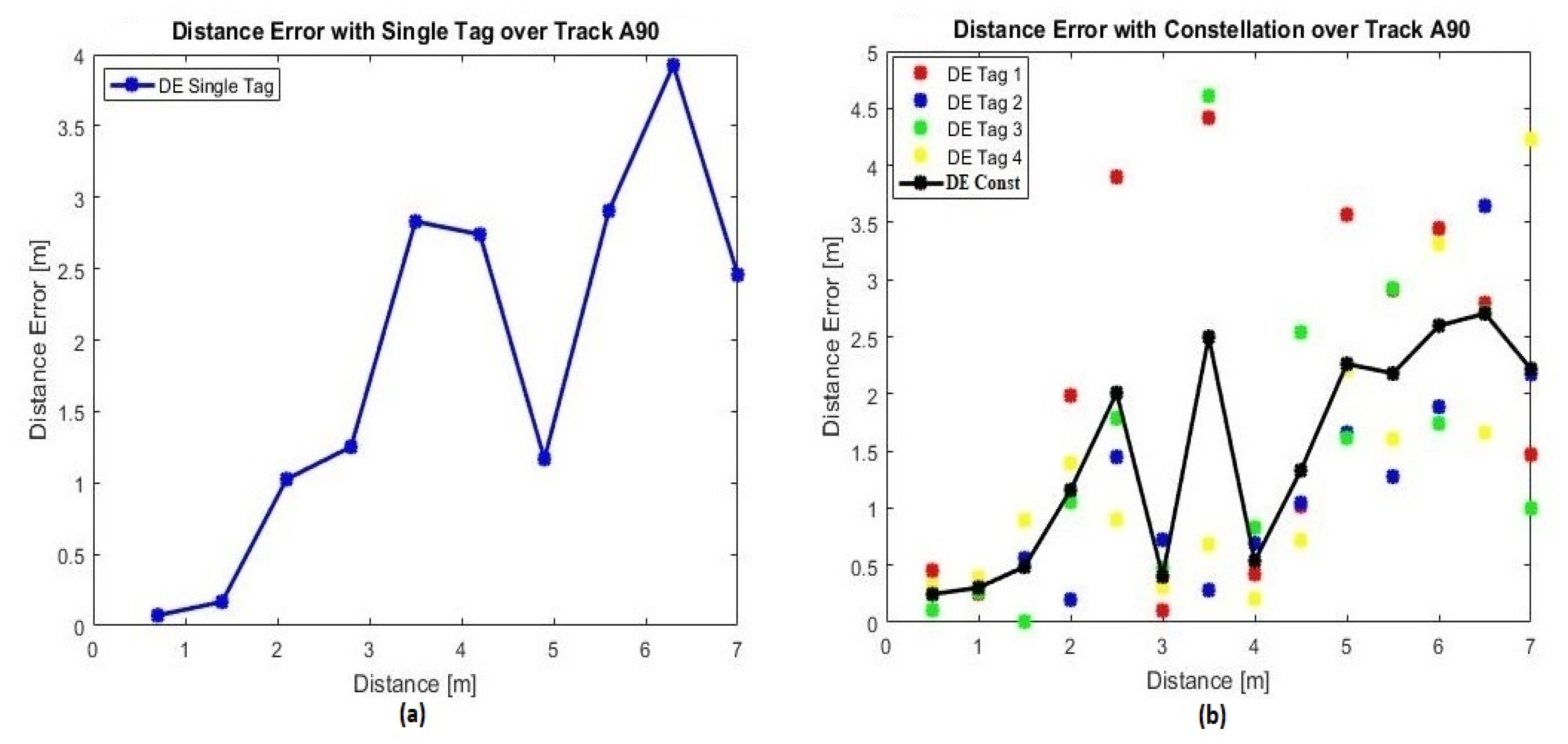
4.3. Evaluation of Distances Estimation
4.3.1. Measurements Accuracy
4.3.2. Simulations
4.4. Radio Map
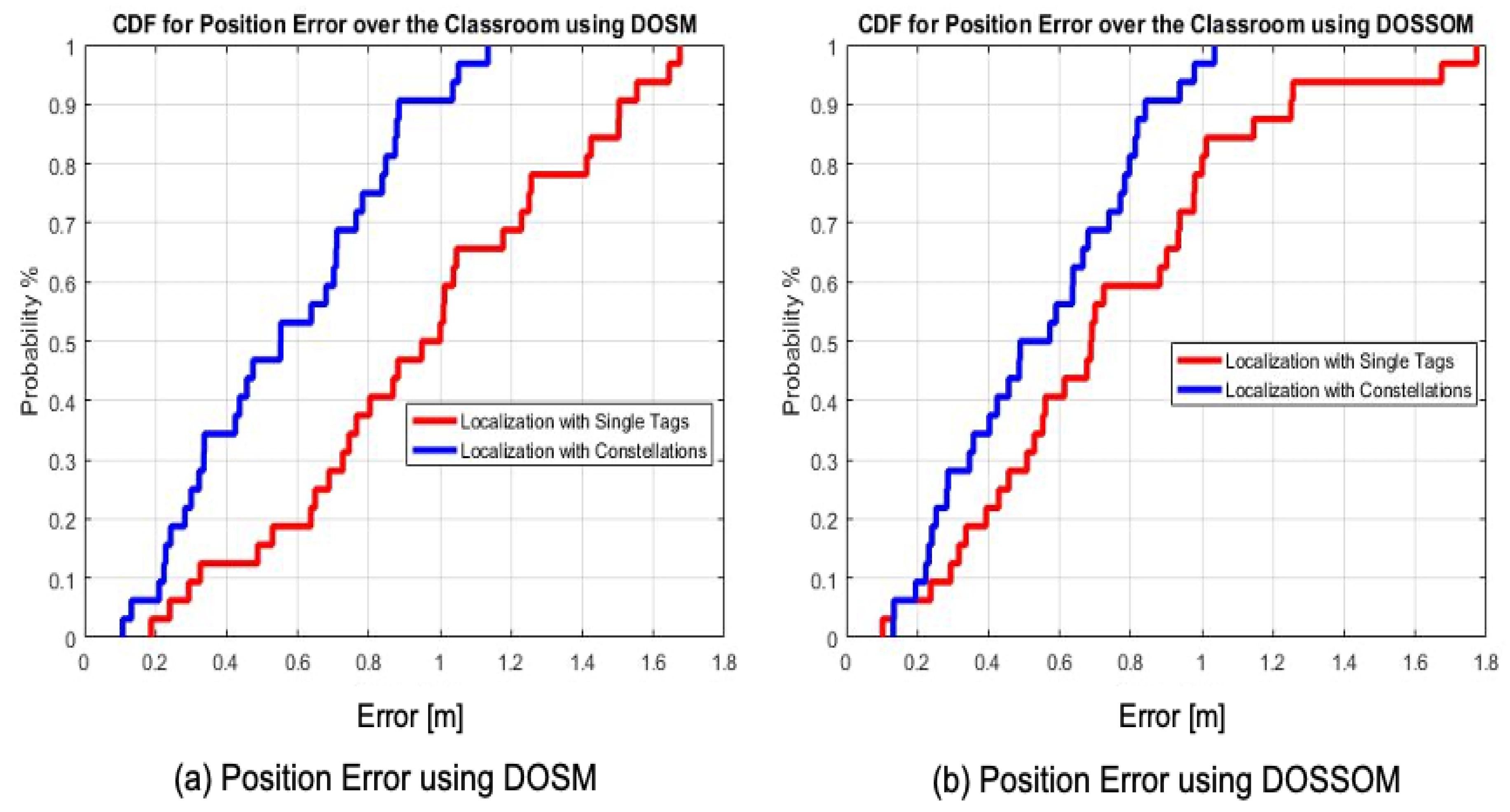
4.5. Assessment of the Positioning Performance
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sarac, A.; Absi, N.; Dauzere-Peres, S. A literature review on the impact of RFID technologies on supply chain managemen. Int. J. Prod. Econ. 2010, 128, 77–95. [Google Scholar] [CrossRef]
- Chawla, K.; Robins, G. An RFID-based object localization framework. Int. J. Radio Freq. Identif. Technol. Appl. 2011, 3, 2–30. [Google Scholar]
- Zhang, H.; Zhu, L. RFID Technology and Structure of Internet of Thing. Comput. Technol. Dev. 2011, 5, 427–429. [Google Scholar]
- Al-Fagih, A.E.; Al-Turjman, F.M.; Hassanein, H.S.; Alsalih, W.M. Coverage-based placement in RFID networks: An overview. In Proceedings of the Third FTRA International Conference on Mobile, Ubiquitous, and Intelligent Computing, Vancouver, BC, Canada, 26 June 2012; pp. 220–224. [Google Scholar]
- Ciurana, M.; Barceló, F.; Cugno, S. Indoor tracking in WLAN location with TOA measurements. In Proceedings of the 4th ACM International Workshop on Mobility Management and Wireless Access, New York, NY, USA, 2–6 October 2006; pp. 121–125. [Google Scholar]
- Chen, P.; Kuang, Y.; Chen, X. A UWB/improved PDR integration algorithm applied to dynamic indoor positioning for pedestrians. Sensors 2017, 17, 2065. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Makki, A.; Siddig, A.; Saad, M.; Cavallaro, J.R.; Bleakley, C.J. Indoor localization using 802.11 time differences of arrival. IEEE Trans. Instrum. Meas. 2016, 65, 614–623. [Google Scholar] [CrossRef]
- Li, S.; Rashidzadeh, R. Hybrid indoor location positioning system. IET Wirel. Sens. Syst. 2019, 9, 257–264. [Google Scholar] [CrossRef] [Green Version]
- Milioris, D.; Tzagkarakis, G.; Papakonstantinou, A.; Papadopouli, M.; Tsakalides, P. Low-dimensional signal-strength fingerprint-based positioning in wireless LANs. Ad Hoc Netw. 2014, 12, 100–114. [Google Scholar] [CrossRef]
- Turgut, Z.; Üstebay, S.; Aydin, Z.G.; Sertbaş, A. Deep learning in indoor localization using WiFi. In Proceedings of the International Telecommunications Conference, Istanbul, Turkey, 28–29 December 2017; pp. 101–110. [Google Scholar]
- Subedi, S.; Pauls, E.; Zhang, Y.D. Accurate localization and tracking of a passive RFID reader based on RSSI measurements. IEEE J. Radio Freq. Identif. 2017, 1, 144–154. [Google Scholar] [CrossRef]
- Yiu, S.; Dashti, M.; Claussen, H.; Perez-Cruz, F. Wireless RSSI fingerprinting localization. Signal Process 2017, 131, 235–244. [Google Scholar] [CrossRef]
- Siachalou, S.; Megalou, S.; Tzitzis, A.; Tsardoulias, E.; Bletsas, A.; Sahalos, J.N.; Yioultsis, T.; Dimitriou, A. Robotic inventorying and localization of rfid tags, exploiting phase-fingerprinting. In Proceedings of the IEEE International Conference on RFID Technology and Applications, Phoenix, AZ, USA, 25 September 2019. [Google Scholar]
- Wang, Q.; Balasingham, I.; Zhang, M.; Huang, X. Improving RSS based ranging in LOS-NLOS scenario using GMMs. IEEE Commun. Lett. 2011, 15, 1065–1067. [Google Scholar] [CrossRef]
- Aguilar-Garcia, A.; Fortes, S.; Barco, R.; Colin, E. Enhancing localization accuracy with multi-antenna UHF RFID fingerprinting. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation (IPIN), Banff, AB, Canada, 13–16 October 2015; pp. 1–9. [Google Scholar]
- Dian, Z.; Kezhong, L.; Rui, M. A precise RFID indoor localization system with sensor network assistance. China Commun. 2015, 12, 13–22. [Google Scholar] [CrossRef]
- Dashti, M.; Claussen, H. A metric to describe access point significance in location estimation. In Proceedings of the 13th Workshop Positioning, Navigation and Communications (WPNC), Bremen, Germany, 19–20 October 2016; pp. 1–6. [Google Scholar]
- Telatar, I.E. Capacity of multi-antenna Gaussian channels. Eur. Trans. Telecommun. 1999, 10, 585–595. [Google Scholar] [CrossRef]
- Fosichini, G.J.; Gans, M.J. On limits of wireless communications in a fading environment when using multiple antennas. Wirel. Pers. Commun. 1998, 6, 311–335. [Google Scholar] [CrossRef]
- Sachdeva, N.; Sharma, D. Diversity: A fading reduction technique. 2012, 6, 58–61. Int. J. Adv. Res. Comput. Sci. Softw. Eng. 2012, 6, 58–61. [Google Scholar]
- Zhong, C.; Wong, K.K.; Jin, S. Capacity bounds for MIMO Nakagami-m fading channels. IEEE Trans. Signal Process. 2009, 57, 3613–3623. [Google Scholar] [CrossRef]
- Chiani, M.; Win, M.Z.; Zanella, A. On the capacity of spatially correlated MIMO Rayleigh-fading channels. IEEE Trans. Inf. Theory 2003, 49, 2363–2371. [Google Scholar] [CrossRef] [Green Version]
- Mckay, M.R.; Collings, I.B. General capacity bounds for spatially correlated Rician MIMO channels. IEEE Trans. Inf. Theory 2005, 51, 3121–3145. [Google Scholar] [CrossRef]
- Hatem, E.; Colin, E.; Abou-Chakra, S.; El-Hassan, B.; Laheurte, J.-M. New empirical indoor path loss model using active uhf-rfid tags for localization purposes. In Proceedings of the IEEE International Conference on RFID Technology & Application (RFID-TA), Macau, China, 25 September 2018; pp. 1–6. [Google Scholar]
- Tuset-Peiró, P.; Anglès-Vazquez, A.; López-Vicario, J.; Vilajosana-Guillén, X. On the suitability of the 433 MHz band for M2M low-power wireless communications: Propagation aspects. Trans. Emerg. Telecommun. Technol. 2014, 25, 1154–1168. [Google Scholar] [CrossRef]
- Zepernick, H.J.; Wysocki, T.A. Multipath channel parameters for the indoor radio at 2.4 GHz ISM band. IEEE Veh. Technol. Conf. 1999, 1, 190–193. [Google Scholar]
- Kumar, S.P.T.; Farhang-Boroujeny, B.; Uysal, S.; Ng, C.S. Microwave indoor radio propagation measurements and modeling at 5 GHz for future wireless LAN systems. In Proceedings of the 1999 Asia Pacific Microwave Conference, Singapore, 30 November–3 December 1999; pp. 606–609. [Google Scholar]
- Remley, K.A.; Anderson, H.R.; Weisshar, A. Improving the accuracy of ray-tracing techniques for indoor propagation modeling. IEEE Veh. Technol. Conf. 2000, 49, 2350–2358. [Google Scholar] [CrossRef]
- Bouet, M.; Santos, A.L.D. RFID tags: Positioning principles and localization techniques. In Proceedings of the 2008 1st IFIP Wireless Days, Dubai, UAE, 24–27 November 2008. [Google Scholar]
- Paulraj, A.J.; Gore, D.A.; Nabar, R.U.; Bolcskei, H. An Overview of MIMO Communications—A Key to Gigabit Wireless; IEEE: Piscataway, NJ, USA, 2004; Volume 92, pp. 198–218. [Google Scholar]
- Nishmoto, H.; Ogawa, Y.; Nishimura, T.; Ongane, T. Performance of MIMO-SDM in indoor line-of-sight environments based on 5.2 GHz Measurements. In Proceedings of the ISAP on IEICE, Sendai, Japan, 23 January 2004; pp. 345–348. [Google Scholar]
- Navidpour, S.M.; Uysal, M.; Jing, L. BER performance of MIMO free–space optical links. In Proceedings of the IEEE 60th Vehicular Technology Conference, Los Angeles, CA, USA, 26–29 September 2004; pp. 3378–3382. [Google Scholar]
- Lee, E.J.; Chan, V.W.S. Part 1: Optical communication over the clear turbulent atmospheric channel using diversity. IEEE J. Sel. Areas Commun. 2004, 22, 1896–1906. [Google Scholar] [CrossRef]
- Hamdoun, S.; Rachedi, A.; Benslimane, A. RSSI-based localization algorithms using spatial diversity in wireless sensor networks. Int. J. Ad Hoc Ubiquitous Comput. 2015, 19, 157–167. [Google Scholar] [CrossRef]
- Zhu, A.; Fan, T.; Gu, Z.; Lv, Q.; Li, C.; Ran, L. Indoor localization based on a single-tone SIMO-structured Doppler radar system. In Proceedings of the 2018 IEEE Radio and Wireless Symposium (RWS), Anaheim, CA, USA, 15–18 January 2018. [Google Scholar]
- Hatem, E.; Colin, E.; Abou-Chakra, S.; El-Hassan, B.; Laheurte, J.-M. Constellations of active UHF-RFID tags for indoor positioning. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation (IPIN), Nantes, France, 24–27 September 2018; pp. 1–4. [Google Scholar]
- Ela Innovation, SA. (2014) Ela Innovation active RFID tag and reader manufacturer. Available online: http://www.rfid-ela.eu/ (accessed on 20 July 2015).
- Hatem, E.; Colin, E.; Abou-Chakra, S.; El-Hassan, B.; Laheurte, J.-M. 3D Modeling for Propagation of UHF-RFID Tags’ Signals in an Indoor Environment. In Proceedings of the 2nd IEEE Middle East and North Africa Communications Conference (MENACOMM), Manama, Bahrain, 19–21 November 2019; pp. 1–6. [Google Scholar]
- Hoppe, R.; Wölfle, G.; Jakobus, U. Wave propagation and radio network planning software WinProp added to the electromagnetic solver package FEKO. In Proceedings of the International Applied Computational Electromagnetics Society Symposium, Firenze, Italy, 26–30 March 2017; pp. 1–2. [Google Scholar]


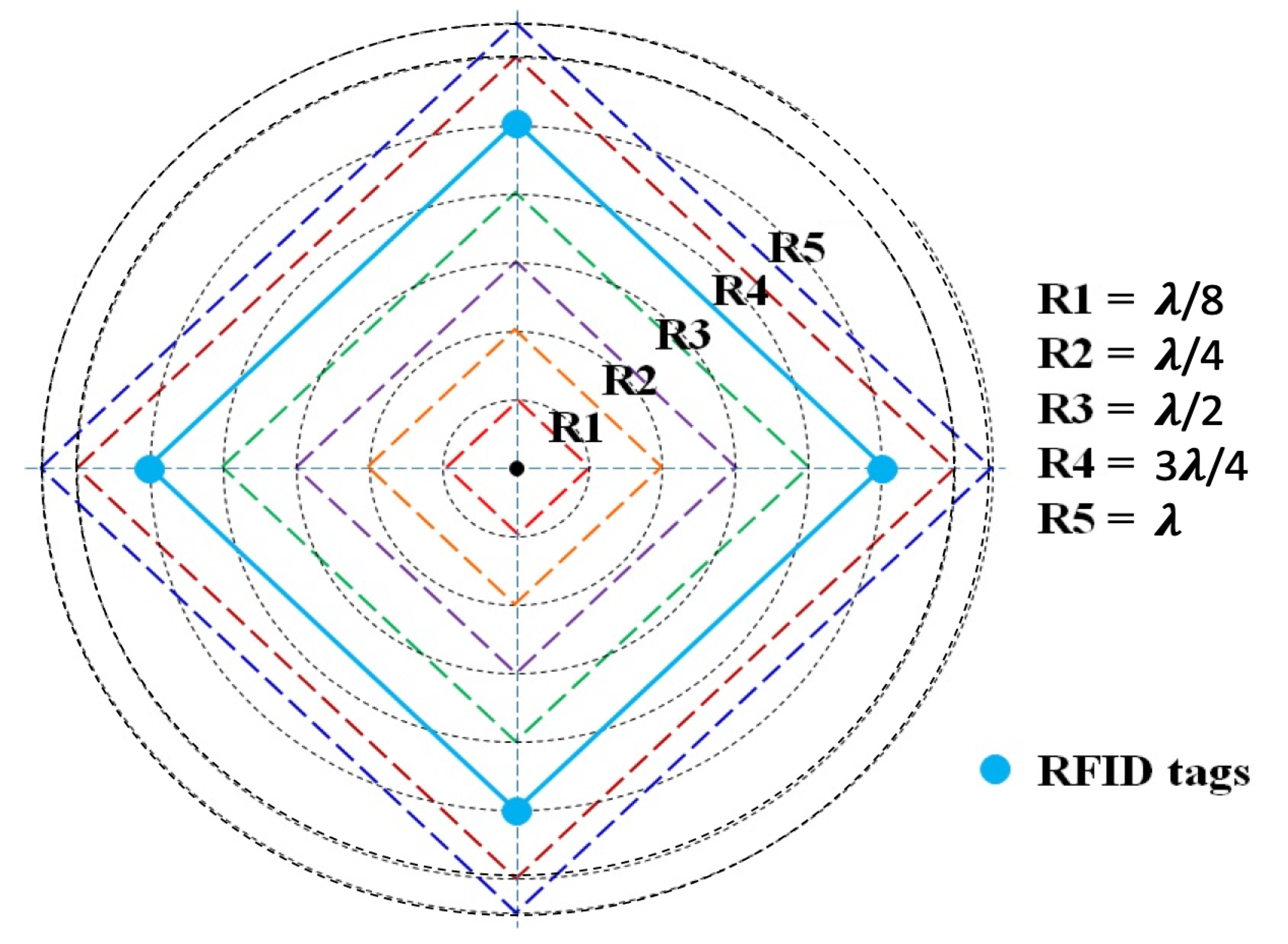




| Constellation’s Radius | λ/8 8.75 | λ/4 17.5 | λ/2 35 | 3λ/4 52.5 | λ 70 | |
|---|---|---|---|---|---|---|
| Track A90 | Mean Distance Error [m] | 2.24 | 2.09 | 2.31 | 2.05 | 1.94 |
| Standard deviation | 1.58 | 1.03 | 1.43 | 1.31 | 1.26 | |
| Constellation Tags’ Number | 3 Tags | 4 Tags | 5 Tags | 5 Tags (Penta) |
|---|---|---|---|---|
| Mean Distance Error [m] | 2.0426 | 1.9421 | 1.9181 | 1.9533 |
| Standard Deviation | 1.0669 | 1.2555 | 1.0519 | 1.3073 |
| Single Tag | Constellation of Tags | ||
|---|---|---|---|
| Track A60 | MDE [m] | 0.99 | 0.82 |
| Standard deviation | 0.59 | 0.49 | |
| Track A90 | MDE [m] | 2.4 | 1.98 |
| Standard deviation | 1.64 | 1.26 | |
| Track A120 | MDE [m] | 0.96 | 0.73 |
| Standard deviation | 1.12 | 0.46 | |
| Single Tag | Constellation of Tags | ||
|---|---|---|---|
| Track A60 | MDE [m] | 1.02 | 0.81 |
| Standard deviation | 0.59 | 0.45 | |
| Track A90 | MDE [m] | 2.41 | 1.93 |
| Standard deviation | 1.62 | 1.21 | |
| Track A120 | MDE [m] | 0.97 | 0.71 |
| Standard deviation | 1.04 | 0.49 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hatem, E.; Abou-Chakra, S.; Colin, E.; Laheurte, J.-M.; El-Hassan, B. Performance, Accuracy and Generalization Capability of RFID Tags’ Constellation for Indoor Localization. Sensors 2020, 20, 4100. https://doi.org/10.3390/s20154100
Hatem E, Abou-Chakra S, Colin E, Laheurte J-M, El-Hassan B. Performance, Accuracy and Generalization Capability of RFID Tags’ Constellation for Indoor Localization. Sensors. 2020; 20(15):4100. https://doi.org/10.3390/s20154100
Chicago/Turabian StyleHatem, Elias, Sara Abou-Chakra, Elizabeth Colin, Jean-Marc Laheurte, and Bachar El-Hassan. 2020. "Performance, Accuracy and Generalization Capability of RFID Tags’ Constellation for Indoor Localization" Sensors 20, no. 15: 4100. https://doi.org/10.3390/s20154100
APA StyleHatem, E., Abou-Chakra, S., Colin, E., Laheurte, J.-M., & El-Hassan, B. (2020). Performance, Accuracy and Generalization Capability of RFID Tags’ Constellation for Indoor Localization. Sensors, 20(15), 4100. https://doi.org/10.3390/s20154100






