Ultimately Bounded Filtering for Time-Delayed Nonlinear Stochastic Systems with Uniform Quantizations under Random Access Protocol
Abstract
:1. Introduction
2. Problem Formulation and Preliminaries
2.1. System Model and Communication Channel
2.2. Structure of the Filter
3. Main Results
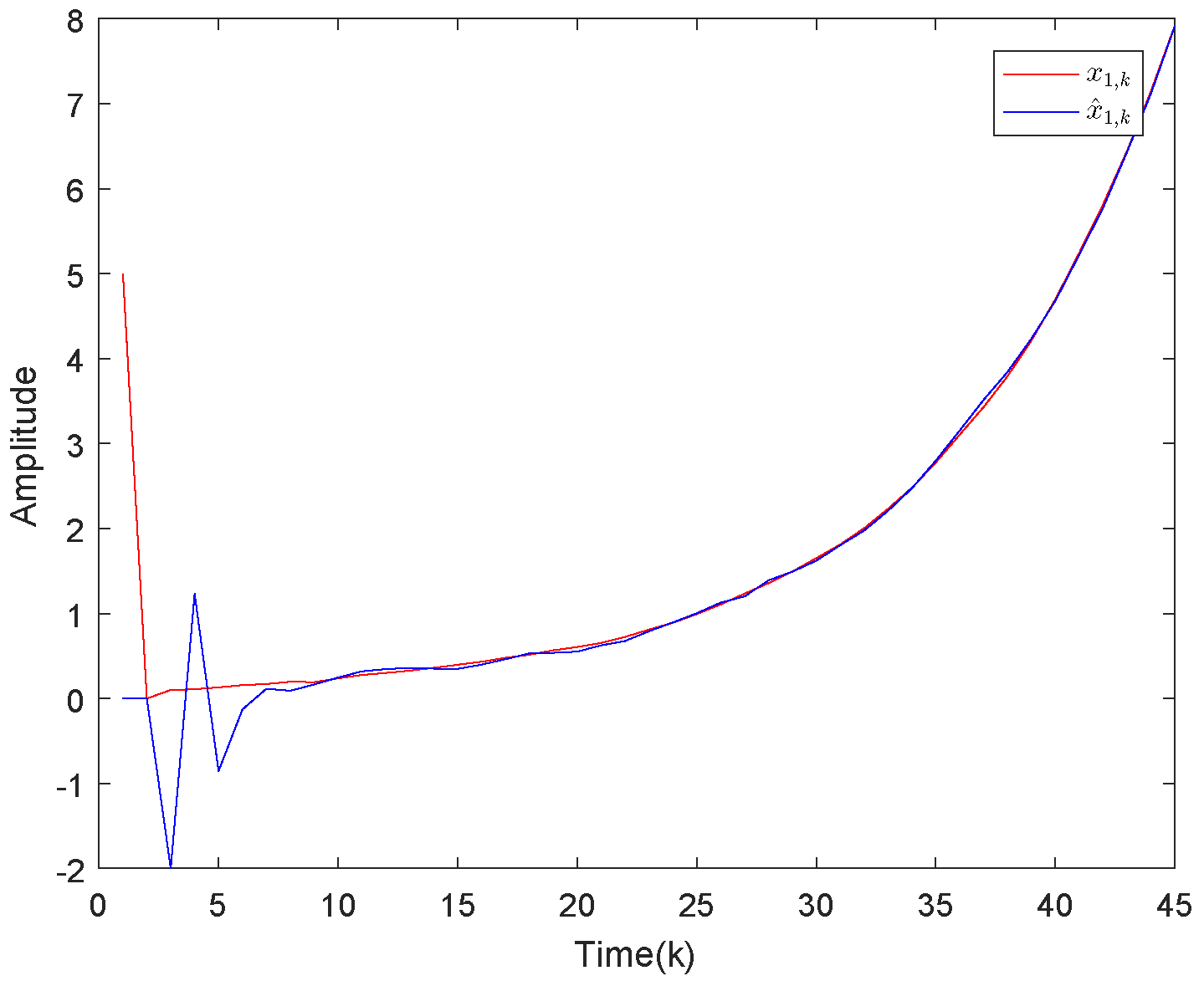
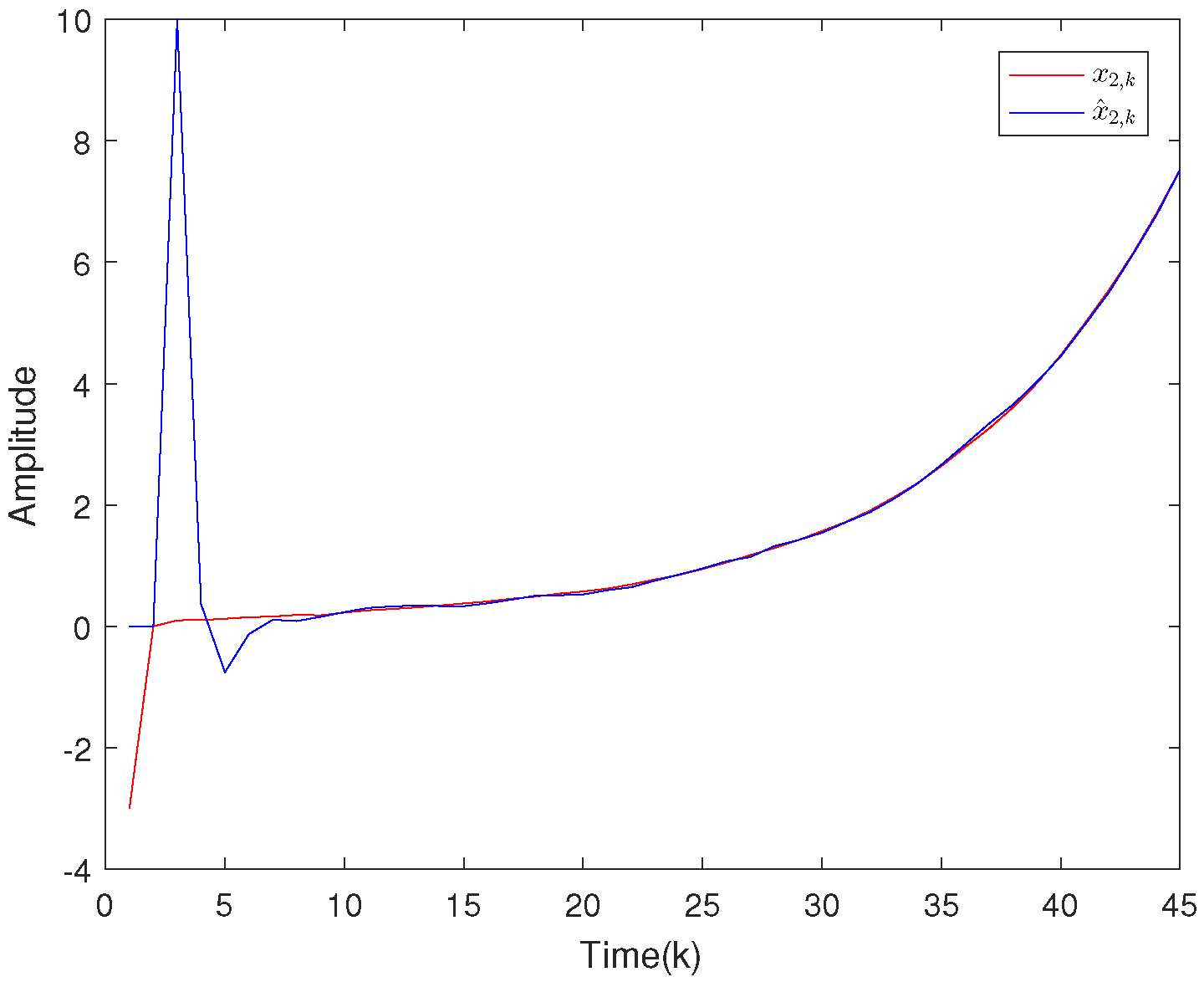
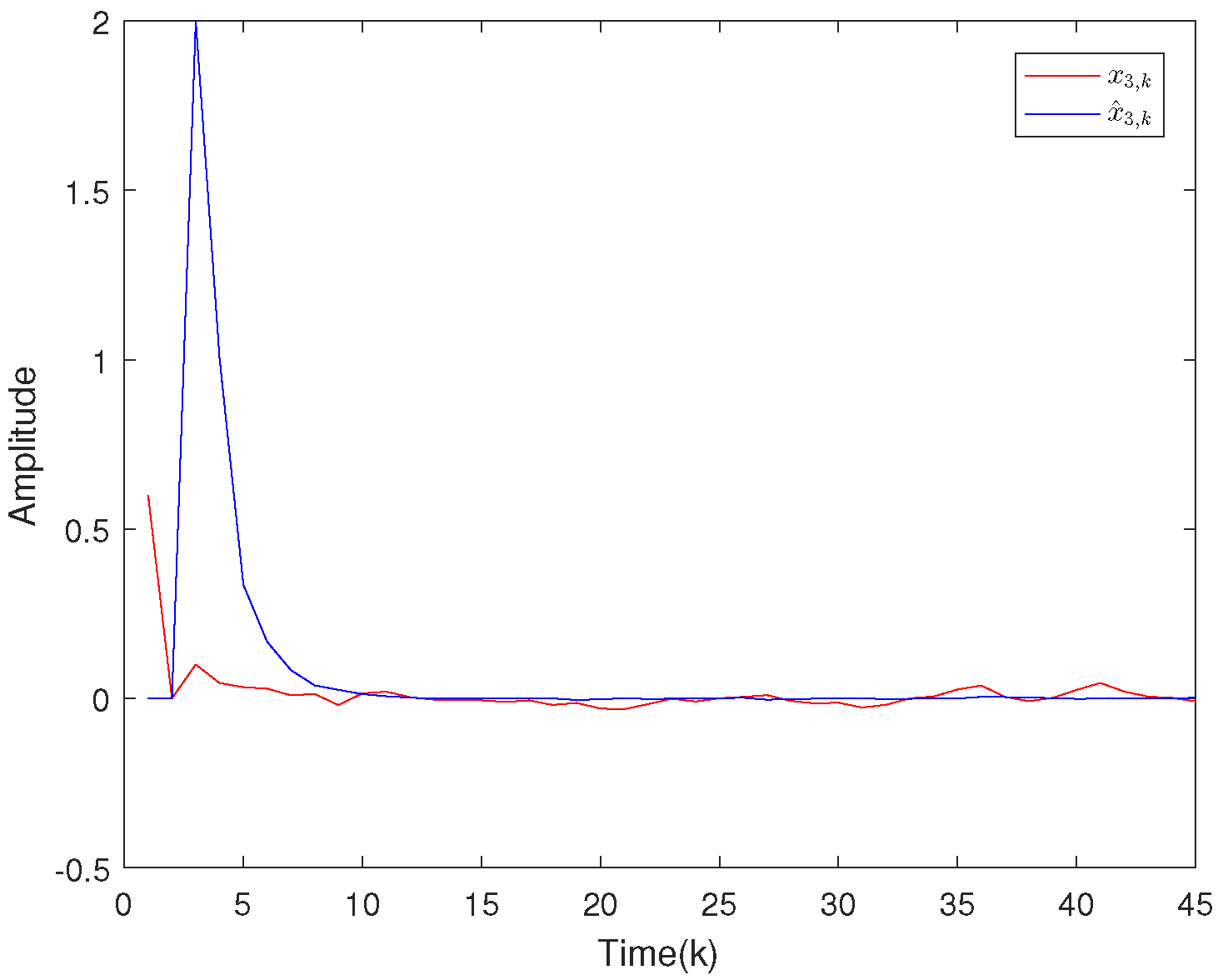
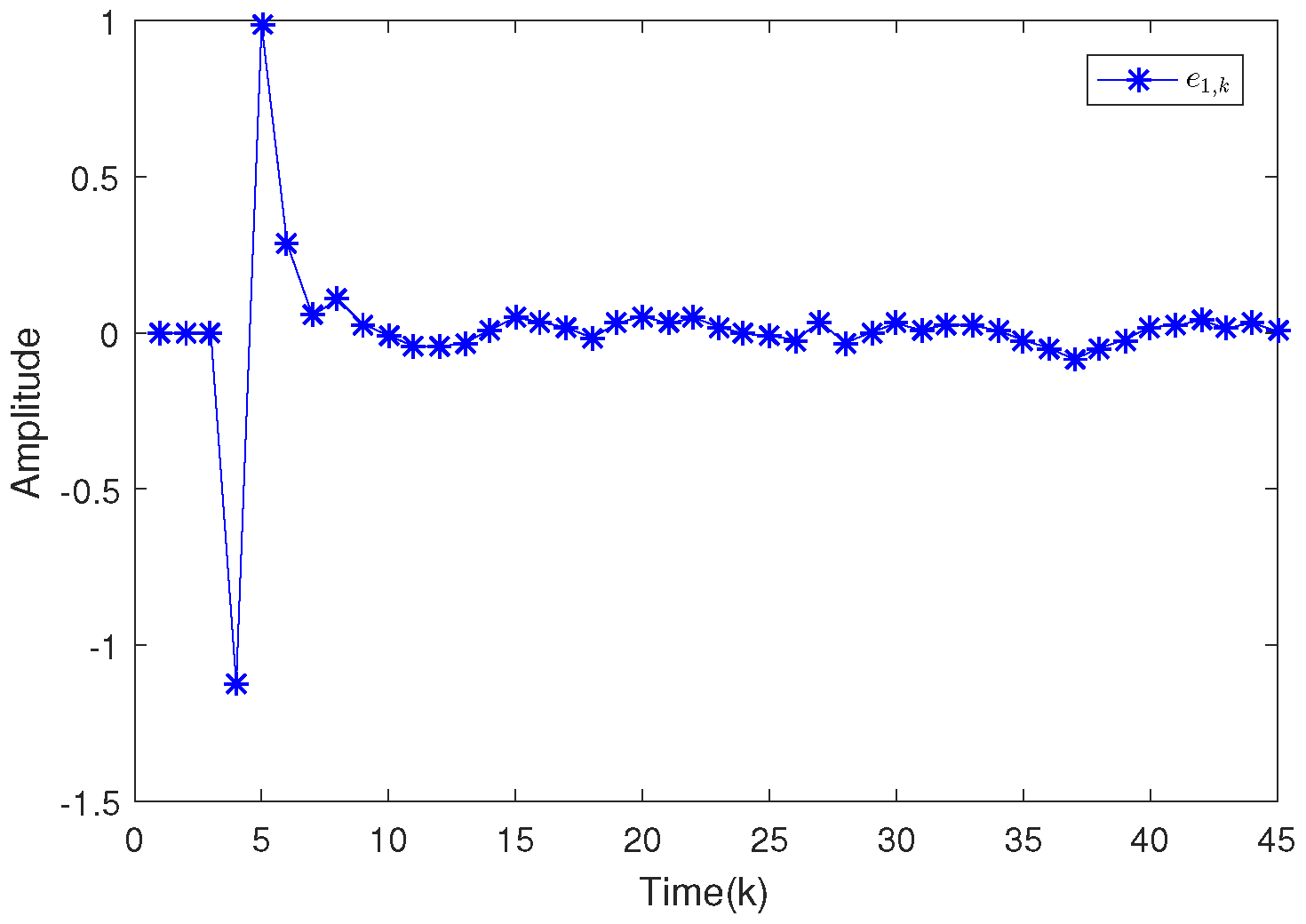
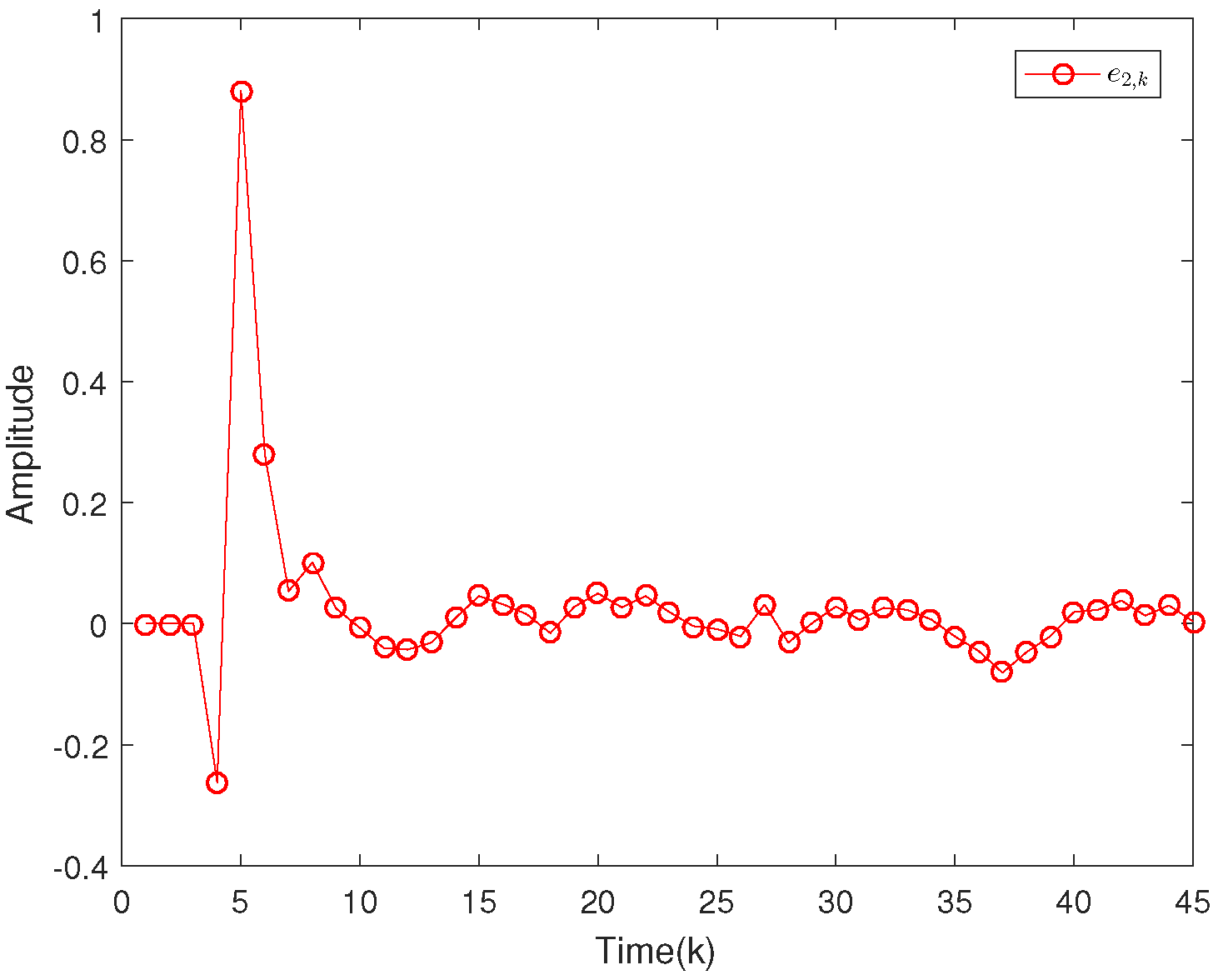
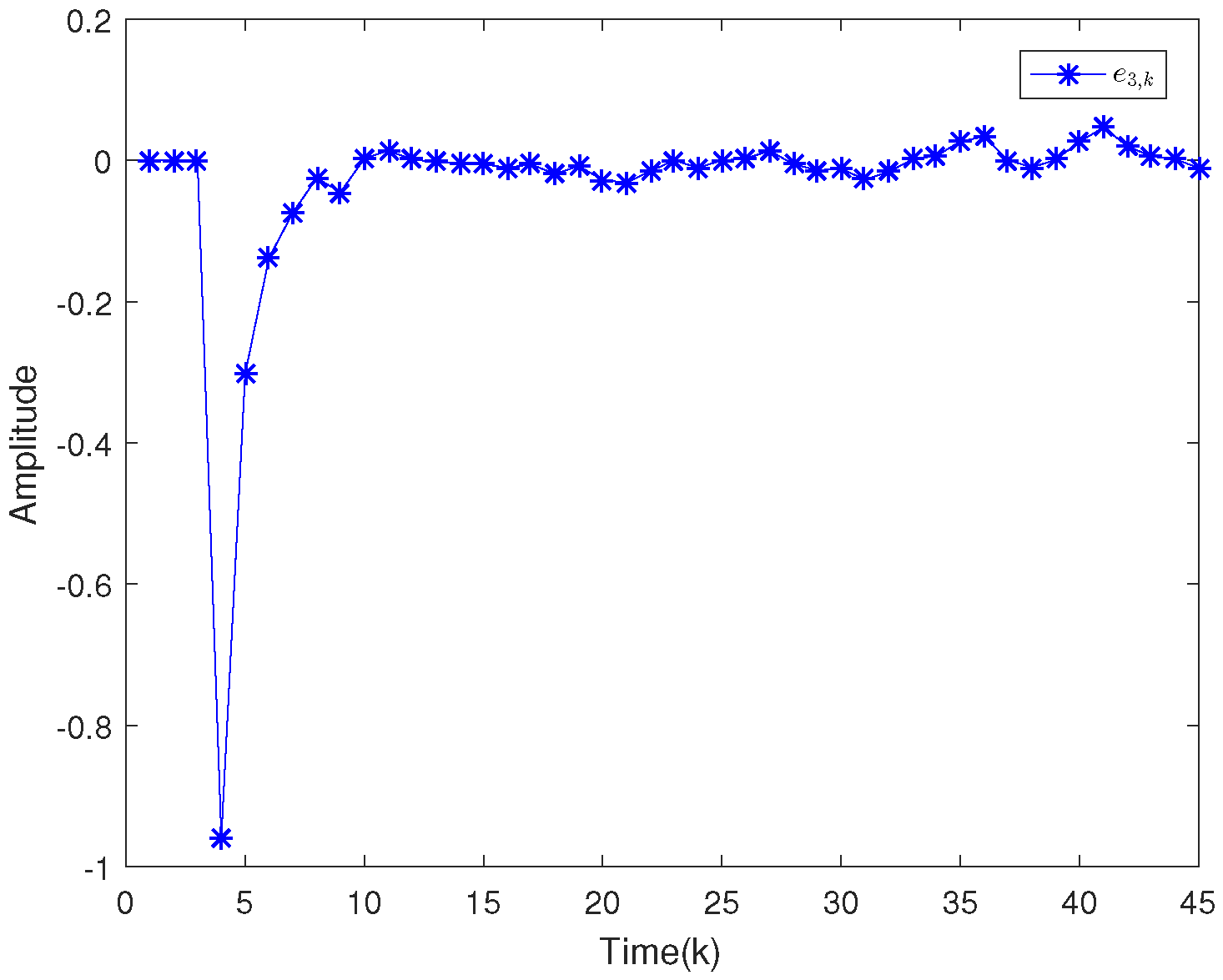
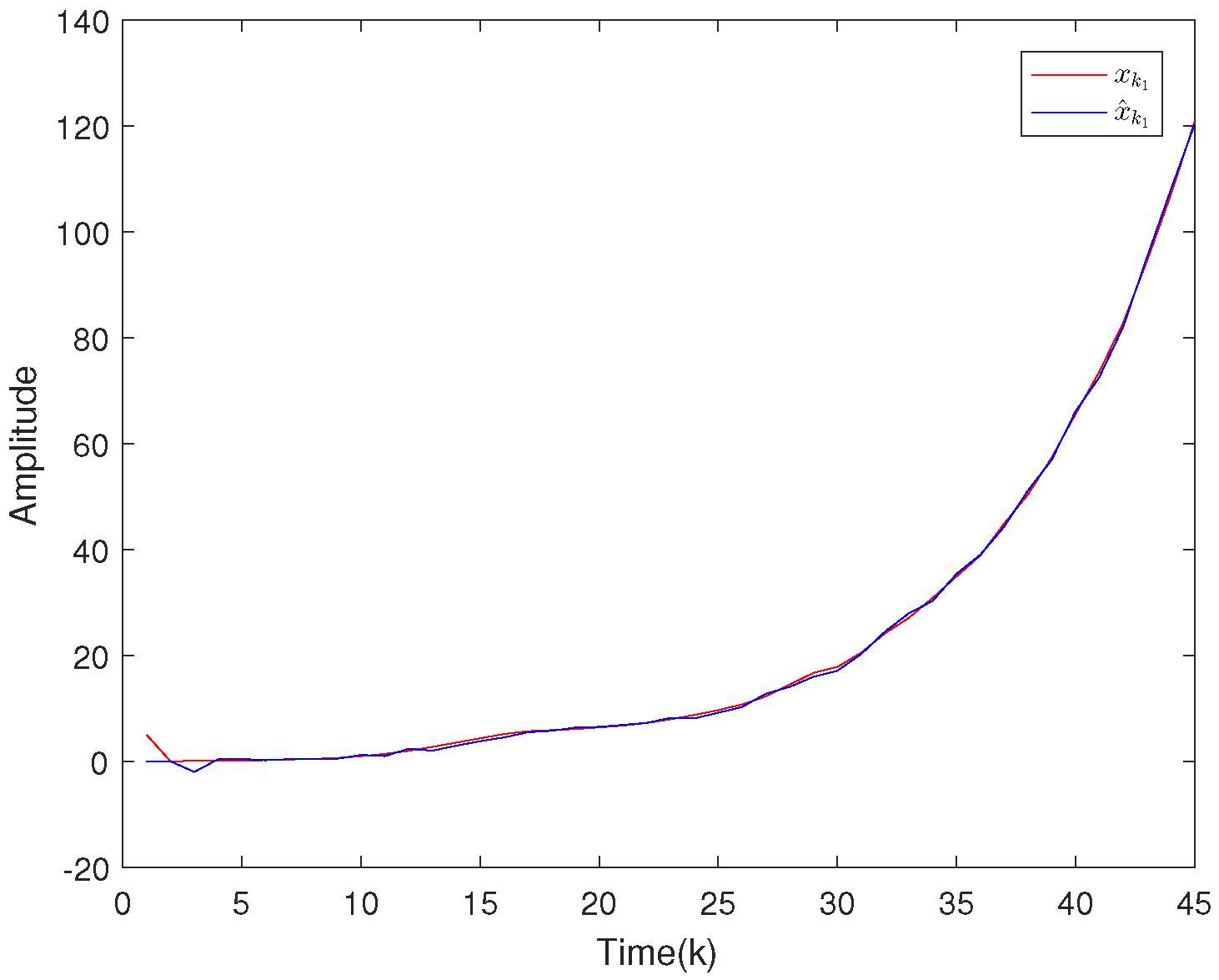
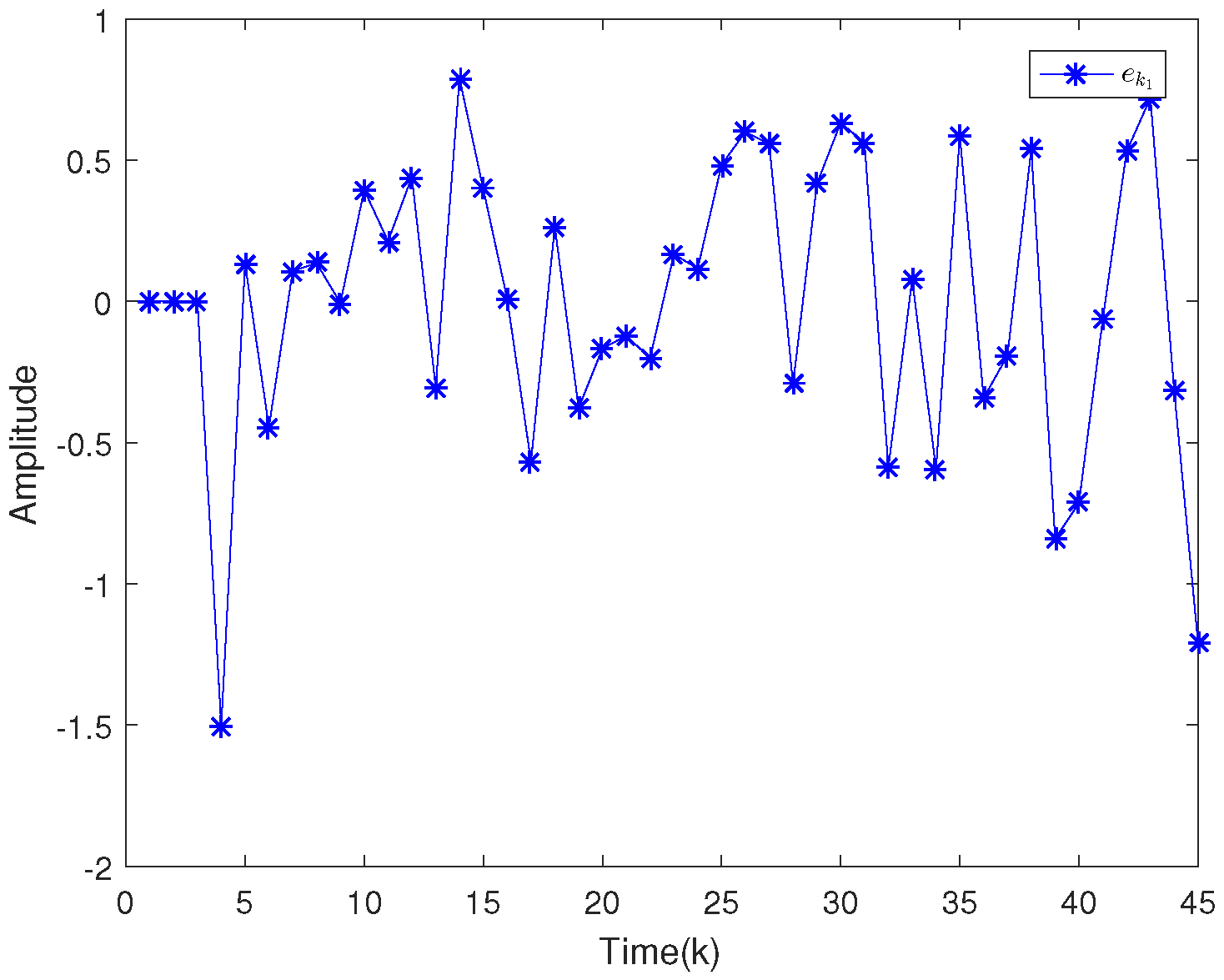
4. Illustrative Examples
4.1. Example 1
4.2. Example 2
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| RAP | random access protocol |
| UQEs | uniform quantization effcets |
| EUBMS | exponentially ultimately bounded in mean square |
| LMIs | linear matrix inequalities |
| EUB | exponential ultimate boundedness |
| ZOH | zero-order holder |
References
- Basin, M.V.; Loukianov, A.G.; Hernandez-Gonzalez, M. Joint state and parameter estimation for uncertain stochastic nonlinear polynomial systems. Int. J. Syst. Sci. 2013, 44, 1200–1208. [Google Scholar] [CrossRef]
- Caballero-Águila, R.; García-Garrido, I.; Linares-Pérez, J. Information fusion algorithms for state estimation in multi-sensor systems with correlated missing measurements. Appl. Math. Comput. 2014, 226, 548–563. [Google Scholar] [CrossRef]
- Donkers, M.C.F.; Heemels, W.P.M.H.; Bernardini, D.; Bemporad, A.; Shneer, V. Stability analysis of stochastic Networked Control Systems. Automatica 2012, 48, 917–925. [Google Scholar] [CrossRef]
- Han, F.; Wei, G.; Ding, D.; Song, Y. Local condition based consensus filtering with stochastic nonlinearities and multiple missing measurements. IEEE Trans. Autom. Control 2017, 62, 4784–4790. [Google Scholar] [CrossRef]
- Liu, M.; Ho, D.W.C.; Niu, Y. Robust filtering design for stochastic system with mode-dependent output quantization. IEEE Trans. Signal Process. 2016, 58, 6410–6416. [Google Scholar] [CrossRef]
- Mao, J.; Ding, D.; Wei, G.; Liu, H. Networked recursive filtering for time-delayed nonlinear stochastic systems with uniform quantisation under Round-Robin protocol. Int. J. Syst. Sci. 2019, 50, 871–884. [Google Scholar] [CrossRef]
- Tabbara, M.; Nesic, D. Input-output stability of Networked Control Systems with stochastic protocols and channels. IEEE Trans. Autom. Control 2008, 53, 1160–1175. [Google Scholar] [CrossRef]
- Wan, X.; Wang, Z.; Han, Q.L.; Wu, M. A recursive approach to quantized H∞ state estimation for genetic regulatory networks under stochastic communication protocols. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 2840–2852. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Song, H.; Yu, L. Robust fuzzy-model-based filtering for nonlinear cyber-physical systems with multiple stochastic incomplete measurements. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 1826–1838. [Google Scholar] [CrossRef]
- Zhang, D.; Yu, L.; Zhang, W.A. Energy efficient distributed filtering for a class of nonlinear systems in sensor networks. IEEE Sens. J. 2015, 15, 3026–3036. [Google Scholar] [CrossRef]
- Hung, Y.; Yang, F. Robust H∞ filtering with error variance constraints for discrete time-varying systems with uncertainty. Automatica 2003, 39, 1185–1194. [Google Scholar] [CrossRef]
- Xu, L.; Dai, Z.; He, D. Exponential ultimate boundedness of impulsive stochastic delay differential equations. Appl. Math. Lett. 2018, 85, 70–76. [Google Scholar] [CrossRef]
- Xu, L.; Ge, S.S. Exponential ultimate boundedness of nonlinear stochastic difference systems with time-varying delays. Int. J. Control 2015, 88, 1–7. [Google Scholar] [CrossRef]
- Xu, L.; Hu, H.; Qin, F. Ultimate boundedness of impulsive fractional differential equations. Appl. Math. Lett. 2016, 62, 110–117. [Google Scholar] [CrossRef]
- Hoecht, L.; Bierling, T.; Holzapfel, F. Ultimate boundedness theorem for model reference adaptive control systems. J. Guid. Control Dyn. 2014, 37, 1595–1603. [Google Scholar] [CrossRef]
- Arbel, A. Sensor placement in optimal filtering and smoothing problems. IEEE Trans. Autom. Control 1982, 27, 94–98. [Google Scholar] [CrossRef]
- Hou, M.; Patton, R.J. Optimal filtering for systems with unknown inputs. IEEE Trans. Autom. Control 1998, 43, 445–449. [Google Scholar] [CrossRef]
- Kwakernaak, H. Optimal filtering in linear systems with time delays. IEEE Trans. Autom. Control 1967, 12, 169–173. [Google Scholar] [CrossRef]
- Lu, X.; Xie, L.; Zhang, H.; Wang, W. Robust Kalman filtering for discrete-time systems with measurement delay. IEEE Trans. Circuits Syst. II 2007, 54, 522–526. [Google Scholar] [CrossRef]
- Xie, L.; Soh, Y.C.; De Souza, C.E. Robust Kalman filtering for uncertain discrete-time systems. IEEE Trans. Autom. Control 1994, 39, 1310–1314. [Google Scholar]
- Jia, C.; Hu, J.; Chen, D.; Liu, Y.; Alsaadi, F.E. Event-triggered resilient filtering with stochastic uncertainties and successive packet dropouts via variance-constrained approach. Int. J. Gen. Syst. 2018, 47, 438–453. [Google Scholar] [CrossRef]
- Chen, S.; Guo, J.; Ma, L. Sliding mode observer design for discrete nonlinear time-delay systems with stochastic communication protocol. Int. J. Control Autom. Syst. 2019, 17, 1666–1676. [Google Scholar] [CrossRef]
- Mao, J.; Ding, D.; Song, Y.; Liu, Y.; Alsaadi, F.E. Event-based recursive filtering for time-delayed stochastic nonlinear systems with missing measurements. Signal Process. 2017, 134, 158–165. [Google Scholar] [CrossRef]
- Wang, Z.; Ho, D.W.C. Filtering on nonlinear time-delay stochastic systems. Automatica 2003, 39, 101–109. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Gao, H.; Kaynak, O. Network-induced constraints in Networked Control Systems—A survey. IEEE Trans. Ind. Inform. 2013, 9, 403–416. [Google Scholar] [CrossRef]
- Han, F.; Wei, G.; Song, Y.; Li, W. Distributed H∞ filtering for piecewise discrete-time linear systems. J. Frankl. Inst. Eng. Appl. Math. 2015, 352, 2029–2046. [Google Scholar] [CrossRef]
- Caballero-Águila, R.; Hermoso-Carazo, A.; Linares-Pérez, J. Distributed fusion filters from uncertain measured outputs in sensor networks with random packet losses. Inf. Fusion 2017, 34, 70–79. [Google Scholar] [CrossRef]
- Liu, Y.; Shen, B.; Li, Q. State estimation for neural networks with Markov-based nonuniform sampling: The partly unknown transition probability case. Neurocomputing 2019, 357, 261–270. [Google Scholar] [CrossRef]
- Tian, E.; Yue, D.; Wei, G. Robust H∞ filter for discrete-time linear system with uncertain missing measurements and non-linearity. IET Signal Process. 2013, 7, 239–248. [Google Scholar] [CrossRef]
- Wei, G.; Liu, S.; Song, Y.; Liu, Y. Probability-guaranteed set-membership filtering for systems with incomplete measurements. Automatica 2015, 60, 12–16. [Google Scholar] [CrossRef]
- Wang, F.; Liang, J. Constrained H∞ estimation for time-varying networks with hybrid incomplete information. Int. J. Robust Nonlinear Control 2018, 28, 699–715. [Google Scholar] [CrossRef]
- Huo, X.; Ma, L.; Zhao, X.; Zong, G. Observer-based fuzzy adaptive stabilization of uncertain switched stochastic nonlinear systems with input quantization. J. Frankl. Inst. 2019, 356, 1789–1809. [Google Scholar] [CrossRef]
- Liu, S.; Wei, G.; Song, Y.; Ding, D. Set-membership state estimation subject to uniform quantization effects and communication constraints. J. Frankl. Inst. 2017, 354, 7012–7027. [Google Scholar] [CrossRef]
- Wang, Y.; Bian, T.; Xiao, J.; Wen, C. Global synchronization of complex dynamical networks through digital communication with limited data rate. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 2487–2499. [Google Scholar] [CrossRef] [PubMed]
- Yun, S.W.; Choi, Y.J.; Park, P. Dynamic output-feedback guaranteed cost control for linear systems with uniform input quantization. Nonlinear Dyn. 2010, 62, 95–104. [Google Scholar] [CrossRef]
- Gaid, M.E.M.B.; Çela, A. Trading quantization precision for update rates for systems with limited communication in the uplink channel. Automatica 2016, 46, 1210–1214. [Google Scholar] [CrossRef]
- Zou, L.; Wang, Z.; Han, Q.-L.; Zhou, D.H. Moving horizon estimation of networked nonlinear systems with random access protocol. IEEE Trans. Syst. Man Cybern. Syst. 2019. [Google Scholar] [CrossRef]
- Liu, K.; Fridman, E.; Hetel, L. Stability and L2-gain analysis of Networked Control Systems under Round-Robin scheduling: A time-delay approach. Syst. Control Lett. 2012, 61, 666–675. [Google Scholar] [CrossRef]
- Ugrinovskii, V.; Fridman, E. A Round-Robin type protocol for distributed estimation with H∞ consensus. Syst. Control Lett. 2014, 69, 103–110. [Google Scholar] [CrossRef]
- Xu, Y.; Lu, R.; Shi, P.; Li, H.; Xie, S. Finite-time distributed state estimation over sensor networks with Round-Robin protocol and fading channels. IEEE Trans. Cybern. 2016, 48, 336–345. [Google Scholar] [CrossRef]
- Zou, L.; Wang, Z.; Han, Q.-L.; Zhou, D.H. Moving horizon estimation for networked time-delay systems under Round-Robin protocol. IEEE Trans. Autom. Control 2019, 64, 5191–5198. [Google Scholar] [CrossRef]
- Cao, Z.; Niu, Y.; Karimi, H.R. Sliding mode control of automotive electronic valve system under weighted Try-Once-Discard protocol. Inf. Sci. 2020, 515, 324–340. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, Z.; Shen, B.; Alsaadi, F.E.; Alsaadi, F.E. Fusion estimation for multi-rate linear repetitive processes under weighted Try-Once-Discard protocol. Inf. Fusion 2020, 55, 281–291. [Google Scholar] [CrossRef]
- Zou, L.; Wang, Z.; Han, Q.-L.; Zhou, D.H. Recursive filtering for time-varying systems with random access protocol. IEEE Trans. Autom. Control 2019, 64, 720–727. [Google Scholar] [CrossRef] [Green Version]
- Liu, A.; Yu, L.; Zhang, W. H∞ control for network-based systems with time-varying delay and packet disordering. J. Frankl. Inst. Eng. Appl. Math. 2011, 348, 917–932. [Google Scholar] [CrossRef]
- Zhang, Y.; Xie, S.; Zhang, L.; Ren, L. Robust sliding mode predictive control of uncertain Networked Control System with random time delay. Discret. Dyn. Nat. Soc. 2018, 85, 1218–1234. [Google Scholar] [CrossRef] [Green Version]
- Åkesson, B.M.; Jørgensen, J.B.; Poulsen, N.K.; Jørgensen, S.B. A generalized autocovariance least-squares method for Kalman filter tuning. J. Process Control 2008, 18, 769–779. [Google Scholar] [CrossRef]
- Dunik, J.; Straka, O.; Simandl, M. On autocovariance least-squares method for noise covariance matrices estimation. IEEE Trans. Autom. Control 2016, 62, 967–972. [Google Scholar] [CrossRef]
- Yuen, K.V.; Liang, P.F.; Kuok, S.C. Online estimation of noise parameters for Kalman filter. Struct. Eng. Mech. 2013, 47, 361–381. [Google Scholar] [CrossRef]
- Boyd, S.; Ghaoul, L.E.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in Systems and Control Theory; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1994. [Google Scholar]





| 0.64 | 0.16 | 0.0064 | |
| 0.81 | 0.225 | 0.0081 | |
| Ultimate bound | 163.9338 | 43.5281 | 1.6394 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Wang, Z.; Zou, L.; Zhao, Z. Ultimately Bounded Filtering for Time-Delayed Nonlinear Stochastic Systems with Uniform Quantizations under Random Access Protocol. Sensors 2020, 20, 4134. https://doi.org/10.3390/s20154134
Guo J, Wang Z, Zou L, Zhao Z. Ultimately Bounded Filtering for Time-Delayed Nonlinear Stochastic Systems with Uniform Quantizations under Random Access Protocol. Sensors. 2020; 20(15):4134. https://doi.org/10.3390/s20154134
Chicago/Turabian StyleGuo, Jiyue, Zidong Wang, Lei Zou, and Zhongyi Zhao. 2020. "Ultimately Bounded Filtering for Time-Delayed Nonlinear Stochastic Systems with Uniform Quantizations under Random Access Protocol" Sensors 20, no. 15: 4134. https://doi.org/10.3390/s20154134
APA StyleGuo, J., Wang, Z., Zou, L., & Zhao, Z. (2020). Ultimately Bounded Filtering for Time-Delayed Nonlinear Stochastic Systems with Uniform Quantizations under Random Access Protocol. Sensors, 20(15), 4134. https://doi.org/10.3390/s20154134





